椭圆及其标准方程(1)
- 格式:docx
- 大小:30.96 KB
- 文档页数:2

椭圆及标准方程椭圆是平面上到定点F1、F2的距离之和等于常数2a的点P的轨迹。
设F1(-c,0),F2(c,0),点P(x,y),则PF1+PF2=2a。
椭圆的标准方程为,x^2/a^2+y^2/b^2=1(a>b>0)。
椭圆的性质:1.椭圆的离心率0<e<1,焦点到中心的距离为ae。
2.椭圆的长轴2a,短轴2b,焦距2ae。
3.椭圆的离心角θ满足e=cosθ,离心率e与离心角θ的关系为e=cosθ。
4.椭圆的面积为πab。
5.椭圆的焦点到直径的距离等于直径的一半。
6.椭圆的焦点到切线的距离等于焦点到法线的距离。
7.椭圆的切线与法线的交点坐标分别为(x1,y1)和(x1,-y1)。
8.椭圆的渐近线方程为y=±b/ax。
9.椭圆的参数方程为x=acosθ,y=bsinθ。
10.椭圆的极坐标方程为r=a(1-e^2)/(1+ecosθ)。
椭圆的标准方程推导:设椭圆的长轴为2a,短轴为2b,焦点为F1(-c,0),F2(c,0),中心为O(0,0),点P(x,y)。
则有PF1+PF2=2a,根据两点之间的距离公式可得。
√((x+c)^2+y^2)+√((x-c)^2+y^2)=2a。
整理得到。
(√((x+c)^2+y^2))^2+(√((x-c)^2+y^2))^2=4a^2。
化简得到。
x^2/a^2+y^2/b^2=1。
从而得到椭圆的标准方程。
椭圆的标准方程性质:1.椭圆的标准方程为x^2/a^2+y^2/b^2=1(a>b>0)。
2.椭圆的中心在原点O(0,0)。
3.椭圆的长轴在x轴上,短轴在y轴上。
4.椭圆的焦点为F1(-c,0),F2(c,0),离心率e=c/a。
5.椭圆的长轴长为2a,短轴长为2b,焦距2ae。
6.椭圆的面积为πab。
7.椭圆的离心角θ满足e=cosθ,离心率e与离心角θ的关系为e=cosθ。
8.椭圆的参数方程为x=acosθ,y=bsinθ。

学案编号:B51 第 1 页 共 2 页P F 2F 1§2.2.1椭圆及其标准方程(1)【使用说明】1、课前完成预习学案,掌握基本题型;2、认真限时规范书写,课上小组合作探讨,答疑解惑。
3、A 、B 层全部掌握,C 层选做。
【学习目标】1.从具体情境中抽象出椭圆的模型;2.掌握椭圆的定义; 3.掌握椭圆的标准方程. 【问题导学】(预习教材理P 38~ P 40,文P 32~ P 34找出疑惑之处) 复习1:过两点(0,1),(2,0)的直线方程 .复习2:方程22(3)(1)4x y -++= 表示以 为圆心, 为半径的 .【合作探究】取一条定长的细绳,把它的两端都固定在图板的同一个点处,套上铅笔,拉紧绳子,移动笔尖,这时笔尖画出的轨迹是一个 .如果把细绳的两端拉开一段距离,分别固定在图板的两个点处,套上铅笔,拉紧绳子,移动笔尖,画出的轨迹是什么曲线? 思考:移动的笔尖(动点)满足的几何条件是什么? 经过观察后思考:在移动笔尖的过程中,细绳的 保持不变,即笔尖 等于常数.新知1: 我们把平面内与两个定点12,F F 的距离之和等于常数(大于12F F )的点的轨迹叫做椭圆,这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距 .反思:若将常数记为2a ,为什么122a F F >? 当122a F F =时,其轨迹为 ; 当122a F F <时,其轨迹为 .试试:已知1(4,0)F -,2(4,0)F ,到1F ,2F 两点的距离之和等于8的点的轨迹是 .小结:应用椭圆的定义注意两点:①分清动点和定点;②看是否满足常数122a F F >.新知2:焦点在x 轴上的椭圆的标准方程 ()222210x y a b a b +=>> 其中222b ac =-若焦点在y 轴上,两个焦点坐标 ,则椭圆的标准方程是 .我的疑惑:记录下你的疑惑,让我们在课堂上共同解决。



课时作业10 椭圆及其标准方程(1)知识点一椭圆的定义及简单应用1。
已知在平面直角坐标系中,点A(-3,0),B(3,0),点P为一动点,且|PA|+|PB|=2a(a≥0),给出下列说法:①当a=2时,点P的轨迹不存在;②当a=4时,点P的轨迹是椭圆,且焦距为3;③当a=4时,点P的轨迹是椭圆,且焦距为6;④当a=3时,点P的轨迹是以AB为直径的圆.其中正确的说法是()A.①②B.①③C.②③D.②④答案B解析当a=2时,2a=4<|AB|,故点P的轨迹不存在,①正确;当a=4时,2a=8>|AB|,故点P的轨迹是椭圆,且焦距为|AB|=6,②错误,③正确;当a=3时,点P的轨迹为线段AB,④错误.2.已知椭圆错误!+错误!=1上一点P到椭圆的一个焦点的距离为3,则点P到另一个焦点的距离为()A.2 B.3 C.5 D.7答案D解析由椭圆方程知a=5,根据椭圆定义有|PF1|+|PF2|=2a=10.若|PF1|=3,则|PF2|=7.3.设F1,F2是椭圆错误!+错误!=1的焦点,P为椭圆上一点,则△PF1F2的周长为()A.16 B.18 C.20 D.不确定答案B解析∵a=5,b=3,∴c=4又|PF1|+|PF2|=2a=10,|F1F2|=2c=8,∴△PF1F2的周长为|PF1|+|PF2|+|F1F2|=2a+2c=10+8=18,故选B。
知识点二求椭圆的标准方程4.写出适合下列条件的椭圆的标准方程.(1)a=5,c=2;(2)经过P1(错误!,1),P2(-错误!,-错误!)两点;(3)以椭圆9x2+5y2=45的焦点为焦点,且经过点M(2,6).解(1)由b2=a2-c2,得b2=25-4=21.∴椭圆的标准方程为错误!+错误!=1或错误!+错误!=1。
(2)解法一:①当焦点在x轴上时,设椭圆方程为错误!+错误!=1(a>b〉0).由已知,得错误!⇒错误!即所求椭圆的标准方程是错误!+错误!=1。



椭圆定义及其标准方程(一)一、教学目标根据课程标准的要求,本节教材的特点及所教学生的认知情况,把教学目标拟定如下:1、知识目标:理解椭圆的定义;明确焦点、焦距的概念;了解用椭圆定义推导椭圆的标准方程的过程;掌握a、b、c之间的关系,会由其中的两个求出第三个;学会运用定义法和数形结合等方法解题2、能力目标:让学生感知数学知识与实际生活的普遍联系;培养学生类比、数形结合的数学思想方法,提高学生的学习能力;培养学生在运用网络和数学工具探究和解决数学问题的能力;培养学生运动、变化的辨证唯物主义观点;3、情感目标:培养学生不怕困难、勇于探索的优良作风;增强学生审美体验,提高数学思维的情趣,给学生以成功的体验;形成学习数学知识的积极态度。
二、重点、难点及关键1、重点:椭圆的定义和标准方程;2、难点:椭圆标准方程的推导;初步掌握椭圆方程求法;3、关键:创设具体的椭圆的直观情景;结合建立坐标系的一般原则,从“对称美”和“简洁美”出发作必要的点拨。
三、教学方法:启发探索式教学法四、教学手段及设施环境运用多媒体和实物投影仪、几何画板和网页辅助教学,在语音多媒体教室网络授课五、教学环节脉络:见后附图六、教学过程1、课前准备活动①(1)指导学生使用“几何画板”,让学生了解几何画板的基本操作,可以自行画出两点之间的线段并测量出线段的长度,会通过拖动相关的点或者线段来观察相应测量值的变化情况;(2)复习圆的标准方程和求一般曲线方程的基本步骤;(3)让学生学会网页浏览的基本要求和方式,会上传或下载一些网络上的信息。
①目的:了解并熟悉如何恰当建立直角坐标系来解决有关数学问题;使学生掌握利用网络查找资料的方法,培养学生的信息素养;了解相关数学软件,培养学生自主创新意识。
2、正课活动(1)、创设情景、引入概念【问】我们在物理和地理课上就已经知道,在我们的银河系中,九大行星和一些彗星在绕太阳运转的轨迹是什么呢?①【学生回答问题】【引入】点击下一页,我们还可以看到一些生活中的实用品也是椭圆形的。

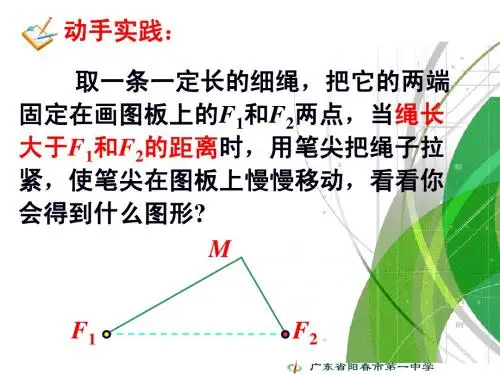
椭圆及其标准方程(1)
一.知识探究
1.椭圆的定义
把平面内与两个定点F 1,F 2的距离的和等于 的点的轨迹叫做椭圆,点 叫做椭圆的焦点, 叫做椭圆的焦距.
2.平面内动点M 满足|MF 1|+|MF 2|=2a ,当2a =|F 1F 2|时,点M 的轨迹是什么?当2a <|F 1F 2|时呢?
4.如何确定焦点的位置?
二.典型选讲:
例1.判断下列椭圆的焦点的位置,并求出焦点的坐标。
①16410022=+y x ②125
92
2=+y x
变式训练1.将方程22525922=+y x 化为标准方程,并求出焦点的坐标。
例2.已知椭圆16x 2+25y 2=400上一点到椭圆左焦点的距离为3,求该点到右焦点的距离。
变式训练2. 椭圆136
642
2=+y x 的弦PQ 过F 1,求△PQF 2的周长
三.课后作业
1.a =6,c =1的椭圆的标准方程是( )
A.x 236+y 235=1
B.y 236+x 235=1
C.x 236+y 25
=1 D .以上都不对 2.设P 是椭圆x 225+y 216
=1上的点.若F 1.F 2是椭圆的两个焦点,则|PF 1|+|PF 2|等于( ) A .4 B .5 C .8 D .10
3.椭圆1100
362
2=+y x 上一点P ,则△PF 1F 2的周长 4.椭圆x 216+y 29
=1的焦距为________,焦点坐标为________. 5.已知椭圆x 29+y 2m 2=1的焦点在x 轴上,则实数m 的取值范围是________. 6.求下列条件的椭圆的标准方程 :
(1)焦点坐标分别为(0,-4),(0,4),a=5;
(2)a+c=10,a -c=4
自助餐
1.已知A (-12,0),B 是圆F :(x -12
)2+y 2=4(F 为圆心)上一动点,线段AB 的垂直平分线交BF 于P ,求动点P 的轨迹方程
2.方程15
102
2=-+-k y k x 表示焦点在y 轴上的椭圆,则k 的取值范围是( ) A.10<k B.5>k C.105<<k D.105.7<<k。