高三数学南方凤凰台高2021届高2018级高三一轮数学提高版完整版第10章第52讲排列与组合

第八章 解析几何第41讲 直线的斜率与方程A 应知应会一、 选择题1. (2019·开封模拟)过点A (－1,－3),斜率是直线y ＝3x 的斜率的－14的直线方程为( )A. 3x ＋4y ＋15＝0B. 3x ＋4y ＋6＝0C. 3x ＋y ＋6＝0D. 3x －4y ＋10＝02. 直线2x cos α－y －3＝0⎝⎛⎭⎫α∈⎣⎡⎦⎤π6，π3 的倾斜角的取值范围是 ( ) A. ⎣⎡⎦⎤π6，π3 B. ⎣⎡⎦⎤π4，π3 C. ⎣⎡⎦⎤π4，π2 D. ⎣⎡⎦⎤π4，2π33. (2019·湖北四地七校联考)已知函数f (x )＝a sin x －b cos x (a ≠0,b ≠0),若f ⎝⎛⎭⎫π4－x ＝f ⎝⎛⎭⎫π4＋x ,则直线ax －by ＋c ＝0的倾斜角为( )A. π4B. π3C. 2π3D. 3π44. 如果A ·C <0且B ·C <0,那么直线Ax ＋By ＋C ＝0不通过( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限5. (2019·张家口模拟)若直线mx ＋ny ＋3＝0在y 轴上的截距为－3,且它的倾斜角是直线3 x －y ＝33 的倾斜角的2倍,则( )A. m ＝－3 ,n ＝1B. m ＝－3 ,n ＝－3C. m ＝3 ,n ＝－3D. m ＝3 ,n ＝1二、 解答题6. 求过点A (1,3),斜率是直线y ＝－4x 的斜率的13的直线方程．7. 求适合下列条件的直线方程．(1) 经过点P(3,2),且在两坐标轴上的截距相等；(2) 求过点(2,1)且在x轴上的截距与在y轴上的截距之和为6的直线方程．B巩固提升一、填空题1. 直线x＋3y＋1＝0的倾斜角是________．2. 过点P(2,3)且在两坐标轴上截距相等的直线方程为________．3. 已知直线l：(a－2)x＋(a＋1)y＋6＝0,则直线l恒过定点________．4. (2019·江苏姜堰中学)已知△ABC的三个顶点A(－5,0),B(3,－3),C(0,2),则BC边上中线所在的直线方程为________．二、解答题5. (2019·启东检测)已知直线l：(2＋m)x＋(1－2m)y＋4－3m＝0.(1) 求证：不论m为何实数,直线l过一定点M；(2) 过定点M作一条直线l1,使夹在两坐标轴之间的线段被M点平分,求直线l1的方程．6. 如图,射线OA,OB分别与x轴正半轴成45°和30°角,过点P(1,0)作直线AB分别交OA,OB于A,B两点,当AB的中点C恰好落在直线y＝12x上时,求直线AB的方程．(第6题)第42讲两条直线的位置关系A应知应会一、选择题1. 若直线2x＋3y－1＝0与直线4x＋my＋11＝0平行,则m的值为()A. 83 B. －83 C. －6 D. 62. 若直线l过点(3,1)且与直线2x－y－2＝0平行,则直线l的方程为()A. 2x－y－5＝0B. 2x－y＋1＝0C. x＋2y－7＝0D. x＋2y－5＝03. (2019·石家庄模拟)若直线2x＋3y－k＝0和直线x－ky＋12＝0的交点在x轴上,则k 的值为()A. －24B. 24C. 6D. ±64. 若直线a1x＋b1y＝2和a2x＋b2y＝2交于点P(3,2),则过点A(a1,b1),B(a2,b2)的直线方程是()A. 2x＋3y－2＝0B. 3x＋2y－2＝0C. 3x＋2y＋2＝0D. 2x＋3y＋2＝05. 已知直线l1：(m－4)x－(2m＋4)y＋2m－4＝0与l2：(m－1)x＋(m＋2)y＋1＝0,则“m ＝－2”是“l1∥l2”的()A. 充要条件B. 充分不必要条件C. 必要不充分条件D. 既不充分也不必要条件二、解答题6. 已知三角形三边所在的直线方程分别为2x－y＋4＝0,x＋y－7＝0,2x－7y－14＝0,求边2x－7y－14＝0上的高所在的直线方程．7. 已知△ABC的顶点B(2,1),C(－6,3),其垂心为H(－3,2),求顶点A的坐标．B 巩固提升一、 填空题1. 若三条直线y ＝2x ,x ＋y ＝3,mx ＋2y ＋5＝0相交于同一点,则m 的值为________．2. 如果直线ax ＋2y ＋3a ＝0与直线3x ＋(a －1)y ＝a －7平行,则a ＝________．3. 已知直线l 1：ax ＋y －6＝0与l 2：x ＋(a －2)y ＋a －1＝0相交于点P ,若l 1⊥l 2,则a ＝________,此时点P 的坐标为________．4. (2019·南通中学)已知直线l 的倾斜角为3π4,直线l 1经过点A (3,2),B (a ,－1),且l 1与l 垂直,直线l 2：2x ＋by ＋1＝0与直线l 1平行,则a ＋b ＝________．二、 解答题5. (2019·海门实验中学)已知两直线l 1：x ＋y sin α－1＝0和l 2：2x ·sin α＋y ＋1＝0,求α的值,使得：(1) l 1∥l 2；(2) l 1⊥l 2.6. 已知点P (a ,b )在x ,y 轴上的射影分别为点A ,B .(1) 求直线AB 的方程；(2) 求过点P 且垂直于AB 的直线m 的方程．第43讲 距离公式与对称问题A 应知应会一、 选择题1. 点A (2,5)到直线l ：x －2y ＋3＝0的距离为( )A. 25B. 55C. 5D. 2552. 两条平行直线3x ＋4y －12＝0与ax ＋8y ＋11＝0之间的距离为( )A. 235B. 2310C. 7D. 723. 已知坐标原点关于直线l 1：x －y ＋1＝0的对称点为A ,设直线l 2经过点A ,则当点B (2,－1)到直线l 2的距离最大时,直线l 2的方程为( )A. 2x ＋3y ＋5＝0B. 3x －2y ＋5＝0C. 3x ＋2y ＋5＝0D. 2x －3y ＋5＝04. 已知动直线l 0：ax ＋by ＋c －2＝0(a ＞0,c ＞0)恒过点P (1,m ),且Q (4,0)到动直线l 的最大距离为3,则12a ＋2c的最小值为( ) A. 92 B. 94C. 1D. 9 5. (多选)在平面直角坐标系中,定义d (P ,Q )＝|x 1－x 2|＋|y 1－y 2|为两点P (x 1,y 1),Q (x 2,y 2)之间的“折线距离”,则下列命题中为真命题的是( )A. 若点A (－1,3),B (1,0),则有d (A ,B )＝5B. 到原点的“折线距离”等于1的所有点的集合是一个圆C. 若点C 在线段AB 上,则有d (A ,C )＋d (C ,B )＝d (A ,B )D. 到M (－1,0),N (1,0)两点的“折线距离”相等的点的轨迹是直线x ＝0二、 解答题6. (2019·江苏启东中学)已知直线l ：y ＝12x －1. (1) 求点P (3,4)关于l 对称的点Q ；(2) 求l 关于点(2,3)对称的直线方程．7. 已知直线l ：(2a ＋b )x ＋(a ＋b )y ＋a －b ＝0及点P (3,4).(1) 证明：直线l 过某定点,并求该定点的坐标；(2) 当点P 到直线l 的距离最大时,求直线l 的方程．B 巩固提升一、 填空题1. 已知点(a ,2)(a ＞0)到直线l ：x －y ＋3＝0的距离为1,则a ＝________．2. 直线l 1：y ＝2x ＋3关于直线l ：y ＝x ＋1对称的直线l 2的方程为________．3. 已知l 1,l 2是分别经过A (2,1),B (0,2)两点的两条平行直线,当l 1,l 2之间的距离最大时,直线l 1的方程是________．4. “c ＝5”是“点(2,1)到直线3x ＋4y ＋c ＝0的距离为3”的________条件．(填“充分不必要”“必要不充分”“充要”或“既不充分也不必要”)二、 解答题5. 已知直线l 经过直线l 1：2x ＋y －5＝0与l 2：x －2y ＝0的交点．(1) 若点A (5,0)到l 的距离为3,求l 的方程；(2) 求点A (5,0)到l 的距离的最大值．6. 已知三条直线l 1：2x －y ＋a ＝0(a ＞0)；l 2：－4x ＋2y ＋1＝0；l 3：x ＋y －1＝0,且l 1与l 2间的距离是7510. (1) 求a 的值；(2) 能否找到一点P ,使P 同时满足下列三个条件：①点P 在第一象限；②点P 到l 1的距离是点P 到l 2的距离的12；③点P 到l 1的距离与点P 到l 3的距离之比是2 ∶5 ？若能,求点P 的坐标；若不能,说明理由．第44讲 圆的方程A 应知应会一、 选择题1. (2019·太原模拟)若两条直线y ＝x ＋2a ,y ＝2x ＋a 的交点P 在圆(x －1)2＋(y －1)2＝4的内部,则实数a 的取值范围是( )A. ⎝⎛⎭⎫－15，1B. ⎝⎛⎭⎫－∞，－15 ∪(1,＋∞) C. ⎣⎡⎭⎫－15，1 D. ⎝⎛⎦⎤－∞，－15 ∪[1,＋∞) 2. (2019·长沙模拟)已知三点A (1,0),B (0,3 ),C (2,3 ),则△ABC 外接圆的圆心到原点的距离为( )A. 53B. 213C. 253D. 433. 方程|x |－1＝1－（y －1）2 所表示的曲线是( )A. 一个圆B. 两个圆C. 半个圆D. 两个半圆4. (2019·邯郸一模)若x ,y 满足约束条件(x －1)2＋(y －1)2≤1,则x 2＋y 2的最小值为( )A. 2 －1B. 3－22C. 2 ＋1D. 3＋225. (2019·黄冈调研)若长度为定值4的线段AB 的两端点分别在x 轴正半轴和y 轴正半轴上移动,P (x ,y )为△OAB 的外心轨迹上一点,则x ＋y 的最大值为( )A. 1B. 4C. 2D. 22二、 解答题6. 已知以点P 为圆心的圆经过点A (－1,0)和B (3,4),线段AB 的垂直平分线交圆P 于点C 和D ,且CD ＝410 .(1) 求直线CD 的方程；(2) 求圆P 的方程．7. 已知圆经过点A (2,－3)和B (－2,－5).(1) 若圆的面积最小,求圆的方程；(2) 若圆心在直线x －2y －3＝0上,求圆的方程．B巩固提升一、填空题1. 若直线3x＋y＋a＝0过圆x2＋y2＋2x－4y＝0的圆心,则a＝________．2. 已知圆C的圆心在x轴上,并且经过点A(－1,1),B(1,3),若M(m,6)在圆C内,则m的取值范围为________．3. (2019·南师附中)经过三点A(－1,0),B(3,0),C(1,2)的圆的面积S＝________．4. 已知点A(－2,0),B(0,2).若点M是圆x2＋y2－2x＋2y＝0上的动点,则△ABM面积的最小值为________．二、解答题5. 已知圆x2＋y2＝4上一定点A(2,0),B(1,1)为圆内一点,P,Q为圆上的动点．(1) 求线段AP中点的轨迹方程；(2) 若∠PBQ＝90°,求线段PQ中点的轨迹方程．6. 如图,已知圆O的直径AB＝4,定直线l到圆心的距离为4,且直线l垂直于直线AB,点P 是圆O上异于A,B的任意一点,直线P A,PB分别交l于M,N两点．(1) 若∠P AB＝30°,求以MN为直径的圆的方程；(2) 当点P变化时,求证：以MN为直径的圆必过圆O内的一定点．(第6题)第45讲直线与圆、圆与圆的位置关系课时1直线与圆相关问题A应知应会一、选择题1. 以点(2,－1)为圆心且与直线3x－4y＋5＝0相切的圆的方程为()A. (x－2)2＋(y＋1)2＝3B. (x＋2)2＋(y－1)2＝3C. (x－2)2＋(y＋1)2＝9D. (x＋2)2＋(y－1)2＝92. (2019·湖南十四校二联)已知直线x－2y＋a＝0与圆O：x2＋y2＝2相交于A,B两点(O 为坐标原点),且△AOB为等腰直角三角形,则实数a的值为()A. 6或－6B. 5或－5C. 6D. 53. “a＝3”是“直线y＝x＋4与圆(x－a)2＋(y－3)2＝8相切”的()A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件4. 已知圆C：x2＋y2＝4,若点P(x0,y0)在圆C外,则直线l：x0x＋y0y＝4与圆C的位置关系为()A. 相离B. 相切C. 相交D. 不确定5. (多选)(2019·合肥模拟)设圆x2＋y2－2x－2y－2＝0的圆心为C,直线l过(0,3),且与圆C交于A,B两点,若|AB|＝23,则直线l的方程为()A. 3x＋4y－12＝0B. 4x－3y＋9＝0C. x＝0D. 4x＋3y＋9＝0二、解答题6. (2019·启东模拟)已知直线l：kx－y＋k－3＝0与圆x2＋y2＝12交于A,B两点,过A,B 分别作l的垂线与x轴交于C,D两点,若|AB|＝43,求|CD|.7. 已知圆C经过点A(2,－1),与直线x＋y＝1相切,且圆心在直线y＝－2x上．(1) 求圆C的方程；(2) 已知直线l经过原点,并且被圆C截得的弦长为2,求直线l的方程．B 巩固提升一、 填空题1. (2019·衡水调研)过M (－3,1),N (0,a )两点的光线经y 轴反射后所在直线与圆x 2＋y 2＝1存在公共点,则实数a 的取值范围为________．2. (2019·扬州期末)已知直线l ：y ＝－x ＋4与圆C ：(x －2)2＋(y －1)2＝1相交于P ,Q 两点,则CP → ·CQ → ＝________．3. 已知过点P ⎝⎛⎭⎫32，32 的直线l 与圆C ：(x －1)2＋y 2＝4交于A ,B 两点,当∠ACB 最小时,直线l 的方程为________,∠ACB ＝________．4. (2019·启东考前卷)如图,已知圆C 与x 轴相切于点T (1,0),与y 轴正半轴交于两点A ,B (B 在A 的上方),且|AB |＝2,则圆C 在点B 处的切线在x 轴上的截距为________．(第4题)二、 解答题5. 已知圆C ：x 2＋y 2－4x －6y ＋12＝0,点A (3,5).(1) 求过点A 的圆的切线方程；(2) 点O 是坐标原点,连接OA ,OC ,求△AOC 的面积S .6. 已知圆C 的方程为x 2＋(y －4)2＝4,点O 是坐标原点,直线l ：y ＝kx 与圆C 交于M ,N 两点．(1) 求k 的取值范围；(2) 直线l 能否将圆C 分割成弧长的比为13的两段弧？若能,求出直线l 的方程；若不能,请说明理由．课时2圆与圆的位置关系A应知应会一、选择题1. 圆C1：x2＋y2＋4x＋8y－5＝0与圆C2：x2＋y2＋4x＋4y－1＝0的位置关系为()A. 相交B. 外切C. 内切D. 外离2. 已知圆O1的方程为x2＋y2＝4,圆O2的方程为(x－a)2＋y2＝1,如果这两个圆有且只有一个公共点,那么a的所有取值构成的集合是()A. {1,－1}B. {3,－3}C. {1,－1,3,－3}D. {5,－5,3,－3}3. 若圆(x－a)2＋(y－b)2＝b2＋1始终平分圆(x＋1)2＋(y＋1)2＝4的周长,则a,b应满足的关系式是()A. a2－2a－2b－3＝0B. a2＋2a＋2b＋5＝0C. a2＋2b2＋2a＋2b＋1＝0D. 3a2＋2b2＋2a＋2b＋1＝04. 两圆x2＋y2＝16与(x－4)2＋(y＋3)2＝r2(r＞0)在交点处的切线互相垂直,则r等于()A. 5B. 4C. 3D. 225. 已知A＝{(x,y)|x2＋y2＝1},B＝{(x,y)|(x－5)2＋(y－5)2＝4},则A∩B等于()A. ∅B. {(0,0)}C. {(5,5)}D. {(0,0),(5,5)}二、解答题6. 已知圆A：x2＋y2＋2x＋2y－2＝0,若圆B平分圆A的周长,且圆B的圆心在直线l：y ＝2x上,求满足上述条件的半径最小的圆B的方程．7. 圆O1的方程为x2＋(y＋1)2＝4,圆O2的圆心坐标为(2,1).(1) 若圆O1与圆O2外切,求圆O2的方程；(2) 若圆O1与圆O2相交于A,B两点,且|AB|＝22,求圆O2的方程．B 巩固提升一、 填空题1. 若圆C 1：x 2＋y 2＝1与圆C 2：x 2＋y 2－6x －8y ＋m ＝0外切,则m ＝________．2. 已知线段AB 的长为2,动点C 满足CA → ·CB →＝λ(λ<0),且点C 总不在以点B 为圆心,12为半径的圆内,则负数λ的最大值是________．3. (2019·江苏天一中学)若圆O ：x 2＋y 2＝5与圆O 1：(x －m )2＋y 2＝20(m ∈R)相交于A ,B 两点,且两圆在点A 处的切线互相垂直,则线段AB 的长度是________．4. 如图,在平面四边形ABCD 中,AB ＝4,AD ＝2,∠DAB ＝60°,AC ＝3BC ,则边CD 长的最小值为________．(第4题)二、 解答题 5. (2019·江苏准阴中学)已知点P (2,2),圆C ：x 2＋y 2－8y ＝0,过点P 的动直线l 与圆C 交于A ,B 两点,线段AB 的中点为M ,O 为坐标原点．(1) 求M 的轨迹方程；(2) 当|OP |＝|OM |时,求l 的方程及△POM 的面积．6. (2019·泰州中学)在平面直角坐标系xOy 中,过点P (0,1)且互相垂直的两条直线分別与圆O ：x 2＋y 2＝4交于点A ,B ,与圆M ：(x －2)2＋(y －1)2＝1交于点C ,D .(1) 若AB ＝327 ,求CD 的长；(2) 若CD 中点为E ,求△ABE 面积的取值范围．(第6题)第46讲 椭圆A 应知应会一、 选择题1. 过点A (3,－2)且与椭圆x 29 ＋y 24 ＝1有相同焦点的椭圆的方程为( )A. x 215 ＋y 210 ＝1B. x 225 ＋y 220 ＝1 C. x 210 ＋y 215 ＝1 D. x 220 ＋y 215 ＝12. 设F 1,F 2分别是椭圆x 225 ＋y 216 ＝1的左、右焦点,P 为椭圆上一点,M 是F 1P 的中点,|OM |＝3,则P 点到椭圆左焦点的距离为( )A. 4B. 3C. 2D. 53. (多选)已知P 为椭圆x 25 ＋y 24 ＝1上一点,以点P 及焦点F 1,F 2为顶点的三角形的面积为S ,则( )A. 若S ＝1,则满足条件的点P 有4个B. 若S ＝2,则满足条件的点P 有2个C. 若S ＝5 ,则满足条件的点P 有2个D. 若S ＝12 ,则满足条件的点P 有4个4. 若中心为(0,0),一个焦点为F (0,52 )的椭圆,截直线y ＝3x －2所得弦中点的横坐标为12,则该椭圆的方程是( ) A. 2x 275 ＋2y 225 ＝1 B. x 275 ＋y 225 ＝1C. x 225 ＋y 275 ＝1D. 2x 225 ＋2y 275 ＝15. 已知椭圆x 2a 2 ＋y 2b 2 ＝1(a ＞b ＞0)的右顶点和上顶点分别为A ,B ,左焦点为F .以原点O 为圆心的圆与直线BF 相切,且该圆与y 轴的正半轴交于点C ,过点C 的直线交椭圆于M ,N 两点．若四边形F AMN 是平行四边形,则该椭圆的离心率为( )A. 35B. 12C. 23D. 34二、 解答题6 . 分别求出满足下列条件的椭圆的标准方程．(1) 与椭圆x 24 ＋y 23＝1有相同的离心率且经过点(2,－3 )；(2) 已知点P 在以坐标轴为对称轴的椭圆上,且P 到两焦点的距离分别为5,3.7. (2019·厦门期中)如图,已知椭圆C ：x 2a 2 ＋y 2b 2 ＝1(a ＞b ＞0)的左、右顶点分别为A ,B ,右焦点为F ,一条准线方程是x ＝－4,短轴一端点与两焦点构成等边三角形,点P ,Q 为椭圆C上异于A ,B 的两点,点R 为PQ 的中点．(1) 求椭圆C 的标准方程；(2) 直线PB 交直线x ＝－2于点M ,记直线P A 的斜率为k P A ,直线FM 的斜率为k FM ,求证：k FM ·k P A 为定值．(第7题)B 巩固提升一、 填空题1. 已知椭圆G 的中心在坐标原点,长轴在x 轴上,离心率为32,且G 上一点到G 的两个焦点的距离之和为12,则椭圆G 的方程为________．2. 已知F 1,F 2分别为椭圆C ：x 2a 2 ＋y 2＝1(a ＞1)的左、右焦点,点F 2关于直线y ＝x 的对称点Q 在椭圆上,则长轴长为________；若P 是椭圆上的一点,且PF 1·PF 2＝43 ,则S △F 1PF 2＝________．3. (2019·江苏海门中学)设F 1,F 2分别为椭圆x 24 ＋y 2＝1的左、右焦点,点P 在椭圆上,且|PF 1＋PF 2|＝23 ,则∠F 1PF 2＝________．4. (2019·淮北一模)在平面直角坐标系xOy 中,点P 是椭圆C ：x 2a 2 ＋y 24 ＝1(a ＞0)上一点,F为椭圆C 的右焦点,直线FP 与圆O ：x 2＋y 2＝1相切于点Q ,若Q 恰为线段FP 的中点,则a ＝________．二、 解答题5. (2019·南昌一模)已知椭圆C ：x 2a 2 ＋y 2b 2 ＝1(a ＞b ＞0)经过点M (0,－1),长轴长是短轴长的2倍．(1) 求椭圆C 的方程；(2) 设直线l 经过点N (2,1)且与椭圆C 相交于A ,B 两点(异于点M ),记直线MA 的斜率为k 1,直线MB 的斜率为k 2,求证：k 1＋k 2为定值．6. (2019·揭阳二模)已知椭圆C ：x 2a 2 ＋y 2＝1(a ＞1)的上顶点为A ,右焦点为F ,直线AF 与圆M ：(x －3)2＋(y －1)2＝3相切．(1) 求椭圆C 的方程；(2) 若不过点A 的动直线l 与椭圆C 交于P ,Q 两点,且AP → ·AQ →＝0,试探究：直线l 是否过定点？若是,求该定点的坐标；若不是,请说明理由．第47讲 双曲线 A 应知应会一、 选择题1. (多选)下列各条件下求得的双曲线标准方程,正确的是( )A. 与x 轴交于两点A (－2,0),B (2,0),c ＝3,则方程为x 24 －y 25 ＝1B. a ＝25 ,过点A (2,－5),焦点在y 轴上,则方程为y 220 －x 216＝1C. 与椭圆x 227 ＋y 236 ＝1有相同的焦点,它们的一个交点的纵坐标为4,则方程为y 24 －x 25＝1D. 过P 1⎝⎛⎭⎫－2，352 ,P 2⎝⎛⎭⎫473，4 两点,则方程是y 29 －x 216 ＝12. 若双曲线E ：x 29 －y 216 ＝1的左、右焦点分别为F 1,F 2,点P 在双曲线E 上,且|PF 1|＝3,则|PF 2|等于( )A. 11B. 9C. 5D. 33. 已知双曲线x 2a 2 －y 2b 2 ＝1(a ＞0,b ＞0)的一个焦点为F (－2,0),且双曲线的两条渐近线的夹角为60°,则双曲线的方程为( )A. x 23 －y 2＝1B. x 26 －y 22＝1C. x 23 －y 2＝1或x 2－y 23 ＝1 D. x 2－y 23 ＝1或x 26 －y 22＝1 4. (2019·济宁期末)已知抛物线C 1：y 2＝2px (p ＞0)的焦点为F ,准线与x 轴的交点为E ,线段EF 被双曲线C 2：x 2a 2 －y 2b 2 ＝1(a ＞0,b ＞0)的顶点三等分,且两曲线C 1,C 2的交点连线过曲线C 1的焦点F ,则双曲线C 2的离心率为( )A. 2B.322 C. 113 D. 2225. (2019·秦皇岛模拟)已知双曲线x 2a 2 －y 2b 2 ＝1(a ＞0,b ＞0)的一条渐近线平行于直线l ：y＝2x ＋10,双曲线的一个焦点在直线l 上,则双曲线的方程为( )A. x 25 －y 220 ＝1B. x 220 －y 25 ＝1C. 3x 225 －3y 2100 ＝1D. 3x 2100 －3y 225 ＝1二、 解答题6. 根据下列条件,求双曲线的标准方程． (1) 虚轴长为12,离心率为54 ；(2) 焦距为26,且经过点M (0,12)；(3) 经过两点P (－3,27 )和Q (－62 ,－7).7. 根据下列条件,求双曲线的标准方程． (1) 经过点P ⎝⎛⎭⎫3，154 ,Q ⎝⎛⎭⎫－163，5 ； (2) c ＝6 ,经过点(－5,2),焦点在x 轴上．B 巩固提升一、 填空题1. (2019·江苏卷)在平面直角坐标系xOy 中,若双曲线x 2－y 2b2 ＝1(b ＞0)经过点(3,4),则该双曲线的渐近线方程是________．2. (2019·晋中二模)过双曲线y 2a 2 －x 2b 2 ＝1(a ＞0,b ＞0)的下焦点F 1作y 轴的垂线,交双曲线于A ,B 两点,若以AB 为直径的圆恰好过其上焦点F 2,则双曲线的离心率为________．3. 已知M (x 0,y 0)是双曲线C ：x 22 －y 2＝1上的一点,F 1,F 2是C 的两个焦点,若MF 1·MF 2<0,则y 0的取值范围是________．4. (2019·马鞍山一检)已知双曲线C ：x 24 －y 25 ＝1的焦点为F 1,F 2,P 为双曲线C 上的一点,且△F 1PF 2的内切圆半径为1,则△F 1PF 2的面积为________．二、 解答题5. 已知双曲线过点(3,－2)且与椭圆4x 2＋9y 2＝36有相同的焦点． (1) 求双曲线的标准方程；(2) 若点M 在双曲线上,F 1,F 2为左、右焦点,且|MF 1|＋|MF 2|＝63 ,试判断△MF 1F 2的形状．6. 已知双曲线y 2a 2 －x 2b 2 ＝1(a ＞0,b ＞0)的两个焦点分别为F 1,F 2,一条渐近线方程为2x ＋y＝0,且焦点到这条渐近线的距离为1.(1) 求此双曲线的方程；(2) 若点M ⎝⎛⎭⎫55，m 在双曲线上,求证：点M 在以F 1F 2为直径的圆上．第48讲 抛物线A 应知应会一、 选择题 1. (2019·南昌一模)已知抛物线方程为x 2＝－2y ,则其准线方程为( ) A. y ＝－1 B. y ＝1 C. y ＝12 D. y ＝－122. 过抛物线y 2＝4x 的焦点的直线l 交抛物线于P (x 1,y 1),Q (x 2,y 2)两点,如果x 1＋x 2＝6,则|PQ |等于( )A. 9B. 8C. 7D. 6 3. (2019·石家庄检测)已知抛物线y 2＝4x 的焦点为F ,过点F 和抛物线上一点M (2,22 )的直线l 交抛物线于另一点N ,则|NF |∶|FM |等于( )A. 1∶2B. 1∶3C. 1∶2D. 1∶3 4. (2019·武汉调研)已知A ,B 为抛物线y 2＝4x 上两点,O 为坐标原点,且OA ⊥OB ,则|AB |的最小值为( )A. 42B. 22C. 8D. 825. (多选)设抛物线y 2＝2px (p ＞0)上有A (x 1,y 1),B (x 2,y 2),C (x 3,y 3)三点,F 是它的焦点,若AF ,BF ,CF 成等差数列,则( )A. x 1,x 2,x 3成等差数列B. x 1,x 2,x 3成等比数列C. y 21 ,y 22 ,y 23 成等差数列D. y 21 ,y 22 ,y 23 成等比数列 二、 解答题6. 已知抛物线y 2＝2px (p ＞0),过点C (－2,0)的直线l 交抛物线于A ,B 两点,坐标原点为O ,且OA → ·OB → ＝12.(1) 求抛物线的方程；(2) 当以AB 为直径的圆与y 轴相切时,求直线l 的方程．7. 一种高脚酒杯的轴截面近似一条抛物线如图所示,已知杯口宽4 cm,杯深8 cm.若将一些大小不等的玻璃球放入酒杯中,试问：半径为多大时,玻璃球触及酒杯底部？(第7题)B 巩固提升一、 填空题1. 若直线l 过抛物线C ：y 2＝2px (p ＞0)的焦点F (1,0),且与抛物线C 交于A ,B 两点,则p ＝________,1AF ＋1BF＝________．2. (2019·河南六市二联)已知抛物线y 2＝4x 的焦点为F ,其准线为直线l ,过点M (5,25 )作直线l 的垂线,垂足为H ,则∠FMH 的平分线所在直线的斜率是________．3. (2019·福州一模)已知直线l 经过抛物线y 2＝4x 的焦点F ,且与抛物线交于A ,B 两点,若AF → ＝5FB →,则直线l 的斜率为________．4. (2019·深圳二调)已知抛物线C ：y 2＝2px (p ＞0)上一点P 到焦点F 和到点(2,0)的距离之和的最小值为3,过点F 作斜率为3 的直线l 与抛物线C 及其准线从上到下依次交于点A ,B ,M ,则|AF ||BF | ＋|AF ||MF |＝________．二、 解答题 5. (2019·唐山摸底)斜率为k (k ≠0)的直线l 与抛物线y ＝x 2交于A (x 1,y 1),B (x 2,y 2)两点,O 为坐标原点．(1) 当x 1＋x 2＝2时,求k ；(2) 若OB ⊥l ,且|AB |＝3|OB |,求|AB |.6. (2019·合肥二模)已知抛物线C ：x 2＝2py (p ＞0)上一点M (m ,9)到其焦点F 的距离为10.(1) 求抛物线C 的方程；(2) 设过焦点F 的直线l 与抛物线C 交于A ,B 两点,且抛物线在A ,B 两点处的切线分别交x 轴于P ,Q 两点,求|AP |·|BQ |的取值范围．第49讲 解析几何的综合问题课时1 解析几何中的最值、范围问题A 应知应会一、 选择题1. 设A ,B 为椭圆C ：x 23 ＋y 2m＝1长轴的两个端点,若C 上存在点M 满足∠AMB ＝120°,则m 的取值范围是( )A. (0,1]∪[9,＋∞)B. (0,3 ]∪[9,＋∞)C. (0,1]∪[4,＋∞)D. (0,3 ]∪[4,＋∞)2. (2019·襄阳调研)已知F 1,F 2是双曲线x 2a 2 －y 2b 2 ＝1(a ＞0,b ＞0)的左、右焦点,若在右支上存在点A 使得点F 2到直线AF 1的距离为2a ,则离心率e 的取值范围是( ) A. [2 ,＋∞) B. (2 ,＋∞) C. (1,2 ) D. (1,2 ]3. (多选)已知O 是坐标原点,A ,B 是抛物线y ＝x 2上不同于O 的两点,OA ⊥OB ,则下列结论中正确的是( )A. OA ·OB ≥2B. OA ＋OB ≥22C. 直线AB 过抛物线y ＝x 2的焦点D. O 到直线AB 的距离小于等于1二、 解答题4. (2019·安庆二模)已知椭圆x 2a 2 ＋y 2b 2 ＝1(a ＞b ＞0)的离心率为22,且过点(2,2 ). (1) 求椭圆C 的标准方程；(2) 设A ,B 为椭圆C 的左、右顶点,过C 的右焦点F 作直线l 交椭圆于M ,N 两点,分别记△ABM ,△ABN 的面积为S 1,S 2,求|S 1－S 2|的最大值．5. (2019·荆州二模)已知椭圆C ：x 2a 2 ＋y 2b2 ＝1(a ＞b ＞0)的左、右焦点分别为F 1,F 2,离心率为13,点P 在椭圆C 上,且△PF 1F 2的面积的最大值为22 . (1) 求椭圆C 的方程；(2) 已知直线l ：y ＝kx ＋2(k ≠0)与椭圆C 交于不同的两点M ,N ,若在x 轴上存在点G ,使得|GM |＝|GN |,求点G 的横坐标的取值范围．B 巩固提升一、 填空题1. (2017·全国卷Ⅱ)若a ＞1,则双曲线x 2a 2 －y 2＝1的离心率的取值范围是________． 2. 已知线段|AB |＝4,|P A |＋|PB |＝6,M 是AB 的中点,当P 点在同一平面内运动时,PM 的长度的最小值为________．3. 已知F 1,F 2是双曲线x 2a 2 －y 2b 2 ＝1(a ＞0,b ＞0)的左、右焦点,若双曲线上存在点P 满足PF 1·PF 2＝－a 2,则双曲线离心率的取值范围为________．二、 解答题4. (2019·新乡三模)已知抛物线E ：y 2＝2px (p ＞0)的准线与x 轴交于点K ,过点K 作圆C ：(x －5)2＋y 2＝9的两条切线,切点为M ,N ,|MN |＝33 .(1) 求抛物线E 的方程；(2) 若直线AB 是过定点Q (2,0)的一条直线,且与抛物线E 交于A ,B 两点,过定点Q 作AB 的垂线与抛物线交于G ,D 两点,求四边形AGBD 面积的最小值．5. (2019·江西质检)已知椭圆C ：x 2a 2 ＋y 2b 2 ＝1(a ＞b ＞0)的离心率e ＝22,过点A (－m ,0),B (m ,0)(m ＞0)分别作两平行直线l 1,l 2,l 1与椭圆C 相交于M ,N 两点,l 2与椭圆C 相交于P ,Q两点,且当直线l 2过右焦点和上顶点时,四边形MNQP 的面积为163. (1) 求椭圆C 的标准方程；(2) 若四边形MNQP 是菱形,求正数m 的取值范围．课时2 解析几何中的定点、定值问题A 应知应会一、 选择题1. (2019·武汉模拟)曲线x 225 ＋y 29 ＝1与曲线x 225－k ＋y 29－k＝1(k ＜9)的( )A. 长轴长相等B. 短轴长相等C. 离心率相等D. 焦距相等2. 已知直线l 与抛物线C ：y 2＝2x 交于A ,B 两点,O 为坐标原点,若直线OA ,OB 的斜率k 1,k 2满足k 1k 2＝23,则l 一定过点( ) A. (－3,0) B. (3,0) C. (－1,3) D. (－2,0)3. (2019·德阳模拟)设P 为椭圆C ：x 249 ＋y 224＝1上一点,F 1,F 2分别是椭圆C 的左、右焦点,且△PF 1F 2的重心为点G ,若|PF 1|∶|PF 2|＝3∶4,那么△GPF 1的面积为( )A. 24B. 12C. 8D. 6二、 解答题4. (2015·全国卷Ⅰ)在直角坐标系xOy 中,曲线C ：y ＝x 24与直线l ：y ＝kx ＋a (a ＞0)交于M ,N 两点．(1) 当k ＝0时,分别求C 在点M 和N 处的切线方程；(2) y 轴上是否存在点P ,使得当k 变动时,总有∠OPM ＝∠OPN ？说明理由．5. 已知椭圆C ：x 23＋y 2＝1,圆O ：x 2＋y 2＝4上一点A (0,2). (1) 过点A 作两条直线l 1,l 2都与椭圆C 相切,求直线l 1,l 2的方程并判断其位置关系；(2) 同学甲：过圆O 上任意一点P 作椭圆C 的两条切线l 1,l 2,则直线l 1,l 2始终相互垂直； 同学乙：过圆O 上任意一点P 作椭圆C 的两条切线l 1,l 2,则直线l 1,l 2始终不垂直． 请判定两个同学观点是否正确,并证明．B 巩固提升一、 填空题1. 过抛物线y 2＝8x 上的任意一点为圆心作与直线x ＋2＝0相切的圆,这些圆必过一定点,则定点的坐标是________．2. 设A (x 1,y 1),B ⎝⎛⎭⎫4，95 ,C (x 2,y 2)是右焦点为F 的椭圆x 225 ＋y 29 ＝1上三个不同的点,若AF ,BF ,CF 成等差数列,则x 1＋x 2＝________．二、 解答题3. (2019·烟台一模)已知F 为抛物线C ：y 2＝2px (p ＞0)的焦点,过F 的动直线交抛物线C 于A ,B 两点．当直线与x 轴垂直时,|AB |＝4.(1) 求抛物线C 的方程；(2) 若直线AB 与抛物线的准线l 相交于点M ,在抛物线C 上是否存在点P ,使得直线P A ,PM ,PB 的斜率成等差数列？若存在,求出点P 的坐标；若不存在,说明理由．4. (2019·池州期末)已知定点A (－3,0),B (3,0),直线AM ,BM 相交于点M ,且它们的斜率之积为－19,记动点M 的轨迹为曲线C . (1) 求曲线C 的方程；(2) 过点T (1,0)的直线l 与曲线C 交于P ,Q 两点,是否存在定点S (s ,0),使得直线SP 与SQ 斜率之积为定值？若存在,求出S 的坐标；若不存在,请说明理由．微难点10 解析几何运算中的常用技巧一、 选择题1. 已知双曲线x 2a 2 －y 2b 2 ＝1(a ＞0,b ＞0)的一条渐近线方程是y ＝3 x ,它的一个焦点在抛物线y 2＝24x 的准线上,则双曲线的方程为( )A. x 236 －y 2108 ＝1B. x 29 －y 227＝1 C. x 2108 －y 236 ＝1 D. x 227 －y 29＝12. 已知椭圆E ：x 2a 2 ＋y 2b 2 ＝1(a ＞b ＞0)的右焦点为F (3,0),过点F 的直线交E 于A ,B 两点．若AB 的中点坐标为(1,－1),则E 的标准方程为( )A. x 245 ＋y 236 ＝1B. x 236 ＋y 227＝1 C. x 227 ＋y 218 ＝1 D. x 218 ＋y 29＝13. 已知双曲线x 2a 2 －y 2b 2 ＝1(a ＞0,b ＞0)的左、右焦点分别为F 1(－c ,0),F 2(c ,0),P 为双曲线上任一点,且PF 1·PF 2最小值的取值范围是⎣⎡⎦⎤－34c 2，－12c 2 ,则该双曲线的离心率的取值范围为( ) A. (1,2 ] B. [2 ,2] C. (0,2 ] D. [2,＋∞)二、 填空题4. (2019·清江中学)已知F (2,0)为椭圆x 2a 2 ＋y 2b 2 ＝1(a ＞b ＞0)的右焦点,过F 且垂直于x 轴的弦长为6,若A (－2,2 ),点M 为椭圆上任一点,则|MF |＋|MA |的最大值为________．5. 如图,已知椭圆C 的中心为原点O ,F (－25 ,0)为C 的左焦点,P 为C 上一点,满足OP ＝OF ,且PF ＝4,则椭圆C 的方程为________．(第5题)三、 解答题6. 已知椭圆C ：x 2a 2 ＋y 2b 2 ＝1(a ＞b ＞0)上的点到两个焦点的距离之和为23 ,短轴长为12,直线l 与椭圆C 交于M ,N 两点．(1) 求椭圆C 的方程；(2) 若直线l 与圆O ：x 2＋y 2＝125相切,求证：OM → ·ON → 为定值.7. 已知椭圆C 的中心在坐标原点,焦点在x 轴上,离心率e ＝12,且椭圆C 经过点P (2,3),过椭圆C 的左焦点F 1且不与坐标轴垂直的直线交椭圆C 于A ,B 两点．(1) 求椭圆C 的方程；(2) 设线段AB 的垂直平分线与x 轴交于点G ,求△PF 1G 的面积S 的取值范围．8. 如图,O 为坐标原点,点F 为抛物线C 1：x 2＝2py (p ＞0)的焦点,且抛物线C 1上点P 处的切线与圆C 2：x 2＋y 2＝1相切于点Q .(1) 当直线PQ 的方程为x －y －2 ＝0时,求抛物线C 1的方程；(2) 当正数p 变化时,记S 1 ,S 2分别为△FPQ ,△FOQ 的面积,求S 1S 2的最小值．(第8题)。

第二章 基本初等函数第6讲 函数的概念及其表示方法A 组 应知应会一、 选择题1. (2019·北京一模)已知函数f (x )＝x 3－2x ,则f (3)等于( )A. 1B. 19C. 21D. 352. (2019·石家庄二模)设集合M ＝{x |0≤x ≤2},N ＝{y |0≤y ≤2},给出如下四个图形,其中能表示从集合M 到集合N 的函数关系的是( )A BCD3. (2019·厦门质检)已知函数f (x )＝⎩⎪⎨⎪⎧3x ，x ≤0，－⎝⎛⎭⎫12x ，x >0， 则f (f (log 23))等于( ) A. －9 B. －1C. －13D. －1274. (2019·河南名校段测)设函数f (x )＝⎩⎪⎨⎪⎧log 3x ，0＜x ≤9，f （x －4），x ＞9，则f (13)＋2f ⎝⎛⎭⎫13 的值为( ) A. 1 B. 0 C. －2 D. 25. (2019·河北衡水)若函数y ＝x 2－3x －4的定义域为[0,m ],值域为⎣⎡⎦⎤－254，－4 ,则实数m的取值范围是( )A. (0,4]B. ⎣⎡⎦⎤32，4C. ⎝⎛⎭⎫32，＋∞D. ⎣⎡⎦⎤32，3二、 解答题6. (1) 已知f (x )是二次函数且f (0)＝2,f (x ＋1)－f (x )＝x －1,求f (x )的解析式．(2) 已知函数f (x )的定义域为(0,＋∞),且f (x )＝2f ⎝⎛⎭⎫1x ·x －1,求f (x )的解析式．7. 已知f (x )＝x 2－1,g (x )＝⎩⎪⎨⎪⎧x －1，x >0，2－x ，x <0.(1) 求f (g (2))和g (f (2))的值；(2) 求f (g (x ))和g (f (x ))的表达式．B 组 能力提升一、 填空题1. 已知函数f (x )＝－x 2＋3x ＋4 ,则函数y ＝f (x )的定义域为________,函数y ＝f (2x ＋1)的定义域为________．2. (2019·南京三模)若函数f (x )＝⎩⎪⎨⎪⎧2x ，x ≤0，f （x －2），x ＞0， 则f (log 23)＝________． 3. (2018·南阳一模)已知函数y ＝f (x )满足f (x )＝2f ⎝⎛⎭⎫1x ＋3x ,则f (x )的解析式为________．4. (2018·郴州质量监测)已知f (x )＝⎩⎪⎨⎪⎧12x ＋1，x ≤0，－（x －1）2，x ＞0，则使f (a )＝－1成立的a 值是________．二、 解答题5. (1) 已知一次函数f (x )满足f (f (x ))＝4x －1,求f (x ).(2) 已知定义在(－1,1)内的函数f (x )满足2f (x )－f (－x )＝lg (x ＋1),求f (x ).6. 对于每个实数x ,设f (x )取y ＝4x ＋1,y ＝x ＋2,y ＝－2x ＋4三个函数中的最小值,用分段函数写出f (x )的解析式,并求f (x )的最大值．第7讲 函数的单调性与最值A 组 应知应会一、 选择题1. (多选)已知f (x )是定义在[0,＋∞)上的函数,根据下列条件可以断定f (x )为增函数的是( )A. 对任意x ≥0,都有f (x ＋1)＞f (x )B. 对任意x 1,x 2∈[0,＋∞),且x 1≥x 2,都有f (x 1)≥f (x 2)C. 对任意x 1,x 2∈[0,＋∞),且x 1－x 2<0,都有f (x 1)－f (x 2)<0D. 对任意x 1,x 2∈[0,＋∞),且x 1≠x 2,都有f （x 1）－f （x 2）x 1－x 2＞0 2. 下列函数中,在区间(－1,1)上为减函数的是( )A. y ＝11－xB. y ＝cos xC. y ＝ln (x ＋1)D. y ＝2－x 3. 若函数y ＝2－x x ＋1,x ∈(m ,n ]的最小值为0,则m 的取值范围是( ) A. (1,2) B. (－1,2) C. [1,2) D. [－1,2)4. (2019·郑州调研)若函数f (x )＝x －1x 2 在x ∈[1,4]上的最大值为M ,最小值为m ,则M －m 的值是( )A. 3116B. 2C. 94D. 1145. (2019·武汉质检)若函数y ＝log 12(x 2－ax ＋3a )在区间(2,＋∞)上是减函数,则a 的取值范围为( )A. (－∞,－4)∪[2,＋∞)B. (－4,4]C. [－4,4)D. [－4,4]二、 解答题6. 已知f (x )＝x x 2＋1,判断并证明函数f (x )在区间[－1,0]上的单调性．7. 求下列函数的值域．(1) f (x )＝⎩⎪⎨⎪⎧x 2－x ＋1，x <1，1x，x >1； (2) y ＝x －x .B 巩固提升一、填空题1. 函数f (x )＝1－2x ＋1的单调增区间是________． 2. (2019·太原期末)已知函数f (x )＝x ＋1x －1,x ∈[2,5],则f (x )的最大值是________． 3. (2018·全国卷Ⅰ)设函数f (x )＝⎩⎪⎨⎪⎧⎝⎛⎭⎫12x，x ≤0，1，x >0，则满足f (x ＋1)<f (2x )的x 的取值范围是________．4. 已知f (x )＝⎩⎪⎨⎪⎧（2－a ）x ＋1，x <1，a x ，x ≥1 满足对任意x 1≠x 2,都有f （x 1）－f （x 2）x 1－x 2 ＞0成立,那么实数a 的取值范围是________．二、 解答题5. 已知函数f (x )＝1a －1x(a ＞0,x ＞0). (1) 求证：f (x )在(0,＋∞)上是增函数；(2) 若f (x )在⎣⎡⎦⎤12，2 上的值域是⎣⎡⎦⎤12，2 ,求a 的值．6. 已知函数f (x )的定义域D ＝{x |x ≠0},且满足对于任意x 1,x 2∈D ,有f (x 1·x 2)＝f (x 1)＋f (x 2).(1) 求f (1)的值；(2) 判断f (x )的奇偶性并证明；(3) 如果f (4)＝1,f (3x ＋1)＋f (2x －6)≤3,且f (x )在(0,＋∞)上是增函数,求x 的取值范围．第8讲 函数的奇偶性与周期性课时1 函数奇偶性判定与周期性A 组 应知应会一、 选择题1. 下列函数中,既是偶函数,又在区间(0,＋∞)上单调递减的函数是( )A. y ＝x 3B. y ＝ln 1|x |C. y ＝2|x |D. y ＝cos x 2. (2019·济宁二模)已知f (x )是定义在R 上的周期为4的奇函数,当x ∈(0,2)时,f (x )＝x 2＋ln x ,则f (2 019)等于( )A. －1B. 0C. 1D. 23. (2019·烟台一模)若函数f (x )是定义在R 上的奇函数,f ⎝⎛⎭⎫14 ＝1,当x <0时,f (x )＝log 2(－x )＋m ,则实数m 等于( )A. －1B. 0C. 1D. 24. 已知f (x )在R 上是奇函数,且满足f (x ＋4)＝f (x ),当x ∈(－2,0)时,f (x )＝2x 2,则f (2 019)等于( )A. －2B. 2C. －98D. 985. (多选)设函数f (x )的定义域为R,且f ⎝⎛⎭⎫π2 ＝0,f (0)≠0,若对于任意实数x ,y ,恒有f (x )＋f (y )＝2f ⎝⎛⎭⎫x ＋y 2 ·f ⎝⎛⎭⎫x －y 2 ,则下列说法正确的是( )A. f (0)＝1B. f (x )＝f (－x )C. f (x ＋2π)＝f (x )D. f (2x )＝2f (x )－1二、 解答题6. 已知f (x )是定义在R 上的奇函数,且当x ∈(－∞,0)时,f (x )＝－x lg (2－x ),求函数f (x )的解析式．7. 已知f (x )是定义在[－1,1]上的奇函数,且f (1)＝1,若a ,b ∈[－1,1],且a ＋b ≠0时,有f （a ）＋f （b ）a ＋b＞0恒成立． (1) 用定义证明函数f (x )在[－1,1]上是增函数；(2) 解不等式：f ⎝⎛⎭⎫x ＋12 <f (1－x ).B 组 能力提升一、 填空题1. (2019·日照一模)若函数f (x )＝x 2＋(3－a )x ＋1为偶函数,则a ＝________．2. 设f (x )是定义在R 上以2为周期的偶函数,当x ∈[0,1]时,f (x )＝log 2(x ＋1),则当x ∈[1,2]时,f (x )＝________．3. (2019·苏州期初调查)已知函数f (x )＝⎩⎪⎨⎪⎧x 2－2x ，x ≥0，－x 2＋ax ，x <0 为奇函数,则实数a 的值为________．4. (2019·南通、泰州、扬州一调)已知函数f (x )是定义在R 上的奇函数,且f (x ＋2)＝f (x ).当0<x ≤1时,f (x )＝x 3－ax ＋1,则实数a 的值为________．二、 解答题5. 设f (x )是(－∞,＋∞)上的奇函数,f (x ＋2)＝－f (x ),当0≤x ≤1时,f (x )＝x .(1) 求f (π)的值；(2) 当－4≤x ≤4时,求f (x )的图象与x 轴所围成图形的面积．6. 设f (x )是定义在R 上的奇函数,且对任意实数x 恒有f (x ＋2)＝－f (x ),当x ∈[0,2]时,f (x )＝2x －x 2.(1) 求证：f (x )是周期函数；(2) 当x ∈[2,4]时,求f (x )的解析式；(3) 计算f (0)＋f (1)＋…＋f (2 020)的值．课时2 函数性质的应用A 组 应知应会一、 选择题1. (2019·山西考前训练)下列函数中,既是奇函数,又在区间(0,1)内是增函数的是( )A. y ＝x ln xB. y ＝x 2＋xC. y ＝sin 2xD. y ＝e x －e －x2. (2018·全国卷Ⅱ)已知f (x )是定义域为(－∞,＋∞)的奇函数,满足f (1－x )＝f (1＋x ).若f (1)＝2,则f (1)＋f (2)＋f (3)＋…＋f (50)等于 ( )A. －50B. 0C. 2D. 503. (2019·九江二模)已知函数f (x )满足：①对任意x ∈R,f (x )＋f (－x )＝0,f (x ＋4)＋f (－x )＝0成立；②当x ∈(0,2]时,f (x )＝x (x －2),则f (2 019)等于( )A. 1B. 0C. 2D. －14. (多选)已知定义在R 上的奇函数y ＝f (x )和偶函数y ＝g (x )满足f (x )＋g (x )＝4x ,下列结论正确的有( )A. f (x )＝4x －4－x 2,且0<f (1)<f (2) B. ∀x ∈R,总有[g (x )]2－[f (x )]2＝1C. ∀x ∈R,总有f (－x )g (－x )＋f (x )g (x )＝0D. ∃x 0∈R,使得f (2x 0)＞2f (x 0)g (x 0)5. (2019·临沂一模)已知函数g (x )＝f (x )＋x 2是奇函数,当x ＞0时,函数f (x )的图象与函数y ＝log 2x 的图象关于y ＝x 对称,则g (－1)＋g (－2)等于( )A. －7B. －9C. －11D. －13二、 解答题6. 若f (x )是定义在(－1,1)上的奇函数,且x ∈[0,1)时f (x )为增函数,求不等式f (x )＋f ⎝⎛⎭⎫x －12 ＜0的解集．7. 已知函数f (x )是(－∞,＋∞)上的偶函数,若对于x ≥0,都有f (x ＋2)＝－f (x ),且当x ∈[0,2)时,f (x )＝log 2(x ＋1).(1) 求f (0)与f (2)的值；(2) 求f (3)的值；(3) 求f (2 021)＋f (－2 022)的值．B 组 能力提升一、 填空题1. 已知函数f (x )同时满足条件：①偶函数；②值域为[0,＋∞)；③周期为2 020,请写出f (x )的一个解析式：______________．2. 已知奇函数f (x )在R 上是增函数,g (x )＝xf (x ).若a ＝g (－log 25.1),b ＝g (20.8),c ＝g (3),则a ,b ,c 的大小关系是________．3. 设函数f (x )＝ln (1＋|x |)－11＋x 2,则使得f (x )＞f (2x －1)成立的x 的取值范围是________． 4. 函数f (x )＝x 3－3x 2的对称中心是________．二、 解答题5. 若f (x )和g (x )都是奇函数,且F (x )＝af (x )＋bg (x )＋2在(0,＋∞)上有最大值8,求F (x )在(－∞,0)上的最小值．6. 设函数f (x )是定义在R 上的奇函数,对任意实数x 都有f ⎝⎛⎭⎫32＋x ＝－f ⎝⎛⎭⎫32－x 成立． (1) 证明：y ＝f (x )是周期函数,并指出其周期；(2) 若f (1)＝2,求f (2)＋f (3)的值；(3) 若g (x )＝x 2＋ax ＋3,且y ＝|f (x )|·g (x )是偶函数,求实数a 的值．第9讲二次函数与幂函数A组应知应会一、选择题1. 若a＝3221⎪⎭⎫⎝⎛,b＝3251⎪⎭⎫⎝⎛,c＝3121⎪⎭⎫⎝⎛,则a,b,c的大小关系是()A. a<b<cB. c<a<bC. b<c<aD. b<a<c2. 若幂函数y＝f(x)的图象过点(4,2),则幂函数y＝f(x)的大致图象是()A BC D3. (2019·安阳模拟)已知函数f(x)＝－x2＋4x＋a,x∈[0,1],若f(x)有最小值－2,则f(x)的最大值为()A. 1B. 0C. －1D. 24. 将进价为40元的商品按50元一件销售,一个月恰好卖500件,而价格每提高1元,就会少卖10个,商店为使该商品利润最大,应将每件商品定价为()A. 50元B. 60元C. 70元D. 100元5. (多选)已知函数f(x)＝|x2－2ax＋b|(x∈R),给出下列命题,其中是真命题的是()A. 若a2－b≤0,则f(x)在区间[a,＋∞)上是增函数B. 存在a∈R,使得f(x)为偶函数C. 若f(0)＝f(2),则f(x)的图象关于x＝1对称D. 若a2－b－2＞0,则函数h(x)＝f(x)－2有2个零点二、解答题6. 已知二次函数f(x)同时满足条件：①对称轴方程是x＝1；②f(x)的最大值为15；③f(x)＝0的两根立方和等于17.求f(x)的解析式．7. 已知函数f(x)＝x2－2tx＋1在(－∞,1]上单调递减,且对任意的x1,x2∈[0,t＋1],总有|f(x1)－f(x2)|≤2,求实数t的取值范围．B 组 能力提升一、 填空题1. 已知函数f (x )＝ax 2－2x －3在区间为(－∞,4)上单调递减,则a 的取值范围是________．2. 若二次函数f (x )＝－x 2＋2ax ＋4a ＋1有一个零点小于－1,一个零点大于3,则实数a 的取值范围是________．3. 函数f (x )＝⎩⎪⎨⎪⎧x 2＋2x －3，－2≤x <0，x 2－2x －3，0≤x ≤3 的值域是________． 4. 已知二次函数f (x )＝ax 2－4x ＋c ＋1(a ≠0)的值域为(－∞,1],则1a ＋4c的最大值是________．二、 解答题5. (1) 已知函数f (x )＝4x 2－kx －8在[5,20]上具有单调性,求实数k 的取值范围．(2) 已知关于x 的方程mx 2＋2(m ＋3)x ＋2m ＋14＝0有两个不同的实根,且一个大于4,另一个小于4,求m 的取值范围．6. 已知函数f (x )＝x 2－kx ＋3.(1) 若f (x )在[－2,2]上存在单调减区间,求k 的取值范围；(2) 从下面三个函数中：①g (x )＝mx ＋5－m ；②h (x )＝2x －m ；③r (x )＝log 2(3－x )－m ,任选一个函数补充在下列问题中,若m 存在,求m 的取值范围；若不存在,请说明理由．问题：当k ＝0时,若对任意的x 1∈[1,2],总存在x 2∈[－1,2],使得f (2x 1)＝k (x 2)成立．(其中k (x )是你选择的函数)第10讲 指数式与指数函数A 组 应知应会一、 选择题1. (多选)下列结论中不正确的是( )A. 函数f (x )＝x x -⎪⎭⎫⎝⎛221的单调增区间为⎝⎛⎭⎫－∞，12 B. 函数f (x )＝2x －12x ＋1为奇函数 C. 函数y ＝1x ＋1的单调减区间是(－∞,1)和(1,＋∞) D. 1x＞1是x <1的必要不充分条件 2. 已知a ＝243 ,b ＝425 ,c ＝2513,则( )A. b <a <cB. a <b <cC. b <c <aD. c <a <b3. 若3x ＝a ,5x ＝b ,则45x 等于( )A. a 2bB. ab 2C. a 2＋bD. a 2＋b 24. (2019·东北三校联考)已知函数f (x )＝a x －1(a ＞0,a ≠1)的图象恒过点A ,下列函数中图象不经过点A 的是( )A. y ＝1－xB. y ＝|x －2|C. y ＝2x －1D. y ＝log 2(2x )5. (多选)已知函数f (x )＝e x －e －x 2 ,g (x )＝e x ＋e －x 2,则f (x ),g (x )满足( ) A. f (－x )＝－f (x ),g (－x )＝g (x )B. f (－2)<f (3)C. f (2x )＝2f (x )g (x )D. [f (x )]2－[g (x )]2＝1二、 解答题6. 已知函数f (x )＝⎝⎛⎭⎫12 ax ,a 为常数,且函数的图象过点(－1,2).(1) 求a 的值；(2) 若g (x )＝4－x －2,且g (x )＝f (x ),求满足条件的x 的值．7. 已知函数f (x )是定义在R 上的奇函数,当x ≥0时,f (x )＝2x －1.(1) 求f (3)＋f (－1)；(2) 求f (x )在R 上的解析式；(3) 求不等式－7≤f (x )≤3的解集．B 组 能力提升一、 填空题1. (2019·菏泽九校联考)已知函数f (x )是定义在R 上的偶函数,且在区间(－∞,0)上单调递增．若实数a 满足f (32a －1)≥f (－3 ),则a 的最大值是________．2. (2019·石家庄二模)若函数f (x ),g (x )分别是定义在R 上的偶函数、奇函数,且满足f (x )＋2g (x )＝e x ,则g (－1),f (－2),f (－3)从大到小的顺序是________．3. (2018·苏锡常镇调研)已知函数f (x )＝⎩⎪⎨⎪⎧a －e x ，x <1，x ＋4x，x ≥1 (e 是自然对数的底).若函数y ＝f (x )的最小值是4,则实数a 的取值范围为________．4. (2019·聊城一模)设函数f (x )＝1e x －1＋a ,若f (x )为奇函数,则不等式f (x )＞1的解集为________．二、解答题5. 已知函数f (x )＝b ·a x (a ＞0,且a ≠1,b ∈R)的图象经过点A (1,6),B (3,24).(1) 设g (x )＝1f （x ）＋3 －16,确定函数g (x )的奇偶性； (2) 若对任意x ∈(－∞,1],不等式⎝⎛⎭⎫a b x≥2m ＋1恒成立,求实数m 的取值范围．6. 设f (x )＝a x ＋a －x 2 ,g (x )＝a x －a －x 2,其中a 为常数,且a ＞0,a ≠1. (1) 求证：g (5)＝g (2)f (3)＋f (2)g (3)；(2) 试写出一个f (x )和g (x )的函数值满足的等式,使得第(1)问的结论是这个等式的一个特例,并证明它在f (x )和g (x )的公共定义域R 上恒成立；(3) 试再写出一个f (x )和g (x )的函数值满足的等式．第11讲 对数与对数函数A 组 应知应会一、 选择题1. (2019·全国卷Ⅰ) 已知a ＝log 20.2,b ＝20.2,c ＝0.20.3,则( )A. a <b <cB. a <c <bC. c <a <bD. b <c <a2. (多选)已知函数f (x )＝ax 3－1x＋b (a ＞0,b ∈Z),选取a ,b 的一组值计算f (lg a )和f ⎝⎛⎭⎫lg 1a 所得出的结果可以是( )A. 3和4B. －2和5C. 6和2D. －2和23. (2019·枣庄一模)已知2x ＝5y ＝t ,1x ＋1y＝2,则t 等于( ) A. 110 B. 1100C. 10D. 100 4. (2019·汕头一模)已知当0<x ≤12时,不等式log a x <－2恒成立,则实数a 的取值范围是( ) A. (2 ,2) B. (1,2 )C. ⎝⎛⎭⎫22，1 D. (0,2 ) 5. (2019·肇庆二模)已知f (x )＝lg (10＋x )＋lg (10－x ),则( )A. f (x )是奇函数,且在(0,10)上是增函数B. f (x )是偶函数,且在(0,10)上是增函数C. f (x )是奇函数,且在(0,10)上是减函数D. f (x )是偶函数,且在(0,10)上是减函数二、 解答题6. 已知函数f (x )＝log 4(ax 2＋2x ＋3).(1) 若f (1)＝1,求f (x )的单调区间；(2) 若f (x )的最小值为0,求a 的值．7. 已知函数f (x )是定义在R 上的偶函数,且f (0)＝0,当x ＞0时,f (x )＝log 12x . (1) 求函数f (x )的解析式；(2) 解不等式f (x 2－1)＞－2.B 组 能力提升一、 填空题1. (2019·南京、盐城一模)已知y ＝f (x )为定义在R 上的奇函数,且当x ＞0时,f (x )＝e x ＋1,则f (－ln 2)的值为________．2. (2019·孝义二模)若函数y ＝log 2(x 2－ax ＋3a )在[2,＋∞)上是增函数,则a 的取值范围是________．3. 若函数f (x )＝log a ⎝⎛⎭⎫x 2＋32x (a ＞0,a ≠1)在区间⎝⎛⎭⎫12，＋∞ 内恒有f (x )＞0,则f (x )的单调增区间为________．4. 设函数f (x )＝⎩⎪⎨⎪⎧e x ，x ≤0，ln x ，x >0， 则f ⎝⎛⎭⎫f ⎝⎛⎭⎫12 ＝________, 方程f (f (x ))＝1的解集是________． 二、 解答题5. 已知函数f (x )＝log a (x ＋1)(a ＞0,a ≠1)在区间[1,7]上的最大值比最小值大12,求a 的值．6. 已知函数f (x )＝ln (1＋x )＋ln (a －x )为偶函数,a ∈R ．(1) 求a 的值,并讨论f (x )的单调性；(2) 若f ⎝⎛⎭⎫12 <f (lg x ),求x 的取值范围．第12讲函数的图象课时1图象变换及识别A组应知应会一、选择题1. (2019·黄山一模)已知图(1)中的图象对应的函数为y＝f(x),则图(2)中的图象对应的函数为()(第1题)A. y＝f(|x|)B. y＝f(－|x|)C. y＝|f(x)|D. y＝－f(|x|)2. (2019·厦门质检)函数y＝cos x＋ln (|x|＋1)(x∈[－2π,2π])的图象大致为()A BC D3. (2019·泉州质检)函数f(x)＝e|x|2x的部分图象大致为()A BC D4. (2019·长沙月考)函数f(x)＝ln (x－1)＋ln (x＋1)＋cos x的大致图象是()A BC D5. (2019·济南一模)若函数f (x )＝a x －a －x (a ＞0)在R 上为减函数,则函数y ＝log a (|x |－1)的图象可以是( )A BC D二、解答题6. 如图,定义在[－1,＋∞)上的函数f (x )的图象由一条线段及抛物线的一部分组成,求f (x )的解析式．(第6题)7. 已知函数f (x )＝1＋|x |－x 2(－2<x ≤2). (1) 用分段函数的形式表示该函数；(2) 画出该函数的图象；(3) 写出该函数的值域．B 组 能力提升一、 填空题1. 设函数f (x )＝⎩⎪⎨⎪⎧|x ＋1|，x ＜1，－x ＋3，x ≥1， 使得f (x )≥1的自变量x 的取值范围是________． 2. 已知函数f (x )＝1x,则y ＝f (x －1)＋1的单调减区间为________． 3. 若函数f (x )＝|2x －4|－a 存在两个零点,且一个为正数,另一个为负数,则a 的取值范围为________．4. (2019·龙岩质检)已知定义在R 上的可导函数f (x ),g (x )满足f (x )＋f (－x )＝6x 2＋3,f (1)－g (1)＝3,g ′(x )＝f ′(x )－6x ,如果g (x )的最大值为M ,最小值为N ,则M ＋N ＝________．二、 解答题5. 已知函数f (x )＝|x |(x －a ),a ＞0.(1) 作出函数f (x )的图象；(2) 写出函数f (x )的单调区间；(3) 当x ∈[0,1]时,由图象写出f (x )的最小值．6. 设函数f (x )＝ax ＋1x ＋b(a ,b 为常数),且方程f (x )＝32 x 的两个实根分别为x 1＝－1,x 2＝2.(1) 求y ＝f (x )的解析式；(2) 证明：函数y ＝f (x )的图象是一个中心对称图形,并求其对称中心．课时2以函数图象为背景的问题A组应知应会一、选择题1. (2019·合肥质检)函数f(x)＝x2＋x sin x的图象大致为()A BC D2. (2019·芜湖期末)函数f(x)＝ln |x＋1|x＋1的部分图象大致为()A BC D3. (2019·广州一模)如图,一高为H且装满水的鱼缸,其底部装有一排水小孔,当小孔打开时,水从孔中匀速流出,水流完所用时间为T.若鱼缸水深为h时,水流出所用时间为t,则函数h ＝f(t)的图象大致是()(第3题)ABCD4. (多选)函数f (x )＝|x |＋ax2 (其中a ∈R)的图象可能是( )ABCD二、 填空题5. 已知函数f (x )＝|log 3x |,实数m ,n 满足0<m <n ,且f (m )＝f (n ),若f (x )在[m 2,n ]上的最大值为2,则nm＝________．6. 若函数f (x )＝⎩⎪⎨⎪⎧ax ＋b ，x <－1，ln （x ＋a ），x ≥－1 的图象如图所示,则f (－3)＝________．(第6题)7. 若函数f (x )＝x ＋1x 的图象与直线y ＝kx ＋1交于不同的两点(x 1,y 1),(x 2,y 2),则y 1＋y 2＝________．8. (2019·长沙统测)已知f (x )＝|e x －1|＋1,若函数g (x )＝[f (x )]2＋(a －2)f (x )－2a 有三个零点,则实数a 的取值范围是________．9. 不等式3sin ⎝⎛⎭⎫π2x －log 12x <0的整数解的个数为________．B 组 能力提升一、 选择题 1. (2019·潍坊模拟)函数y ＝4cos x －e |x |的图象可能是( )ABCD2. (2019·河南省六市联考)设实数a ,b ,c 分别满足a ＝5－12 ,b ln b ＝1,3c 3＋c ＝1,则a ,b ,c 的大小关系为( )A. c ＞b ＞aB. b ＞c ＞aC. b ＞a ＞cD. a ＞b ＞c3. 已知函数f (2x ＋1)是奇函数,则函数y ＝f (2x )的图象成中心对称的点为( )A. (1,0)B. (－1,0)C. ⎝⎛⎭⎫12，0D. ⎝⎛⎭⎫－12，04. 若函数f (x )＝（2－m ）xx 2＋m的图象如图所示,则m 的取值范围为( )(第4题)A. (－∞,－1)B. (－1,2)C. (0,2)D. (1,2)二、 填空题 5. (2019·新余模拟)若函数y ＝f (x )的图象过点(1,1),则函数y ＝f (4－x )的图象一定经过点________．6. (2019·荆州三模)已知偶函数f (x )和奇函数g (x )的图象如图所示,若关于x 的方程f (g (x ))＝1,g (f (x ))＝2的实根个数分别为m ,n ,则m ＋n ＝________．(第6题)7. 已知函数f (x )＝log a x (a ＞0且a ≠1)和函数g (x )＝sin π2 x ,若f (x )与g (x )的图象有且只有3个交点,则a 的取值范围是________．8. 已知函数f (x )对于任意实数x ∈[a ,b ],当a ≤x 0≤b 时,记|f (x )－f (x 0)|的最大值为D [a ,b ](x 0). (1) 若f (x )＝(x －1)2,则D [0,3](2)＝________；(2) 若f (x )＝⎩⎪⎨⎪⎧－x 2－2x ，x ≤0，2－|x －1|，x >0， 则D [a ,a ＋2](－1)的取值范围是________．第13讲 函数与方程A 组 应知应会一、 选择题1. 若函数f (x )＝2x －2x －a 的一个零点在区间(1,2)内,则实数a 的取值范围是( )A. (1,3)B. (1,2)C. (0,3)D. (0,2)2. 已知函数f (x )＝⎩⎪⎨⎪⎧2x －1，x ≤1，1＋log 2x ，x >1， 则函数f (x )的零点为( )A. 12 ,0B. －2,0C. 12D. 0 3. 已知函数f (x )＝2x ＋x ＋1,g (x )＝log 2x ＋x ＋1,h (x )＝log 2x －1的零点依次为a ,b ,c ,则( )A. a <b <cB. a <c <bC. b <c <aD. b <a <c4. 已知函数y ＝f (x )的周期为2,当x ∈[－1,1]时f (x )＝x 2,那么函数y ＝f (x )的图象与函数y ＝|lg x |的图象的交点共有( )A. 10个B. 9个C. 8个D. 1个 5. (2019·九江模拟)已知函数f (x )＝a ＋log 2(x 2＋a )(a ＞0)的最小值为8,则实数a 的取值范围是( )A. (5,6)B. (7,8)C. (8,9)D. (9,10) 二、 解答题6. 若关于x 的方程3x 2－5x ＋a ＝0的一个根在(－2,0)内,另一个根在(1,3)内,求a 的取值范围．7. 已知函数f (x )＝x 2＋ax ＋2,a ∈R ．(1) 若不等式f (x )≤0的解集为[1,2],求不等式f (x )≥1－x 2 的解集；(2) 若函数g (x )＝f (x )＋x 2＋1在区间(1,2)上有两个不同的零点,求实数a 的取值范围．B 组 能力提升一、 填空题1. 方程log 2(x －1)＝2－log 2(x ＋1)的解集为________．2. 设f (x )是定义在R 上的偶函数,满足f (x )＝f (2－x ),当0≤x ≤1时,f (x )＝－x 2＋1,方程f (x )＝⎝⎛⎭⎫12 |x |在区间[－5,5]内实根的个数为________．3. 在平面直角坐标系xOy 中,若直线y ＝2a 与函数y ＝|x －a |－1的图象只有一个交点,则a 的值为________．4. 设函数f (x )＝⎩⎪⎨⎪⎧3x －a ，x <1，π（x －3a ）（x －2a ），x ≥1， 若f (x )恰有2个零点,则实数a 的取值范围是________．二、 解答题5. 已知y ＝f (x )是定义域为R 的奇函数,当x ∈[0,＋∞)时,f (x )＝x 2－2x . (1) 求函数y ＝f (x )的解析式；(2) 若方程f (x )＝a 恰有3个不同的解,求a 的取值范围．6. (2019·全国卷Ⅰ)已知函数f (x )＝2sin x －x cos x －x ,f ′(x )为f (x )的导数． (1) 求证：f ′(x )在区间(0,π)上存在唯一零点； (2) 若x ∈[0,π]时,f (x )≥ax ,求a 的取值范围．第14讲数学建模——函数的模型及其应用A组应知应会一、选择题1. 国家规定个人稿费纳税办法为：不超过800元的不纳税；超过800元而不超过4 000元的按超过部分的14%纳税；超过4 000元的按全稿酬的11%纳税．若某人共纳税420元,则这个人的稿费为()A. 3 000元B. 3 800元C. 3 818元D. 5 600元2. 某公司为激励创新,计划逐年加大研发资金投入．若该公司2017年全年投入研发资金130万元,在此基础上,每年投入的研发资金比上一年增长12%,则该公司全年投入的研发资金开始超过200万元的年份是(参考数据：lg 1.12≈0.05,lg 1.3≈0.11,lg 2≈0.30)()A. 2020年B. 2021年C. 2022年D. 2023年3. (2019·三明联考)用清水洗衣服,若每次能洗去污垢的34,要使存留的污垢不超过1%,则至少要洗的次数是(参考数据：lg 2≈0.3 010)()A. 3B. 4C. 5D. 64. (2019·安庆二模)设甲、乙两地的距离为a(a＞0),小王骑自行车以匀速从甲地到乙地用了20 min,在乙地休息10 min后,他又以匀速从乙地返回到甲地用了30 min,则小王从出发到返回原地所经过的路程y和其所用的时间x的函数图象为()A BC D5. (多选)汽车的“燃油效率”是指汽车每消耗1 L汽油行驶的里程．如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况,则下列叙述不正确的是()(第5题)A. 消耗1 L汽油,乙车最多可行驶5 kmB. 以相同速度行驶相同路程,三辆车中,甲车消耗汽油最少C. 甲车以80 km/h的速度行驶1 h,消耗10 L汽油D. 某城市机动车最高限速80 km/h,相同条件下,在该市用丙车比用乙车更省油二、解答题6. 网店销售某一品牌的商品,购买人数n是商品标价x的一次函数,标价越高,购买人数越少．已知标价为每件300元时,购买人数为零；标价为每件225元时,购买人数为75人．若这种商品的成本价是100元/件,网店以高于成本价的相同价格(标价)出售．(1) 网店要获取最大利润,商品的标价应定为每件多少元？(2) 通常情况下,获取最大利润只是一种“理想结果”,如果网店要获得最大利润的75%,那么商品的标价为每件多少元？7. 某商场销售某种商品的经验表明,该商品每日的销售量y(单位：kg)与销售价格x(单位：元/kg)满足关系式y＝ax－3＋10(x－6)2,其中3<x<6,a为常数．已知销售价格为5元/kg时,每日可售出该商品11 kg.(1) 求a的值；(2) 若该商品的成本为3元/kg,试确定销售价格x的值,使商场每日销售该商品所获得的利润最大．B组能力提升一、填空题1. (2019·唐山联考)“好酒也怕巷子深”,许多著名品牌是通过广告宣传进入消费者视线的．已知某品牌商品靠广告销售的收入R与广告费A之间满足关系R＝a A (a为常数),广告效应为D＝a A －A.那么精明的商人为了取得最大广告效应,投入的广告费应为________．(用常数a表示)2. (2019·湖北八校联考)某人根据经验绘制了2019年春节前后,从12月21日至1月8日自己种植的西红柿的销售量y(kg)随时间x(天)变化的函数图象,如图所示,则此人在12月26日大约卖出了西红柿________kg.(第2题）3. 某公司一年购买某种货物600 t,每次购买x t,运费为6万元/次, 一年的总存储费用为4x万元．要使一年的总运费与总存储费用之和最小,则x的值是________．4. 根据相关规定,机动车驾驶员血液中的酒精含量大于(等于)20毫克/100毫升时属于醉酒驾车．假设饮酒后,血液中的酒精含量为p0毫克/100毫升,经过x h,酒精含量降为p毫克/100毫升,且满足关系式p＝p0·e rx(r为常数).若某人饮酒后血液中的酒精含量为89毫克/100毫升,2 h后,测得其血液中酒精含量降为61毫克/100毫升,则此人饮酒后需经过________h方可驾车．(精确到h)二、解答题5. 某创业团队拟生产A、B两种产品,根据市场预测,A产品的利润与投资额成正比(如图(1)),B产品的利润与投资额的算术平方根成正比(如图(2)).(注：利润与投资额的单位均为万元)(1) 分别将A、B两种产品的利润f(x)、g(x)表示为投资额x的函数；(2) 该团队已筹集到10万元资金,并打算全部投入A、B两种产品的生产,问：当B产品的投资额为多少万元时,生产A、B两种产品能获得最大利润？最大利润为多少？图(1)图(2)(第5题)6. 某快递公司在某市的货物转运中心,拟引进智能机器人分拣系统,以提高分拣效率和降低物流成本,已知购买x 台机器人的总成本p (x )＝1600x 2＋x ＋150(万元). (1) 若使每台机器人的平均成本最低,则应买多少台？(2) 现按(1)中的数量购买机器人,需要安排m 人将邮件放在机器人上,机器人将邮件送达指定落袋格口完成分拣(如图),经实验知,每台机器人的日平均分拣量q (m )＝⎩⎪⎨⎪⎧815m （60－m ），1≤m ≤30，480，m ＞30(单位：件),已知传统人工分拣每人每日的平均分拣量为1 200件,问：引进机器人后,日平均分拣量达最大值时,用人数量比引进机器人前的用人数量最多可减少百分之多少？(第6题)微难点2 分段函数的研究一、 选择题1. (2019·湖北四地联考)已知函数f (x )＝⎩⎪⎨⎪⎧⎝⎛⎭⎫12x－7，x <0，log 2（x ＋1），x ≥0， 若f (a )<1,则实数a 的取值范围是( )A. (－∞,－3)∪[0,1)B. (－3,0)∪(－1,1)C. (－3,1)D. (1,＋∞)2. (2019·开封一模)已知函数f (x )＝⎩⎪⎨⎪⎧e x －1，x <2，log 3（x 2－1），x ≥2， 若f (a )≥1,则a 的取值范围是( )A. [1,2)B. [1,＋∞)C. [2,＋∞)D. (－∞,－2]3. (2019·廊坊三模)若函数f (x )＝⎩⎪⎨⎪⎧e 2x －2x ＋a ，x >0，ax ＋3a －2，x ≤0 在(－∞,＋∞)上是单调函数,且f (x )存在负的零点,则a 的取值范围是( )A. ⎝⎛⎭⎫23，1B. ⎝⎛⎦⎤23，32C. ⎝⎛⎦⎤0，32D. ⎝⎛⎭⎫23，＋∞4. 已知函数f (x )＝⎩⎪⎨⎪⎧|log 3x |，0<x <3，13x 2－103x ＋8，x ≥3， 若存在实数a ,b ,c ,d ,满足f (a )＝f (b )＝f (c )＝f (d ),其中d ＞c ＞b ＞a ＞0,则abcd 的取值范围是( )A. (21,25)B. (21,24)C. (20,24)D. (20,25)5. (2019·驻马店期末)已知函数f (x )＝⎩⎪⎨⎪⎧2x 3＋3x 2＋2，x ≤0，e ax x >0 在[－2,2]上的最大值为3,则实数a 的取值范围是( )A. (ln 3,＋∞)B. ⎣⎡⎦⎤0，12ln 3C. ⎝⎛⎦⎤－∞，12ln 3 D. (－∞,ln 3]二、 填空题6. (2019·佛山二模)若函数f (x )＝⎩⎪⎨⎪⎧e x ，x ≥0，－x 2＋2x ＋1，x <0 (其中e 是自然对数的底数),且函数y＝|f (x )|－mx 有两个不同的零点,则实数m 的取值范围是________．7. 设f (x )＝⎩⎪⎨⎪⎧（1－2a ）x，x ≤1，log a x ＋13，x >1. 若存在x 1,x 2∈R,x 1≠x 2,使得f (x 1)＝f (x 2)成立,则实数a 的取值范围是________．8. (2019·滨州期末)已知函数f (x )＝⎩⎪⎨⎪⎧|x ＋1|，x ≤0，|log 2x |，x >0.若方程f (x )＝a 恰有4个不同的实根x 1,x 2,x 3,x 4,且x 1<x 2<x 3<x 4,则x 3(x 1＋x 2)＋1x 23 x 4的取值范围为________．微难点3 由函数的性质求参数范围一、 填空题1. 已知函数f (x )＝⎩⎪⎨⎪⎧－x 2，x ≥0，x 2，x <0， 若f (a －1)＋f (a )＞0,则实数a 的取值范围是________．2. 若f (x )＝－x 2＋2ax 与g (x )＝ax ＋1在区间[1,2]上都是减函数,则a 的取值范围是________．3. 已知函数f (x )＝⎩⎪⎨⎪⎧x 2－mx ，x >1，⎝⎛⎭⎫4－m 2x ＋2，x ≤1 是R 上的增函数,则实数m 的取值范围是________．4. 若函数f (x )＝ax 2＋x ＋a ＋1在(－2,＋∞)上单调递增,则a 的取值范围是________．5. 已知f (x )＝log a (8－3ax )在[－1,2]上是减函数,则实数a 的取值范围是________．6. 已知函数f (x )＝ax ＋1x ＋2 在区间(－2,＋∞)上为增函数,则实数a 的取值范围是________．7. 已知函数f (x )＝⎩⎪⎨⎪⎧x 2＋2x ，x ≥0，－x 2＋2x ，x <0， 若f (2－a 2)<f (a ),则实数a 的取值范围是________．二、解答题8. 设定义在[－2,2]上的函数f(x)在区间[0,2]上单调递减,且f(1－m)＜f(3m).(1) 若函数f(x)在区间[－2,2]上是奇函数,求实数m的取值范围；(2) 若函数f(x)在区间[－2,2]上是偶函数,求实数m的取值范围．。

第三章 导数及其应用第15讲 导数的几何意义和四则运算A 应知应会一、 选择题1. 已知f (x )＝x (2 018＋ln x ),若f ′(x 0)＝2 019,则x 0等于( )A. e 2B. 1C. ln 2D. e2. 若函数f (x )＝33x 3＋ln x －x ,则曲线y ＝f (x )在点(1,f (1))处的切线的倾斜角是( ) A. π6 B. π3 C. 2π3 D. 5π63. 已知函数f (x )＝ln (x ＋1)·cos x －ax 在(0,f (0))处的切线倾斜角为45°,则a 等于( )A. －2B. －1C. 0D. 34. (2019·泰安一模)已知函数f (x )满足f ⎝⎛⎭⎫x 2 ＝x 3－3x ,则函数f (x )的图象在x ＝1处的切线斜率为( )A. 0B. 9C. 18D. 275. 已知曲线y ＝sin x 在点P (x 0,sin x 0)(0≤x 0≤π)处的切线为l ,则下列各点中不可能在直线l 上的是( )A. (－1,－1)B. (－2,0)C. (1,－2)D. (4,1)二、 解答题6. 求下列函数的导数．(1) y ＝5x 3 ； (2) y ＝1x4 ； (3) y ＝－2sin x 2 ⎝⎛⎭⎫1－2cos 2x 4 ； (4)y ＝log 2x 2－log 2x .7. 已知曲线y ＝x 3＋x －2在点P 0处的切线l 1平行于直线4x －y －1＝0,且点P 0在第三象限．(1) 求P 0的坐标；(2) 若直线l ⊥l 1,且l 也过切点P 0,求直线l 的方程．B 巩固提升一、 填空题1. (2019·全国卷Ⅰ)曲线y ＝3(x 2＋x )e x 在点(0,0)处的切线方程为________．2. 已知函数f (x )满足满足f (x )＝f ′(1)e x －1－f (0)x ＋12x 2,则f (x )的解析式为________________.3. (2019·江苏卷)在平面直角坐标系xOy 中,点A 在曲线y ＝ln x 上,且该曲线在点A 处的切线经过点(－e,－1)(e 为自然对数的底数),则点A 的坐标是________．4. (2019·厦门一模)在平面直角坐标系xOy 中,已知x 21 －ln x 1－y 1＝0,x 2－y 2－2＝0,则(x 1－x 2)2＋(y 1－y 2)2的最小值为________．二、 解答题5. 已知曲线y ＝(ax －1)e x 在点A (x 0,y 1)处的切线为l 1,曲线y ＝1－x e x 在点B (x 0,y 2)处的切线为l 2.若存在x 0∈⎣⎡⎦⎤0，32 ,使得l 1⊥l 2,求实数a 的取值范围．6. 已知函数f (x )＝ax 3＋3x 2－6ax －11,g (x )＝3x 2＋6x ＋12和直线m ：y ＝kx ＋9,且f ′(－1)＝0.(1) 求a 的值；(2) 是否存在k ,使直线m 既是曲线y ＝f (x )的切线,又是曲线y ＝g (x )的切线？如果存在,求出k 的值；如果不存在,请说明理由．第16讲 导数与函数的单调性A 应知应会一、 选择题1. (2019·福建四校二联)函数f (x )＝(x 2－2x )e x 的图象大致是( )A BC D2. 若函数y ＝f (x )的导函数f ′(x )的图象如图所示,则下列判断中正确的是 ( )(第2题)A. 在区间(－3,1)内f (x )是增函数B. 在区间(1,3)内f (x )是增函数C. 在区间(5,6)内f (x )是增函数D. 在区间(－∞,1)内f (x )是增函数3. (2019·宣城二调)若函数f (x )＝43x 3－2ax 2－(a －2)x ＋5恰好有三个单调区间,则实数a 的取值范围为( )A. [－1,2]B. [－2,1]C. (－∞,－1)∪(2,＋∞)D. (－∞,－2)∪(1,＋∞)4. 若函数f (x )＝e x (－x 2＋2x ＋a )在区间[a ,a ＋1]上单调递增,则实数a 的最大值为( )A. －1＋52B. 1＋52C. 1－52D. －1－525. (多选)已知函数f (x )＝e x －1,对于满足0<x 1<x 2<e 的任意x 1,x 2,下列结论中正确的是( )A. (x 2－x 1)[f (x 2)－f (x 1)]<0B. x 2f (x 1)＞x 1f (x 2)C. f (x 2)－f (x 1)＞x 2－x 1D. f （x 1）＋f （x 2）2 ＞f ⎝⎛⎭⎫x 1＋x 22二、 解答题 6. (2019·太原一模节选)已知函数f (x )＝x 3－32 ax 2(a ＞0),若函数h (x )＝f （x ）·e x x 在(0,1)上单调递减,求a 的取值范围．7. (2019·南昌一模)已知函数f (x )＝(x ＋a )e x (x ＞－3),其中a ∈R ．(1) 若曲线y ＝f (x )在点A (0,a )处的切线l 与直线y ＝|2a －2|x 平行,求直线l 的方程；(2) 讨论函数y ＝f (x )的单调性．B 巩固提升一、 填空题1. (2019·泰州一模)已知函数f (x )＝2x 4＋4x 2,若f (a ＋3)＞f (a －1),则实数a 的取值范围为________．2. 已知函数f (x )的定义域为R,f (0)＝2,对任意x ∈R,都有f (x )＋f ′(x )＞1,则不等式e x ·f (x )＞e x ＋1的解集为________．3. 已知函数f (x )＝－12x 2＋4x －3ln x 在区间[t ,t ＋1]上不单调,则t 的取值范围是________．4. (2019·盐城期中)已知函数f (x )＝(x －a )ln x (a ∈R),若函数f (x )存在三个单调区间,则实数a 的取值范围是________．二、 解答题5. 已知函数f (x )＝x e x －a ⎝⎛⎭⎫x 22＋x (a ∈R),讨论函数f (x )的单调性．6. 已知函数f (x )＝e x ln x －a e x (a ∈R).(1) 若f (x )在点(1,f (1))处的切线与直线y ＝1ex ＋1垂直,求a 的值； (2) 若f (x )在(0,＋∞)上是单调函数,求实数a 的取值范围．第17讲 导数与函数的极值、最值A 应知应会一、 选择题1. 函数f (x )＝x 3＋3x 2＋3x －a 的极值点的个数为( )A. 0B. 1C. 2D. 32. (2019·安庆二模)已知函数f (x )＝2e f ′(e)ln x －x e(e 是自然对数的底数),则f (x )的极大值为( )A. 2e －1B. －1eC. 1D. 2ln 2 3. 若函数f (x )＝x 3－3x 在(a ,6－a 2)上有最小值,则实数a 的取值范围是( )A. (－5 ,1)B. [－5 ,1)C. [－2,1)D. (－2,1)4. 设直线x ＝t 与函数f (x )＝x 2,g (x )＝ln x 的图象分别交于点M ,N ,则当|MN |达到最小时t 的值是( )A. 1B. 12C. 52D. 225. (多选)设函数f (x )＝ax 22e－ln |ax |(a ＞0),若f (x )有4个零点,则a 的可能取值个数为( ) A. 1 B. 2 C. 3 D. 4二、 解答题6. 已知函数f (x )＝e x cos x －x .(1) 求曲线y ＝f (x )在点(0,f (0))处的切线方程；(2) 求函数f (x )在区间⎣⎡⎦⎤0，π2 上的最大值和最小值．7. (2019·邵阳期末)已知a ∈R,函数f (x )＝a x＋ln x －1. (1) 当a ＝1时,求曲线y ＝f (x )在点(2,f (2))处的切线方程；(2) 求f (x )在区间(0,e]上的最小值．B 巩固提升一、 填空题1. 若函数f (x )＝12x 2f ′(2)＋ln x ,则f (x )的极大值点为________,极大值为________． 2. 已知函数f (x )＝13x 3＋x 2－2ax ＋1,若函数f (x )在(1,2)上有极值,则实数a 的取值范围为________．3. (2019·滁州期末)已知函数f (x )＝⎩⎪⎨⎪⎧2x 3－3x 2＋1，x ≥0，e ax ＋1，x <0 在[－2,2]上的最大值为5,则实数a 的取值范围是________．4. (2019·唐山一模)在△ABC 中,a ,b ,c 分别为A ,B ,C 所对的边,若函数f (x )＝13x 3＋bx 2＋(a 2＋c 2－ac )x ＋1有极值点,则sin ⎝⎛⎭⎫2B －π3 的最小值为________． 二、 解答题5. (2019·全国卷Ⅲ)已知函数f (x )＝2x 3－ax 2＋2.(1) 讨论f (x )的单调性；(2) 当0<a <3时,记f (x )在区间[0,1]的最大值为M ,最小值为m ,求M －m 的取值范围．6. 解答一个问题后,将结论作为条件之一,提出与原问题有关的新问题,我们把它称为原问题的一个“逆向问题”．例如：原问题是“若矩形的边长为3和4,则其周长为14”,它的一个“逆向问题”是：“若矩形的周长为14,一边长为3,求另一边长”,也可以是“若矩形的周长为14,求其面积的最大值”等等．已知函数f (x )＝⎩⎪⎨⎪⎧－x 3＋x 2，x <1，a ln x ，x ≥1. (1) 求f (x )在[－1,e](e 为自然对数的底数)上的最大值； (2) 请对(1)提出两个“逆向问题”,并作解答．第18讲生活中的优化问题举例A应知应会一、解答题1. 某连锁分店销售某种商品,每件商品的成本为4元,并且每件商品需向总店交a(1≤a≤3)元的管理费,预计当每件商品的售价为x(8≤x≤9)元时,一年的销售量为(10－x)2万件．(1) 求该连锁分店一年的利润L(万元)与每件商品的售价x的函数关系式L(x)；(2) 当每件商品的售价为多少元时,该连锁分店一年的利润L最大？并求出L的最大值．2. 如图所示是一个帐篷,它下部分的形状是一个正六棱柱,上部分的形状是一个正六棱锥,其中帐篷的高为PO,正六棱锥的高为PO1,且PO＝3PO1.设PO1＝x.(1) 当x＝2 m,P A1＝4 m时,求搭建的帐篷的表面积；(2) 在P A1的长为定值l m的条件下,已知当且仅当x＝23m时,帐篷的容积V最大,求l的值．(第2题)B 巩固提升一、 解答题1. (2019·徐州期中)如图所示是一个半径为2 km,圆心角为π3的扇形游览区的平面示意图,点C 是半径OB 上一点,点D 是圆弧AB 上一点,且CD ∥OA .现在线段OC 、线段CD 及圆弧DB 三段所示位置设立广告位,经测算广告位出租收入是：线段OC 处每千米为2a 元,线段CD 及圆弧DB 处每千米均为a 元．设∠AOD ＝x 弧度,广告位出租的总收入为y 元．(1) 求y 关于x 的函数解析式,并指出该函数的定义域；(2) 试问x 为何值时,广告位出租的总收入最大？并求出其最大值．(第1题)2. (2019·盐城期中)某厂生产一种仪器,由于受生产能力和技术水平的限制,会产生一些次品．根据以往的经验知道,该厂生产这种仪器次品率P 与日产量x (件)之间近似满足关系：P ＝⎩⎨⎧196－x ，1≤x ≤c ，x ∈N ，1≤c <96，23，x >c ，x ∈N (注：次品率P ＝次品数总生产量,如P ＝0.1表示每生产10件产品,约有1件为次品,其余为合格品).已知每生产一件合格的仪器可以盈利A 元,但每生产一件次品将亏损A 2元,故厂方希望定出合适的日产量． (1) 试将生产这种仪器每天的盈利额T (元)表示为日产量x (件)的函数；(2) 当日产量x 为多少时,可获得最大利润？微难点4 构造函数研究不等关系一、 选择题1. 当x ∈[－2,1]时,不等式ax 3－x 2＋4x ＋3≥0恒成立,则实数a 的取值范围是( )A. [－5,－3]B. ⎣⎡⎦⎤－6，－98 C. [－6,－2] D. [－4,－3] 2. (2019·上饶一模)已知函数f (x )＝ln x ＋a 的导数为f ′(x ),若方程f ′(x )＝f (x )的根x 0小于1,则实数a 的取值范围为( )A. (1,＋∞)B. (0,1)C. (1,2 )D. (1,3 )3. 已知函数f (x )＝x ＋1x 2 ,g (x )＝log 2x ＋m ,若对x 1∈[1,2],x 2∈[1,4],使得f (x 1)≥g (x 2),则m 的取值范围是( )A. ⎝⎛⎦⎤－∞，－54B. (－∞,2]C. ⎝⎛⎦⎤－∞，34 D. (－∞,0] 二、 填空题4. 设函数f (x )在R 上存在导数f ′(x ),对任意的x ∈R,有f (－x )＋f (x )＝x 2,当x ∈(0, ＋∞)时,f ′(x )＜x .若f (4－m )－f (m )≥8－4m ,则实数m 的取值范围为________．5. 已知f (x )是定义在R 上的偶函数,其导函数为f ′(x ),若f ′(x )＜f (x ),且f (x ＋1)＝f (3－x ),f (2 019)＝2,则不等式f (x )＜2e x －1的解集为________．6. 若定义在R 上的函数f (x )满足f (x )＋f ′(x )＞1,f (0)＝4,则不等式e x f (x )＞e x ＋3(其中e 为自然对数的底数)的解集为________．三、 解答题7. 已知函数f (x )＝(x 2－3x ＋3)e x ,若不等式f （x ）ex ＋7x －2＞k (x ln x －1)(k 为正整数)对任意正实数x 恒成立,求k 的最大值．(参考数据：ln 7≈1.95,ln 8≈2.08)8. 已知函数f (x )＝ln x －ax 3,g (x )＝a e xe. (1) 若直线y ＝x 与y ＝g (x )的图象相切,求实数a 的值；(2) 若存在x 0∈[1,e],使得f (x 0)＞(1－3a )x 0＋1成立,求实数a 的取值范围．微难点5 利用导数研究函数的零点一、 解答题1. 已知函数f (x )＝2e x ＋ax .(1) 求f (x )的单调区间；(2) 讨论f (x )在(0,＋∞)上的零点个数．2. (2019·抚州调研)已知函数f (x )＝a 6 x 3－a 4x 2－ax －2的图象过点A ⎝⎛⎭⎫4，103 . (1) 求函数f (x )的单调增区间；(2) 若函数g (x )＝f (x )－2m ＋3有3个零点,求m 的取值范围．3. 已知函数f (x )＝ln x ,g (x )＝3x －2a 2x. (1) 求函数F (x )＝f (x )－x ＋2在x ∈[4,＋∞)上的最大值；(2) 若函数H (x )＝2f (x )－ln [g (x )]在区间⎣⎡⎦⎤12，1 上有零点,求实数a 的取值范围．4. 已知函数f (x )＝(2－a )(x －1)－2ln x (a ∈R,e 为自然对数的底数).(1) 当a ＝1时,求f (x )的单调区间；(2) 若函数f (x )在⎝⎛⎭⎫0，12 上无零点,求a 的最小值．。

[高2021届高2018级高三数学一轮专题训练64]第三讲 二项式定理A 组基础巩固一、单选题1.(2020·郑州模拟)(x －1x )9的展开式中的常数项为( D )A.64B.－64C.84D.－84【试题解答】 (x －1x )9的展开式的通项公式为T r ＋1＝C r 9·(x )9－r ·(－1x )r ＝(－1)r ·C r 9·x 9－3r 2，由9－3r 2＝0，得r ＝3，∴(x －1x)9的展开式中的常数项为T 4＝(－1)3×C 39＝－84.故选D. 2.(2020·河北保定期末)(3x －1x)6的展开式中，有理项共有( D ) A.1项 B.2项 C.3项D.4项【试题解答】 (3x －1x)6的展开式的通项公式为T r ＋1＝C r 6·(－1)r ·36－r ·x 6－32r ，令6－32r 为整数，求得r ＝0,2,4,6，共计4项.3.(2019·甘肃张掖诊断)已知(1＋x )n 的展开式中第4项与第8项的二项式系数相等，则奇数项的二项式系数和为( D )A.212B.211C.210D.29【试题解答】 已知(1＋x )n 的展开式中第4项与第8项的二项式系数相等，可得C 3n ＝C 7n，可得n ＝3＋7＝10.(1＋x )10的展开式中奇数项的二项式系数和为：12×210＝29.故选D.4.(2020·广州调研)(x －12x )9的展开式中x 3的系数为( A )A.－212B.－92C.92D.212【试题解答】 二项展开式的通项T r ＋1＝C r 9x 9－r (－12x )r ＝(－12)r C r 9x 9－2r ，令9－2r ＝3，得r ＝3，展开式中x 3的系数为(－12)3C 39＝－212.故选A. 5.(2019·烟台模拟)已知(x 3＋2x )n 的展开式的各项系数和为243，则展开式中x 7的系数为( B )A.5B.40C.20D.10【试题解答】 由(x 3＋2x )n 的展开式的各项系数和为243，令x ＝1得3n ＝243，即n ＝5，∴(x 3＋2x )n ＝(x 3＋2x )5，则T r ＋1＝C r 5·(x 3)5－r ·(2x )r ＝2r ·C r 5·x 15－4r ，令15－4r ＝7，得r ＝2，∴展开式中x 7的系数为22×C 25＝40.6.(ax ＋1x )(2x －1)5的展开式中各项系数的和为2，则该展开式中常数项为( C )A.－20B.－10C.10D.20【试题解答】 令x ＝1，可得a ＋1＝2，所以a ＝1，所以(ax ＋1x )(2x －1)5＝(x ＋1x)(2x －1)5，则展开式中常数项为(2x －1)5展开式中x 项的系数，即2C 45(－1)4＝10.7.(2019·内蒙古包头模拟)已知(2x －1)5＝a 5x 5＋a 4x 4＋a 3x 3＋a 2x 2＋a 1x ＋a 0，则|a 0|＋|a 1|＋…＋|a 5|＝( B )A.1B.243C.121D.122【试题解答】 令x ＝1，得a 5＋a 4＋a 3＋a 2＋a 1＋a 0＝1，① 令x ＝－1，得－a 5＋a 4－a 3＋a 2－a 1＋a 0＝－243，② ①＋②，得2(a 4＋a 2＋a 0)＝－242， 即a 4＋a 2＋a 0＝－121.①－②，得2(a 5＋a 3＋a 1)＝244， 即a 5＋a 3＋a 1＝122.所以|a 0|＋|a 1|＋…＋|a 5|＝122＋121＝243.故选B.8.(2019·广州测试)使(3x ＋1x x )n(n ∈N ＋)的展开式中含有常数项的最小的n 为( B )A.4B.5C.6D.7【试题解答】 T r ＋1＝C r n (3x )n －r·x －32r ＝C r n ·3n －r ·xn －5r 2(r ＝0,1,2，…，n )，若T r ＋1是常数项，则有n －52r ＝0，即2n ＝5r (r ＝0,1，…，n )，当r ＝0,1时，n ＝0，52，不满足条件：当r ＝2时，n ＝5，故选B.9.(2020·四川省联合诊断)(1－x 3)(1－x )9的展开式中x 4的系数为( B ) A.124 B.135 C.615D.625【试题解答】 (1－x )9的展开式的通项公式为T r ＋1＝C r 9(－x )r ，故所求x 4项的系数为C 49－(－1)C 19＝135.故选B.二、多选题10.若(1x －x x )n 展开式中含有x 2项，则n 的值可以是( BD )A.15B.8C.7D.3【试题解答】 注意到二项式(1x －x x )n 的展开式的通项是T r ＋1＝C r n ·(1x )n －r ·(－x x )r ＝C r n ·(－1)r ·x 52r －n .令52r －n ＝2，即r ＝2(n ＋2)5有正整数解；又2与5互质，因此n ＋2必是5的倍数，即n ＋2＝5k ，n ＝5k －2，故选BD.11.已知(x ＋1)10＝a 1＋a 2x ＋a 3x 2＋…＋a 11x 10.若数列a 1，a 2，a 3，…，a k (1≤k ≤11，k ∈Z )是一个单调递增数列，则k 的值可以是( ABC )A.4B.5C.6D.7【试题解答】 由二项式定理知a n ＝C n －110(n ＝1,2,3，…，n ).又(x ＋1)10展开式中二项式系数最大项是第6项.∴a 6＝C 510，则k 的最大值为6.故选ABC.三、填空题12.(2018·天津高考)在(x －12x )5的展开式中，x 2的系数为 52 .【试题解答】 (x －12x)5的展开式的通项为T r ＋1＝C r 5x5－r (－12x)r ＝(－12)r C r 5x 5－3r2. 令5－3r2＝2，可得r ＝2.所以(x －12x)5的展开式中的x 2的系数为(－12)2C 25＝52. 13.(2020·河南八校重点高中联盟联考)已知(2x －1)(x ＋a )6的展开式中x 5的系数为24，则a ＝ 1或－45. 【试题解答】 根据题意，(x ＋a )6的展开式的通项为T r ＋1＝C r 6x 6－r a r ，其中当r ＝1时，有T 2＝C 16x 5a ，当r ＝2时，有T 3＝C 26x 4a 2，则(2x －1)(x ＋a )6的展开式中x 5的系数为－C 16a ＋2C 26a 2＝－6a ＋30a 2，则有－6a＋30a 2＝24，可得5a 2－a －4＝0，∴(a －1)(5a ＋4)＝0，∴a ＝1或a ＝－45.14.(2020·广东省东莞市期末)若(3＋ax )(1＋x )4展开式中x 的系数为13，则展开式中各项系数和为__64__.(用数字作答)【试题解答】 由题意得3C 14＋a ＝13，∴a ＝1.令x ＝1得(3＋ax )(1＋x )4的展开式中各项系数和为(3＋1)(1＋1)4＝64.15.(2019·陕西西安模拟)已知(1＋x )10＝a 0＋a 1(1－x )＋a 2(1－x )2＋…＋a 10(1－x )10，则a 8＝__180__. 【试题解答】 令1－x ＝t ，则x ＝1－t ， ∴(2－t )10＝a 0＋a 1t ＋a 2t 2＋…＋a 10t 10，由T r ＋1＝C r 10210－r (－t )r 知r ＝8时， a 8＝22C 810(－1)8＝180.B 组能力提升1.(2019·浙江，13)在二项式(2＋x )9的展开式中，常数项是 162 ，系数为有理数的项的个数是__5__.【试题解答】 (2＋x )9展开式的通项T r ＋1＝C r 9(2)9－r x r＝C r 9·29－r 2·x r(r ＝0,1,2，…，9)，令r ＝0，得常数项T 1＝C 09·292·x 0＝292＝162，要使系数为有理数，则只需9－r 2∈Z ，则r 必为奇数，满足条件的r 有1,3,5,7,9，共五种，故系数为有理数的项的个数是5.2.(2020·广西柳州铁路一中、玉林一中联考)(2－x )·(1＋2x )5展开式中，含x 2项的系数为__70__. 【试题解答】 (1＋2x )5展开式的通项公式为：T k ＋1＝C k 5(2x )k ＝2k·C k 5·x k ， 故所求x 2项的系数为2×22C 25－2C 15＝70.3.(2019·上海普陀区二模)502 019＋1被7除后的余数为__2__.【试题解答】 502 019＋1＝(1＋72)2019＋1＝1＋C 12 019·72＋C 22 019·74＋…＋C 2 0192 01974 038＋1＝72C 12 019＋C 22 01974＋…＋C 2 0192 01974 038＋2.故余数为2. 4.(2019·吉林实验中学月考)若(2x －3)5＝a 0＋a 1x ＋a 2x 2＋a 3x 3＋a 4x 4＋a 5x 5，则a 1＋2a 2＋3a 3＋4a 4＋5a 5＝__10__.【试题解答】 等式两边求导得10(2x －3)4＝a 1＋2a 2x ＋3a 3x 2＋4a 4x 3＋5a 5x 4， 令x ＝1得a 1＋2a 2＋3a 3＋4a 4＋5a 5＝10(2－3)4＝10. 5.(2020·广东茂名联考)在(x ＋x )6(1＋1y )6的展开式中，x 4y2项的系数为( C ) A.200 B.180 C.150D.120【试题解答】 (x ＋x )6展开式的通项公式为T r ＋1＝C r 6(x )6－r x r ＝C r 6x 6＋r 2，令6＋r 2＝4，得r ＝2，则T 3＝C 26x 6＋22＝15x 4. (1＋1y )5展开式的通项公式为T r ＋1＝C r 5(1y )r ＝C r 5y －r ，令r ＝2可得T 3＝C 25y －2＝10y －2.故x 4y 2项的系数为15×10＝150.6.(2019·衡水模拟)S ＝C 127＋C 227＋…＋C 2727除以9的余数为( B )A.8B.7C.6D.5【试题解答】 依题意S ＝C 127＋C 227＋…＋C 2727＝227－1＝89－1＝(9－1)9－1＝C 09×99－C 19×98＋…＋C 89×9－C 99－1＝9(C 09×98－C 19×97＋…＋C 89)－2.∵C 09×98－C 19×97＋…＋C 89是正整数，∴S 被9除的余数为7.7.(2020·河北省邢台市期末)(x ＋y －1x －1y )4的展开式中的常数项为( A )A.36B.－36C.48D.－48【试题解答】 ∵(x ＋y －1x －1y )4＝(x ＋y －x ＋y xy )4＝(x ＋y )4(1－1xy )4，∴(x ＋y －1x －1y)4的展开式中的常数项为C 24×C 24＝36.8.(2019·江西重点中学联考)若多项式(2x＋3y)n展开式仅在第5项的二项式系数最大，则多项式(x2＋1x2－4)n－4展开式中x2的系数为(A)A.－304B.304C.－208D.208【试题解答】多项式(2x＋3y)n展开式仅在第5项的二项式系数最大，故n＝8，多项式(x2＋1x2－4)4展开式中x2的系数为C14·(－4)3＋C24·C12·(－4)＝－256－48＝－304，故选A.。

§10.1分类计数原理与分步计数原理1.分类计数原理如果完成一件事,有n类方式,在第1类方式中有m1种不同的方法,在第2类方式中有m2种不同的方法,……,在第n类方式中有m n种不同的方法,那么完成这件事共有N＝m1＋m2＋…＋m n 种不同的方法.2.分步计数原理如果完成一件事,需要分成n个步骤,做第1步有m1种不同的方法,做第2步有m2种不同的方法,……,做第n步有m n种不同的方法,那么完成这件事共有N＝m1×m2×…×m n种不同的方法.3.分类和分步的区别,关键是看事件能否一步完成,事件一步完成了就是分类；必须要连续若干步才能完成的则是分步.分类要用分类计数原理将种数相加；分步要用分步计数原理,将种数相乘.概念方法微思考1.在解题过程中如何判定是用分类计数原理还是分步计数原理？提示如果已知的每类办法中的每一种方法都能完成这件事,应该用分类计数原理；如果每类办法中的每一种方法只能完成事件的一部分,就用分步计数原理.2.两种原理解题策略有哪些？提示①明白要完成的事情是什么；②分清完成该事情是分类完成还是分步完成,“类”间互相独立,“步”间互相联系；③有无特殊条件的限制；④检验是否有重复或遗漏.题组一思考辨析1.判断下列结论是否正确(请在括号中打“√”或“×”)(1)在分类计数原理中,两类不同方案中的方法可以相同.(×)(2)在分类计数原理中,每类方案中的方法都能直接完成这件事.(√)(3)在分步计数原理中,每个步骤中完成这个步骤的方法是各不相同的.(√)(4)在分步计数原理中,事情是分两步完成的,其中任何一个单独的步骤都能完成这件事.(×)题组二教材改编2.已知集合M＝{1,－2,3},N＝{－4,5,6,－7},从M,N这两个集合中各选一个元素分别作为点的横坐标,纵坐标,则这样的坐标在直角坐标系中可表示第一、第二象限内不同的点的个数是()A.12B.8C.6D.4答案 C解析分两步:第一步先确定横坐标,有3种情况,第二步再确定纵坐标,有2种情况,因此第一、二象限内不同点的个数是3×2＝6,故选C.3.(2020·山东模拟)某元宵灯谜竞猜节目,有6名守擂选手和6名复活选手,从复活选手中挑选1名选手为攻擂者,从守擂选手中挑选1名选手为守擂者,则攻擂者、守擂者的不同构成方式共有__________种.答案36解析从6名守擂选手中选1名,选法有C16＝6(种)；复活选手中挑选1名选手,选法有C16＝6(种).由分步计数原理,不同的构成方式共有6×6＝36(种).4.书架的第1层放有4本不同的计算机书,第2层放有3本不同的文艺书,第3层放有2本不同的体育书.从书架中任取1本书,则不同取法的种数为________.答案9解析分三类:第一类,从第1层取一本书有4种,第二类,从第2层取一本书有3种,第三类,从第3层取一本书有2种.共有4＋3＋2＝9(种).题组三易错自纠5.从0,2中选一个数字,从1,3,5中选两个数字,组成无重复数字的三位数,其中奇数的个数为()A.24B.18C.12D.6答案 B解析分两类情况讨论:第1类,奇偶奇,个位有3种选择,十位有2种选择,百位有2种选择,共有3×2×2＝12(个)奇数；第2类,偶奇奇,个位有3种选择,十位有2种选择,百位有1种选择,共有3×2×1＝6(个)奇数.根据分类计数原理知,共有12＋6＝18(个)奇数.6.某人有3个电子邮箱,他要发5封不同的电子邮件,则不同的发送方法有________种.答案243解析因为每个邮件选择发的方式有3种不同的情况.所以要发5个电子邮件,发送的方法有3×3×3×3×3＝35＝243(种).分类计数原理1.满足a,b∈{－1,0,1,2},且关于x的方程ax2＋2x＋b＝0有实数解的有序数对(a,b)的个数为()A.14B.13C.12D.10答案 B解析方程ax2＋2x＋b＝0有实数解的情况应分类讨论.①当a＝0时,方程为一元一次方程2x ＋b＝0,不论b取何值,方程一定有解.此时b的取值有4个,故此时有4个有序数对.②当a≠0时,需要Δ＝4－4ab≥0,即ab≤1.显然有3个有序数对不满足题意,分别为(1,2),(2,1),(2,2).a≠0时,(a,b)共有3×4＝12(个)实数对,故a≠0时满足条件的实数对有12－3＝9(个),所以答案应为4＋9＝13.2.如果一个三位正整数如“a1a2a3”满足a1＜a2,且a2＞a3,则称这样的三位数为凸数(如120,343,275等),那么所有凸数的个数为()A.240B.204C.729D.920答案 A解析若a2＝2,则百位数字只能选1,个位数字可选1或0,“凸数”为120与121,共2个.若a2＝3,则百位数字有两种选择,个位数字有三种选择,则“凸数”有2×3＝6(个).若a2＝4,满足条件的“凸数”有3×4＝12(个),…,若a2＝9,满足条件的“凸数”有8×9＝72(个).所以所有凸数有2＋6＋12＋20＋30＋42＋56＋72＝240(个).3.如果把个位数是1,且恰有3个数字相同的四位数叫做“好数”,那么在由1,2,3,4四个数字组成的有重复数字的四位数中,“好数”共有________个.答案12解析当组成的数字有三个1,三个2,三个3,三个4时共有4种情况.当有三个1时:2111,3111,4111,1211,1311,1411,1121,1131,1141,有9种,当有三个2,3,4时:2221,3331,4441,有3种,根据分类计数原理可知,共有12种结果.思维升华分类标准是运用分类计数原理的难点所在,应抓住题目中的关键词,关键元素,关键位置.(1)根据题目特点恰当选择一个分类标准.(2)分类时应注意完成这件事情的任何一种方法必须属于某一类,并且分别属于不同种类的两种方法是不同的方法,不能重复.(3)分类时除了不能交叉重复外,还不能有遗漏.分步计数原理例1(1)如图,小明从街道的E处出发,先到F处与小红会合,再一起到位于G处的老年公寓参加志愿者活动,则小明到老年公寓可以选择的最短路径条数为()A.24B.18C.12D.9答案 B解析从E点到F点的最短路径有6条,从F点到G点的最短路径有3条,所以从E点到G点的最短路径有6×3＝18(条),故选B.(2)有六名同学报名参加三个智力项目,每项限报一人,且每人至多参加一项,则共有________种不同的报名方法.答案120解析每项限报一人,且每人至多参加一项,因此可由项目选人,第一个项目有6种选法,第二个项目有5种选法,第三个项目有4种选法,根据分步计数原理,可得不同的报名方法共有6×5×4＝120(种).本例(2)中若将条件“每项限报一人,且每人至多参加一项”改为“每人恰好参加一项,每项人数不限”,则有多少种不同的报名方法？解每人都可以从这三个比赛项目中选报一项,各有3种不同的报名方法,根据分步计数原理,可得不同的报名方法共有36＝729(种).本例(2)中若将条件“每项限报一人,且每人至多参加一项”改为“每项限报一人,但每人参加的项目不限”,则有多少种不同的报名方法？解每人参加的项目不限,因此每一个项目都可以从这六人中选出一人参赛,根据分步计数原理,可得不同的报名方法共有63＝216(种).思维升华(1)利用分步计数原理解决问题要按事件发生的过程合理分步,即分步是有先后顺序的,并且分步必须满足:完成一件事的各个步骤是相互依存的,只有各个步骤都完成了,才算完成这件事.(2)分步必须满足两个条件:一是步骤互相独立,互不干扰；二是步与步之间确保连续,逐步完成. 跟踪训练1(1)(2020·洛阳联考)2019年牡丹花会期间,5名志愿者被分配到我市3个博物馆为外地游客提供服务,其中甲博物馆分配1人,另2个博物馆各分配2人,则不同的分配方法共有()A.15种B.30种C.90种D.180种答案 B解析分两步完成:第一步,选1人到甲博物馆,有5种分配方法；第二步,将余下的4人各分配2人到另2个博物馆,有6种分配方法.根据分步计数原理可得,不同的分配方法共有5×6＝30(种).(2)已知a∈{1,2,3},b∈{4,5,6,7},则方程(x－a)2＋(y－b)2＝4可表示不同的圆的个数为()A.7B.9C.12D.16答案 C解析得到圆的方程分两步:第一步:确定a有3种选法；第二步:确定b有4种选法,由分步计数原理知,共有3×4＝12(个).两个计数原理的综合应用例2(1)现有5种不同颜色的染料,要对如图所示的四个不同区域进行涂色,要求有公共边的两个区域不能使用同一种颜色,则不同的涂色方法的种数是()A.120B.140C.240D.260答案 D解析由题意,先涂A处共有5种涂法,再涂B处有4种涂法,然后涂C处,若C处与A处所涂颜色相同,则C处共有1种涂法,D处有4种涂法；若C处与A处所涂颜色不同,到C处有3种涂法,D处有3种涂法,由此可得不同的涂色方法有5×4×(1×4＋3×3)＝260(种).故选D. (2)中国古代儒家要求学生掌握六种基本才能(六艺):礼、乐、射、御、书、数,某校国学社团周末开展“六艺”课程讲座活动,一天连排六节,每艺一节,排课有如下要求:“射”不能排在第一,“数”不能排在最后,则“六艺”讲座不同的排课顺序共有________种.答案504解析 根据题意,分2种情况讨论:①“数”排在第一,将剩下的“五艺”全排列,安排在剩下的5节,有A 55＝120(种)情况.②“数”不排在第一,则“数”的排法有4种,“射”的排法有4种,将剩下的“四艺”全排列,安排在剩下的4节,有A 44＝24(种)情况,则此时有4×4×24＝384(种)情况.则一共有120＋384＝504(种)排课顺序.(3)用0,1,2,3,4,5,6这7个数字可以组成________个无重复数字的四位偶数.(用数字作答) 答案 420解析 要完成的“一件事”为“组成无重复数字的四位偶数”,所以千位数字不能为0,个位数字必须是偶数,且组成的四位数中四个数字不重复,因此应先分类,再分步.①第1类,当千位数字为奇数,即取1,3,5中的任意一个时,个位数字可取0,2,4,6中的任意一个,百位数字不能取与这两个数字重复的数字,十位数字不能取与这三个数字重复的数字. 根据分步计数原理,有3×4×5×4＝240(种)取法.②第2类,当千位数字为偶数,即取2,4,6中的任意一个时,个位数字可以取除首位数字的任意一个偶数数字,百位数字不能取与这两个数字重复的数字,十位数字不能取与这三个数字重复的数字.根据分步计数原理,有3×3×5×4＝180(种)取法.③根据分类计数原理,共可以组成240＋180＝420(个)无重复数字的四位偶数.思维升华 利用两个计数原理解决应用问题的一般思路(1)弄清完成一件事是做什么.(2)确定是先分类后分步,还是先分步后分类.(3)弄清分步、分类的标准是什么.(4)利用两个计数原理求解.跟踪训练2 (1)(2020·郑州质检)将数字“124467”重新排列后得到不同的偶数的个数为( )A.72B.120C.192D.240答案 D解析 将数字“124467”重新排列后所得数字为偶数,则末位数应为偶数,(1)若末位数字为2,因为含有2个4,所以有5×4×3×2×12＝60(种)情况；(2)若末位数字为6,同理有60种情况；(3)若末位数字为4,因为有两个相同数字4,所以共有5×4×3×2×1＝120(种)情况.综上,共有60＋60＋120＝240(种)情况.(2)从正方体六个面的对角线中任取两条作为一对,其中所成的角为60°的共有( )A.24对B.30对C.48对D.60对答案 C解析 如图,在正方体ABCD －A 1B 1C 1D 1中,与面对角线AC 成60°角的面对角线有B 1C ,BC 1,A 1D ,AD 1,AB 1,A 1B ,D 1C ,DC 1,共8条,同理与DB 成60°角的面对角线也有8条.因此一个面上的2条面对角线与其相邻的4个面上的8条对角线共组成16对.又正方体共有6个面,所以共有16×6＝96(对).又因为每对被计算了2次,因此成60°的面对角线有12×96＝48(对).1.有不同的语文书9本,不同的数学书7本,不同的英语书5本,从中选出不属于同一学科的书2本,则不同的选法有()A.21种B.315种C.143种D.153种答案 C解析可分三类:一类:语文、数字各1本,共有9×7＝63(种)；二类:语文、英语各1本,共有9×5＝45(种)；三类:数字、英语各1本,共有7×5＝35(种),∴共有63＋45＋35＝143(种)不同选法.2.(2020·南京质检)三个人踢毽子,互相传递,每人每次只能踢一下,由甲开始踢,经过4次传递后,毽子又被踢回给甲,则不同的传递方式共有()A.4种B.6种C.10种D.16种答案 B解析分两类:甲第一次踢给乙时,满足条件的有3种传递方式(如图),同理,甲先传给丙时,满足条件的也有3种传递方式. 由分类计数原理可知,共有3＋3＝6(种)传递方式.3.十字路口来往的车辆,如果不允许回头,则行车路线共有( ) A.24种 B.16种 C.12种 D.10种 答案 C解析 根据题意,车的行驶路线起点有4种,行驶方向有3种,所以行车路线共有4×3＝12(种),故选C.4.若a ∈{1,2,3,4},b ∈{1,2,3,4},则y ＝ba x 表示不同直线的条数为( )A.8B.11C.14D.16 答案 B解析 若使ba 表示不同的实数,则当a ＝1时,b ＝1,2,3,4；当a ＝2时,b ＝1,3；当a ＝3时,b ＝1,2,4；当a ＝4时,b ＝1,3.故y ＝bax 表示的不同直线的条数共有4＋2＋3＋2＝11.5.从2,3,4,5,6,7,8,9这8个数中任取2个不同的数分别作为一个对数的底数和真数,则可以组成不同对数值的个数为( ) A.56 B.54 C.53 D.52 答案 D解析 在8个数中任取2个不同的数共有8×7＝56(个)对数值；但在这56个数值中,log 24＝log 39,log 42＝log 93,log 23＝log 49,log 32＝log 94,即满足条件的对数值共有56－4＝52(个). 6.(2020·石家庄模拟)将“福”“禄”“寿”填入到如图所示的4×4小方格中,每格内只填入一个汉字,且任意的两个汉字既不同行也不同列,则不同的填写方法有( )A.288种B.144种C.576种D.96种答案 C解析依题意可分为以下3步:(1)先从16个格子中任选一格放入第一个汉字,有16种方法；(2)任意的两个汉字既不同行也不同列,第二个汉字只有9个格子可以放,有9种方法；(3)第三个汉字只有4个格子可以放,有4种方法,根据分步计数原理可得不同的填写方法有16×9×4＝576(种).7.(2020·安阳模拟)如图为我国数学家赵爽(约3世纪初)在为《周髀算经》作注时验证勾股定理的示意图,现在提供5种颜色给其中5个小区域涂色,规定每个区域只涂一种颜色,相邻区域颜色不相同,则不同的涂色方案共有()A.120种B.260种C.340种D.420种答案 D解析由题意可知上下两块区域可以相同,也可以不同,则共有5×4×3×1×3＋5×4×3×2×2＝180＋240＝420(种).故选D.8.(多选)将四个不同的小球放入三个分别标有1,2,3号的盒子中,不允许有空盒子,下列结果正确的有( )A.C 13C 12C 11C 13B.C 24A 33C.C 13C 24A 22D.18答案 BC解析 根据题意,四个不同的小球放入三个分别标有1,2,3号的盒子中,且没有空盒,则三个盒子中有1个放2个球,剩下的2个盒子各放1个, 有2种解法: (1)分2步进行分析:①先将四个不同的小球分成3组,有C 24种分组方法； ②将分好的3组全排列,对应放到3个盒子中,有A 33种放法,则没有空盒的放法有C 24A 33种.(2)分2步进行分析:①在4个小球中任选2个,在3个盒子中任选1个,将选出的2个小球放入选出的小盒中,有C 13C 24种情况； ②将剩下的2个小球全排列,放入剩下的2个小盒中,有A 22种放法,则没有空盒的放法有C 13C 24A 22种.故选BC.9.若椭圆x 2m ＋y 2n ＝1的焦点在y 轴上,且m ∈{1,2,3,4,5},n ∈{1,2,3,4,5,6,7},则这样的椭圆的个数为________. 答案 20解析 当m ＝1时,n ＝2,3,4,5,6,7,共6个； 当m ＝2时,n ＝3,4,5,6,7,共5个； 当m ＝3时,n ＝4,5,6,7,共4个； 当m ＝4时,n ＝5,6,7,共3个； 当m ＝5时,n ＝6,7,共2个.故共有6＋5＋4＋3＋2＝20(个)满足条件的椭圆.10.直线方程Ax ＋By ＝0,若从0,1,2,3,5,7这6个数字中任取两个不同的数作为A ,B 的值,则可表示________条不同的直线. 答案 22解析 分成三类:A ＝0,B ≠0；A ≠0,B ＝0和A ≠0,B ≠0,前两类各表示1条直线；第三类先取A 有5种取法,再取B 有4种取法,故5×4＝20(种). 所以可以表示22条不同的直线.11.如果一条直线与一个平面垂直,那么称此直线与平面构成一个“正交线面对”.在一个正方体中,由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是________.答案36解析第1类,对于每一条棱,都可以与两个侧面构成“正交线面对”,这样的“正交线面对”有2×12＝24(个)；第2类,对于每一条面对角线,都可以与一个对角面构成“正交线面对”,这样的“正交线面对”有12个.所以正方体中“正交线面对”共有24＋12＝36(个).12.如图所示,用五种不同的颜色分别给A,B,C,D四个区域涂色,相邻区域必须涂不同颜色,若允许同一种颜色多次使用,则不同的涂色方法共有________种.答案180解析按区域分四步:第一步,A区域有5种颜色可选；第二步,B区域有4种颜色可选；第三步,C区域有3种颜色可选；第四步,D区域也有3种颜色可选.由分步计数原理,可得共有5×4×3×3＝180(种)不同的涂色方法.13.从集合{1,2,3,4,…,10}中,选出5个数组成该集合的子集,使得这5个数中任意两个数的和都不等于11,则这样的子集有()A.32个B.34个C.36个D.38个答案 A解析先把数字分成5组:{1,10},{2,9},{3,8},{4,7},{5,6},由于选出的5个数中,任意两个数的和都不等于11,所以从每组中任选一个数字即可,故共可组成2×2×2×2×2＝32(个)这样的子集.14.工人在安装一个正六边形零件时,需要固定如图所示的六个位置的螺栓.若按一定顺序将每个螺栓固定紧,但不能连续固定相邻的2个螺栓.则不同的固定螺栓方式的种数是________.答案60解析根据题意,第一个可以从6个螺栓里任意选一个,共有6种选择方法,并且是机会相等的,若第一个选1号螺栓,第二个可以选3,4,5号螺栓,依次选下去,共可以得到10种方法,所以总共有10×6＝60(种)方法,故答案是60.15.(2019·凌源模拟)中国有十二生肖,又叫十二属相,每一个人的出生年份对应了十二种动物(鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪)中的一种,现有十二生肖的吉祥物各一个,三位同学依次选一个作为礼物,甲同学喜欢牛和马,乙同学喜欢牛、狗和羊,丙同学哪个吉祥物都喜欢,如果让三位同学都选取到喜欢的礼物,则不同的选法有()A.30种B.50种C.60种D.90种答案 B解析①甲同学选择牛,乙有2种选择,丙有10种选择,选法有1×2×10＝20(种)；②甲同学选择马,乙有3种选择,丙有10种选择,选法有1×3×10＝30(种),所有总共有20＋30＝50(种)选法.16.若给一个各边不等的凸五边形的各边染色,每条边可以染红、黄、蓝三种颜色中的一种,但是不允许相邻的边有相同的颜色,则不同的染色方法共有________种.答案30解析方法一如图,染五条边总体分五步,染每一边为一步.当染边1时有3种染法,则染边2有2种染法.(1)当3与1同色时有1种染法,则4有2种,5有1种,此时染法总数为3×2×1×2×1＝12(种).(2)当3与1不同色时,3有1种,①当4与1同色时,4有1种,5有2种；②当4与1不同色时,4有1种,5有1种,则此时有3×2×1×(1×2＋1×1)＝18(种).综合(1)、(2),由分类计数原理,可得染法的种数为30种.方法二通过分析可知,每种颜色至少要涂1次,至多只能涂2次,即有一色涂1次,剩余两种颜色各涂2次.一次的有C13C15种涂法,涂2次的有2种涂法,故一共有2C13C15＝30(种)涂法.。

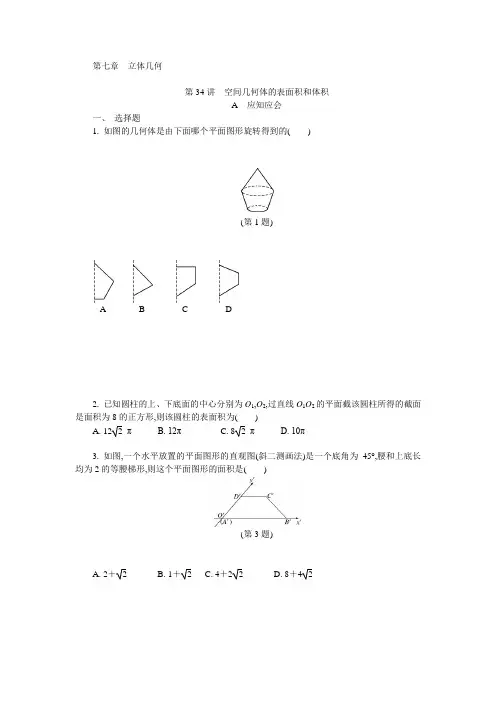
第七章立体几何第34讲空间几何体的表面积和体积A应知应会一、选择题1. 如图的几何体是由下面哪个平面图形旋转得到的()(第1题)A B C D2. 已知圆柱的上、下底面的中心分别为O1,O2,过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为()A. 122πB. 12πC. 82πD. 10π3. 如图,一个水平放置的平面图形的直观图(斜二测画法)是一个底角为45°,腰和上底长均为2的等腰梯形,则这个平面图形的面积是()(第3题)A. 2＋2B. 1＋2C. 4＋22D. 8＋424. 已知正方体外接球的体积是323 π,那么正方体的棱长等于( )A. 22B.233 C. 423 D. 4335. (2019·江西重点中学联考)《算术书》竹简于上世纪八十年代在湖北省江陵县张家山出土,这是我国现存最早的有系统的数学典著,其中记载有求“囷盖”的术：置如其周,令相乘也,又以高乘之,三十六成一,该术相当于给出圆锥的底面周长l 与高h ,计算其体积V 的近似公式V ＝136 l 2h ,它实际上是将圆锥体积公式中的圆周率π近似取3,那么,近似公式V ≈25942 l 2h 相当于将圆锥体积公式中的π近似取( )A.227 B. 258 C. 15750 D. 355113二、 解答题6. 已知正四棱锥底面正方形的边长为4 cm,高与斜高的夹角为30°,求正四棱锥的侧面积和表面积．(单位：cm 2 )7. 如图,四棱锥P ABCD 的底面ABCD 是半径为R 的圆的内接四边形,其中BD 是圆的直径,∠ABD ＝60°,∠BDC ＝45°,△ADP ∽△BAD .(1) 求线段PD 的长；(2) 若PC ＝11 R ,求三棱锥P ABC 的体积．(第7题)B巩固提升一、填空题1. 如图,一个底面半径为R的圆柱形量杯中装有适量的水．若放入一个半径为r的实心铁球,水面高度恰好升高r,则Rr＝________．(第1题)2. (2019·通州、海门、启东期末)已知正三棱柱ABC A1B1C1的各棱长均为2,点D在棱AA1上,则三棱锥D BB1C1的体积为________．(第2题)3. 如图,已知正三棱柱ABC A1B1C1的底面边长为2 cm,高为5 cm,一质点自点A出发,沿着三棱柱的侧面绕行两周到达点A1的最短路线的长为________cm.(第3题)4. 给出下列命题：①棱柱的侧棱都相等,侧面都是全等的平行四边形；②若三棱锥的三条侧棱两两垂直,则其三个侧面也两两垂直；③在四棱柱中,若两个过相对侧棱的截面都垂直于底面,则该四棱柱为直四棱柱；④存在每个面都是直角三角形的四面体．其中正确的命题是________．(填序号)二、解答题5. 已知等边圆柱(轴截面是正方形的圆柱)的全面积为S,求其内接正四棱柱的体积．6. 如图,四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD.(1) 求证：平面AEC⊥平面BED；(2) 若∠ABC＝120°,AE⊥EC,三棱锥E ACD的体积为63,求该三棱锥的侧面积．(第6题)第35讲空间点、线、面之间的位置关系A应知应会一、选择题1. 下列图形中不一定是平面图形的是()A. 三角形B. 菱形C. 梯形D. 四边相等的四边形2. 如图,ABCD A1B1C1D1是长方体,O是B1D1的中点,直线A1C交平面AB1D1于点M,则下列结论正确的是()(第2题)A. A,M,O三点共线B. A,M,O,A1不共面C. A,M,C,O不共面D. B,B1,O,M共面3. 如图,平面α∩平面β＝l,A∈α,B∈α,AB∩l＝D,C∈β,C l,则平面ABC与平面β的交线是()(第3题)A. 直线ACB. 直线ABC. 直线CDD. 直线BC4. (多选)下列四个命题中正确的是()A. 存在与两条异面直线都平行的平面B. 过空间一点,一定能作一个平面与两条异面直线都平行C. 过平面外一点可作无数条直线与该平面平行D. 过直线外一点可作无数个平面与该直线平行5. (2019·湖北八校联考)已知直三棱柱ABC A1B1C1中,∠ABC＝120°,AB＝2,BC＝CC1＝1,则异面直线AB1与BC1所成角的余弦值为()A.32 B.155 C.105 D.33二、解答题6. 如图,在棱长为a的正方体ABCD A1B1C1D1中,M,N分别是AA1,D1C1的中点,过D,M,N 三点的平面与正方体的下底面相交于直线l.(1) 画出l的位置；(2) 设l∩A1B1＝P,求PB1的长．(第6题)7. 如图,A是△BCD所在平面外的一点,E,F分别是BC,AD的中点．(1) 求证：直线EF与BD是异面直线；(2) 若AC⊥BD,AC＝BD,求EF与BD所成的角．(第7题)B巩固提升一、填空题1. 下列命题正确的是________．(填序号)①三个点确定一个平面；②一条直线和一个点确定一个平面；③两条相交直线确定一个平面；④两条平行直线确定一个平面．2. 已知l1,l2,l3是空间三条不同的直线,给出下列四个命题：①l1⊥l2,l2⊥l3⇒l1∥l3；②l1⊥l2,l2∥l3⇒l1⊥l3；③l1∥l2∥l3⇒l1,l2,l3共面；④l1,l2,l3共点⇒l1,l2,l3共面．其中正确的命题是________．(填序号)3. (2019·深圳调研)若P是两条异面直线l,m外的任意一点,给出四个命题：①过点P有且仅有一条直线与l,m都平行；②过点P有且仅有一条直线与l,m都垂直；③过点P有且仅有一条直线与l,m都相交；④过点P有且仅有一条直线与l,m都异面．其中正确的是________．(填序号)4. 设E,F,G,H依次是空间四边形ABCD的边AB,BC,CD,DA的中点,且AC＋BD＝a,AC·BD＝b,则EG2＋FH2＝________．二、解答题5. 已知a,b,c,d是不共点且两两相交的四条直线,求证：a,b,c,d共面．6. 已知三棱柱ABC A1B1C1的侧棱长和底面边长均为2,A1在底面ABC内的射影O为底面三角形ABC的中心,如图所示．(1) 连接BC1,求异面直线AA1与BC1所成角的大小；(2) 连接A1C,A1B,求三棱锥C1-BCA1的体积．(第6题)第36讲直线、平面平行的判定与性质A应知应会一、选择题1. 已知平面α,β和直线m,若α⊥β,m⊥α,则()A. m⊥βB. m∥βC. m⊂βD. m∥β或m⊂β2. (2019·湘中名校联考)已知m,n是两条不同的直线,α,β,γ是三个不重合的平面,下列命题中正确的是()A. 若m∥α,n∥α,则m∥nB. 若m∥α,m∥β,则α∥βC. 若α⊥γ,β⊥γ,则α∥βD. 若m⊥α,n⊥α,则m∥n3. (2019·泰安调研)已知α,β,γ是三个不重合的平面,l是直线．给出下列命题：①若l上两点到α的距离相等,则l∥α；②若l⊥α,l∥β,则α⊥β；③若α∥β,lβ,且l∥α,则l∥β.其中正确的命题是()A. ①②B. ①②③C. ①③D. ②③4. 设l,m,n表示不同的直线,α,β,γ表示不重合的平面,给出下列三个命题：①若m∥l,且m⊥α,则l⊥α；②若α∩β＝l,β∩γ＝m,γ∩α＝n,则l∥m∥n；③若α∩β＝m,β∩γ＝l,γ∩α＝n,且n∥β,则l∥m.其中正确命题的个数是()A. 0B. 1C. 2D. 35. (2019·深圳调研)在空间四边形ABCD中,E,F分别为AB,AD上的点,且AE∶EB＝AF∶FD＝1∶4.又H,G分别为BC,CD的中点,则()A. BD∥平面EFG,且四边形EFGH是平行四边形B. EF∥平面BCD,且四边形EFGH是梯形C. HG∥平面ABD,且四边形EFGH是平行四边形D. EH∥平面ADC,且四边形EFGH是梯形二、解答题6. 如图,四棱锥P ABCD的底面为平行四边形,PD⊥平面ABCD,M为PC的中点．求证：AP∥平面MBD.(第6题)7. (2019·南昌模拟)如图,在四棱锥P ABCD中,∠ABC＝∠ACD＝90°,∠BAC＝∠CAD ＝60°,P A⊥平面ABCD,P A＝2,AB＝1.设M,N分别为PD,AD的中点．(1) 求证：平面CMN∥平面P AB；(2) 求三棱锥P-ABM的体积．(第7题)B巩固提升一、填空题1. 若一直线上有相异的三个点A,B,C到平面α的距离相等,那么直线l与平面α的位置关系是________．2. 如图,正方体ABCD-A1B1C1D1中,AB＝2,点E为AD的中点,点F在CD上．若EF∥平面AB1C,则线段EF的长度等于________．(第2题)3. 在空间中,用a,b,c表示三条不同的直线,γ表示平面,给出下列四个命题：①若a∥b,b∥c,则a∥c；②若a⊥b,b⊥c,则a⊥c；③若a∥γ,b∥γ,则a∥b；④若a⊥γ,b⊥γ,则a∥b.其中真命题为________．(填序号)4. (2019·九江调研)如图,正方体的底面与正四面体的底面在同一平面α上,且AB∥CD,则直线EF与正方体的六个面所在的平面相交的平面个数为________．(第4题)二、解答题5. 如图,四边形ABCD与四边形ADEF为平行四边形,M,N,G分别是AB,AD,EF的中点．(1) 求证：BE∥平面DMF；(2) 求证：平面BDE∥平面MNG.(第5题)6. 如图,四棱锥P ABCD中,AB∥CD,AB＝2CD,E为PB的中点．(1) 求证：CE∥平面P AD；(2) 在线段AB上是否存在一点F,使得平面P AD∥平面CEF？若存在,证明你的结论,若不存在,请说明理由．(第6题)第37讲直线、平面垂直的判定与性质A应知应会一、选择题1. 已知互相垂直的平面α,β交于直线l,若直线m,n满足m∥α,n⊥β,则()A. m∥lB. m∥nC. n⊥lD. m⊥n2. (2019·焦作期中)设m,n是两条不同的直线,α,β,γ是三个不重合的平面,给出下列命题,正确的是()A. 若mβ,α⊥β,则m⊥αB. 若m∥α,m⊥β,则α⊥βC. 若α⊥β,α⊥γ,β⊥γD. 若α∩γ＝m,β∩γ＝n,m∥n,则α∥β3. (2019·合肥调研)如图,在正方体ABCD-A1B1C1D1中,M,N分别是BC1,CD1的中点,则下列说法错误的是()(第3题)A. MN与CC1垂直B. MN与AC垂直C. MN与BD平行D. MN与A1B1平行4. 如图,在斜三棱柱ABC A1B1C1中,∠BAC＝90°,BC1⊥AC,则点C1在底面ABC上的射影H必在()(第4题)A. 直线AB上B. 直线BC上C. 直线AC上D. △ABC内部5. 如图,在四面体D ABC中,若AB＝CB,AD＝CD,E是AC的中点,则下列结论正确的是()(第5题)A. 平面ABC⊥平面ABDB. 平面ABD⊥平面BDCC. 平面ABC⊥平面BDE,且平面ADC⊥平面BDED. 平面ABC⊥平面ADC,且平面ADC⊥平面BDE二、解答题6. (2019·潍坊期末)如图,四棱锥E ABCD中,底面ABCD是平行四边形,∠ADC＝60°,CD ＝2AD,EC⊥底面ABCD.(1) 求证：平面ADE⊥平面ACE；(2) 若AD＝CE＝2,求三棱锥C ADE的高．(第6题)7. (2019·蚌埠二模)在如图所示的几何体中,四边形ABCD是正方形,P A⊥平面ABCD,E,F 分别是线段AD,PB的中点,P A＝AB＝1.(1) 求证：EF∥平面PDC；(2) 求点F到平面PDC的距离．(第7题)B巩固提升一、填空题1. (2019·青岛调研)已知P为△ABC所在平面外一点,且P A,PB,PC两两垂直,有下列结论：①P A⊥BC；②PB⊥AC；③PC⊥AB；④AB⊥BC.其中正确的有________．(填序号)2. 如图,在棱长为2的正方体ABCD A1B1C1D1中,E为BC的中点,点P在线段D1E上,则点P到直线CC1的距离的最小值为________．(第2题)3. (2019·武汉调研)在矩形ABCD中,AB＜BC,现将△ABD沿矩形的对角线BD所在的直线进行翻折,在翻折的过程中,给出下列结论：①存在某个位置,使得直线AC与直线BD垂直；②存在某个位置,使得直线AB与直线CD垂直；③存在某个位置,使得直线AD与直线BC垂直．其中正确的结论是________．(填序号)4. (2019·滨州期末)已知正方体ABCD A1B1C1D1的棱长为2,点P是棱AA1的中点,则过点P且与直线BC1垂直的平面截正方体所得的截面的面积为________．二、解答题5. 如图,在正三棱柱ABC A1B1C1中,D为AB的中点．(1) 求证：BC1∥平面A1CD.(2) 请从图中所标点中,选择直线或平面将命题补充完整,并证明．求证：__________⊥平面ABB1A1.(第5题)6. (2019·漳州调研)在如图所示的五面体ABCDEF中,四边形ABCD为菱形,且∠DAB＝60°,EA＝ED＝AB＝2EF＝2,EF∥AB,M为BC的中点．(1) 求证：FM∥平面BDE；(2) 若平面ADE⊥平面ABCD,求点F到平面BDE的距离．(第6题)第38讲直线、平面平行与垂直的综合问题A应知应会一、选择题1. 若直线a⊥b,且直线a∥平面α,则直线b与平面α的位置关系是()A. b⊂αB. b∥αC. b⊂α或b∥αD. b与α相交或b⊂α或b∥α2. 设平面α与平面β相交于直线m,直线a在平面α内,直线b在平面β内,且b⊥m,则“α⊥β”是“a⊥b”的()A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件3. 给出下列关于互不相同的直线l,m,n和平面α,β,γ的三个命题：①若l与m为异面直线,l⊂α,m⊂β,则α∥β；②若α∥β,l⊂α,m⊂β,则l∥m；③若α∩β＝l,β∩γ＝m,γ∩α＝n,l∥γ,则m∥n.其中真命题的个数为()A. 3B. 2C. 1D. 04. (2019·深圳调研)已知a,b,c是空间中三条不同的直线,α,β,γ为空间三个不重合的平面,则下列说法中正确的是()A. 若α⊥β,aα,a⊥β,则a∥αB. 若α⊥β,且α∩β＝a,b⊥a,则b⊥αC. 若α∩β＝a,β∩γ＝b,α∩γ＝c,则a∥b∥cD. 若α∩β＝a,b∥a,则b∥α5. (多选)已知平面α,β,γ和直线l,m,且l⊥m,α⊥γ,α∩γ＝m,β∩γ＝l,下列结论中一定正确的是()A. β⊥γB. l⊥αC. m⊥βD. α⊥β二、解答题6. 如图,在直四棱柱ABCD A1B1C1D1中,DB＝BC,DB⊥AC,点M是棱BB1上一点．(1) 求证：B1D1∥平面A1BD；(2) 求证：MD⊥AC；(3) 试确定点M的位置,使得平面DMC1⊥平面CC1D1D.(第6题)7. 如图,在三棱柱ABC A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1＝AC＝2,BC＝1,E,F分别是A1C1,BC的中点．(1) 求证：平面ABE⊥平面B1BCC1；(2) 求证：C1F∥平面ABE；(3) 求三棱锥E ABC的体积．(第7题)B 巩固提升一、 填空题1. (多选)如图,正三棱柱ABC A 1B 1C 1的各条棱的长度均相等,D 为AA 1的中点,M ,N 分别是线段BB 1和线段CC 1上的动点(含端点),且满足BM ＝C 1N ,当点M ,N 运动时,下列结论正确的是( )(第1题)A. 在△DMN 内总存在与平面ABC 平行的线段B. 平面DMN ⊥平面BCC 1B 1C. 三棱锥A 1 DMN 的体积为定值D. △DMN 可能为直角三角形2. (多选)如图,在棱长为1的正方体ABCD A 1B 1C 1D 1中,P 为线段A 1B 上的动点,则下列结论中正确的是( )(第2题)A. 平面D 1A 1P ⊥平面A 1APB. ∠APD 1的取值范围是⎝⎛⎭⎫0，π2C. 三棱锥B 1 D 1PC 的体积为定值D. DC 1⊥D 1P3. (多选)如图,一张A4纸的长、宽分别为22 a ,2a ,A ,B ,C ,D 分别是其四条边的中点,现将其沿图中虚线折起,使得P 1,P 2,P 3,P 4四点重合为一点P ,从而得到一个多面体,下列关于该多面体的命题,正确的是( )(第3题)A. 该多面体是三棱锥B. 平面BAD⊥平面BCDC. 平面BAC⊥平面ACDD. 该多面体外接球的表面积为5πa2二、解答题4. 如图,在四棱锥P ABC中,P A⊥底面ABCD,AD∥BC,AB＝AD＝AC＝3,P A＝BC＝4,M 为线段AD上一点,AM＝2MD,N为PC的中点．(1) 求证：MN∥平面P AB；(2) 求直线AN与平面PMN所成角的正弦值．(第4题)5. 如图(1),在Rt△ABC中,∠C＝90°,D,E分别为AC,AB的中点,点F为线段CD上的一点．将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图(2).(1) 求证：DE∥平面A1CB；(2) 求证：A1F⊥BE；(3) 线段A1B上是否存在点Q,使A1C⊥平面DEQ？说明理由．图(1)图(2)(第5题)第39讲 用向量法解决空间中的位置关系A 应知应会一、 选择题1. 已知a ＝(2,1,－3),b ＝(－1,2,3),c ＝(7,6,λ),若a,b,c 三向量共面,则λ等于( ) A. 9 B. －9 C. －3 D. 32. 若平面α,β的法向量分别为n 1＝(2,－3,5),n 2＝(－3,1,－4),则( ) A. α∥β B. α⊥βC. α,β相交但不垂直D. 以上均不正确3. 在空间四边形ABCD 中,AB → ·CD → ＋AC → ·DB → ＋AD → ·BC →等于( )A. －1B. 0C. 1D. 不确定4. 已知平面α内有一点M (1,－1,2),平面α的一个法向量为n ＝(6,－3,6),则下列点P 中,在平面α内的是( )A. P (2,3,3)B. P (－2,0,1)C. P (－4,4,0)D. P (3,－3,4)5. 如图,F 是正方体ABCD A 1B 1C 1D 1的棱CD 的中点,E 是BB 1上一点,若D 1F ⊥DE ,则有( )(第5题)A. B 1E ＝EBB. B 1E ＝2EBC. B 1E ＝12EB D. E 与B 重合二、 解答题6. 已知a ＝(1,－3,2),b ＝(－2,1,1),A (－3,－1,4),B (－2,－2,2). (1) 求|2a ＋b|；(2) 在直线AB 上,是否存在一点E ,使得OE →⊥b(O 为原点)?7. (2019·江西调研)如图,在直三棱柱ABC A 1B 1C 1中,侧面AA 1C 1C 和侧面AA 1B 1B 都是正方形且互相垂直,M 为AA 1的中点,N 为BC 1的中点．(1) 求证：MN ∥平面A 1B 1C 1；(2) 求证：平面MBC 1⊥平面BB 1C 1C .(第7题)B 巩固提升一、 填空题1. 已知法向量为n ＝(1,－1,1)的平面σ过点M (1,2,－1),则平面σ上任意一点P 的坐标(x ,y ,z )满足的方程为________．2. 已知a ＝(x ,4,1),b ＝(－2,y ,－1),c ＝(3,－2,z ),若a ∥b,b ⊥c,则c ＝________．3. 已知V 为矩形ABCD 所在平面外一点,且VA ＝VB ＝VC ＝VD ,VP →＝13 VC → ,VM → ＝23VB → ,VN →＝23VD → ,则VA 与平面PMN 的位置关系是________．4. (2019·丽水调研)如图,圆锥的轴截面SAB 是边长为2的等边三角形,O 为底面中心,M 为SO 的中点,动点P 在圆锥底面内(包括圆周).若AM ⊥MP ,则点P 形成的轨迹长度为________．(第4题)二、 解答题5. 如图,正方形ABCD 所在平面与四边形ABEF 所在平面互相垂直,△ABE 是等腰直角三角形,AB ＝AE ,F A ＝FE ,∠AEF ＝45°.(1) 求证：EF ⊥平面BCE ；(2) 设线段CD ,AE 的中点分别为P ,M ,求证：PM ∥平面BCE .(第5题)6. (2019·芜湖调研)如图,在长方体ABCD A 1B 1C 1D 1中,AA 1＝AD ＝1,E 为CD 中点． (1) 求证：B 1E ⊥AD 1；(2) 在棱AA 1上是否存在一点P ,使得DP ∥平面B 1AE ？若存在,求AP 的长；若不存在,说明理由．(第6题)第40讲 空间角的计算课时1 线线角与线面角A 应知应会一、 选择题1. 已知A (－1,0,1),B (0,0,1),C (2,2,2),D (0,0,3),则sin 〈AB → ,CD →〉等于( ) A. －23 B. 23 C. 53 D. －532. (2019·江门调研)如图,在三棱柱ABC A 1B 1C 1中,AA 1⊥底面ABC ,AB ＝BC ＝AA 1,∠ABC＝90°,点E ,F 分别是棱AB ,BB 1的中点,则直线EF 和BC 1所成的角是( )(第2题)A. 30°B. 45°C. 60°D. 90°3. 已知空间三点A (0,2,3),B (－2,1,6),C (1,－1,5).若|a|＝3 ,且a 分别与AB → ,AC →垂直,则向量a 为( )A. (1,1,1)B. (－1,－1,－1)C. (1,1,1)或(－1,－1,－1)D. (1,－1,1)或(－1,1,－1) 4. (2019·日照调研)如图,已知长方体ABCD A 1B 1C 1D 1中,AD ＝AA 1＝1,AB ＝3,E 为线段AB 上一点,且AE ＝13AB ,则DC 1与平面D 1EC 所成角的正弦值为( )A.33535 B. 277 C. 33 D. 24(第4题)5.如图,正方形ACDE 与等腰直角三角形ACB 所在的平面互相垂直,且AC ＝BC ＝2,∠ACB ＝90°,F ,G 分别是线段AE ,BC 的中点．则AD 与GF 所成角的余弦值为( )(第5题)A.36 B. －36 C.33 D. －33二、解答题6. 如图,在四棱锥P ABCD中,底面ABCD是矩形,P A⊥底面ABCD,E是PC的中点．已知AB＝2,AD＝22,P A＝2.求异面直线BC与AE所成的角的大小．(第6题)7. (2019·宿迁调研)如图,在四棱锥P ABCD中,P A⊥底面ABCD,AD⊥AB,AB∥DC,AD＝DC＝AP＝2,AB＝1,点E为棱PC的中点．(1) 求证：BE⊥DC；(2) 求直线BE与平面PBD所成角的正弦值．(第7题)B 巩固提升一、 填空题1. 已知O 点为空间直角坐标系的原点,向量OA → ＝(1,2,3),OB → ＝(2,1,2),OP →＝(1,1,2),且点Q 在直线OP 上运动,当QA → ·QB → 取得最小值时,OQ →的坐标是________．2. 如图,已知正四面体ABCD 中,AE ＝14 AB ,CF ＝14 CD ,则直线DE 和BF 所成角的余弦值为________．(第2题)3. 在正四棱柱ABCD A 1B 1C 1D 1中,AA 1＝2AB ,则直线CD 与平面BDC 1所成角的正弦值为________．4. 如图,菱形ABCD 中,∠ABC ＝60°,AC 与BD 相交于点O ,AE ⊥平面ABCD ,CF ∥AE ,AB ＝2,CF ＝3.若直线OF 与平面BED 所成的角为45°,则AE ＝________．(第4题)二、解答题5. (2019·宁波调研)如图,在三棱锥P ABC中,P A⊥底面ABC,∠BAC＝90°.点D,E,N分别为棱P A,PC,BC的中点,M是线段AD的中点,P A＝AC＝4,AB＝2.(1) 求证：MN∥平面BDE；(2) 已知点H在棱P A上,且直线NH与直线BE所成角的余弦值为721,求线段AH的长．(第5题)6. (2019·洛阳二模)如图,在四棱柱ABCD A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD＝CD＝1,AA1＝AB＝2,E为棱AA1的中点．(1) 求证：B1C1⊥CE；(2) 设点M在线段C1E上,且直线AM与平面ADD1A1所成角的正弦值为26,求线段AM的长．(第6题)课时2二面角A应知应会一、解答题1. (2019·保定期末)如图,正三棱柱(底面为正三角形,侧棱垂直于底面)ABC A1B1C1中,侧棱长AA1＝2,底面边长AB＝1,N是CC1的中点．(1) 求证：平面ANB1⊥平面AA1B1B；(2) 设M是线段AB1的中点,求直线C1M与平面ABC1所成的角的正弦值．(第1题)2. (2019·江苏天一中学)如图,在直三棱柱ABC A1B1C1中,AB＝4,AC＝BC＝3,D为AB的中点．(1) 求点C到平面A1ABB1的距离；(2) 若AB1⊥A1C,求二面角A1-CD-C1的平面角的余弦值．(第2题)3. (2019·临汾一模)在四棱锥P ABCD中,平面ABCD⊥平面PCD,底面ABCD为梯形,AB∥CD,AD⊥PC且AB＝1,AD＝DC＝DP＝2,∠PDC＝120°.(1) 求证：AD⊥平面PDC；(2) 求二面角B-PD-C的余弦值．(第3题)4. (2019·如皋中学)如图,以正四棱锥V ABCD 的底面中心O 为坐标原点建立空间直角坐标系O-xyz ,其中Ox ∥BC ,Oy ∥AB ,E 为VC 的中点．正四棱锥V-ABCD 的底面边长为2a ,高为h ,且有cos 〈BE → ,DE →〉＝－1549.(1) 求ha的值；(2) 求二面角B-VC-D 的余弦值．(第4题)B 巩固提升一、 填空题1. 如图,在直三棱柱ABC A 1B 1C 1中,AA 1＝BC ＝AB ＝2,AB ⊥BC ,则二面角B 1-A 1C-C 1的大小是________．(第1题)2. 如图,在四棱锥P ABCD 中,底面ABCD 是矩形,PD ⊥平面ABCD ,且PD ＝AD ＝1,AB ＝2,点E 是AB 上一点,当AE ＝________时,二面角P-EC- D 的平面角为π4.(第2题)二、 解答题3. 如图,四棱锥P ABCD 的底面ABCD 是平行四边形,P A ⊥底面ABCD ,P A ＝3,AD ＝2,AB ＝4,∠ABC ＝60°.(1) 求证：BC ⊥平面P AC ；(2) 若E 是侧棱PB 上一点,记PEPB ＝λ(0<λ<1),且________,求λ的值．①二面角E-AD-B 为30°； ②二面角E-AD-P 为60°；③二面角E-AD-B 与E-AD-P 相等．请从上面三个条件中任选一个,填入横线处,并完成．(第3题)4. (2019·合肥调研)如图,在梯形ABCD 中,AB ∥CD ,AD ＝DC ＝CB ＝1,∠BCD ＝2π3 ,四边形BFED 为矩形,平面BFED ⊥平面ABCD ,BF ＝1.(1) 求证：AD ⊥平面BFED ；(2) 点P 在线段EF 上运动,设平面P AB 与平面ADE 所成锐二面角为θ,试求θ的最小值．(第4题)微难点8翻折问题一、填空题1. 如图表示一个正方体表面的一种展开图,图中的四条线段AB,CD,EF和GH在原正方体中相互异面的有______对．(第1题)2.如图所示是一个正方体的表面展开图,A,B,C均为棱的中点,D是顶点,则在正方体中,异面直线AB,CD所成角的余弦值为________．(第2题)3. 已知一个凸多面体共有9个面,所有棱长均为1,其平面展开图如图所示,则该凸多面体的体积V＝________．(第3题)4. 如图是一几何体的平面展开图,其中四边形ABCD 为正方形,E ,F 分为P A ,PD 的中点,在此几何体中,给出下面四个结论：①直线BE 与直线CF 是异面直线；②直线BE 与直线AF 是异面直线；③直线EF ∥平面PBC ；④平面BCE ⊥平面P AD .其中正确的结论是________．(填序号)(第4题)二、 解答题5. 如图(1),四边形ABCD 为等腰梯形,AD ∥BC ,且AD ＝13 BC ＝a ,∠BAD ＝135°,AE ⊥BC于点E ,F 为BE 的中点．将△ABE 沿着AE 折起至△AB ′E 的位置,得到如图(2)所示的四棱锥B ′ ADCE .图(1)图(2) (第5题)(1) 求证：AF ∥平面B ′CD ；(2) 若平面AB ′E ⊥平面AECD ,求二面角B ′- CD-E 的余弦值．6. 如图,在平面四边形ABCD 中,△ABC 等边三角形,AC ⊥DC ,以AC 为折痕将△ABC 折起,使得平面ABC ⊥平面ACD .(1) 设E 为BC 的中点,求证：AE ⊥平面BCD .(2) 若BD 与平面ABC 所成角的正切值为32,求二面角A-BD-C 的余弦值．(第6题)7. 如图,已知等边三角形ABC 中,E ,F 分别为AB ,AC 边的中点,M 为EF 的中点,N 为BC 边上一点,且CN ＝14BC ,将△AEF 沿EF 折到△A ′EF 的位置,使平面A ′EF ⊥平面EFCB .(1) 求证：平面A ′MN ⊥平面A ′BF ； (2) 求二面角E-A ′F-B 的余弦值．(第7题)微难点9 球的相关问题一、 选择题1. 若球的表面积扩大为原来的2倍,则球的体积比原来增加了( )A. 2倍B. 4倍C. 2 2D. (2 2 －1)倍2. (2019·长沙调研)圆柱形容器的内壁底半径为5 cm,两个直径为5 cm 的玻璃小球都浸没于容器的水中,若取出这两个小球,则容器内水面将下降( )A. 53 cmB. 103 cmC. 403 cmD. 56cm3. 在四面体S ABC 中,SA ⊥平面ABC ,∠BAC ＝120°,SA ＝AC ＝2,AB ＝1,则该四面体的外接球的表面积为( )A. 11πB. 7πC.103 π D. 4034. 已知某球半径为R ,则该球内接长方体的表面积的最大值是( ) A. 8R 2 B. 6R 2 C. 4R 2 D. 2R 25. 两球O 1和O 2在棱长为1的正方体ABCD A 1B 1C 1D 1的内部,且互相外切,若球O 1与过点A 的正方体的三个面相切,球O 2与过点C 1的正方体的三个面相切,则球O 1和O 2的表面积之和的最小值为( )A. (6－33 )πB. (8－43 )πC. (6＋33 )πD. (8＋43 )π二、 填空题6. 如果三棱锥的三个侧面两两垂直,它们的面积分别为6,4,3,那么它的外接球的表面积是________．7. 将长、宽分别为4和3的长方形ABCD 沿对角线AC 折起,得到四面体A BCD ,则四面体A BCD 的外接球的体积为________．8. 底面半径为1 cm 的圆柱形容器里放有四个半径为12 cm 的实心铁球,四个球两两相切,其中底层两球与容器底面相切．现往容器里注水,使水面恰好浸没所有铁球,则需要注水________cm 3.9. 已知三棱锥S ABC 的所有顶点都在球O 的球面上,SC 是球O 的直径．若平面SCA ⊥平面SCB ,SA ＝AC ,SB ＝BC ,三棱锥S ABC 的体积为9,则球O 的表面积为________．10. 已知一个四面体的一条边长为6 ,其余边长均为2,则此四面体的外接球的半径为________．三、解答题11. 有一个倒圆锥形容器,它的轴截面是一个正三角形,在容器内放一个半径为r的铁球,并注入水,使水面与球正好相切,然后将球取出,求这时容器中水的深度．(第11题)。

§1.4 不等关系与不等式1.两个实数比较大小的方法(1)作差法⎩⎪⎨⎪⎧a －b >0⇔a >b a －b ＝0⇔a ＝b a －b <0⇔a <b(a ,b ∈R )(2)作商法⎩⎪⎨⎪⎧ab>1⇔a >b ab ＝1⇔a ＝ba b <1⇔a <b(a ∈R ,b ＞0)2.不等式的基本性质概念方法微思考1.若a ＞b ,且a 与b 都不为0,则1a 与1b的大小关系确定吗？提示 不确定.若a ＞b ,ab ＞0,则1a ＜1b ,即若a 与b 同号,则分子相同时,分母大的反而小；若a ＞0＞b ,则1a ＞1b ,即正数大于负数.2.两个同向不等式可以相加和相乘吗？提示 可以相加但不一定能相乘,例如2＞－1,－1＞－3.题组一 思考辨析1.判断下列结论是否正确(请在括号中打“√”或“×”)(1)两个实数a ,b 之间,有且只有a ＞b ,a ＝b ,a ＜b 三种关系中的一种.( √ ) (2)若ab＞1,则a ＞b .( × )(3)一个不等式的两边同加上或同乘以同一个数,不等号方向不变.( × )(4)a ＞b ＞0,c ＞d ＞0⇒a d ＞bc .( √ )题组二 教材改编2.若a ,b 都是实数,则“a －b ＞0”是“a 2－b 2＞0”的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分又不必要条件答案 A 解析a －b ＞0⇒a ＞b ⇒a ＞b ⇒a 2＞b 2,但a 2－b 2＞0⇏a －b ＞0.3.若a ＞b ＞0,c ＜d ＜0,则一定有( ) A.a c －bd ＞0 B.a c －b d ＜0 C.a d ＞b c D.a d ＜b c答案 D解析 ∵c ＜d ＜0,∴0＜－d ＜－c , 又0＜b ＜a ,∴－bd ＜－ac ,即bd ＞ac , 又∵cd ＞0,∴bd cd ＞ac cd ,即b c ＞ad .题组三 易错自纠4.设a ,b ∈R ,则“a ＞2且b ＞1”是“a ＋b ＞3且ab ＞2”的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分又不必要条件 答案 A解析 若a ＞2且b ＞1,则由不等式的同向可加性可得a ＋b ＞2＋1＝3,由不等式的同向同正可乘性可得ab ＞2×1＝2.即“a ＞2且b ＞1”是“a ＋b ＞3且ab ＞2”的充分条件；反之,若“a ＋b ＞3且ab ＞2”,则“a ＞2且b ＞1”不一定成立,如a ＝6,b ＝12.所以“a ＞2且b ＞1”是“a＋b ＞3且ab ＞2”的充分不必要条件.故选A. 5.(多选)下列命题为真命题的是( ) A.若a ＞b ＞0,则ac 2＞bc 2 B.若a ＜b ＜0,则a 2＞ab ＞b 2 C.若a ＞b ＞0且c ＜0,则c a 2＞cb 2D.若a ＞b 且1a ＞1b ,则ab ＜0答案 BCD解析 当c ＝0时,不等式不成立,∴A 命题是假命题；⎩⎪⎨⎪⎧ a <b ，a <0⇒a 2＞ab ,⎩⎪⎨⎪⎧a <b ，b <0⇒ab ＞b 2,∴a 2＞ab ＞b 2,∴B 命题是真命题；a ＞b ＞0⇒a 2＞b 2＞0⇒0＜1a 2＜1b 2,∵c ＜0,∴c a 2＞cb 2,∴C 命题是真命题；1a ＞1b ⇒1a －1b ＞0⇒b －a ab ＞0,∵a ＞b ,∴b －a ＜0,ab ＜0,∴D 命题是真命题,∴本题选BCD.6.(2019·北京市海淀区育英学校期中)若实数a, b 满足0＜a ＜2, 0＜b ＜1,则a －b 的取值范围是________. 答案 (－1,2)解析 ∵0＜b ＜1,∴－1＜－b ＜0, ∵0＜a ＜2,∴－1＜a －b ＜2.比较两个数(式)的大小例1 (1)若a ＜0,b ＜0,则p ＝b 2a ＋a 2b 与q ＝a ＋b 的大小关系为( )A.p ＜qB.p ≤qC.p ＞qD.p ≥q答案 B解析 (作差法)p －q ＝b 2a ＋a 2b －a －b＝b 2－a 2a ＋a 2－b 2b ＝(b 2－a 2)·⎝⎛⎭⎫1a －1b ＝(b 2－a 2)(b －a )ab ＝(b －a )2(b ＋a )ab ,因为a ＜0,b ＜0,所以a ＋b ＜0,ab ＞0. 若a ＝b ,则p －q ＝0,故p ＝q ； 若a ≠b ,则p －q ＜0,故p ＜q . 综上,p ≤q .故选B.(2)已知a ＞b ＞0,比较a a b b 与a b b a 的大小. 解 ∵a a b b a b b a ＝a a －b b a －b ＝⎝⎛⎭⎫a b a －b,又a ＞b ＞0,故ab ＞1,a －b ＞0,∴⎝⎛⎭⎫a b a －b ＞1,即a a b ba b b a ＞1, 又a b b a ＞0,∴a a b b ＞a b b a ,∴a a b b 与a b b a 的大小关系为a a b b ＞a b b a . 思维升华 比较大小的常用方法(1)作差法:①作差；②变形；③定号；④结论.(2)作商法:①作商；②变形；③判断商与1的大小关系；④结论.跟踪训练1 (1)已知p ∈R ,M ＝(2p ＋1)(p －3),N ＝(p －6)(p ＋3)＋10,则M ,N 的大小关系为________. 答案 M ＞N解析 因为M －N ＝(2p ＋1)(p －3)－[(p －6)(p ＋3)＋10]＝p 2－2p ＋5＝(p －1)2＋4＞0,所以M ＞N .(2)若a ＞0,且a ≠7,则( ) A.77a a ＜7a a 7 B.77a a ＝7a a 7 C.77a a ＞7a a 7D.77a a 与7a a 7的大小不确定 答案 C解析 77a a 7a a7＝77－a a a －7＝⎝⎛⎭⎫7a 7－a ,则当a ＞7时,0＜7a ＜1,7－a ＜0,则⎝⎛⎭⎫7a 7－a＞1,∴77a a ＞7a a 7； 当0＜a ＜7时,7a ＞1,7－a ＞0,则⎝⎛⎭⎫7a 7－a＞1,∴77a a ＞7a a 7. 综上,77a a ＞7a a 7.不等式的基本性质例2 (1)(2020·武汉部分市级示范高中联考)下列命题中正确的是( ) A.若a ＞b ,则ac 2＞bc 2 B.若a ＞b ,c ＜d ,则a c ＞bdC.若a ＞b ,c ＞d ,则a －c ＞b －dD.若ab ＞0,a ＞b ,则1a ＜1b答案 D解析 对于A 选项,当c ＝0时,不成立,故A 选项错误；当a ＝1,b ＝0,c ＝－2,d ＝－1时,a c ＜bd ,故B 选项错误；当a ＝1,b ＝0,c ＝1,d ＝0时,a －c ＝b －d ,故C 选项错误,故D 选项正确. (2)(多选)若1a ＜1b ＜0,则下列结论正确的是( )A.a 2＜b 2B.ab ＜b 2C.a ＋b ＜0D.|a |＋|b |＞|a ＋b |答案 ABC解析 由题意可知b ＜a ＜0,所以A,B,C 正确,而|a |＋|b |＝－a －b ＝|a ＋b |,故D 错误.思维升华判断不等式的常用方法:一是用性质逐个验证；二是用特殊值法排除.利用不等式的性质判断不等式是否成立时要特别注意前提条件.跟踪训练2(1)(多选)(2019·天津市河北区模拟)若a,b,c∈R,给出下列命题中,正确的有()A.若a＞b,c＞d,则a＋c＞b＋dB.若a＞b,c＞d,则b－c＞a－dC.若a＞b,c＞d,则ac＞bdD.若a＞b,c＞0,则ac＞bc答案AD解析∵a＞b,c＞d,由不等式的同向可加性得a＋c＞b＋d,故A正确；由A正确,可知B不正确；取4＞－2,－1＞－3,则4×(－1)＜(－2)×(－3),故C不正确；∵a＞b,c＞0,∴ac＞bc.故D 正确.综上可知,只有AD正确.故选AD.(2)已知a,b,c满足c＜b＜a,且ac＜0,那么下列选项中一定成立的是()A.ab＞acB.c(b－a)＜0C.cb2＜ab2D.ac(a－c)＞0答案 A解析由c＜b＜a且ac＜0,知c＜0且a＞0.由b＞c,得ab＞ac一定成立.不等式性质的综合应用命题点1判断不等式是否成立例3(2019·北京师范大学附属中学期中)若b＜a＜0,则下列不等式:①|a|＞|b|；②a＋b＜ab；③a2b＜2a－b中,正确的不等式有()A.0个B.1个C.2个D.3个答案 C解析 对于①,因为b ＜a ＜0,所以|b |＞|a |,故①错误；对于②,因为b ＜a ＜0,所以a ＋b ＜0,ab ＞0,a ＋b ＜ab ,故②正确；对于③,a 2b －2a ＋b ＝a 2－2ab ＋b 2b ＝(a －b )2b ＜0,a 2b ＜2a －b ,故③正确.故选C.命题点2 求代数式的取值范围例4 已知－1＜x ＜4,2＜y ＜3,则x －y 的取值范围是________,3x ＋2y 的取值范围是________. 答案 (－4,2) (1,18)解析 ∵－1＜x ＜4,2＜y ＜3,∴－3＜－y ＜－2, ∴－4＜x －y ＜2.由－1＜x ＜4,2＜y ＜3,得－3＜3x ＜12,4＜2y ＜6, ∴1＜3x ＋2y ＜18.若将本例条件改为－1＜x ＋y ＜4,2＜x －y ＜3,求3x ＋2y 的取值范围.解 设3x ＋2y ＝m (x ＋y )＋n (x －y ),则⎩⎪⎨⎪⎧m ＋n ＝3，m －n ＝2，∴⎩⎨⎧m ＝52，n ＝12.即3x ＋2y ＝52(x ＋y )＋12(x －y ),又∵－1＜x ＋y ＜4,2＜x －y ＜3, ∴－52＜52(x ＋y )＜10,1＜12(x －y )＜32,∴－32＜52(x ＋y )＋12(x －y )＜232,即－32＜3x ＋2y ＜232,∴3x ＋2y 的取值范围为⎝⎛⎭⎫－32，232. 思维升华 (1)判断不等式是否成立的方法 ①逐一给出推理判断或反例说明.②结合不等式的性质,对数函数、指数函数的性质进行判断. (2)求代数式的取值范围一般是利用整体思想,通过“一次性”不等关系的运算求得整体范围. 跟踪训练3 (1)设b ＞a ＞0,c ∈R ,则下列不等式中不一定成立的是( ) A.1122<a b B.1a －c ＞1b －c C.a ＋2b ＋2＞ab D.ac 2＜bc 2答案 D解析 因为y ＝12x 在(0,＋∞)上是增函数,所以1122<a b ； 因为y ＝1x －c 在(0,＋∞)上是减函数,所以1a －c ＞1b －c ；因为a ＋2b ＋2－a b ＝2(b －a )(b ＋2)b ＞0,所以a ＋2b ＋2＞ab ；当c ＝0时,ac 2＝bc 2,所以D 不成立.故选D.(2)已知π＜α＋β＜5π4,－π＜α－β＜－π3,则2α－β的取值范围是________.答案 ⎝⎛⎭⎫－π，π8 解析 设2α－β＝m (α＋β)＋n (α－β),则⎩⎪⎨⎪⎧m ＋n ＝2，m －n ＝－1，∴⎩⎨⎧m ＝12，n ＝32，即2α－β＝12(α＋β)＋32(α－β),∵π＜α＋β＜5π4,－π＜α－β＜－π3,∴π2＜12(α＋β)＜5π8,－3π2＜32(α－β)＜－π2, ∴－π＜12(α＋β)＋32(α－β)＜π8,即－π＜2α－β＜π8,∴2α－β的取值范围是⎝⎛⎭⎫－π，π8.1.(2019·张家界期末)下列不等式中,正确的是( )A.若ac 2＞bc 2,则a ＞bB.若a ＞b ,则a ＋c ＜b ＋cC.若a ＞b ,c ＞d ,则ac ＞bdD.若a ＞b ,c ＞d ,则a c ＞b d答案 A解析 若a ＞b ,则a ＋c ＞b ＋c ,故B 错；设a ＝3,b ＝1,c ＝－1,d ＝－2,则ac ＜bd ,a c ＜b d所以C,D 错,故选A.2.若a ,b ∈R ,且a ＞|b |,则( )A.a ＜－bB.a ＞bC.a 2＜b 2D.1a ＞1b答案 B 解析 由a ＞|b |得,当b ≥0时,a ＞b ,当b ＜0时,a ＞－b ,综上可知,当a ＞|b |时,则a ＞b 成立,故选B.3.若a ＜b ＜0,则下列不等式一定成立的是( )A.1a －b ＞1b B.a 2＜abC.|b ||a |＜|b |＋1|a |＋1 D.a n ＞b n答案 C解析 (特值法)取a ＝－2,b ＝－1,n ＝0,逐个检验,可知A,B,D 项均不正确；C 项,|b ||a |＜|b |＋1|a |＋1⇔|b |(|a |＋1)＜|a |(|b |＋1)⇔|a ||b |＋|b |＜|a ||b |＋|a |⇔|b |＜|a |,∵a ＜b ＜0,∴|b |＜|a |成立,故选C.4.已知c 3a ＜c 3b ＜0,则下列选项中错误的是( )A.|b |＞|a |B.ac ＞bcC.a －b c ＞0D.ln a b ＞0答案 D解析 c 3a ＜c 3b ＜0,当c ＜0时, 1a ＞1b ＞0,即b ＞a ＞0,∴|b |＞|a |, ac ＞bc, a －b c ＞0成立,即A,B,C 成立；此时0＜a b ＜1,∴ln a b ＜0,D 错误.同理,当c ＞0时,A,B,C 也正确.故选D.5.设M ＝3x＋3y 2,N ＝(3)x ＋y ,P ＝其中0＜x ＜y ),则M ,N ,P 的大小顺序是() A.P ＜N ＜M B.N ＜P ＜MC.P ＜M ＜ND.M ＜N ＜P答案 A解析 M ＝3x ＋3y 2＞3x ＋y ＝(3)x ＋y ＝N ,又N ＝(3)x ＋y ＝23x y＞P ,∴M ＞N ＞P .6.(2020·天津模拟)若α,β满足－π2＜α＜β＜π2,则2α－β的取值范围是( ) A.－π＜2α－β＜0B.－π＜2α－β＜πC.－3π2＜2α－β＜π2D.0＜2α－β＜π 答案 C解析 ∵－π2＜α＜π2,∴－π＜2α＜π. ∵－π2＜β＜π2,∴－π2＜－β＜π2, ∴－3π2＜2α－β＜3π2. 又α－β＜0,α＜π2,∴2α－β＜π2. 故－3π2＜2α－β＜π2. 7.(多选)若a ＜b ＜0,则下列不等式关系中,正确的有( )A.1a ＞1bB.1a ＞1a －bC.2233>a bD.1a 2＞1b 2 答案 ABC解析 对于A,∵a ＜b ＜0,∴1a ＞1b,故A 正确；对于B,∵a ＜b ＜0 ,∴a ＜a －b ＜0,两边同时除以a (a －b )可得1a ＞1a －b,故B 正确；根据幂函数的单调性可知C 正确；对于D,∵a ＜b ＜0,∴a 2＞b 2＞0,∴1a 2＜1b 2,故D 错误. 8.(多选)已知a ,b ∈(0,1),若a ＞b ,则下列所给命题中错误的为( ) A.1(1-)>(1-)aa b b B.2(1-)>(1-)a a b bC.(1＋b )b ＞(1＋a )aD.(1－b )b ＞(1－a )a答案 ABC解析 因为a ,b ∈(0,1)且a ＞b ,所以1＞1－b ＞1－a ＞0,因为指数函数y ＝a x (0＜a ＜1)单调递减,1＞a ＞b ＞0,所以1a ＞a ,a ＞a 2,故A,B 错误. (1＋b )b ＜(1＋a )b ＜(1＋a )a ,故C 错误.(1－b )b ＞(1－b )a ＞(1－a )a ,故D 正确.9.已知a ＋b ＞0,则a b 2＋b a 2与1a ＋1b的大小关系是________. 答案a b 2＋b a 2≥1a ＋1b 解析 a b 2＋b a 2－⎝⎛⎭⎫1a ＋1b ＝a －b b 2＋b －a a 2 ＝(a －b )·⎝⎛⎭⎫1b 2－1a 2＝(a ＋b )(a －b )2a 2b 2. ∵a ＋b ＞0,(a －b )2≥0,∴(a ＋b )(a －b )2a 2b 2≥0. ∴a b 2＋b a 2≥1a ＋1b. 10.已知有三个条件:①ac 2＞bc 2；②a c ＞b c；③a 2＞b 2,其中能成为a ＞b 的充分条件的是________.(填序号)答案 ①解析 由ac 2＞bc 2可知c 2＞0,即a ＞b ,故“ac 2＞bc 2”是“a ＞b ”的充分条件；②当c ＜0时,a ＜b ；③当a ＜0,b ＜0时,a ＜b ,故②③不是a ＞b 的充分条件.11.(1)若bc －ad ≥0,bd ＞0,求证:a ＋b b ≤c ＋d d； (2)已知c ＞a ＞b ＞0,求证:a c －a ＞b c －b. 证明 (1)∵bc ≥ad ,bd ＞0,∴c d ≥a b, ∴c d ＋1≥a b ＋1,∴a ＋b b ≤c ＋d d. (2)∵c ＞a ＞b ＞0,∴c －a ＞0,c －b ＞0.∵a ＞b ＞0,∴1a ＜1b, 又∵c ＞0,∴c a ＜c b ,∴c －a a ＜c －b b,又c －a ＞0,c －b ＞0,∴a c －a ＞bc －b .12.已知1＜a ＜4,2＜b ＜8,试求a －b 与a b 的取值范围.解 因为1＜a ＜4,2＜b ＜8,所以－8＜－b ＜－2.所以1－8＜a －b ＜4－2,即－7＜a －b ＜2.又因为18＜1b ＜12,所以18＜a b ＜42＝2,即18＜a b ＜2.故a －b 的取值范围为(－7,2),a b 的取值范围为⎝⎛⎭⎫18，2.13.已知a ,b ,c ,d 为实数,则“a ＞b 且c ＞d ”是“ac ＋bd ＞bc ＋ad ”的() A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分又不必要条件答案 A解析 因为c ＞d ,所以c －d ＞0.又a ＞b ,所以两边同时乘(c －d ),得a (c －d )＞b (c －d ),即ac ＋bd ＞bc ＋ad .若ac ＋bd ＞bc ＋ad ,则a (c －d )＞b (c －d ),也可能a ＜b 且c ＜d ,所以“a ＞b 且c ＞d ”是“ac ＋bd ＞bc ＋ad ”的充分不必要条件.14.若a ＝ln 33,b ＝ln 44,c ＝ln 55,则( )A.a ＜b ＜cB.c ＜b ＜aC.c ＜a ＜bD.b ＜a ＜c答案 B解析 方法一 对于函数y ＝f (x )＝ln x x (x ＞e),y ′＝1－ln xx 2,易知当x ＞e 时,函数f (x )单调递减.因为e ＜3＜4＜5,所以f (3)＞f (4)＞f (5),即c ＜b ＜a .方法二 易知a ,b ,c 都是正数,因为b a ＝3ln 44ln 3＝log 8164＜1,所以a ＞b ；因为b c ＝5ln 44ln 5＝log 6251 024＞1,所以b ＞c .即c ＜b ＜a .15.(2019·抚州临川第一中学模拟)设m ＝log 0.30.6,n ＝12log 20.6,则() A.m －n ＞mn ＞m ＋n B.m －n ＞m ＋n ＞mnC.mn ＞m －n ＞m ＋nD.m ＋n ＞m －n ＞mn答案 B解析 因为m ＝log 0.30.6＞log 0.31＝0,n ＝12log 20.6＜12log 21＝0,所以mn ＜0,m －n ＞0,因为－1n ＝－2log 0.62＝log 0.60.25＞0,1m ＝log 0.60.3＞0,而log 0.60.25＞log 0.60.3,所以－1n ＞1m＞0,即可得m ＋n ＞0, 因为(m －n )－(m ＋n )＝－2n ＞0,所以m －n ＞m ＋n ,所以m －n ＞m ＋n ＞mn .故选B.16.设0＜b ＜a ＜1,则下列不等式成立的是( )A.a ln b ＞b ln aB.a ln b ＜b ln aC.a e b ＜b e aD.a e b ＝b e a答案 B解析 观察A,B 两项,实际上是在比较ln b b 和ln a a 的大小,引入函数y ＝ln x x ,0＜x ＜1.则y ′＝1－ln x x 2,可见函数y ＝ln x x 在(0,1)上单调递增.所以ln b b ＜ln a a,B 正确.对于C,D 两项,引入函数f (x )＝e x x ,0＜x ＜1,则f ′(x )＝x e x －e x x 2＝(x －1)e x x 2＜0,所以函数f (x )＝e x x在(0,1)上单调递减,又因为0＜b ＜a ＜1,所以f (a )＜f (b ),即e a a ＜e b b ,所以a e b ＞b e a ,故选B.。

多维层次练59[A 级 基础巩固]1．已知⎝ ⎛⎭⎪⎫x －1x 7的展开式的第4项等于5，则x 等于( )A.17 B ．－17C ．7D ．－7解析：由T 4＝C 37x 4⎝⎛⎭⎪⎫－1x 3＝5，得x ＝－17.答案：B2．(2020·合肥八校联考)已知(1＋x )n 的展开式中第5项与第7项的二项式系数相等，则奇数项的二项式系数和为( )A ．29B ．210C ．211D ．212解析：由题意得C 4n ＝C 6n ，由组合数性质得n ＝10，则奇数项的二项式系数和为2n －1＝29.答案：A3．(x 2＋x ＋y )5的展开式中，x 5y 2的系数为( ) A ．10 B ．20 C ．30D ．60解析：(x 2＋x ＋y )5＝[(x 2＋x )＋y ]5的展开式中只有C 25(x 2＋x )3y 2中含x 5y 2，易知x 5y 2的系数为C 25C 13＝30.答案：C4．(2020·佛山质检)若⎝⎛⎭⎪⎫ax －1x 6的展开式的常数项是60，则a 的值为( )A ．4B ．±4C ．2D ．±2解析：⎝ ⎛⎭⎪⎫ax －1x 6的展开式的通项为T r ＋1＝C r 6(ax )6－r ·⎝⎛⎭⎪⎫－1x r ＝(－1)r a 6－r ·C r 6x 6－32r ， 令6－32r ＝0，解得r ＝4.所以常数项为(－1)4a 2C 46＝15a 2＝60，则a ＝±2. 答案：D5．C 1n ＋2C 2n ＋4C 3n ＋…＋2n －1C n n 等于( ) A ．3n B ．2·3n C.3n2－1 D.3n －12解析：C 1n ＋2C 2n ＋4C 3n ＋…＋2n －1C n n ＝12(C 0n ＋2C 1n ＋22C 2n ＋…＋2n C nn )－12＝12(1＋2)n－12＝3n－12. 答案：D6．(x ＋y )(2x －y )5的展开式中x 3y 3的系数为( ) A ．－80 B ．－40 C ．40D ．80解析：因为x 3y 3＝x ·(x 2y 3)，其系数为－C 35·22＝－40， x 3y 3＝y ·(x 3y 2)，其系数为C 25·23＝80.所以x 3y 3的系数为80－40＝40. 故选C. 答案：C7．(2020·青岛质检)在⎝ ⎛⎭⎪⎫x ＋2x 2n(n ∈N *)的展开式中，若二项式系数最大的项仅是第六项，则展开式中常数项是( )A ．180B ．120C ．90D ．45解析：依题意，展开式共11项，所以n ＝10.则⎝ ⎛⎭⎪⎫x ＋2x 210展开式的通项T r ＋1＝C r 10·2r·x 5－5r 2. 令5－5r2＝0，所以r ＝2.所以展开式中的常数项T 3＝C 210·22＝180. 答案：A8．(2020·衡水中学调研)(1＋x 2)·⎝⎛⎭⎪⎫1－1x 6的展开式中，常数项为( )A ．－15B ．16C ．15D ．－16解析：⎝ ⎛⎭⎪⎫1－1x 6的展开式的通项为T r ＋1＝C r 6⎝ ⎛⎭⎪⎫－1x r ＝C r 6(－1)r ·x －r， 令－r ＝0，得r ＝0；令－r ＝－2，得r ＝2.所以展开式的常数项为C 06(－1)0＋C 26(－1)2＝16.答案：B9．若⎝ ⎛⎭⎪⎫ax 2＋b x 6的展开式中x 3项的系数为20，则a 2＋b 2的最小值为________．解析：T r ＋1＝C r6(ax 2)6－r ⎝⎛⎭⎪⎫b x r ＝C r 6a 6－r b r x 12－3r ， 令12－3r ＝3，则r ＝3.所以C 36a 3b 3＝20，即ab ＝1.所以a 2＋b 2≥2ab ＝2，即a 2＋b 2的最小值为2. 答案：210．已知幂函数y ＝x a的图象过点(3，9)，则⎝ ⎛⎭⎪⎫a x －x 8的展开式中x 的系数为________．解析：由幂函数的图象过点(3，9)，可得a ＝2.则⎝ ⎛⎭⎪⎫2x －x 8展开式的第r ＋1项为T r ＋1＝C r8⎝ ⎛⎭⎪⎫2x 8－r ·(－x )r ＝(－1)r C r 8·28－r x 32r －8，由32r －8＝1，得r ＝6，故含x 的项的系数为C 68×22×(－1)6＝112.答案：11211．(2017·浙江卷)已知多项式(x ＋1)3(x ＋2)2＝x 5＋a 1x 4＋a 2x 3＋a 3x 2＋a 4x ＋a 5，则a 4＝________，a 5＝________．解析：a 4是x 项的系数，由二项式的展开式得a 4＝C 33·C 12·2＋C 23·C 22·22＝16； a 5是常数项，由二项式的展开式得a 5＝C 33·C 22·22＝4. 答案：16 412.⎝ ⎛⎭⎪⎫x ＋a x ⎝ ⎛⎭⎪⎫2x －1x 5的展开式中各项系数的和为2，则该展开式中常数项为________．解析：令x ＝1，得展开式各项系数的和为(1＋a )·(2－1)5＝2， 所以a ＝1.因为二项式⎝ ⎛⎭⎪⎫2x －1x 5的展开式的通项公式为T r ＋1＝C r 5(－1)r ·25－r ·x 5－2r，所以⎝ ⎛⎭⎪⎫x ＋1x ⎝ ⎛⎭⎪⎫2x －1x 5展开式中的常数项为x ·C 35(－1)3·22·x －1＋1x·C 25·(－1)2·23·x ＝－40＋80＝40. 答案：40[B 级 能力提升]13．(一题多解)(2020·广州模拟)(2－x 3)(x ＋a )5的展开式的各项系数和为32，则该展开式中x 4的系数是( )A ．5B ．10C ．15D ．20解析：法一 因为(2－x 3)(x ＋a )5的展开式的各项系数和为32，所以(2－1)(1＋a )5＝32，所以a ＝1，因为(x ＋1)5的展开式的通项为T r ＋1＝C r 5·x 5－r ，所以原多项式的展开式中x 4的系数是2×C 15＋(－1)×C 45＝5.法二 因为(2－x 3)(x ＋a )5的展开式的各项系数和为32，所以(2－1)·(1＋a )5＝32，所以a ＝1，因为(x ＋1)5＝x 5＋5x 4＋10x 3＋10x 2＋5x ＋1，所以(2－x 3)(x ＋a )5的展开式中x 4的系数是2×5＋(－1)×5＝5.答案：A14．在(1＋x )6(1＋y )4的展开式中，记x m y n 项的系数为f (m ，n )，则f (3，0)＋f (2，1)＋f (1，2)＋f (0，3)＝( )A ．45B ．60C ．120D ．210解析：在(1＋x )6的展开式中，x m 的系数为C m 6，在(1＋y )4的展开式中，y n 的系数为C n 4，故f (m ，n )＝C m6·C n 4， 所以f (3，0)＋f (2，1)＋f (1，2)＋f (0，3)＝C 36C 04＋C 26C 14＋C 16C 24＋C 06C 34＝120.答案：C15．(2019·江苏卷节选)设(1＋x )n ＝a 0＋a 1x ＋a 2x 2＋…＋a n x n ，n ≥4，n ∈N *，已知a 23＝2a 2a 4.则n ＝________．解析：因为(1＋x )n ＝C 0n ＋C 1n x ＋C 2n x 2＋…＋C n n x n，n ≥4，所以a 2＝C 2n ＝n （n －1）2，a 3＝C 3n ＝n （n －1）（n －2）6， a 4＝C 4n ＝n （n －1）（n －2）（n －3）24.因为a 23＝2a 2a 4，所以⎣⎢⎡⎦⎥⎤n （n －1）（n －2）62＝2×n （n －1）2×n （n －1）（n －2）（n －3）24.解得n ＝5. 答案：5[C 级 素养升华]16．(2019·浙江卷)在二项式(2＋x )9的展开式中，常数项是________，系数为有理数的项的个数是________．解析：由二项展开式的通项公式可知T r ＋1＝C r 9·(2)9－r ·x r ，r ∈N ，0≤r ≤9，当为常数项时，r ＝0，T 1＝C 09·(2)9·x 0＝(2)9＝16 2.当项的系数为有理数时，9－r 为偶数，可得r ＝1，3，5，7，9，即系数为有理数的项的个数是5. 答案：162 5。

[考案1]第一章综合过关规范限时检测(时间：45分钟满分100分)一、单选题(本大题共7个小题，每小题5分，共35分，在每小题给出的四个选项中只有一个是符合题目要求的)1.(2020·兰州市高三诊断考试)已知集合A＝{x∈N|－1＜x＜4}，B⊆A，则集合B中的元素个数至多是(B)A.3B.4C.5D.6【试题解答】因为A＝|x∈N|－1＜x＜4}＝{0,1,2,3}，且B⊆A，所以集合B中的元素个数至多是4，故选B.2.(2018·课标全国Ⅲ，1)已知集合A＝{x|x－1≥0}，B＝{0,1,2}，则A∩B＝(C)A.{0}B.{1}C.{1,2}D.{0,1,2}【试题解答】本题考查集合的运算.∵A＝{x|x－1≥0}＝{x|x≥1}，B＝{0,1,2}，∴A∩B＝{1,2}，故选C.3.(2020·成都市二诊)设全集U＝R，集合A＝{x|－1＜x＜3}，B＝{x|x≤－2或x≥1}，则A∩(∁U B)＝(A)A.{x|－1＜x＜1}B.{x|－2＜x＜3}C.{x|－2≤x＜3}D.{x|x≤－2或x>－1}【试题解答】由题意知∁U B＝{x|－2＜x＜1}，则A∩(∁U B)＝{x|－1＜x＜3}∩{x|－2＜x＜1}＝{x|－1＜x＜1}.4.(2020·宁夏中卫模拟)命题“若a2＋b2＝0，则a＝0且b＝0”的逆否命题是(D)A.若a2＋b2≠0，则a≠0且b≠0B.若a2＋b2≠0，则a≠0或b≠0C.若a＝0且b＝0，则a2＋b2≠0D.若a≠0或b≠0，则a2＋b2≠0【试题解答】命题“若a2＋b2＝0，则a＝0且b＝0”的逆否命题是“若a≠0或b≠0，则a2＋b2≠0”，故选D.5.(2020·山东潍坊重点高中联考)毛泽东同志在《清平乐·六盘山》中的两句诗为“不到长城非好汉，屈指行程二万”，假设诗句的前一句为真命题，则“到长城”是“好汉”的(B)A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【试题解答】解法一：由“不到长城非好汉”可知，要想成为好汉必须到过长城，因此“到长城”是“好汉”的必要不充分条件.解法二：设¬p为不到长城，推出¬q非好汉，即¬p⇒¬q，由原命题与其逆否命题等价可知q⇒p，即好汉⇒到长城，故“到长城”是“好汉”的必要不充分条件.故选B.6.下列命题中，真命题是( D )A.命题“若a >b ，则ac 2>bc 2”B.命题“若a ＝b ，则|a |＝|b |”的逆命题C.命题“当x ＝2时，x 2－5x ＋6＝0”的否命题D.命题“终边相同的角的同名三角函数值相等”的逆否命题【试题解答】 命题“若a >b ，则ac 2>bc 2”是假命题，如a >b 且c ＝0时，ac 2＝bc 2；命题“若a ＝b ，则|a |＝|b |”的逆命题为“若|a |＝|b |，则a ＝b ”是假命题；命题“当x ＝2时，x 2－5x ＋6＝0”的否命题为“若x ≠2，则x 2－5x ＋6≠0”是假命题；命题“终边相同的角的同名三角函数值相等”是真命题，其逆否命题与原命题等价，为真命题，故选D.7.(2020·广东汕头模拟)已知命题p ：关于x 的方程x 2＋ax ＋1＝0没有实根；命题q ：∀x >0，均有2x －a >0.若“¬p ”和“p ∧q ”都是假命题，则实数a 的取值范围是( C )A.(－∞，－2)B.(－2,1]C.(1,2)D.(1，＋∞)【试题解答】 若方程x 2＋ax ＋1＝0没有实根，则判别式Δ＝a 2－4＜0，即－2＜a ＜2，即p ：－2＜a ＜2.∀x >0,2x －a >0则a ＜2x ，当x >0时，2x >1，则a ≤1，即q ：a ≤1.∵¬p 是假命题，∴p 是真命题.∵p ∧q 是假命题，∴q 是假命题，即⎩⎪⎨⎪⎧－2<a <2，a >1，得1＜a ＜2.故选C. 二、多选题(本大题共3个小题，每小题5分，共15分，在每小题给出的四个选项中，有多项符合题目要求全部选对的得5分，部分选对的得3分，有选错的得0分)8.(2020·重庆市第一次调研抽测改编)已知集合A ＝{1,2，m }，B ＝{3,4}，若A ∪B ＝{1,2,3,4}，则实数m 可以为( CD )A.1B.2C.3D.4 【试题解答】 解法一：由题意知m 是B 中的元素，则m ＝3或4，故选C 、D.解法二：由集合中元素的互异性知，m ≠1且m ≠2，故排除选项A 、B ，选C 、D.9.(2020·福建三明一中期中改编)下列选项中错误的有( ABC )A.命题“若x 2＝1，则x ＝1”的否命题为：“若x 2＝1，则x ≠1”B.“A ≠∅”是“A ∩B ≠∅”的充分不必要条件C.命题“∃x ∈R ，使得x 2＋x －1＜0”的否定是“∀x ∈R ，均有x 2＋x －1>0”D.命题“若x ＝y ，则sin x ＝sin y ”的逆否命题为真命题【试题解答】 对于A ，命题“若x 2＝1，则x ＝1”的否命题为：“若x 2≠1，则x ≠1”∴A 错误； 对于B ，由“A ≠∅”是得不到“A ∩B ≠∅”，即“A ≠∅”是“A ∩B ≠∅”不充分条件，由“A ∩B ≠∅”可知“A ≠∅”，即“A ≠∅”是“A ∩B ≠∅”必要条件，故“A ≠∅”是“A ∩B ≠∅”必要不充分条件，∴B 错误；对于C ，命题“∃x ∈R ，使得x 2＋x －1＜0”的否定是“∀x ∈R ，使得x 2＋x －1≥0”，∴C 错误； 对于D ，命题“若x ＝y ，则sin x ＝sin y ”为真命题，根据互为逆否命题的两个命题同真假，可知，命题“若x ＝y ，则sin x ＝sin y ”的逆否命题为真命题，∴D 正确；故A 、B 、C.10.(2020·凤城市第一中学高一月考改编)不等式1≤|x |≤4成立的充分不必要条件为( AB )A.[－4，－1]B.[1,4]C.[－4，－1]∪[1,4]D.[－4,4]【试题解答】 由不等式1≤|x |≤4，解得：－1≤x ≤－1或1≤x ≤4，对于A ，B 选项中的集合是不等式解集的真子集，∴不等式1≤|x |≤4成立的充分不必要条件为A ，B.故选A 、B.三、填空题(本大题共4小题，每小题5分，共20分.把答案填在题中的横线上)11.(2018·湖南卷)已知集合U ＝{1,2,3,4}，A ＝{1,3}，B ＝{1,3,4}，则A ∪(∁U B )＝__{1,2,3}__. 【试题解答】 ∵∁U B ＝{2}，∴A ∪(∁U B )＝{1,2,3}.12.(2020·江西上饶模拟)命题“∀x ∈R ，|x |＋x 2≥0”的否定是 ∃x 0∈R ，|x 0|＋x 20＜0 .【试题解答】 因为全称命题的否定是特称命题，所以命题“∀x ∈R ，|x |＋x 2≥0”的否定是“∃x 0∈R ，|x 0|＋x 20＜0”.13.(2020·湖南常德一中模拟)条件p ：1－x ＜0，条件q ：x >a ，若p 是q 的充分不必要条件，则a 的取值范围是__(－∞，1)__.【试题解答】 p ：x >1，若p 是q 的充分不必要条件，则p ⇒q 但qp ，也就是说，p 对应的集合是q 对应的集合的真子集，所以a ＜1.14.(2020·衡水金卷A 信息卷(五)，14)命题p ：若x >0，则x >a ；命题q ：若m ≤a －2，则m ＜sin x (x ∈R )恒成立.若p 的逆命题，q 的逆否命题都是真命题，则实数a 的取值范围是__[0,1)__.【试题解答】 命题p 的逆命题是若x >a ，则x >0，故a ≥0.因为命题q 的逆否命题为真命题，所以命题q 为真命题，则a －2＜－1，解得a ＜1.则实数a 的取值范围是[0,1).四、解答题(本大题共2个小题，共30分，解答应写出文字说明、证明过程或演算步骤)15.(本小题满分15分)已知集合A ＝{x |x 2－6x ＋8＜0}，B ＝{x |(x －a )(x －3a )＜0}，a ∈R .(1)若x ∈A 是x ∈B 的充分条件，求实数a 的取值范围；(2)若A ∩B ＝∅，求实数a 的取值范围.【试题解答】 A ＝{x |x 2－6x ＋8＜0}＝{x |2＜x ＜4}，B ＝{x |(x －a )(x －3a )＜0}.(1)当a ＝0时，B ＝∅，不符合题意，当a >0时，B ＝{x |a ＜x ＜3a }，要满足题设条件，则⎩⎪⎨⎪⎧a ≤2，3a ≥4，解得43≤a ≤2. 当a ＜0时，B ＝{x |3a ＜x ＜a }，要满足题设条件，则⎩⎪⎨⎪⎧3a ≤2，a ≥4，无解. 综上可知：43≤a ≤2. (2)要满足A ∩B ＝∅.当a >0时，B ＝{x |a ＜x ＜3a }，则a ≥4或3a ≤2，即0＜a ≤23或a ≥4， 当a ＜0时，B ＝{x |3a ＜x ＜a }，则a ≤2或3a ≥4，即a ＜0，当a ＝0时，B ＝∅，满足题意.综上可知：a ≤23或a ≥4. 16.(本小题满分15分)设命题p ：方程x 28－a ＋y 2a －4＝1表示焦点在x 轴上的椭圆，命题q ：函数f (x )＝13x 3＋3(3－a )2x 2＋9x 无极值. (1)若p 为真命题，求实数a 的取值范围；(2)若“p ∧q ”为假命题，“p ∨q ”为真命题，求实数a 的取值范围.【试题解答】 (1)由⎩⎪⎨⎪⎧ 8－a >0a －4>08－a >a －4得4＜a ＜6， ∴实数a 的取值范围为(4,6).(2)由题意知p ，q 一真一假，q 为真时，则f ′(x )＝x 2＋3(3－a )x ＋9≥0恒成立，∴Δ＝9(3－a )2－36≤0得1≤a ≤5，若p 真q 假，5＜a ＜6；若q 真p 假，1≤a ≤4.综上，实数a 的取值范围是[1,4]∪(5,6).。

第五章 平面向量与复数第26讲 平面向量的概念与线性运算A 应知应会一、 选择题1. (多选)如图,若D ,E ,F 分别是△ABC 的边AB ,BC ,CA 的中点,则下列等式中正确的是( )(第1题)A. FD → ＋DA → ＋DE →＝0 B. AD → ＋BE → ＋CF →＝0C. FD → ＋DE → ＋AD → ＝AB →D. AD → ＋EC → ＋FD → ＝BD →2. 在平行四边形ABCD 中,对角线AC 与BD 交于点O ,若AB → ＋AD → ＝λAO →,则λ等于( )A. 1B. 2C. 4D. 63. 在等腰梯形ABCD 中,AB → ＝－2CD → ,M 为BC 的中点,则AM →等于( ) A. 12 AB → ＋12 AD → B. 34 AB → ＋12 AD → C. 34 AB → ＋14 AD → D. 12 AB → ＋34AD → 4. 在△ABC 中,设三边AB ,BC ,CA 的中点分别为E ,F ,D ,则EC → ＋F A →等于( ) A. BD → B. 12 BD → C. AC →D. 12AC →5. (2019·河北三市联考)已知e 1,e 2是不共线向量,a ＝m e 1＋2e 2,b ＝n e 1－e 2,且mn ≠0,若a ∥b,则mn等于( )A. －12B. 12 C. －2 D. 2二、 解答题6. 设e 1,e 2是两个不共线向量,已知AB → ＝2e 1－8e 2,CB → ＝e 1＋3e 2,CD →＝2e 1－e 2. (1) 求证：A ,B ,D 三点共线；(2) 若BF →＝3e 1－k e 2,且B ,D ,F 三点共线,求k 的值．7. 在△ABC 中,D ,E 分别为BC ,AC 边上的中点,G 为BE 上一点,且GB ＝2GE ,设AB →＝a,AC → ＝b,试用a,b 表示AD → ,AG → .B 组 能力提升一、 填空题1. 在△ABC 中,若AD → ＝2DB → ,CD → ＝13 CA → ＋λCB →,则λ＝________．2. (2019·无锡期末)在四边形 ABCD 中,已知AB → ＝a ＋2b,BC → ＝－4a －b,CD →＝－5a －3b,其中a,b 是不共线的向量,则四边形ABCD 的形状是________．3. (2019·潍坊一模改编)若M 是△ABC 内一点,且满足BA → ＋BC → ＝4BM → ,则△ABM 与△ACM 的面积之比为________.4. (2019·泰州期末)已知点P 为平行四边形ABCD 所在平面上一点,且满足P A → ＋PB → ＋2PD → ＝0,λP A → ＋μPB → ＋PC →＝0,则λμ＝________．二、 解答题5. 在直角梯形ABCD 中,∠A ＝90°,∠B ＝30°,AB ＝23 ,BC ＝2,点E 在线段CD 上,若AE →＝AD → ＋μAB →,求μ的取值范围．6. (1) 如图(1),在同一个平面内,向量OA → ,OB → ,OC → 的模分别为1,1,2 ,OA → 与OC →的夹角为α,且tan α＝7,OB → 与OC → 的夹角为45°.若OC → ＝mOA → ＋nOB →(m ,n ∈R),求m ＋n 的值．(2) 如图(2),在△ABC 中,AH ⊥BC 于点H ,M ∈AH ,AM ＝13 AH ,若AM → ＝xAB → ＋yAC →,求x＋y 的值．图(1)图(2)(第6题)第27讲 平面向量的基本定理与坐标表示A 应知应会一、 选择题1. 已知a ＝(3,－1),b ＝(－1,2),则－3a －2b 等于( )A. (7,1)B. (－7,－1)C. (－7,1)D. (7,－1)2. 已知A ,B ,C 三点共线,且A (3,－6),B (－5,2),若点C 的横坐标为6,则点C 的纵坐标为( )A. －13B. 9C. －9D. 133. 已知a ＝(1,2),b ＝(x ,1),若a ＋2b 与2a －b 平行,则x 等于( )A. 12B. 1C. －1D. 2 4. 在△ABC 中,P ,Q 分别是AB ,BC 的三等分点,且AP → ＝13 AB → ,BQ → ＝13 BC → .若AB →＝a,AC → ＝b,则PQ →等于( )A. 13 a ＋13 bB. －13 a ＋13 bC. 13 a －13 bD. －13 a －13b5. (多选)设e 1,e 2为平面α上不共线的两个向量,则下列命题中正确的是( ) A. λe 1＋u e 2(λ,u ∈R)可以表示平面α内的所有向量B. 对于平面α内任一向量a,使a ＝λe 1＋u e 2的实数对(λ,u )有无穷多个C. 若向量λ1e 1＋u 1e 2与λ2e 1＋u 2e 2共线,则有且只有一个实数λ,使得λ1e 1＋u 1e 2＝λ(λ2e 1＋u 2e 2)D. 若实数λ,u 使得λe 1＋u e 2＝0,则λ＝u ＝0二、 解答题6. 设OA → ＝(1,－2),OB → ＝(a ,－1),OC →＝(－b ,0),a ＞0,b ＞0,O 为坐标原点,若A ,B ,C 三点共线,求1a ＋2b的最小值．7. 如图,以向量OA → ＝a,OB → ＝b 为邻边作OADB ,BM →＝13 BC → ,CN → ＝13 CD → ,用a,b 表示OM → ,ON → ,MN →.(第7题)B 组 能力提升一、 填空题1. 已知梯形ABCD 中,AB ∥CD ,且DC ＝2AB ,若三个顶点分别为A (1,2),B (2,1),C (4,2),则点D 的坐标为________．2. 已知|OA → |＝1,|OB → |＝3 ,OA → ·OB → ＝0,点C 在∠AOB 内,且OC → 与OA →的夹角为30°,设OC → ＝mOA → ＋nOB →(m ,n ∈R),则m n的值为________．3. (2019·南昌十校二模)已知向量a ＝(1,－2),b ＝(x ,3y －5),且a ∥b,若x ,y 均为正数,则xy 的最大值是________．4. 在平面直角坐标系xOy 中,已知A (1,0),B (0,1),C 为坐标平面内第一象限内一点且∠AOC ＝π4,且|OC |＝2,若OC → ＝λOA → ＋μOB →,则λ＋μ＝________．二、 解答题5. (2019·长沙模拟改编)在平面直角坐标系xOy 中,已知点A (3 ,0),B (1,2),动点P 满足OP → ＝λOA → ＋μOB →,其中λ,μ∈[0,1],λ＋μ∈[1,2],求所有点P 构成的图形的面积．6. 已知正三角形ABC 的边长为23 ,平面ABC 内的动点P ,M 满足|AP → |＝1,PM → ＝MC →,求|BM →|2的最大值．第28讲 平面向量数量积的应用A 应知应会一、 选择题 1. (2019·深圳二调)已知向量a ＝(1,－1),b ＝(－2,3).若a ⊥(a ＋m b),则m 等于( ) A. 25 B. －25 C. 0 D. 152. (2019·芜湖期末)已知向量a,b 满足a ＝(cos α,sin α),α∈R,a·b ＝－1,则a·(2a －b)等于( )A. 3B. 2C. 1D. 03. (2019·太原期末)设向量a,b,c 都是单位向量,且2a ＝b －3 c,则a,b 的夹角为( ) A. π6 B. π4 C. π3 D. 2π34. (2019·长沙检测)在△ABC 中,AB ＝10,BC ＝6,CA ＝8,且O 是△ABC 的外心,则CA → ·AO → 等于( )A. 16B. 32C. －16D. －325. (多选)给出下列四个命题,其中正确的选项有( )A. 非零向量a,b 满足|a|＝|b|＝|a －b|,则a 与a ＋b 的夹角是30°B. 若(AB → ＋AC → )·(AB → －AC → )＝0,则△ABC 为等腰三角形C. 若单位向量a,b 的夹角为120°,则当|2a ＋x b|(x ∈R)取最小值时x ＝1D. 若OA → ＝(3,－4),OB → ＝(6,－3),OC →＝(5－m ,－3－m ),∠ABC 为锐角,则实数m 的取值范围是m ＞－34二、 解答题6. 已知两向量e 1,e 2满足|e 1|＝2,|e 2|＝1,e 1,e 2所成的角为60°,若向量2t e 1＋7e 2与向量e 1＋t e 2所成的角为钝角,求实数t 的取值范围．7. 已知|a|＝4,|b|＝3,(2a －3b)·(2a ＋b)＝61. (1) 求a 与b 的夹角θ； (2) 求|a ＋b|；(3) 若AB → ＝a,BC →＝b,求△ABC 的面积．B 组 能力提升一、 填空题1. (2019·合肥检测)若非零向量a,b 满足a ⊥(a ＋2b),则|a ＋b||b|＝________．2. (2019·福州抽测改编)已知点O 是△ABC 内部一点,且满足OA → ＋OB → ＋OC →＝0,又AB → ·AC → ＝23 ,∠BAC ＝60°,则△OBC 的面积为________．3. (2019·郑州模拟)已知平面向量a,b,c 满足|a|＝|b|＝|c|＝1,若a·b ＝12 ,则(a ＋b)·(2b －c)的最小值为________．4. (2019·江苏淮阴中学)在△ABC 中,∠A ＝60°,AB ＝3,AC ＝2.若BD → ＝2DC → ,AE → ＝λAC →－AB → (λ∈R),且AD → ·AE → ＝－4,则λ的值为________．二、 解答题5. 已知在△ABC 中,角A ,B ,C 的对边分别为a,b,c,向量m ＝(sin A ,sin B ),n ＝(cos B ,cos A ),m·n ＝sin 2C .(1) 求角C 的大小；(2) 若sin A ,sin C ,sin B 成等差数列,且CA → ·(AB → －AC →)＝18,求边c 的长．6. (2019·山东德州模拟)在平面直角坐标系xOy 中,已知四边形OABC 是等腰梯形,A (6,0),C (1,3 ),点M 满足OM →＝12OA → ,点P 在线段BC 上运动(包括端点),如图所示．(1) 求∠OCM 的余弦值；(2) 是否存在实数λ,使(OA → －λOP → )⊥CM →？若存在,求出满足条件的实数λ的取值范围；若不存在,请说明理由．(第6题)第29讲 复 数 A 应知应会一、 选择题1. 若复数z 满足(2－i)z ＝|1＋2i|,则z 的虚部为( ) A.55 B. 55i C. 1 D. i 2. 已知复数z ＝|(3 －i)i|＋i 5(i 为虚数单位),则复数z 的共轭复数为( ) A. 2－i B. 2＋i C. 4－i D. 4＋i3. 设i 是虚数单位,如果复数a ＋i2－i 的实部与虚部相等,那么实数a 的值为( )A. 13B. －13C. 3D. －3 4. 设复数z ＝lg (m 2－1)＋1－m i,则z 在复平面内对应的点( ) A. 一定不在第一、二象限 B. 一定不在第二、三象限 C. 一定不在第三、四象限D. 一定不在第二、三、四象限5. (多选)(2019·山东枣庄模拟改编)设z 1,z 2是复数,则下列命题中的真命题是( ) A. 若|z 1－z 2|＝0,则z 1＝z 2 B. 若z 1＝z 2,则z 1＝z 2 C. 若|z 1|＝|z 2|,则z 1·z 1＝z 2·z 2D. 若|z 1|＝|z 2|,则z 21 ＝z 22二、 解答题6. 已知z 是复数,z ＋2i,z2－i 均为实数(i 为虚数单位),且复数(z ＋a i)2在复平面内对应的点在第一象限,求实数a 的取值范围．7. 设z 1是虚数,z 2＝z 1＋1z 1 是实数,且－1≤z 2≤1.(1) 求|z 1|的值以及z 1的实部的取值范围； (2) 若ω＝1－z 11＋z 1,求证：ω为纯虚数．B 组 能力提升一、 填空题1. 设z 2＝z 1－i z 1(其中z 1表示z 1的共轭复数),已知z 2的实部是－1,则z 2的虚部为________．2. 已知i 是虚数单位,若⎝ ⎛⎭⎪⎫2＋i 1＋m i 2＜0(m ∈R),则m 的值为________．3. 定义：若z 2＝a ＋b i(a ,b ∈R,i 为虚数单位),则称复数z 是复数a ＋b i 的平方根．根据定义,复数－3＋4i 的平方根是________．4. 已知复数z ＝a 2－b 2＋(|a |＋a )i(a ,b ∈R),使复数z 为纯虚数的充要条件是________,写出一个使复数z 为纯虚数的充分不必要条件是________．二、 解答题5. 已知O 为坐标原点,向量OZ 1,OZ 2分别对应的复数z 1,z 2,且z 1＝3a ＋5＋(10－a 2)i,z 2＝21－a＋(2a －5)i(a ∈R),若z 1＋z 2是实数． (1) 求实数a 的值；(2) 求以OZ 1,OZ 2为邻边的平行四边形的面积．6. 已知复数z 和ω满足：zω＋2i z －2i ω＋1＝0. (1) 若ω －z ＝2i,求z 和ω；(2) 求证：若|z |＝3 ,则|ω－4i|的值是一个常数,并求出这个常数．。

第1讲 集合及其运算A 应知应会一、 选择题 1. (2019·全国卷Ⅱ)设集合A ＝{x |x 2－5x ＋6＞0},B ＝{x |x －1<0},则A ∩B 等于( ) A. (－∞,1) B. (－2,1) C. (－3,－1) D. (3,＋∞) 2. (2019·全国卷Ⅲ)已知集合A ＝{－1,0,1,2},B ＝{x |x 2≤1},则A ∩B 等于( ) A. {－1,0,1} B. {0,1} C. {－1,1} D. {0,1,2} 3. (2019·宁德质检)已知集合A ＝{x |x ≥1},B ＝{x |x 2－2x －3<0},则A ∪B 等于( ) A. {x |1≤x <3} B. {x |x ＞－1} C. {x |1<x <3} D. {x |x ≥1}4. (多选)设集合A ＝{x |x 2－8x ＋15＝0},B ＝{x |ax －1＝0},若A ∩B ＝B ,则实数a 的值可以为( )A. 15B. 0C. 3D. 135. (多选)给出下列关系,其中正确的选项是( ) A. ∈{{}} B. ⊆{{}} C. ∈{} D. ⊆{}二、 解答题6. 已知M ＝{2,a ,b },N ＝{2a ,2,b 2},且M ＝N ,求实数a ,b 的值．7. 若A ＝{x |x 2－ax ＋a 2－19＝0},B ＝{x |x 2－5x ＋6＝0},C ＝{x |x 2＋2x －8＝0}． (1) 若A ＝B ,求a 的值；(2) 若B ∩A ≠,C ∩A ＝,求a 的值．∅∅∅∅∅∅∅∅∅∅B 巩固提升一、 填空题 1. (2018·南通模拟)已知集合A ＝{0,e x },B ＝{－1,0,1},若A ∪B ＝B ,则x ＝________． 2. (2018·青岛模拟)设集合A ＝{x |(x ＋3)(x －6)≥0},B ＝⎩⎨⎧⎭⎬⎫x |2x ≤14 ,则(∁R A )∩B ＝________．3. (2019·张家口期末)已知全集U ＝Z,A ＝{x |x ＝3n －1,n ∈Z},B ＝{x ||x |＞3,x ∈Z},则A ∩(∁U B )中元素的个数为________．4. (2019·深圳调研)已知集合M ＝{x |x ＞0},N ＝{x |x 2－4≥0},则M ∪N ＝________． 二、 解答题5. 设集合U ＝{2,3,a 2＋2a －3},A ＝{|2a －1|,2},∁U A ＝{5},求实数a 的值．6. 已知全集S ＝{1,3,x 3＋3x 2＋2x },A ＝{1,|2x －1|},如果∁S A ＝{0},则这样的实数x 是否存在？若存在,请说明理由．第2讲 充分条件与必要条件A 应知应会一、 选择题1. 设a ,b ,c ,d 是非零实数,则“ad ＝bc ”是“a ,b ,c ,d 成等比数列”的( ) A. 充分不必要条件 B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件 2. (2019·淄博诊断)若a ,b ∈R,则“|a |＋|b |＞1”是“|a ＋b |＞1”的( ) A. 充分不必要条件 B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件3. 已知直线b 和平面α,则“b α”是b 与α平行的( ) A. 充分不必要条件 B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件4. (2019·江西九校联考)已知命题p ：A ＝⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x －21－x ≤0 ,命题q ：B ＝{x |x －a <0},若命题p 是命题q 的必要不充分条件,则实数a 的取值范围是( )A. (2,＋∞)B. [2,＋∞)C. (－∞,1)D. (－∞,1]5. “a ＝b ＝1”是“直线ax －y ＋1＝0与直线x －by －1＝0平行”的( ) A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件6. (2019·烟台一模)已知a ,b ∈R,则“ab ＞0”是“b a ＋ab ＞2”的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件7. (2019·济宁一模)将函数f (x )＝sin (2x ＋φ)的图象向左平移π6 个单位长度后,得到函数g (x )的图象,则“φ＝π6”是“g (x )为偶函数”的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件 8. (2019·枣庄一模)设a ,b 都是不等于1的正数,则“0<b <a <1”是“log a 3<log b 3”的 ( ) A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件二、 解答题9. 已知p ：(x －m )2＞3(x －m ),q ：x 2＋3x －4<0.若p 是q 的必要不充分条件,求实数m 的取值范围．⊂B巩固提升一、填空题1. (2019·合肥质检)若“x＞2”是“x＞m”的必要不充分条件,则m的取值范围是________．2. “|x|<3”是“x2－x－6<0”的________条件．3. 设a∈R ,则“a＝1”是“直线l1：ax＋2y＝0与直线l2 ：x＋(a＋1)y＋4＝0平行”的________条件．4. (2019·郴州三模)已知p：x2－3x－4≤0；q：x2－6x＋9－m2≤0,若非q是非p的充分不必要条件,则实数m的取值范围是________．二、解答题5. (2020·江苏八校联考)已知集合A＝{x|y＝log2(－4x2＋15x－9),x∈R},B＝{x||x－m|≥1,x∈R}．(1) 求集合A；(2) 若p：x∈A,q：x∈B,且p是q的充分不必要条件,求实数m的取值范围．6. 已知数列{a n}的前n项和S n＝3n＋t(n∈N*).求证：数列{a n}是等比数列的充要条件是t＝－1.第3讲全称量词和存在量词A应知应会一、选择题1. (多选)下列命题中是全称命题并且是假命题的是()A. π是无理数B. 若2x为偶数,则任意x∈NC. 对任意x∈R,x2＋2x＋1＞0D. 所有菱形的四条边都相等2. (2019·南昌调研)下列命题中的假命题是( ) A. 存在x 0∈R,lg x 0＝1 B. 存在x 0∈R,sin x 0＝0 C. 任意x ∈R,x 3＞0 D. 任意x ∈R,2x ＞03. 命题“任意n ∈N *,f (n )∈N *且f (n )≤n ”的否定形式是( ) A. 任意n ∈N *,f (n )∉N *且f (n )＞n B. 任意n ∈N *,f (n )N *或f (n )＞n C. 存在n 0∈N *,f (n 0)N *且f (n 0)＞n 0 D. 存在n 0∈N *,f (n 0)N *或f (n 0)＞n 04. (2019·中原名校联盟)已知命题“x ∈R,4x 2＋(a －2)x ＋14 ≤0”是假命题,则实数a 的取值范围为( )A. (－∞,0)B. [0,4]C. [4,＋∞)D. (0,4)5. 若命题p ：x 0∈⎣⎡⎦⎤0，π4 ,sin 2x 0＋cos 2x 0<a 是假命题,则实数a 的取值范围是( )A. (－∞,1]B. (－∞,2 ]C. [1,＋∞)D. [2 ,＋∞) 二、 解答题6. 判断下列命题的真假．(1) 已知a ,b ,c ,d ∈R,若a ≠c 或b ≠d ,则a ＋b ≠c ＋d ； (2) ∀x ∈N,x 3＞x 2；(3) 若m ＞1,则方程x 2－2x ＋m ＝0无实数根； (4) 存在一个三角形没有外接圆．7. 已知命题“∀x ∈R,x 2－5x ＋152a ＞0”的否定为假命题,求实数a 的取值范围．∉∉∉∃∃B 巩固提升一、 填空题1. 若命题p ：x ∈⎣⎡⎦⎤12，2 ,使得2x 2－λx ＋1<0成立,则非p 为_______________． 2. 若命题p 的否定是“对所有正数x ,x ＞x ＋1”,则命题p 可写为________________． 3. 若命题“t ∈R, t 2－2t －a <0”是假命题,则实数a 的取值范围是________．4. 已知函数f (x )＝x ＋4x ,g (x )＝2x ＋a ,若任意x 1∈⎣⎡⎦⎤12，1 ,存在x 2∈[2,3],使得f (x 1)≤g (x 2),则实数a 的取值范围是________． 二、 解答题5. 已知函数f (x )＝x 2－2ax ＋5(a ＞1).若f (x )在区间(－∞,2]上是减函数,且对任意的x 1,x 2∈[1,a ＋1],总有|f (x 1)－f (x 2)|≤4,求实数a 的取值范围．6. 已知函数f (x )＝x 2－2ax ＋1,g (x )＝ax,其中a ＞0,x ≠0.(1) 对任意x ∈[1,2],都有f (x )＞g (x )恒成立,求实数a 的取值范围；(2) 对任意x 1∈[1,2],x 2∈[2,4],都有f (x 1)＞g (x 2)恒成立,求实数a 的取值范围．∃∃第4讲 不等式的性质、一元二次不等式一、 选择题1. (2019·南昌模拟)下列三个不等式：①x ＋1x ≥2(x ≠0)；②c a <cb (a ＞b ＞c ＞0)；③a ＋m b ＋m＞ab(a ,b ,m ＞0且a <b ),恒成立的个数为( ) A. 3 B. 2 C. 1 D. 02. (多选)已知a ,b ,c ,d 均为实数,则下列命题中正确的是( ) A. 若ab ＞0,bc －ad ＞0,则c a －db ＞0B. 若ab ＞0,c a －db ＞0,则bc －ad ＞0C. 若bc －ad ＞0,c a －db＞0,则ab ＞0D. 若a ＞b ＞0,c ＞d ＞0,则ac ＞bd3. (多选)已知关于x 的不等式kx 2－2x ＋6k <0(k ≠0),下列判断正确的是( ) A. 若不等式的解集为{x |x <－3或x ＞－2},则k ＝－25B. 若不等式的解集为⎩⎨⎧⎭⎬⎫x |x ∈R ，x ≠1k ,则k ＝66C. 若不等式的解集为R,则k <－66 D. 若不等式的解集为,则k ≥664. (2019·黄冈联考)若关于x 的不等式ax ＋b ＞0的解集是(1,＋∞),则关于x 的不等式(ax ＋b )(x －2)<0的解集是( )A. (－∞,1)∪(2,＋∞)B. (－1,2)C. (1,2)D. (－∞,－1)∪(2,＋∞)5. (2019·合肥模拟)若不等式2kx 2＋kx －38 <0对一切实数x 都成立,则k 的取值范围为( )A. (－3,0)B. [－3,0)C. [－3,0]D. (－3,0] 二、 解答题6. 已知不等式ax 2＋bx ＋c ＞0的解集为{x |2<x <3},求不等式ax 2－bx ＋c ＞0的解集．7. 若对于满足0≤p ≤3的任意实数p ,不等式x 2＋2px ＞4x ＋p －3恒成立,求x 的取值范围．∅B 巩固提升一、 填空题1. 不等式4x －2x ＋2＞0的解集为________．2. 若关于x 的不等式kx 2－6kx ＋k ＋8<0的解集为空集,则实数k 的取值范围为________．3. 已知函数f (x )是定义在R 上的奇函数,当x ＞0时,f (x )＝x 2－4x ,则不等式f (x )＞x 的解集为________．4. 已知集合A ＝{x |x 2＋a ≤(a ＋1)x ,a ∈R},∃a ∈R,使得集合A 中所有整数的元素和为28,则a 的取值范围是________．二、 解答题5. 若不等式ax 2＋5x －2＞0的解集是⎩⎨⎧⎭⎬⎫x |12<x <2 .(1) 求实数a 的值；(2) 求不等式ax 2－5x ＋a 2－1＞0的解集．6. 已知f (x )＝x 2－2ax ＋2(a ∈R),当x ∈[－1,＋∞)时,f (x )≥a 恒成立,求a 的取值范围．第5讲 基本不等式一、 选择题1. (多选)有下面四个不等式,其中恒成立的有( ) A.a ＋b2≥ab B. a (1－a )≤14C. a 2＋b 2＋c 2≥ab ＋bc ＋caD. b a ＋ab≥2 2. (多选)下列四个函数中,最小值为2的是( ) A. y ＝sin x ＋1sin x ⎝⎛⎭⎫0<x ≤π2 B. y ＝ln x ＋1ln x (x ＞0,x ≠1)C. y ＝x 2＋6x 2＋5D. y ＝4x ＋4－x3. 已知a ＞0,b ＞0,若不等式3a ＋1b ≥ma ＋3b 恒成立,则m 的最大值为( )A. 9B. 12C. 18D. 244. (2019·豫南九校一联)若a ＞0,b ＞0,且2a ＋b ＝4,则1ab 的最小值为( )A. 2B. 12C. 4D. 145. (2019·济宁期末)已知圆C 1：x 2＋y 2－kx ＋2y ＝0与圆C 2：x 2＋y 2＋ky －4＝0的公共弦所在直线恒过定点(a ,b ),且点P 在直线mx －ny －2＝0上,则mn 的取值范围是( )A. ⎝⎛⎭⎫0，14B. ⎝⎛⎦⎤0，14C. ⎝⎛⎭⎫－∞，14D. ⎝⎛⎦⎤－∞，14 二、 解答题6. (2019·黄山质检)已知f (x )＝x 2＋3x ＋6x ＋1 (x ＞0),求f (x )的最小值．7. 已知lg 3x ＋lg y ＝lg (x ＋y ＋1). (1) 求xy 的最小值； (2) 求x ＋y 的最小值．B 巩固提升一、 填空题1. (2017·山东卷)若直线x a ＋yb ＝1(a ＞0,b ＞0)过点(1,2),则2a ＋b 的最小值为________．2. (2017·天津卷)若a ,b ∈R,ab ＞0,则a 4＋4b 4＋1ab 的最小值为________．3. 若a ＞0,b ＞0,且12a ＋b ＋1b ＋1＝1,则a ＋2b 的最小值为________．4. 已知a ,b 均为正数,且ab －a －2b ＝0,则a 2 ＋b 的最小值为________,a 24 －2a ＋b 2－1b的最小值为________．二、 解答题5. (1) 设x 为正实数,且x 2＋y 22＝1,求x 1＋y 2 的最大值． (2) 若a ,b 均为大于1的正数,且ab ＝10,求lg a ·lg b 的最大值．6. 某单位拟建一个扇环面形状的花坛(如图所示),该扇环面是由以点O 为圆心的两个同心圆弧和延长后通过点O 的两条直线段围成．按设计要求扇环面的周长为30 m,其中大圆弧所在圆的半径为10 m ．设小圆弧所在圆的半径为x m,圆心角为θ(弧度).(1) 求y 关于x 的函数关系式；(2) 已知在花坛的边缘(实线部分)进行装饰时,直线部分的装饰费用为4元/米,弧线部分的装饰费用为9元/米．设花坛的面积与装饰总费用的比为y ,求y 关于x 的函数关系式,并求出x 为何值时,y 取得最大值．(第6题)微难点1 “三个二次”关系一、 选择题1. 若函数f (x )＝x 2＋2x ＋a 没有零点,则实数a 的取值范围是( )A. (－∞,1)B. (1,＋∞)C. (－∞,1]D. [1,＋∞)2. 若函数f (x )＝x 2＋ax ＋b 的图象与x 轴的交点为(1,0)和(3,0),则函数f (x )( )A. 在(－∞,2]上单调递减,在(2,＋∞)上单调递增B. 在(－∞,3)上单调递增C. 在[1,3]上单调递增D. 单调性不能确定二、 填空题3. (2019·南昌质检)若二次函数f (x )＝ax 2－x ＋b (a ≠0)的最小值为0,则a ＋4b 的取值范围是________．4. 已知函数f (x )＝x 2＋abx ＋a ＋2b .若f (0)＝4,则f (1)的最大值为________．5. 已知二次函数f (x )＝ax 2－x ＋c (x ∈R)的值域为[0,＋∞),则c ＋2a ＋a ＋2c的最小值为________．6. 已知函数f (x )＝x 2－2|x |＋4的定义域为[a ,b ],其中a <b ,值域为[3a ,3b ],则满足条件的数组(a ,b )为________．三、 解答题7. 对任意a ∈[－1,1],函数f (x )＝x 2＋(a －4)x ＋4－2a 的值总大于零,求x 的取值范围．8. 已知函数f (x )＝ax 2＋2x ＋c 的零点为－13 ,12. (1) 试求a ＋c 的值；(2) 解不等式－cx 2＋2x －a ＞0.9. 设a ∈R,关于x 的一元二次方程7x 2－(a ＋13)x ＋a 2－a －2＝0有两实数根x 1,x 2,且0<x 1<1<x 2<2,求a 的取值范围．10. 已知二次函数f (x )＝ax 2＋bx ＋1(a ,b ∈R 且a ≠0),x ∈R ．(1) 若函数f (x )的最小值为f (－1)＝0,求f (x )的解析式,并写出单调区间；(2) 在(1)的条件下,f (x )＞x ＋k 在区间[－3,－1]上恒成立,试求k 的取值范围．。

§1.5一元二次不等式及其解法一元二次不等式的解集概念方法微思考1.一元二次不等式ax2＋bx＋c＞0(a＞0)的解集与其对应的函数y＝ax2＋bx＋c的图象有什么关系？提示ax2＋bx＋c＞0(a＞0)的解集就是其对应函数y＝ax2＋bx＋c的图象在x轴上方的部分所对应的x的取值范围.2.一元二次不等式ax2＋bx＋c＞0(＜0)恒成立的条件是什么？提示 显然a ≠0.ax 2＋bx ＋c ＞0恒成立的条件是⎩⎪⎨⎪⎧a >0，Δ<0；ax 2＋bx ＋c ＜0恒成立的条件是⎩⎪⎨⎪⎧a <0，Δ<0.题组一 思考辨析1.判断下列结论是否正确(请在括号中打“√”或“×”) (1)若不等式ax 2＋bx ＋c ＜0的解集为(x 1,x 2),则必有a ＞0.( √ )(2)若方程ax 2＋bx ＋c ＝0(a ≠0)没有实数根,则不等式ax 2＋bx ＋c ＞0的解集为R .( × ) (3)不等式ax 2＋bx ＋c ≤0在R 上恒成立的条件是a ＜0且Δ＝b 2－4ac ≤0.( × )(4)若二次函数y ＝ax 2＋bx ＋c 的图象开口向下,则不等式ax 2＋bx ＋c ＜0的解集一定不是空集.( √ ) 题组二 教材改编2.已知集合A ＝{x |x 2－x －6＞0},则∁R A 等于( ) A.{x |－2＜x ＜3} B.{x |－2≤x ≤3} C.{x |x ＜－2或x ＞3} D.{x |x ≤－2或x ≥3} 答案 B解析 ∵x 2－x －6＞0,∴(x ＋2)(x －3)＞0,∴x ＞3或x ＜－2,即A ＝{x |x ＞3或x ＜－2}.在数轴上表示出集合A ,如图所示.由图可得∁R A ＝{x |－2≤x ≤3}. 故选B.3.y ＝log 2(3x 2－2x －2)的定义域是________________. 答案 ⎝ ⎛⎭⎪⎫－∞，1－73∪⎝ ⎛⎭⎪⎫1＋73，＋∞ 解析 由题意,得3x 2－2x －2＞0,令3x 2－2x －2＝0,得x 1＝1－73,x 2＝1＋73,∴3x 2－2x －2＞0的解集为 ⎝ ⎛⎭⎪⎫－∞，1－73∪⎝ ⎛⎭⎪⎫1＋73，＋∞. 题组三 易错自纠4.(多选)关于x 的不等式(ax －1)(x ＋2a －1)＞0的解集中恰有3个整数,则a 的值可以为( ) A.－12 B.1 C.－1 D.2答案 AC解析 由题意知a ＜0,则排除B,D ； 对于A 项,当a ＝－12时,⎝⎛⎭⎫－12x －1(x －2)＞0, 即(x ＋2)(x －2)＜0,解得－2＜x ＜2,恰有3个整数,符合题意；对于C 项,当a ＝－1时,(－x －1)(x －3)＞0,即(x ＋1)(x －3)＜0,解得－1＜x ＜3,恰有3个整数,符合题意,故选AC. 5.不等式－x 2－3x ＋4＞0的解集为________.(用区间表示) 答案 (－4,1)解析 由－x 2－3x ＋4＞0可知,(x ＋4)(x －1)＜0,得－4＜x ＜1.6.若关于x 的不等式ax 2＋bx ＋2＞0的解集是⎝⎛⎭⎫－12，13,则a ＋b ＝________. 答案 －14解析 ∵x 1＝－12,x 2＝13是方程ax 2＋bx ＋2＝0的两个根,∴⎩⎨⎧a 4－b2＋2＝0，a 9＋b3＋2＝0，解得⎩⎪⎨⎪⎧a ＝－12，b ＝－2，∴a ＋b ＝－14.7.不等式(a －2)x 2＋2(a －2)x －4＜0,对一切x ∈R 恒成立,则实数a 的取值范围是________.答案 (－2,2]解析 当a －2≠0时,由⎩⎪⎨⎪⎧a －2<0，Δ<0，得－2＜a ＜2；当a ＝2时,原式化为－4＜0,不等式恒成立, ∴－2＜a ≤2.即实数a 的取值范围是(－2,2].一元二次不等式的求解命题点1 不含参的不等式例1 (2019·济宁模拟)已知全集U ＝R ,集合A ＝{x |x 2－3x ＋2≥0},则∁R A 等于( ) A.(1,2)B.[1,2]C.(－∞,1]∪[2,＋∞)D.(－∞,1)∪(2,＋∞)答案 A解析 由题意可得,∁R A ＝{x |x 2－3x ＋2＜0}＝{x |1＜x ＜2},表示为区间形式即(1,2).故选A. 命题点2 含参不等式例2 解关于x 的不等式ax 2－(a ＋1)x ＋1＜0(a ＞0). 解 原不等式变为(ax －1)(x －1)＜0, 因为a ＞0,所以⎝⎛⎭⎫x －1a (x －1)＜0. 所以当a ＞1时,解得1a ＜x ＜1；当a ＝1时,解集为∅； 当0＜a ＜1时,解得1＜x ＜1a.综上,当0＜a ＜1时,不等式的解集为⎩⎨⎧⎭⎬⎫x |1<x <1a ；当a ＝1时,不等式的解集为∅；当a ＞1时,不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪1a<x <1. 思维升华 对含参的不等式,应对参数进行分类讨论 (1)根据二次项系数为正、负及零进行分类. (2)根据判别式Δ与0的关系判断根的个数. (3)有两个根时,有时还需根据两根的大小进行讨论.跟踪训练1 (1)(2020·北京市海淀区期末)不等式x 2＋2x －3＜0的解集为( ) A.{x |x ＜－3或x ＞1} B.{x |x ＜－1或x ＞3} C.{x |－1＜x ＜3} D.{x |－3＜x ＜1}答案 D解析 由x 2＋2x －3＜0得(x ＋3)(x －1)＜0,解得－3＜x ＜1.故选D.(2)已知不等式ax 2－bx －1＞0的解集是⎩⎨⎧⎭⎬⎫x ⎪⎪－12<x <－13,则不等式x 2－bx －a ≥0的解集是________.答案 {x |x ≥3或x ≤2}解析 由题意,知－12,－13是方程ax 2－bx －1＝0的两个根,且a ＜0,所以⎩⎨⎧a ×⎝⎛⎭⎫－122－b ×⎝⎛⎭⎫－12－1＝0，a ×⎝⎛⎭⎫－132－b ×⎝⎛⎭⎫－13－1＝0，解得⎩⎪⎨⎪⎧a ＝－6，b ＝5.故不等式x 2－bx －a ≥0为x 2－5x ＋6≥0, 解得x ≥3或x ≤2.(3)解不等式12x 2－ax ＞a 2(a ∈R ). 解 原不等式可化为12x 2－ax －a 2＞0, 即(4x ＋a )(3x －a )＞0,令(4x ＋a )(3x －a )＝0, 解得x 1＝－a 4,x 2＝a3.当a ＞0时,不等式的解集为⎝⎛⎭⎫－∞，－a 4∪⎝⎛⎭⎫a3，＋∞； 当a ＝0时,不等式的解集为(－∞,0)∪(0,＋∞)； 当a ＜0时,不等式的解集为⎝⎛⎭⎫－∞，a 3∪⎝⎛⎭⎫－a4，＋∞.一元二次不等式恒成立问题命题点1 在R 上的恒成立问题例3 已知函数f (x )＝mx 2－mx －1.若对于x ∈R ,f (x )＜0恒成立,求实数m 的取值范围. 解 当m ＝0时,f (x )＝－1＜0恒成立.当m ≠0时,则⎩⎪⎨⎪⎧m <0，Δ＝m 2＋4m <0，即－4＜m ＜0. 综上,－4＜m ≤0,故m 的取值范围是(－4,0]. 命题点2 在给定区间上的恒成立问题例4 已知函数f (x )＝mx 2－mx －1.若对于x ∈[1,3],f (x )＜5－m 恒成立,求实数m 的取值范围. 解 要使f (x )＜－m ＋5在x ∈[1,3]上恒成立, 即m ⎝⎛⎭⎫x －122＋34m －6＜0在x ∈[1,3]上恒成立. 有以下两种方法:方法一 令g (x )＝m ⎝⎛⎭⎫x －122＋34m －6,x ∈[1,3]. 当m ＞0时,g (x )在[1,3]上是增函数, 所以g (x )max ＝g (3),即7m －6＜0, 所以m ＜67,所以0＜m ＜67；当m ＝0时,－6＜0恒成立； 当m ＜0时,g (x )在[1,3]上是减函数, 所以g (x )max ＝g (1),即m －6＜0, 所以m ＜6,所以m ＜0.综上所述,m 的取值范围是⎩⎨⎧⎭⎬⎫m ⎪⎪m <67.方法二 因为x 2－x ＋1＝⎝⎛⎭⎫x －122＋34＞0, 又因为m (x 2－x ＋1)－6＜0,所以m ＜6x 2－x ＋1.因为函数y ＝6x 2－x ＋1＝6⎝⎛⎭⎫x －122＋34在[1,3]上的最小值为67,所以只需m ＜67即可. 所以m 的取值范围是⎩⎨⎧⎭⎬⎫m ⎪⎪m <67. 若将“f (x )＜5－m 恒成立”改为“f (x )＜5－m 无解”,如何求m 的取值范围？解 若f (x )＜5－m 无解,即f (x )≥5－m 恒成立, 即m ≥6x 2－x ＋1恒成立,又x ∈[1,3]时,⎝⎛⎭⎫6x 2－x ＋1max ＝6,得m ≥6, 即m 的取值范围为[6,＋∞).若将“f (x )＜5－m 恒成立”改为“存在x ,使f(x )＜5－m 成立”,如何求m 的取值范围？ 解 由题意知f (x )＜5－m 有解,即m ＜6x 2－x ＋1有解,则m ＜⎝⎛⎭⎫6x 2－x ＋1max ,又x ∈[1,3],得m ＜6,即m 的取值范围为(－∞,6). 命题点3 给定参数范围的恒成立问题例5 若mx 2－mx －1＜0对于m ∈[1,2]恒成立,求实数x 的取值范围.解 设g (m )＝mx 2－mx －1＝(x 2－x )m －1,其图象是直线,当m ∈[1,2]时,图象为一条线段,则⎩⎪⎨⎪⎧ g (1)<0，g (2)<0，即⎩⎪⎨⎪⎧x 2－x －1<0，2x 2－2x －1<0， 解得1－32＜x ＜1＋32,故x 的取值范围为⎝⎛⎭⎪⎫1－32，1＋32. 思维升华 解决恒成立问题一定要搞清谁是主元,谁是参数,一般地,知道谁的范围,谁就是主元,求谁的范围,谁就是参数.跟踪训练2 函数f (x )＝x 2＋ax ＋3.(1)若当x ∈R 时,f (x )≥a 恒成立,求实数a 的取值范围； (2)若当x ∈[－2,2]时,f (x )≥a 恒成立,求实数a 的取值范围； (3)若当a ∈[4,6]时,f (x )≥0恒成立,求实数x 的取值范围. 解 (1)∵当x ∈R 时,x 2＋ax ＋3－a ≥0恒成立, 需Δ＝a 2－4(3－a )≤0,即a 2＋4a －12≤0, 解得－6≤a ≤2,∴实数a 的取值范围是[－6,2].(2)由题意可转化为x 2＋ax ＋3－a ≥0在x ∈[－2,2]上恒成立,则(x 2＋ax ＋3－a )min ≥0(x ∈[－2,2]). 令g (x )＝x 2＋ax ＋3－a ,x ∈[－2,2], 函数图象的对称轴方程为x ＝－a2.当－a 2＜－2,即a ＞4时,g (x )min ＝g (－2)＝7－3a ≥0,解得a ≤73,舍去；当－2≤－a 2≤2,即－4≤a ≤4时,g (x )min ＝g ⎝⎛⎭⎫－a 2＝－a 24－a ＋3≥0,解得－6≤a ≤2,∴－4≤a ≤2；当－a2＞2,即a ＜－4时,g (x )min ＝g (2)＝7＋a ≥0,解得a ≥－7,∴－7≤a ＜－4.综上可得,满足条件的实数a 的取值范围是[－7,2]. (3)令h (a )＝xa ＋x 2＋3. 当a ∈[4,6]时,h (a )≥0恒成立.只需⎩⎪⎨⎪⎧ h (4)≥0，h (6)≥0，即⎩⎪⎨⎪⎧x 2＋4x ＋3≥0，x 2＋6x ＋3≥0，解得x ≤－3－6或x ≥－3＋ 6. ∴实数x 的取值范围是(－∞,－3－6]∪[－3＋6,＋∞).设方程ax 2＋bx ＋c ＝0(a ≠0,Δ＞0)有不相等的两根为x 1,x 2,且x 1＜x 2,相应的二次函数为f (x )＝ax 2＋bx ＋c ,方程的根即为二次函数的图象与x 轴交点的横坐标,它们的分布情况见下面各表(每种情况对应的均是充要条件).表一:(两根与0的大小比较即根的正负情况)表二:(两根与k的大小比较)表三:(根在区间上的分布)根在区间上的分布还有一种情况:两根分别在区间(m,n)外,即在区间两侧x1＜m,x2＞n,(图形分别如下)需满足的条件是(1)a ＞0时,⎩⎪⎨⎪⎧ f (m )<0，f (n )<0；(2)a ＜0时,⎩⎪⎨⎪⎧f (m )>0，f (n )>0.对以上的根的分布表中,两根有且仅有一根在(m ,n )内有以下特殊情况:(ⅰ)若f (m )＝0或f (n )＝0,则此时f (m )·f (n )＜0不成立,但对于这种情况是知道了方程有一根为m 或n ,可以求出另外一根,然后可以根据另一根在区间(m ,n )内,从而可以求出参数的值.如方程mx 2－(m ＋2)x ＋2＝0在区间(1,3)上有一根,因为f (1)＝0,所以mx 2－(m ＋2)x ＋2＝(x －1)(mx －2),另一根为2m ,由1＜2m ＜3得23＜m ＜2即为所求；(ⅱ)方程有两个相等的根,且这个根在区间(m ,n )内,即Δ＝0,此时由Δ＝0可以求出参数的值,然后再将参数的值带入方程,求出相应的根,检验根是否在给定的区间内,如若不在,舍去相应的参数.如方程x 2－4mx ＋2m ＋6＝0有且只有一根在区间(－3,0)内,求m 的取值范围.分析:①由f (－3)·f (0)＜0即(14m ＋15)(m ＋3)＜0得出－3＜m ＜－1514；②由Δ＝0即16m 2－4(2m ＋6)＝0得出m ＝－1或m ＝32,当m ＝－1时,根x ＝－2∈(－3,0),即m ＝－1满足题意；当m ＝32时,根x ＝3∉(－3,0),故m ＝32不满足题意.综上分析,得出－3＜m ＜－1514或m ＝－1.例1 已知二次方程(2m ＋1)x 2－2mx ＋(m －1)＝0有一正根和一负根,求实数m 的取值范围. 解 设f (x )＝(2m ＋1)x 2－2mx ＋(m －1), 由(2m ＋1)·f (0)＜0 ,即(2m ＋1)(m －1)＜0, 解得－12＜m ＜1,即m 的取值范围为⎝⎛⎭⎫－12，1. 例2 已知方程2x 2－(m ＋1)x ＋m ＝0有两个不等正实根,求实数m 的取值范围.解 设f (x )＝2x 2－(m ＋1)x ＋m ,由⎩⎪⎨⎪⎧Δ>0，－－(m ＋1)2×2>0，f (0)>0⇒ ⎩⎪⎨⎪⎧(m ＋1)2－8m >0，m >－1，m >0⇒⎩⎪⎨⎪⎧m <3－22或m >3＋22，m >0⇒0＜m ＜3－22或m ＞3＋22,即m 的取值范围为(0,3－22)∪(3＋22,＋∞).例3 已知二次函数f (x )＝(m ＋2)x 2－(2m ＋4)x ＋3m ＋3与x 轴有两个交点,一个大于1,一个小于1,求实数m 的取值范围. 解 由(m ＋2)·f (1)＜0 ,即(m ＋2)·(2m ＋1)＜0 ⇒－2＜m ＜－12,即m 的取值范围为⎝⎛⎭⎫－2，－12.1.(2019·武汉调研)已知集合A ＝{x |x 2－x －2＜0},B ＝{x |x 2＋3x ＜0},则A ∩B 等于( ) A.(0,2) B.(－1,0) C.(－3,2) D.(－1,3)答案 B解析 A ＝{x |－1＜x ＜2},B ＝{x |－3＜x ＜0},∴A ∩B ＝(－1,0).故选B.2.(2020·黄冈调研)关于x 的不等式ax ＋b ＞0的解集是(1,＋∞),则关于x 的不等式(ax ＋b )(x －2)＜0的解集是( ) A.(－∞,1)∪(2,＋∞) B.(－1,2)C.(1,2)D.(－∞,－1)∪(2,＋∞) 答案 C解析 关于x 的不等式ax ＋b ＞0的解集是(1,＋∞), ∴a ＞0,且－ba＝1,∴关于x 的不等式(ax ＋b )(x －2)＜0可化为⎝⎛⎭⎫x ＋ba (x －2)＜0,即(x －1)(x －2)＜0, ∴不等式的解集为{x |1＜x ＜2}.故选C.3.“不等式x 2－x ＋m ＞0在R 上恒成立”的充要条件是( ) A.m ＞14B.m ＜14C.m ＜1D.m ＞1 答案 A解析 ∵不等式x 2－x ＋m ＞0在R 上恒成立, ∴Δ＝(－1)2－4m ＜0,解得m ＞14,又∵m ＞14,∴Δ＝1－4m ＜0,∴“m ＞14”是“不等式x 2－x ＋m ＞0在R 上恒成立”的充要条件.故选A.4.若不等式x 2－(a ＋1)x ＋a ≤0的解集是[－4,3]的子集,则a 的取值范围是( ) A.[－4,1] B.[－4,3] C.[1,3] D.[－1,3]答案 B解析 原不等式为(x －a )(x －1)≤0,当a ＜1时,不等式的解集为[a,1],此时只要a ≥－4即可,即－4≤a ＜1；当a ＝1时,不等式的解为x ＝1,此时符合要求；当a ＞1时,不等式的解集为[1,a ],此时只要a ≤3即可,即1＜a ≤3,综上可得－4≤a ≤3.5.若存在实数x ∈[2,4],使x 2－2x ＋5－m ＜0成立,则m 的取值范围为( ) A.(13,＋∞) B.(5,＋∞) C.(4,＋∞) D.(－∞,13)答案 B解析 m ＞x 2－2x ＋5,设f (x )＝x 2－2x ＋5＝(x －1)2＋4,x ∈[2,4], 当x ＝2时f (x )min ＝5,∃x ∈[2,4]使x 2－2x ＋5－m ＜0成立, 即m ＞f (x )min ,∴m ＞5.故选B.6.在关于x 的不等式x 2－(a ＋1)x ＋a ＜0的解集中至多包含1个整数,则a 的取值范围是( ) A.(－3,5) B.(－2,4) C.[－1,3] D.[－2,4]答案 C解析 因为关于x 的不等式x 2－(a ＋1)x ＋a ＜0可化为(x －1)(x －a )＜0, 当a ＞1时,不等式的解集为{x |1＜x ＜a }, 当a ＜1时,不等式的解集为{x |a ＜x ＜1}, 当a ＝1时,不等式的解集为∅,要使得解集中至多包含1个整数,则a ＝1或1＜a ≤3或－1≤a ＜1, 所以实数a 的取值范围是a ∈[－1,3],故选C. 7.(多选)下列四个解不等式,正确的有( ) A.不等式2x 2－x －1＞0的解集是{x |x ＞2或x ＜1}B.不等式－6x 2－x ＋2≤0的解集是⎩⎨⎧⎭⎬⎫x ⎪⎪x ≤－23或x ≥12C.若不等式ax 2＋8ax ＋21＜0的解集是{x |－7＜x ＜－1},那么a 的值是3D.关于x 的不等式x 2＋px －2＜0的解集是(q,1),则p ＋q 的值为－1 答案 BCD解析 对于A,∵2x 2－x －1＝(2x ＋1)(x －1), ∴由2x 2－x －1＞0得(2x ＋1)(x －1)＞0, 解得x ＞1或x ＜－12,∴不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪x >1或x <－12.故A 错误； 对于B,∵－6x 2－x ＋2≤0,∴6x 2＋x －2≥0, ∴(2x －1)(3x ＋2)≥0,∴x ≥12或x ≤－23.故B 正确；对于C,由题意可知－7和－1为方程ax 2＋8ax ＋21＝0的两个根.∴a －8a ＋21＝0,∴a ＝3.故C 正确；对于D,依题意q,1是方程x 2＋px －2＝0的两根, q ＋1＝－p ,即p ＋q ＝－1,故D 正确.8.(多选)已知关于x 的不等式kx 2－2x ＋6k ＜0(k ≠0),则下列说法正确的是( ) A.若不等式的解集为{x |x ＜－3或x ＞－2},则k ＝－25B.若不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪x ∈R ，x ≠1k ,则k ＝66 C.若不等式的解集为R ,则k ＜－66D.若不等式的解集为∅,则k ≥66答案 ACD解析 对于A,∵不等式的解集为{x |x ＜－3或x ＞－2},∴k ＜0,且－3与－2是方程kx 2－2x ＋6k ＝0的两根,∴4k ＋4＋6k ＝0,解得k ＝－25.故A 正确；对于B,∵不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪x ∈R ，x ≠1k , ∴⎩⎪⎨⎪⎧k <0，Δ＝4－24k 2＝0，解得k ＝－66.故B 错误； 对于C,由题意,得⎩⎪⎨⎪⎧k <0，Δ＝4－24k 2<0，解得k ＜－66.故C 正确；对于D,由题意,得⎩⎪⎨⎪⎧k >0，Δ＝4－24k 2≤0，解得k ≥66.故D 正确.9.(2019·北京市顺义区模拟)满足关于x 的不等式(ax －b )(x －2)＞0的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪12<x <2,则满足条件的一组有序实数对(a ,b )的值可以是________. 答案 (－2,－1)(答案不唯一)解析 不等式(ax －b )(x －2)＞0的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪12<x <2, ∴方程(ax －b )(x －2)＝0的实数根为12和2,且⎩⎪⎨⎪⎧a <0，b a ＝12，即a ＝2b ＜0,则满足条件的一组有序实数对(a ,b )的值可以是(－2,－1).10.在R 上定义运算⊗:x ⊗y ＝x (1－y ),若不等式(x －a )⊗(x ＋a )＜1对任意实数x 恒成立,则实数a 的取值范围为________. 答案 ⎝⎛⎭⎫－12，32 解析 由题意,可知不等式(x －a )⊗(x ＋a )＜1对任意实数x 都成立, 又由(x －a )⊗(x ＋a )＝(x －a )(1－x －a ), 即x 2－x －a 2＋a ＋1＞0对任意实数x 都成立, 所以Δ＝1－4(－a 2＋a ＋1)＜0,即4a 2－4a －3＜0, 解得－12＜a ＜32.11.已知关于x 的不等式－x 2＋ax ＋b ＞0. (1)若该不等式的解集为(－4,2),求a ,b 的值； (2)若b ＝a ＋1,求此不等式的解集.解 (1)根据题意得⎩⎪⎨⎪⎧－16－4a ＋b ＝0，－4＋2a ＋b ＝0，解得a ＝－2,b ＝8.(2)当b ＝a ＋1时,－x 2＋ax ＋b ＞0⇔x 2－ax －(a ＋1)＜0, 即[x －(a ＋1)](x ＋1)＜0.当a ＋1＝－1,即a ＝－2时,原不等式的解集为∅； 当a ＋1＜－1,即a ＜－2时,原不等式的解集为(a ＋1,－1)； 当a ＋1＞－1,即a ＞－2时,原不等式的解集为(－1,a ＋1).综上,当a ＜－2时,不等式的解集为(a ＋1,－1)；当a ＝－2时,不等式的解集为∅；当a ＞－2时, 不等式的解集为(－1,a ＋1).12.甲厂以x 千克/小时的速度匀速生产某种产品(生产条件要求1≤x ≤10),每小时可获得的利润是100⎝⎛⎭⎫5x ＋1－3x 元. (1)要使生产该产品2小时获得的利润不低于3 000元,求x 的取值范围；(2)要使生产900千克该产品获得的利润最大,则甲厂应该选取何种生产速度？并求最大利润.解 (1)根据题意,得200⎝⎛⎭⎫5x ＋1－3x ≥3 000, 整理得5x －14－3x≥0,即5x 2－14x －3≥0, 又1≤x ≤10,可解得3≤x ≤10.故要使生产该产品2小时获得的利润不低于3 000元,x 的取值范围是[3,10].(2)设利润为y 元,则y ＝900x·100⎝⎛⎭⎫5x ＋1－3x ＝9×104⎝⎛⎭⎫5＋1x －3x 2 ＝9×104⎣⎡⎦⎤－3⎝⎛⎭⎫1x －162＋6112, 故当x ＝6时,y max ＝457 500.故甲厂以6千克/小时的生产速度生产900千克该产品时获得的利润最大,最大利润为457 500元.13.设a ＜0,(4x 2＋a )(2x ＋b )≥0在(a ,b )上恒成立,则b －a 的最大值为( )A.12B.13C.14D.22答案 C解析 由题意知a ＜0,a ＜b ,则①当b ＜0时,∀x ∈(a ,b ),2x ＋b ＜0,所以(4x 2＋a )(2x ＋b )≥0在(a ,b )上恒成立可转化为∀x ∈(a ,b ),a ≤－4x 2,所以a ≤－4a 2,所以－14≤a ＜0,所以0＜b －a ＜14； ②当b ＞0时,(4x 2＋a )(2x ＋b )≥0在(a ,b )上恒成立,当x ＝0时,(4x 2＋a )(2x ＋b )＝ab ＜0,不符合题意；③当b ＝0时,由题意知x ∈(a,0),(4x 2＋a )2x ≥0恒成立,所以4x 2＋a ≤0,所以－14≤a ＜0,所以0＜b －a ≤14. 综上所述,b －a 的最大值为14. 14.已知对于任意的x ∈(－∞,1)∪(5,＋∞),都有x 2－2(a －2)x ＋a ＞0,则实数a 的取值范围是________.答案 (1,5]解析 设f (x )＝x 2－2(a －2)x ＋a ,当Δ＝4(a －2)2－4a ＜0,即1＜a ＜4 时,f (x )＞0 对x ∈R 恒成立,符合题意；当a ＝1时,f (－1)＝0,不符合题意；当a ＝4时,f (x )＝x 2－4x ＋4＝(x －2)2＞0对x ∈(－∞,1)∪(5,＋∞)恒成立,符合题意；当Δ＞0 时,由⎩⎪⎨⎪⎧ Δ>0，1<a －2<5，f (1)≥0，f (5)≥0，得⎩⎪⎨⎪⎧ a <1或a >4，3<a <7，a ≤5，a ≤5，即4＜a ≤5.综上所述,实数a 的取值范围是(1,5].15.若集合A ＝{x ∈Z |x 2－(a ＋2)x ＋2－a ＜0}中有且只有一个元素,则正实数a 的取值范围是________.答案 ⎝⎛⎦⎤12，23解析 f (x )＝x 2－(a ＋2)x ＋2－a ＜0,即x 2－2x ＋1＜a (x ＋1)－1,分别令y 1＝x 2－2x ＋1,y 2＝a (x ＋1)－1,易知y 2过定点(－1,－1),在同一坐标系中画出两个函数的图象,如图所示,若集合A ＝{x ∈Z |f (x )＜0}中有且只有一个元素,结合图象可得,即点(0,1)和点(2,1)在直线上或者在直线上方,点(1,0)在直线下方,∴⎩⎪⎨⎪⎧ a －1≤1，2a －1>0，3a －1≤1，解得12＜a ≤23. 16.(2020·南京六校联考)已知函数f (x )＝x 2－2ax ＋2a －1.若对任意的a ∈(0,3),存在x 0∈[0,4],使得t ≤|f (x 0)|成立,求实数t 的取值范围.解 ∵f (x )＝x 2－2ax ＋2a －1的对称轴为x ＝a ,且a ∈(0,3),∴函数f (x )＝x 2－2ax ＋2a －1在[0,a ]上是减函数,在[a,4]上是增函数；∴函数f (x )＝x 2－2ax ＋2a －1在[0,4]上的最小值为f (a )＝－(a －1)2∈(－4,0],|f (a )|＝(a －1)2, ①当2≤a ＜3时,函数f (x )＝x 2－2ax ＋2a －1(x ∈[0,4])在x ＝0时取得最大值,且最大值为2a －1,由于此时2≤a ＜3,则3≤2a －1＜5,易知当2≤a ＜3时,(a －1)2＜2a －1,所以|f (x )|max ＝max{|f (a )|,|f (0)|}＝|f (0)|＝2a －1∈[3,5).∴t ≤3.②当0＜a ＜2时,函数f (x )＝x 2－2ax ＋2a －1(x ∈[0,4])在x ＝4时取得最大值,且最大值为42－8a ＋2a －1＝15－6a ,由于此时0＜a ＜2,所以3＜15－6a ＜15,且15－6a ＞(a －1)2,|f (x )|max ＝max{|f (a )|,|f (4)|}＝|f (4)|＝15－6a ∈(3,15),∴t ≤3.综上, t 的取值范围是(－∞,3].。

§10.3二项式定理1.二项式定理2.二项式系数的性质＋C m n.(1)C0n＝1,C n n＝1,C m n＋1＝C m－1n(0≤m≤n).C m n＝C n－mn(2)二项式系数先增后减中间项最大.当n 为偶数时,第n 2＋1项的二项式系数最大,最大值为2C nn ,当n 为奇数时,第n ＋12项和第n ＋32项的二项式系数最大,最大值为12Cn n -或12Cn n+.(3)各二项式系数和:C 0n ＋C 1n ＋C 2n ＋…＋C n n ＝2n ,C 0n ＋C 2n ＋C 4n ＋…＝C 1n ＋C 3n ＋C 5n ＋…＝2n －1. 概念方法微思考1.(a ＋b )n 与(b ＋a )n 的展开式有何区别与联系？提示 (a ＋b )n 的展开式与(b ＋a )n 的展开式的项完全相同,但对应的项不相同而且两个展开式的通项不同.2.二项展开式中二项式系数最大时该项的系数就最大吗？提示 不一定最大,当二项式中a ,b 的系数为1时,此时二项式系数等于项的系数,否则不一定.题组一 思考辨析1.判断下列结论是否正确(请在括号中打“√”或“×”)(1)C r n an －r b r是(a ＋b )n 的展开式的第r 项.( × ) (2)(a ＋b )n 的展开式中某一项的二项式系数与a ,b 无关.( √ ) (3)二项展开式中,系数最大的项为中间一项或中间两项.( × )(4)(a ＋b )n 某项的系数是该项中非字母因数部分,包括符号等,与该项的二项式系数不同.( √ ) 题组二 教材改编2.(1＋2x )5的展开式中,x 2的系数等于( ) A.80 B.40 C.20 D.10 答案 B解析 T r ＋1＝C r 5(2x )r ＝C r 52r x r ,当r ＝2时,x 2的系数为C 25·22＝40. 3.若⎝⎛⎭⎫x ＋1x n 展开式的二项式系数之和为64,则展开式的常数项为( ) A.10 B.20 C.30 D.120 答案 B解析 二项式系数之和2n ＝64,所以n ＝6,T r ＋1＝C r 6·x 6－r ·⎝⎛⎭⎫1x r ＝C r 6x 6－2r,当6－2r ＝0,即当r ＝3时为常数项,T 4＝C 36＝20.4.若(x －1)4＝a 0＋a 1x ＋a 2x 2＋a 3x 3＋a 4x 4,则a 0＋a 2＋a 4的值为( ) A.9 B.8 C.7 D.6 答案 B解析 令x ＝1,则a 0＋a 1＋a 2＋a 3＋a 4＝0,令x ＝－1,则a 0－a 1＋a 2－a 3＋a 4＝16,两式相加得a 0＋a 2＋a 4＝8.题组三 易错自纠5.(x －y )n 的二项展开式中,第m 项的系数是( )A.C m nB.C m ＋1nC.C m －1nD.(－1)m －1C m －1n答案 D解析 (x －y )n 二项展开式第m 项的通项为T m ＝C m －1n(－y )m －1x n－m ＋1,所以系数为C m －1n(－1)m －1. 6.已知⎝⎛⎭⎪⎫x ＋a 3x n (a 为常数)的展开式的二项式系数之和为32,常数项为80,则a 的值为( ) A.1 B.±1 C.2 D.±2 答案 C解析 根据题意,该二项式的展开式的二项式系数之和为32,则有2n ＝32,可得n ＝5,则二项式的展开式通项为T r ＋1＝C r 5(x )5－r·⎝ ⎛⎭⎪⎫a 3x r ＝a r C r 51556r x -,令15－5r 6＝0,得r ＝3,则其常数项为C 35a 3,根据题意,有C 35a 3＝80,可得a ＝2.7.在⎝⎛⎭⎫2x 2－1x n 的展开式中,所有二项式系数的和是32,则展开式中各项系数的和为________. 答案 1解析 因为所有二项式系数的和是32,所以2n ＝32,解得n ＝5. 在⎝⎛⎭⎫2x 2－1x 5中,令x ＝1可得展开式中各项系数的和为(2－1)5＝1.多项展开式的特定项命题点1 二项展开式问题例1 (1)(2020·山东模拟)⎝⎛⎭⎫1x －x 10的展开式中x 4的系数是( ) A.－210 B.－120 C.120 D.210答案 B解析 由二项展开式,知其通项为T r ＋1＝C r 10⎝⎛⎭⎫1x 10－r (－x )r ＝(－1)r C r 10x 2r －10, 令2r －10＝4,解得r ＝7.所以x 4的系数为(－1)7C 710＝－120.(2)(2019·浙江)在二项式(2＋x )9的展开式中,常数项是________,系数为有理数的项的个数是________. 答案 162 5解析 该二项展开式的第r ＋1项为T r ＋1＝C r 9(2)9－r x r ,当r ＝0时,第1项为常数项,所以常数项为(2)9＝162；当r ＝1,3,5,7,9时,展开式的项的系数为有理数,所以系数为有理数的项的个数为5.命题点2 两个多项式积的展开式问题例2 (1)(1＋2x 2)(1＋x )4的展开式中x 3的系数为( ) A.12 B.16 C.20 D.24 答案 A解析 展开式中含x 3的项可以由“1与x 3”和“2x 2与x ”的乘积组成,则x 3的系数为C 34＋2C 14＝4＋8＝12.(2)⎝⎛⎭⎫1＋1x 2(1＋x )6的展开式中x 2的系数为( )A.15B.20C.30D.35 答案 C解析 因为(1＋x )6的通项为C r 6x r ,所以⎝⎛⎭⎫1＋1x 2(1＋x )6的展开式中含x 2的项为1·C 26x 2和1x 2·C 46x 4. 因为C 26＋C 46＝2C 26＝2×6×52×1＝30, 所以⎝⎛⎭⎫1＋1x 2(1＋x )6的展开式中x 2的系数为30. 故选C.命题点3 三项展开式问题例3 (1)(x 2＋x ＋y )5的展开式中,x 5y 2的系数为( ) A.10 B.20 C.30 D.60答案 C解析 方法一 利用二项展开式的通项求解. (x 2＋x ＋y )5＝[(x 2＋x )＋y ]5,含y 2的项为T 3＝C 25(x 2＋x )3·y 2. 其中(x 2＋x )3中含x 5的项为C 13x 4·x ＝C 13x 5. 所以x 5y 2的系数为C 25C 13＝30.故选C.方法二 利用排列组合知识求解.(x 2＋x ＋y )5为5个x 2＋x ＋y 之积,其中有两个因式取y ,剩余的三个因式中两个取x 2,一个取x即可,所以x 5y 2的系数为C 25C 23C 11＝30.故选C.(2)(2020·合肥检测)⎝⎛⎭⎫x －1x ＋15展开式中的常数项为( ) A.1 B.11 C.－19 D.51 答案 B解析 ⎝⎛⎭⎫x －1x ＋15＝⎣⎡⎦⎤⎝⎛⎭⎫x －1x ＋15 展开式的通项为T r ＋1＝C r 5⎝⎛⎭⎫x －1x 5－r 当r ＝5时,常数项为C 55＝1,当r ＝3时,常数项为－C 12C 35＝－20, 当r ＝1时,常数项为C 45C 24＝30.综上所述,常数项为1－20＋30＝11.思维升华 (1)求二项展开式中的特定项,一般是化简通项公式后,令字母的指数符合要求(求常数项时,指数为零；求有理项时,指数为整数等),解出项数r ＋1,代回通项公式即可.(2)对于几个多项式积的展开式中的特定项问题,一般都可以根据因式连乘的规律,结合组合思想求解,但要注意适当地运用分类方法,以免重复或遗漏. (3)对于三项式问题一般先变形化为二项式再解决.跟踪训练1 (1)(x 2＋x ＋1)(x －1)4的展开式中,x 3的系数为( ) A.－3 B.－2 C.1 D.4 答案 B解析 (x －1)4的通项为T r ＋1＝C r 4x 4－r (－1)r ,(x 2＋x ＋1)(x －1)4的展开式中,x 3的系数为C 34(－1)3＋C 24(－1)2＋C 14(－1)＝－2,故选B.(2)(x ＋a )10的展开式中,x 7项的系数为15,则a ＝______.(用数字填写答案) 答案 12解析 通项为T r ＋1＝C r 10x 10－r a r ,令10－r ＝7, ∴r ＝3,∴x 7项的系数为C 310a 3＝15,∴a 3＝18,∴a ＝12.(3)(1＋2x －3x 2)5展开式中x 5的系数为________. 答案 92解析 方法一 (1＋2x －3x 2)5＝[(1＋2x )－3x 2]5＝C 05(1＋2x )5＋C 15(1＋2x )4(－3x 2)＋C 25(1＋2x )3(－3x 2)2＋…＋C 55(－3x 2)5, 所以x 5的系数为C 05C 5525＋C 15C 34×23×(－3)＋C 25C 13×2×(－3)2＝92.方法二 (1＋2x －3x 2)5＝(1－x )5(1＋3x )5,所以x 5的系数为C 05C 5535＋C 15(－1)C 4534＋C 25(－1)2C 3533＋C 35(－1)3C 2532＋C 45(－1)4C 1531＋C 55(－1)5C 0530＝92.二项式系数的和与各项系数的和问题命题点1 二项式系数和与系数和例4 (1)(2019·郑州一中测试)若二项式⎝⎛⎭⎫x 2－2x n 的展开式的二项式系数之和为8,则该展开式每一项的系数之和为( ) A.－1 B.1 C.27 D.－27 答案 A解析 依题意得2n ＝8,解得n ＝3.取x ＝1得,该二项展开式每一项的系数之和为(1－2)3＝－1. (2)(2019·宣城调研)若(2－x )7＝a 0＋a 1(1＋x )＋a 2(1＋x )2＋…＋a 7(1＋x )7,则a 0＋a 1＋a 2＋…＋a 6的值为( ) A.1 B.2 C.129 D.2 188答案 C解析 令x ＝0得a 0＋a 1＋a 2＋…＋a 7＝27＝128, 又(2－x )7＝[3－(x ＋1)]7,则a 7(1＋x )7＝C 77·30·[－(x ＋1)]7,解得a 7＝－1. 故a 0＋a 1＋a 2＋…＋a 6＝128－a 7＝128＋1＝129. 命题点2 二项式系数的最值问题例5 (2019·马鞍山模拟)二项式⎝⎛⎭⎪⎫3x ＋13x n 的展开式中只有第11项的二项式系数最大,则展开式中x 的指数为整数的项的个数为( ) A.3 B.5 C.6 D.7 答案 D解析 根据⎝⎛⎭⎪⎫3x ＋13x n的展开式中只有第11项的二项式系数最大,得n ＝20,∴⎝ ⎛⎭⎪⎫3x ＋13x n 的展开式的通项为T r ＋1＝C r20·(3x )20－r ·⎝ ⎛⎭⎪⎫13x r ＝(3)20－r ·C r 20·420-3r x ,要使x 的指数是整数,需r 是3的倍数,∴r ＝0,3,6,9,12,15,18,∴x 的指数是整数的项共有7项.思维升华 (1)形如(ax ＋b )n ,(ax 3＋bx ＋c )m (a ,b ,c ∈R )的式子求其展开式的各项系数之和,常采用赋值法,只需令x ＝1即可.(2)当n 为偶数时,展开式中第n 2＋1项的二项式系数最大,最大值为2C nn ；当n 为奇数时,展开式中第n ＋12项和第n ＋32项的二项式系数最大,最大值为12C n n -或12C n n +.跟踪训练2 (1)(2019·山西八校联考)已知(1＋x )n 的展开式中第5项和第7项的二项式系数相等,则奇数项的二项式系数和为( ) A.29 B.210 C.211 D.212 答案 A解析 由题意知C 4n ＝C 6n ,由组合数性质得n ＝10,则奇数项的二项式系数和为2n －1＝29.(2)已知m 为正整数,(x ＋y )2m 展开式的二项式系数的最大值为a ,(x ＋y )2m ＋1展开式的二项式系数的最大值为b .若13a ＝7b ,则m 等于( ) A.5 B.6 C.7 D.8 答案 B解析 由题意可知,a ＝C m 2m ,b ＝C m2m ＋1,∵13a ＝7b ,∴13·(2m )！m ！m ！＝7·(2m ＋1)！m ！(m ＋1)！,即137＝2m ＋1m ＋1,解得m ＝6. (3)(2019·合肥质检)已知m 是常数,若(mx －1)5＝a 5x 5＋a 4x 4＋a 3x 3＋a 2x 2＋a 1x ＋a 0且a 1＋a 2＋a 3＋a 4＋a 5＝33,则m ＝________. 答案 3解析 当x ＝0时,(－1)5＝－1＝a 0.当x ＝1时,(m －1)5＝a 0＋a 1＋a 2＋a 3＋a 4＋a 5＝33－1＝32,则m －1＝2,m ＝3.1.(2020·湖北龙泉中学、钟祥一中、京山一中,沙洋中学联考)在⎝⎛⎭⎫x 2－2x 6的展开式中,常数项为( )A.－240B.－60C.60D.240 答案 D解析 ⎝⎛⎭⎫x 2－2x 6的二项展开式的通项为T r ＋1＝C r 6·(x 2)6－r ⎝⎛⎭⎫－2x r ＝C r 6(－2)r x 12－3r , 令12－3r ＝0得r ＝4,即常数项为T 5＝C 46(－2)4＝240.2.⎝⎛⎭⎫2x －1x 5的展开式中x 3项的系数为( ) A.80 B.－80 C.－40 D.48 答案 B解析 ⎝⎛⎭⎫2x －1x 5的展开式的通项为T r ＋1＝C r 5(2x )5－r ·⎝⎛⎭⎫－1x r ＝(－1)r ·25－r ·C r 5·x 5－2r ,令5－2r ＝3,得r ＝1.于是展开式中x 3项的系数为(－1)·25－1·C 15＝－80,故选B.3.(2019·十堰调研)若⎝⎛⎭⎫x 6＋1x x n 的展开式中含有常数项,则n 的最小值等于( )A.3B.4C.5D.6 答案 C解析 ⎝⎛⎭⎫x 6＋1x x n展开式的通项为C r n (x 6)n －r 32rx -⎛⎫ ⎪⎝⎭＝C r n 1562n r x - ,r ＝0,1,2,…n , 则依题设,由6n －152r ＝0,得n ＝54r ,∴n 的最小值等于5. 4.(2020·广州海珠区模拟)(x ＋y )(2x －y )6的展开式中x 4y 3的系数为( )A.－80B.－40C.40D.80答案 D解析 (2x －y )6的展开式的通项为T r ＋1＝C r 6(2x )6－r (－y )r ,当r ＝2时,T 3＝240x 4y 2,当r ＝3时,T 4＝－160x 3y 3,故x 4y 3的系数为240－160＝80,故选D.5.(2019·江淮十校考前最后一卷)已知(x ＋1)(2x ＋a )5的展开式中各项系数和为2,则其展开式中含x 3项的系数是( )A.－40B.－20C.20D.40答案 D解析 令x ＝1,可得(x ＋1)(2x ＋a )5的展开式中各项系数和为2(2＋a )5＝2.∴a ＝－1.二项式(2x －1)5的展开式的通项为T r ＋1＝C r 5(2x )5－r ·(－1)r ＝25－r ·(－1)r ·C r 5·x 5－r , 所以(x ＋1)(2x －1)5的展开式中含x 3项的系数为22(－1)3C 35＋23(－1)2C 25＝40. 6.在⎝⎛⎭⎫x ＋3x n 的展开式中,各项系数和与二项式系数和之比为32∶1,则x 2的系数为( ) A.50 B.70 C.90 D.120答案 C解析 令x ＝1,则⎝⎛⎭⎫x ＋3x n ＝4n ,所以⎝⎛⎭⎫x ＋3x n 的展开式中,各项系数和为4n ,又二项式系数和为2n,所以4n2n ＝2n ＝32,解得n ＝5. 二项展开式的通项T r ＋1＝C r 5x 5－r ⎝⎛⎭⎫3x r ＝C r 53r 352r x －,令5－32r ＝2,得r ＝2,所以x 2的系数为C 2532＝90.7.(多选)二项式(2x －1)7的展开式的各项中,二项式系数最大的项是( )A.第2项B.第3项C.第4项D.第5项答案 CD解析 本题考查二项式系数的性质.因为二项式(2x －1)7展开式的各项的二项式系数为C r 7(r ＝0,1,2,3,4,5,6,7),易知当r ＝3或r ＝4时,C r 7最大,即二项展开式中,二项式系数最大的为第4项和第5项.8.(多选)对于二项式⎝⎛⎭⎫1x ＋x 3n (n ∈N *),以下判断正确的有( ) A.存在n ∈N *,展开式中有常数项B.对任意n ∈N *,展开式中没有常数项C.对任意n ∈N *,展开式中没有x 的一次项D.存在n ∈N *,展开式中有x 的一次项答案 AD解析 该二项展开式的通项为T r ＋1＝C r n ⎝⎛⎭⎫1x n －r (x 3)r ＝C r n x 4r －n , ∴当n ＝4r 时,展开式中存在常数项,A 选项正确,B 选项错误；当n ＝4r －1时,展开式中存在x 的一次项,D 选项正确,C 选项错误.故选AD.9.(2020·镇江质检)(x －x )6的展开式中,含x 5项的系数为________.答案 15解析 展开式的通项为T r ＋1＝C r 6·(－1)r ·62r x －,令6－r 2＝5,得r ＝2, 故含x 5的系数为C 26＝15. 10.(2019·晋城模拟)(2－3x )2(1－x )7的展开式中,x 3的系数为________.答案 －455解析 依题意,x 3的系数为4C 37×(－1)3－12C 27(－1)2＋9C 17(－1)＝－455. 11.已知⎝⎛⎭⎫ax ＋1x (2x ＋1)5(a ≠0),若其展开式中各项的系数和为81,则a ＝________,展开式中常数项为________.答案 －2310 解析 在⎝⎛⎭⎫ax ＋1x (2x ＋1)5中, 令x ＝1,得(a ＋1)·35＝81,解得a ＝－23, 所以⎝⎛⎭⎫－23x ＋1x (2x ＋1)5的展开式中的常数项为 1x ·C 45·2x ＝10. 12.(2019·怀化模拟)若在⎝⎛⎭⎫2x ＋1x n 的二项展开式中,第3项和第4项的二项式系数相等且最大,则⎝⎛⎭⎫x －2x ·⎝⎛⎭⎫2x ＋1x n 的展开式中的常数项为________. 答案 －120解析 由⎝⎛⎭⎫2x ＋1x n 的二项展开式中二项式系数的最大项是第3项和第4项, 则展开式共6项,即n ＝6－1＝5,又⎝⎛⎭⎫2x ＋1x n 展开式的通项为T r ＋1＝C r 5(2x )5－r ⎝⎛⎭⎫1x r ＝25－r C r 5x 5－2r ,则⎝⎛⎭⎫x －2x ·⎝⎛⎭⎫2x ＋1x n 的展开式中的常数项为22C 35－2·23C 25＝－120.13.已知(x cos θ＋1)5的展开式中x 2的系数与⎝⎛⎭⎫x ＋544的展开式中x 3的系数相等,且θ∈(0,π),则θ等于( )A.π4B.π4或3π4C.π3D.π3或2π3答案 B解析 由二项式定理知(x cos θ＋1)5的展开式中x 2的系数为C 35cos 2θ,⎝⎛⎭⎫x ＋544的展开式中x 3的系数为C 14×54,所以C 35cos 2θ＝C 14×54,解得cos 2θ＝12,解得cos θ＝±22,又θ∈(0,π),所以θ＝π4或3π4,故选B.14.⎝⎛⎭⎫2x ＋1x －35的展开式中常数项是________. 答案 －1 683解析 ⎝⎛⎭⎫2x ＋1x －35表示五个⎝⎛⎭⎫2x ＋1x －3相乘,则展开式中的常数项由三种情况产生,第一种是从五个⎝⎛⎭⎫2x ＋1x －3中分别抽取2x ,2x ,1x ,1x,－3,则此时的常数项为C 25·C 23·22·(－3)＝－360,第二种情况是从五个⎝⎛⎭⎫2x ＋1x －3中都抽取－3,则此时的常数项为(－3)5＝－243,第三种情况是从五个⎝⎛⎭⎫2x ＋1x －3中分别抽取2x ,1x,－3,－3,－3,则此时的常数项为C 15·C 14·21·(－3)3＝－1 080,则展开式中常数项为－360－243－1 080＝－1 683.15.(2019·衡水中学调研卷)设a ,b ,m 为整数(m ＞0),若a 和b 被m 除得的余数相同,则称a 和b对模m 同余,记为a ≡b (mod m ).若a ＝C 020＋C 120·2＋C 220·22＋…＋C 2020·220,a ≡b (mod10),则b 的值可以是( )A.2 018B.2 019C.2 020D.2 021答案 D解析 a ＝C 020＋C 120·2＋C 220·22＋…＋C 2020·220＝(1＋2)20＝320＝(80＋1)5,它被10除所得余数为1,又a ≡b (mod10),所以b 的值可以是2 021.16.若⎝ ⎛⎭⎪⎫x ＋24x n 展开式中前三项的系数和为163,求: (1)展开式中所有x 的有理项；(2)展开式中系数最大的项.解 易求得展开式前三项的系数为1,2C 1n ,4C 2n .由题意得1＋2C 1n ＋4C 2n ＝163,可得n ＝9.(1)设展开式中的有理项为T r ＋1,由T r ＋1＝C r 9(x )9－r⎝ ⎛⎭⎪⎫24x r ＝2r C r 91834r x -, 又∵0≤r ≤9,∴r ＝2,6.故有理项为T 3＝22C 29·18324x -⨯＝144x 3, T 7＝26·C 69·18364x -⨯＝5 376.(2)设展开式中T r ＋1项的系数最大,则⎩⎪⎨⎪⎧2r C r 9≥2r ＋1C r ＋19，2r C r 9≥2r －1C r －19， ∴173≤r ≤203, 又∵r ∈N ,∴r ＝6,故展开式中系数最大的项为T 7＝5 376.。