2018北京市朝阳区初二(上)期末数学

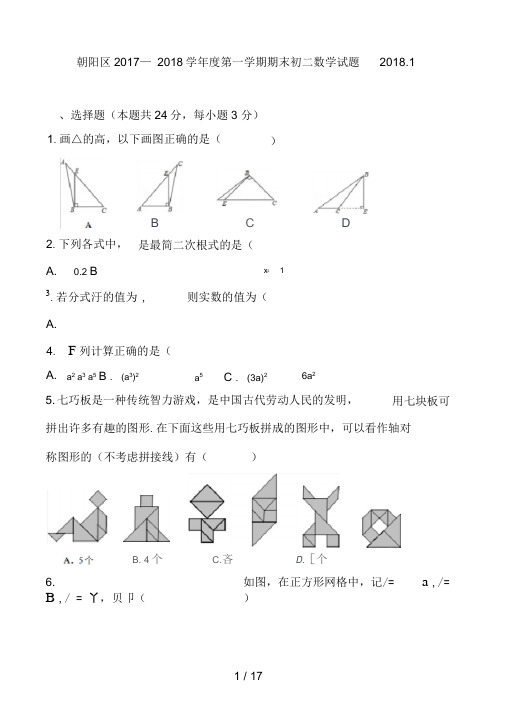
朝阳区2017— 2018学年度第一学期期末初二数学试题 2018.1、选择题（本题共24分，每小题3 分）5. 七巧板是一种传统智力游戏，是中国古代劳动人民的发明， 拼出许多有趣的图形.在下面这些用七巧板拼成的图形中，可以看作轴对 称图形的（不考虑拼接线）有（ ）6.如图，在正方形网格中，记/= a ,/=B ,/ = 丫，贝卩（ ）1.画△的高，以下画图正确的是（2.下列各式中， BC 是最简二次根式的是（A. 0.2 B x 2 1 3.若分式汙的值为°, 则实数的值为（A.4.F 列计算正确的是（ A.a 2 a 3 a 5 B . (a 3)2 a 5 C . (3a)2 6a 2用七块板可）D B. 4个C.吝D.［个A7. 下列各式中，从左到右的变形属于因式分解的是( )A. a(a b 1) a2ab a B . a a 2 a(a 1) 2C. 4a2 9b2 (2a 3b)(2a 3b) D . 2x 1 x(2 -)x8. 如图，等腰ABC中，AB AC , MN是边BC上一条运动的线段(点M不与点B重合，点N不与点C重合)，且MN -BC，MD BC交AB于点D，NE BC 2交AC于点E，在MN从左至右的运动过程中，BMD和CNE的面积之和( )A.保持不变 B .先变小后变大 C .先变大后变小D直变大二、填空题(本题共24分，每小题3分)9. 分解因式：3x2 6x 3 ________________ .10. ________________________________________________ 若二次根式有意义，则x的取值范围是__________________________________ .11 .下图中X的值为___________________ .12.如图，在长方形ABCD中，AF BD，垂足为E , AF交BC于点F，连接DF .图中有全等三角形_____________ 对，有面积相等但不全等的三角形对.13.在你所学过的几何知识中，可以证明两个角相等的定理有_____________________ .(写出三个定理即可)14. 在平面直角坐标系xOy中，A(0,2) , B(4,0)，点P与A, B不重合.若以P ,O , B三点为顶点的三角形与ABO全等，则点P的坐标为_________________________________ .15. 如图，在ABC中，AD BC , CE AB，垂足分别为 D , E , AD , CE交于点F .请你添加一个适当的条件，使AEF旦CEB .添加的条件是：____________________ .(写出一个即可)17.计算:x x 4x x 2 x 2 x 216 .如图，点 D 是线段 AB 上一点， CAB ADE ABF 90 , AC BD , AD BF ,AB DE .若 AEB ，贝卩CEF ___________________________ .（用含 的式子 表示）三、解答题（本题共 52分，17-18题每小题4分，19-23题每小题5分， 24-25题每小题6分，26题7分）18•解分式方程：具& i19.已知a b 0，求代数式a(a 4b) (a 2b)(a 2b)的值.20.已知：如图，点A ,D ,C在同一直线上，AB // CE , AC CE , B CDE .求证：BC DE .匚21.八年级学生去距学校10的博物馆参观，一部分学生骑自行车先走，过了20后，其余学生乘汽车出发，结果他们同时到达.已知汽车的速度是骑车学生速度的2倍，求骑车学生的速度.22.能被2整除的整数叫做偶数，不能被2整除的整数叫做奇数.弓I入负数后，如1, -3等是奇数，0, -2等是偶数.任意两个连续整数的平方差能确定是奇数还是偶数吗？写出你的判断并证明.23.已知：如图，点D ,E在ABC的边BC上，AB AC , AD AE .求证：BD CE .24.分式中，在分子、分母都是整式的情况下，如果分子的次数低于分母的次数，称这样的分式为真分式.例如，分式丄，壬是真分式.如果x 2 x 4x分子的次数不低于分母的次数，称这样的分式为假分式.例如，分式x 12 —是假分式.x 1一个假分式可以化为一个整式与一个真分式的和.例如，x 1 (x 1) 2 1 2x 1 x 1 x 1(1 )将假分式化为一个整式与一个真分式的和；x 12(2)若分式亠的值为整数，求x的整数值.x 125.请按要求完成下面三道小题.(1)如图1, AB AC .这两条线段一定关于某条直线对称吗？如果是，请画出对称轴a (尺规作图，保留作图痕迹)；如果不是，请说明理由.图1(2)如图2，已知线段AB和点C .求作线段CD (不要求尺规作图)，使它与AB成轴对称，且A与C是对称点，标明对称轴b，并简述画图过程.02(3)如图3,任意位置的两条线段AB , CD , AB CD .你能通过对其中一条线段作有限次的轴对称使它们重合吗？如果能，请描述操作方法；如果不能，请说明理由.D26 .在等边ABC外作射线AD，使得AD和AC在直线AB的两侧，BAD(0 180 )，点B关于直线AD的对称点为P，连接PB , PC .(1)依题意补全图1；(2)在图1中，求BPC的度数；(3)直接写出使得PBC是等腰三角形的的值.1北京市朝阳区2017〜2018学年度第一学期期末检测八年级数学试卷参考答案及评分标准2018.1一、选择题（本题共24分，每小题3 分）二、填空题（本题共24分，每小题3 分）三、解答题（本题共52分，17-18题每小题4分，19-23题每小题5分，24-25题每小题6分，26题7分）17.解:4xx(x 2) x(x 2) x 2 (x 2)( x 2) 4x4x x 2 (x 2)( x 2) 4x1 ..........................・・・ ・・・ ・・・ ・・・ 18解 (2)分得5 3・・・・・・ ・・・3经检验，x 5是原方程的解. 3所以这个方程的 解5 (4)319.解： a(a 4b) (a 2b)(a 2b)a 2 4ab (a 2 4b 2)24ab 4b ...................................................................................................................... … … … … … 3 分T a b 0, 二原 式4b(a b) 0 ..... .........................................................................................................… … … … 4 分 去 分 母，得20.证明：T AB // CE ,二A= DCE ........ ..................................................................................・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・ 1在ABC禾口CDE中，’ B CDE ,. A DCE ,AC CE ,/. ABC CDE . ...........................................................................・・・・・・・・・・・・・・・・・・・・・・・・・・・4二BC DE ... .........................................................................................・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・521 .解：设骑车学生的速度为x千米/时，则汽车的速度为2x千米/时. .................................................................................................. 1 分由题意，得10 10 20 0 (3)x 2x 60分解得x 15 . .................................................................................................................... ………… 4 分经检验，x 15是原方程的解，且符合题意. ................................5 分答：骑车学生的速度为15千米/时.2 2 .答：任意两个连续整数的平方差一定是奇13 / 17•••任意两个连续整数的平方差一定是奇数.T AB AC , AD AE ,HB HC二 HB HD HC HE .n 1 ..................................................................................................... 2 ................................................... 分这两个连续整数的 平方差 为(n 1)2 n 2n 2 2n 1 n 2 2n 1. … ・・・ ・・・ ・・・ ・・・ ・・・ ・・・ ・・・ 4分•/ n 为整数，2n 1为 奇证明：设较小的整数为n5则较大的整数为数.过 点 A 作 AH BC占HD HE .BD CE .22x43 12•.•分式—的值为整数，且x 为整数，x 1.............................................. 3 分① 连接AC ；② 作线段 AC 的垂直平分线，即为对称轴b ； (4)分③ 作点B 关于直线b 的对称点D ； ④ 连接CD即 为 所求.或图 分… … … … 5 分(3)先类比(2)的步骤画图，通过一次轴对称，把问题转化为( 1)的情 况， 再做一次轴对称即可满足条 件. ..................................... ………………………6 分PAD BAD .T ABC 是等边三角形， 二 AB AC , BAC 60 . 二 AP AC .APC ACP .26.(2)解：连接AP ，如图. 由点B 关于直线AD 的对称点为 二 AP AB .(1)补全的图形如图所示.• ••在 APC 中，2 APC 2 PAD BAC 180 .APC PAD 60 ． BPC 303 ) 3075 ， 1207分说明：各解答题的其他正确解法请参照以上标准给分祝各位老师寒假愉快！3分165 .。

2018-2019学年北京市朝阳区初二（上）期末数学及答案一．选择题（共8小题，满分24分）1. 画△ABC的边AB上的高，下列画法中，正确的是（）【答案】D【解析】试题分析：三角形的高即从三角形的顶点向对边引垂线，顶点和垂足间的线段．根据概念可知．解：过点C作边AB的垂线段，即画AB边上的高CD，所以画法正确的是D．故选：D．考点：三角形的角平分线、中线和高．2.下列各式属于最简二次根式的是（）A. B. C. D.【答案】B【解析】试题解析：A、含有能开方的因式，不是最简二次根式，故本选项错误；B、符合最简二次根式的定义，故本选项正确；C、含有能开方的因式，不是最简二次根式，故本选项错误；D、被开方数含分母，故本选项错误；故选B．3.若分式的值为0，则x的值是（）A. 2或﹣2B. 2C. ﹣2D. 0【答案】A【解析】【分析】直接利用分式的值为零则分子为零进而得出答案．【详解】∵分式的值为0，∴x2﹣4=0，解得：x=2或﹣2．故选：A．【点睛】此题主要考查了分式的值为零的条件，正确把握定义是解题关键．4.下列运算：①a2•a3=a6，②（a3）2=a6，③a5÷a5=a，④（ab）3=a3b3，其中结果正确的个数为（）A. 1B. 2C. 3D. 4【答案】B【解析】分析：根据同底数幂的除法法则：底数不变，指数相减；同底数幂的乘法法则：同底数幂相乘，底数不变，指数相加；幂的乘方法则：底数不变，指数相乘；积的乘方法则：把每一个因式分别乘方，再把所得的幂相乘进行计算即可．详解：①a2•a3=a5，故原题计算错误；②（a3）2=a6，故原题计算正确；③a5÷a5=1，故原题计算错误；④（ab）3=a3b3，故原题计算正确；正确的共2个，故选B．点睛：此题主要考查了同底数幂的除法、乘法、幂的乘方、积的乘方，关键是熟练掌握各计算法则．5.以下图形中，不是轴对称图形的是（）A. B. C. D.【答案】D【解析】试题分析：A、沿一条直线对折后可以重合，是轴对称图形，故本选项错误；B、沿一条直线对折后可以重合，是轴对称图形，故本选项错误；C、沿一条直线对折后可以重合，是轴对称图形，故本选项错误；D、沿任何一条直线对折后都不能重合，不是轴对称图形，故本选项正确．故选：D．点睛：本题考查了轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．6.已知∠A=60°24′，∠B=60.24°，∠C=60°14′24″，则( )A. ∠A>∠B>∠CB. ∠A>∠B=∠CC. ∠B>∠C>∠AD. ∠B=∠C>∠A【答案】B【解析】【分析】将∠A、∠B、∠C统一单位后比较即可．【详解】∵∠A=60°24′=60.4°，∠B=60.24°，∠C=60°14′24″=60.24°，∴∠A>∠B=∠C．故选B．【点睛】本题考查了度、分、秒的转化计算，比较简单，注意以60为进制即可．7.下列各式变形中，是因式分解的是（）A. a2﹣2ab+b2﹣1=（a﹣b）2﹣1B. x4﹣1=（x2+1）（x+1）（x﹣1）C. （x+2）（x﹣2）=x2﹣4D. 2x2+2x=2x2（1+）【答案】B【解析】【分析】利用因式分解的定义判断即可．【详解】A选项：它的结果不是乘积的形式，不是因式分解，故是错误的；B选项：x4﹣1=（x2+1）（x+1）（x﹣1）结果是乘积形式，是因式分解，故是正确的；C选项：（x+2）（x﹣2）=x2﹣4中结果不是乘积的形式，不是因式分解，故是错误的；D选项：2x2+2x=2x2（1+）结果不是整式乘积的形式，不是因式分解，故是错误的；故选:B.【点睛】考查了因式分解的定义，理解因式分解的定义（把一个多项式在一个范围化为几个整式的积的形式，这种式子变形叫做这个多项式的因式分解，也叫作把这个多项式分解因式）是解题的关键。

北京市朝阳区2017—2018学年度第一学期期末检测一、单项选择题（共30分,每小题2分）题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 答案 D C B B B B C C A D A C C D D 二、多项选择题（共18分，每小题2分）题号16 17 18 19 20 21 22 23 24答案ABC AB ABC ACD AB BD ABD AC AB三、实验解答题（共40分）25．2.826．OD27．振动音调28．物体导热性跟物质种类是否有关？（答案合理同样给分）29．（1）时间（2）88 （3）观察是否有大量的气泡冒出（4）不变（5）水可以通过烧杯继续吸热（答案合理同样给分）30．（1）（2）停表（3）大于（4）不同相同时间（答案合理同样给分）31．（1）不能（2）A （3）不能32．（1）小于增大等于（2）水（玻璃）空气（答案合理同样给分）33．（1）相同（2）不同物质（3）密度（答案合理同样给分）34．透明玻璃板距离判断像与物位置的连线是否与镜面垂直（答案合理同样给分）35．（1）物距焦距（2）没有改变焦距，改变了物距u/cm h/cm四、科普阅读题（共4分）36．（1）射电（2）反射面板（3）长度（4）会聚（答案合理同样给分）五、计算题（共8分）37．由列出时刻表可得t= 4.5h= =146km/h（其他方法正确同样给分）38．（1）V＝30cm×20cm×10cm×60%＝3600cm3（2）= =2g/ cm3（3）V空＝30cm×20cm×10cm×40%＝2400cm3m空＝ρV空＝2g/ cm3×2400cm3＝4800g。

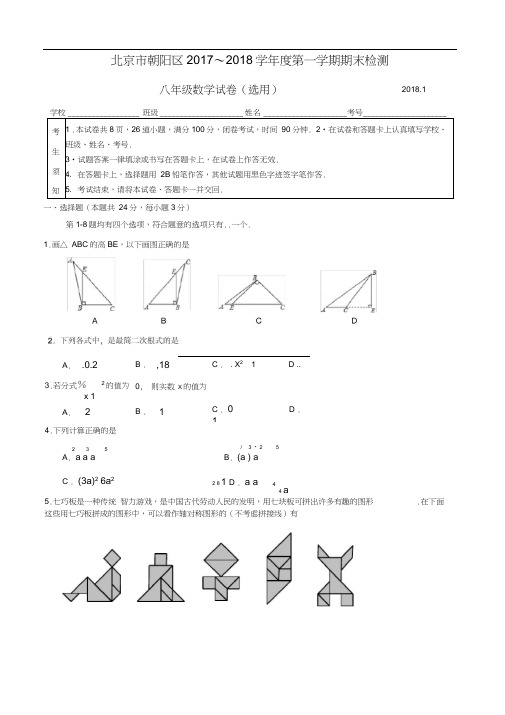
北京市朝阳区2017〜2018学年度第一学期期末检测八年级数学试卷（选用）考生须知1 .本试卷共8页，26道小题，满分100分，闭卷考试，时间90分钟. 2•在试卷和答题卡上认真填写学校、班级、姓名、考号.3•试题答案一律填涂或书写在答题卡上，在试卷上作答无效.4. 在答题卡上，选择题用2B铅笔作答，其他试题用黑色字迹签字笔作答.5. 考试结束，请将本试卷、答题卡一并交回.一、选择题（本题共24分，每小题3分）第1-8题均有四个选项，符合题意的选项只有..一个.1.画△ ABC的高BE，以下画图正确的是A. .0.2 B . ,18 C . . X2 1 D ..3.若分式％2的值为0, 则实数X的值为x 1A. 2 B . 1 C . 0 D .14.下列计算正确的是2 3 5/ 3、2 5A. a a aB. (a ) aC . (3a)26a2 2 8 1D . a a 44 a5.七巧板是一种传统智力游戏，是中国古代劳动人民的发明，用七块板可拼出许多有趣的图形.在下面这些用七巧板拼成的图形中，可以看作轴对称图形的（不考虑拼接线）有2018.129.分解因式：3x 6x 310.若二次根式■■一厂X 有意义，则x 的取值范围是 第11题图12 .如图，在长方形 ABCD 中，AF 13•在你所学过的几何知识中，可以证明两个角相等的定理有.（写出三个定理即可）14 .在平面直角坐标系 xOy 中，A （0, 2） , B （4,0），点P 与A , B 不重合.若以P , O , B 三点为顶点 的三角形与 ABO 全等，则点 P 的坐标为 ____________________________________ .6.如图，在正方形网格中，记/ABD = a, / DEF =卩，/ CGH = Y ，则7•下列各式中，从左到右的变形属于因式分解的是\ B E77/&如图,2a(a b 1) a ab aa 2 a4a 2 2x 1等腰C 重合），且 运动过程中, 2 a(a 1) 29b 2 (2a 3b)(2a 3b)x(2 -)xABC 中，AB 1MN BC ,2BMD 和AC , MN 是边BC 上一条运动的线段（点M 不与点B 重合，点N 不与点MD BC 交 AB 于点 D , NE BC 交AC 于点E ,在MN 从左至右的A •保持不变 C .先变大后变小CNE 的面积之和B .先变小后变大 D .一直变大二、填空题（本题共 24分，每小题3分）角形对，有面积相等但不全等的三角形A11 .下图中连接DF .图中有全等三对.15•如图，在ABC中，AD BC , CE AB，垂足分别为D , E , AD , CE交于点F .请你添加一个适当的条件，使AEF也CEB .添加的条件是：•（写出一个即可）16.如图，点D 是线段AB 上一点，CAB ADE ABF 90 , AC BD , AD BF ,AB DE •若AEB，则CEF•（用含的式子表示）三、解答题（本题共52分，17-18题每小题4分，19-23题每小题5分，24-25题每小题6分，26题7分）、、十x x4x17•计算：—x2x2x 23x 118.解分式方程： ---- 一.2x 4x 2 2第15题图第16题图19.已知a b 0，求代数式a(a 4b) (a 2b)(a 2b)的值.20.已知：如图，点A, D , C在同一直线上，AB II CE , AC CE , B CDE .求证：BC DE .匚21.八年级学生去距学校10 km的博物馆参观，一部分学生骑自行车先走，过了20 min后，其余学生乘汽车出发，结果他们同时到达.已知汽车的速度是骑车学生速度的2倍，求骑车学生的速度.22 .能被2整除的整数叫做偶数，不能被2整除的整数叫做奇数.弓I入负数后，女口 1 , -3等是奇数，0, -2等是偶数.任意两个连续整数的平方差能确定是奇数还是偶数吗？写出你的判断并证明.23.已知：如图，点D , E在ABC的边BC上，AB AC , AD AE .求证：BD CE .24•分式中，在分子、分母都是整式的情况下，如果分子的次数低于分母的次数， 称这样的分式为真分式.例x 1 x分式D ，厶是假分式.x 1 x 1一个假分式可以化为一个整式与一个真分式的和.例如，2x 1(1) 将假分式 丝」化为一个整式与一个真分式的和;x 12(2) 若分式 —的值为整数，求x 的整数值.x 125•请按要求完成下面三道小题.(1) 如图1, AB AC .这两条线段一定关于某条直线对称吗？如果是，请画出对称轴如，分式3x 2 x 34x是真分式•如果分子的次数不低于分母的次数，称这样的分式为假分式•例如,x 1 (x 1) 2 12 x 1 x 1x 1a (尺规作图,CA保留作图痕迹）；如果不是，请说明理由.述画图过程.(2)如图2,已知线段AB 和点C •求作线段CD （不要求尺规作图），使它与 AB 成轴对称，且A 与C 是对称点，标明对称轴 b ，并简(3)如图3,任意位置的两条线段 AB , CD , AB CD •你能通过对其中一条线段作有限次的轴对称使它们重合吗？如果能，请描述操作方法；如果不能，请说明理由. /CD26 •在等边 ABC 外作射线AD ，使得AD 和AC 在直线AB 的两侧， BADB 关于直线AD 的对称点为P ，连接PB , PC .(0180 ),点A北京市朝阳区2017〜2018学年度第一学期期末检测八年级数学试卷参考答案及评分标准(1)依题意补全图1;(2) 在图1中，求 BPC 的度数;(3) 直接写出使得 PBC 是等腰三角形的 的值.备用图2018.11、解答题（本题共-2分，17-18题每小题4分，19-23题每小题-分，24-2-题每小题6分，26题7分）x x4x17•解：——x 2x 2x 2x(x 2)x(x2) x 2........................................................................... 2分(x 2)( x 2) 4x4x x 2 八................................................................................................... 3分(x 2)(x 2) 4x—• ................................................................ 4 分x 218 •解：去分母，得 3 2x x 2 • ........................................................................................................ 2分5解得x - • .................................................................................................................. 3分3-经检验，x 是原方程的解.3-所以这个方程的解是x 5•........................................................................................ 4分319.解：a(a 4b) (a 2b)(a 2b)a2 4ab (a2 4b2) ....................................................................................................... 2 分4ab 4b2•........................................................................................................... 3 分；a b 0,•••原式4b(a b) 0 •............................................................................................ -分20•证明：••• AB // CE ,•- A= DCE • ............................................................................................................................. 1 分在ABC和CDE中，< B CDE,21 •22 •23 •24 •25 •A DCE ,AC CE ,ABC CDE •••• BC DE •解：设骑车学生的速度为由题意，得10X解得x 15 •x千米/时，则汽车的速度为2x千米/时.10 202X 60经检验，X 15是原方程的解，且符合题意.答：骑车学生的速度为15千米/时.答：任意两个连续整数的平方差一定是奇证明：设较小的整数为n，则较大的整数为这两个连续整数的平方差为(n 1)2•/ n为整数,• 2n 1为奇数.•••任意两个连续整数的平方差一定是奇证明：过点A作AH解：(1)—XBC于点H .•/ABAC , AD AE ,• HB HC , HDHE•• HB HD HC HE •即BDCE•2X 1 -32 2 2n2 n2 2n 1 n2 2n 1 •分式—X解得X的值为整数，且X为整数,BAC的平分线所在直线•图略.如：作(1)答案不唯一,............................................................................. 3分① 连接AC ;② 作线段 AC 的垂直平分线，即为对称轴 b ； .............................................. 4分 ③ 作点B 关于直线b 的对称点D ;④ 连接CD 即为所求. ................................................................... 5分 (3)先类比(2)的步骤画图，通过一次轴对称，把问题转化为(1)的情况，再做一次轴对称即可满足条件. ............................................................................. 6分 26. ( 1)补全的图形如图所示.(2 )解：连接AP ，如图.由点B 关于直线 AD 的对称点为P ，可得AD 垂直平分PB .••• AP AB . ••• PAD BAD . ••• ABC 是等边三角形，•- AB AC , BAC 60 • AP AC . .................................................................. 2 分•APC ACP .•••在 APC 中，2 APC 2 PAD BAC 180 . • APC PAD 60 .•BPC 30 ................................................................................................................. 3 分(3) 30 , 75 , 120 , 165。

北京市朝阳区名校2018-2019学年八上数学期末试卷一、选择题1．数﹣0.00000324，用科学记数法表示为（ ）A ．﹣324×10﹣8B ．3.24×10﹣6C ．﹣3.24×10﹣6D ．0.324×10﹣52．分式x y x y-+--可变形为( ) A ．x y x y--- B ．-x y x y -+ C ．x y x y +- D ．x y x y -+ 3．已知（x ﹣1）|x|﹣1有意义且恒等于1，则x 的值为（ ）A ．﹣1或2B ．1C ．±1D ．0 4．下列计算中正确的是（ ）A ．23325x x x +=B ．()34312x x --=-+C ．224(3)412x x x -⋅=-D ．623x x x ÷= 5．已知2m a =，12n a =，则23m n a +的值为（ ） A ．6 B ．12 C ．2 D ．1126．下列等式从左往右因式分解正确的是（ ）A ．()ab ac b a b c d ++=++B ．()()23212x x x x -+=--C ．()222121m n m mn n +-=++-D ．()()2414141x x x -=+- 7．在下列图案中，不是．．轴对称图形的是( )A ．B ．C ．D ．8．如图，在第1个△ABA 1中，∠B=20°，AB=A 1B ，在A 1B 上取一点C,延长AA 1到A 2，使得A 1A 2=A 1C ；在A 2C 上取一点D ，延长A 1A 2到A 3，使得A 2A 3=A 2D ；…，按此做法进行下去，第n 个三角形的以A n 为顶点的内角的度数为（ ）A ．n 1802︒- B ．n 802︒ C ．n 1802︒+ D ．n 2802︒+ 9．如图，在等腰直角△ABC 中，腰长AB=4，点D 在CA 的延长线上，∠BDA=30°，则△ABD 的面积是( )A.4B.4C.8D.8 10．如图，在△ABC 中，边AC 的垂直平分线交边AB 于点D ，连结CD ．若∠A ＝50°，则∠BDC 的大小为（ ）A ．90°B ．100°C ．120°D ．130°11．如图：D 、E 是△ABC 的边AC 、BC 上的点，△ADB ≌△EDB ≌△EDC ，下列结论：①AD=ED ；②BC=2AB ；③∠1=∠2=∠3；④∠4=∠5=∠6；⑤∠A=90°；⑥DE ⊥BC ．其中正确的有（ ）个．A ．6B ．5C ．4D ．212．如图，△ABC 中，BC=a ，AC=b ，AB=c （b ＜c ＜a ），BC 的垂直平分线DG 交∠BAC 的角平分线AD 于点D ，DE ⊥AB 于E ，DF ⊥AC 于F ，则下列结论一定成立的是（ ）A ．()12DG a b =+B ．CF c b =-C ．()12BE a b =-D ．()12AE b c =+ 13．如图，小林从P 点向西直走12米后，向左转，转动的角度为α，再走12米，如此重复，小林共走了108米回到点P ，则α﹣5︒的值是（ ）A ．35°B ．40°C ．50°D ．不存在 14．如图，已知O 为直线AB 上一点，OC 平分∠AOD ，∠BOD=4∠DOE ，∠COE=α，则∠BOE 的度数为( )A ．360°-4αB ．180°-4αC ．αD ．270°-3α 15．已知等腰三角形的两条边长分别是2和4，则它的周长是（ ） A ．8B ．10C ．810或D ．无法确定 二、填空题16．如果方程23111x k x x x +=---会产生增根，那么k 的值是_______________. 17．若ab+bc+ca ＝﹣3，且a+b+c ＝0，则a 4+b 4+c 4＝_____．18．如图，AC ⊥BC ，AD ⊥DB ，下列条件中: ①∠ABD=∠BAC ；②∠DAB=∠CBA ；③AD=BC ；④∠DAC=∠CBD ，能使△ABC ≌△BAD 的有_____（把所有正确结论的序号都填在横线上）19．已知a ，b ，c 是ΔABC 的三边长，a ，b 满足()2a 7b 10-+-=，c 为奇数，则c =__________．20．如图，已知∠AOB ＝40°，在∠AOB 的两边OA 、OB 上分别存在点Q 、点P ，过点Q 作直线QR ∥OB ，当OP ＝QP 时，∠PQR 的度数是_____．三、解答题21．某图书馆计划选购甲、乙两种图书.甲图书每本价格是乙图书每本价格的2.5倍，如果用900元购买图书，则单独购买甲图书比单独购买乙图书要少18本.（1）甲、乙两种图书每本价格分别为多少元？（2）如果该图书馆计划购买乙图书的本数比购买甲图书本数的2倍多8本，且用于购买甲、乙两种图书的总费用不超过1725元，那么该图书馆最多可以购买多少本乙图书？22．(1)已知 xy=2,2225x y +=,求x-y 的值・（2）求证：无论x 、y 为何值，代数式22245x y x y +--+的值不小023．如图，在中，，D 为AB 边上一点，连接CD ，E 为CD 中点，连接BE 并延长至点F ，使得，连接DF 交AC 于点G ，连接CF ．（1）求证：四边形DBCF 是平行四边形；（2）若，，，求CD的长．24．如图，直线AB、CD相交于点O，OE平分∠BOD.(1)若∠AOC=70°,∠DOF=90°，求∠EOF的度数；(2)若OF平分∠COE,∠BOF=15°，求∠AOC的度数。

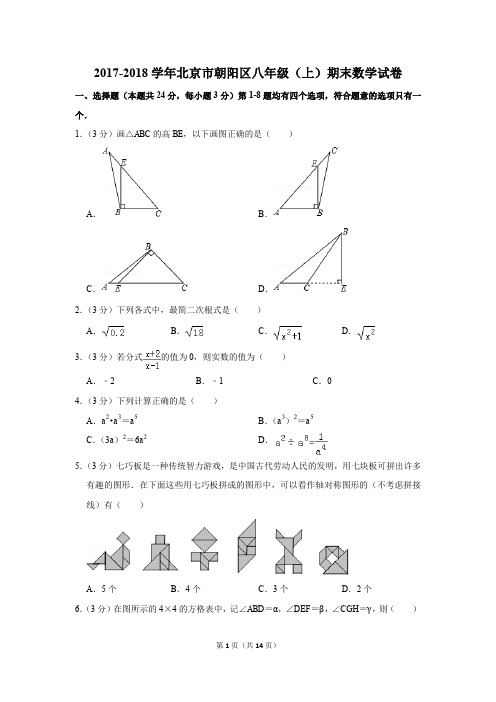
2018北京市朝阳区初二（上）期末数 学 2018.1一、选择题（本题共24分，每小题3分）第1-8题均有四个选项，符合题意的选项只有．．一个． 1．画△ABC 的高BE ，以下画图正确的是A B C D2．下列各式中，是最简二次根式的是A ．2.0B ．18C ．12+xD ．2x 3．若分式21x x +-的值为0，则实数x 的值为 A ．2- B ．1- C ．0 D ．1 4．下列计算正确的是A ．235a a a ⋅=B ．325()a a =C ．22(3)6a a = D ．2841a a a ÷=5．七巧板是一种传统智力游戏，是中国古代劳动人民的发明，用七块板可拼出许多有趣的图形．在下面这些用七巧板拼成的图形中，可以看作轴对称图形的（不考虑拼接线）有A ．5个B ．4个C ．3个D ．2个 6．如图，在正方形网格中，记∠ABD ＝α，∠DEF ＝β，∠CGH ＝γ，则A ．αβγ<<B ．αγβ<<C ．βαγ<<D ．βγα<<7．下列各式中，从左到右的变形属于因式分解的是A ．2(1)+-=+-a a b a ab aB ．22(1)2--=--aaa aABCDEFGHβγαC ．2249(23)(23)a b a b a b -+=-+-D ．)12(12xx x +=+8．如图，等腰ABC ∆中，AB AC =,MN 是边BC 上一条运动的线段(点M 不与点B 重合，点N 不与点C 重合)，且12MN BC =，MD BC ⊥交AB 于点D ，NE BC ⊥交AC 于点E ，在MN 从左至右的运动过程中，BMD ∆和CNE ∆的面积之和A ．保持不变B ．先变小后变大C ．先变大后变小D ．一直变大 二、填空题（本题共24分，每小题3分） 9．分解因式：2363x x -+= ．10．若二次根式4x -有意义，则x 的取值范围是 ． 11．下图中x 的值为 ．12．如图，在长方形ABCD 中，AF BD ⊥，垂足为E ，AF 交BC 于点F ，连接DF ．图中有全等三角形 对，有面积相等但不全等的三角形 对．13．在你所学过的几何知识中，可以证明两个角相等的定理有．（写出三个定理即可）14．在平面直角坐标系xOy 中，(0,2)A ，(4,0)B ，点P 与A ，B 不重合．若以P ，O ，B 三点为顶点的三角形与ABO ∆全等，则点P 的坐标为 ．15．如图，在ABC ∆中，AD BC ⊥，CE AB ⊥，垂足分别为D ，E ，AD ，CE 交于点F ．请你添加一个适当的条件，使AEF ∆≌CEB ∆．添加的条件是： ．（写出一个即可）第12题图 FEDCBA第16题图FEDC BA第15题图DF ECBANMED CBA第11题图80°(x －20)°x°x°16．如图，点D 是线段AB 上一点，90CAB ADE ABF ∠=∠=∠=︒，AC BD =，AD BF =，AB DE =．若AEB α∠=，则CEF ∠= ．（用含α的式子表示） 三、解答题（本题共52分，17-18题每小题4分，19-23题每小题5分，24-25题每小题6分，26题7分） 17．计算：4222xx x x x x ⎛⎫-÷⎪-+-⎝⎭．18．解分式方程：312422x x x -=--．19．已知0a b +=，求代数式(4)(2)(2)a a b a b a b +-+-的值．20．已知：如图，点A ，D ，C 在同一直线上，AB ∥CE ，AC CE =，B CDE ∠=∠． 求证：BC DE =．ED CBA21．八年级学生去距学校10 km 的博物馆参观，一部分学生骑自行车先走，过了20 min 后，其余学生乘汽车出发，结果他们同时到达．已知汽车的速度是骑车学生速度的2倍，求骑车学生的速度．22．能被2整除的整数叫做偶数，不能被2整除的整数叫做奇数．引入负数后，如1，-3等是奇数，0，-2等是偶数．任意两个连续整数的平方差能确定是奇数还是偶数吗？写出你的判断并证明．23．已知：如图，点D ，E 在ABC ∆的边BC 上，AB AC =，AD AE =．求证：BD CE =．EDCBA24．分式中，在分子、分母都是整式的情况下，如果分子的次数低于分母的次数，称这样的分式为真分式．例如，分式42x +，2334x x x -是真分式．如果分子的次数不低于分母的次数，称这样的分式为假分式．例如，分式11x x +-，21x x +是假分式． 一个假分式可以化为一个整式与一个真分式的和．例如，1(1)221111x x x x x +-+==+---． （1）将假分式211x x -+化为一个整式与一个真分式的和； （2）若分式21x x +的值为整数，求x 的整数值．25．请按要求完成下面三道小题．（1）如图1，AB AC =．这两条线段一定关于某条直线对称吗？如果是，请画出对称轴a （尺规作图，保留作图痕迹）；如果不是，请说明理由．（2）如图2，已知线段AB 和点C ．求作线段CD （不要求尺规作图），使它与AB 成轴对称，且A 与C 是对称点，标明对称轴b ，并简述画图过程．ABC图1ABC 图2（3）如图3，任意位置的两条线段AB ，CD ，AB CD =．你能通过对其中一条线段作有限次的轴对称使它们重合吗？如果能，请描述操作方法；如果不能，请说明理由．26．在等边ABC ∆外作射线AD ，使得AD 和AC 在直线AB 的两侧，BAD α∠=（0180α︒<<︒），点B 关于直线AD 的对称点为P ，连接PB ，PC ． （1）依题意补全图1；（2）在图1中，求BPC ∆的度数；（3）直接写出使得PBC ∆是等腰三角形的α的值．CB A备用图图1DCBA CDBA 图3数学试题答案一、选择题（本题共24分，每小题3分）题号 1 2 3 4 5 6 7 8 答案 DCAABDCB二、填空题（本题共24分，每小题3分）三、解答题（本题共52分，17-18题每小题4分，19-23题每小题5分，24-25题每小题6分，26题7分） 17．解：4222x x x x x x ⎛⎫-÷⎪-+-⎝⎭(2)(2)2(2)(2)4x x x x x x x x +---=⋅+- ……………………………………………………………………2分42(2)(2)4x x x x x-=⋅+- …………………………………………………………………………3分12x =+． ...................................................................................................4分 18．解：去分母，得 322x x -=-． (2)分 解得 53x =． (3)分经检验，53x =是原方程的解．所以这个方程的解是53x =． (4)分19．解： (4)(2)(2)a a b a b a b +-+-2224(4)a ab a b =+--……………………………………………………………………………2分 244ab b =+． …………………………………………………………………………………3分∵0a b +=，∴原式4()0b a b =+=．…………………………………………………………………………5分20．证明：∵AB ∥CE ，题号 9 10 11 12 答案 23(1)x -4x ≤130 1；4 题号 13141516答案答案不唯一，如：对顶角相等．(0,2)-，(4,2)，(4,2)-．答案不唯一，如：EF EB =90α︒-∴=A DCE ∠∠ ．………………………………………………………………………………1分 在ABC ∆和CDE ∆中，B CDE ∠=∠, A DCE ∠=∠， AC CE =,∴ABC CDE ∆≅∆． …………………………………………………………………………4分 ∴BC DE =． …………………………………………………………………………………5分21．解：设骑车学生的速度为x 千米/时，则汽车的速度为2x 千米/时． ……………………………1分 由题意，得101020260x x =+． …………………………………………………………………3分 解得 15x =． …………………………………………………………………………………4分 经检验，15x =是原方程的解，且符合题意． ………………………………………………5分 答：骑车学生的速度为15千米/时．22．答：任意两个连续整数的平方差一定是奇数． …………………………………………………1分证明：设较小的整数为n ，则较大的整数为1n +． ………………………………………………2分这两个连续整数的平方差为2222(1)2121n n n n n n +-=++-=+．……………………4分 ∵n 为整数，∴21n +为奇数．………………………………………………………………………………5分 ∴任意两个连续整数的平方差一定是奇数．23．证明：过点A 作AH BC ⊥于点H ． ………………………………………………………………1分 ∵AB AC =，AD AE =，∴HB HC =，HD HE =． ………………………………………………………………3分 ∴HB HD HC HE -=-．即BD CE =． ………………………………………………………………………………5分 24．解：（1）213211x x x -=-++． …………………………………………………………………………2分 （2）21111x x x x =-+++．…………………………………………………………………………4分 ∵分式21x x +的值为整数，且x 为整数，∴11x +=或11x +=-．解得 0x =或2x =-． ……………………………………………………………………6分b A BD C 25．（1）答案不唯一，如：作BAC ∠的平分线所在直线．图略．………………………………………2分（2）如图所示．…………………………………………………………3分①连接AC ；②作线段AC 的垂直平分线，即为对称轴b ；……………………………………………………………4分 ③作点B 关于直线b 的对称点D ；④连接CD 即为所求． ………………………………………………………………………………………5分 （3）先类比（2）的步骤画图，通过一次轴对称，把问题转化为（1）的情况，再做一次轴对称即可满足条件．………………………………………………………………………………………………………6分 26．（1）补全的图形如图所示．……………………………………………………………1分（2）解：连接AP ，如图．由点B 关于直线AD 的对称点为P ，可得AD 垂直平分PB ． ∴AP AB =． ∴PAD BAD ∠=∠． ∵ABC ∆是等边三角形， ∴AB AC =，60BAC ∠=︒．∴AP AC =． …………………………………………………………………………………………2分 ∴APC ACP ∠=∠．∴在APC ∆中，22180APC PAD BAC ∠+∠+∠=︒． ∴60APC PAD ∠+∠=︒．∴30BPC ∠=︒． ……………………………………………………………………………………3分 （3）30︒，75︒，120︒，165︒．……………………………………………………………………7分PDC B A PDCB A。

2018-2019学年北京市朝阳区八年级（上）期末数学试卷一、选择题（本大题共8小题，共16.0分）1.下列各式中，是最简二次根式的是（）B. √5C. √18D. √a2A. √122.下列图形中，有稳定性的是（）A. 长方形B. 梯形C. 平行四边形D. 三角形3.若分式x−1的值等于0，则x的值为（）xA. −1B. 1C. 0D. 24.汉语言文字博大精深，丰富细腻易于表达，比如形容时间极短的词语有“一刹那”、“眨眼间”、“弹指一挥间”等根据唐玄奘《大唐西域记》中记载，一刹那大约是0.013秒．将0.013用科学记数法表示应为（）A. 1.3×10−2B. 1.3×10−3C. 13×10−3D. 1.3×1035.若如图中的两个三角形全等，图中的字母表示三角形的边长，则∠1的度数为（）A. 40∘B. 50∘C. 60∘D. 70∘6.如图，在△ABC中，AC=BC，D在BC的延长线上，∠ABC与∠ACD的平分线相交于点P，则下列结论中不一定正确的是（）A. ∠ACD=2∠AB. ∠A=2∠PC. BP⊥ACD. BC=CP7.下列各式从左边到右边的变形中，是因式分解的是（）A. ax−ay=a(x−y)B. x2−4x+4=x(x−4)+4C. x2−9+8x=(x+3)(x−3)+8xD. (3a−2)(−3a−2)=4−9a28.我国古代数学的许多发现都曾位居世界前列，其中“杨辉三角”（如图）就是一例，这个三角形给出了（a+b）n（n=1，2，3，4，5，6）的展开式（按a的次数由大到小的顺序排列）的系数规律．例如，在三角形中第三行的三个数1，2，1，恰好对应着（a+b）2=a2+2ab+b2展开式中各项的系数；第五行的五个数1，4，6，4，1，恰好对应着（a+b）4=a4+4a3b+6a2b2+4ab3+b4展开式中各项的系数，等等．有如下三个结论：①当a=1，b=1时，代数式a4+4a3b+6a2b2+4ab3+b4的值是1．②当a=-1，b=2时，代数式a4+4a3b+6a2b2+4ab3+b4的值是1③当代数式a4+4×3a3+6×9a2+4×27a+81的值是1时，a的值是-2或-4．上述结论中，所有正确结论的序号为（）A. ①②B. ②C. ③D. ②③二、填空题（本大题共8小题，共16.0分）9.若式子√x+1在实数范围内有意义，则x的取值范围是______．10.计算（x+3）（x-2）=______．11.如图，在五边形ABCDE中，∠1+∠2+∠3+∠4+∠5=______．12.已知x2-6x+a是完全平方式，则a的值为______．13.等腰三角形的一个内角是80°，则它顶角的度数是______．14.如图，线段AB，CD相交于点O，AO=BO，添加一个条件，能使△AOC≌△BOD，所添加的条件可以是______15.如图，两车从南北方向的路段AB的A端出发，分别向东、向西行进相同的距离，到达C，D两地，此时可以判断C，D到B的距离相等，用到的数学道理是______．16.已知，∠AOB=30°，点M，N是射线OA上的动点（都不与点O重合），且MN=2，点P在射线OB上，若△MPN为等腰直角三角形，则PO的长为______．三、计算题（本大题共2小题，共10.0分）17.计算：1a−b -aa2−b2．18.已知x-y=√2，求代数式（x+1）2+y（y-2x）-2x-1的值．四、解答题（本大题共10小题，共58.0分）19.计算：√12+（-2019）0-|2√3|．20.（12a3-6a2+3a）÷3a．21.已知：如图，D是BC上一点，AB=BD，DE∥AB，∠A=∠DBE．求证：AC=BE．22.如图，在△ABC中，AB=AC，∠BAC=80°，D是AC上一点，E是BC延长线上一点，连接BD，DE，若∠ABD=20°，BD=DE，求∠CDE的度数．23.阅读材料：，那么这如果一个三角形的三边长分别为a，b，c，记p=a+b+c2个三角形的面积为S=√p(p−a)(p−b)(p−c)．这个公式叫“海伦公式”，它是利用三角形的三条边的边长直接求三角形面积的公式，中国秦九韶也得出了类似的公式，称三斜求积术，故这个公式又被称为“海伦-秦九韶公式”．完成下列问题：如图，在△ABC中，a=7，b=5，c=6．（1）求△ABC的面积；（2）过点C作CD⊥AB，垂足为D，求线段CD的长．24.研学活动继承和发展了我国传统游学“读万卷书，行万里路”的教育理念和人文精神，成为教育的新内容和新方式．朝阳区一所中学组织学生去某市进行研学活动，原计划乘坐特快列车前往，为了节省时间，现改为乘坐高铁列车前往．已知北京与该市的距离约为1200千米，高铁列车的平均速度是特快列车的平均速度的2.4倍，且乘坐高铁列车比乘坐特快列车少用7小时，求特快列车的平均速度．25.如图，在△ABC中，AB=AC，D是三角形内一点，连接AD，BD，CD，∠BDC=90°，∠DBC=45°．（1）求证：∠BAD=∠CAD；（2）求∠ADB 的度数．26. 观察下列式子： 22−4+66−4=2，55−4+33−4=2，−2−2−4+1010−4=2，1313−4+−5−5−4=2…… 按照上面式子的规律，完成下列问题：（1）填空：()()−4+11−4=2；（2）再写出两个式子；（3）把这个规律用字母表示出来，并说明其正确性（不必写出字母的取值范围）．27. 已知C 是线段AB 垂直平分线m 上一动点，连接AC ，以AC 为边作等边三角形ACD ，点D 在直线AB 的上方，连接DB 与直线m 交于点E ，连接BC ，AE ．（1）如图1，点C 在线段AB 上．①根据题意补全图1②求证：∠EAC =∠EDC ；（2）如图2，点C 在直线AB 的上方，0°＜∠CAB ＜30°，用等式表示线段BE ，CE ，DE 之间的数量关系，并证明．28.对于平面直角坐标系xOy中的线段AB及点P，给出如下定义：若点P满足PA=PB，则称P为线段AB的“轴点”，其中，当0°＜∠APB＜60°时，称P为线段AB的“远轴点”；当60°≤∠APB≤180°时，称P为线段AB的“近轴点”．（1）如图1，点A，B的坐标分别为（-2，0），（2，0），则在P1（-1，3），P2（0，2），P3（0，-1），P4（0，4）中，线段AB的“近轴点”是______．（2）如图2，点A的坐标为（3，0），点B在y轴正半轴上，∠OAB=30°．①若P为线段AB的“远轴点”，直接写出点P的横坐标t的取值范围______；②点C为y轴上的动点（不与点B重合且BC≠AB），若Q为线段AB的“轴点”，当线段QB与QC的和最小时，求点Q的坐标．答案和解析1.【答案】B【解析】解：A、被开方数含分母，故A不是最简二次根式；B、是最简二次根式；C、被开方数含能开得尽方的因数，故C不是最简二次根式；D、被开方数含能开得尽方的因数，故D不是最简二次根式；故选：B．根据最简二次根式必须满足两个条件进行判断即可．本题考查最简二次根式的定义．根据最简二次根式的定义，最简二次根式必须满足两个条件：（1）被开方数不含分母；（2）被开方数不含能开得尽方的因数或因式．2.【答案】D【解析】解：因为三角形具有稳定性，所以下面图形中稳定性最好的是三角形．故选：D．根据三角形具有稳定性，四边形具有不稳定性进行判断．此题考查了三角形的稳定性，关键是根据三角形的稳定性和四边形的不稳定性解答．3.【答案】B【解析】解：依题意得：x-1=0且x≠0，解得x=1．故选：B．分式值为零的条件是分子等于零且分母不等于零．本题主要考查的是分式值为零的条件，掌握分式值为零的条件是解题的关键．4.【答案】A【解析】解：0.013=1.3×10-2．故选：A．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．5.【答案】B【解析】解：在左图中，边a所对的角为180°-60°-70°=50°，因为图中的两个三角形全等，所以∠1的度数为50°．故选：B．在左图中，先利用三角形内角和计算出边a所对的角为50°，然后根据全等三角形的性质得到∠1的度数．本题考查了全等三角形的性质：全等三角形的对应边相等；全等三角形的对应角相等．6.【答案】C【解析】解：∵AC=BC，∴∠A=∠ABC，∴∠ACD=∠A+∠ABC=2∠A，故A正确；∵∠ABC与∠ACD的平分线相交于点P，∴∠PBC=∠ABC，∠PCD=∠ACD，∴∠ACD=∠A+∠ABC，∠PCD=∠P+∠PBC，∴ACD=A+∠ABC=∠P+∠PBC=∠P+PBC，∴∠A=2∠P，故B正确；∵∠A≠∠ACB，∴无法判断BP⊥AC，故C错误；∵∠PBC=∠ABC，∵∠P=∠A，∵∠A=∠ABC，∴∠P=∠PBC，∴BC=CP，故D正确，故选：C．根据等腰三角形的性质得到∠ACD=∠A+∠ABC=2∠A，故A正确；根据角平分线的性质得到∠PBC=∠ABC，∠PCD=∠ACD，根据三角形的外角的性质即可得到∠A=2∠P，故B正确；由于∠A≠∠ACB，无法判断BP⊥AC，故C错误；根据等量代换得到∠P=∠PBC，根据等腰三角形的性质得到BC=CP，故D正确．本题考查了等腰三角形的性质，角平分线的定义，三角形的外角的性质，熟练掌握等腰三角形的性质是解题的关键．7.【答案】A【解析】解：A、是因式分解，正确；B、结果不是整式的积的形式，故不是因式分解，选项错误；C、结果不是整式的积的形式，故不是因式分解，选项错误；D、结果不是整式的积的形式，故不是因式分解，选项错误．故选：A．因式分解就是把多项式分解成整式的积的形式，依据定义即可判断．本题主要考查了因式分解的定义，因式分解与整式的乘法互为逆运算．是中考中的常见题型．8.【答案】D【解析】解：∵（a+b）4=a4+4a3b+6a2b2+4ab3+b4，∴当a=1，b=1时，代数式a4+4a3b+6a2b2+4ab3+b4的值是16，故①错误；当a=-1，b=2时，代数式a4+4a3b+6a2b2+4ab3+b4的值是1，故②正确；当代数式a4+4×3a3+6×9a2+4×27a+81的值是1时，（a+3）4=1，∴a的值是-2或-4，故③正确．故选：D．依据（a+b）4=a4+4a3b+6a2b2+4ab3+b4，即可代入a，b的值，得到代数式a4+4a3b+6a2b2+4ab3+b4的值．本题考查了完全平方公式，（a+b）n展开后各项是按a的降幂排列的，系数依次是从左到右（a+b）n-1系数之和，它的两端都是由数字1组成的，而其余的数则是等于它肩上的两个数之和．9.【答案】x≥-1【解析】解：根据题意得：x+1≥0，解得x≥-1，故答案为：x≥-1．根据二次根式的定义可知被开方数必须为非负数，列不等式求解．主要考查了二次根式的意义和性质．概念：式子（a≥0）叫二次根式．性质：二次根式中的被开方数必须是非负数，否则二次根式无意义．10.【答案】x2+x-6【解析】解：原式=x2-2x+3x-6=x2+x-6．故答案为：x2+x-6原式利用多项式乘多项式法则计算即可得到结果．此题考查了多项式乘多项式，熟练掌握运算法则是解本题的关键．11.【答案】360°【解析】解：根据多边形外角和定理得到：∠1+∠2+∠3+∠4+∠5=360°．故答案为：360°．根据多边形的外角和定理即可求解．本题主要考查了多边形的外角和定理，熟记多边形的外角和定理是解题的关键．12.【答案】9【解析】解：a=（）2=9．故答案是：9．根据完全平方式的结构是：a2+2ab+b2和a2-2ab+b2两种，据此即可求解．此题考查了完全平方式，熟练掌握完全平方公式是解本题的关键．13.【答案】80°或20°【解析】解：当80°是等腰三角形的顶角时，则顶角就是80°；当80°是等腰三角形的底角时，则顶角是180°-80°×2=20°．故答案为：80°或20°．先分情况讨论：80°是等腰三角形的底角或80°是等腰三角形的顶角，再根据三角形的内角和定理进行计算．本题考查了等腰三角形的性质及三角形的内角和定理；若题目中没有明确顶角或底角的度数，做题时要注意分情况进行讨论，这是十分重要的，也是解答问题的关键．14.【答案】OC=OD或∠A=∠B或∠C=∠D【解析】解：∵∠AOC=∠BOC，AO=BO，∴当OC=OD时，△AOC≌△BOD；当∠A=∠B时，△AOC≌△BOD；当∠C=∠D时，△AOC≌△BOD．故答案为OC=OD或∠A=∠B或∠C=∠D．利用对顶角相等得到∠AOC=∠BOC，加上AO=BO，当OC=OD时，根据“SAS“可判断△AOC≌△BOD；当∠A=∠B时，可根据“ASA”判断△AOC≌△BOD；当∠C=∠D时，根据“AAS”可判断△AOC≌△BOD．本题考查了全等三角形的判定：全等三角形的5种判定方法中，选用哪一种方法，取决于题目中的已知条件，若已知两边对应相等，则找它们的夹角或第三边；若已知两角对应相等，则必须再找一组对边对应相等，且要是两角的夹边，若已知一边一角，则找另一组角，或找这个角的另一组对应邻边．15.【答案】垂直平分线上的点到线段两端点的距离相等【解析】解：∵AB⊥CD，AC=AD，∴AB垂直平分CD，∴BC=BD，即C，D到B的距离相等．故答案为：垂直平分线上的点到线段两端点的距离相等．先根据题意得到AB垂直平分CD，然后根据线段垂直平分线的性质可判断C，D到B的距离相等．本题考查了线段垂直平分线的性质：垂直平分线上任意一点，到线段两端点的距离相等．16.【答案】2或4【解析】解：若△MPN为等腰直角三角形，①如图1，当∠MNP=90°，PN=MN=2，∵∠AOB=30°，∴OP=2PN=4；②如图2，当∠NPM=90°，PM=PN时，过P作PH⊥MN于H，则PH=MN=1，∵∠AOB=30°，∴OP=2PH=2，③如图3，当∠NMP=90°，PM=MN=2，∵∠AOB=30°，∴OP=2PM=4；综上所述，PO的长为4或2，故答案为：2或4．分三种情况①如图1，当∠MNP=90°，PN=MN=2，②如图2，当∠NPM=90°，PM=PN时，过P作PH⊥MN于H，③如图3，当∠NMP=90°，PM=MN=2，根据直角三角形的性质即可得到结论．本题考查了等腰直角三角形的性质，含30°直角三角形的性质，分类思想的运用是解题的关键17.【答案】解：原式=a+b−a (a+b)(a−b)=b (a+b)(a−b)=ba 2−b 2．【解析】原式通分并利用同分母分式的减法法则计算，约分即可得到结果．此题考查了分式的加减法，熟练掌握运算法则是解本题的关键．18.【答案】解：原式=x 2+1+2x +y 2-2xy -2x -1=x 2+y 2-2xy=（x -y ）2，当x -y =√2时，原式=（√2）2=2．【解析】首先利用整式乘法运算法则化简，进而将已知代入求出答案．此题主要考查了整式的混合运算，正确运用乘法公式是解题关键．19.【答案】解：原式=2√3+1-2√3=1．【解析】直接利用二次根式的性质以及零指数幂的性质分别化简得出答案． 此题主要考查了实数运算，正确化简各数是解题关键．20.【答案】解：（12a 3-6a 2+3a ）÷3a =4a 2-2a +1． 【解析】直接利用整式的除法的运算法则求解即可求得答案．此题考查了整式的除法．此题难度不大，注意掌握指数的变化是解此题的关键．21.【答案】证明：∵DE ∥AB ，∴∠EDB =∠CBA ，而∠A =∠DBE ，AB =BD ，∴△ABC ≌△BDE （ASA ），∴AC =BE ．【解析】证明△ABC≌△BDE（AAS），即可求解．本题主要考查的是利用角角边定理，判断三角形全等，涉及到了平行线的性质，本题较为容易．22.【答案】解：∵在△ABC中，AB=AC，∠BAC=80°，∴∠ABC=∠ACB=1（180°-80°）=50°，2∵∠ABD=20°，∴∠DBC=∠ABC-∠ABD=30°．∵BD=DE，∴∠E=∠DBC=30°，∴∠CDE=∠ACB-∠E=20°．【解析】由等腰三角形的性质以及三角形内角和定理可得∠ABC=∠ACB=50°，那么∠DBC=∠ABC-∠ABD=30°．因为△BDE是等腰三角形，所以∠E=∠DBC=30°，然后根据三角形外角的性质即可求出∠CDE的度数．本题考查了等腰三角形的性质、三角形内角和定理以及三角形外角的性质，求出∠ACB与∠E的度数是解题关键．23.【答案】解：（1）∵a=7，b=5，c=6．∴p=7+5+6=9，2∴△ABC的面积S=√9×(9−7)×(9−5)×(9−6)=6√6；AB•CD，（2）如图，∵△ABC的面积=12∴1×6×CD=6√6，2∴CD=2√6．【解析】（1）利用阅读材料，先计算出p的值，然后根据海伦公式计算△ABC的面积；（2）利用面积法求CD的长．本题考查了三角形的面积：三角形的面积等于底边长与高线乘积的一半，即S△=×底×高．也考查了阅读理解能力．24.【答案】解：设特快列车的平均速度为x 千米/小时，则高铁列车的平均速度2.4x 千米/小时，由题意得，1200x -12002.4x =7，解得，x =100，经检验，x =100是原方程的根，并且符合题意，答：特快列车的平均速度为100千米/小时．【解析】根据列分式方程解应用题的一般步骤解答．本题考查的是分式方程的应用，列分式方程解应用题的一般步骤：设、列、解、验、答．25.【答案】（1）证明：∵∠BDC =90°，∠DBC =45°， ∴∠BCD =180°-∠BDC -∠DBC =45°，∴∠DBC =∠BCD ，∴DB =DC ．在△ABD 与△ACD 中，{AB =AC DB =DC AD =AD，∴△ABD ≌△ACD （SSS ），∴∠BAD =∠CAD ；（2）解：∵△ABD ≌△ACD （SSS ），∴∠ADB =∠ADC ，∵∠ADB +∠ADC +∠BDC =360°，∠BDC =90°，∴∠ADB =12（360°-90°）=135°．【解析】（1）先根据三角形内角和定理求出∠BCD=180°-∠BDC-∠DBC=45°，利用等角对等边得出DB=DC ．再根据SSS 证明△ABD ≌△ACD ，那么∠BAD=∠CAD ； （2）根据全等三角形的对应角相等得出∠ADB=∠ADC ，再利用周角的定义即可求出∠ADB 的度数．本题考查了全等三角形的判定与性质，三角形内角和定理，等腰三角形的判定，周角的定义．证明出△ABD ≌△ACD 是解题的关键．26.【答案】解：（1）77−4+11−4=2；（2）88−4+00−4=2，−1−1−4+99−4=2；（3）x x−4+8−x 8−x−4=2， ∵左边=x x−4+8−x 4−x=x x−4+x−8x−4 =2x−8x−4=2=右边，∴x x−4+8−x 8−x−4=2．【解析】（1）由已知等式得出+=2，据此求解可得；（2）利用所得规律求解可得；（3）根据分式的加减运算法则计算即可验证．本题主要考查数字的变化规律，解题的关键是得出规律+=2，及分式的加减运算法则．27.【答案】解：（1）①根据题意补全图1，如图所示．②证明：∵直线m 是线段AB 的垂直平分线，∴AC =BC ，EA =EB ，∴∠EAC =∠EBC ．∵△ACD 为等边三角形，∴CD =AC =BC ，∴∠EDC =∠EBC ，∴∠EAC =∠EDC ．（2）如图2中，结论：EB =EC +ED ．理由：设CD交AE于J，在EA上取一点H，使得EH=ED．∵△ADC是等边三角形，∴DA=DC=AC，∠ADC=DCA=60°，∵直线m垂直平分线段AB，∴CA=CB=CD，∴∠CDB=∠CBE，∵EA=EB，CA=CB，∴∠EAB=∠EBA，∠CAB=∠CBA，∴∠EAC=∠EBC，∴∠JDE=∠JAC，∵∠DJE=∠AJC，∴△DJE∽△AJC，∴∠DEJ=∠JCA=60°，∵ED=EH，∴△DEH是等边三角形，∴∠ADJ=∠HDE，DH=DE，∵DA=DC，∴△ADH≌△CDE（SAS），∴AH=EC，∴EA=EH+AH=DE+EC，∵直线m垂直平分线段AB，∴EA=EB，∴EB=EC+ED．【解析】（1）①根据题意画出图形即可；②只要证明CA=CD=CB，利用等腰三角形的性质即可解决问题；（2）如图2中，结论：EB=EC+ED．设CD交AE于J，在EA上取一点H，使得EH=ED．只要证明△ADH≌△CDE（SAS），EA=EB即可解决问题；本题属于三角形综合题，考查了线段的垂直平分线的性质，全等三角形的判定和性质，相似三角形的判定和性质，等边三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考压轴题．28.【答案】P2，P3t＞3或t＜0【解析】解：（1）如图作等边△ABC，△ABC′．由题意C（0，2），C′（0，-2），当点P在线段CC′上时，点P是“近轴点”，所以P2（0，2），P3（0，-1）是“近轴点”，故答案为P2，P3．（2）①如图2-1中，以AB为边作等边△ABK，△ABK′，由题意可知K（3，），k′（0，-），若P为线段AB的“远轴点”，∴点P的横坐标t的取值范围为t＞3或t＜0．故答案为t＞3或t＜0．②如图2-2中，由题意点Q在线段AB的垂直平分线上．连接QA，QB，作QC⊥OB于C．∵点Q在AB的垂直平分线上，∴QB=QA，∴QB+QC=QA+QC，根据垂线段最短可知：当A，Q，C共线且AC⊥OB时，QB+QC的值最小，最小值为线段OA的长，∵直线AB的解析式为y=-x+，∴线段AB的垂直平分线的解析式为y=x-，令y=0，得到x=1，∴此时点Q坐标为（1，0）．（1）如图1中作等边△ABC，△ABC′．根据点C，C′的坐标即可判断；（2）①如图2-1中，以AB为边作等边△ABK，△ABK′，根据K，K′的坐标即可判断；②如图2-2中，由题意点Q在线段AB的垂直平分线上．连接QA，QB，作QC⊥OB于C．根据垂线段最短可知：当A，Q，C共线且AC⊥OB时，QB+QC 的值最小，最小值为线段OA的长，求出线段AB的垂直平分线的解析式即可解决问题；本题属于三角形综合题，考查了等边三角形的判定和性质，线段的垂直平分线的性质，一次函数的应用等知识，解题的关键是理解题意，灵活运用所学知识解决问题，学会利用数形结合的思想解决问题，属于中考压轴题．。

北京市朝阳区2017～2018学年度第一学期期末检测八年级数学试卷参考答案及评分标准2018.1一、选择题（本题共24分，每小题3分）二、填空题（本题共24分，每小题3分）三、解答题（本题共52分，17-18题每小题4分，19-23题每小题5分，24-25题每小题6分，26题7分） 17．解：4222xx x x x x ⎛⎫-÷⎪-+-⎝⎭ (2)(2)2(2)(2)4x x x x x x x x +---=⋅+- ……………………………………………………………………2分42(2)(2)4x x x x x-=⋅+- …………………………………………………………………………3分12x =+． ………………………………………………………………………………………4分 18．解：去分母，得 322x x -=-． ……………………………………………………………………2分解得 53x =． ……………………………………………………………………………………3分经检验，53x =是原方程的解．所以这个方程的解是53x =． …………………………………………………………………4分19．解： (4)(2)(2)a a b a b a b +-+-2224(4)a ab a b =+--……………………………………………………………………………2分 244ab b =+． …………………………………………………………………………………3分∵0a b +=，∴原式4()0b a b =+=．…………………………………………………………………………5分20．证明：∵AB ∥CE ，∴=A DCE ∠∠ ．………………………………………………………………………………1分 在ABC ∆和CDE ∆中，B CDE ∠=∠, A DCE ∠=∠， AC CE =,∴ABC CDE ∆≅∆． …………………………………………………………………………4分 ∴BC DE =． …………………………………………………………………………………5分21．解：设骑车学生的速度为x 千米/时，则汽车的速度为2x 千米/时． ……………………………1分 由题意，得101020260x x =+． …………………………………………………………………3分 解得 15x =． …………………………………………………………………………………4分 经检验，15x =是原方程的解，且符合题意． ………………………………………………5分 答：骑车学生的速度为15千米/时．22．答：任意两个连续整数的平方差一定是奇数． …………………………………………………1分证明：设较小的整数为n ，则较大的整数为1n +． ………………………………………………2分这两个连续整数的平方差为2222(1)2121n n n n n n +-=++-=+．……………………4分 ∵n 为整数，∴21n +为奇数．………………………………………………………………………………5分 ∴任意两个连续整数的平方差一定是奇数．23．证明：过点A 作AH BC ⊥于点H ． ………………………………………………………………1分 ∵AB AC =，AD AE =，∴HB HC =，HD HE =． ………………………………………………………………3分 ∴HB HD HC HE -=-．即BD CE =． ………………………………………………………………………………5分 24．解：（1）213211x x x -=-++． …………………………………………………………………………2分 （2）21111x x x x =-+++．…………………………………………………………………………4分 ∵分式21x x +的值为整数，且x 为整数，∴11x +=或11x +=-．解得 0x =或2x =-． ……………………………………………………………………6分BD 25．（1）答案不唯一，如：作BAC ∠的平分线所在直线．图略．………………………………………2分（2…………………………………………………………3分①连接AC ；②作线段AC 的垂直平分线，即为对称轴b ；……………………………………………………………4分 ③作点B 关于直线b 的对称点D ； ④连接CD 即为所求． ………………………………………………………………………………………5分 （3）先类比（2）的步骤画图，通过一次轴对称，把问题转化为（1）的情况，再做一次轴对称即可满足条件．………………………………………………………………………………………………………6分 26．（1）补全的图形如图所示．……………………………………………………………1分（2）解：连接AP ，如图．由点B 关于直线AD 的对称点为P ，可得AD 垂直平分PB ． ∴AP AB =． ∴PAD BAD ∠=∠．∵ABC ∆是等边三角形， ∴AB AC =，60BAC ∠=︒．∴AP AC =． …………………………………………………………………………………………2分 ∴APC ACP ∠=∠．∴在APC ∆中，22180APC PAD BAC ∠+∠+∠=︒． ∴60APC PAD ∠+∠=︒．∴30BPC ∠=︒． ……………………………………………………………………………………3分 （3）30︒，75︒，120︒，165︒．……………………………………………………………………7分说明：各解答题的其他正确解法请参照以上标准给分.祝各位老师寒假愉快！PDC B A PD CA。

北京市朝阳区2018～2019学年度第一学期期末检测八年级数学试卷 2019.1（考试时间90分钟 满分100分）学校_________________ 班级_________________ 姓名_________________ 考号_________________考 生须知1．本试卷共6页，共三道大题，28道小题．2．在试卷和答题卡上认真填写学校、班级、姓名、考号． 3．试题答案一律填涂或书写在答题卡上，在试卷上作答无效． 4．在答题卡上，选择题、作图题用2B 铅笔作答，其他试题用黑色字迹签字笔作答． 5．考试结束，请将本试卷、答题卡和草稿纸一并交回．一、选择题（本题共16分，每小题2分）第1-8题均有四个选项，符合题意的选项只有．．一个． 1．下列各式中，是最简二次根式的是A ．12B ．5C ．18D ．2a 2．下列图形中，有稳定性的是A ．长方形B ．梯形C ．平行四边形D ．三角形 3．若分式1x x-的值等于0，则x 的值为 A ．-1 B ． 1 C ．0 D ．24．汉语言文字博大精深，丰富细腻，易于表达.比如形容时间极短的词语有“一刹那”、“眨眼间”、“弹指一挥间”等.根据唐玄奘《大唐西域记》中记载，一刹那大约是0.013秒．将0.013用科学记数法表示应为 A ．2103.1-⨯ B ．3103.1-⨯ C ．31013-⨯D ．3103.1⨯ 5．若右图中的两个三角形全等，图中的字母表示三角形的边长，则∠1的度数为A ．40°B ．50°C ．60°D ．70°6．如图，在△ABC 中，AC=BC ，D 在BC 的延长线上，∠ABC 与∠ACD 的平分线相交于点P ，则下列结论中不一定．．．正确的是 A. ∠ACD =2∠A B.∠A =2∠P C. BP ⊥AC D. BC =CP7．下列各式从左边到右边的变形中，是因式分解的是A. ()ax ay a x y -=-B. 244(4)4x x x x -+=-+C. 298(3)(3)8x x x x x -+=+-+D. 2(32)(32)49a a a ---=- 8. 我国古代数学的许多发现都曾位居世界前列，其中“杨辉三角” (如图)就是一例.这个三角形给出了()na b +（n =1，2，3，4，5，6）的展开式（按a 的次数由大到小的顺序排列）的系数规律.例如，在三角形中第三行的三个数1，2，1，恰好对应()2222a b a ab b +=++展开式中各项的系数；第五行的五个数1，4，6，4，1，恰好对应着()4432234464a b a a b a b ab b +=++++展开式中各项的系数，等等.有如下三个结论：①当a =1,b =1时，代数式432234464a a b a b ab b ++++的值是1； ②当a =-1,b =2时，代数式432234464a a b a b ab b ++++的值是1；③当代数式432436942781a a a a +⨯+⨯+⨯+的值是1时，a 的值是-2或-4. 上述结论中，所有正确结论的序号为A ．①②B ．②C ．③D ．②③ 二、填空题（本题共16分，每小题2分）9．若1+x 在实数范围内有意义，则实数x 的取值范围是 ．10．计算：(3)(2)x x +-= ．11．如图，在五边形ABCDE 中，∠1+∠2+∠3+∠4+∠5= °．12．已知26x x a -+是完全平方式，则a 的值为 ．13．如果等腰三角形的一个内角是80°，那么它的顶角的度数是 ．14．如图，线段AB ，CD 相交于点O ，AO=BO ，添加一个条件， 能使△AOC ≌△BOD ，所添加的条件的是 ．15．如图，两车从南北方向的路段AB 的A 端出发，分别向东、向西行进相同的距离，到达C ，D 两地，此时可以判断C ，D 到B 的距离相等，用到的数学道理是 ．16．如图，∠AOB =30°，点M ，N 在射线OA 上（都不与点O 重合），且MN =2，点P 在射线OB 上，若△MPN 为等腰直角三角形，则PO 的长为 ___．三、解答题（本题共68分，第17-22题每题5分，第23-26题每题6分，第27-28每题7分） 17．计算：()012201923.---18．计算：()32126+33a a a a -÷．19．已知：如图，D 是BC 上的一点，AB=BD ， DE ∥AB ，∠A=∠DBE ． 求证： AC=BE ．20．计算：221aa b a b ---．21．如图，在△ABC 中，AB ＝AC ，∠BAC ＝80°，D 是AC 上一点，E 是BC 延长线上一点，连接BD ，DE ，若∠ABD ＝20°，BD =DE ，求∠CDE 的度数．22．已知2x y -=，求代数式()()21221x y y x x ++---的值.23．阅读材料：如果一个三角形的三边长分别为a ，b ，c ，记2a b cp ++=，那么这个三角形的面积为()()()S p p a p b p c =---．这个公式叫“海伦公式”，它是利用三角形的三条边的边长直接求三角形面积的公式，中国秦九韶也得出了类似的公式，称三斜求积术，故这个公式又被称为“海伦——秦九韶公式”．完成下列问题：如图，在△ABC 中，6,5,7===c b a .（1）求△ABC 的面积；（2）过点C 作CD ⊥AB ，垂足为D ，求线段CD 的长.24．研学活动继承和发展了我国传统游学“读万卷书，行万里路”的教育理念和人文精神，成为教育的新内容和新方式．朝阳区一所中学组织学生去某市进行研学活动，原计划乘坐特快列车前往，为了节省时间，现改为乘坐高铁列车前往．已知北京与该市的距离约为1200千米，高铁列车的平均速度是特快列车的平均速度的2.4倍，且乘坐高铁列车所用时间比乘坐特快列车所用时间少用7小时，求特快列车的平均速度．25．如图，在△ABC 中，AB=AC ，D 是三角形内一点，连接AD ，BD ，CD ，∠BDC =90°，∠DBC =45°．(1)求证：∠BAD =∠CAD ；(2)求∠ADB 的度数．26． 观察下列式子：2622464+=--，5325434+=--，210224104-+=---，135213454-+=---…… 按照上面式子的规律，完成下列问题： （1）填空：12414+=-( )( )-；（2）再写出两个式子；（3）把这个规律用字母表示出来，并说明其正确性(不必写出字母的取值范围).27．已知C是线段AB垂直平分线m上一动点，连接AC，以AC为边作等边三角形ACD，点D在直线AB 的上方，连接DB与直线m交于点E，连接BC，AE．（1）如图1，点C在线段AB上．①根据题意补全图1；②求证：∠EAC=∠EDC；（2）如图2，点C在直线AB的上方，0°＜∠CAB＜30°，用等式表示线段BE，CE，DE之间的数量关系，并证明．图1 图228．对于平面直角坐标系xOy 中的线段AB 及点P ，给出如下定义：若点P 满足P A=PB ，则称P 为线段AB 的“轴点”，其中，当0°＜∠APB ＜60°时，称P 为线段AB 的“远轴点”；当60°≤∠APB ≤180°时，称P 为线段AB 的“近轴点”.（1）如图1，点A ，B 的坐标分别为（-2，0），（2，0），则在)3,1(1-P ，)2,0(2P ，)1,0(3-P ，)4,0(4P 中，线段AB 的“近轴点”是 .（2）如图2，点A 的坐标为（3，0），点B 在y 轴正半轴上，且∠OAB =30°.①若P 为线段AB 的“远轴点”，直接写出点P 的横坐标t 的取值范围 ；②点C 为y 轴上的动点（不与点B 重合且BC ≠AB ），若Q 为线段AB 的“轴点”，当线段QB 与QC 的和最小时，求点Q 的坐标.图2图1北京市朝阳区2018～2019学年度第一学期期末检测八年级数学试卷参考答案及评分标准一、选择题题号 1 2 3 4 5 6 7 8 答案BDBABCAD二、填空题 三、解答题17．解：原式=32132-+=1．18．解：()32126+33a a a a -÷2421a a =-+．19．证明：∵DE ∥AB ，∴∠ABC=∠EDB ． 在△ABC 和△BDE 中 = A DBE ∠∠, AB BD =， ABC EDB ∠=∠,∴△ABC ≌△BDE ． ∴AC=BE ．题号 91011 12 答案 1x ≥-2+6x x -360 9 题号1314 1516答案 20°或80°答案不唯一，如：OC =OD答案不唯一，如：线段垂直平分线上的点与这条线段两个端点的距离相等2或420．解：221aa b a b --- ()()1a a b a b a b =--+- ()()()()a b aa b a b a b a b +=-+-+-22ba b =-．21．解：∵AB ＝AC ，∠BAC ＝80°，∴=50ABC ACB ∠∠=︒ ． ∵∠ABD ＝20°， ∴∠DBC ＝30°． ∵BD =DE ，∴︒=∠=∠30DBC E ． ∵∠ACB =∠CDE +∠E ， ∴∠CDE =20°．22．解：()()21221x y y x x ++---2221221x x y xy x =+++---222x y xy =+-()2x y =-．时，当2=-y x 原式=2．23．解：（1）根据题意=92a b cp ++=． ∴()()()S p p a p b p c =---()()()9979596=---66=．（2）∵1=2S AB CD ，∴1662AB CD =． ∴26CD =．24．解：设特快列车的平均速度为x 千米/时，则高铁列车的平均速度为2.4x 千米/时．由题意，得1200120072.4x x=+． 解得 100x =．经检验，100x =是原方程的解，且符合题意．答：特快列车的平均速度为100千米/时．25．(1)证明：∵∠BDC =90°，∠DBC =45°，∴∠DCB=∠DBC =45°． ∴DB =DC ． 在△ABD 和△ACD 中 = AB AC ,AD AD =，BD CD =,∴△ABD ≌△ACD ．∴∠BAD =∠CAD ．(2)解：∵△ABD ≌△ACD ，∴∠ADB =∠ADC ．∵∠BDC =90°，∴∠ADB =135°．26．解：（1）24114)7()7(=-+-． （2）答案不唯一，如：243341111=---+-，9129414-+=---． （3）2484=--+-xx x x ． 其中x ≠4．说明如下：482 484 484--=--+-=--+-=x x x x x x xx x x 左边 =2=右边． ∴2484=--+-xx x x 成立．27．解：（1）①补全图形如图所示．②证明：∵直线m是AB的垂直平分线，∴EA=EB，CA=CB．∴∠EAC=∠B．∵△ACD是等边三角形，∴CA=CD．∴CD=CB．∴∠EDC=∠B．∴∠EAC=∠EDC．（2）BE=CE+DE．证明：如图，在EB上截取EF，使EF=CE，连接CF．∵直线m是AB的垂直平分线，∴EA=EB，CA=CB．∴∠EAB=∠EBA，∠CAB=∠CBA．∴∠EAC=∠EBC．∵△ACD是等边三角形，∴CA=CD，∠ACD=60°．∴CD=CB．∴∠EDC=∠EBC．∴∠EDC=∠EAC．∵∠1=∠2，∴∠DEA =∠ACD =60°．∴∠AEB =120°．∵EA=EB ，m ⊥AB ，∴∠AEC =∠BEC =60°．∴△CEF 是等边三角形．∴∠CEF=∠CFE =60°．∴△CDF ≌△CBE ．∴DF=BE ．∴BE=CE+DE ．28．解：（1）P 2 , P 3．（2）t ＜0或t ＞3．（3）根据题意，点Q 在线段AB 的垂直平分线l 上．当点B ，C 在直线l 的同侧时，对于满足题意的点C 的每一个位置，都有QB +QC =QA +QC ． ∵QA +QC ≥AC ，AC ≥AO∴当点C 与点O 重合，Q 为AO 与直线l 交点时，QB +QC 最小． ∵∠OAB =30°，AQ =BQ ，∴∠QBA =∠QBO =30°．∴OQ =21BQ ．在Rt △BOQ 中，设OQ =x ，则AQ =BQ =2x ．∴3x =3．解得 x =1．∴Q （1，0）．当点B ，C 在直线l 的异侧时，QB +QC ＞3．综上所述，当点Q的坐标为（1，0）时，线段QB与QC的和最小．。