初二上册数学练习题及答案大全

12.1.1平方根（第一课时）◆随堂检测1、若x 2=a ，则叫的平方根，如16的平方根是，972的平方根是 2、3±表示的平方根，12-表示12的3、196的平方根有个，它们的和为4、下列说法是否正确？说明理由（1）0没有平方根；（2）—1的平方根是1±；（3）64的平方根是8；（4）5是25的平方根；（5）636±=5、求下列各数的平方根（1）100（2）)8()2(-⨯-（3）1.21（4）49151 ◆典例分析例若42-m 与13-m 是同一个数的平方根，试确定m 的值◆课下作业●拓展提高一、选择1、如果一个数的平方根是a+3和2a-15，那么这个数是（）A 、49B 、441C 、7或21D 、49或4412、2)2(-的平方根是（）A 、4B 、2C 、-2D 、2±二、填空3、若5x+4的平方根为1±，则x=4、若m —4没有平方根，则|m —5|=5、已知12-a 的平方根是4±，3a+b-1的平方根是4±，则a+2b 的平方根是三、解答题6、a 的两个平方根是方程3x+2y=2的一组解（1）求a 的值（2）2a 的平方根7、已知1-x +∣x+y-2∣=0求x-y 的值●体验中考1、（09河南）若实数x ，y 满足2-x +2)3(y -=0，则代数式2x xy -的值为2、（08咸阳）在小于或等于100的非负整数中，其平方根是整数的共有个3、（08荆门）下列说法正确的是（）A 、64的平方根是8B 、-1的平方根是1±C 、-8是64的平方根D 、2)1(-没有平方根◆随堂检测1、259_____ 2、一个数的算术平方根是9，则这个数的平方根是3x 的取值范围是，若a ≥04、下列叙述错误的是（）A 、-4是16的平方根B 、17是2(17)-的算术平方根C 、164的算术平方根是18D 、0.4的算术平方根是0.02 ◆典例分析例：已知△ABC 的三边分别为a 、b 、c 且a 、b |4|0b -=，求c 的取值范围分析：根据非负数的性质求a 、b 的值，再由三角形三边关系确定c 的范围◆课下作业●拓展提高一、选择12=，则2(2)m +的平方根为（）A 、16B 、16±C 、4±D 、2±2A 、4B 、4±C 、2D 、2±二、填空3、如果一个数的算术平方根等于它的平方根，那么这个数是42(4)y +=0，则x y =三、解答题5、若a 是2(2)-的平方根，b 是16的算术平方根，求2a +2b 的值6、已知a 为170的整数部分，b-1是400的算术平方根，求a b +的值●体验中考．(2009年山东潍坊)一个自然数的算术平方根为a ，则和这个自然数相邻的下一个自然数是（）A ．1a +B ．21a +C ．21a +D ．1a +2、（08年泰安市）88的整数部分是；若a<57<b ，（a 、b 为连续整数），则a=，b=3、（08年广州）如图，实数a 、b 在数轴上的位置，化简222()a b a b ---=4、（08年随州）小明家装修用了大小相同的正方形瓷砖共66块铺成10.56米2的房间，小明想知道每块瓷砖的规格，请你帮助算一算.12.1.2立方根◆随堂检测1、若一个数的立方等于—5，则这个数叫做—5的，用符号表示为，—64的立方根是，125的立方根是；的立方根是—5.2、如果3x =216，则x =.如果3x =64，则x =.3、当x 为时，32x -有意义.4、下列语句正确的是（）A 、64的立方根是2B 、3-的立方根是27C 、278的立方根是32±D 、2)1(-立方根是1- 典例分析例若338x 51x 2+-=-，求2x 的值.●拓展提高一、选择1、若22)6(-=a ，33)6(-=b ，则a+b 的所有可能值是（）A 、0B 、12-C 、0或12-D 、0或12或12-2、若式子3112a a -+-有意义，则a 的取值范围为（） A 、21≥aB 、1≤aC 、121≤≤a D 、以上均不对 二、填空 3、64的立方根的平方根是4、若162=x ，则（—4+x ）的立方根为三、解答题5、求下列各式中的x 的值（1）1253)2(-x =343（2）64631)1(3-=-x 6、已知：43=a ，且03)12(2=-++-c c b ，求333c b a ++的值●体验中考1、（09宁波）实数8的立方根是2、（08泰州市）已知0≠a ，a ，b 互为相反数，则下列各组数中，不是互为相反数的一组是（）A 、3a 与3bB 、a +2与b +2C 、2a 与2b -D 、3a 与3b3、（08益阳市）一个正方体的水晶砖，体积为100cm 3，它的棱长大约在（）A 、4～5cm 之间B 、5～6cm 之间C 、6～7cm 之间D 、7～8cm 之间12.2实数与数轴◆随堂检测1、下列各数：23，722-，327-，414.1，3π-，12122.3，9-，••9641.3中，无理数有个，有理数有个，负数有个，整数有个.2、33-的相反数是，|33-|=57-的相反数是，21-的绝对值=3、设3对应数轴上的点A ，5对应数轴上的点B ，则A 、B 间的距离为4、若实数a<b<0，则|a||b|；大于17小于35的整数是； 比较大小：6334112535、下列说法中,正确的是()A .实数包括有理数,0和无理数B .无限小数是无理数C .有理数是有限小数D .数轴上的点表示实数.◆典例分析例：设a 、b 是有理数，并且a 、b 满足等式2522-=++b b a ，求a+b 的平方根◆课下作业●拓展提高一、选择1、如图，数轴上表示1，2的对应点分别为A 、B ，点B 关于点A 的对称点为C ，则点C 表示的实数为（）A ．2－1B ．1－2C ．2－2D ．2－22、设a 是实数，则|a|-a 的值（）A ．可以是负数B ．不可能是负数C ．必是正数D ．可以是整数也可以是负数二、填空3、写出一个3和4之间的无理数4、下列实数1907，3π-，0，49-，21，31-1…（每两个1之间的0的个数逐次加1）中，设有m 个有理数，n 个无理数，则n m =三、解答题5、比较下列实数的大小（1）|8-|和3（2）52-和9.0-（3）215-和87 6、设m 是13的整数部分，n 是13的小数部分，求m-n 的值.●体验中考．（2011年青岛二中模拟）如图，数轴上A B ，两点表示的数分别为1-，点B 关于点A 的对称点为C ，则点C 所表示的数为（）A．2-B．1- C．2- D．1+．（2011年湖南长沙）已知实数a在数轴上的位置如图所示，则化简|1|a -的结果为（）C A 0B（第46题图）A ．1B ．1-C ．12a -D ．21a - 3、（2011年江苏连云港）实数a b ，在数轴上对应点的位置如图所示，则必有（）A ．0a b +>B ．0a b -<C ．0ab >D ．0a b< 4、（2011年浙江省杭州市模2）如图，数轴上点A 所表示的数的倒数是（ ）A .2-B .2C .12D .12- §13.1幂的运算1.同底数幂的乘法试一试（1）23×２4＝（）×（）＝２()；（2）53×５4＝5()；（3）a 3·a 4＝a ()．概括：a m ·a n ＝（）（）＝＝a n m +．可得a m ·a n ＝a n m +这就是说，同底数幂相乘，．例1计算：（1）103×１０4；（2）a ·a 3；（3）a ·a 3·a 5．练习1.判断下列计算是否正确，并简要说明理由．（1）a ·a 2＝a 2；（2）a ＋a 2＝a 3；（3）a 3·a 3＝a 9；（4）a 3＋a 3＝a 6．2.计算：（1）102×105；（2）a 3·a 7；（3）x ·x 5·x 7．3．填空：（1）ma 叫做a 的m 次幂，其中a 叫幂的________，m 叫幂的________；（2）写出一个以幂的形式表示的数，使它的底数为c ，指数为3，这个数为________；（第8题图）（3）4)2(-表示________，42-表示________；（4）根据乘方的意义，3a ＝________，4a ＝________，因此43a a ⋅＝)()()(+同底数幂的乘法练习题1．计算：（1）=⋅64a a （2）=⋅5b b（3）=⋅⋅32m mm （4）=⋅⋅⋅953c c c c （5）=⋅⋅p n m a a a（6）=-⋅12m t t （7）=⋅+q q n 1（8）=-+⋅⋅112p p n n n 2．计算：（1）=-⋅23b b （2）=-⋅3)(a a（3）=--⋅32)()(y y （4）=--⋅43)()(a a （5）=-⋅2433（6）=--⋅67)5()5(（7）=--⋅32)()(q q n （8）=--⋅24)()(m m （9）=-32（10）=--⋅54)2()2(（11）=--⋅69)(b b （12）=--⋅)()(33a a3．下面的计算对不对？如果不对，应怎样改正？ （1）523632=⨯；（2）633a a a =+；（3）n n n yy y 22=⨯；（4）22m m m =⋅； （5）422)()(a a a =-⋅-；（6）1243a a a=⋅； （7）334)4(=-；（8）6327777=⨯⨯；（9）42-=-a ；（10）32n n n =+．4．选择题：（1）22+m a 可以写成（ ）．A ．12+m a B ．22a a m +C ．22a a m ⋅D ．12+⋅m a a（2）下列式子正确的是（ ）．A ．4334⨯=B ．443)3(=-C ．4433=-D ．3443=（3）下列计算正确的是（ ）．A ．44a a a =⋅B ．844a a a =+C ．4442a a a =+D ．1644a a a =⋅2.幂的乘方根据乘方的意义及同底数幂的乘法填空：（1）（23）2＝×＝２()；（2）（32）3＝×＝３()；（3）（a 3）4＝×××＝a ()．概括（a m ）n ＝（n 个）＝（n 个）=a mn可得（a m ）n ＝a mn （m 、n 为正整数）．这就是说，幂的乘方，．例2计算：（1） （103）5；（2）（b 3）4．练习1.判断下列计算是否正确，并简要说明理由．（1）（a 3）5＝a 8；（2）a 5·a 5＝a 15；（3）（a 2）3·a 4＝a 9．2.计算：（1）（22）2；（2）（y 2）5；（3）（x 4）3；（4）（y 3）2·（y 2）3．3、计算: （1）x·（x 2）3（2）（x m ）n ·（x n ）m （3）（y 4）5－（y 5）4（4）（m 3）4+m 10m 2+m·m 3·m 8（5）[（a －b ）n ]2[（b －a ）n －1]2（6）[（a －b ）n ]2[（b －a ）n －1]2（7）（m 3）4+m 10m 2+m·m 3·m 8幂的乘方一、基础练习1、幂的乘方,底数_______,指数____.（a m ）n =___(其中m 、n 都是正整数)2、计算：（1）（23）2=_____；（2）（－22）3=______；（3）－（－a 3）2=______；（4）（－x 2）3=_______。

初二上册数学练习题带答案本文为初二上册数学练习题带答案，旨在帮助同学们巩固课堂所学知识，提升数学运算能力。

第一章：基本运算一、计算题1. 求下列各实数的和：(1) 2.5 + 3.7 + (-0.5) + 1.8解：2.5 + 3.7 + (-0.5) + 1.8 = 7.5(2) (-3) + 5 + (-1) + 3.2解：(-3) + 5 + (-1) + 3.2 = 4.2(3) 1.73 + 0.8 + (-0.43) + (-1)解：1.73 + 0.8 + (-0.43) + (-1) = 1.12. 请计算下列各算式的值：(1) (9 - 4) × 2 + 7解：(9 - 4) × 2 + 7 = 19(2) (14 - 7) ÷ 3 - 1解：(14 - 7) ÷ 3 - 1 = 0(3) (2.6 × 10^2 - 1.5 × 10^1) ÷ 5解：(2.6 × 10^2 - 1.5 × 10^1) ÷ 5 = 5.02 × 10二、填空题1. 用大写字母表示下列各式：(1) 2a + b - 3c + d解：A = 2a, B = b, C = -3c, D = d(2) 5(x - y) + a^2 - b^2解：A = 5(x - y), B = a^2, C = -b^2(3) p ÷ 4q - r^2 + s^3解：A = p ÷ 4q, B = -r^2, C = s^32. 将下列各算式化简：(1) 4^3 ÷ 2^3解：4^3 ÷ 2^3 = 64 ÷ 8 = 8(2) 5 × 10^3 ÷ 2 × 10^2解：5 × 10^3 ÷ 2 × 10^2 = 5 × 10^1 = 50(3) -3(x + 2) + 5(x - 1)解：-3(x + 2) + 5(x - 1) = -3x - 6 + 5x - 5 = 2x - 11三、解方程1. 解下列方程：(1) 3x + 4 = 16解：3x + 4 = 163x = 12x = 4(2) 5y - 2 = 23解：5y - 2 = 235y = 25y = 5(3) -2z + 3 = 7解：-2z + 3 = 7-2z = 4z = -22. 若2(x - 1) = 10，求x的值。

初二数学上册三角形练习题含答案一、选择题1. 在锐角三角形ABC中，已知角A的度数为45°，边AC的长度为3，边AB的长度为4，则边BC的长度为A. 3B. 4C. 5D. 62. 设一舞蹈场馆的跳跃板为一个等腰梯形，已知两腰边长分别为5米和8米，底边长为6米，则该跳跃板的面积为A. 15平方米B. 24平方米C. 30平方米D. 48平方米3. 已知一个锐角三角形的两个角的度数分别为30°和60°，则第三个角的度数为A. 30°B. 60°C. 90°D. 120°4. 在直角三角形ABC中，已知边AB的长度为5，边BC的长度为12，则角B的度数为A. 30°B. 45°C. 60°D. 90°5. 将一个边长为10的正方形对角线上的一点与其两个端点相连，形成一个直角三角形，该直角三角形的斜边长为A. 10B. 10√2C. 14D. 14√2二、填空题1. 若一三角形的两边长分别为5cm和8cm，且这两边夹角的度数为60°，则该三角形的面积为_________。

2. 在锐角三角形ABC中，已知边AC的长度为4cm，边BC的长度为6cm，角A的度数为45°，则边AB的长度为_________。

3. 若一等腰直角三角形的斜边长为10cm，则其腰边长为_________。

4. 若一角度为30°的角的两边的长度比为1:√3，则其中一边的长度为_________。

5. 设一锐角三角形的两腰边分别为3cm和4cm，夹角的度数为60°，则该三角形的面积为_________。

三、解答题1. 已知锐角三角形ABC中，边AB的长度为6cm，边AC的长度为8cm。

请计算角B的度数。

解答:根据余弦定理可得：cosB = (AC^2 + BC^2 - AB^2) / (2 * AC * BC)= (8^2 + BC^2 - 6^2) / (2 * 8 * BC)= (64 + BC^2 - 36) / (16 * BC)= (BC^2 + 28) / (16 * BC)又知0 < B < 90°，所以cosB > 0，故BC^2 + 28 > 0。

人教八年级数学上册同步练习题及详细答案————————————————————————————————作者：————————————————————————————————日期：23 / 104图1ABCED第十一章 全等三角形11.1全等三角形1、 已知⊿ABC ≌⊿DEF ，A 与D ，B 与E 分别是对应顶点，∠A=52°，∠B=67 °，BC =15cm ，则F = ，FE = .2、∵△ABC ≌△DEF∴AB= ，AC= BC= ，（全等三角形的对应边 ）∠A= ，∠B= ，∠C= ； （全等三角形的对应边 ） 3、下列说法正确的是（ ）A ：全等三角形是指形状相同的两个三角形B ：全等三角形的周长和面积分别相等C ：全等三角形是指面积相等的两个三角形D ：所有的等边三角形都是全等三角形4、 如图1：ΔABE ≌ΔACD ，AB=8cm ，AD=5cm ，∠A=60°，∠B=40°，则AE=_____，∠C=____。

4 / 104课堂练习1、已知△ABC ≌△CDB ，AB 与CD 是对应边，那么AD= ，∠A= ；2、如图，已知△ABE ≌△DCE ，AE=2cm ，BE=1.5cm ，∠A=25°∠B=48°； 那么DE= cm ，EC= cm ，∠C= 度.3、如图，△ABC ≌△DBC ，∠A=800，∠ABC=300，则∠DCB= 度；（第1小题） （第2小题） （第3小题） （第4小题）4、如图，若△ABC ≌△ADE ，则对应角有 ； 对应边有 （各写一对即可）；E B A D CFE DC B AED C B A D CB A5 / 10411.2.1全等三角形的判定（sss ）课前练习1、如图1：AB=AC ，BD=CD ，若∠B=28°则∠C= ；2、如图2：△EDF ≌△BAC ，EC=6㎝，则BF= ；3、如图，AB ∥EF ∥DC ，∠ABC ＝900，AB ＝DC ，那么图中有全等三角形 对。

江苏初二数学上册练习题答案题目一：计算题1. 计算 (3+4) x 5 - 6 ÷ 2 = ?解答：(3+4) x 5 - 6 ÷ 2 = (7) x 5 - 6 ÷ 2 = 35 - 3 = 32 2. 计算 12 x 5 - 6 ÷ 2 + 3 = ?解答：12 x 5 - 6 ÷ 2 + 3 = 60 - 3 + 3 = 603. 计算 20 ÷ 5 + 6 x (4 - 3) = ?解答：20 ÷ 5 + 6 x (4 - 3) = 4 + 6 x 1 = 4 + 6 = 104. 计算 10 + 5 x 2 - 3 ÷ 6 = ?解答：10 + 5 x 2 - 3 ÷ 6 = 10 + 10 - 0.5 = 20 - 0.5 = 19.5 5. 计算 8 ÷ (4 + 5) x 2 = ?解答：8 ÷ (4 + 5) x 2 = 8 ÷ 9 x 2 ≈ 1.7778 x 2 ≈ 3.5556题目二：代数表达式1. 化简表达式：2x + 3x - 4x + 5 = ?解答：2x + 3x - 4x + 5 = x + 52. 化简表达式：3(x - 2) + 4(2x + 1) = ?解答：3(x - 2) + 4(2x + 1) = 3x - 6 + 8x + 4 = 11x - 23. 计算已知 x = 2，求 3x^2 - 4x + 1 的值。

解答：将 x = 2 代入表达式，得到 3(2)^2 - 4(2) + 1 = 12 - 8 + 1 = 54. 计算已知 x = 3/4，求 (2x)^3 的值。

解答：将 x = 3/4 代入表达式，得到 (2(3/4))^3 = (3/2)^3 = 27/85. 计算已知 x = -1，求 2x^4 - 3x^3 + 5 的值。

八年级数学上册练习题及答案
1. 整数运算
题目：
a) 两个整数相加得到0，其中一个整数为-15，求另一个
整数是多少？
b) 三个整数相加得到-16，其中两个整数分别为-9和12，求第三个整数是多少？
答案：
a) 另一个整数为15。

b) 第三个整数为-19。

2. 百分数
把小数转换为百分数：
a) 0.25
b) 0.075
答案：
a) 0.25 转化为百分数为25%。

b) 0.075 转换为百分数为7.5%。

3. 几何图形
题目：
计算正方形的面积和周长，其中一条边长为5 cm。

正方形的面积 = 边长× 边长= 5 cm × 5 cm = 25 平方厘米
正方形的周长= 4 × 边长= 4 × 5 cm = 20 厘米
4. 代数方程
题目：
解方程：2x + 3 = 11
答案：
2x + 3 = 11
将3移到方程右边：
2x = 11 - 3
将2移到方程右边：
x = 8 / 2
x = 4
5. 比例
题目：
已知6个苹果的价格是30元，求10个苹果的价格。

答案：
6个苹果的价格 = 30元
1个苹果的价格 = 30元÷ 6 = 5元
10个苹果的价格 = 5元× 10 = 50元
这样的例子还有很多很多，一本数学练习册包含很多章节和各种类型的问题。

希望以上的例子可以帮助您对八年级数学上册的练习题有一个初步的了解。

如果您需要更详细和全面的练习题及答案，建议您参考课本或向数学老师寻求帮助。

初二上册数学同步练习训练题含答案八年级数学上册同步测试题含答案一、填空题(共13小题，每小题2分，满分26分)1.已知：2某-3y=1，若把看成的函数，则可以表示为2.已知y是某的一次函数，又表给出了部分对应值，则m的值是3.若函数y=2某+b经过点(1，3)，则b=_________.4.当某=_________时，函数y=3某+1与y=2某-4的函数值相等。

5.直线y=-8某-1向上平移___________个单位，就可以得到直线y=-8某+3.6.已知直线y=2某+8与某轴和y轴的交点的坐标分别是______________;与两条坐标轴围成的三角形的面积是__________ 7一根弹簧的原长为12cm，它能挂的重量不能超过15kg并且每挂重1kg就伸长0.5cm写出挂重后的弹簧长度y(cm)与挂重某(kg)之间的函数关系式是_______________.8.写出同时具备下列两个条件的一次函数表达式:(写出一个即可)___.(1)y随着某的增大而减小;(2)图象经过点(0，-3).9.若函数是一次函数，则m=_______，且随的增大而_______.10.如图是某工程队在“村村通”工程中，修筑的公路长度y(米)与时间某(天)之间的关系图象.根据图象提供的信息，可知该公路的长度是______米.11.如图所示，表示的是某航空公司托运行李的费用y(元与托运行李的质量某(千克)的关系，由图中可知行李的质量只要不超过_________千克，就可以免费托运.12.正方形A1B1C1O，A2B2C2C1，A3B3C3C2，…按如图所示的方式放置.点A1，A2，A3，…和点C1，C2，C3，…分别在直线(k>0)和某轴上，已知点B1(1，1)，B2(3，2)，B3(7，4)，则Bn的坐标是______________.13.如下图所示，利用函数图象回答下列问题：(1)方程组的解为__________;(2)不等式2某>-某+3的解集为___________;二、选择题(每小题3分，满分24分)1.一次函数y=(2m+2)某+m中，y随某的增大而减小，且其图象不经过第一象限，则m的取值范围是()A.B.C.D.2.把直线y=-2某向上平移后得到直线AB，直线AB经过点(m，n)，且2m+n=6则直线AB的解析式是().A、y=-2某-3B、y=-2某-6C、y=-2某+3D、y=-2某+63.下列说法中：①直线y=-2某+4与直线y=某+1的交点坐标是(1,1);②一次函数=k某+b，若k>0，b<0，那么它的图象过第一、二、三象限;③函数y=-6某是一次函数，且y随着某的增大而减小;④已知一次函数的图象与直线y=-某+1平行，且过点(8，2)，那么此一次函数的解析式为y=-某+6;⑤在平面直角坐标系中，函数的图象经过一、二、四象限⑥若一次函数中，y随某的增大而减小，则m的取值范围是m>3学⑦点A的坐标为(2，0)，点B在直线y=-某上运动，当线段AB最短时，点B的坐标为(-1,1);⑧直线y=某—1与坐标轴交于A、B两点，点C在坐标轴上，△ABC为等腰三角形，则满足条件的点C最多有5个.正确的有()A.2个B.3个C.4个D.5个4.已知点(-2，y1)，(-1，y2)，(1，y3)都在直线y=-3某+b上，则y1，y2，y3的值的大小关系是()A.y1>y2>y3B.y1y1>y2D.y35.下列函数中，其图象同时满足两个条件①у随着χ的增大而增大;②与ỵ轴的正半轴相交，则它的解析式为()(A)у=-2χ-1(B)у=-2χ+1(C)у=2χ-1(D)у=2χ+16.已知y-2与某成正比例，且某=2时，y=4，若点(m，2m+7)，在这个函数的图象上，则m的值是()A.-2B.2C.-5D.57.某公司市场营销部的个人月收入与其每月的销售量成一次函数关系，其图象如图所示，由图中给出的信息可知，营销人员没有销售时的收入是()A.310元B.300元C.290元D.280元8.已知函数y=k某+b的图象如图，则y=2k某+b的图象可能是()三、解答题(共50分)1.(10分)两摞相同规格的饭碗整齐地叠放在桌面上，请根据图中给出的数据信息，解答问题：(1)求整齐叠放在桌面上饭碗的高度y(cm)与饭碗数某(个)之间的一次函数解析式(不要求写出自变量某的取值范围);(2)若桌面上有12个饭碗，整齐叠放成一摞，求出它的高度。

初二数学练习题及答案上册第一题：计算四则运算已知 a = 3，b = 5，c = 2，请计算以下表达式的结果：1) a + b * c - a2) (b + c) * a3) b / a + c解答：1) a + b * c - a = 3 + 5 * 2 - 3 = 102) (b + c) * a = (5 + 2) * 3 = 213) b / a + c = 5 / 3 + 2 ≈ 1.67 + 2 = 3.67第二题：解方程解以下方程：1) 3x + 4 = 162) 2(x + 5) = 183) 4x - 7 = 9解答：1) 3x + 4 = 16首先将方程两边减去4，得到 3x = 12然后将方程两边除以3，得到 x = 42) 2(x + 5) = 18首先将方程中的括号展开，得到 2x + 10 = 18然后将方程两边减去10，得到 2x = 8最后将方程两边除以2，得到 x = 43) 4x - 7 = 9首先将方程两边加上7，得到 4x = 16然后将方程两边除以4，得到 x = 4第三题：找规律根据下面的数列，找出规律并补充下一个数：1, 2, 4, 7, 11, ?解答：观察数列可以发现，每个数是前一个数加上一个递增的数字而得到的。

第一个数是 1，递增的数字为 1，所以下一个数是 11 + 1 = 12。

第四题：判断正误判断下列各命题是真（T）还是假（F）：1) 2 + 2 = 52) 5 / 0 = 03) 8 - 3 * 2 = 2解答：1) 2 + 2 = 5 - 假（F）2) 5 / 0 = 0 - 假（F）（除数不能为零）3) 8 - 3 * 2 = 2 - 假（F）（左侧是8减去3乘以2等于2，而正确的结果是2）。

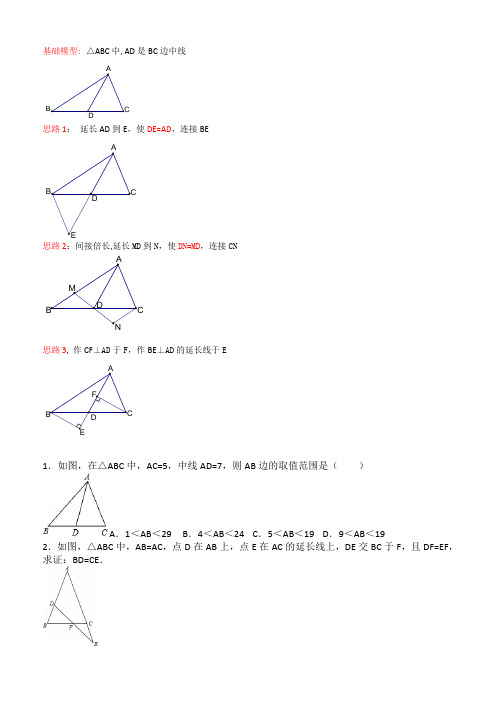
基础模型: △ABC 中, AD 是BC 边中线思路1： 延长AD 到E ，使DE=AD ，连接BE思路2：间接倍长,延长MD 到N ，使DN=MD ，连接CN思路3, 作CF ⊥AD 于F ，作BE ⊥AD 的延长线于E1．如图，在△ABC 中，AC=5，中线AD=7，则AB 边的取值范围是（ ）A ．1＜AB ＜29 B ．4＜AB ＜24C ．5＜AB ＜19D ．9＜AB ＜192．如图，△ABC 中，AB=AC ，点D 在AB 上，点E 在AC 的延长线上，DE 交BC 于F ，且DF=EF ，求证：BD=CE ．D A B C ED A B FE DB A ND BAM3．如图，在△ABC中，AD为中线，求证：AB+AC＞2AD．4．小明遇到这样一个问题，如图1，△ABC中，AB=7，AC=5，点D为BC的中点，求AD的取值范围．小明发现老师讲过的“倍长中线法”可以解决这个问题，所谓倍长中线法，就是将三角形的中线延长一倍，以便构造出全等三角形，从而运用全等三角形的有关知识来解决问题的方法，他的做法是：如图2，延长AD到E，使DE=AD，连接BE，构造△BED≌△CAD，经过推理和计算使问题得到解决．请回答：（1）小明证明△BED≌△CAD用到的判定定理是：（用字母表示）（2）AD的取值范围是小明还发现：倍长中线法最重要的一点就是延长中线一倍，完成全等三角形模型的构造．参考小明思考问题的方法，解决问题：如图3，在正方形ABCD中，E为AB边的中点，G、F分别为AD，BC边上的点，若AG=2，BF=4，∠GEF=90°，求GF的长．5．已知：在△ABC中，AD是BC边上的中线，E是AD上一点，且BE=AC，延长BE交AC于F，求证：AF=EF．6．已知：如图，△ABC（AB≠AC）中，D、E在BC上，且DE=EC，过D作DF∥BA交AE于点F，DF=AC．求证：AE平分∠BAC．7-10,换汤不换药(多题一解)7．如图，D是△ABC的BC边上一点且CD=AB，∠BDA=∠BAD，AE是△ABD的中线．求证：∠C=∠BAE．8．如图，已知D是△ABC的边BC上的一点，CD=AB，∠BDA=∠BAD，AE是△ABD的中线．（1）若∠B=60°，求∠C的值；（2）求证：AD是∠EAC的平分线．9．如图，已知：CD=AB，∠BAD=∠BDA，AE是△ABD的中线，求证：AC=2AE．10．已知，如图，AB=AC=BE，CD为△ABC中AB边上的中线，求证：CE=2CD．11．已知：如图，△ABC中，∠C=90°，CM⊥AB于M，AT平分∠BAC交CM于D，交BC于T，过D作DE∥AB交BC于E，求证：CT=BE．12．如图①，点O为线段MN的中点，PQ与MN相交于点O，且PM∥NQ，可证△PMO≌△QNO．根据上述结论完成下列探究活动：如图②，在四边形ABCD中，AB∥DC，E为BC边的中点，∠BAE=∠EAF，AF与DC的延长线相交于点F．试探究线段AB与AF、CF之间的数量关系，并证明你的结论；(图3是原题的第2问)13．如图，在△ABC中，AD交BC于点D，点E是BC的中点，EF∥AD交CA的延长线于点F，交EF与于点G．若BG=CF，求证：AD为△ABC的角平分线．14．如图，已知在△ABC中，∠CAE=∠B，点E是CD的中点，若AD平分∠BAE．（1）求证：AC=BD；（2）若BD=3，AD=5，AE=x，求x的取值范围．15．已知在△ABC中，AD是BC边上的中线，分别以AB边、AC边为直角边各向外作等腰直角三角形，如图，求证：EF=2AD．1.解：如图，延长AD至E，使DE=AD，∵AD是△ABC的中线，∴BD=CD，在△ABD和△ECD中，，∴△ABD≌△ECD（SAS），∴AB=CE，∵AD=7，∴AE=7+7=14，∵14+5=19，14﹣5=9，∴9＜CE＜19，2．证明：如图，过点D作DG∥AE，交BC于点G；3．证明：4．解：（1）如图2中，延长AD到E，使DE=AD，连接BE．在△BED和△CAD中，，∴△BED≌△CAD（SAS）．（2）∵△BED≌△CAD，∴BE=AC=5，∵AB=7，∴2＜AE＜12，∴2＜2AD＜12，∴1＜AD＜6．解决问题：如图3中，解：延长GE交CB的延长线于M．∵四边形ABCD是正方形，∴AD∥CM，∴∠AGE=∠M，在△AEG和△BEM中，，∴△AEG≌△BEM，∴GE=EM，AG=BM=2，∵EF⊥MG，∴FG=FM，∵BF=4，∴MF=BF+BM=2+4=6，∴GF=FM=6．5．证明：如图，延长AD到点G，使得AD=DG，连接BG．∵AD是BC边上的中线（已知），∴DC=DB，在△ADC和△GDB中，∴△ADC≌△GDB（SAS），∴∠CAD=∠G，BG=AC又∵BE=AC，∴BE=BG，∴∠BED=∠G，∵∠BED=∠AEF，∴∠AEF=∠CAD，即：∠AEF=∠FAE，∴AF=EF．6．证明：如图，延长FE到G，使EG=EF，连接CG．在△DEF和△CEG中，∵，∴△DEF≌△CEG．∴DF=GC，∠DFE=∠G．∵DF∥AB，∴∠DFE=∠BAE．∵DF=AC，∴GC=AC．∴∠G=∠CAE．∴∠BAE=∠CAE．即AE平分∠BAC．7．证明：延长AE到F，使EF=AE，连接DF，∵AE是△ABD的中线∴BE=ED，在△ABE与△FDE中∵，∴△ABE≌△FDE（SAS），∴AB=DF，∠BAE=∠EFD，∵∠ADB是△ADC的外角，∴∠DAC+∠ACD=∠ADB=∠BAD，∴∠BAE+∠EAD=∠BAD，∠BAE=∠EFD，∴∠EFD+∠EAD=∠DAC+∠ACD，∴∠ADF=∠ADC，∵AB=DC，∴DF=DC，在△ADF与△ADC中∵，∴△ADF≌△ADC（SAS）∴∠C=∠AFD=∠BAE．8．（1）解：∵∠B=60°，∠BDA=∠BAD，∴∠BAD=∠BDA=60°，∴AB=AD，∵CD=AB，∴CD=AD，∴∠DAC=∠C，∴∠BDA=∠DAC+∠C=2∠C，∵∠BAD=60°，∴∠C=30°；（2）证明：延长AE到M，使EM=AE，连接DM，在△ABE和△MDE中，，∴△ABE≌△MDE，∴∠B=∠MDE，AB=DM，∵∠ADC=∠B+∠BAD=∠MDE+∠BDA=∠ADM，在△MAD与△CAD，，∴△MAD≌△CAD，∴∠MAD=∠CAD，∴AD是∠EAC的平分线．9．证明：延长AE至F，使AE=EF，连接BF，在△ADE与△BFE中，，∴△AED≌△FEB，∴BF=DA，∠FBE=∠ADE，∵∠ABF=∠ABD+∠FBE，∴∠ABF=∠ABD+∠ADB=∠ABD+∠BAD=∠ADC，在△ABF与△ADC中，，∴△ABF≌△CDA，∴AC=AF，∵AF=2AE，∴AC=2AE．10．证明：取AC的中点F，连接BF；∵B为AE的中点，∴BF为△AEC的中位线，∴EC=2BF；在△ABF与△ACD中，，∴△ABF≌△ACD（SAS），∴CD=BF，∴CE=2CD．11．证明：过T作TF⊥AB于F，∵AT平分∠BAC，∠ACB=90°，∴CT=TF（角平分线上的点到角两边的距离相等），∵∠ACB=90°，CM⊥AB，∴∠ADM+∠DAM=90°，∠ATC+∠CAT=90°，∵AT平分∠BAC，∴∠DAM=∠CAT，∴∠ADM=∠ATC，∴∠CDT=∠CTD，∴CD=CT，又∵CT=TF（已证），∴CD=TF，∵CM⊥AB，DE∥AB，∴∠CDE=90°，∠B=∠DEC，在△CDE和△TFB中，，∴△CDE≌△TFB（AAS），∴CE=TB，∴CE﹣TE=TB﹣TE，即CT=BE．12．解：（1）AB=AF+CF．如图2，分别延长DC、AE，交于G点，根据图①得△ABE≌△GCE，∴AB=CG，又AB∥DC，∴∠BAE=∠G而∠BAE=∠EAF，∴∠G=∠EAF，∴AF=GF，∴AB=CG=GF+CF=AF+CF；13．解：延长FE，截取EH=EG，连接CH，∵E是BC中点，∴BE=CE，∴∠BEG=∠CEH，在△BEG和△CEH中，，∴△BEG≌△CEH（SAS），∴∠BGE=∠H，∴∠BGE=∠FGA=∠H，∴BG=CH，∵CF=BG，∴CH=CF，∴∠F=∠H=∠FGA，∵EF∥AD，∴∠F=∠CAD，∠BAD=∠FGA，∴∠CAD=∠BAD，∴AD平分∠BAC．14．（1）证明：延长AE到F，使EF=EA，连接DF，∵点E是CD的中点，∴EC=ED，在△DEF与△CEA中，，∴△DEF≌△CEA，∴AC=FD，∴∠AFD=∠CAE，∵∠CAE=∠B，∴∠AFD=∠B，∵AD平分∠BAE，∴∠BAD=∠FAD，在△ABD与△AFD中，，∴△ABD≌△AFD，∴BD=FD，∴AC=BD；（2）解：由（1）证得△ABD≌△AFD，△DEF≌△CEA，∴AB=AF，∵AE=x，∴AF=2AE=2x，∴AB=2x，∵BD=3，AD=5，∴在△ABD中，，解得：1＜x＜4，∴x的取值范围是1＜x＜4．15证明：延长AD至点G，使得AD=DG，连接BG，CG，∵AD=DG，BD=CD，∴四边形ABGC是平行四边形，∴AC=AF=BG，AB=AE=CG，∠BAC+∠ABG=180°，∵∠EAF+∠BAC=180°，∴∠EAF=∠ABG，在△EAF和△BAG中，，∴△EAF≌△BAG（SAS），∴EF=AG，∵AG=2AD，∴EF=2AD．。

初二上册数学练习题及答案大全This model paper was revised by LINDA on December 15, 2012.初二上册数学练习题及答案大全一、选择题 1、如图，两直线a∥b，与∠1相等的角的个数为 A、1个B、2个C、3个D、4个x>32、不等式组的解集是x A、33D、无解、如果a>b，那么下列各式中正确的是 A、a3 a3 C、a>bD、2a4、如图所示，由∠D=∠C,∠BAD=∠ABC推得△ABD≌△BAC，所用的的判定定理的简称是A、AASB、ASAC、SASD、SSS5、已知一组数据1，7，10，8，x，6，0，3，若=5，则x应等于 A、B、C、D、6、下列说法错误的是A、长方体、正方体都是棱柱；B、三棱住的侧面是三角形；C、六棱住有六个侧面、侧面为长方形；D、球体的三种视图均为同样大小的图形；、△ABC的三边为a、b、c，且=c2，则 A、△ABC是锐角三角形； B、c边的对角是直角；C、△ABC是钝角三角形；D、a边的对角是直角；8、为筹备班级的初中毕业联欢会，班长对全班学生爱吃哪几种水果作了民意调查，那么最终买什么水果，下面的调查数据中最值得关注的是A、中位数；B、平均数；C、众数；D、加权平均数；、如右图，有三个大小一样的正方体，每个正方体的六个面上都按照相同的顺序，依次标有1，2，3，4，5，6这六个数字，并且把标有“6”的面都放在左边，那么它们底面所标的3个数字之和等于A、8B、9C、10D、1110、为鼓励居民节约用水，北京市出台了新的居民用水收费标准：若每月每户居民用水不超过4立方米，则按每立方米2米计算；若每月每户居民用水超过4立方米，则超过部分按每立方米米计算。

现假设该市某户居民某月用水x立方米，水费为y元，则y与x的函数关系用图象表示正确的是BA、B、C、D、二、填空题11、不等式2x-1>3的解集是__________________；12、已知点A在第四象限，且到x轴，y轴的距离分别为3，5，则A点的坐标为_________；13、为了了解某校初三年级400名学生的体重情况，从中抽查了50名学生的体重进行统计分析，在这个问题中，总体是指__________________________________；14、某班一次体育测试中得100分的有4人，90分的有11人，80分的有11人，70分的有8人，60分的有5人，剩下的8人一共得了300分，则中位数是_____________。

初二(八年级)上册数学书练习题答案(北师大版)第一章实数1.1 实数的概念1. 实数包括哪些数？实数可以分为哪几类？答：实数包括有理数和无理数。

有理数可以进一步分为整数、分数和有限小数；无理数则包括无限不循环小数。

2. 如何判断一个数是有理数还是无理数？答：如果一个数可以表示为两个整数的比，即分数形式，那么它是有理数；否则，它是无理数。

1.2 实数的运算1. 如何进行实数的加减运算？答：实数的加减运算遵循交换律和结合律。

对于加法，同号相加取相同符号，异号相加取绝对值较大的符号，并用较大的绝对值减去较小的绝对值。

对于减法，可以将减法转换为加法，即减去一个数等于加上它的相反数。

2. 如何进行实数的乘除运算？答：实数的乘除运算也遵循交换律和结合律。

乘法中，同号相乘得正，异号相乘得负；除法中，除以一个数等于乘以它的倒数。

1.3 实数的应用1. 如何应用实数解决实际问题？答：实数在日常生活中有着广泛的应用，例如计算长度、面积、体积、质量等。

在解决实际问题时，需要将问题转化为数学模型，然后使用实数进行计算。

2. 实数在科学研究中有什么作用？答：实数是科学研究的基础，它用于描述物理量、化学量、生物量等。

在科学研究中，实数用于建立数学模型，进行实验数据的分析和处理。

第二章整式2.1 整式的概念1. 什么是整式？整式有哪些基本形式？答：整式是由常数和变量的乘积组成的代数式，其中变量的指数为非负整数。

整式的基本形式包括单项式和多项式。

2. 如何判断一个代数式是否为整式？答：如果一个代数式中只包含常数和变量的乘积，且变量的指数为非负整数，那么它是一个整式。

2.2 整式的运算1. 如何进行整式的加减运算？答：整式的加减运算遵循交换律和结合律。

对于加法，将同类项合并；对于减法，将减法转换为加法，即减去一个整式等于加上它的相反数。

2. 如何进行整式的乘除运算？答：整式的乘除运算也遵循交换律和结合律。

乘法中，将同类项相乘；除法中，将整式除以一个非零的整式，结果为商式和余式。

初二上册数学练习题及答案初二上册数学练习题及答案数学是一门需要不断练习和巩固的学科，通过练习题，我们可以更好地理解和掌握数学知识。

初二上册数学练习题涵盖了各个章节的内容，包括代数、几何、函数等。

在这篇文章中，我将为大家提供一些初二上册数学练习题及其答案，希望对大家的学习有所帮助。

一、代数1. 化简下列代数式：(3x^2 + 4x - 2) + (2x^2 - 3x + 5)答案：5x^2 + x + 32. 解方程：2(x + 3) = 5(x - 1)答案：x = 73. 求解不等式：2x - 5 < 3x + 2答案：x > -7二、几何1. 计算下列图形的面积：一个边长为5cm的正方形答案：25平方厘米2. 计算下列图形的周长：一个底边长为6cm，高为8cm的梯形答案：26厘米3. 判断下列说法是否正确：一个正方形的对角线相等答案：正确三、函数1. 已知函数y = 2x + 3，求当x = 4时，y的值。

答案：y = 112. 已知函数y = x^2 - 4x + 3，求当x = 2时，y的值。

答案：y = 33. 判断下列函数是否为一次函数：y = 3x^2 + 2x - 1答案：不是一次函数通过以上的练习题，我们可以巩固代数、几何和函数等各个章节的知识点。

在解题的过程中，我们要注意运用所学的知识和方法，灵活运用公式和定理，理清思路，正确计算。

同时，我们还要注意审题，将问题转化为数学语言，避免出现理解偏差。

在学习数学的过程中，练习题是不可或缺的一部分。

通过大量的练习，我们可以提高解题的能力和思维逻辑能力，培养数学思维，提高数学素养。

同时，通过练习题，我们也可以发现自己的不足和薄弱环节，有针对性地进行学习和巩固。

除了完成教材中的练习题，我们还可以寻找其他来源的数学练习题，如习题集、试卷等。

多样化的练习题可以帮助我们更全面地掌握知识点，提高解题的能力。

总之，数学练习题是我们学习数学的好帮手，通过不断的练习和巩固，我们可以更好地理解和掌握数学知识。

初二上册数学练习题及答案数学作为一门重要的学科，需要通过大量的练习来提高自己的数学能力。

本文将为大家提供初二上册数学练习题及答案，帮助同学们更好地巩固所学知识。

第一章：有理数1. 计算下列各题：(1) $5 - (\frac{3}{2} - \frac{4}{3} + 1)$;(2) $(\frac{2}{3} - \frac{1}{4}) \cdot (\frac{4}{5} - \frac{3}{10}) + 1$;答案：(1) $5 - (\frac{3}{2} - \frac{4}{3} + 1) = 5 - \frac{5}{6} =\frac{25}{6}$;(2) $(\frac{2}{3} - \frac{1}{4}) \cdot (\frac{4}{5} - \frac{3}{10}) + 1 = (\frac{1}{12}) \cdot (\frac{7}{10}) + 1 = \frac{7}{120} + 1 =\frac{127}{120}$.第二章：代数式与方程1. 计算下列各题：(1) $5a - (2a - 3b + a)$，其中$a = 2$，$b = 3$;(2) $2(x + 1) - (x - 2)$，其中$x = 3$。

答案：(1) $5a - (2a - 3b + a) = 5 \cdot 2 - (2 \cdot 2 - 3 \cdot 3 + 2) = 10 - (4 - 9 + 2) = 10 - (-3) = 13$;(2) $2(x + 1) - (x - 2) = 2(3 + 1) - (3 - 2) = 2(4) - 1 = 8 - 1 = 7$.第三章：图形的认识1. 完成下面的图形：(1) 正方形，边长为5cm;(2) 五角星，外接圆半径为3cm。

答案：(1) (2) 第四章：数据的收集与分类1. 图表中的数据如下所示，请完成所需的统计：答案：(1) 小于35岁的人数：20 + 12 + 18 = 50人。

八年级数学上册--分式练习题及答案1.下列各式a-bx+35+y/3.x/ (x^2+1)。

π/4.(a+b)/(a-b)。

m/(x-y)中，分式共有（C.3个）。

2.如果分式(x^2-4)/(x-2)的值等于0，那么（B.x=2）。

3.与分式(-a+b)/(-a-b)相等的是（A。

(a+b)/(a-b)）。

4.若把分式(x+y)/(2xy)中的x和y都扩大3倍，那么分式的值（D.缩小6倍）。

5.化简(m^2-3m)/(9-m^2)的结果是（B。

-m/(m+3)）。

6.下列算式中，你认为正确的是（B。

1/(ba)=1）。

7.甲乙两个码头相距s千米，某船在静水中的速度为a千米/时，水流速度为b千米/时，则船一次往返两个码头所需的时间为（2s/(a-b)）小时。

8.甲、乙两班学生参加植树造林，已知甲班每天比乙班多植5棵树，甲班植80棵树所用的天数与乙班植70棵树所用的天数相等，若设甲班每天植树x棵，则根据题意得出的方程是（80/(x+5)=70/x）。

9.用科学计数法表示的数-3.6×10^-4写成小数是（C。

-0.）。

10.若分式(a-b)(b-c)/(a-b)(b+c)+(b-c)(c-a)/(b+c)(c-a)+(c-a)(a-b)/(c-a)(a+b)的值为0，则a、b、c构成等边三角形。

填空题：11.当x≠1/2时，分式1+2x/1-2x有意义。

12.利用分式的基本性质，得到：(a+b)/(a-b)×(a-b)/(a+b)=1.3a1.$\frac{a+2}{1}=\frac{5xy}{10axy}$，化简得：$a=\frac{xy}{2}$。

2.$a^2-4a+29=0$，解得：$a=2\pm 5i$。

3.计算：$\frac{3a}{a-b}=\frac{3a}{a-b}\cdot\frac{ab}{ab}=\frac{3ab}{a^2b-ab}= \frac{3b}{a-b}$。

初二数学上册同步练习册习题与答案大全初中数学与小学不同，会比较难，学好初中数学需要平时的练习，练习越多,掌握越熟练。

下面是小编为大家整理的关于初二数学上册同步练习册习题与答案，希望对您有所帮助!初二数学上册练习题及答案1.下列四个说法中，正确的是( )A.一元二次方程有实数根;B.一元二次方程有实数根;C.一元二次方程有实数根;D.一元二次方程_2+4_+5=a(a≥1)有实数根.【答案】D2.一元二次方程有两个不相等的实数根，则满足的条件是A. =0B. 0C. 0D. ≥0【答案】B3.(20__四川眉山)已知方程的两个解分别为、，则的值为A. B. C.7 D.3【答案】D4.(20__浙江杭州)方程 _2 + _ – 1 = 0的一个根是A. 1 –B.C. –1+D.【答案】D5.(20__年上海)已知一元二次方程_2 + _ ─ 1 = 0，下列判断正确的是( )A.该方程有两个相等的实数根B.该方程有两个不相等的实数根C.该方程无实数根D.该方程根的情况不确定【答案】B6.(20__湖北武汉)若是方程 =4的两根，则的值是( )A.8B.4C.2D.0【答案】D7.(20__山东潍坊)关于_的一元二次方程_2-6_+2k=0有两个不相等的'实数根，则实数k的取值范围是( ).A.k≤B.kC.k≥D.k【答案】B初二数学练习及答案一、选择题：(每小题3分，共30分)1. 如右图，图中共有三角形( )A、4个B、5个C、6个D、8个2.下面各组线段中，能组成三角形的是( )A.1，2，3B.1，2，4C.3，4，5D.4，4，83.下列图形中具有不稳定性的是( )A、长方形B、等腰三角形C、直角三角形D、锐角三角形4. 在△ABC中，∠A=39°，∠B=41°，则∠C的度数为( )A.70°B. 80°C.90°D. 100°5. 如右图所示，AB∥CD，∠A=45°，∠C=29°，则∠E的度数为( )A.22.5°B. 16°C.18°D.29°6. 下列几何图形中，是轴对称图形且对称轴的条数大于1的有( )①长方形;②正方形;③圆;④三角形;⑤线段;⑥射线.A. 3个B. 4个C. 5个D. 6个7. 如图所示，∠A+∠B+∠C+∠D+∠E的结果为( )A.90°B.1 80°C.360°D. 无法确定8. 正多边形的一个内角等于144°，则该多边形是正( )边形.A.8B.9C.10D.119. 如图所示，BO，CO分别是∠ABC，∠ACB的两条角平分线，∠A=100°，则∠BOC的度数为( ).A.80°B.90°C.120°D.140°10. 如图，△ABC中，∠A=90°，AB=AC，BD平分∠ABC交AC于D,DE⊥BC于点E，且BC=6，则△DEC的周长是( )(A)12 cm (B)10 cm (C)6cm (D)以上都不对二、填空题：(每小题3分，共24分)11. 已知三角形两边长分别为4和9，则第三边的取值范围是 .12. 等腰三角形的周长为20cm，一边长为6cm，则底边长为______.13. 已知在△ABC中，∠A=40°，∠B-∠C=40°，则∠B=_____，∠C=______.14. 如图，所示，在△ABC中，D在AC上，连结BD，且∠ABC=∠C=∠1，∠A=∠3，则∠A 的度数为 .15. 把边长相同的正三角形和正方形组合镶嵌，若用2个正方形，则还需要____个正三角形才可以镶嵌.16. 如果一个多边形的内角和为1260°，那么从这个多边形的一个顶点可以连_____•条对角线.17. 如图，△ABC中，∠C=90°，AD平分∠BAC，AB=5，CD=2，则△ABD的面积是____________.18. 已知△ABC的三边长a、b、c，化简│a+b-c│-│b-a-c│的结果是_________.三、解答下列各题：19. 如图所示，在△ABC中：(1)画出BC边上的高AD和中线AE.(2分)(2)若∠B=30°，∠ACB=130°，求∠BAD和∠CAD的度数.(4分)20. 如图，△ABC中，DE是AC的垂直平分线，AE=3cm，△ABD 的周长为13cm.求△ABC的周长.21如图，点A、F、C、D在同一直线上，点B和点E分别在直线AD的两侧，且AB=DE，∠A=∠D，AF=DC.求证：BC∥EF.22. 如图所示，BE平分∠ABD，DE平分∠CDB，BE和DE相交于AC上一点E，•如果∠BED=90°，试说明AB∥CD.23. 请完成下面的说明:(1)如图①所示，△ABC的外角平分线交于G，试说明∠BGC=90°- ∠A.说明：根据三角形内角和等于180°，可知∠ABC+∠ACB=180°-∠_____.根据平角是180°，可知∠ABE+∠ACF=180°×2=360°，所以∠EBC+∠FCB=360°-(∠ABC+∠ACB)=360°-(180°-∠_____)=180 °+ ∠______.根据角平分线的意义，可知∠2+∠3= (∠EBC+∠FCB)= (180°+∠_____)=90°+ ∠_______.所以∠BGC=180°-(∠2+∠3)=90°-∠____.(2)如图②所示，若△ABC的内角平分线交于点点I，试说明∠BIC=90°+ ∠A.(3)用(1)，(2)的结论，你能说出∠BGC和∠BIC的关系吗?24. 在△ABC中,AB=CB,∠ABC=90º,F为AB延长线上一点,点E在BC上,且AE=CF.(1)求证:Rt△ABE≌Rt△CBF;(2)若∠CAE=30º,求∠ACF度数.参考答案：一、选择题：(每小题3分，共30分)1. D2. C3. A4. D5.B6.B7.B8.C9.D 10.C二、填空题：(每小题3分，共24分)三、解答下列各题：(19-20题，每小题6分;21-23题，每小题6分;24题10分，本大题共46分)19. 解：(1)如答图所示.(2)∠BAD=60°，∠CAD=40°.20. 解：∵DE是线段AC的垂直平分线∴AD=CD∵△ABD的周长为13cm∴AB+BC=13cm∵AE=3cm∴AC=2AE=6cm. ∴△ABC的周长为：AB+BC+AC=19cm.21. 证明：∵AF=DC，∴AC=DF，又∠A=∠D，AB=DE，∴△ABC≌△DEF，∴∠ACB=∠DFE，∴BC∥EF.22.证明：在△BDE中，∵∠BED=90°，∠BED+∠EBD+∠EDB=180°，∴∠EBD+∠EDB=180°-∠BED=180°-90°=90°.又∵BE平分∠ABD，DE平分∠CDB，∴∠ABD=2∠EBD，∠CDB=2∠EDB，∴∠ABD+∠CDB=2(∠EBD+∠EDB)=2×90°=180°，∴AB∥CD.24.(1)∵∠ABC=90°,∴∠CBF=∠ABE=90°.在Rt△ABE和Rt△CBF中,∵AE=CF,AB=BC,∴Rt△ABE≌Rt△CBF(HL)(2)∵AB=BC,∠ABC=90°,∴∠CAB=∠ACB=45°.∵∠BAE=∠CAB-∠CAE=45°-30°=15°.由(1)知Rt△ABE≌Rt△CBF，∴∠BCF=∠BAE=15°,∴∠ACF=∠BCF+∠ACB=45°+15°=60°.八年级上册数学练习及答案一、请细心推敲，写出正确结果(每小题3分，共27分)1、已知方程3_+5y—3=0，用含_的代数式表示y，则y=________、2、若_a—b—2—2ya+b=3是二元一次方程，则a=________。

初二数学上册三角形练习题含答案题一：已知△ABC中，∠B=90°，AB=5cm，BC=12cm，求AC的长度。

解：根据勾股定理，直角三角形的两个直角边的平方和等于斜边的平方。

假设AC=x，则AC²=AB²+BC²。

代入已知数据，得到x²=5²+12²，即x²=25+144，x²=169，解方程得x=13。

所以AC的长度为13cm。

题二：已知△DEF中，DE=6cm，DF=8cm，EF=10cm，判断△DEF的形状。

解：根据三角形的边长关系，任意两边之和必须大于第三边。

以DE、DF、EF作为三角形的三条边，计算它们的和：DE+DF=6+8=14cmDE+EF=6+10=16cmDF+EF=8+10=18cm由于DE+DF=14cm小于EF=10cm，所以三边不能构成△DEF。

因此，题目中给出的边长不能构成三角形。

题三：已知△GHI中，∠G=60°，IH=6cm，GH=3cm，求HI的长度。

条边的长度相等，每个角都是60°。

因此，HI的长度等于GH=3cm。

题四：已知△JKL中，∠J=90°，JK=8cm，JL=10cm，求KL的长度。

解：根据勾股定理，直角三角形的两个直角边的平方和等于斜边的平方。

假设KL=x，则KL²=JK²+JL²。

代入已知数据，得到x²=8²+10²，即x²=64+100，x²=164，解方程得x=√164。

所以KL的长度为√164 cm。

题五：已知△MNO中，MN=15cm，NO=20cm，MO=25cm，判断△MNO的形状。

解：根据三角形的边长关系，任意两边之和必须大于第三边。

以MN、NO、MO作为三角形的三条边，计算它们的和：MN+NO=15+20=35cmMN+MO=15+25=40cmNO+MO=20+25=45cm由于MN+NO=35cm小于MO=25cm，所以三边不能构成△MNO。

初二数学上册练习题及答案一、选择题1.若甲、乙两个角相等，则它们的补角一定是（）。

A.锐角B.直角C.钝角D.全等角2.已知直角三角形的长边是5cm，短边是4cm，求斜边的长。

A.1cmB.3cmC.8cmD.9cm3.解方程2x + 5 = 11，求x的值。

A.6B.3C.2D.74.一个平行四边形的邻角是（）。

A.互补角B.对顶角C.对边角D.内角5.计算（-3）×（-4）的结果：A.-7B.7C.12D.-12二、填空题1.一类图形的边长都是2cm，这类图形有4个，它们的总周长是__cm。

2.已知正方形的边长是8cm，它的周长是__cm。

3.若a = 3，b = 4，则a² + b²的值是__。

4.计算π的近似值，保留两位小数：__。

5.化简表达式2x + 3x - (4 + 2x)的结果是__。

三、解答题1.已知两个角互补，其中一个角的度数是60°，求另一个角的度数。

解：设互补角的度数为x，则有：x + 60° = 90°x = 90° - 60°x = 30°所以，另一个角的度数为30°。

2.小明父亲的年龄是小明年龄的3倍，两人年龄总和是36岁，请问小明的父亲多少岁？解：设小明的年龄为x岁，则小明父亲的年龄为3x岁。

根据题意，有：x + 3x = 364x = 36x = 9所以，小明的父亲36岁。

3.已知一个正方形的面积是16平方厘米，求其边长。

解：设正方形的边长为a厘米。

根据题意，有：a² = 16a = √16a = 4所以，正方形的边长为4厘米。

四、综合题现有一个长方形的长是6cm，宽是4cm，请计算：1.该长方形的面积是多少？解：长方形的面积 = 长 ×宽面积 = 6cm × 4cm面积 = 24平方厘米2.该长方形的周长是多少？解：长方形的周长 = 2 × (长 + 宽)周长 = 2 × (6cm + 4cm)周长 = 2 × 10cm周长 = 20厘米3.该长方形的对角线长是多少？解：设对角线长为d厘米。

初二数学上册练习题及答案一、选择题1. 已知函数y = 2x + 3，若x = 5，则y的值是多少？A. 8B. 13C. 15D. 28答案：C. 152. 一只小船顺流而下以恒定的速度航行，全程96千米，若顺流速度为12千米/小时，航行时间是多少？A. 4小时B. 6小时C. 8小时D. 12小时答案：C. 8小时3. 若a + b = 10，且a = 2x，b = 3x，则x的值为多少？A. 1B. 2C. 3D. 4答案：A. 14. 矩形的长是宽的2倍，若矩形的面积为18平方米，则它的长和宽分别是多少？A. 2m和1mB. 3m和6mC. 2m和4mD. 3m和9m答案：C. 2m和4m5. 若x = -3，求y = 2x^2 + 3x - 2的值。

A. 4B. -4C. -22D. 22答案：A. 4二、填空题1. 把2小时20分钟转换为分钟数，结果是多少？（填写数字）答案：1402. 若一个角的度数为90°，则这个角是一个________。

（填写“锐角”或“直角”或“钝角”）答案：直角3. 在一张矩形纸片上，画一个以对角线为轴的对称图形，可用的常见图形有________。

（填写常见图形名称，可多填）答案：正方形、矩形、菱形4. 在一个底面半径为6cm，高度为8cm的圆柱体内，若装满水，则水的体积为________立方厘米。

（填写数字）答案：2885. 若x为3的奇数次放大，y为3的偶数次缩小的倍数，则xy的值为________。

（填写数字）答案：3三、计算题1. 小明从家到学校的路上，首先骑自行车12km，然后步行2km，最后乘公交车8km。

请计算小明总共走了多少千米？解答：小明骑自行车的距离：12km小明步行的距离：2km小明乘公交车的距离：8km小明总共走的距离 = 骑自行车的距离 + 步行的距离 + 乘公交车的距离= 12km + 2km + 8km= 22km所以，小明总共走了22千米。

初二数学上册练习题和答案1. 解方程：求x的值(a) 3x + 5 = 20解：首先将等式中的常数项移项，得到3x = 20 - 5然后计算得 3x = 15最后将方程两边同时除以3，得到 x = 5(b) 2(x + 3) = 14解：首先将括号内的表达式展开，得到 2x + 6 = 14然后将等式中的常数项移项，得到 2x = 14 - 6最后将方程两边同时除以2，得到 x = 42. 求平均数：计算一组数据的平均数(a) 2, 4, 6, 8, 10解：将这些数相加，得到 2 + 4 + 6 + 8 + 10 = 30然后将总和除以个数，即 30 ÷ 5 = 6，所以平均数为6(b) 5, 10, 15, 20, 25, 30解：将这些数相加，得到 5 + 10 + 15 + 20 + 25 + 30 = 105然后将总和除以个数，即 105 ÷ 6 = 17.5，所以平均数为17.5 3. 梯形面积计算：已知梯形的上底、下底和高，求梯形的面积(a) 上底为3cm，下底为7cm，高为4cm解：梯形的面积可以通过上底、下底和高来计算，公式为：面积= (上底 + 下底) ÷ 2 ×高将已知的数值代入公式，得到面积 = (3 + 7) ÷ 2 × 4 = 10 × 4 = 40cm²(b) 上底为5cm，下底为9cm，高为6cm解：同样使用梯形的面积公式进行计算，得到面积 = (5 + 9) ÷ 2 ×6 = 14 × 6 = 84cm²4. 分数运算：进行分数的四则运算(a) 1/2 + 1/3解：首先求出最小公倍数，3和2的最小公倍数为6将两个分数的分母统一为6，得到 3/6 + 2/6 = 5/6(b) 3/4 - 1/4解：两个分数的分母相同，直接对分子进行相减，得到 3/4 - 1/4 = 2/4 = 1/25. 图形的面积计算：已知图形的形状和尺寸，求图形的面积(a) 正方形的边长为5cm解：正方形的面积公式为边长的平方，所以面积 = 5cm × 5cm = 25cm²(b) 圆的半径为3cm解：圆的面积公式为πr²，其中π取近似值3.14，所以面积 = 3.14 × 3cm × 3cm = 28.26cm²以上是初二数学上册练习题和答案，通过解方程、求平均数、计算梯形面积、进行分数运算以及计算图形面积等多个题目的练习，能够帮助同学们提升数学能力，更好地理解和掌握数学知识。

初二数学上册练习题答案1. 填空题答案：1. 302. 1/43. 484. 7/155. 856. 1207. 88. 179. 3/810. 712. 选择题答案：1. C2. D3. A4. B5. C6. D7. A8. B9. D10. C3. 计算题答案：1. 1602. 19.53. 3814. 155. 7.66. 4357. 128. 639. 44.810. 514. 解答题答案：1. 解：设未知数为x，则方程可以表示为：2x + 5 = 17解得：2x = 12x = 6因此，未知数x的值为6。

2. 解：设未知数为x，则方程可以表示为：3x - 2 = 4x + 1解得：-x = 3x = -3因此，未知数x的值为-3。

3. 解：设未知数为x，则方程可以表示为：5(x + 3) = 7x - 2解得：5x + 15 = 7x - 215 + 2 = 7x - 5x17 = 2xx = 8.5因此，未知数x的值为8.5。

5. 证明题答案：题目：证明等腰三角形的底角相等。

证明：设等腰三角形ABC中，AB = AC，目标是证明∠B = ∠C。

证明过程：由等腰三角形的定义可知，AB = AC，即两边相等。

根据三角形内角和定理可知，∠A + ∠B + ∠C = 180°。

由等腰三角形的性质可知，∠A = ∠C（顶角相等）。

代入上述等式得：∠C + ∠B + ∠C = 180°。

化简得：2∠C + ∠B = 180°。

移项得：∠B = 180° - 2∠C。

又由于已知∠A = ∠C，代入上述等式得：∠B = 180° - 2∠A。

再次化简得：∠B + ∠A = ∠A。

移项得：∠B = ∠A。

故证明了等腰三角形的底角相等。

总结：通过上述证明过程，我们证明了等腰三角形的底角相等，即∠B = ∠C。

综上所述，我们得出了等腰三角形的底角相等的结论。