绍兴市XX中学2016-2017学年八年级上数学期中试卷含答案

2016-2017学年八年级第一学期期中联考数学试卷参考答案一、选择题（每题3分，共30分）1C;2C;3D;4A;5A;6C;7B;8B;9A;10B二.填空题（每题4分，共24分）11 148°.12 -8a3b613 -4 14 20 15 8 16 60°17．解：（x+1）（x﹣1）﹣x（1﹣x）-2x2，=x2-1-x+x2-2x2……………4 分=-1-x ………5分当x=2时，原式=-1-2=-3．………6 分18．如图，AC=BD且∠A=∠B，求证：AO=BO．证明：∵在△AOC和△BOD中∴△AOC≌△BOD（AAS），…………4 分∴AO=BO．………6 分19．评分说明：1.全对6分；2.只画对一种得2分3.P点坐标2分、四、解答题（本大题共21分．解答应写出文字说明、证明过程或演算步骤．）20解：∵∠BAC=100°，∠B=40°，∴∠ACB=180°﹣∠B﹣∠BAC=40°，………1分∴∠ACB=∠B，………2…分∴AC=AB=3，………3分…∵∠D=30°，∴∠DAC=∠ACB﹣∠D=30°………4分∴∠DAC=∠D，………5分∴CD=AC=3．…………7分21如图，在△ABC和△DBC中，∠ACB=∠DBC=90°，E是BC的中点，EF⊥AB于点F，且AB=DE．（1）求证：△ACB≌△EBD；（2）若DB=8，求AC的长．（1）证明：∵∠DEB+∠ABC=90°，∠A+∠ABC=90°，∴∠DEB=∠A，………2分在△ACB和△EBD中，，∴△ACB≌△EBD，（AAS）；………4分（2）解：∵△ACB≌△EBD，∴BC=DB，AC=EB，………5分∵E是BC的中点，∴EB=，………6分∵DB=8，BC=DB，∴BC=8，∴AC=EB==4．………7分解：连接AF………1分∵AB=AC, ∠BAC=120°∴∠B=∠C=30°………2分∵AC的垂直平分线EF∴AF=CF=3………4分∴∠C=∠EAF=30°∴∠BAF=120°-30°=90°………5分又∵∠B=30°∴BF=2AF=6cm………7分五、解答题（本大题共27分．解答应写出文字说明、证明过程或演算步骤．）23．证明：（1）如图1，在等边△ABC中，AB=BC=AC，∴∠ABC=∠ACB=∠A=60°，………1分∵AE=EB，AE=BD∴BD=BE∴∠EDB=∠DEB=∠A BC=30°………2分∵BC=AC，AE=EB∴∠ECB=∠ACB=30°………3分∴∠EDB=∠ECB，∴EC=ED；………4分（2）如图2，∵EF∥BC，∴∠AEF=∠ABC=60°，∠AFE=∠C=60°，………5分∴△AEF为等边三角形；………6分（3）答EC=ED ；理由：∵∠AEF=∠ABC=60°，∴∠EFC=∠DBE=120°，∵AB=AC，AE=AF ，∴AB﹣AE=AC ﹣AF ，即BE=FC ，………7分在△DBE 和△EFC 中，，∴△DBE≌△EFC（SAS ），………8分∴ED=EC．………9分24：评分说明：（1）过程省略 2分（2）共5分 画对辅助线延长AD,BE 交于P ……1分证到△ABE ≌△APE,得BE=EP …3分证到△DEP ≌△CEB,得DE=CE ……5分(3)面积 48 ……2分E CB A D P25在△ABC中，∠ACB=90°，AC=BC，AB=8，CD⊥AB，垂足为D，M为边AB上任意一点，点N在射线CB上（点N与点C不重合），且MC=MN，NE⊥AB，垂足为E．评分说明解：（1）CD=4．………1分（2）ME=4．………1分（3）共7分答：ME的长度不会改变理由：①如图2所示，若点N在BC上（与B不重合），∵AC=BC，∴∠ACB=90°，∴∠A=∠B=45°．∵AC=BC，CD⊥AB，AB=8，∴CD=BD=4，即∠BCD=45°．∵MN=MN，∴∠MCN=∠MNC．∵∠MCN=∠MCD+∠BCD，∠MNC=∠B+∠BMN，∴∠MCD=∠NME．在△MCD与△NME中，，∴△MCD≌△NME（AAS），∴ME=CD=4．……3分②当点N与点B重合时，点M与点D重合，此时，ME=MN=4．……4分③如图3所示，若点N在边CB上，可知点M在线段BD上，且点E在边AB的延长线上．∵∠ABC=∠MNC+∠BMN=45°，∠BCD=∠MCD+∠MNC=45°，MC=MN，∴∠MCN=∠MNC，∴∠MCD=∠BMN．在△MCD与△NME中，，∴△MCD≌△NME（AAS），∴ME=CD=4．……6分综上所述：由①②③可知，当点M在边AB上移动时，线段ME的长不变，ME=4．…7分．。

浙江省绍兴市八年级上学期数学期中考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题；共24分)1. （2分）(2017·房山模拟) 下列图案是轴对称图形的是（）A .B .C .D .2. （2分） (2019八上·武安期中) 如图，△ABC≌△A′B′C′，其中∠A＝36°，∠C＝24°，则∠B′＝（）A . 150°B . 120°C . 90°D . 60°3. （2分） (2016八上·柘城期中) 如图，CE⊥AB，DF⊥AB，垂足分别为E、F，AC∥DB，且AC=BD，那么Rt△AEC≌Rt△BFD的理由是（）A . SSSB . AASC . SASD . HL4. （2分） (2016八上·蓬江期末) 点M（1，3）关于y轴对称点的坐标为（）A . （﹣1，﹣3）B . （﹣1，3）C . （1，﹣3）D . （3，﹣1）5. （2分）在下列命题中，正确的是（）A . 等腰三角形是锐角三角形B . 等腰三角形两腰上的高相等C . 等腰三角形的腰一定大于其腰上的高D . 等腰三角形一边长为7，另一边长为15，则它的周长是29或376. （2分） (2018八上·西华期末) 若一个三角形两边长分别是3、7，则第三边长可能是（）A . 4B . 8C . 10D . 117. （2分）若三角形的三边长分别为3，4，x ，则x的值可能是（）A . 1B . 6C . 7D . 108. （2分） (2017八下·定安期末) 如果一个四边形的面积正好等于它的两条对角线乘积的一半，•那么这个四边形一定是（）A . 菱形B . 矩形C . 正方形D . 对角线互相垂直的四边形9. （2分）在如图所示的5×5方格中，每个小方格都是边长为1的正方形，△ABC是格点三角形（即顶点恰好是正方形的顶点），则与△ABC有一条公共边且全等的所有格点三角形的个数是（）A . 1B . 2C . 3D . 410. （2分）如图，在△ABC中，分别以点A和点C为圆心，大于 AC长为半径画弧，两弧相交于点M，N，作直线MN分别交BC，AC于点D，E．若AE=3cm，△ABD的周长为13cm，则△ABC的周长为（）A . 16cmB . 19cmC . 22cmD . 25cm11. （2分）如图，点O是△ABC的内切圆的圆心，若∠BAC=80°，则∠BOC=（）A . 130°B . 100°C . 50°D . 65°12. （2分） (2019八下·南岸期中) 等腰三角形的两边长是6cm和3cm，那么它的周长是A . 9cmB . 12 cmC . 12 cm或15 cmD . 15 cm二、填空题 (共10题；共10分)13. （1分）(2014·连云港) 一个正多边形的一个外角等于30°，则这个正多边形的边数为________．14. （1分）(2014·常州) 已知P（1，﹣2），则点P关于x轴的对称点的坐标是________．15. （1分）如图，在△ABC中，∠BAD=∠B，∠EAC=∠C，BC=12，则△ADE的周长为________．16. （1分） (2016八上·滨州期中) 如图，正三角形ABC的周长为12cm，DC∥AB，AD⊥CD于D．则CD=________cm．17. （1分）(2018·和平模拟) 如图，矩形ABCD的对角线AC，BD相交于点O，分别过点C，D作BD，AC的平行线，相交于点E．若AD=6，则点E到AB的距离是________．18. （1分）如图，在Rt△ABC中，∠ACB=90°，CD⊥AB，CD=4，cosA=，那么BC=________19. （1分） (2019八下·太原期中) 如图，△ABC和△DCB中，∠A=∠D=90°，边AC与DB相交于点O，要使△ABC≌△DCB，则需要添加的一个条件是________．（写出一种情况即可）20. （1分）(2019·盘锦) 如图，点A1 ， A2 ，A3…，An在x轴正半轴上，点C1 ， C2 ， C3 ，…，在y轴正半轴上，点B1 ， B2 ， B3 ，…，Bn在第一象限角平分线OM上，OB1＝B1B2＝B1B3＝…＝Bn﹣1Bn＝ a，A1B1⊥B1C1 ，A2B2⊥B2C2 ，A3B3⊥B3C3 ，…，，…，则第n个四边形的面积是________.21. （1分） (2017八上·东台期末) 小聪用刻度尺画已知角的平分线，如图，在∠MAN两边上分别量取AB=AC，AE=AF，连接FC，EB交于点D，作射线AD，则图中全等的三角形共有________对．22. （1分）在△ABC中，∠A=60°，要使是等边三角形，则需要添加一条件是________三、解答题 (共8题；共105分)23. （15分）(2019·碑林模拟) 如图，已知矩形ABCD中，连接AC，请利用尺规作图法在对角线AC上求作一点E使得△ABC∽△CDE．（保留作图痕迹不写作法）24. （15分） (2016八下·黄冈期中) 已知：如图，在四边形ABCD中，AB∥CD，E，F为对角线AC上两点，且AE=CF，DF∥BE．求证：四边形ABCD为平行四边形．25. （5分）若多边形所有内角与它的一个外角的和为600°，求这个多边形的边数及内角和．26. （15分） (2016八上·桐乡月考) 已知：如图在△ABC，∠BAC=80°，AD⊥BC于D，AE平分∠DAC，∠B=60°，求∠C的度数求∠DAE的度数27. （10分） (2017八下·孝义期中) 如图，将平行四边形ABCD的边AB延长至点E，使BE=AB，连接DE，EC，DE，交BC于点O．（1）求证：△ABD≌△BEC；（2）连接BD，若∠BOD=2∠A，求证：四边形BECD是矩形．28. （15分） (2016八上·吉安开学考) 在如图所示的正方形网格中，已知△ABC的三个顶点分别是格点A ，B ，C ．（1）请在正方形网格中作△A1B1C1，使它与△ABC关于直线m成轴对称，其中点A1，B1，C1分别是A，B，C 的对称点．（2）若网格中小正方形的边长为1，求四边形BCC1B1的面积．29. （15分） (2020八上·中山期末) 如图，△ABC中，AE=BE，∠AED=∠ABC。

CAD BE2016-2017学年第一学期期中教学质量检测卷八年级 数学试卷（时间100分钟，总分100分）得分：一、选择题（本题共10小题，每小题3分，共30分） 1、下列各数中是无理数的是（ ）ABCD 2、在△ABC 中AB=1、、BC=2则这个三角形是（ ）A ．锐角三角形B ．直角三角形C ．钝角三角形D ．等腰三角形 3、设1a =，a 在两个相邻整数之间，则这两个数是（ ） A ．1和2B ．2和3C ．3和4D ．4和54、函数y kx =的图象经过点P （3，－1）则k 的值为（ ）A ．3B ．－3C ．13D ．13-5）A ．12±B ．12C ．D 6、面积为9㎝2的正方形以对角线为边长的正方形面积为（ ）A ．18㎝2B ．20㎝2C ．24㎝2D ．28㎝27、若点A （2，m ）在x 轴上，则点B （m-1，m+1）在（ ）A ．第一象限B．第二象限C ．第三象限D ．第四象限8、下列计算正确的是（ ）A=B=C4=D =9、函数已知一次函数y kx b =+，y 随x 的增大而减小，且kb ＜0则在直角坐标系内大致图象是（A B C D10、“黄金1号”玉米种子的价格为5元/千克，如果一次购买2千克以上的种子，超过2千克部分的种子价格打6折，设购买种子数量为x 千克，付款金额为y 元，则y 与x 的函数关系的图象大致是（ ）A B C D 二、填空题（本大题8小题，每小题3分共24分）11、在电影院5排3号用（5,3）表示，那么6排2号可表示为。

12= ；= 。

13、一次函数21y x =-的图象经过点（a ，3），则a = 。

14、已知x 轴上的点P 到y 轴的距离为3，则P 点坐标为 。

152(3)0b +=，则M (,)a b 关于x 轴对称的点的坐标为 。

16、写出一个图象不经过第二象限的一次函数表达式 。

17、已知过点A (52,2)a a -+，B (1,4)a a --的直线与y 轴平行，则a 的值为 。

2017学年第一学期八年级期中考试数学试卷（答题时间：90分钟满分：100分）一、 CAABD DBBCB二、（11） 120,60︒︒ （12） 〈 （13）（3，2） （ 14）4 （15）36三、（16）解：16、①解：原式=24222+-····················2分=25····················4分②解：原式=12+···················2分=3+··················4分 ③解：原式=4)3()7(22--····················2分 =437--····················3分=0····················4分④解：原式=3333632-⨯+····················2分 =333232-+····················3分=3····················4分（17）略（18）过程略（每个1.5分）A (0,BCD ( 19、（答案不唯一）答：是平行四边形···················1分 理由：如图，连接DB ，与AC 交于O 点。

浙江省绍兴市八年级上学期数学期中考试试卷姓名:________ 班级:________ 成绩:________一、选择题(本大题共10小题每小题3分，共30分) (共10题；共30分)1. （3分）《九章算术》是我国古代第一部自成体系的数学专著，代表了东方数学的最高成就．它的算法体系至今仍在推动着计算机的发展和应用．书中记载：“今有圆材埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何？”译为：“今有一圆柱形木材，埋在墙壁中，不知其大小，用锯去锯这木材，锯口深1寸（ED=1寸），锯道长1尺（AB=1尺=10寸）”，问这块圆柱形木材的直径是多少？”如图所示，请根据所学知识计算：圆柱形木材的直径AC是（）A . 13寸B . 20寸C . 26寸D . 28寸2. （3分） (2018八上·叶县期中) 在实数，π，﹣，，3.14，3.1212212221……（两个2之间依次增加1个2）中，无理数有（）A . 2个B . 3个C . 4个D . 5个3. （3分） (2018七下·合肥期中) 在下列所给出的坐标中，在第二象限的是（）A . （2，3）B . （2，-3）C . （-2，-3）D . （-2，3）4. （3分）若函数y=（k+1）x+k2﹣1是正比例函数，则k的值为（）A . 0B . 1C . ±1D . -15. （3分）以直角三角形的三边为边长分别向外作正方形，已知其中两个正方形的面积分别为20和16，则第三个正方形的边长为（）A .B . 4或6C . 或4D . 2或66. （3分） (2017八下·个旧期中) 下列计算错误的是（）A .B .C .D .7. （3分） (2018八上·番禺期末) 在平面直角坐标系中，点（2，1）关于y轴对称的点的坐标是（）.A . （－2 ，0 ）B . （－2 ，1 ）C . （－2 ，－1）D . （2 ，－1）8. （3分）如图，在平面直角坐标系中，有若干个整数点，其顺序按图中“→”方向排列，如（1，0），（2，0），（2，1），（3，1），（3，0），（3，﹣1）…根据这个规律探索可得，第100个点的坐标为（）A . （14，0）B . （14，﹣1）C . （14，1）D . （14，2）9. （3分）如图，在矩形ABCD中，AB=3，AD=4，P是AD上的动点，PE⊥AC于E，PF⊥BD 于F，则PE+PF的值是（）A .B . 2C .D .10. （3分）如图，数轴上点P表示的数可能是（）A . -B .C . -D .二、细心填一填(本大题共6小题，每小题4分，共24分 (共6题；共24分)11. （4分） (2019七下·老河口期中) 在平面直角坐标系中，点A在x轴下方，到x轴的距离为3，到原点的距离为5，则点A的坐标为________.12. （4分）(2020·如皋模拟) 化简： =________.13. （4分）(2017·东营) 我国古代有这样一道数学问题：“枯木一根直立地上，高二丈，周三尺，有葛藤自根缠绕而上，五周而达其顶，问葛藤之长几何？”题意是：如图所示，把枯木看作一个圆柱体，因一丈是十尺，则该圆柱的高为20尺，底面周长为3尺，有葛藤自点A处缠绕而上，绕五周后其末端恰好到达点B处，则问题中葛藤的最短长度是________尺．14. （4分）(2017·永定模拟) 在平面直角坐标系中，对于平面内任一点（m，n），规定以下两种变换：⑴f（m，n）=（m，﹣n），如f（2，1）=（2，﹣1）；⑵g（m，n）=（﹣m，﹣n），如g（2，1）=（﹣2，﹣1）．按照以上变换有：f[g（3，4）]=f（﹣3，﹣4）=（﹣3，4），那么g[f（2，﹣3）]=________．15. （4分） (2017八下·蒙城期末) 如图，一透明的圆柱体玻璃杯，从内部测得底部直径为6cm，杯深8cm．今有一根长为16cm的吸管如图放入杯中，露在杯口外的长度为h，则h的变化范围是：________．16. （4分）(2016·镇江) 若代数式有意义，则实数x的取值范围是________．三、用心做一做(本大题共3个小题，每小题6分，共18分) (共3题；共18分)17. （6分） (2016八上·无锡期末) 计算：（1）；（2）（- ）2+|1- |+（- ）-1．18. （6分） (2017八上·揭西期中) 如图，每个小正方形的边长是1（1）在图①中画出一个面积为2的直角三角形；（2）在图②中画出一个面积是2的正方形．19. （6分）(2018·安徽模拟) △ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.①将△ABC向右平移2个单位长度,作出平移后的△A1B1C1,并写出△A1B1C1各顶点的坐标.②若将△ABC绕点(-1,0)顺时针旋转180°后得到△A2B2C2,并写出△A2B2C2各顶点的坐标.③观察△A1B1C1和△A2B2C2,它们是否关于某点成中心对称?若是,请写出对称中心的坐标;若不是,说明理由.四、沉着冷静，缜密思考(本大题共3个小题每小题7分，共21分) (共3题；共21分)20. （7.0分） (2017八下·潮阳期末) 计算： + （﹣1）﹣30﹣| ﹣2|．21. （7分）(2018·定兴模拟) 阅读以下作图过程：第一步：在数轴上，点O表示数0，点A表示数1，点B表示数5，以AB为直径作半圆（如图）；第二步：以B点为圆心，1为半径作弧交半圆于点C（如图）；第三步：以A点为圆心，AC为半径作弧交数轴的正半轴于点M．请你在下面的数轴中完成第三步的画图（保留作图痕迹，不写画法），并写出点M表示的数22. （7.0分）已知函数y=（m2﹣m）x2+（m﹣1）x+2﹣2m．（1）若这个函数是二次函数，求m的取值范围．（2）若这个函数是一次函数，求m的值．（3）这个函数可能是正比例函数吗？为什么？五、灵动智慧超越自我(本大题共3小题每小题9分共27分) (共3题；共21分)23. （7.0分） (2019八上·泰州月考) 如图，，垂足为 . 如果，（1）直接写出 ________， ________；（2）是直角三角形吗？证明你的结论.24. （7.0分）观察下列一组式子的变形过程，然后回答问题：例 1： = = = = ﹣1．例 2： = ， = ﹣， = ﹣，…（1）填空： =________； =________．（2）请你用含 n（n为正整数）的关系式表示上述各式子的变形规律：________．（3）利用上面的结论，求下列式子的值（要有计算过程）. + + +…+．25. （7.0分） (2019八上·新兴期中) 如图，在平面直角坐标系中，A(a，0)，B(b，0)，C(-1，2)，且|a+2|+(b-4)2=0（1）求a，b的值（2）在y轴上是否存在一点M，使△COM的面积= △ABC的面积求出点M的坐标。

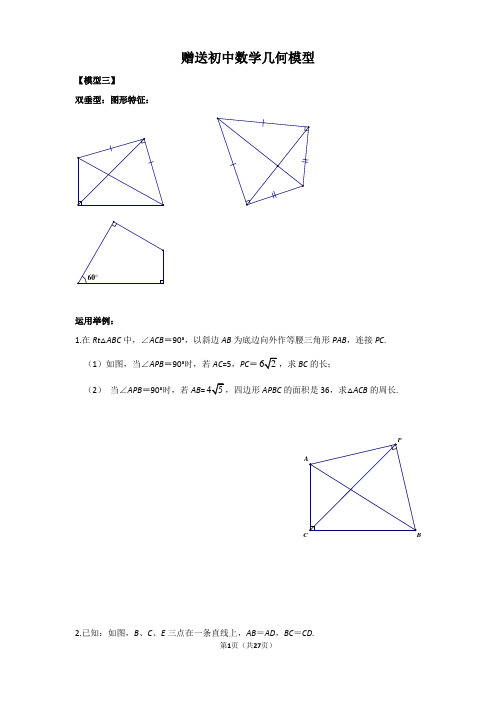
赠送初中数学几何模型【模型三】双垂型：图形特征：60°运用举例：1.在Rt△ABC中，∠ACB＝90°，以斜边AB为底边向外作等腰三角形PAB，连接PC. （1）如图，当∠APB＝90°时，若AC=5，PC＝62，求BC的长；（2）当∠APB＝90°时，若AB=45APBC的面积是36，求△ACB的周长.P 2.已知：如图，B、C、E三点在一条直线上，AB＝AD，BC＝CD.（1）若∠B＝90°，AB＝6，BC＝23，求∠A的值；（2）若∠BAD＋∠BCD＝180°，cos∠DCE＝35，求ABBC的值.3.如图，在四边形ABCD中，AB=AD，∠DAB=∠BCD=90°，（1）若AB=3，BC+CD=5，求四边形ABCD的面积（2）若p= BC+CD，四边形ABCD的面积为S，试探究S与p之间的关系。

DBC2016-2017学年浙江省绍兴市嵊州市剡城中学八年级（上）期中数学试卷一、仔细选一选（本大题有10小题，每小题2分，共20分.请选出每个小题中一个符合题意的正确选项，不选、多选、错选，均不给分）1．（2分）下列每组数分别是三根木棒的长度，能用它们摆成三角形的是（）A．3cm，4cm，8cm B．8cm，7cm，15cmC．5cm，5cm，11cm D．13cm，12cm，20cm2．（2分）如果一个三角形的三个内角的度数之比为2：3：5，那么这个三角形是（）A．锐角三角形B．直角三角形C．钝角三角形D．无法判断3．（2分）对于命题“如果∠1+∠2=90°，那么∠1≠∠2”，能说明它是假命题的反例是（）A．∠1=50°，∠2=40°B．∠1=50°，∠2=50°C．∠1=∠2=45° D．∠1=40°，∠2=40°4．（2分）如图，已知EB=FD，∠EBA=∠FDC，下列不能判定△ABE≌△CDF的条件是（）A．∠E=∠F B．AB=CD C．AE=CF D．AE∥CF5．（2分）如图，△ABC中，∠C=90°，AB的中垂线DE交AB于E，交BC于D，若AB=10，AC=6，则△ACD的周长为（）A．16 B．14 C．20 D．186．（2分）如图，△ABC中，AD⊥BC于D，BE⊥AC于E，AD与BE相交于F，若BF=AC，则∠ABC的大小是（）A．40°B．45°C．50°D．60°7．（2分）工人师傅常用角尺平分一个任意角．做法如下：如图，∠AOB是一个任意角，在边OA，OB上分别取OM=ON，移动角尺，使角尺两边相同的刻度分别与M，N重合．过角尺顶点C作射线OC．由此做法得△MOC≌△NOC的依据是（）A．AAS B．SAS C．ASA D．SSS8．（2分）如图，在△ABC中，∠B=55°，∠C=30°，分别以点A和点C为圆心，大于AC的长为半径画弧，两弧相交于点M，N，作直线MN，交BC于点D，连接AD，则∠BAD的度数为（）A．65°B．60°C．55°D．45°9．（2分）如图，已知AB=A1B，A1B1=A1A2，A2B2=A2A3，A3B3=A3A4…，若∠A=70°，则∠A nA nB n﹣1的度数为（）﹣1A．B．C．D．10．（2分）如图，等边△ABC的边长为6，AD是BC边上的中线，M是AD上的动点，E是边AC上一点，若AE=2，则EM+CM的最小值为（）A． B．3 C．2 D．4二．细心填一填，相信你一定会填对的！（每小题3分，共30分）11．（3分）把命题“对顶角相等”改写成“如果…那么…”的形式：．12．（3分）在Rt△ABC中，∠C=Rt∠，BC=3，AC=4，则斜边上的高线长为．13．（3分）某楼梯的侧面视图如图所示，其中AB=4米，∠BAC=30°，∠C=90°，因某种活动要求铺设红色地毯，则在AB段楼梯所铺地毯的长度应为米．14．（3分）把一副常用的三角板如图所示拼在一起，那么图中∠ADE是度．15．（3分）如图，已知∠ABC=∠DCB，现要说明△ABC≌△DCB，则还要补加一个条件是或或．16．（3分）在直线l上依次摆放着七个正方形（如图所示）．已知斜放置的三个正方形的面积分别是1，2，3，正放置的四个正方形的面积依次是S1，S2，S3，S4，则S1+S2+S3+S4=．17．（3分）如图，点P是∠BAC的平分线上一点，PB⊥AB于B，且PB=5cm，AC=12cm，则△APC的面积是cm2．18．（3分）如图所示，线段AB与直线a所夹锐角为30°，AB=，在直线a上有一动点C，当△ABC为等腰三角形时，则线段AC的长为．19．（3分）如图，在△ABC中，BD⊥AC于点D，DE是△ABD的中线，AD=6，DE=5，则线段BD的长等于．20．（3分）如图，Rt△ABC，∠ACB=90°，AC=3，BC=4，将边AC沿CE翻折，使点A落在AB上的点D处；再将边BC沿CF翻折，使点B落在CD的延长线上的点B′处，两条折痕与斜边AB分别交于点E、F，则线段B′F的长为．三、解答题（共50分）21．（6分）如图所示：已知DF⊥AB于点F，∠A=25°，∠D=40°，求∠ACD的度数．22．（8分）如图，在长方形ABCD中，将△ABC沿AC对折至△AEC位置，CE与AD交于点F．（1）试说明：AF=FC；（2）如果AB=3，BC=4，求AF的长．23．（8分）如图，已知AC平分∠BAD，CE⊥AB于E，CF⊥AD于F，且BC=CD，（1）求证：BE=DF；（2）若AB=21，AD=9，BC=CD=10，求AC的长．24．（8分）在△ABC中，BC=a，AC=b，AB=c，若∠C=90°，如图1，则有a2+b2=c2；若△ABC为锐角三角形时，小明猜想：a2+b2＞c2，理由如下：如图2，过点A作AD⊥CB于点D，设CD=x．在Rt△ADC中，AD2=b2﹣x2，在Rt△ADB中，AD2=c2﹣（a﹣x）2∴a2+b2=c2+2ax∵a＞0，x＞0∴2ax＞0∴a2+b2＞c2∴当△ABC为锐角三角形时，a2+b2＞c2所以小明的猜想是正确的．（1）请你猜想，当△ABC为钝角三角形时，a2+b2与c2的大小关系．（2）温馨提示：在图3中，作BC边上的高．（3）证明你猜想的结论是否正确．25．（10分）问题背景：在△ABC中，AB、BC、AC三边的长分别为、、，求此三角形的面积．小辉同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处），如图①所示．这样不需求△ABC的高，而借用网格就能计算出它的面积．（1）请你将△ABC的面积直接填写在横线上：．思维拓展：（2）我们把上述求△ABC面积的方法叫做构图法．如果△ABC三边的长分别为a、a、a（a＞0），请利用图②的正方形网格（每个小正方形的边长为a）画出相应的△ABC，并求出它的面积．探索创新：（3）若△ABC三边的长分别为、、（m＞0，n＞0，且m≠n），试运用构图法画出示意图并求出这三角形的面积．26．（10分）如图1，已知△ABC，以AB、AC为边分别向△ABC外作等边△ABD 和等边△ACE，连结BE、CD，则有BE=CD；（1）如图2，已知△ABC，以AB、AC为边分别向外作等腰直角三角形ABD和等腰直角三角形ACE，连结BE、CD，猜想BE与CD有什么数量关系？并说明理由；（2）运用图（1），图（2）中所积累的经验和知识，完成下题：如图（3），要测量池塘两岸相对的两点B、E的距离，已经测得∠ABC=45°，∠CAE=90°，AB=BC=100米，AC=AE，求BE的长（结果保留根号）．2016-2017学年浙江省绍兴市嵊州市剡城中学八年级（上）期中数学试卷参考答案与试题解析一、仔细选一选（本大题有10小题，每小题2分，共20分.请选出每个小题中一个符合题意的正确选项，不选、多选、错选，均不给分）1．（2分）下列每组数分别是三根木棒的长度，能用它们摆成三角形的是（）A．3cm，4cm，8cm B．8cm，7cm，15cmC．5cm，5cm，11cm D．13cm，12cm，20cm【解答】解：A、3+4＜8，故以这三根木棒不可以构成三角形，不符合题意；B、8+7=15，故以这三根木棒不能构成三角形，不符合题意；C、5+5＜11，故以这三根木棒不能构成三角形，不符合题意；D、12+13＞20，故以这三根木棒能构成三角形，符合题意．故选：D．2．（2分）如果一个三角形的三个内角的度数之比为2：3：5，那么这个三角形是（）A．锐角三角形B．直角三角形C．钝角三角形D．无法判断【解答】解：设其三个内角分别是2k，3k，5k．根据三角形的内角和定理，得2k+3k+5k=180，k=18．则2k=36，3k=54，5k=90．则该三角形是直角三角形．故选：B．3．（2分）对于命题“如果∠1+∠2=90°，那么∠1≠∠2”，能说明它是假命题的反例是（）A．∠1=50°，∠2=40°B．∠1=50°，∠2=50°C．∠1=∠2=45° D．∠1=40°，∠2=40°【解答】解：A、满足条件∠1+∠2=90°，也满足结论∠1≠∠2，故A选项错误；B、不满足条件，故B选项错误；C、满足条件，不满足结论，故C选项正确；D、不满足条件，也不满足结论，故D选项错误．故选：C．4．（2分）如图，已知EB=FD，∠EBA=∠FDC，下列不能判定△ABE≌△CDF的条件是（）A．∠E=∠F B．AB=CD C．AE=CF D．AE∥CF【解答】解：A、符合全等三角形的判定定理ASA，能推出△ABE≌△CDF，故本选项错误；B、符合全等三角形的判定定理SAS，能推出△ABE≌△CDF，故本选项错误；C、不符合全等三角形的判定定理，不能推出△ABE≌△CDF，故本选项正确；D、∵AE∥CF，∴∠A=∠FCD，∴符合全等三角形的判定定理AAS，能推出△ABE≌△CDF，故本选项错误；故选：C．5．（2分）如图，△ABC中，∠C=90°，AB的中垂线DE交AB于E，交BC于D，若AB=10，AC=6，则△ACD的周长为（）A．16 B．14 C．20 D．18【解答】解：∵△ABC中，∠C=90°，AB=10，AC=6，∴BC===8，∵DE是线段AB的垂直平分线，∴AD=BD，∴AD+CD=BD+CD，即AD+CD=BC，∴△ACD的周长=AC+CD+AD=AC+BC=6+8=14．故选：B．6．（2分）如图，△ABC中，AD⊥BC于D，BE⊥AC于E，AD与BE相交于F，若BF=AC，则∠ABC的大小是（）A．40°B．45°C．50°D．60°【解答】解：∵AD⊥BC于D，BE⊥AC于E，∴∠BEA=∠ADC=90°．∵∠FBD+∠BFD=90°，∠AFE+∠FAE=90°，∠BFD=∠AFE，∴∠FBD=∠FAE，在△BDF和△ADC中，，∴△BDF≌△ADC（AAS），∴BD=AD，∴∠ABC=∠BAD=45°，故选：B．7．（2分）工人师傅常用角尺平分一个任意角．做法如下：如图，∠AOB是一个任意角，在边OA，OB上分别取OM=ON，移动角尺，使角尺两边相同的刻度分别与M，N重合．过角尺顶点C作射线OC．由此做法得△MOC≌△NOC的依据是（）A．AAS B．SAS C．ASA D．SSS【解答】解：∵OM=ON，CM=CN，OC为公共边，∴△MOC≌△NOC（SSS）．故选：D．8．（2分）如图，在△ABC中，∠B=55°，∠C=30°，分别以点A和点C为圆心，大于AC的长为半径画弧，两弧相交于点M，N，作直线MN，交BC于点D，连接AD，则∠BAD的度数为（）A．65°B．60°C．55°D．45°【解答】解：由题意可得：MN是AC的垂直平分线，则AD=DC，故∠C=∠DAC，∵∠C=30°，∴∠DAC=30°，∵∠B=55°，∴∠BAC=95°，∴∠BAD=∠BAC﹣∠CAD=65°，故选：A．9．（2分）如图，已知AB=A1B，A1B1=A1A2，A2B2=A2A3，A3B3=A3A4…，若∠A=70°，则∠A nA nB n﹣1的度数为（）﹣1A．B．C．D．【解答】解：∵在△ABA1中，∠A=70°，AB=A1B，∴∠BA1A=70°，∵A1A2=A1B1，∠BA1A是△A1A2B1的外角，∴∠B1A2A1==35°；同理可得，∠B2A3A2=17.5°，∠B3A4A3=×17.5°=，∴∠A nA nB n﹣1=．﹣1故选：C．10．（2分）如图，等边△ABC的边长为6，AD是BC边上的中线，M是AD上的动点，E是边AC上一点，若AE=2，则EM+CM的最小值为（）A． B．3 C．2 D．4【解答】解：如图所示，在AB上取AE′=AE，连接CE′，过点E′作E′F⊥BC．∵△ABC为等边三角形，∴AB=AC=BC=6．∵AB=AC，AD是BC边上的中线，∴∠BAD=∠CAD．在△AE′M和△AEM中，，∴△AE′M≌△AEM，∴E′M=EM．由两点之间线段最短可知：当E′、M、C在一条直线上时，EM+MC有最小值．∵AE=2，∴BE′=AB﹣AE′=4在Rt△E′BF中，∠B=60°，∴，=．∴BF=，E′F==．∴FC=BC﹣BF=4．在Rt△E′FC中，E′C===2．∴EM+MC=2．故选：C．二．细心填一填，相信你一定会填对的！（每小题3分，共30分）11．（3分）把命题“对顶角相等”改写成“如果…那么…”的形式：如果两个角是对顶角，那么它们相等．【解答】解：题设为：对顶角，结论为：相等，故写成“如果…那么…”的形式是：如果两个角是对顶角，那么它们相等，故答案为：如果两个角是对顶角，那么它们相等．12．（3分）在Rt△ABC中，∠C=Rt∠，BC=3，AC=4，则斜边上的高线长为 2.4．【解答】解：如图，在Rt△ABC中，CD是高，∠C=Rt∠，BC=3，AC=4，由勾股定理得：AB==5，∵CD是Rt△ABC斜边上的高，∴S=AB×CD，S△ABC=AC×BC，△ABC∴AB×CD=AC×BC，即5×CD=3×4，∴CD=2.4．故答案为：2.4．13．（3分）某楼梯的侧面视图如图所示，其中AB=4米，∠BAC=30°，∠C=90°，因某种活动要求铺设红色地毯，则在AB段楼梯所铺地毯的长度应为（2+2）米．【解答】解：根据题意，Rt△ABC中，∠BAC=30°．∴BC=AB÷2=4÷2=2，AC==2，∴AC+BC=2+2，即地毯的长度应为（2+2）米．14．（3分）把一副常用的三角板如图所示拼在一起，那么图中∠ADE是135度．【解答】解：因为∠BDE=45°，所以∠ADE=135°．15．（3分）如图，已知∠ABC=∠DCB，现要说明△ABC≌△DCB，则还要补加一个条件是∠A=∠D或AB=CD或∠ACB=∠DBC．【解答】解：补充∠A=∠D．∵∠ABC=∠DCB，BC=BC，∠A=∠D∴△ABC≌△DCB（AAS）补充∠ACB=∠DBC．∵∠ABC=∠DCB，BC=BC，∠ACB=∠DBC∴△ABC≌△DCB（ASA）补充AB=CD．∵∠ABC=∠DCB，AB=CD，BC=BC∴△ABC≌△DCB（SAS）．∴故填∠A=∠D或AB=CD或∠ACB=∠DBC．16．（3分）在直线l上依次摆放着七个正方形（如图所示）．已知斜放置的三个正方形的面积分别是1，2，3，正放置的四个正方形的面积依次是S1，S2，S3，S4，则S1+S2+S3+S4=4．【解答】解：观察发现，∵AB=BE，∠ACB=∠BDE=90°，∴∠ABC+∠BAC=90°，∠ABC+∠EBD=90°，∴∠BAC=∠EBD，∴△ABC≌△BDE（AAS），∴BC=ED，∵AB2=AC2+BC2，∴AB2=AC2+ED2=S1+S2，即S1+S2=1，同理S3+S4=3．则S1+S2+S3+S4=1+3=4．故答案为：4．17．（3分）如图，点P是∠BAC的平分线上一点，PB⊥AB于B，且PB=5cm，AC=12cm，则△APC的面积是30cm2．【解答】解：∵AP平分∠BAC交BC于点P，∠ABC=90°，PB=5cm，∴点P到AC的距离等于5cm，∵AC=12cm，∴△APC的面积=12×5÷2=30cm2，故答案为30．18．（3分）如图所示，线段AB与直线a所夹锐角为30°，AB=，在直线a上有一动点C，当△ABC为等腰三角形时，则线段AC的长为2或2或6．【解答】解：当AB=AC1=AC3=2时，△ABC为等腰三角形；当AB=BC2时，△ABC为等腰三角形，过B作BD⊥a，可得∠BAD=∠BC2D=30°，且AD=C2D，∴BD=AB=，根据勾股定理得：AD==3，此时AC2=2AD=6；当AC4=BC4时，△ABC为等腰三角形，过C4作C4E⊥AB，故∠BAC4=∠ABC4=30°，AE=BE=，设C4E=x，则有AC4=2x，根据勾股定理得：x2+（）2=（2x）2，解得：x=1，此时AC4=2x=2，综上△ABC为等腰三角形时，AC的值为2或2或6．故答案为：2或2或6．19．（3分）如图，在△ABC中，BD⊥AC于点D，DE是△ABD的中线，AD=6，DE=5，则线段BD的长等于8．【解答】解：∵BD⊥AC于D，点E为AB的中点，∴AB=2DE=2×5=10，∴在Rt△ABD中，BD==8．故答案为：8．20．（3分）如图，Rt△ABC，∠ACB=90°，AC=3，BC=4，将边AC沿CE翻折，使点A落在AB上的点D处；再将边BC沿CF翻折，使点B落在CD的延长线上的点B′处，两条折痕与斜边AB分别交于点E、F，则线段B′F的长为．【解答】解：根据折叠的性质可知CD=AC=3，B′C=BC=4，∠ACE=∠DCE，∠BCF=∠B′CF，CE⊥AB，∴B′D=4﹣3=1，∠DCE+∠B′CF=∠ACE+∠BCF，∵∠ACB=90°，∴∠ECF=45°，∴△ECF是等腰直角三角形，∴EF=CE，∠EFC=45°，∴∠BFC=∠B′FC=135°，∴∠B′FD=90°，=AC•BC=AB•CE，∵S△ABC∴AC•BC=AB•CE，∵根据勾股定理求得AB=5，∴CE=，∴EF=，ED=AE=，∴DF=EF﹣ED=，∴B′F=．故答案为：．三、解答题（共50分）21．（6分）如图所示：已知DF⊥AB于点F，∠A=25°，∠D=40°，求∠ACD的度数．【解答】解：∵DF⊥AB∴∠AFE=90°，∴∠AEF=90°﹣∠A=90°﹣25°=65°，∴∠CED=∠AEF=65°，∴∠ACD=180°﹣∠CED﹣∠D=180°﹣65°﹣40°=75°．答：∠ACD的度数为75°．22．（8分）如图，在长方形ABCD中，将△ABC沿AC对折至△AEC位置，CE与AD交于点F．（1）试说明：AF=FC；（2）如果AB=3，BC=4，求AF的长．【解答】（1）证明：∵将△ABC沿AC对折至△AEC位置，∴∠ACB=∠ACE，又∵在矩形ABCD中，AD∥BC，∴∠ACB=∠DAC，∴∠DAC=∠ACE，∴AF=CF；（2）解：设AF=x，则DF=4﹣x，CF=AF=x，在直角△CDF中，∵∠D=90°，∴CF2=CD2+DF2，即x2=9+（4﹣x）2，解得：x=，即AF的长为．23．（8分）如图，已知AC平分∠BAD，CE⊥AB于E，CF⊥AD于F，且BC=CD，（1）求证：BE=DF；（2）若AB=21，AD=9，BC=CD=10，求AC的长．【解答】解（1）∵AC平分∠BAD，CE⊥AB，CF⊥AD，∴CE=CF，△BCE与△DCF都是直角三角形，在Rt△BEC和Rt△DFC中，∴Rt△BEC≌Rt△DFC（HL），∴BE=DF．（2）∵Rt△BEC≌Rt△DFC，∴BE=DF，∵CF⊥AF，CE⊥AB，∴∠F=∠CEA=90°，∵AC平分∠BAF，∠FAC=∠EAC，在△FAC和△EAC中，∴△FAC≌△EAC（AAS），∴AE=AF，设BE=x，则AE=21﹣x，DF=x，AF=9+x，∴21﹣x=9+x，∴x=6，即BE=6，在Rt△BCE中，∵BC=10，BE=6，∴由勾股定理得：CE=8．24．（8分）在△ABC中，BC=a，AC=b，AB=c，若∠C=90°，如图1，则有a2+b2=c2；若△ABC为锐角三角形时，小明猜想：a2+b2＞c2，理由如下：如图2，过点A作AD⊥CB于点D，设CD=x．在Rt△ADC中，AD2=b2﹣x2，在Rt△ADB中，AD2=c2﹣（a﹣x）2∴a2+b2=c2+2ax∵a＞0，x＞0∴2ax＞0∴a2+b2＞c2∴当△ABC为锐角三角形时，a2+b2＞c2所以小明的猜想是正确的．（1）请你猜想，当△ABC为钝角三角形时，a2+b2与c2的大小关系．（2）温馨提示：在图3中，作BC边上的高．（3）证明你猜想的结论是否正确．【解答】解：（1）当△ABC为钝角三角形时，a2+b2与c2的大小关系为：a2+b2＜c2；（2）如图3，过点A作AD⊥BC于点D，（3）证明：如图3，设CD=x．在Rt△ADC中，AD2=b2﹣x2，在Rt△ADB中，AD2=c2﹣（a+x）2∴a2+b2=c2﹣2ax∵a＞0，x＞0∴2ax＞0∴a2+b2＜c2∴当△ABC为钝角三角形时，a2+b2＜c2．25．（10分）问题背景：在△ABC中，AB、BC、AC三边的长分别为、、，求此三角形的面积．小辉同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处），如图①所示．这样不需求△ABC的高，而借用网格就能计算出它的面积．（1）请你将△ABC的面积直接填写在横线上：．思维拓展：（2）我们把上述求△ABC面积的方法叫做构图法．如果△ABC三边的长分别为a、a、a（a＞0），请利用图②的正方形网格（每个小正方形的边长为a）画出相应的△ABC，并求出它的面积．探索创新：（3）若△ABC三边的长分别为、、（m＞0，n＞0，且m≠n），试运用构图法画出示意图并求出这三角形的面积．【解答】解：（1）S=3×3﹣×1×2﹣×1×3﹣×2×3=．△ABC故答案为：．（2）如图1，在边长为a的正方形网格中，△ABC即为所求作三角形，S△ABC=2a×4a﹣×2a×2a﹣×2a×a﹣×4a×a=3a2；（3）如图2，在长为m、宽为n的网格中，△ABC即为所求作三角形，其中AB=、AC=、BC=，S△ABC=4m×4n﹣×m×4n﹣×3m×2n﹣×4m×2n=7mn．26．（10分）如图1，已知△ABC，以AB、AC为边分别向△ABC外作等边△ABD 和等边△ACE，连结BE、CD，则有BE=CD；（1）如图2，已知△ABC，以AB、AC为边分别向外作等腰直角三角形ABD和等腰直角三角形ACE，连结BE、CD，猜想BE与CD有什么数量关系？并说明理由；（2）运用图（1），图（2）中所积累的经验和知识，完成下题：如图（3），要测量池塘两岸相对的两点B、E的距离，已经测得∠ABC=45°，∠CAE=90°，AB=BC=100米，AC=AE，求BE的长（结果保留根号）．【解答】解：（1）BE=DC，理由如下：∵△ABD和△ACE都为等腰直角三角形，∴AD=AB，AE=AC，∠DAB=∠EAC=90°，∴∠DAB+∠BAC=∠EAC+∠BAC，即∠DAC=∠BAE，在△DAC和△BAE中，，∴△DAC≌△BAE（SAS）∴BE=DC，（2）在AB的外侧作AD⊥AB，使AD=AB，连结CD，BD，∴∠DAB=90°，∴∠ABD=∠ADB=45°．∵∠ABC=45°，∴∠ABD+∠ABC=45°+45°=90°，即∠DBC=90°．∴∠CAE=90°，∴∠DAB=∠CAE，∴∠DAB+∠BAC=∠CAE+∠BAC，即∠DAC=∠BAE．在△ADC和△ABE中，∴△ADC≌△ABE（SAS），∴CD=BE．∵AB=100m，在直角△ABD中，由勾股定理，得BD=100．∴CD==100，∴BE=CD=100，答：BE的长为100米。

浙江省绍兴市八年级上学期期中数学试卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题；共24分)1. （2分）下列式子是分式的是（）A .B .C .D .2. （2分） (2017八上·中江期中) 已知点P（2，﹣1），那么点P关于y轴对称的点Q的坐标是（）A . （﹣2，1）B . （﹣2，﹣1）C . （﹣1，2）D . （2，1）3. （2分）在平面直角坐标中，已知点A（2，1），O为坐标原点，在y轴上确定点P，使得△AOP为等腰三角形，则符合条件的点P的个数为（）A . 3B . 4C . 5D . 64. （2分）下列各式中正确的是（）A .B .C .D .5. （2分）(2016·漳州) 如图，在△ABC中，AB=AC=5，BC=8，D是线段BC上的动点（不含端点B、C）．若线段AD长为正整数，则点D的个数共有（）A . 5个B . 4个C . 3个D . 2个6. （2分）如图，在△ABC中，∠ACB=90°，CD是AB边上的高，∠A=30°，则下列结论中正确的是（）A . AD=2CDB . CD=2BDC . AC=2BCD . AB=4BD7. （2分）能使分式的值为零的所有x的值是（）A . x=1B . x=-1C . x=1或x=-1D . x=2或x=18. （2分）思考下列命题：（1）等腰三角形一腰上的高线等于腰长的一半，则顶角为75度；（2）两圆圆心距小于两圆半径之和，则两圆相交；（3）在反比例函数y= 2 x 中，如果函数值y＜1时，那么自变量x＞2；（4）圆的两条不平行弦的垂直平分线的交点一定是圆心；（5）三角形的重心是三条中线的交点，而且一定在这个三角形的内部；其中正确命题的有几个（）A . 1B . 2C . 3D . 49. （2分） (2017八上·上城期中) 如图，已知的六个元素，下面甲、乙、丙三个三角形中标出了某些元素，则与全等的三角形是（）．A . 甲和乙B . 乙和丙C . 只有乙D . 只有丙10. （2分）(2018·新北模拟) AD与BE是△ABC的角平分线，D，E分别在BC，AC上，若AD=AB，BE=BC，则∠C=（）A . 69°B .C .D . 不能确定11. （2分）(2017·东营模拟) 边长为a的等边三角形，记为第1个等边三角形，取其各边的三等分点，顺次连接得到一个正六边形，记为第1个正六边形，取这个正六边形不相邻的三边中点，顺次连接又得到一个等边三角形，记为第2个等边三角形，取其各边的三等分点，顺次连接又得到一个正六边形，记为第2个正六边形（如图），…，按此方式依次操作，则第6个正六边形的边长为（）A .B .C .D .12. （2分）(2017·广州模拟) 如图，在平行四边形ABCD中，BF平分∠ABC，交AD于点F，CE平分∠BCD，交AD于点E，AB=7，EF=3，则BC长为（）A . 9B . 10C . 11D . 12二、填空题 (共6题；共6分)13. （1分） (2019八上·鸡东期末) 当x________时，分式有意义．14. （1分） (2017七上·绍兴期中) 已知一个数的平方根是3a+1和a+11，求这个数的立方根________。

2016-2017 人教版第一學期 八年級數學期中試卷一．用心選一選：（每小題3分,共30分）1.下列各式是因式分解且完全正確の是（ ）A ．ab ＋ac ＋d =b a (＋c ）＋dB ．)1(23-=-x x x x C ．（a ＋2）（a －2）=2a －4 D ．2a －1=（a ＋1）（a －1） 2.醫學研究發現一種新病毒の直徑約為0.000043毫米，這個數用科學記數法表 示為( )A. 41043.0-⨯ B. 41043.0⨯ C. 5103.4-⨯ D. 5103.4⨯3. 下列各式：()xxx x y x x x 2225,1,2 ,34 ,151+---π其中分式共有（ ）個。

A ．2 B. 3 C. 4 D. 5 4. 多項式 2233449-18-36a x a x a x 各項の公因式是（ ）A ．22a xB ．33a xC ．229a xD ．449a x5. 如圖，用三角尺可按下面方法畫角平分線：在已知の∠AOBの兩邊上分別取點M 、N ，使OM ＝ON ，再分別過點M 、N 作OA 、OB の垂線，交點為P ，畫射線OP ．可證得△POM ≌△PON ，OP 平分∠AOB ．以上依畫法證明 △POM ≌△PON 根據の是（ ） A ．SSS B ．HL C ．AAS D ．SAS6. 甲、乙二人做某種機械零件，已知甲每小時比乙多做6個，甲做90個所用の時間與乙做60個所用の時間相等。

如果設甲每小時做x 個零件，那麼下面所列方程中正確の是（ ）. A.9060-6x x = B. 90606x x =+ C. 90606x x =+ D. 9060-6x x=7. 如圖，已知△ABC ，則甲、乙、丙三個三角形中和△ABC 全等の是（ ）baca cc aa丙72︒50︒乙50︒甲50︒CBA50︒72︒58︒A. 只有乙B. 乙和丙C. 只有丙D. 甲和乙8. 下列各式中，正確の是（ ）A ．122b a b a =++ B ．2112236d cd cd cd++= C ． -a b a bc c++= D ．222-4-2(-2)a a a a += 9.如圖，正方形ABCD の邊長為4，將一個足夠大の直角三角板の直角頂點放於點A 處，該三角板の兩條直角邊與CD 交於點F ，與CB 延長線交於點E ．四邊形AECF の面積是（ ）A. 16 B ．4 C ．8 D. 1210．在數學活動課上，小明提出這樣一個問題：如右圖, ∠B =∠C = 90︒, E 是BC の中點, DE 平分∠ADC, ∠CED = 35︒, 則∠EAB の度數 是 ( )A ．65︒B ．55︒C ．45︒D ．35︒二．細心填一填:(每小題3分,共24分) ． 11．計算：2220042003-= .ED CBA12. 04= 212-⎛⎫- ⎪⎝⎭= ()312a b -=13. 如果分式 242x x -+ の值是零，那麼x の值是 _________________ .14. 將一張長方形紙片按如圖所示の方式折疊，BC BD ，為折痕， 則CBD ∠の度數為_ _.15. 計算： 2422x x x --- = __________________. 16. 如圖，AC 、BD 相交於點O ，∠A ＝∠D ，請你再補充一個條件， 使得△AOB ≌△DOC ，你補充の條件是 .17. 如圖，點P 是∠BAC の平分線AD 上一點，PE ⊥AC 於點E ． 已知PE =3，則點P 到AB の距離是_________________.18. 在平面直角坐標系中，已知點A （1，2），B （5，5），C （5，2），存在點E ， 使△ACE 和△ACB 全等，寫出所有滿足條件のE 點の坐標 ．三.用心做一做（19、20題每題3分，21、22、23題每題4分，共26分）19.因式分解: 24a -32a +64 20．計算：3222)()(---⋅a ab (結果寫成分式)21.計算: （1） 22819369269a a a a a a a --+÷⋅++++ （2） (m 1＋n1)÷nn m ＋22.解分式方程:（1）3221+=x x （2）214111x x x +-=--23. 先化簡： 21x +21+x +1x -1⎛⎫÷ ⎪⎝⎭，再選擇一個恰當の數代入求值.四．應用題（本題5分）24. 甲乙兩站相距1200千米，貨車與客車同時從甲站出發開往乙站，已知客車の速度是貨車速度の2倍，結果客車比貨車早6小時到達乙站，求客車與貨車の速度分別是多少？解:DCB五、作圖題（本題2分）25．畫圖 (不用寫作法,要保留作圖痕跡．．．．．．)尺規作圖：求作AOB∠の角平分線OC．六、解答題：（28題5分，其他每題4分，共17分）26.已知，如圖，在△AFD和△CEB中，點A，E，F，C在同一直線上，AE=CF，DF=BE，AD=CB. 求證：AD∥BC.27.已知：如圖，AB=AD，AC=AE，且BA⊥AC，DA⊥AE．求證：(1)∠B=∠D (2) AM=AN.28.如圖，已知∠1=∠2，P為BN上の一點，PF⊥BC於F，PA=PC，求證：∠PCB+∠BAP=180º.29. 已知：在平面直角坐標系中，△ABCの頂點A、C別在y軸、x軸上，且∠ACB=90°,AC=BC.（1）如圖1，當(0,2),(1,0)A C-，點B則點Bの坐標為；（2）如圖2，當點C在x軸正半軸上運動，點A在y軸正半軸上運動，點B在第四象限時，作BD⊥y軸於點D，試判斷OABDOC+與OABDOC-哪一個是定值，並說明定值是多少？請證明你の結論.F CFDCBAEO附加題1.選擇題：以右圖方格紙中の3個格點為頂點，有多少個不全等の三角形（ ） A ．6 B ．7 C ．8 D ．92．填空題：考察下列命題：（1）全等三角形の對應邊上の中線、高線、角平分線對應相等；（2）兩邊和其中一邊上の中線對應相等の兩個三角形全等；（3）兩邊和第三邊上の中線對應相等の兩個三角形全等；（4）兩角和其中一角の角平分線對應相等の兩個三角形全等；（5）兩角和第三角の角平分線對應相等の兩個三角形全等；（6）兩邊和其中一邊上の高線對應相等の兩個三角形全等；（7）兩邊和第三邊上の高線對應相等の兩個三角形全等；其中正確の命題是 （填寫序號）.3．解答題：我們知道，假分數可以化為帶分數. 例如： 83=223+=223. 在分式中，對於只含有一個字母の分式，當分子の次數大於或等於分母の次數時，我們稱之為“假分式”；當分子の次數小於分母の次數時，我們稱之為“真分式”. 例如：11x x -+，21x x -這樣の分式就是假分式；31x + ，221xx + 這樣の分式就是真分式 . 類似の，假分式也可以化為帶分式（即：整式與真分式和の形式）. 例如：1(1)22=1111x x x x x -+-=-+++； 22111(1)1111111x x x )x x x x x x -++-+===++----（. （1）將分式12x x -+化為帶分式； （2）若分式211x x -+の值為整數，求x の整數值；解：參考答案1-5 DCACB 6-10 ABDBD 11 . 4007 12. 1， 4， 338a b - 13. -2 14 . 90︒ 15. 2 16. OC OB ，或CD AB ，或===OD OA17. 3 18.(5,-1),(1,5),(1,-1) 19. 2)4(4-a 20. 48b a21. （1）-2 （2）1m 22. (1) x=1 (2)無解 23. -1 24. x=625.略 26. SSS 證全等 27.(1)SAS 證全等 （2）ASA 證全等 28. 過點P 作PE 垂直BA 於點E ，HL 證全等. 29.（1） （3，-1） （2）OC BDOA-是定值.附加題1.選擇題： C2．填空題： 正確の命題是 1,2,3,4 ,5 3．解答題：解：（1）12331222x x x x x -(+)-==-+++； （2）2121332111x x x x x -(+)-==-+++. 當211x x -+為整數時，31x +也為整數.1x ∴+可取得の整數值為1±、3±.x ∴の可能整數值為0,-2，2，-4.。

浙江省绍兴市八年级数学上册期中试卷姓名:________ 班级:________ 成绩:________一、选择题 (共10题；共20分)1. （2分） (2017八上·金华期中) 下列四组线段中，能组成三角形的是（）A . 2cm，3 cm，4 cmB . 3 cm，4 cm，7 cmC . 4 cm，6 cm，2 cmD . 5cm，11 cm，5cm2. （2分） (2017九上·宜城期中) 下列图形中，既是轴对称图形又是中心对称图形的是（）A .B .C .D .3. （2分） (2016八上·平凉期中) 点P（2，3）关于x轴的对称的点的坐标是（）A . （﹣2，3）B . （2，﹣3）C . （2，3）D . （﹣2，﹣3）4. （2分）如图，△AOC≌△BOD，∠A和∠B，∠C和∠D是对应角，下列几组边中是对应边的是（）A . AC与BDB . AO与ODC . OC与OBD . OC与BD5. （2分） (2019七上·马山期中) （﹣2）3的值是（）A . ﹣5B . ﹣6C . ﹣8D . ﹣96. （2分） (2016八上·抚顺期中) 如图所示，三角形纸片中，有一个角为60°，剪去这个角后，得到一个四边形，则∠1+∠2的度数为（）A . 120°B . 180°C . 240°D . 300°7. （2分）不能确定△ABC与△DEF全等的是（）A . AC=DF，AB=DE，BC=EF,B . AB=DE，∠A=∠D， BC=EFC . AC= DF，∠A=∠D，∠C=∠FD . AC= DF，∠B=∠E，∠A=∠D8. （2分）如图所示的尺规作图是作（）A . 线段的垂直平分线B . 一个半径为定值的圆C . 一条直线的平行线D . 一个角等于已知角9. （2分）(2019·河南模拟) 如图，在Rt△ABC中，∠C＝90°，按以下步骤作图：①以点A为圆心，以小于AC的长为半径作弧，分别交AC，AB于点M，N；②分别以点M，N为圆心，以大于 MN的长为半径作弧，两弧相交于点O；③连接AP，交BC于点E．若CE＝3，BE＝5，则AC的长为（）A . 4B . 5C . 6D . 710. （2分）(2017·裕华模拟) 如图，是四张形状不同的纸片，用剪刀沿一条直线将它们分别剪开（只允许剪一次），不能够得到两个等腰三角形纸片的是（）A .B .C .D .二、填空题 (共6题；共6分)11. （1分） (2015七下·泗阳期中) 如果等式（x﹣3）2x﹣1=1，则x=________．12. （1分） (2017八上·官渡期末) 如果一个多边形的内角和是1800°，那么这个多边形的边数是________．13. （1分） (2020八上·铁力期末) 如图，在平面直角坐标系中，已知点A（2，-2），在坐标轴上确定一点B ，使得△AOB是等腰三角形，则符合条件的点B共有________个．14. （1分）随着人们生活水平的不断提高,汽车逐步进入到千家万户,小红的爸爸想在本镇的三条相互交叉的公路(如图所示),建一个加油站,要求它到三条公路的距离相等,这样可供选择的地址有________处.15. （1分） (2020八上·河池期末) 等腰三角形ABC中，∠A＝40°，则∠B的度数是________.16. （1分） (2017八上·湖北期中) 如图，△ABC与△DEF为等边三角形，其边长分别为a，b，则△AEF的周长为________．三、解答题 (共9题；共70分)17. （15分） (2017七下·山西期末) 计算：（1）简便计算：（2）计算：（3）先化简再求值：，其中x= ，y=218. （5分） (2019八上·广州期中) 如图，处在的南偏西方向，处在处的南偏东方向，处在处的北偏东方向，求的度数．19. （5分）如图，在平面直角坐标系中，已知点A、B、C的坐标分别为（－1,0），（5,0），（0,2）（1）求过A、B、C三点的抛物线解析式．（2）若点P从Ａ点出发，沿x轴正方向以每秒1个单位长度的速度向B点移动，连接PC并延长到点E，使CE=PC，将线段PE绕点P顺时针旋转90°得到线段PF,连接FB．若点P运动的时间为ｔ秒，（0≤t≤6）设△PBF的面积为S．①求S与ｔ的函数关系式．②当ｔ是多少时，△PBF的面积最大，最大面积是多少？（3）点P在移动的过程中，△PBF能否成为直角三角形？若能，直接写出点F的坐标；若不能，请说明理由．20. （10分）计算：（1）（﹣2）2+[18﹣（﹣3）×2]÷4．（2）﹣3（2x2y﹣3xy2+2）﹣（x2y﹣xy2+2）﹣x．21. （5分）如图,在四边形ABCD中，∠A=∠BCD=90°,BC=CD,CE⊥AD,垂足为E,求证:AE=CE.22. （5分）(2019·南京) 如图，⊙O的弦AB、CD的延长线相交于点P，且AB＝CD.求证PA＝PC.23. （15分） (2019八上·仙居月考) 如图，△ABC中，AB＝AC，（1）请你利用直尺和圆规完成如下操作：①作△ABC的角平分线AD；②作边AB的垂直平分线EF，EF与AD相交于点P；③连接PB，PC．（2）写出线段PA，PB，PC之间的数量关系，并说明理由．（3）若∠ABC＝70°，求∠BPC的度数．24. （5分）如图，在正方形ABCD中，E为BC边上的点（不与B，C重合），F为CD边上的点（不与C，D重合），且AE=AF，AB=4，设△AEF的面积为y，EC的长为x，求y关于x的函数关系式，并写出自变量x的取值范围．25. （5分） (2016八上·阳信期中) 已知，如图：A、E、F、B在一条直线上，AE=BF，∠C=∠D，CF∥DE，求证：AC∥BD．参考答案一、选择题 (共10题；共20分)答案：1-1、考点：解析：答案：2-1、考点：解析：答案：3-1、考点：解析：答案：4-1、考点：解析：答案：5-1、考点：解析：答案：6-1、考点：解析：答案：7-1、考点：解析：答案：8-1、考点：解析：答案：9-1、考点：解析：答案：10-1、考点：解析：二、填空题 (共6题；共6分)答案：11-1、考点：解析：答案：12-1、考点：解析：答案：13-1、考点：解析：答案：14-1、考点：解析：答案：15-1、考点：解析：答案：16-1、考点：解析：三、解答题 (共9题；共70分)答案：17-1、答案：17-2、答案：17-3、考点：解析：答案：18-1、考点：解析：答案：19-1、考点：解析：答案：20-1、答案：20-2、考点：解析：答案：21-1、考点：解析：答案：22-1、考点：解析：答案：23-1、答案：23-2、答案：23-3、考点：解析：答案：24-1、考点：解析：答案：25-1、考点：解析：。

2016-2017学年浙江省绍兴市嵊州市马寅初中学八年级（上）期中数学试卷、选择题（共10小题，每小题2分，满分20 分）A • 2B • 43 •下列语句不是命题的是（） A •两直线平行，同位角相等2 2C •若 |a|=|b|,则 a =b C • 6D • 8B •作直线AB 垂直于直线CDD •同角的补角相等4.在厶ABC 和厶AB'C 中,已知/ A= / A ； AB=A B ；添加下列条件中的一个，不能使厶ABC AB'C 一定成立的 是（ ）A • AC=AC 'B • BC=B 'C ' C ./ B= / B 'D ./ C= / C '5•工人师傅常用角尺平分一个任意角. 作法如下：如图所示，/ AOB 是一个任意角，在边OA,OB 上分别取OM=ON ,移动角尺，使角尺两边相同的刻度分别与M , N 重合，过角尺顶点 C 的射线OC 即是/ AOB 的平分线•这种作法的道理是（ ）6・如图，一副分别含有30。

和45。

角的两个直角三角板， 拼成如下图形，其中/ C=90 ° / B=45 ° / E=30。

，则/ BFD 的度数是（ ）1 •如图所示，图中不是轴对称图形的是（A 2 •如果一个三角形的两边长分别为 2和4,则第三边长可能是（ A • HL B• SSS C . SASD • ASA的周长为（10 .等边△ ABC 中，AB=7 , DE 绕点D 逆时针转过 60 °E 点落在BC 边的F 处，已知 AE=2，贝U BF=7. 8. A . 15 ° D . 10 °如图，△ ABC 中，已知/ B 和/ C 的平分线相交于点 F , 经过点F 作DE // BC ,交AB 于D ，交AC 于点E ,若BD+CE=9，则线段DE 的长为（ ）C. 如图，△ ABC 中, AB=AC=10, BC=8, AD 平分/ BAC 交BC 于点D ，点E 为AC 的中点，连接DE ，则△ CDE 9. A . 20如图，△ABCB . 12C . 14D . 13中，AB=AC ,Z BAC=120 °, D 是 BC 中点，DE 丄 AB 于点 E ,贝U BE 是 AE 的(EC.7D . 4倍C . 3倍C. 3.5二、填空题（每小题3分，共30分）11 .若直角三角形的一个锐角为20 °则另一个锐角等于12•命题等腰三角形的两个底角相等”的逆命题是13•已知直角三角形的两直角边的长分别为5和12,则斜边中线长为在△ ABC 中，/ C=90 ° AD 平分/BAC, BC=10,且CD :BD=2：3,则点D 到AB 的距离是19.如图，在Rt A ABC中，/ C=90 ° BC=6cm, AC=8cm,按图中所示方法将△ BCD沿BD折叠，使点C落在AB边的C处，那么CD =14 •在△ ABC中，D是中点, △ ADC的面积是3，则△ ABC的面积是15 .在△ ABC与厶ADC中,/ BAC= / DAC ,添加一个条件,使得△ ABCADC.16.如图, 已知 / BAC=130 ,AB=AC, AC的垂直平分线交BC于点D，则/ ADB= ________ 度.17•如图,，咼线长为18.如图,等腰△ ABC 中，AB=AC,则AD= ____cm.B20•如图，Rt A ABC 中，AC=BC=4，点D , E 分别是AB , AC 的中点，在CD 上找一点P ，使PA+PE 最小，则这个 最小值是.三、解答题（共5小题，满分50分）21.如图，有分别过 A 、B 两个加油站的公路11、12相交于点O ,现准备在/ AOB 内建一个油库，要求油库的位置点P 满足到A 、B 两个加油站的距离相等，而且P 到两条公路l i 、I 2的距离也相等.请用尺规作图作出点 P （不写作法，保留作图痕迹）I .22 .如图，AB=AE , / 1 = / 2, / C= / D .求证：△ ABC ^A AED .23. 如图，已知 AE // BC , AE 平分/ DAC .求证：AB=AC.□ E24. 已知：如图，在△ ABC 中，AB=AC, BF=CD , BD=CE, / FDE= a，(1)求证：△ BFD ◎△ CDE ;(2)求/ A的度数.25 .如图，在△ ABC中，AD丄BC, AE平分/ BAC .(1)若/ A=80°, / C=30°,求 / DAE 的度数；(2)若/ B=80°, / C=40°,求 / DAE 的度数；(3)探究：小明认为如果只知道 / B - Z C=40°,也能得出/ DAE的度数？你认为可以吗？若能，请你写出求解过程；若不能，请说明理由.附加题26. 如图所示，在△ ABC中，AB=5, AC=13, BC边上的中线AD=6,求27. 如图，在△ ABC 中/ABC=45 ° CD 丄BA, BE 丄AC, F 为BC 中点,(1)线段BH与线段AC相等吗？若相等给予证明，若不相等，请说明理由.(2)若AC=12, BC=10,求BG 的长.BC的长./ ABE= / CBE。