高中数学人教A版必修一优化练习：第二章 2.1 2.1.1 第2课时 指数幂及运算 Word版含解析

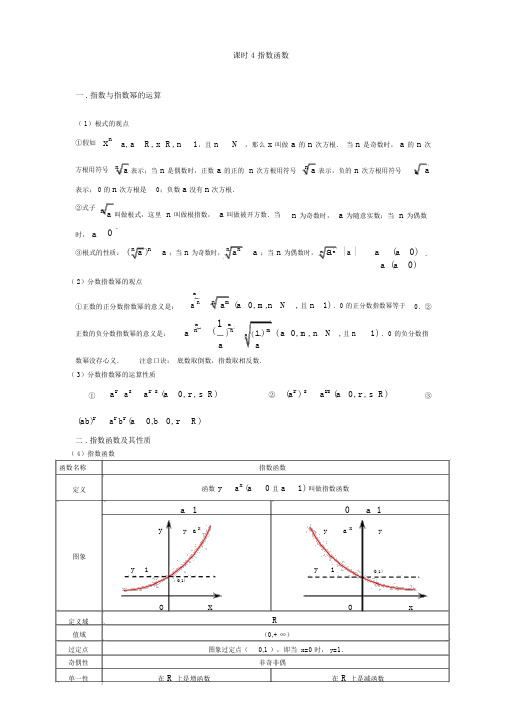
课时 4 指数函数一 . 指数与指数幂的运算（ 1）根式的观点①假如xna, a R, x R, n 1，且 nN ，那么 x 叫做 a 的 n 次方根． 当 n 是奇数时， a 的 n 次方根用符号 na 表示；当 n 是偶数时，正数 a 的正的 n 次方根用符号na 表示，负的 n 次方根用符号na表示； 0 的 n 次方根是 0；负数 a 没有 n 次方根．②式子 n a 叫做根式，这里 n 叫做根指数， a 叫做被开方数．当n 为奇数时， a 为随意实数；当 n 为偶数时， a．③根式的性质： (na )n a ；当 n 为奇数时， n a n a ；当 n 为偶数时， n a n | a |a (a 0) ．a (a 0)（ 2）分数指数幂的观点mna m (a①正数的正分数指数幂的意义是：a n 0, m,n N , 且 n 1) ．0 的正分数指数幂等于0．②m(1m1 ) m( a正数的负分数指数幂的意义是：a n)n n (0, m, n N , 且 n1) ．0 的负分数指aa数幂没存心义． 注意口诀： 底数取倒数，指数取相反数．（ 3）分数指数幂的运算性质①a r a s a r s (a 0, r , s R)② (ar) sa rs (a 0, r , s R)③(ab)ra rb r (a0,b 0, rR)二 . 指数函数及其性质（ 4）指数函数函数名称指数函数定义函数 ya x (a 0 且 a1) 叫做指数函数a 1a 1yy a xya xy图象y1y1(0,1)(0,1)OxOx定义域 R值域（0,+ ∞）过定点 图象过定点（0,1 ），即当 x=0 时， y=1．奇偶性非奇非偶单一性在 R 上是增函数在 R 上是减函数函数值的 y ＞ 1(x ＞ 0), y=1(x=0), 0＜ y ＜ 1(x ＜ 0)y ＞ 1(x ＜ 0), y=1(x=0), 0＜ y ＜ 1(x ＞ 0)变化状况a 变化对在第一象限内， a 越大图象越高，越凑近 y 轴； 在第一象限内， a 越小图象越高，越凑近 y 轴； 图象影响在第二象限内，a 越大图象越低，越凑近x 轴．在第二象限内，a 越小图象越低，越凑近x 轴．三 .例题剖析1.设 a 、 b 知足 0<a<b<1,以下不等式中正确的选项是 ( C)A.a a <a bB.b a <b bC.a a <b aD.b b <a b 分析： A 、B 不切合底数在 (0,1) 之间的单一性 ; C 、 D 指数同样 , 底小值小 . 应选 C. 2.若 0<a<1,则函数 y=a x 与 y=(a-1)x 2 的图象可能是 (D )分析： 当 0<a<1 时 ,y=a x 为减函数 ,a-1<0, 因此 y=(a-1)x2张口向下 , 应选 D.3.设指数函数 f(x)=a x (a>0 且 a ≠ 1),则以下等式中不正确的选项是 ( D )A.f(x+y)=f(x)f(y)f (x)B.f(x-y)=f ( y)C.f(nx)= ［ f(x) ］ nD.f ［ (xy) n ］ =［ f(x) ］ n ［ f(y) ］ n (n ∈ N * )分析： 易知 A 、 B 、 C 都正确 .对于 D,f ［(xy)n］ =a (xy)n , 而［ f(x) ］ n ·［f(y) ］ n =(a x ) n ·(a y ) n =a nx+ny , 一般状况下 D 不建立 .11 34.设 a= ( 3) 3,b= ( 4)4,c= ( 3) 4,则 a 、b 、 c 的大小关系是 ( B )43 2A.c<a<b3分析： a= ( )B.c<b<aC.b<a<cD.b<c<a1 111(8133( 4)3 ( 4) 4=b, b=(4) 4)4(3) 4 =c.∴ a>b>c.3 332725.设 f(x)=4 x -2x+1,则 f -1 (0)=______1____________. 分析： 令 f -1 (0)=a, 则 f(a)=0 即有 4a -2 · 2a =0.2a · (2 a -2)=0, 而 2a >0,∴ 2a =2 得 a=1.6.函数 y=a x-3 +4(a>0 且 a ≠ 1)的反函数的图象恒过定点 ______(5,3)____________.分析： 因 y=a x 的图象恒过定点 (0,1), 向右平移 3 个单位 , 向上平移 4 个单位获得 y=a x-3 +4 的图象 , 易知恒过定点 (3,5).故其反函数过定点 (5,3).10 x 10 x.证明 f(x) 在 R 上是增函数 .7.已知函数 f(x)=x10 x10x1010x102x1,设 x 1<x 2∈ R,则f(x 1)-f(x2)=10x 1 1010x 1 10x 110x 210 x 2102 x 11 102 x 21 2(102 x 1102 x2).x 110x2 10x2 102 x1 1102 x21(102 x11)(102 x 2 1)∵ y=10 x是增函数 ,∴ 10 2x 1 10 2x 2 <0.而 10 2x 1 +1>0, 102 x 2 +1>0,故当 x <x 时 ,f(x)-f(x )<0,1212即 f(x 1)<f(x 2). 因此 f(x) 是增函数 .8.若定义运算 a b=b, ab,则函数 f(x)=3 x3-x 的值域为 ( A )a, a b,A.(0,1]B. ［ 1,+∞ )C.(0,+ ∞ )D.(- ∞ ,+∞ )分析： 当 3x ≥3-x , 即 x ≥ 0 时 ,f(x)=3-x∈(0,1 ］ ;x-x, 即 x<0 时 ,f(x)=3x∈ (0,1).3 x , x 0, 当 3<3∴ f(x)=x值域为 (0,1).3x ,0,9.函数 y=a x 与 y=-a -x (a>0,a ≠1) 的图象 ( C )A. 对于 x 轴对称B.对于 y 轴对称C.对于原点对称D.对于直线 y=-x 对称分析： 可利用函数图象的对称性来判断两图象的关系.10.当 x ∈［ -1,1］时 ,函数 f(x)=3 x-2 的值域为 _______［ -5,1 ］ ___________.3分析： f(x) 在［ -1,1 ］上单一递加 .11.设有两个命题 :(1)对于 x 的不等式 x 2+2ax+4>0对全部 x ∈ R 恒建立 ;(2) 函数 f(x)=-(5-2a) x是减函数 .若命题 (1)和 (2)中有且仅有一个是真命题 ,则实数 a 的取值范围是 _______(- ∞ ,-2)__________.分析： (1) 为真命题=(2a) 2-16<0-2<a<2. (2)为真命题 5-2a>1 a<2.若 (1) 假 (2) 真 , 则 a ∈ (- ∞ ,-2]. 若 (1) 真 (2) 假, 则 a ∈ (-2,2)∩［ 2,+ ∞］=.故 a 的取值范围为 (- ∞ ,-2).12.求函数 y=4 -x -2-x +1,x ∈［ -3,2］的最大值和最小值 .解： 设 2-x=t, 由 x ∈［ -3,2 ］得 t ∈［ 1,8 ］ , 于是 y=t 2-t+1=(t-1)2+3. 当 t= 1时 ,y3 .424有最小值 这时 x=1.当 t=8 时 ,y 有最大值57.这时 x=-3.2413.已知对于 x 的方程 2a2x-2-7a x-1 +3=0 有一个根是 2,求 a 的值和方程其他的根 . 解： ∵ 2 是方程 2a2x-2-9a x-1+4=0 的根 , 将 x=2 代入方程解得 a= 1或 a=4.2(1) 当 a= 1时 , 原方程化为 2· ( 1)2x-2-9(1) x-1 +4=0.①222x-1 2令 y=( 1) , 方程①变成 2y -9y+4=0,2解得 y 1=4,y 2= 1.∴ ( 1) x-1 =42x=-1,2( 1 ) x-1 = 1x=2.22(2) 当 a=4 时 , 原方程化为 2· 42x-2 -9 · 4x-1 +4=0. ②令 t=4 x-1 , 则方程②变成 2t 2-9t+4=0. 解得 t 1=4,t 2= 1.x-12=4x=2,∴44x-1 = 1x=- 1 .22故方程此外两根是当 a= 1时 ,x=-1;1 .2当 a=4 时 ,x=-214.函数 y= (1) 3 4xx 2的单一递加区间是 ( D )3A. ［ 1,2］B.［ 2,3］C.(-∞ ,2]D.［ 2,+∞ )分析： 由于 y=3x2-4x+3 , 又 y=3t 单一递加 ,t=x 2-4x+3 在 x ∈［ 2,+ ∞ ) 上递加 , 故所求的递加区间为［ 2,+ ∞ ).15.已知 f(x)=3 x-b (2≤ x ≤ 4,b 为常数 ) 的图象经过点 (2,1), 则 F(x)=f 2(x)-2f(x) 的值域为 ( B )A. ［ -1,+∞ )B. ［ -1,63)C.［ 0,+∞ )D.(0,63 ］分析： 由 f(2)=1, 得 32-b =1,b=2,f(x)=3 x-2.∴ F (x)= ［ f(x)-1 ］2-1=(3 x-2 -1) 2-1. 令 t=3 x-2 ,2 ≤x ≤4.2∴g(t)=(t-1) - 1,t ∈［ 1,9 ］.2.1 指数函数练习1．以下各式中建立的一项A ． ( n)71n 7 m 7B ．12 ( 3)433m3C ． 4 x 3y 3( x y) 4D ．393321111 1 52．化简 (a 3 b 2 )( 3a 2 b 3 ) ( a 6 b 6 ) 的结果3D ． 9a 2 A ． 6aB ． aC ． 9a3．设指数函数 f ( x)a x ( a 0, a1) ，则以下等式中不正确的选项是f (x) A ． f(x+y)=f(x) ·f(y)B ． f （ x y ）f ( y)C ． f (nx)[ f ( x)]n (nQ )D ． f ( xy) n [ f ( x)] n ·[f ( y)] n1 4．函数 y (x5) 0 ( x 2)2A ． { x | x 5, x 2}B ． { x | x 2}C ． { x | x 5}D ． { x | 2 x 5或 x 5}（）（）（）(n N )（ ）5．若指数函数 y a x 在 [－ 1,1]上的最大值与最小值的差是1，则底数 a 等于 （）A ．15 B ．1 5 C ．15D ．5 122 226．当 a0 时，函数 y axb 和 yb ax 的图象只可能是（）7．函数 f ( x)2 |x| 的值域是（）A ． (0,1]B ． (0,1)C ． (0, )D ． R8．函数 f ( x)2 x 1, x 0，知足 f ( x)1的 x 的取值范围1x 2 , x（）A ． ( 1,1)B ． ( 1, )C ． { x | x 0或 x2}D ． { x | x 1或 x1}9．函数 y(1) x 2x2得单一递加区间是2（）A ．[ 1,1]B ． ( , 1]C ．[2,)D ．[ 1,2]2exe x210．已知 f ( x)（）2 ，则以下正确的选项是A ．奇函数，在 R 上为增函数B ．偶函数，在 R 上为增函数C ．奇函数，在 R 上为减函数D ．偶函数，在 R 上为减函数11．已知函数 f (x)的定义域是（1， 2），则函数 f (2 x ) 的定义域是.12．当 a ＞0 且 a ≠1 时，函数 f (x)=a x －2－ 3 必过定点.三、解答题：13．求函数 y1的定义域 .x5 x 1114．若 a ＞0， b ＞ 0，且 a+b=c ，求证： (1) 当r ＞1时， a r +b r ＜ c r ； (2) 当r ＜ 1时， a r +b r ＞ c r .a x 1 15．已知函数 f ( x)(a ＞1) .a x1（ 1）判断函数 f (x) 的奇偶性；（ 2）证明 f (x)在 (－∞， +∞ )上是增函数 .xa16．函数 f(x) ＝ a (a>0 ，且 a ≠1) 在区间 [1,2] 上的最大值比最小值大2，求 a 的值．参照答案一、 DCDDD AADDA二、 11． (0,1)；12． (2，－ 2) ；三、 13． 解：要使函数存心义一定：x 1 0x 1x0 x 0x 1∴ 定义域为 ： x xR 且 x0, x 1a rrrb r此中a1,0b114． 解：ba，c rcccc.r ＞1 ，a rb ra b 1，r r r当因此+b＜ c ；时c c c crrrrr当 r ＜ 1 时， aba b1， 因此 a +b ＞c .ccc c15． 解 ：(1)是奇函数 .(2) 设x ＜x ，则 f (x 1 )ax11 ax21 。

[课时作业] [A 组 基础巩固]1．化简[3(－5)2]34的结果是( )A ．5 B. 5 C ．－ 5 D ．－5解析：[3(－5)2]34＝(352)34＝52334⨯＝512＝ 5.答案：B 2．设a 12－a 12-＝m ，则a 2＋1a 等于( )A ．m 2－2 B.2－m 2 C ．m 2＋2 D ．m 2解析：对a 12－a12-＝m 平方得：a ＋1a －2＝m 2，∴a 2＋1a ＝a ＋1a ＝m 2＋2. 答案：C3.222的值是( ) A ．278B.258C ．234D ．232解析：222278. 答案：A4． (112)0－(1－0.5－2)÷(278)23的值为( )A ．－13 B.13 C.43D ．73解析：原式＝1－(1－1⎝ ⎛⎭⎪⎫122)÷⎝ ⎛⎭⎪⎫32233⨯＝1－(－3)÷⎝ ⎛⎭⎪⎫322＝1＋3×49＝1＋43＝73. 答案：D5．若102x ＝25，则10－x ＝( ) A ．－15 B.15 C.150D ．1625解析：102x ＝(10x )2＝25，∵10x >0，∴10x ＝5,10－x ＝110x ＝15. 答案：B6．已知102m ＝2,10n ＝3，则10－2m －10－n ＝________. 解析：由102m ＝2，得10－2m＝1102m ＝12；由10n ＝3，得10－n ＝110n ＝13； ∴10－2m －10－n ＝12－13＝16. 答案：167．已知2x ＝(2)y ＋2，且9y ＝3x －1，则x ＋y ＝________. 解析：2x＝(2)y ＋2＝222y +，9y ＝32y ＝3x －1， ∴⎩⎪⎨⎪⎧x ＝y ＋22，2y ＝x －1，解得{ x ＝1y ＝0，∴x ＋y ＝1.答案：18．已知x ＋y ＝12，xy ＝9，且x ＜y ，则11221122x y x y-+的值是________．解析：∵11221122x y x y-+=()122()x y xy x y+--又∵x ＋y ＝12，xy ＝9，∴(x －y )2＝(x ＋y )2－4xy ＝108.又x ＜y ，∴x －y ＝－108＝－6 3. 代入化简后可得结果为－33. 答案：－33 9．化简求值：(1)(279)0.5＋0.1－2＋⎝ ⎛⎭⎪⎫2102723-－3π0＋3748；(2)⎝ ⎛⎭⎪⎫－338 23-＋(0.002)12-－10(5－2)－1＋(2－3)0.解析：(1)原式＝⎝ ⎛⎭⎪⎫25912＋10.12＋⎝ ⎛⎭⎪⎫642723-－3＋3748＝53＋100＋916－3＋3748＝100.(2)原式＝(－1)23-×(338)23-＋(1500)12－105－2＋1＝⎝ ⎛⎭⎪⎫27823-＋(500) 12－10(5＋2)＋1＝49＋105－105－20＋1＝－1679. 10．完成下列式子的化简： (1)(a －2b －3)·(－4a －1b )÷(12a －4b －2c )； (2)23a ÷46a ·b ×3b 3.解析：(1)原式＝－4a －2－1b －3＋1÷(12a －4b －2c ) ＝－13a －3－(－4)b －2－(－2)c －1＝－13ac －1＝－a 3c . (2)原式＝2a 13÷(4a 16b 16)×(3b 32)＝12a 1136-b 16-·3b 32＝32a 16b 43.[B 组 能力提升]1．若S ＝(1＋2132-)(1＋2116-)(1＋218-)(1＋214-)(1＋212-)，则S 等于( )A.12(1－2132-)－1B.(1－2132-)－1C ．1－2132-D ．12(1－2132-)解析：令2132-＝a ，则S ＝(1＋a )(1＋a 2)(1＋a 4)(1＋a 8)(1＋a 16)．因为1－a ≠0，所以(1－a )S ＝(1－a )(1＋a )(1＋a 2)(1＋a 4)(1＋a 8)(1＋a 16) ＝(1－a 2)(1＋a 2)(1＋a 4)(1＋a 8)(1＋a 16) ＝…＝1－a 32＝1－2－1＝12.所以S ＝12(1－a )－1＝12(1－2132-)－1.故选A.答案：A2．如果x ＝1＋2b ，y ＝1＋2－b ，那么用x 表示y 等于( ) A.x ＋1x －1 B.x ＋1x C.x －1x ＋1D ．x x －1解析：∵x ＝1＋2b ，∴2b ＝x －1，∴2－b ＝12b ＝1x －1，∴y ＝1＋2－b ＝1＋1x －1＝x x －1. 答案：D 3．已知10a＝212-，10b＝332，则1 032+4a b＝________.解析：1032+4a b＝(10a )2·(10b )34＝(212-)2·(3213)34＝2－1·254＝214. 答案：2144．若x 1，x 2为方程2x ＝(12)1+1x -的两个实数根，则x 1＋x 2＝________. 解析：∵2x＝(12)1+1x-＝21-1x ，∴x ＝11x-，∴x 2＋x －1＝0. ∵x 1，x 2是方程x 2＋x －1＝0的两根，∴x 1＋x 2＝－1. 答案：－1 5．已知a ＝3，求11144211241111aaaa+++++-+ 的值 解析：11144211241111aaa a+++++-+ 1114422241(1)(1)1aa a a++++-+ 1122224111a aa+++-+ 1122441(1)(1)aa a +++-+ ＝41－a ＋41＋a ＝81－a 2＝－1. 6．已知x ＝12(51n－51n-)，n ∈N ＋，求(x ＋1＋x 2)n 的值．解析：∵1＋x 2＝1＋14(51n－51n -)2＝1＋14(52n－2＋52n -) ＝14(52n＋2＋52n-)＝[12(51n＋51n -)]2， ∴1＋x 2＝12(51n ＋51n -)，∴x ＋1＋x 2＝12(51n －51n -)＋12(51n ＋51n -)＝51n.1∴(x＋1＋x2)n＝(5n)n＝5.。