不完全信息静态博弈:贝叶斯纳什均衡
- 格式:ppt
- 大小:689.50 KB
- 文档页数:20









12 不完全信息静态博弈贝叶斯纳什均衡不完全信息静态博弈Bayesian Game完全信息complete information不完全信息incomplete information完美信息perfect information不完美信息imperfect information信息不对称的例子拍卖暗标拍卖密封递交标书统一时间公正开标标价最高者以所报标价中标中标者的支付取决于标价和其对标的物的估价信息不对称的例子结婚信息不对称的例子市场进入在位者新企业信息不对称的例子信用困境良商奸商2 2信念Belief1 11 1商人B有两种可能的类型 type 良商奸商商人B的类型是自己的私人信息private information商人A对商人B有不同的信念 belief信念不同收益不确定信念不同均衡解也不同商人A如何确定B的类型如何作出理性的选择海萨尼转换The Harsanyi transformationNature良商 p奸商 1-pBelief共同知识海萨尼转换The Harsanyi transformationA的类型B的类型A知道自己的类型知道B的概率分布B知道自己的类型知道A的概率分布1212商人ANature1212A的选择H CB的选择HH HC CH CC商人A的期望收益厂商A的最优反应B选HH A选H B选HC A选HB选CH A选H B选CC A选C1212厂商B的最优反应A选H良商B选H奸商B选CA选C良商B选C奸商B选C均衡解 H HC BNE不完全信息的古诺模型假设两个厂商 A B市场需求厂商A的成本函数厂商B的成本函数以的概率为以的概率为信息是不对称的B知道自己的成本函数和A的成本函数A知道自己的成本函数但却只知道B为高成本或低成本的概率共同知识A的成本B的成本概率分布A知道B享有信息优势B知道A知道自己的信息优势利润函数如果B是高成本厂商如果B是低成本厂商情况1 情况2B是高成本厂商 B是低成本厂商B的选择 B选择概率为概率为A 面临的可能情况厂商A的目标同时求解三个最大化问题期望收益最大反应函数不完全信息的古诺均衡解完全信息的古诺均衡解不完全信息条件下贝叶斯博弈的战略表达式参与者空间参与者的行动空间参与者的类型空间参与者的信念参与者的收益函数参与者i 的类型 ti 是参与者i 的私人信息决定其效用函数 ui ai a-i ti参与者i 只知道自己的类型ti 而不知道其他参与者的类型 t-i参与者i 的信念 pit-i|ti 表示i 在给定自己的类型 ti 时对其他n-1个参与者可能的类型 t-i 的概率参与者i 的期望效用函数为贝叶斯纳什均衡在静态贝叶斯博弈 G A1An T1Tn p1pn u1un 中战略组合 a a1 an 是一个单纯战略贝叶斯纳什均衡如果对每一参与者i 及对i 的类型Ti 集中的每一 ti ai ti 满足古巴导弹危机苏联美国Cuban Missile Crisis1962古巴导弹危机假设Va Vb∈ 1 -7如果双方都选择进攻则会发生一场战争如果一方撤退则会避免战争苏每一方都知道自己属于哪一派但这一信息是自己的隐私美国的选择苏美国的选择如果苏联采取进攻当Vb1 鹰派时最好反应是进攻当Vb -7 鸽派时最好反应是撤退如果苏联选择撤退那么无论私人信息是什么最好反应都是进攻如果苏联是鹰派则进攻将是苏联的占优战略如果苏联选择进攻则美国的最优反应为如果美国是鹰派进攻如果美国是鸽派撤退美国的选择如果苏联是鸽派若美国进攻苏联将撤退若美国撤退苏联将进攻美国的选择美国的信念美国情报部门所掌握的信息赫鲁晓夫强硬的姿态苏联决策集团内部各种意见的综合苏联的实力赫鲁晓夫执行其意旨的能力美国的选择赫鲁晓夫可能断定美国人太胆小肯尼迪是个软弱的总统不敢冒核战争的风险美国人一旦实际面对着这些导弹除了抗议之外不会做什么别的苏联的选择赫鲁晓夫错误地估计了对方的反应认为美国会容忍这种后果而事实相反古巴导弹危机的结果美国施行封锁态度强硬苏联寻求妥协撤回在古巴的导弹1962年11月苏联从古巴撤回导弹。
4.1 不完全信息静态博弈和贝叶斯纳什均衡4.1.1 不完全信息博弈在前两章,我们介绍了完全信息博弈。
在这种博弈中,每个参与人对所有其他参与人的支付收益函数是完全了解的,即支付收益函数是所有参与者的共同知识。
但是在现实的博弈应用,许多博弈并不满足完全信息的要求。
比方说,当你新接触一个陌生人时,并不能确定他的喜爱偏好是什么,通常需要寻找话题进行沟通来获取信息;而在一次古玩交易中,当你作为买家时,你并不清楚卖主愿意脱手的最低价格是多少。
类似上述这些不满足完全信息假设的,称为不完全信息博弈。
在不完全信息博弈中,至少有一个参与者不能确定另一参与者的支付收益函数。
【例 4.1】下面是一个不完全信息的市场博弈例子。
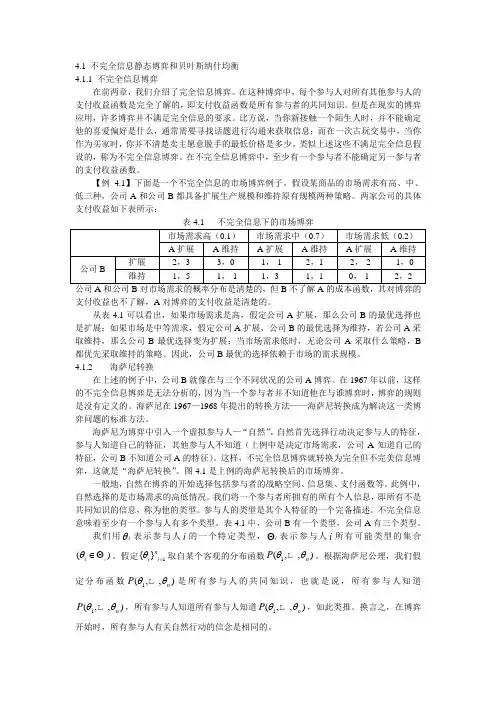
假设某商品的市场需求有高、中、低三种,公司A 和公司B 都具备扩展生产规模和维持原有规模两种策略。
两家公司的具体支付收益如下表所示:公司A 和公司B 对市场需求的概率分布是清楚的,但B 不了解A 的成本函数,其对博弈的支付收益也不了解,A 对博弈的支付收益是清楚的。
从表4.1可以看出,如果市场需求是高,假定公司A 扩展,那么公司B 的最优选择也是扩展;如果市场是中等需求,假定公司A 扩展,公司B 的最优选择为维持,若公司A 采取维持,那么公司B 最优选择变为扩展;当市场需求低时,无论公司A 采取什么策略,B 都优先采取维持的策略。
因此,公司B 最优的选择依赖于市场的需求规模。
4.1.2 海萨尼转换在上述的例子中,公司B 就像在与三个不同状况的公司A 博弈。
在1967年以前,这样的不完全信息博弈是无法分析的,因为当一个参与者并不知道他在与谁博弈时,博弈的规则是没有定义的。
海萨尼在1967—1968年提出的转换方法——海萨尼转换成为解决这一类博弈问题的标准方法。
海萨尼为博弈中引入一个虚拟参与人—“自然”,自然首先选择行动决定参与人的特征,参与人知道自己的特征,其他参与人不知道(上例中是决定市场需求,公司A 知道自己的特征,公司B 不知道公司A 的特征)。
