压电加速度传感器安装谐振频率分析及应用

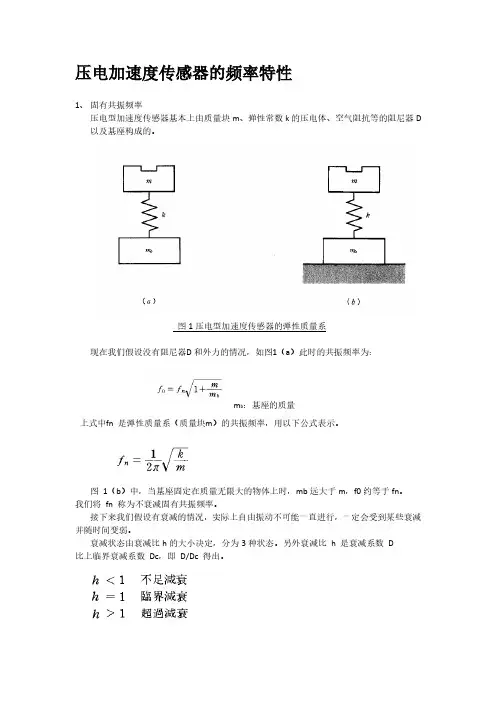
压电加速度传感器的频率特性1、固有共振频率压电型加速度传感器基本上由质量块m、弹性常数k的压电体、空气阻抗等的阻尼器D 以及基座构成的。

图1压电型加速度传感器的弹性质量系现在我们假设没有阻尼器D和外力的情况，如图1（a）此时的共振频率为：m b：基座的质量上式中f n 是弹性质量系（质量块m）的共振频率，用以下公式表示。

图1（b）中，当基座固定在质量无限大的物体上时，mb远大于m，f0约等于fn。

我们将fn 称为不衰减固有共振频率。

接下来我们假设有衰减的情况，实际上自由振动不可能一直进行，一定会受到某些衰减并随时间变弱。

衰减状态由衰减比h的大小决定，分为3种状态。

另外衰减比h 是衰减系数 D比上临界衰减系数Dc，即D/Dc 得出。

图2 衰减自由振动h＜1 时，后续振幅比如下式所示。

由此我们可以得知，包络线会随时间以指数函数减少。

此时将fd 作为共振频率的话，可用以下公式表示。

fd 就称作衰减固有共振频率。

h≥1 时，则fd=0。

变为失去振动性的无周期运动。

从振动测量精度上来看，自由衰减振动需要尽可能快得使其衰减，但衰减比h并不是越大越好。

这一点可从图上记公式中得知。

衰减比h 的大小也受到谐振锐度即Qm 值的影响。

h 越小Qm 就越大，形成尖锐的共振。

其关系由下记公式来表示。

在设计压电型加速度传感器时，会尽可能使h 值小，Qm 值大，形成尖锐共振后，扩大平坦的频率范围。

2、 电荷增幅中的低频截止频率上述已经提到，电荷放大器中传感器产生的电荷全部储存在反馈电容 Cf 中。

因此低频特性与输入电路中的时间常数（电缆电容 Cc 、传感器电容 Cd 等）没有关系， 而是由反馈电路的时间常数 Cf ・Rf 决定。

即低频截止频率 fc 为：由于一般情况下Rf 会选定10MΩ 以上的高阻抗值，比 Cf 的电感器大很多，因此实际上 fc 的值主要由 Cf 的值来决定。

Cf 值越大 fc 就越小，适合低频的振动测量。

生产的YD-5型加速度传感器。

该传感器的质量块的质量约为g m 47.01=，加速度传感器的固有谐振频率为kHz u f 50=。

由(2-27)式有 )/(100437.181m N k ×=2.3.2 2m 的确定2m 为传感器基座与磁座及双头螺栓的总质量,由于传感器中的质量块的质量非常的小,所以2m 近似为YD-5型传感器的质量与CZ −4型磁座(试验中所选用的磁座的一种)质量及双头螺栓质量的总和,即g m 692=。

2.3.3 磁座与轴承外圈接触力的计算磁座与轴承外圈接触时的接触力主要是磁座的磁场对轴承外圈的吸力。

在分析磁座与轴承外圈的接触力时，作如下相关假设：(1) 磁座与轴承的接触表面是理想的光滑面；(2) 磁座在与轴承外圈接触时，不在轴承表面滑动,即摩擦阻力忽略不计；(3) 考虑到接触变型的局部性，即接触面的边界尺寸总是远小于弹性体的几何尺寸；(4) 磁座的磁场是匀强磁场，即不考虑磁力线 的发散现象，且设磁力线的方向是垂直于磁座的底面向下的。

基于以上假设，可以用半空间体（当物体本身的尺寸与接触面尺寸相比很大时，则在此区域中的应力就不大依赖于物体远离接触区的形状，也不依赖于支撑物体的确切方式，这样形成的接触空间为半空间[9]）分析方法来分析磁座与轴承的接触问题。

当磁座与轴承外圈接触的时候，轴承外圈宽度与磁座的底面直径不一定正好相同，在此主要讨论磁座的底面直径小于轴承外圈宽度的情况。

一 永磁圆柱磁场的计算永磁圆柱磁场示意图如图2.4所示，以磁座中心为坐标原点建立柱坐标系。

根据文献[10]的方法，计算整个永磁圆柱在p 点所产生的磁场，可视永磁圆柱为一系列的永磁圆盘的叠加，于是可以写出图2.4永磁圆柱 磁场示意图∫−+=H L H L dB B 220ρρ∫−+×⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧++−=H L H L z R z J 2221220])[(2ρπρdz E z R z R K ⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎦⎤⎢⎢⎣⎡+−++−22222)(ρρ (2-28) ∫−+=H L H L z z dB B 220dz E z R z R K z R J H L H L ⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧+−+−−×++=∫−+])([])[(1.222222221220ρρρπ (2-29) 上式中z B B ,ρ分别为圆柱型永磁圆柱在点),,(z p ϕρ点处的磁场强度各分量大小，0J 是材料的剩磁向量大小，K 和E 分别表示第一类和第二类完全椭圆积分，分别定义如下∫−−=202122)sin 1()(πθθd k k K (2-30) ∫−=20122)sin 1()(πθθd k k E (2-31)式中k 称为积分模数，它的定义如下：2122)(4⎥⎥⎦⎤⎢⎢⎣⎡++=z R R k ρρ (2-32)式中R 为圆柱型永磁圆柱的底面半径，z,ρ分别为p 点的两个坐标分量。

压电换能器谐振频率
压电换能器的谐振频率是指在其固有频率下，换能器产生最大振幅的频率。

这个频率与压电材料的介电常数和机械刚度有关。

在应用中，根据具体需求选择合适的换能器谐振频率，例如在超声波成像中，需要使用合适的谐振频率以获得清晰的成像效果。

要确定压电换能器的谐振频率，可以通过以下方法：
1. 使用阻抗分析仪测试阻抗最大值和阻抗最小值，对应的频率即为谐振频率和反谐振频率。

推荐使用如omicron-lab公司的BODE100阻抗分析仪等设备。

2. 持两个超声转换器（一个是发射，一个是接收）的距离不变，改变信号源的输出频率，观察示波器上的波形变化。

当波形峰峰值最大时，即为谐振频率。

3. 通过驻波法（共振干涉法）和行波法（相位比较法）测量超声波的波长，从而计算出谐振频率。

总之，在测量谐振频率时，要确保换能器端面的平行，以及信号发生器的输出信号频率与压电换能器谐振频率保持一致。

参数说明及工作原理：1.电荷灵敏度加速度计一般采用PZT压电陶瓷材料，利用晶体材料在承受一定方向的应力或形变时，其极化面会产生与应力相应的电荷，压电元件表面产生的电荷正比于作用力，因此有Q=dF其中，Q为电荷量，d为压电元件的压电常数，F为作用力。

加速度计的电荷灵敏度则是加速度计输出的电荷量与其输入的加速度值之比。

电荷量的单位取pC，加速度单位为m/s2。

（1g=9.8m/s2）2.电压灵敏度如果要换算加速度计的电压灵敏度，则可用下面公式得到SqSa = （v/ms-2）CaSq为电荷灵敏度，单位pC/ms-2；Ca为电容量，单位pF。

Sa电压灵敏度单位V。

3.频率响应（1）谐振频率，为加速度计安装时的共振频率，随产品附有谐振频率曲线（低频传感器不附图）。

（2）频率响应一般采用谐振频率的1/3—1/5。

加速度计频响在1/3谐振频率时，频响与参考灵敏度偏差≤1dB，（误差<10%）。

频响在1/5谐振频率时，频响与参考灵敏度≤ 0.5dB （误差<5%）。

我公司传感器频响均以1/3谐振频率计算。

4.最大横向灵敏度比加速度计受到垂直于安装轴线的振动时，仍有信号输出，即垂直于轴线的加速度灵敏度与轴线加速度之比称横向灵敏度。

5. 电荷输出的压电式加速度计配合电荷放大器，其系统的低频响应下限主要取决于放大器的频响。

二、安装技术及注意事项：（一）安装方式用加速度计进行测量，为使数据准确和使用方便，可使用多种方法安装，现介绍几种供选用。

1.螺钉安装RC6000系列加速度计有M5、M3安装孔及传感器自带螺栓等形式，以M5孔居多。

加速度计随产品附有安装螺钉。

使用螺钉安装，它的使用频率响应可近似原标定的频率响应，且称刚性安装。

螺钉安装是在允许打孔的被测物上沿振源轴线方向打孔攻丝。

2.粘接安装在被测物体不允许钻孔时，可使用各种粘接剂，如“502”、环氧树脂胶、双面粘胶带、橡皮泥。

应注意，前二种方法的使用频率接近刚性安装方法，后两种一般用于低频现场，且会使被测频率大大降低。

压电陶瓷片的谐振频率压电陶瓷片的谐振频率导言压电陶瓷片是一种具有压电效应的材料，可以将机械能转化为电能或者将电能转化为机械能。

在实际应用中，压电陶瓷片常常被用来制作振动器、传感器、滤波器等元件。

而这些元件的性能与谐振频率密切相关。

因此，了解压电陶瓷片的谐振频率对于优化元件性能具有重要意义。

一、压电效应和谐振频率的基本概念1. 压电效应压电效应是指某些晶体材料在受到外力作用时会产生极化现象，即正负电荷分离。

同时，当施加外部电场时，这些晶体材料也会发生形变。

这种特殊的物理现象被称为压电效应。

2. 谐振频率谐振频率是指某个系统在受到周期性外力作用时达到最大振幅所对应的频率。

在压电陶瓷片中，谐振频率通常指其固有模式下的共振频率。

二、影响压电陶瓷片谐振频率的因素1. 材料的物理性质压电陶瓷片的谐振频率与其物理性质密切相关。

具体来说，压电陶瓷片的密度、弹性模量、压电系数等参数都会影响其固有频率。

例如，材料密度越大，谐振频率越高；弹性模量越大，谐振频率也越高。

2. 尺寸和形状压电陶瓷片的尺寸和形状也会对其谐振频率产生影响。

通常来说，尺寸越小，谐振频率越高；形状也会影响谐振频率。

例如，在同样大小的圆盘形和方形压电陶瓷片中，圆盘形压电陶瓷片的固有频率要高于方形压电陶瓷片。

3. 电极结构在实际应用中，为了方便控制和测量，压电陶瓷片通常需要加上两个金属电极。

这些金属电极的结构也会影响压电陶瓷片的谐振频率。

例如，在同样大小的圆盘形和方形压电陶瓷片中，采用不同的电极结构会导致谐振频率的差异。

三、压电陶瓷片谐振频率的计算方法1. 等效电路法等效电路法是一种常用的计算压电陶瓷片谐振频率的方法。

该方法将压电陶瓷片等效为一个LC回路，其中L表示压电陶瓷片的等效感性，C表示金属电极之间的等效电容。

根据LC回路共振频率公式可得：f = 1 / (2π√(LC))其中，f表示谐振频率。

2. 有限元法有限元法是一种基于数值分析的方法，可以通过计算模拟出复杂结构下的物理现象。

附录2 仿真程序1. 磁座底面半径－安装谐振频率关系程序% Mounting Resonant Frequency of the Sensor Diagram Generator% This program plots out the Resonant Frequency Diagram% The sensor mounts on a magnetic base% The Diagram reflect the relation between Resonant Frequency% and Radius of the bottom surface% Initialization% format longclearfor i=1:40;R(i)=(i/2.5)*10^(-3);R2=40*10^(-3); % Radius of bearing in meterJ0=1.24; % Magnetization intensity of the base (Wb/m) L=12*10^(-3); % Height of the magnetic basemu=4*pi*10^(-7); % permeability of free space (H/m)n1=0.1875*10^(-11);n2=0.1399*10^(-11);R1=inf; % curvature redius of contacted magnetic base KK1=1.0437*10^8; % equivalent elastic coefficientm1=0.47; % mass of piezoelectricity crystal (g)rho=0.023322;% density of the magnetic base (g/mm^3)for j=1:20;r(i,j)=R(i)*j/20;zz(i,j)=R2-sqrt(R2^2-r(i,j)^2);k(i,j)=sqrt(4*R(i)*r(i,j)/((r(i,j)+R(i))^2+zz(i,j)^2));% Computation of the first class elliptical integral in Simpsonfor w=1:10;x(w)=w*(pi/2)/10;c(i,j,w)=sqrt(1-k(i,j)^2*(sin(x(w)))^2);d(i,j,w)=1/c(i,j,w);endK(i,j)=(pi/2)*((1+c(i,j,10))+2*(c(i,j,2)+c(i,j,4)+c(i,j,6)+c(i,j,8))+...4*(c(i,j,1)+c(i,j,3)+c(i,j,5)+c(i,j,7)+c(i,j,9)))/(3*10);E(i,j)=(pi/2)*((1+d(i,j,10))+2*(d(i,j,2)+d(i,j,4)+d(i,j,6)+d(i,j,8))+...4*(d(i,j,1)+d(i,j,3)+d(i,j,5)+d(i,j,7)+d(i,j,9)))/(3*10);% Computation of magnetization intensity of magnetic base in Simpsonfor q=1:10;z(i,j,q)=zz(i,j)+(q-1)*L/9;e(i,j,q)=(J0/(2*pi))*(1/sqrt((R(i)+r(i,j))^2+z(i,j,q)^2))*...(K(i,j)-(r(i,j)^2-R(i)^2+z(i,j,q)^2)/((r(i,j)-R(i))^2+z(i,j,q)^2)*E(i,j)); endBz(i,j)=-(L/(3*10))*((e(i,j,1)+e(i,j,10))+2*(e(i,j,2)+e(i,j,4)+e(i,j,6)+...e(i,j,8))+4*(e(i,j,1)+e(i,j,3)+e(i,j,5)+e(i,j,7)+e(i,j,9)));endBBz(i)=sum((Bz(i,j))');BBzz(i)=BBz(i);% Computation of the area of the bottom surface of magnetic baseS(i)=pi*(R(i)^2);% Computation of magnetic force of magnetic base to the bearingF(i)=(BBzz(i)^2)*S(i)/(2*mu);% Computation of deformation magnitude of contacted two objectsdelta(i)=(9*pi^2*F(i)^2*(n1+n2)^2*(1/R1+1/R2)/16)^(1/3);% Equivalent elastic coefficientKK2(i)=F(i)/delta(i);aa=KK1/(m1*10^(-3));% mass of magnetic basem2(i)=rho*pi*(R(i)*10^3)^2*L*10^3;bb(i)=KK2(i)/((11+m2(i))*10^(-3));cc(i)=KK1/((11+m2(i))*10^(-3));% Mounting Resonant Frequency of the Sensoromegar(i)=sqrt((aa+bb(i)+cc(i))/2-(1/2)*sqrt(aa^2+2*aa*cc(i)+...(bb(i))^2+2*bb(i)*cc(i)+(cc(i))^2-2*aa*bb(i)));end% plot omegar Vs Rsubplot(2,1,1);plot(R*10^3, omegar,'r'); % FrequencyXlabel('磁座底面半径/mm');Ylabel('安装谐振频率/Hz');2. 磁座的高度－安装谐振频率关系程序% Mounting Resonant Frequency of the Sensor Diagram Generator% This program plots out the Resonant Frequency Diagram% The sensor mounts on a magnetic base% The Diagram reflect the relation between Resonant Frequency% and Heigh of the magnetic base% Initialization% format longclearfor i=1:60;L(i)=(i/2.5)*10^(-3);R2=40*10^(-3); % Radius of bearing in meterJ0=1.24; % Magnetization intensity of the base (Wb/m) R=8*10^(-3); % Radius of bottom surface of magnetic base (m) mu=4*pi*10^(-7); % permeability of free space (H/m)n1=0.1875*10^(-11);n2=0.1399*10^(-11);R1=inf; % curvature redius of contacted magnetic baseKK1=1.0437*10^8; % equivalent elastic coefficientm1=0.47; % mass of piezoelectricity crystal (g)rho=0.023322; % density of the magnetic base (g/mm^3)for j=1:20;r(j)=R*j/20;zz(j)=R2-sqrt(R2^2-r(j)^2);k(j)=sqrt(4*R*r(j)/((r(j)+R)^2+zz(j)^2));% Computation of the first class elliptical integral in Simpsonfor w=1:10;x(w)=w*(pi/2)/10;c(j,w)=sqrt(1-k(j)^2*(sin(x(w)))^2);d(j,w)=1/c(j,w);endK(j)=(pi/2)*((1+c(j,10))+2*(c(j,2)+c(j,4)+c(j,6)+c(j,8))+...4*(c(j,1)+c(j,3)+c(j,5)+c(j,7)+c(j,9)))/(3*10);E(j)=(pi/2)*((1+d(j,10))+2*(d(j,2)+d(j,4)+d(j,6)+d(j,8))+...4*(d(j,1)+d(j,3)+d(j,5)+d(j,7)+d(j,9)))/(3*10);% Computation of magnetization intensity of magnetic base in Simpson for q=1:10;z(i,j,q)=zz(j)+(q-1)*L(i)/9;e(i,j,q)=(J0/(2*pi))*(1/sqrt((R+r(j))^2+z(i,j,q)^2))*...(K(j)-(r(j)^2-R^2+z(i,j,q)^2)/((r(j)-R)^2+z(i,j,q)^2)*E(j));endBz(i,j)=(L(i)/(3*10))*((1+e(i,j,10))+2*(e(i,j,2)+e(i,j,4)+e(i,j,6)+...e(i,j,8))+4*(e(i,j,1)+e(i,j,3)+e(i,j,5)+e(i,j,7)+e(i,j,9)));endBBz(i)=sum((Bz(i,j))');BBzz(i)=BBz(i);% Computation of the area of the bottom surface of magnetic baseS=pi*R^2;% Computation of magnetic force of magnetic base to the bearingF(i)=(BBzz(i)^2)*S/(2*mu);% Computation of deformation magnitude of contacted two objectsdelta(i)=(9*pi^2*F(i)^2*(n1+n2)^2*(1/R1+1/R2)/16)^(1/3);% Equivalent elastic coefficientKK2(i)=F(i)/delta(i);aa=KK1/(m1*10^(-3));% Mass of the magnetic basem2(i)=rho*pi*(R*10^3)^2*L(i)*10^3;bb(i)=KK2(i)/((11+m2(i))*10^(-3));cc(i)=KK1/((11+m2(i))*10^(-3));% Mounting Resonant Frequency of the Sensoromegar (i)=sqrt((aa+bb(i)+cc(i))/2-(1/2)*sqrt(aa^2+2*aa*cc(i)+...(bb(i))^2+2*bb(i)*cc(i)+(cc(i))^2-2*aa*bb(i)));end% plot omegar Vs Lsubplot(2,1,1);plot(L*10^3, omegar,'r'); % FrequencyXlabel('磁座高度/mm');Ylabel('安装谐振频率/Hz');3. 剩磁大小－安装谐振频率关系程序% Mounting Resonant Frequency of the Sensor Diagram Generator% This program plots out the Resonant Frequency Diagram% The sensor mounts on a magnetic base% The Diagram reflect the relation between Resonant Frequency% Initialization% format longclearfor i=1:160% Choose variable valuesJ0(i)=0.1+i*0.02; % Magnetization intensity ranges of the base (Wb/m) R=8*10^(-3); % Radius of bottom surface of magnetic base (m) L=12*10^(-3); % Height of the magnetic basemu=4*pi*10^(-7); % permeability of free space (H/m)R2=40*10^(-3); % Radius of bearing in meterKK1=1.0437*10^8; % equivalent elastic coefficientm1=0.47; % mass of piezoelectricity crystal (g)m2=69; % mass of sensor and magnetic basen1=0.1875*10^(-11);n2=0.1399*10^(-11);R1=inf; % curvature redius of contacted magnetic base for j=1:20;r(j)=R*j/20;zz(j)=R2-sqrt(R2^2-r(j)^2);k(j)=sqrt(4*R*r(j)/((r(j)+R)^2+zz(j)^2));% Computation of the first class elliptical integral in Simpsonfor w=1:10;x(w)=w*(pi/2)/10;c(j,w)=sqrt(1-k(j)^2*(sin(x(w)))^2);d(j,w)=1/c(j,w);endK(j)=(pi/2)*((1+c(j,10))+2*(c(j,2)+c(j,4)+c(j,6)+c(j,8))+...4*(c(j,1)+c(j,3)+c(j,5)+c(j,7)+c(j,9)))/(3*10);E(j)=(pi/2)*((1+d(j,10))+2*(d(j,2)+d(j,4)+d(j,6)+d(j,8))+...4*(d(j,1)+d(j,3)+d(j,5)+d(j,7)+d(j,9)))/(3*10);% Computation of magnetization intensity of magnetic base in Simpsonfor q=1:10;z(j,q)=zz(j)+(q-1)*L/9;e(i,j,q)=(J0(i)/(2*pi))*(1/sqrt((R+r(j))^2+z(j,q)^2))*...(K(j)-(r(j)^2-R^2+z(j,q)^2)/((r(j)-R)^2+z(j,q)^2)*E(j));endBz(i,j)=(L/(3*10))*((e(i,j,1)+e(i,j,10))+2*(e(i,j,2)+e(i,j,4)+e(i,j,6)+...e(i,j,8))+4*(e(i,j,1)+e(i,j,3)+e(i,j,5)+e(i,j,7)+e(i,j,9)));end% Computation of magnetization intensityBBz(i)=sum((Bz(i,j))');BBzz(i)=BBz(i);% Computation of the area of the bottom surface of magnetic baseS=pi*R^2;% Computation of magnetic force of magnetic base to the bearing F(i)=(BBzz(i)^2)*S/(2*mu);% Computation of deformation magnitude of contacted two objectsdelta(i)=(9*pi^2*F(i)^2*(n1+n2)^2*(1/R1+1/R2)/16)^(1/3);% Equivalent elastic coefficientKK2(i)=F(i)/delta(i);aa=KK1/(m1*10^(-3));bb(i)=KK2(i)/(m2*10^(-3));cc(i)=KK1/(m2*10^(-3));% Mounting Resonant Frequency of the Sensoromegar(i)=sqrt((aa+bb(i)+cc(i))/2-(1/2)*sqrt(aa^2+2*aa*cc(i)+...(bb(i))^2+2*bb(i)*cc(i)+(cc(i))^2-2*aa*bb(i)));end% plot omegar Vs J0% Display output on screensubplot(2,1,1);plot(J0, omegar,'r'); % FrequencyXlabel('剩磁大小/T');Ylabel('安装谐振频率/HZ');4. 磁座端面半径、磁座高度－安装谐振频率关系程序% Mounting Resonant Frequency of the Sensor Diagram Generator% This program plots out the Resonant Frequency Diagram% The sensor mounts on a magnetic base% The Diagram reflect the relation between Resonant Frequency% and Radius of the bottom surface% Initialization% format longclearfor i=1:50;R(i)=(i/2.5)*10^(-3);R2=40*10^(-3); % Radius of bearing in meterJ0=1.24; % Magnetization intensity of the base (Wb/m) L=[4,8,12,16]*10^(-3); % Height of the magnetic basemu=4*pi*10^(-7); % permeability of free space (H/m)n1=0.1875*10^(-11);n2=0.1399*10^(-11);R1=inf; % curvature redius of contacted magnetic baseKK1=1.0437*10^8; % equivalent elastic coefficientm1=0.47; % mass of piezoelectricity crystal (g) rho=0.023322; % density of the magnetic base (g/mm^3)for j=1:20;r(i,j)=R(i)*j/20;zz(i,j)=R2-sqrt(R2^2-r(i,j)^2);k(i,j)=sqrt(4*R(i)*r(i,j)/((r(i,j)+R(i))^2+zz(i,j)^2));% Computation of the first class elliptical integral in Simpsonfor w=1:10;x(w)=w*(pi/2)/10;c(i,j,w)=sqrt(1-k(i,j)^2*(sin(x(w)))^2);d(i,j,w)=1/c(i,j,w);endK(i,j)=(pi/2)*((1+c(i,j,10))+2*(c(i,j,2)+c(i,j,4)+c(i,j,6)+c(i,j,8))+...4*(c(i,j,1)+c(i,j,3)+c (i,j,5)+c(i,j,7)+c(i,j,9)))/(3*10);E(i,j)=(pi/2)*((1+d(i,j,10))+2*(d(i,j,2)+d(i,j,4)+d(i,j,6)+d(i,j,8))+...4*(d(i,j,1)+d(i,j,3)+ d(i,j,5)+d(i,j,7)+d(i,j,9)))/(3*10);% Computation of magnetization intensity of magnetic base in Simpsonfor q=1:10;z1(i,j,q)=zz(i,j)+(q-1)*L(1)/9;e1(i,j,q)=(J0/(2*pi))*(1/sqrt((R(i)+r(i,j))^2+z1(i,j,q)^2))*...(K(i,j)-(r(i,j)^2-R(i)^2+z1(i,j,q)^2)/((r(i,j)-R(i))^2+z1(i,j,q)^2)*E(i,j));endBz1(i,j)=-(L(1)/(3*10))*((e1(i,j,1)+e1(i,j,10))+2*(e1(i,j,2)+e1(i,j,4)+e1(i,j,6)+e1(i,j,8))+4*( e1(i,j,1)+e1(i,j,3)+e1(i,j,5)+e1(i,j,7)+e1(i,j,9)));for q=1:10;z2(i,j,q)=zz(i,j)+(q-1)*L(2)/9;e2(i,j,q)=(J0/(2*pi))*(1/sqrt((R(i)+r(i,j))^2+z2(i,j,q)^2))*...(K(i,j)-(r(i,j)^2-R(i)^2+z2(i,j,q)^2)/((r(i,j)-R(i))^2+z2(i,j,q)^2)*E(i,j));endBz2(i,j)=-(L(2)/(3*10))*((e2(i,j,1)+e2(i,j,10))+2*(e2(i,j,2)+e2(i,j,4)+e2(i,j,6)+e2(i,j,8)) +4*(e2(i,j,1)+e2(i,j,3)+e2(i,j,5)+e2(i,j,7)+e2(i,j,9)));for q=1:10;z3(i,j,q)=zz(i,j)+(q-1)*L(3)/9;e3(i,j,q)=(J0/(2*pi))*(1/sqrt((R(i)+r(i,j))^2+z3(i,j,q)^2))*...(K(i,j)-(r(i,j)^2-R(i)^2+z3(i,j,q)^2)/((r(i,j)-R(i))^2+z3(i,j,q)^2)*E(i,j));end Bz3(i,j)=-(L(3)/(3*10))*((e3(i,j,1)+e3(i,j,10))+2*(e3(i,j,2)+e3(i,j,4)+e3(i,j,6)+...e3(i,j,8))+4*(e3(i,j,1)+e3(i,j,3)+e3(i,j,5)+e3(i,j,7)+e3(i,j,9)));for q=1:10;z4(i,j,q)=zz(i,j)+(q-1)*L(4)/9;e4(i,j,q)=(J0/(2*pi))*(1/sqrt((R(i)+r(i,j))^2+z4(i,j,q)^2))*...(K(i,j)-(r(i,j)^2-R(i)^2+z4(i,j,q)^2)/((r(i,j)-R(i))^2+z4(i,j,q)^2)*E(i,j));end Bz4(i,j)=-(L(4)/(3*10))*((e4(i,j,1)+e4(i,j,10))+2*(e4(i,j,2)+e4(i,j,4)+e4(i,j,6)+...e4(i,j,8))+4*(e4(i,j,1)+e4(i,j,3)+e4(i,j,5)+e4(i,j,7)+e4(i,j,9)));endBBz1(i)=sum((Bz1(i,j))'); BBzz1(i)=BBz1(i);BBz2(i)=sum((Bz2(i,j))'); BBzz2(i)=BBz2(i);BBz3(i)=sum((Bz3(i,j))'); BBzz3(i)=BBz3(i);BBz4(i)=sum((Bz4(i,j))'); BBzz4(i)=BBz4(i);% Computation of the area of the bottom surface of magnetic baseS(i)=pi*(R(i)^2);% Computation of magnetic force of magnetic base to the bearingF1(i)=(BBzz1(i)^2)*S(i)/(2*mu); F2(i)=(BBzz2(i)^2)*S(i)/(2*mu);F3(i)=(BBzz3(i)^2)*S(i)/(2*mu); F4(i)=(BBzz4(i)^2)*S(i)/(2*mu);% Computation of deformation magnitude of contacted two objectsdelta1(i)=(9*pi^2*F1(i)^2*(n1+n2)^2*(1/R1+1/R2)/16)^(1/3);delta2(i)=(9*pi^2*F2(i)^2*(n1+n2)^2*(1/R1+1/R2)/16)^(1/3);delta3(i)=(9*pi^2*F3(i)^2*(n1+n2)^2*(1/R1+1/R2)/16)^(1/3);delta4(i)=(9*pi^2*F4(i)^2*(n1+n2)^2*(1/R1+1/R2)/16)^(1/3);% Equivalent elastic coefficientKK21(i)=F1(i)/delta1(i);KK22(i)=F2(i)/delta2(i);KK23(i)=F3(i)/delta3(i);KK24(i)=F4(i)/delta4(i);aa=KK1/(m1*10^(-3));% mass of magnetic basem21(i)=rho*pi*(R(i)*10^3)^2*L(1)*10^3;m22(i)=rho*pi*(R(i)*10^3)^2*L(2)*10^3;m23(i)=rho*pi*(R(i)*10^3)^2*L(3)*10^3;m24(i)=rho*pi*(R(i)*10^3)^2*L(4)*10^3;bb1(i)=KK21(i)/((11+m21(i))*10^(-3));bb2(i)=KK22(i)/((11+m22(i))*10^(-3));bb3(i)=KK23(i)/((11+m23(i))*10^(-3));bb4(i)=KK24(i)/((11+m24(i))*10^(-3));cc1(i)=KK1/((11+m21(i))*10^(-3));cc2(i)=KK1/((11+m22(i))*10^(-3));cc3(i)=KK1/((11+m23(i))*10^(-3));cc4(i)=KK1/((11+m24(i))*10^(-3));% Mounting Resonant Frequency of the Sensoromegar1(i)=sqrt((aa+bb1(i)+cc1(i))/2-(1/2)*sqrt(aa^2+2*aa*cc1(i)+...(bb1(i))^2+2*bb1(i)*cc1(i)+(cc1(i))^2-2*aa*bb1(i))); omegar2(i)=sqrt((aa+bb2(i)+cc2(i))/2-(1/2)*sqrt(aa^2+2*aa*cc2(i)+...(bb2(i))^2+2*bb2(i)*cc2(i)+(cc2(i))^2-2*aa*bb2(i))); omegar3(i)=sqrt((aa+bb3(i)+cc3(i))/2-(1/2)*sqrt(aa^2+2*aa*cc3(i)+...(bb3(i))^2+2*bb3(i)*cc3(i)+(cc3(i))^2-2*aa*bb3(i))); omegar4(i)=sqrt((aa+bb4(i)+cc4(i))/2-(1/2)*sqrt(aa^2+2*aa*cc4(i)+...(bb4(i))^2+2*bb4(i)*cc4(i)+(cc4(i))^2-2*aa*bb4(i)));end% plot omegar Vs Laxis autosubplot(2,1,1);plot(R*10^3,omegar1,'b',R*10^3,omegar2,'g'); % Frequencyhold onplot(R*10^3,omegar3,'R',R*10^3,omegar4,'k'); % FrequencyXlabel('磁座底面半径/mm');Ylabel('安装谐振频率/Hz');附录3 振动测量系统图及传感器安装图图1 振动测量系统图Array图2 传感器安装图53。

目录一、概述 (2)二、主要技术指标 (3)三、传感器的选配 (7)四、传感器的使用操作步骤 (9)五、附件及随机文件 (13)一、概述LC01系列内装IC压电加速度传感器是内装微型IC放大器的压电加速度传感器，它将传统的压电加速度传感器与电荷放大器集于一体，能直接与记录和显示仪器连接，简化了测试系统，提高了测试精度和可靠性。

广泛用于核爆炸、航空航天、铁路、桥梁、建筑、车船、机械、水利、电力、石油、地质、环保、地震等领域。

其突出特点如下：1.低阻抗输出，抗干扰，噪声小。

2.性能价格比高，安装方便，尤其适用于多点测量。

3.稳定可靠、抗潮湿、抗粉尘、抗有害气体。

二、主要技术指标注：1.凡后缀T者为顶端输出，不缀T者为侧端输出。

2.每只传感器配1.5m电缆线一根(其中一端M5，另一端BNC接头)，安装螺钉一个。

如用户有特殊要求时，请在定货时说明。

3.LC01内装IC压电加速度传感器系列有如下共同指标：△线性：≤1% △横向灵敏度：≤5% 典型值：≤3% △输出偏压：8-12VDC △恒定电流：2-20mA，典型值：4mA△输出阻抗：＜150Ω△激励电压：15-30VDC 典型值：24VDC △温度范围：-40～+120℃△放电时间常数：≥0.2秒△壳绝缘电阻：＞108Ω△安装力矩：约20-30Kgf.cm(M5螺纹) 三、传感器的选配1.体积、重量：传感器作为被测物体的附加质量，必然会影响其运动状态。

因此要求传感器的质量m a远小于被测物体传感器安装点的动态质量m ，对于有些被测构件虽然作为一个整体质量很大，但是在传感器安装的局部，例如一些薄壁结构，传感器的质量已经可以与结构局部质量相比拟，将会使结构的局部运动状态受到影响。

在这种情况下，要求传感器体积和重量都尽可能小。

由于传感器质量的影响，会使被测构件的振动频率f n降低,其降低的频率△f n用下式估算：△f n = f n [ 1－m /( m a＋m ) ] 。