农作物施肥效果分析

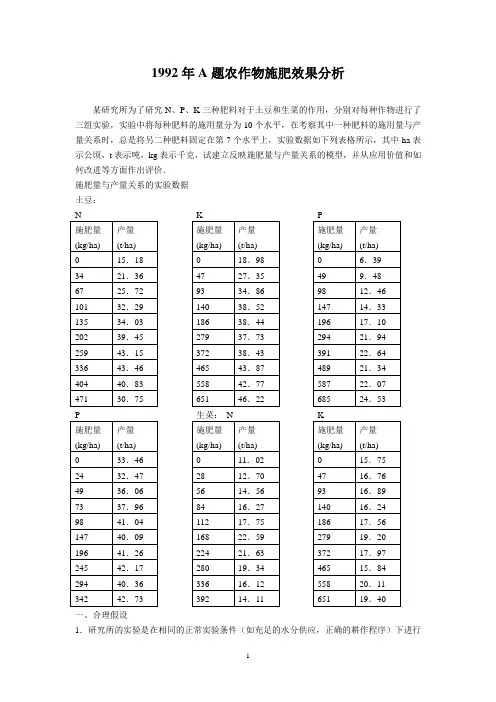
1992年A题农作物施肥效果分析某研究所为了研究N、P、K三种肥料对于土豆和生菜的作用，分别对每种作物进行了三组实验，实验中将每种肥料的施用量分为10个水平，在考察其中一种肥料的施用量与产量关系时，总是将另二种肥料固定在第7个水平上，实验数据如下列表格所示，其中ha表示公顷，t表示吨，kg表示千克，试建立反映施肥量与产量关系的模型，并从应用价值和如何改进等方面作出评价．施肥量与产量关系的实验数据土豆：一、合理假设1．研究所的实验是在相同的正常实验条件（如充足的水分供应，正确的耕作程序）下进行的，产量的变化是由施肥量的改变引起的，产量与施肥量之间满足一定的规律. 2．土壤本身已含有一定数量的氮、磷、钾肥，即具有一定的天然肥力. 3．每次实验是独立进行的，互不影响. 符号说明： W ：农作物产量. x ：施肥量.N 、P 、K ：氮、磷、钾肥的施用量. Tw ：农产品价格. Tx ：肥料价格.Tn,Tp,Tk ：氮、磷、钾肥的价格.a,b,b 0,b 1,b 2,c,c 0,c 1,c ’0,c ’1：常数（对特定肥料，特定农作物而言）. 二、问题分析农学规律[2]表明，施肥量与产量满足下图所示关系，它分成三个不同的区段，在第一区段，当施肥量比较小时，作物产量随施肥量的增加而迅速增加，第二区段，随着施肥量的增加，作物产量平缓上升，第三区段，施肥量超过一定限度后，产量反而随施肥量的增加而下降. 图14-1 施肥量与产量的一般关系为考察氮、磷、钾三种肥料对作物的施肥效果，我们以氮、磷、钾的施用量为自变量；土豆和生菜的产量为因变量描点作图.从中看出，氮肥对于作物产量的贡献大致呈指数关系，磷肥对于作物产量的关系大致为分段直线形式，至于钾肥，对土豆而言，大致呈指数关系，对生菜而言，随着施用量的增加，产量的上升幅度很小.这样，我们得到了对施肥效果的定性认识.在长期的实践中，农学家们已经总结出关于作物施肥效果的经验规律，并建立了相应的理论[3].1.Nicklas 和Miller 理论：设h 为达到最高产量时的施肥量，边际产量（即产量W 对施肥量x 的导数）dxdW 与(h-x)成正比例关系.dW/dx=a(h-x),(1) 从而 W=b 0+b 1x+b 2x 2.(2)2.米采利希学说：只增加某种养分时，引起产量的增加与该种养分供应充足时达到的最高产量A 与现在产量W 之差成正比. dW/dx=c(A-W),(3)从而 W=A （1-exp(-cx)）.(4)考虑到土壤本身的天然肥力，上式可修正为 W=A （1-exp(-cx+b)）.(5)3．英国科学家博伊德发现，在某些情况下，将施肥对象按施肥水平分成几组，则各组的效应曲线就呈直线形式.若按水平分成二组，可以用下式表示：,)x x x (x c c )x x 0(x c c n i 10i 10⎩⎨⎧<≤'+'<≤+（6） 我们假设该研究所的实验是在正常条件下进行的，因而表14-1所示的施肥量与产量的数据应该满足上述规律（对不同肥料，不同作物而言可以满足不同的规律）.以这些理论为依据，就可以对作物施肥效果进行回归分析.从实验设计的角度来看，该研究所采用的设计方案是因素轮换法，即在考察每一种肥料的效应时，总将另二种肥料的施用量固定在第7个水平上.采用这种设计方法，无法估算出三种肥料间的交互效应，因此，我们将每组实验看成单因素实验，并根据实验结果，给出反映施肥量与产量关系的一元肥料效应方程及效应曲线. 三、模型与结果我们建立了一元肥料效应回归模型，并在回归分析之前，用Chauvenent 准则进行修正，剔除异常值.根据对问题的初步分析，氮肥的施肥效果应满足Nicklas 和Miller 理论所描述的关系，运用二次多项式回归，得到氮肥对土豆的效应方程：W=14.74+0.197n-0.00034n 2.（7） 氮肥对生菜的效应方程：W=10.23+0.101n-0.00024n 2.（8） 氮肥的效应曲线如图14-2，图14-3所示．磷肥的施用对作物产量的增加表现为分段直线形式，运用线性回归，得到磷肥对土豆的效应方程：⎩⎨⎧≤≤+<≤+=).342p 04.101(p 0059.0968.39),04.101p 0(p 084.0077.32w （9）磷肥对生菜的效应方程：⎩⎨⎧≤≤+<≤+=).685k 54.202(k 00472.0196.20),54.202k 0(k 052.0809.6w （10）磷肥对作物的效应曲线如图14-4，图14-5所示.从钾肥对土豆的实验数据可以看出，当施用量超过一定限度后，产量的增加很不明显，因此用（5）式来描述其施肥效果是合理的，用指数回归分析得到 钾肥对土豆的效应方程：W(k)=42.17(1-exp(-0.01k-0.641)).(11) 对生菜来说，钾肥的施用对产量的影响很小.通过线性回归得到 钾肥对生菜的效应方程：W （k ）=16.2269+0.00395k.(12) 钾肥对生菜的效应曲线如图14-6，图14-7所示.可以得到每种肥料的最佳施用量，这无疑为生产提供了极为重要的信息.此外，模型的建立并不依赖于任何特殊条件，这种方法可以适用于任何地区，考察任意一种肥料对于作物产量的效应，具有一定的推广价值.本文没有给出三种肥料用量的最佳组合，因为试验方法本身决定了无法估计肥料的交互效应，因而无法计算最佳施肥比例.如果对实验方法加以改进，可以将我们的模型推广为总效应模型，并根据下列式子（当肥料的边际产量之比等于其价格的反比时，即为肥料施用量的最佳配比）来计算最佳施肥比例：⎪⎪⎩⎪⎪⎨⎧=∂∂∂∂=∂ω∂∂∂.T :T K )k ,p ,n (w :P )k ,p ,n (W ,T :T P)k ,p ,n (:N )k ,p ,n (W p k N p （14） 七、关于交互效应的深入讨论和实验方法的建议 在农业学中[4]，可以用三元二次多项式来描述氮、磷、钾三种肥料的综合施肥效果，用下列式子表示：W （N ，P ，K ）=B 0+B N N+B P P+B K K+B NN N 2+B PP P 2+B KK K 2+B NP NP+B NK NK+B KP KP ． 可以用回归的方法，求出回归系数，但对本题而言，下列处理[1]表明，交互系数是无法确定的，由于所给出的实验全都分布于三条平行于坐标轴的直线上，并且这三条直线交于公共点（n0,p0,k0），以n=N-n0,p=P-p0,k=K-k0作为现的变量，称为相对施肥量，则相对产量W(n,p,k)可表示为w(n,p,k)=b0+b n n+b p p+b k k+b nn n2+b pp p2+b kk k2+b np np+b nk nk+b kp kp.在新的坐标系中，所有的试验点都在坐标轴上，至少有两个坐标为0，这样所有的交叉项全消失了，即不可能由实验结果来确定交互系数，因而试验方法本身注定了交互效应是无法求出的.为估计肥料的交互效应，我们建议该研究所进行正交试验设计[5]，将氮、磷、钾肥的用量以第7个水平为中心等问题分为五个水平，作一个五水平三因子的正交表，总共需进行15次实验，将所得数据运用直观分析和方差分析，可以方便地得到氮、磷、钾肥对作物的总效应.试验安排如下.表正交设计表。

数学建模课程设计报告---施肥效果分析设计报告标题：施肥效果分析一、问题描述：在农作物种植过程中，施肥是提高农作物产量和质量的重要手段之一。

然而，在实际操作中，由于施肥的时间、剂量和方法等因素的不同，施肥效果也会有所差异。

本课程设计旨在通过数学建模的方法，分析施肥对农作物产量的影响，找出最佳施肥方案。

二、问题分析：1. 施肥时间：不同时间段施肥对农作物产量的影响不同，需要确定最佳的施肥时间；2. 施肥剂量：过少的施肥剂量无法满足农作物的生长需要，过多的施肥剂量可能造成浪费和环境污染，需要确定最佳的施肥剂量；3. 施肥方法：不同施肥方法对农作物产量的影响也不同，需要确定最佳的施肥方法；4. 施肥效果评价：需要建立一个评价指标体系来评价不同施肥方案的效果。

三、数学模型的建立：1. 施肥时间模型：假设农作物生长过程分为若干个时期，每个时期的生长速度是不同的。

我们可以建立一个函数来描述农作物在不同施肥时间下的生长速度变化，通过求函数的最大值或最小值来确定最佳的施肥时间。

2. 施肥剂量模型：假设农作物的生长速度与施肥剂量是线性相关的。

建立一个方程，使得农作物的生长速度最大化，然后通过求解该方程来确定最佳的施肥剂量。

3. 施肥方法模型：假设农作物的生长速度与施肥方法有关，可以建立一个函数来描述农作物在不同施肥方法下的生长速度变化。

通过求函数的最大值或最小值来确定最佳的施肥方法。

4. 施肥效果评价模型：建立一个评价指标体系，包括农作物产量、养分利用率、土壤质量等指标，通过加权计算得到一个综合评分来评价不同施肥方案的效果。

四、数据分析与结果验证：根据实际的农作物生长数据和施肥实验数据，进行数据分析，验证所建立的数学模型的有效性和准确性。

五、结论与改进：根据数学模型的分析结果得出最佳的施肥方案，同时提出改进意见和建议，为农作物种植提供科学的施肥指导。

附录：1. 农作物生长数据和施肥实验数据的详细信息；2. 用于建模和计算的数学公式和算法的详细说明；3. 模拟计算和数据分析的代码和程序。

施肥效果分析本文研究了营养素对作物的产量的影响，分析了不同营养素对不同作物生长产量的差异，建立了施肥效果模型。

并采用控制变量法和计算机数据拟合法建立了营养素对作物生长影响的模型。

根据研究所所得的营养素与作物产量的数据，运用MATLAB得到营养素与作物产量关系的散点图。

进一步运用拟合工具进行拟合数据，得到多项式的二次，三次函数和正弦函数一项，两项和三项函数。

利用方差比较，得到N在三次多项式时拟合度最好，而P和K 在二次多项式时拟合度最好。

本文最后总结了模型的优点和不足之处，并对施肥效果改进意见。

关键词：散点图，方差比较，拟合方程，控制变量一．问题重述作物生长所需的营养素主要是氮（N）、钾（K）、磷（P）。

为研究三种营养素对作物生长的影响，某作物研究所在该地区选取土豆与生菜做了一定数量的实验，实验过程中当一个营养素的施肥量变化时，总将另二个营养素的施肥量保持在最适宜植物生长状态。

分析数据得出施肥量与产量之间关系，并对所得结果从应用价值与如何改进等方面作出估价。

二．问题分析氮元素可促进植株茎叶的生长，更好的进行光合作用。

磷元素具有一部分促根发育的作用还具有促进开花的作用。

钾元素主要是促进果实的干物质积累，用来膨大果实。

增加产量。

由施肥量与产量的关系表格可得营养素对土豆生菜的产量有明显的促进作用。

根据农业期刊《Biology and fertility of soils》，一般来说，产量W可以用营养素施肥量的多项正弦函数表示，故做拟合曲线并代入试验数据求得关系表达式；同时联想到Logistic函数的导函数曲线为二次多项式（也是随着自变量先增后减），因此作一次二次以及三次多项式拟合，并进行比较。

三．基本假设①每次试验独立且试验条件（如环境条件，种植密度，土壤条件）相同；②由于数据由研究所提供，所以假设试验数据不会出现较大误差；③三种元素的使施用量同作物产量有一定的函数关系，同一种元素对不同作物的作用表现为同一类的函数关系；④忽略土壤中原有的N、P、K对作物生长的影响；⑤三种元素对作物增长的作用是相互独立的；四．名词解释和符号说明名词解释:种植密度：单位面积作物种植量符号说明：①pi（i=1,2,3.....)多项式系数②ai，bi，ci正弦函数各项系数和常数项五.模型建立和求解采用MATLAB2021b中配置的curve fitting tool（曲线拟合工具），直接输入数据，进行曲线拟合。

水稻配方施肥同田肥效对比试验效果分析2012年，道真自治县上坝土家族乡对主要粮食作物实施了测土配方施肥肥效对比试验，展示和推广测土配方施肥技术，实现了“增产、经济、环保”的三大目标，为全县全面普及推广测土配方施肥技术，不断提高农民科学施肥水平，提高肥料利用率奠定了坚实基础。

一、实施情况2012年，我乡科学制定水稻测土配方施肥肥效对比试验实施方案，严格按照方案组织实施。

水稻田按上中下三等，各抽1户，每户在同一田块中（面积不少于1亩）设三个处理（配方施肥区、常规施肥区、无肥区），上等落实在八一村下石组冉贤勇农户的田块里，中等落实在新田坝村申尚奎农户田块里，下等落实在双河村朱福木农户田块里。

全乡水稻田6500亩，其中上等田占40%，中等田占30%，下等田占30%。

二、采取措施在测土配方施肥同田肥效对比试验农户中，一律选择介绍推广的优良杂交水稻组合，并采取以下农艺措施：（1）一律采用高产栽培技术组装；（2）采取旱育秧和无纺布盖膜，培育多糵壮秧，实行宽窄行拉绳插秧；（3）合理密植，加强病虫草鼠害的综合防治。

三、试验设计上等农户冉贤勇选择t优6135品种，中等农户申尚奎选择中优117品种，下等农户朱福木选择富优325品种，各农户在同一田块中实施，设置配方施肥区、常规施肥区、无肥区，要把配方施肥区和习惯施肥区隔离开来，水稻田间要求筑田埂，防止养分相互渗透，影响肥效，要重点突出测土配方施肥技术的领航作用，严格按照我县土肥站制定的不同肥料品种、施肥数量、施肥时期、施肥方法的要求进行操作。

试验农户每户试验地设置三个处理，每个小区面积为200㎡。

在试验处理过程中，配方施肥区和常规施肥区除施肥要求不一样外，其他管理措施完全相同，随时做好灾害性天气，田间作业（如中耕除草、施药、施肥量、施肥时期、用工投入）等记录；无肥区不施肥，但要同步进行田间除草和病虫防治。

四、试验结果附表：水稻测土配方施肥肥效试验产量验收结果单位：公斤/亩通过产量验收结果说明，水稻配方施肥区产量比习惯施肥区平均增产9.3%，比无肥区产量明显增长1—2倍。

玉米肥料效应试验分析报告1. 引言1.1 背景介绍玉米是我国重要的粮食作物之一，也是农民种植面积较大的作物之一。

玉米的产量直接影响到国家粮食安全和农民的经济收入。

而肥料是提高玉米产量的重要手段之一，施肥合理与否直接关系到玉米的生长发育和产量水平。

探究不同玉米施肥处理的效果，分析土壤肥力状况和玉米产量之间的关系，研究不同种类肥料对玉米产量的影响以及不同施肥时间对玉米生长的影响，对于提高玉米产量、改善土壤质量具有重要的理论和实践意义。

本次试验旨在通过对不同施肥处理下玉米生长的对比观察和数据分析，探讨玉米施肥对产量的影响，揭示土壤肥力状况与产量之间的关系，从而为农业生产提供科学的肥料施用建议和技术支持。

1.2 研究目的研究目的是为了探究不同施肥处理对玉米产量的影响，进一步分析土壤肥力状况与玉米产量之间的关系，揭示玉米产量与肥料施用量、种类以及施肥时间的相关性。

通过这些研究，我们可以为玉米生产提供科学依据和合理推荐，从而提高玉米的产量和质量，实现农业生产的可持续发展。

通过对不同施肥处理及其效果的分析，可以为农业生产者提供肥料施用的合理建议，并为农业生产的环境友好性和资源利用效率提供指导。

研究目的就是要通过实验数据和分析结果，全面揭示玉米肥料效应对玉米产量的影响规律，为农业生产提供科学依据和技术支持。

1.3 研究方法本研究采用了田间试验的方法，选取了玉米生长期不同阶段的实验地点进行施肥处理。

在实验开始前，我们对实验地点的土壤进行了详细的调查和分析，包括土壤类型、pH值、有机质含量等指标。

根据前期的调查结果，我们选择了不同种类的肥料进行试验，包括有机肥、化肥和复合肥等。

在施肥处理上，我们设置了不同的施肥量和施肥时间，以探究不同施肥条件下玉米生长的效果。

为了保证实验的准确性和可靠性，我们在试验过程中对各处理组进行了严格的监测和记录，包括土壤湿度、植株生长情况、叶片颜色等指标。

我们还进行了对照组的设置，以便对实验结果进行比较和分析。

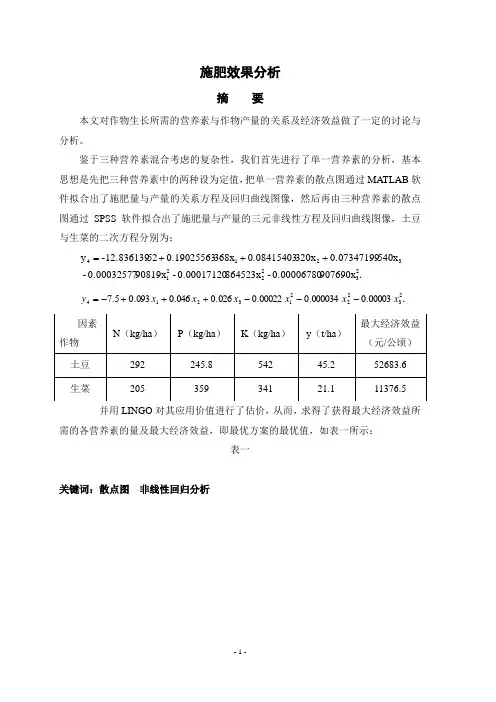
施肥效果分析摘 要本文对作物生长所需的营养素与作物产量的关系及经济效益做了一定的讨论与分析。

鉴于三种营养素混合考虑的复杂性，我们首先进行了单一营养素的分析，基本思想是先把三种营养素中的两种设为定值，把单一营养素的散点图通过MATLAB 软件拟合出了施肥量与产量的关系方程及回归曲线图像，然后再由三种营养素的散点图通过SPSS 软件拟合出了施肥量与产量的三元非线性方程及回归曲线图像，土豆与生菜的二次方程分别为：．2322213214907690x 0.00006780-864523x 0.00017120-90819x 0.00032577- 540x 0.0734*******x 0.08415403368x 0.1902556352-12.836139y +++=．232221321400003.0000034.000022.0026.0046.0093.05.7x x x x x x y ---+++-=并用LINGO 对其应用价值进行了估价，从而，求得了获得最大经济效益所需的各营养素的量及最大经济效益，即最优方案的最优值，如表一所示：表一关键词：散点图 非线性回归分析一、问题重述N P某地区作物生长所需的营养素主要是(N)、钾(K)、磷(P)。

某作物研究所在该地区对土豆和生菜做了一定数量的实验，实验数据如下列表格所示，其中ha表示公顷，t表示吨，kg表示公斤。

当一个营养素的施肥量变化时，总将另二个营养素的施肥量保持在第七个水平上，如对土豆产量关于N的施肥量分别取为196kg/ha与372kg/ha。

试分析施肥量与产量之间关系，并对所得结果从应用价值与如何改进等方面做出估价。

二、符号说明x表示氮肥的施肥量；1x表示磷肥的施肥量；2x表示钾肥的施肥量；3y表示氮肥作为变量时土豆或生菜的产量；1y表示磷肥作为变量时土豆或生菜的产量；2y表示钾肥作为变量时土豆或生菜的产量；3y表示氮肥、磷肥、钾肥都为变量时土豆或生菜的产量；4k表示氮肥作为变量时每公顷土豆或生生菜的纯收入；1k表示磷肥作为变量时每公顷土豆或生菜的纯收入；2k表示钾肥作为变量时每公顷土豆或生菜的纯收入；3k表示氮肥、磷肥、钾肥都为变量时每公顷土豆或生菜的纯收入；4三、模型假设1．气候、温度等外界自然条件适宜作物生长；2．作物水分充足，生长良好；3．其他营养素(除氮、磷、钾)都充足，不对作物生长造成影响； 4．忽略所喷洒的农药对作物生长的影响； 5．忽略施其他营养素(除氮、磷、钾)所需费用； 6．假设土豆和生菜的价格是一定值，不随季节变化；四、模型的建立与求解市场价格[1]模型一：首先分析施氮肥的量与土豆产量的关系。

肥料施用对作物生长和生产的影响分析肥料是农业生产中不可或缺的重要物质。

肥料可以提供植物所需要的增长物质，促进植物的生长和发育。

随着化肥的广泛使用，其对环境的影响也引起了越来越多的关注。

本文将从肥料施用的角度分析其对作物生长和生产的影响。

一、肥料对作物生长的影响肥料对作物生长的影响主要表现在以下几个方面：1、提高作物产量肥料中的微量元素和营养物质是植物生长和繁殖的必要条件。

适量施用肥料可促进植物的光合作用、养分吸收和利用，提高养分利用率和抗逆性，从而提高作物产量。

2、促进作物生长氮肥是促进作物生长的重要肥料，同时也是制造叶绿素及其他生物分子的基础原料。

施用适量的氮肥，可以促进植物生长，增加叶面积，从而提高作物数量和品质。

3、改善作物品质磷是植物生长的重要元素，对作物的花、果、器皮等品质形成和增加营养成分具有重要作用。

适量施用磷肥能够改善作物品质，增加作物的营养价值。

二、肥料对环境的影响肥料施用不当可能对环境造成一些不良影响。

1、污染土壤使用化肥过量或施用不当，会导致土壤中氮、磷等养分物质超标，产生污染，影响土壤的生态环境和作物的生长发育。

由于养分的流失会导致污染，因此定期监测土壤质量是非常必要的。

2、影响水质肥料的污染也会影响到水中的生态环境。

当肥料被施用在田地上后，随着降雨水或地下水循环，可能会沉降到水源中，影响水质。

过量的养分物质会导致水藻繁殖、藻类的生长过程中产生的毒素等，会严重影响水生生物及人类的健康。

3、增加空气污染施用过量的氮肥会导致大气中氮的含量急速增加，产生一些氮气化合物，如氨气、硝酸和一氧化二氮等。

这些气体不仅会影响环境，还会对人类造成危害。

如硝酸和一氧化二氮在大气中还会形成臭氧，对人体有害。

三、肥料施用对农作物的正确姿势为了避免肥料使用不当的不良效果，建议采取以下几点：1、根据作物的养分需求进行施肥因为不同的作物养分需求不同，应根据不同作物的需求进行合理施肥。

同时不同地区的养分状况不同，也应进行适当调整。

《数学建模》课程设计报告施肥效果分析04组摘要首先分别确定产量与施肥量之间的函数曲线类型，考虑函数所对应曲线的类型, 通常有三个参照指标: 一是绘制两个变量的散点图, 从图象的角度判断函数关系的类型; 二是根据给出变量的数据关系以及数据走向来判断; 三是根据所考虑变量之间内在的规律来讨论。

本问题中, 我们需要考察的是土豆和生菜产量与各营养素之间的函数关系, 因此其间的内在规律是未知的, 所以我们采用前两种方法。

对土豆和生菜利用DPS 软件分别绘制出他们的产量与三种营养元素之间关系的散点图，拟合三变量之间的关系式。

然后根据曲线类型对所求函数的对应关系进行假设，并利用已知数据计算出所需参数，最终确定变量之间的函数关系。

利用F 检验法对其函数进行检验。

利用微分法得到土豆最佳施肥量541.7563k 245.7645,p 292, n ===生菜最佳施肥量8888.264k 666.331, p 212.878,n ===和最优产量 t/ha 1302 23.。

关键词：施肥效果、散点图、曲线拟合、dps 、微分法、F 检验法一、 问题重述某地区作物生长所需的营养素主要是氮（ N ）、钾（ K ）、磷（ P ）。

某作物研究所在某地区对土豆与生菜做了一定数量的实验，实验数据如下列表所示，其中 ha 表示公顷， t 表示吨， kg 表示公斤。

当一个营养素的施肥量变化时，总将另两个营养素的施肥量保持在第七个水平上，如对土豆产量关于 N 的施肥量做实验时，p 与k 的施肥量分别取为 196kg ／ ha 与 372kg ／ ha 。

表1土豆产量与施肥量的关系施肥量（N ） (kg/ha)产量 (t/ha) 施肥量（P ） (kg/ha) 产量 (t/ha) 施肥量(K) (kg/ha) 产量 (t/ha)0 15.18 0 33.46 0 18.98 34 21.36 24 32.47 47 27.35 67 25.72 49 36.06 93 34.86 101 32.29 73 37.96 140 39.52 135 34.03 98 41.04 186 38.44 202 39.45 147 40.09 279 37.73 259 43.15 196 41.26 372 38.43 336 43.46 245 42.17 465 43.87 40440.83 294 40.36 55842.77表2生菜产量与施肥量的关系由于当一种肥料施肥量改变时，另外的两种肥料都保持在第7个水平上，于是有如下3个方案：(n,245,465)，(259,p,465)，(259,245,k)。