下载文档原格式
小学数学苏教版六年级上册《第1课时用假设法解决问题1》教案第一篇：小学数学苏教版六年级上册《第1课时用假设法解决问题1》教案小学数学苏教版六年级上册第1课时：用“假设”法解决问题（1）教学内容：P68－69例1和“练一练”，练习十一第1－3题。
教学目标：1.让学生初步学会用“假设”的策略分析数量关系，并能根据问题的特点确定合理的解题步骤。
2.让学生在对解决实际问题过程的不断反思中，感受“假设”策略对于解决特定问题的价值，进一步发展分析、综合和简单推理的能力。
3.让学生进一步积累解决问题的经验，增强解决问题的策略意识，获得解决问题的成功体验，提高学好数学的信心。
教学重点：让学生掌握用“假设”的策略解决一些简单问题的方法。
教学难点：弄清在有差数关系的问题中假设后总量发生的变化。
课前准备：小黑板课时安排：1课时教学过程二次备课一、游戏导入谈话：同学们，咱们先来做一个数学游戏,注意听了。
一种易拉罐饮料搞促销活动，4个有奖拉环换一个杯子。
老师收集了8个有奖拉环，可以换几个杯子？要想换5个杯子，需要几个有奖拉环？二、探究新知，初步理解假设的策略1.谈话：下面，咱们再来做一个抢答游戏。
开始：（1）小明把720毫升果汁倒入9个相同的小杯，正好都倒满，每个小杯的容量是多少毫升？（2）小明把720毫升果汁倒入3个相同的大杯，正好都倒满，每个大杯的容量是多少毫升？谈话：下一题，看谁反应快。
（3）出示例题2.谈话：能用720÷7吗？为什么？（题目中出现了两种不同的杯子了）出示例题图这两种杯子有关系吗？（小杯的容量是大杯的13）这什么意思呢？“正好都倒满”又怎么理解？要解决什么问题？“各多少毫升”意思是…… 3.探索假设的过程。
谈话：这道题中有两种不同的杯子了，同学们，能解决吗？请拿出作业纸，先在图上画一画，然后解答，并且把你的想法说给同桌听。
选择两名学生展示不同解法。
（1）提问：你怎样想的？（把大杯换成小杯）怎么想到的？明白他的意思吗？（找学生再说一遍）方法和他一样的同学请举手。
第一讲运用假设法解应用题【知识要点】所谓“假设法”就是通过假设，再依照已知条件进行推算，根据数量上出现的矛盾，进行比较，作适当调整，从而找到正确答案的方法。
一．笼子里有鸡和兔共30只，总共有70条腿，问鸡和兔各有几只？【分析】如果假设全是鸡，则30只鸡的腿数应为2×30=60条，比题目中少了10条，因为每只鸡比兔少2条腿，所以少了10条腿，说明有5只兔子。
解：假设笼中全是鸡，则兔的只数为：(70-2×30)÷(4-2)=5(只)鸡的只数为：30-5=25(只)答：这只笼子里装有25只鸡，5只兔。
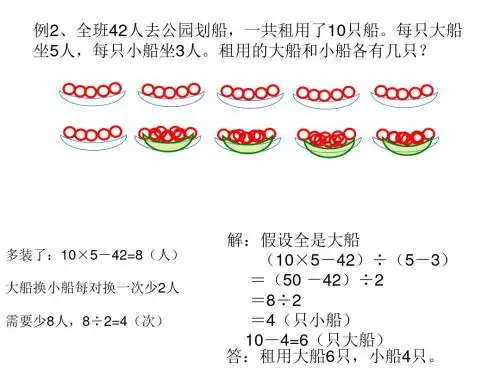
二．三(2)班学生52人，到公园去划船，共租用11条船，每条大船坐6人，每条小船坐4人，刚好坐满，求租用的大船、小船各多少只？解答：大船______只，小船______只。
三．一辆卡车运矿石，睛天每天可运20次，雨天每天只能运12次，它一连运了112次，平均每天运14次，问这几天当中有几个晴天？解：答：这几天中有______个晴天。
四．仓库所存的苹果是香蕉的3倍，春节前夕，平均每天批发出250千克香蕉，600千克苹果，几天后香蕉全部批发完，苹果还剩900千克。
这个仓库原有苹果，香蕉各多少千克？解：答：苹果______千克，香蕉______千克。
五．三、四、五年级同学共植树108棵，三年级比四年级少植18棵，五年级比三年级多植30棵，三个年级同学各植树多少棵？解：答：三年级植树______棵，四年级植树______棵，五年级植树______棵。
六．搬运1000只玻璃瓶，规定安全运到1只可得搬运费3角，但打碎一只，不仅不给搬运费，还要赔5角，如果运完后共得运费260元，那么搬运中打碎了几只玻璃瓶？解：答：搬运中打碎了______只玻璃瓶。
七．鸡兔共100只，共有脚280只，鸡兔各有多少只？解：答：鸡______只，兔______只。
八．10元和5元一张的人民共40张，计325元，两种人民币各几张？解：答：10元人民币______张，5元人民币______张。
苏教版六年级数学上册苏教版六年级数学上册 解决问题的策略（假设法解题）解决问题的策略（假设法解题）解决问题的策略（假设法解题）知识概述知识概述有一些应用题要求两个或两个以上的未知数，有一些应用题要求两个或两个以上的未知数，解答时可以先作出一种假设，解答时可以先作出一种假设，解答时可以先作出一种假设，假设要求的两个或假设要求的两个或几个未知数相等，或者假设有一个具体数量，然后按照题中的已知条件进行推算，找出推算结果与已知条件的差距，并进行适当的调整，求出正确结果，这种思考方法叫做假设法。
果与已知条件的差距，并进行适当的调整，求出正确结果，这种思考方法叫做假设法。
假设法是数学中的一个重要思想，通过假设可以使复杂的问题简单化，使所求的问题明朗化，帮助我们很快地找到解决问题的突破口，从而使问题化难为易。
帮助我们很快地找到解决问题的突破口，从而使问题化难为易。
例1、果园里有桃树、梨树、苹果树共146棵。
桃树比梨树少7棵，苹果树比桃树多4棵，三种树各有多少棵种树各有多少棵? ?练习：练习：1、有三块铁块，共重4千克，已知第二块比第一块轻400克，第三块的重量是第二块的2倍。
求每块各重多少克求每块各重多少克? ?2、小华、小宇、小宇、小红、小红、小红、小叶到森林里去采蘑菇，小叶到森林里去采蘑菇，小叶到森林里去采蘑菇，他们共采了他们共采了80个蘑菇，个蘑菇，小华比小宇少采小华比小宇少采8个，小红比小华少采14个，小叶和小红采的一样多。
他们每人采了多少个蘑菇个，小叶和小红采的一样多。
他们每人采了多少个蘑菇? ?3.3.三筐苹果共三筐苹果共130个，第二筐的苹果数是第一筐的3倍，第三筐的苹果数是第二筐的2倍多10个，三筐苹果各有多少个个，三筐苹果各有多少个? ?例2、学校买了8张办公桌和12把椅子，共用了2200元。
元。
44把子的价钱和一张办公桌的价钱正好相等。
每张办公桌和每把椅子各多少元正好相等。
每张办公桌和每把椅子各多少元? ?练习：练习：1、12张乒乓球台上共有34人在打球，问人在打球，问::正在进行单打和双打的台子各有几张正在进行单打和双打的台子各有几张? ?2、李丽用10元钱买8角邮票和4角邮票共16枚，买的8角邮票和邮票相差几校角邮票和邮票相差几校? ?3、一个大人一餐吃2个面包，两个孩子一餐吃1个面包，现在有大人和孩子共99人，一餐刚好吃了99个面包。
用假设的策略解决问题
1.红山动物园有一群鸵鸟和长颈鹿，它们共有30只眼睛和44条腿，问鸵鸟和长颈鹿各有多少只？
2.小轿车和三轮车共有24辆，这些车共有86个轮子。
三轮车比小轿车少多少辆？
3.运输队要运2000件玻璃器皿，按合同规定，完好无损运到的每件付运费1.2元，如有损坏，每件没有运输费外，还有赔偿6.7元，最后运输队得到2005元，运输中损坏了多少玻璃器皿？
4.一次数学竞赛共20题，规定:做对1题给5分，做错1题不给分还倒扣3分，不做的题不给分，小刚在这次竞赛中全部题都做了，总分84分，他做对了几道题？
5.某粮店运来6袋大米和8袋面粉，共重820千克，已经每袋大米比每袋面粉重20千克，每袋大米重多少千克？
6.林老师买30本语文书、20本数学书，一共用去432元，已知一本语文书比一本数学书贵1.4元，语文书和数学书的单价各是多少元/本？。
11．解决问题的策略——假设法姓名：___________一、填空1．如果△+△+△=○，那么○+○+○=（）个△，△+△+△+○相当于（）个△或者（）个○。
2．如果1只兔的重量相当于2只鸡的重量，那么6只鸡相当于（）只兔的重量，8只兔的重量相当于（）只鸡的重量。
10只鸡和10只兔的总重量相当于（）只鸡或（）只兔的重量。
3．如果1只小兔的重量相当于一只小狗的，那么3只小狗的重量相当于（）只小兔的重量；8只小兔和3只小狗的重量相当于（）只小狗的重量或者相当于（）只小兔的重量。
4．如果1个梨比1个苹果重30克，那么5个梨比5个苹果重（）克；如果把一堆水果中的4个苹果看作4个梨，总重要会（）（填“增加”或“减少”）（）克。
5．某味精厂11月份上旬生产的味精包装成400克一袋，共生产1200袋。
如果包装成100克一袋，那么可生产（）袋。
6．一个玻璃杯的价格是一个保温杯的，王叔叔买了10个玻璃杯和3个保温杯，所花的钱相当于（）个玻璃杯的钱，或（）个保温杯的钱。
7．如果4袋味精的质量=2袋盐的质量，1袋盐的质量=袋面粉的质量，那么一袋面粉的质量等于（）袋味精的质量。
8．2本笔记本的价钱与8本数学本的价钱相等，5本笔记本的价钱等于（）本数学本的价钱。
9．商店里一文具组合包括一副尺子和一把圆规，售价3.9元。
其中圆规的价格比尺子贵1.1元，圆规售价（）元，尺子售价（）元。
10．快餐店里一个汉堡、一杯饮料和两个蛋黄派，一共25元。
汉堡的单价是饮料的3倍，饮料的单价是蛋黄派的2倍，那么，汉堡的单价是（）元，蛋黄派的单价是（）元。
11．张大爷家养了4头牛和12头猪，如果1头牛的重量相当于3头猪的重，那么这些牛和猪的总重量相当于（）头牛的重量，或者相当于（）头猪的重量。
12．小明和小华出同样多的钱买一箱苹果，结果小明拿了8千克，小华拿了12千克，这样，小华就要给小明12元，苹果的单价是（）元。
13，小汤身上的钱可以买12支铅笔或4 块橡皮，她先买了3支铅笔，剩下的钱可以买橡皮（）块。
