完整版,五年级求阴影部分面积

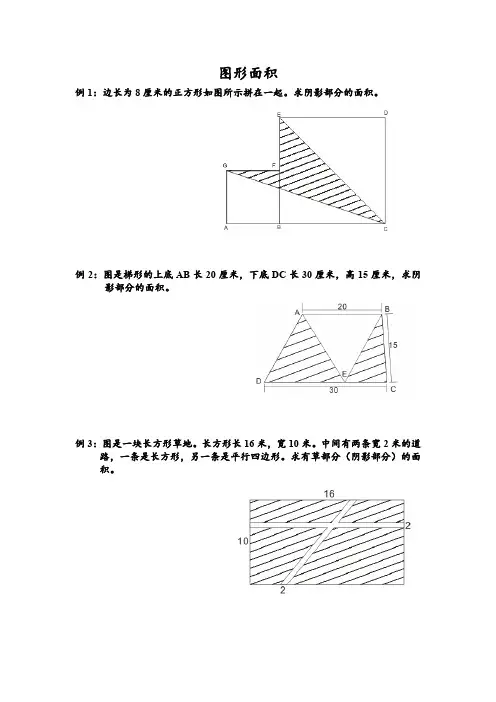
图形面积例1：边长为8厘米的正方形如图所示拼在一起。

求阴影部分的面积。

例2：图是梯形的上底AB长20厘米，下底DC长30厘米，高15厘米，求阴影部分的面积。

例3：图是一块长方形草地。

长方形长16米，宽10米。

中间有两条宽2米的道路，一条是长方形，另一条是平行四边形。

求有草部分（阴影部分）的面积。

例4：图是由两个完全一样的直角三角形重叠在一起，求阴影部分的面积。

例5：图中四边形ABCD和四边形DEFG都是正方形，一直△AFH的面积为6平方厘米，求△CDH的面积。

例6：梯形ABCD的上底CD为12厘米，高AD为10厘米，三角形BCF的面积为24平方厘米，求梯形ABCD的面积。

例7：如图，已知正方形ABCD和正方形CEFG，且正方形ABCD每边长为10厘米，则图中阴影（三角形BFD）部分的面积是多少平方厘米？练习：1.图中，大正方形和小正方形的边长分别是4厘米和3厘米。

求阴影部分的面积。

2.图中，梯形的下底为8厘米，高为4厘米。

求阴影部分的面积。

3.如图，求阴影部分的面积的总和。

（单位：厘米）4.图中，ABCD是平行四边形。

求阴影部分的面积。

（单位：厘米）7.求图中阴影部分的面积。

（单位：厘米）8.图是两个完全一样的直角三角形重叠在一起，按图中的已知条件求阴影部分的面积。

（单位：厘米）9.图是正方形ABCD是有三个长方形拼成。

长方形EFGH的宽式正方形的一半，甲阴影部分的面积是30平方厘米。

求阴影部分的总面积。

10.把边长是10厘米的正方形卡片按图所示的方法重叠起来。

3张这样的卡片重叠以后组成的图形面积是多少平方厘米？11.图中，ABCD是正方形，三角形DEF的面积比三角形ABF的面积大6平方厘米。

CD长4厘米。

求DE的长度。

12.图中，梯形ABCF的下底BC为12厘米，高AB为18厘米，CE的长度是ED的2倍。

求DF的长度。

13.如图，已知ABCD是直角梯形，AB长6厘米。

阴影部分的面积是6平方厘米，三角形ABC的面积是阴影部分面积的3倍。

五年级上册求阴影部分的面积一、求阴影面积例1、两个相同的直角三角形如图所示（单位：厘米）重叠在一起，求阴影部分的面积？巩固练习1、在图中，平行四边形ABCD的边BC 长10厘米，直角三角形ECB的直角边EC 长8厘米。

已知阴影部分的总面积比三角形EFG的面积大10平方厘米，求平行四边形ABCD面积。

例2、右图所示的等腰直角三角形中，剪去一个三角形后，剩下的部分是一个直角梯形（阴影部分）。

已知梯形的面积为36平方厘米，上底为3厘米，求下底和高？巩固练习2、如图，BD、DE、EC的长分别是2厘米，4厘米，2厘米，F是线段AE的中点，三角形ABC的高为4厘米，求三角形DEF的面积。

例3、下图中，有四条线段的长度已知，还有两个角是直角，那么四边形ABCD（阴影部分）的面积是多少？巩固练习3、在右图中，阴影部分A的面积比阴影部分B的面积大10.5平方厘米，求线段BC的长度？二、课堂练习简便计算4.4+5.6×2.5÷5.6×2.5 （3.8－7.7÷2.5）×2.81、一块长方形钢板，长截下4分米，宽截下1分米后，成了一块正方形钢板，如右图，面积比原来减少了49平方米。

原来长方形钢板的面积是多少平方米？2、在边长为6的正方形内有一个三角形BEF，线段AE＝3，DF＝2，求三角形BEF的面积。

3、在右图中，ABCD是长方形，三条线段的长度如图所示，M是线段DE的中点，求四边形ABMD（阴影部分）的面积。

家庭作业一、直接写得数1.52－（－0.48）= －1.25×6= 3.062÷3.2≈ (保留两位小数)二、解方程（带*号的要检验）6X+0.4×6=9.6 42.8+X=2.6+1.2 * 2.5X－9.4=0.5（X－4.8）三、递等式计算，能简便的用简便方法计算（7.5+7.5+7.5+7.5）×2.5 3.65×62+0.28×365+36.5（49.5÷7.5+49.5÷2.5）÷0.01 [3.25－3.25÷（10.3+2.2）]×0.1四、文字题9.1减去2.5与0.4的积所得的差除以0.9，商是多少？甲、乙两数的和是3.8，甲数比乙数的3倍多0.2，求乙数？五应用题1、小红和小明做同样多的口算题，小红每分钟做60道口算题，小明每分钟做75道口算题，当小明做完时，小红还有45道没有做，小明做了几分钟？2、红光足球俱乐部有一线队员45人，二线队员65人，二线队员要抽调多少人到一线，才能使一线队员人数是二线队员人数的1.2倍？3、两辆汽车都从A地开往B地，甲车每小时行40千米，先行2小时后，乙车才出发，经过5小时乙车追上甲车。

五年级求阴影部分面积
1、已知长方形的长为8厘米，宽为3厘米，求阴影部分的面积。

答案应为(14平方厘米)。

2、已知大正方形的边长为5厘米，小正方形的边长为3厘米，求阴影部分的面积。

答案应为(4平方厘米)。

3、已知梯形的上底为6厘米，下底为11厘米，高为8厘米，求阴影部分的面积。

答案应为(64平方厘米)。

4、如图所示，梯形的上底为8厘米，下底比上底长6厘米，高为10厘米，求阴影部分的面积。

答案应为(84平方厘米)。

5、已知大正方形的边长为10厘米，小正方形的边长为2厘米，求阴影部分的面积。

答案应为(96平方厘米)。

6、已知大小两正方形的边长分别为3厘米和2厘米，求阴影部分的面积。

答案应为(1平方厘米)。

7、已知大小两正方形的边长分别为3厘米和2厘米，求阴影部分的面积。

答案应为(1平方厘米)。

8、已知大小两正方形的边长分别为5厘米和2厘米，求阴影部分的面积。

答案应为(6平方厘米)。

9、已知大小两正方形的边长分别为5厘米和4厘米，求阴影部分的面积。

答案应为(9平方厘米)。

10、已知大小两正方形的边长分别为5厘米和4厘米，求阴影部分的面积。

答案应为(9平方厘米)。

阴影部分面积计算一、直接与间接方法求阴影部分面积例1:已知右面得两个正方形边长分别为６分米与４分米,求图中阴影部分得面积。

1、如图,ＡBDC就就是一个长１2厘米,宽5厘米得长方形,已知DE长3厘米,求阴影部分三角形ＡCE得面积。

二、等量代换法求阴影部分得面积例2:右图就就是两个相同得直角三角形叠在一起,求阴影部分得面积。

(单位：厘米)１、下图中两个完全一样得三角形重叠在一起,求阴影部分得面积。

(单位：厘米)例3：在右图中,平行四边形ＡBCD得边BＣ长10厘米，直角三角形EＣB得直角边EＣ长8厘米。

已知阴影部分得总面积比三角形EFＧ得面积大10平方厘米,求平行四边形ABCＤ得面积。

1、在右图中,三角形EDＦ得面积比三角形AＢE得面积大75平方厘米，已知正方形ABＣD得边长为１5厘米,(1)求三角形ＡCＦ得面积（2)ＤF得长就就是多少厘米?四、平移法求面积例4:右图就就是一块长方形公园绿地，绿地长24米,宽16米，中间有一条宽为2米得道路，求草地(阴影部分）得面积。

1、下图得长方形就就是一块草坪，中间有两条宽１米得走道,求植草得面积。

五、等高求面积例5:求下图中阴影部分得面积。

六、按一定得比求面积把下图三角形得底边BＣ四等分,在下面括号里填上“>”、“<”或“=”。

甲得面积( )乙得面积。

例6:（选讲）两条对角线把梯形ABＣＤ分割成四个三角形。

已知两个三角形得面积(如图所示),求另两个三角形得面积各就就是多少?(单位:平方厘米)1、如下图，图中BＯ=２ＤO，阴影部分得面积就就是4平方厘米,求梯形ABCD得面积就就是多少平方厘米?作业:1、已知正方形甲得边长就就是８厘米，正方形乙得面积就就是３6平方厘米,那么图中阴影部分得面积就就是多少？2、图中两个正方形得边长分别就就是6厘米与4厘米,求阴影部分得面积。

3、求下图长方形AＢＣD得面积（单位:厘米)。

4、图中两个正方形得边长分别就就是1０厘米与６厘米，求阴影部分得面积。

阴影图形面积应知应会基础图形的面积：【1】平行四边形的面积=底×高字母公式：S=ah÷2【2】三角形的面积=底×高字母公式：S=ah÷2【3】梯形的面积=（上底＋下底）×高÷2字母公式：s梯形=(a＋b)×h÷2a=s梯形×2÷h-bb=s梯形×2÷h-ah=s梯形×2÷(a＋b)二、求阴影图形的面积的方法（一）分析思路：计算时需转化成已学的基本图形，通过加、减进行计算。

（二）具体方法：1、分割法：将组合图形分成几个基本图形，通过加，求几个基本图形的和。

2、填补法：将组合图形补成一个基本图形，通过大面积减小面积，求两个基本图形的差。

阴影图形的面积直接计算：根据公式计算阴影三角形的面积【1】分析：图中的阴影三角形和平行四边形等底等高，因此三角形的面积等于平行四边形面积的一半。

解：S阴影三角形=底×高÷2=14×10÷2 =70（平方厘米）根据图中已知图形面积和所求图形面积之间的关系计算：S 三角形形=S 大平行四边形面积÷2【2】如图，空白部分的面积是13.5平方厘米，求平行四边形的面积是多少平方分米？ 解：S 空白部分=S 阴影三角形=平行四边形的底×高÷2 =S 平行四边形面积÷2所以S 平行四边形面积=S 空白部分×2=13.5×2=27(平方厘米） 先求出所需数据，再根据公式计算阴影三角形的面积【3】分析： 图中的阴影三角形和平行四边形等高，因此只需计算出三角形的底，再计算出三角形的面积。

解：14-10=6（厘米） S 阴影三角形=底×高÷2 =14×10÷2 =70（平方厘米）先求出所学数据，再计算梯形面积。

【4】寻找合适的条件，求出下面涂色部分的面积。

【史上最全小学求阴影部分面积专题—含答案】小学及小升初复习专题-圆与求阴影部分面积----完整答案在最后面目标：通过专题复习，加强学生对于图形面积计算的灵活运用。

并加深对面积和周长概念的理解和区分。

面积求解大致分为以下几类：1、从整体图形中减去局部；2、割补法，将不规则图形通过割补，转化成规则图形。

重难点：观察图形的特点，根据图形特点选择合适的方法求解图形的面积。

能灵活运用所学过的基本的平面图形的面积求阴影部分的面积。

例1.求阴影部分的面积。

例2.正方形面积是7平方厘米，求阴影部分的面积。

(单位:厘米)(单位:厘米)例3.求图中阴影部分的面积。

(单位:厘米) 例4.求阴影部分的面积。

(单位:厘米)例5.求阴影部分的面积。

(单位:厘米) 例6.如图：已知小圆半径为2厘米，大圆半径是小圆的3倍，问：空白部分甲比乙的面积多多少厘米？例7.求阴影部分的面积。

(单位:厘米)例8.求阴影部分的面积。

(单位:厘米)例9.求阴影部分的面积。

(单位:厘米)例10.求阴影部分的面积。

(单位:厘米)例11.求阴影部分的面积。

(单位:厘米)例12.求阴影部分的面积。

(单位:厘米)例13.求阴影部分的面积。

(单位:厘米)例14.求阴影部分的面积。

(单位:厘米)例16.求阴影部分的面积。

(单位:厘米)例15.已知直角三角形面积是12平方厘米，求阴影部分的面积。

例17.图中圆的半径为5厘米,求阴影部分的面积。

(单位:厘米) 例18.如图，在边长为6厘米的等边三角形中挖去三个同样的扇形,求阴影部分的周长。

例19.正方形边长为2厘米，求阴影部分的面积。

例20.如图，正方形ABCD的面积是36平方厘米，求阴影部分的面积。

例21.图中四个圆的半径都是1厘米，求阴影部分的面积。

例22.如图，正方形边长为8厘米，求阴影部分的面积。

例23.图中的4个圆的圆心是正方形的4个顶点，，它们的公共点是该正方形的中心，如果每个圆的半径都是1厘米，那么阴影部分的面积是多少？例24.如图，有8个半径为1厘米的小圆，用他们的圆周的一部分连成一个花瓣图形，图中的黑点是这些圆的圆心。

五年级数学上册必考题求图形阴影部分的面积方法一：直接求法。

根据已知条件直接求出阴影面积。

方法二：相减法。

用整体图形的面积减去非阴影部分面积既得阴影部分面积。

方法三：辅助线法。

将复杂的图形通过做辅助线的方法简单化，形成可一直接求面积的图形，如三角形、平行四边形、梯形等。

方法四：割补法。

将不规则的图形通过割补法变为规则图形从而进行计算。

方法五：等积变换法。

通过平面图形间的等积变换，化繁为易，计算阴影面积。

1、求梯形中阴影部分的面积。

（单位：厘米）（32+18）×15÷2-32×15÷2=375-240=135（平方厘米）答：阴影部分的面积是135平方厘米。

2、求图中阴影部分的面积。

（单位：厘米）已知平行四边形面积是24平方厘米。

24-（5+6）×4÷2=2（平方厘米）答：阴影部分的面积是2平方厘米。

3、求图中阴影部分的面积。

（单位：厘米）6×6+4×4-6×6÷2-4×10÷2=14（平方厘米）答：阴影部分的面积是14平方厘米。

4、下图是平行四边形，面积是36平方米，求阴影部分的面积。

（单位：米）36÷6=6（米）6-1.5=4.5（米）4.5×6÷2=13.5（平方米）答：阴影部分的面积是13.5平方米。

5、如图，一个梯形的上、下底分别是6厘米、10厘米，已知阴影部分的面积是24平方厘米，这个梯形的面积是？三角形的高：24×2÷10=4.8（厘米），梯形面积：（6+10）×4.8÷2=38.4（平方厘米）答：这个梯形的面积是38.4平方厘米。

《求阴影部分面积》含答案
例4. 图中的4个圆的圆心是正方形的4个顶点，它们的公共点是该正方形的中心，如果每个圆的半径都是1厘米，那么阴影部分的面积是多少？
解：面积为４个圆减去８个叶形，叶形面积为：
1 2 π(1²)-1×1= 1
2
π-1。

所以阴影部分的面积为:
4π(1²)-8( 1
2
π-1)=8 平方厘米
例5.求阴影部分的面积。

(单位:厘米)
解：这是一个用最常用的方法解最常见的题，为方便起见，我们把阴影部分的每一个小部分称为“叶形”，是用两个圆减去一个正方形，
π(2²)Χ2-16=8π-16=9.12平方厘米
另外：此题还可以看成是1题中阴影部分的8倍。

《求阴影部分面积》含答案
例5.求阴影部分的面积。

(单位:厘米)
解：这是最基本的方法：圆面积减去等腰直角三角形的面积，
π
×2²-2×1=1.14（平方厘米）
4
例6.求阴影部分的面积。

(单位:厘米)
解：正方形面积可用(对角线长×对角线长÷2，求)
正方形面积为：5×5÷2=12.5
所以阴影面积为：π5²÷4-12.5=7.125平方厘米
例7.求阴影部分的面积。

(单位:厘米)
解：右面正方形上部阴影部分的面积，等于左面正方形下部
圆，
空白部分面积，割补以后为1
4。

五年级必学：求阴影面积求阴影部分面积之差？五年级一定要学会的几何问题！阴影部分面积之差就是问甲比乙大多少，你是不是要说，套公式不就行了吗？可是呢，乙底是多少，高是多少，都不知道，所以直接套公式是不靠谱的。

那怎么办呢？在这里，甲可以看作是一个大三角形-空白，这个乙+空白=长方形，所以现在我们可以给甲和乙都补上同一块空白图形，那差肯定是不变的，但是通过这个神操作，我们就可以转换成大三角形-长方形的面积。

对于这个大三角形来说，底是15，高是9+5=14，然后再用底×高÷2，就是三角形的面积了。

解：阴影部分面积之差：甲-乙=（甲+空白）-（乙+空白）=（9+5）×15÷2-5×15=30你做对了吗？对于这类问题的处理，除了要熟练地掌握平面图形的概念和面积公式之外，关键还在于“巧用方法、妙在变形”，才能获得顺利地解答。

在小学平面几何图形教学中，经常碰到求阴影部分面积问题。

归纳一下，常用的方法有以下八种:（1）直接求法。

根据已知条件，从整体出发，直接求出阴影部分的面积。

（2）相减法。

这种方法就是把整个图形的面积减去非阴影部分的面积，即得阴影之面积。

这是用得较多的一种方法，是求阴影面积的基础。

（3）辅助线法。

此法即添作适当的辅助线，直接或者结合相减法求出阴影面积。

（4）重组法。

此法就是根据具体情况和计算上的需要把原来图形拆开，并加以重新组合，然后结合相减法求出阴影面积。

（5）割补法。

一个不规则的图形通过割和补的方法，变成一个规则的图形，从而进行计算。

（6）翻转法。

翻转法是根据图形的特征，将原图的某一部分进行翻转或旋转，最后得到便于求解的新图形。

（7）等积变换法。

它通过平面图形之间的等积变换，化难为易，求出阴影部分的面积。