编译原理 第2章习题课教学文案
- 格式:doc
- 大小:195.00 KB
- 文档页数:17

编译原理第二版课后习答案《编译原理》课后习题答案第一章第 1 章引论第 1 题解释下列术语:(1)编译程序(2)源程序(3)目标程序(4)编译程序的前端(5)后端(6)遍答案:(1)编译程序:如果源语言为高级语言,目标语言为某台计算机上的汇编语言或机器语言,则此翻译程序称为编译程序。
(2)源程序:源语言编写的程序称为源程序。
(3)目标程序:目标语言书写的程序称为目标程序。
(4)编译程序的前端:它由这样一些阶段组成:这些阶段的工作主要依赖于源语言而与目标机无关。
通常前端包括词法分析、语法分析、语义分析和中间代码生成这些阶段,某些优化工作也可在前端做,也包括与前端每个阶段相关的出错处理工作和符号表管理等工作。
(5)后端:指那些依赖于目标机而一般不依赖源语言,只与中间代码有关的那些阶段,即目标代码生成,以及相关出错处理和符号表操作。
(6)遍:是对源程序或其等价的中间语言程序从头到尾扫视并完成规定任务的过程。
第 2 题一个典型的编译程序通常由哪些部分组成?各部分的主要功能是什么?并画出编译程序的总体结构图。
答案:一个典型的编译程序通常包含 8 个组成部分,它们是词法分析程序、语法分析程序、语义分析程序、中间代码生成程序、中间代码优化程序、目标代码生成程序、表格管理程序和错误处理程序。
其各部分的主要功能简述如下。
词法分析程序:输人源程序,拼单词、检查单词和分析单词,输出单词的机内表达形式。
语法分析程序:检查源程序中存在的形式语法错误,输出错误处理信息。
语义分析程序:进行语义检查和分析语义信息,并把分析的结果保存到各类语义信息表中。
中间代码生成程序:按照语义规则,将语法分析程序分析出的语法单位转换成一定形式的中间语言代码,如三元式或四元式。
中间代码优化程序:为了产生高质量的目标代码,对中间代码进行等价变换处理。
目标代码生成程序:将优化后的中间代码程序转换成目标代码程序。
表格管理程序:负责建立、填写和查找等一系列表格工作。


第2章可计算函数程序设计语言2.1 引言本章提出一种用于对可计算函数进行编程的语言,叫做PCF语言。
它是基于类型化λ演算的函数式语言。
该语言的设计目的是便于后面各章的分析和讨论,而不是把它作为编写大程序的实际语言。
但是若改进它的外观语法,则还是可用它来方便地写出很多函数式程序。
本章还讨论该语言的公理语义、操作语义和指称语义,但不深入到有关基本定理的证明。
本章的主要议题如下:(1)通过一些例子来介绍类型化λ演算及基于它的语言的语法和语义。
(2)用不动点算子来处理函数的递归定义。
(3)讨论该语言的公理语义、操作语义和指称语义,并总结它们之间的联系。
(4)通过一些例子来说明,该语言虽然简单,但是一些基本的编程方法都可以用该语言来实现。
(5)用操作语义来研究该语言的表达能力和局限。
(6)介绍PCF的一些扩充和衍生。
本章主要目的是通过对基于λ演算的语言的介绍,获得这种语言编程能力的感性认识,并总结可用于多种语言研究一般性质和技术。
其中操作语义在本章将比指称语义讨论得深入一些,因为以后各章将集中在指称语义和公理语义上。
本章通过阐明一些熟悉的程序设计构造可以用λ演算来表示,由此看出λ演算在程序设计中的表达能力,并且是从正反两面展示PCF的表达能力。
本章以PCF的扩充和衍生的简短概述结束,它们有实际或理论的意义。
对那些熟悉指称语义的人来说,需要指出的是,本书中λ演算的使用和指称语义中λ演算的传统使用是有区别的。
一个区别是定型,在指称语义的早期研究中,通常把无类型的λ演算作为描述指称语义的元语言,而现在用类型化λ演算。
使用类型化λ演算可以区分每个表达式定义的值的种类,因而可从几方面简化技术分析。
另一个区别是,本书把PCF本身当成一个程序设计语言,而不是作为给出其它语言语义的元语言。
这样做的一个理由是体现类型化λ演算的表达能力,另一个理由是暗示λ演算不仅可用于指称语义,在程序设计语言分析和设计方面,它还用来研究操作和语用(pragmatic)问题。

![[高等教育]编译原理与技术讲义-第2章_OK](https://uimg.taocdn.com/20305b646bec0975f565e261.webp)
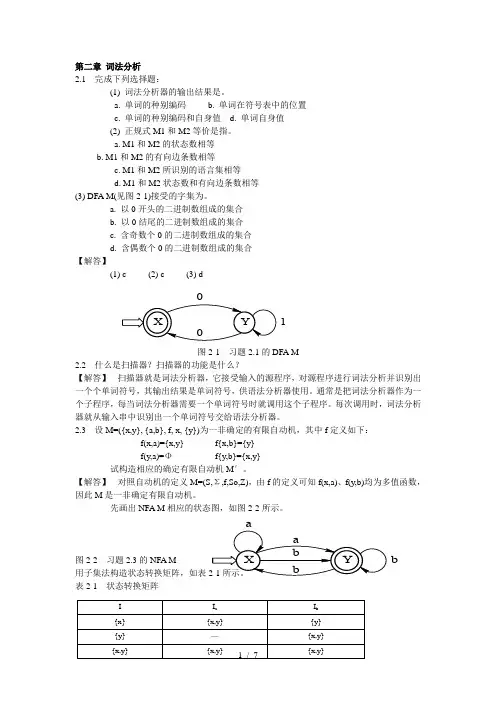
第二章 词法分析2.1 完成下列选择题:(1) 词法分析器的输出结果是。
a. 单词的种别编码b. 单词在符号表中的位置c. 单词的种别编码和自身值d. 单词自身值(2) 正规式M1和M2等价是指。
a. M1和M2的状态数相等b. M1和M2的有向边条数相等c. M1和M2所识别的语言集相等d. M1和M2状态数和有向边条数相等(3) DFA M(见图2-1)接受的字集为。
a. 以0开头的二进制数组成的集合b. 以0结尾的二进制数组成的集合c. 含奇数个0的二进制数组成的集合d. 含偶数个0的二进制数组成的集合【解答】(1) c (2) c (3) d图2-1 习题2.1的DFA M2.2 什么是扫描器?扫描器的功能是什么?【解答】 扫描器就是词法分析器,它接受输入的源程序,对源程序进行词法分析并识别出一个个单词符号,其输出结果是单词符号,供语法分析器使用。
通常是把词法分析器作为一个子程序,每当词法分析器需要一个单词符号时就调用这个子程序。
每次调用时,词法分析器就从输入串中识别出一个单词符号交给语法分析器。
2.3 设M=({x,y}, {a,b}, f, x, {y})为一非确定的有限自动机,其中f 定义如下:f(x,a)={x,y} f {x,b}={y}f(y,a)=Φ f{y,b}={x,y}试构造相应的确定有限自动机M ′。
【解答】 对照自动机的定义M=(S,Σ,f,So,Z),由f 的定义可知f(x,a)、f(y,b)均为多值函数,因此M 是一非确定有限自动机。
先画出NFA M 相应的状态图,如图2-2所示。
图2-2 习题2.3的NFA M 用子集法构造状态转换矩阵,如表表2-1 状态转换矩阵1b将转换矩阵中的所有子集重新命名,形成表2-2所示的状态转换矩阵,即得到 M ′=({0,1,2},{a,b},f,0,{1,2}),其状态转换图如图2-3所示。
表2-2 状态转换矩阵将图2-3所示的DFA M ′最小化。

编译原理教案说明:一、参考书:1、陈意云、张昱:《编译原理》,高等教育出版社,2003年。
2、陈意云、张昱:《编译原理习题精选》,中国科技大学出版社,2003年。
3、吕映芝、张素琴、蒋维杜:《编译原理》,清华大学出版社,1998年第二版。
4、王生原、吕映芝、张素琴:《编译原理课程辅导》,清华大学出版社,2007年。
5、伍春香:《编译原理习题与解析》,清华大学出版社,2001年。
6、Andrew W.Appel:《现代编译原理—C语言描述》,人民邮电出版社,2005年。
7、Noam Nison等:《计算机系统要素》,电子工业出版社,2007年。
8、Randall Hyde:《编程卓越之道(第二卷)》,电子工业出版社,2007年。
二、教学目的:通过学习形式语言与自动机理论、词法分析、语法分析、语义分析、代码优化和生成等内容使学生掌握构造编译程序的基本原理和基本方法,并通过上机实习使学生进一步掌握开发应用程序的基本方法,为深入理解计算机系统、程序设计语言与开发大型应用程序打下良好的基础。
三、教学时数:课堂教学51学时,上机实验30学时。
四、授课内容:第一章编译程序概述第二章 PL/0编译程序的实现第三章文法和语言第四章词法分析第五章自顶向下语法分析方法第六章自底向上优先分析方法第七章 LR分析方法第八章语法制导翻译和中间代码生成第九章符号表第一○章目标程序运行时的存储组织第一一章代码优化第一二章代码生成第一章概述一、说明:1、教学目的与要求:了解编译程序的概念、结构以及工作流程。
2、主要内容:什么是编译程序、编译过程概述、编译程序的结构、编译阶段的组合、编译技术和软件工具以及实例分析。
3、教学重点:编译程序的结构以及每一阶段的任务。
4、教学难点:理解编译程序各模块的判错功能、编译方式和解释方式执行速度上的不同。
二、教学内容第一节编译程序1、机器语言:直接用计算机能够识别的二进制代码指令来编写程序的语言。




1.构造正规式的DFA。
(1)1(0|1)*101首先构造NFA:1 NFA化为DFA:状态转换表:化简后得:(2)(a|b)*(aa|bb)(a|b)*化简后得;2.将下图确定化和最小化。
⇒解: 首先取A=ε-CLOSURE({0})={0},NFA确定化后的状态矩阵为:NFA确定化后的DFA为:⇒将A,B 合并得:⇒3.构造一个DFA ,它接受∑={0,1}上所有满足如下条件的字符串,每个1都有0直接跟在后边。
解:按题意相应的正规表达式是0*(0 | 10)*0*构造相应的DFA ,首先构造NFA 为DFA 为4.给出NFA等价的正规式R。
方法一:首先将状态图转化为得0,1消去其余结点NFA等价的正规式为(0|1)*11方法二:NFA→右线性文法→正规式A→0A|1A|1BB→1CC→εA=0A+1A+1BB=1A=0A+1A+11A=(0+1)*11→(0|1)*115.试证明正规式(a|b )*与正规式(a *|b *)*是等价的。
证明: (1)正规式(a|b)*的NFA 为=>其最简DFA 为(2)正规式(a*|b*)*的 NFA 为: 其最简化DFA 为:由于这两个正规式的最小DFA 相同,所以正规式(a|b)*等价于正规式(a*|b*)*。
6.设字母表∑={a,b},给出∑上的正规式R=b*ab(b|ab)*。
(1)试构造状态最小化的DFA M,使得L(M)=L(R)。
(2)求右线性文法G,使L(G)=L(M)。
解: (1)构造NFA:b(2)将其化为DFA,转换矩阵为:b再将其最小化得:b(2)对应的右线性文法G=({X,W,Y},{a,b},P,X)P: X→aW|bX W→b Y|b y→a W|bY|b3.8文法G[〈单词〉]为:〈单词〉-〉〈标识符〉|〈整数〉〈标识符〉-〉〈标识符〉〈字母〉|〈标识符〉〈数字〉|〈字母〉〈整数〉-〉〈数字〉|〈整数〉〈数字〉〈字母〉-〉A|B|C〈数字〉|->1|2|3(1)改写文法G为G’,使L(G’)=L(G)。
(2)给出相应的有穷自动机。
解:(1)令D代表单词,I代表标识符,Z代表整数,有G’(D):D→I | ZI→A | B | C | IA | IB | IC | I1 | I2 | I3Z→1 | 2 | 3 | Z1 | Z2 | Z3(2) 左线性文法G’所对应的有穷自动机为:M=({S,D,I,Z},{1,2,3,A,B,C},f,S,{D})f: f(S,A)=I, f(S,B)=I, f(S,C)=If(S,1)=Z f(S,2)=Z f(S,3)=Zf(I,A)=I f(I,B)=I f(I,C)=If(I,1)=I f(I,2)=I f(I,3)=I f(I,ε)=If(Z,1)=Z f(Z,2)=Z f(Z,3)=Z f(Z, ε)=D3.10给出下述文法所对应的正规式。
S→0A|1BA→1S|1B→0S|0解: 相应的正规式方程组为:S=0A+1B ①A=1S+1 ②B=0S+0 ③将②,③代入①,得S=01S+01+10S+10 ④对④使用求解规则,得 (01|10)* (01|10)为所求。
3.4给出文法G[S],构造相应最小的DFA 。
S->aS|bA|b A-> aS方法一: S=aS+bA+b A=aSS=aS+baS+bS=(a+ba)*b即:S=(a|ba)*b正规式(a|ba)*b 对应的NFA :正规式(a|ba)*b 对应的DFA :化简后:b方法二:P43 右线性正规文法到有穷自动机的转换。
文法S->aS|bA|bA-> aS对应的NFA为:M=({S,A,D},{a,b},f,{S},{D})其中:f (S,a)=S, f(S,b)=A, f(S,b)=D, f(A,a)=S其NFA图为:⇒NFA确定化后的DFA为:⇒3.5给出下述文法所对应的正规式:S->aAA->bA+aB+bB->aA解:将文法改为:S=aA ①A=bA+aB+b ②B=aA ③将③代入②,得A=bA+aaA+b ④将④用求解规则,得A= (b|aa)*b ⑤,带入①得,S= a(b|aa)*b,故文法所对应的正规式为R= a(b|aa)*b。
3.6给出与下图等价的正规文法G。
答: 该有穷自动机为:M=({A,B,C,D},{a,b},f,{A},{C,D})其中f(A,a)=B, f(A,b)=D, f(B,a)=φ, f(B,b)=C, f(C,a)=A, f(C,b)=D, f(D,a)=B, f(D,b)=D根据其转换规则,与其等价的正规文法G为G=({A,B,C,D},{a,b},P,A),其中P : A→aB|bD B→bC C→aA|bD|εD→aB|b D|ε3.12.解释下列术语和概念:(1)确定有穷自动机答:一个确定有穷自动机M是一个五元组M=(Q,Σ,f,S,Z),其中:Q是一个有穷状态集合,每一个元素称为一个状态;Σ是一个有穷输入字母表,每个元素称为一个输入字符;f是一个从Q*Σ到Q的单值映射;f(qi ,a)=qj(qi,qj∈Q,a∈Σ)表示当前状态为qi ,输入字符为a时,自动机将转换到下一个状态qj,qj称为 qi 的一个后继状态。
我们说状态转换函数是单值函数,是指 f(qi,a)惟一地确定了下一个要转移的状态,即每个状态的所有输出边上标记的输入字符不同。
S∈Q,是惟一的一个初态;Z 真包含于Q,是一个终态集。
(2)非确定有穷自动机一个非确定有穷自动机M是一个五元组M=(Q,Σ,f,S,Z),其中:Q是一个有穷状态集合,每一个元素称为一个状态;Σ是一个有穷输入字母表,每个元素称为一个输入字符;状态转换函数是一个多值函数。
f(qi ,a)={某些状态的集合}(qi∈Q),表示不能由当前状态、当前输入字符惟一地确定下一个要转移的状态,即允许同一个状态对同一输入字符有不同的输出边。
S 包含于A,是非空初态集。
Z 真包含于 Q,是一个终态集。
(3)正规式和正规集有字母表Σ={a1,a2,…an},在字母表Σ上的正规式和它所表示的正规集可用如下规则来定义:(1)φ是Σ是的正规式,它所表示的正规集是φ,即空集{}。
(2)ε是Σ上的正规式,它所表示的正规集仅含一空符号串,即{ε} 。
(3)是Σ上的一个正规式,它所表示的正规集是由单个符号ai 所组成,即{ai}。
(4)e1和e2是Σ是的正规式,它们所表示的正规集分别为L(e1)和L(e2),则①e1 | e2是Σ上的一个正规式,它所表示的正规集为L(e1 | e2)=L(e1)∪L(e2).②e1e2是Σ上的一个正规式,它所表示的正规集为L(e1e2)=L(e1)L(e2).③(e1)*是Σ上的一个正规式,它所表示的正规集为L((e1)*)=L((e1))*.3.1构造下列正规式相应的DFA。
(1) 1 ( 0 | 1)*101(2)( a | b )*( aa | bb )( a | b )*(3)(( 0 | 1 )* | ( 11 ))*(4)( 0 | 11*0 )*3.2将下面图(a)和(b)分别确定化和最小化.⇒(a)a(b)3.3构造一个DFA,他接收∑={0,1}上所有满足如下条件的字符串,每个1都有0直接跟在右边。
3.4给出文法G[S],构造相应最小的DFA。
S aS | bA | bA aS3.5给出下述文法所对应的正规式:S->AaA->bA+aB+bB->aA3.6给出与下图等价的正规文法G。
⇒b a b3.7给出与图3.29中的NFA等价的正规式R。
3.8 文法G[〈单词〉]为:〈单词〉〈标识符〉| 〈整数〉〈标识符〉〈标识符〉〈字母〉| 〈标识符〉〈数字〉|〈字母〉〈整数〉〈数字〉|〈整数〉〈数字〉〈字母〉 A | B | C〈数字〉 1 | 2 | 3(1)改写文法G为G’,使L(G’)=L(G).(2)给出相应的有穷自动机。
3.9试证明正规式(a|b)*与正规式(a*|b*)*是等价的。
3.10给出下述文法所对应的正规式:S 0A | 1BA 1S | 1B 0S | 03.11设字母表Σ={a,b},给出Σ上的正规式R=b*ab(b | ab)*.(1)试构造状态最小化的DFA M,使得L(M)=L(R)。
(2) 求右线性文法G,使L(G)=L(M)。
3.12解释下列术语和概念。
(1)确定有穷自动机(2)非确定有穷自动机(3)正规式和正规集。