大学物理_第十七章_光的衍射
- 格式:ppt
- 大小:1.37 MB
- 文档页数:50


大学物理光的衍射课件CONTENTS •光的衍射现象与基本原理•典型衍射实验及其分析•衍射光栅及其应用•晶体中的X射线衍射•激光全息与光学信息处理•总结与展望光的衍射现象与基本原理01光在传播过程中遇到障碍物或小孔时,偏离直线传播的现象。
包括菲涅尔衍射和夫琅禾费衍射等。
衍射是光波遇到障碍物后产生的偏离直线传播的现象,而干涉是光波叠加产生的加强或减弱的现象。
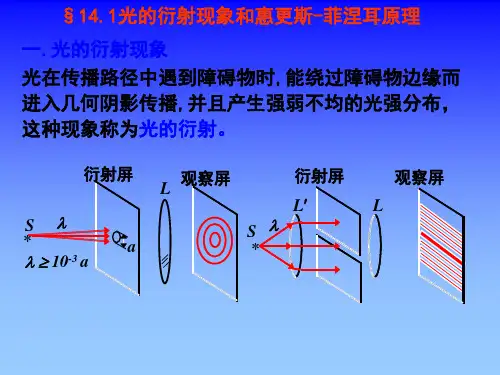
衍射现象的定义衍射的种类衍射与干涉的区别光的衍射现象惠更斯-菲涅尔原理惠更斯原理介质中任一波面上的各点,都可以看做发射子波的波源,即可作为新波源产生球面次波,其后任意时刻这些子波的包迹面就是新的波面。
菲涅尔原理在光传播的过程中,光波前上的每一点都可以看作是新的光源,发出球面次波,这些次波在空间中相遇并相互叠加,形成新的光波前。
惠更斯-菲涅尔原理的意义解释了光的衍射现象,并为波动光学的发展奠定了基础。
03基尔霍夫衍射公式的应用用于计算各种衍射现象的振幅和相位分布,如单缝衍射、双缝干涉等。
01基尔霍夫衍射公式的表达式描述了光波在衍射屏上的振幅分布与观察屏上的振幅分布之间的关系。
02公式中各物理量的含义包括衍射屏上的复振幅分布、观察屏上的复振幅分布、光源到衍射屏的距离、衍射屏到观察屏的距离等。
基尔霍夫衍射公式典型衍射实验及其分析02单缝衍射实验装置与原理01通过单缝的衍射实验,可以观察到光波通过狭窄缝隙后的衍射现象。
实验装置包括光源、单缝、屏幕等部分。
当单色光波通过宽度与波长相当的单缝时,会在屏幕上形成明暗相间的衍射条纹。
衍射条纹特点02单缝衍射条纹呈现中间亮、两侧暗的特点。
亮条纹的间距随着衍射角的增大而减小,暗条纹则相反。
条纹间距与单缝宽度、光波长以及观察距离有关。
衍射公式与计算03根据惠更斯-菲涅尔原理,可以推导出单缝衍射的公式,用于计算衍射条纹的位置和强度分布。
双缝干涉与衍射实验装置与原理双缝干涉与衍射实验采用双缝作为分波前装置,通过两束相干光波的叠加产生干涉和衍射现象。

一、选择题 [ B ]1、(基础训练1)在单缝夫琅禾费衍射实验中,波长为λ的单色光垂直入射在宽度为a =4 λ 的单缝上,对应于衍射角为30°的方向,单缝处波阵面可分成的半波带数目为(A ) 2 个 (B ) 4 个 (C ) 6 个 (D ) 8 个 【答】已知a =4 λ,θ=30°,1sin 4422a λθλ∴=⨯=⨯,半波带数目N = 4. [ C ]2、(基础训练5)一单色平行光束垂直照射在宽度为1.0 mm 的单缝上,在缝后放一焦距为2.0 m的会聚透镜。
已知位于透镜焦平面处的屏幕上的中央明条纹宽度为2.0 mm ,则入射光波长约为(A )100 nm (B )400 nm (C )500 nm (D )600 nm 【答】中央明条纹宽度为2, 5002x ax fnm afλλ∆⋅∆≈∴== [ B ]3、(基础训练6)一束平行单色光垂直入射在光栅上,当光栅常数(a + b )为下列哪种情况时(a代表每条缝的宽度),k =3、6、9 等级次的主极大均不出现?(A )a +b =2 a (B )a +b =3 a (C )a +b =4 a (A )a +b =6 a【答】光栅缺级:()sin sin 'a b k a k θλθλ+=⎧⎨=⎩,缺级的主极大的级次为',2,3,...a b a b a b a bk k a a a a++++==,k 应为整数,依题意,k=3,6,9缺级,所以a+b=3a 符合。
[ D ]4、(基础训练10)孔径相同的微波望远镜和光学望远镜相比较,前者分辨本领较小的原因是 (A ) 星体发出的微波能量比可见光能量小 (B ) 微波更易被大气所吸收 (C ) 大气对微波的折射率较小 (D ) 微波波长比可见光波长大 【答】分辨本领为11.22RdR θλ==,孔径d 相同时,R 与波长λ成反比关系。
微波波长比可见光波长大,所以微波望远镜分辨本领较小。

第十七章 光的衍射17-1 波长为700nm 的红光正入射到一单缝上,缝后置一透镜,焦距为0.70m ,在透镜焦距处放一屏,若屏上呈现的中央明条纹的宽度为2mm ,问该缝的宽度是多少?假定用另一种光照射后,测得中央明条纹的宽度为1.5mm ,求该光的波长。
解:单缝衍射中央明条纹的宽度为afx λ2=∆m xf a 739109.4102107007.022---⨯=⨯⨯⨯⨯=∆=λfx a2∆=λ代入数据得 nm 5257.02105.1109.437=⨯⨯⨯=--λ17-2一单缝用波长为λ1和λ2的光照明,若λ1的第一级衍射极小与λ2的第二级衍射极小重合。
问(1)这两种波长的关系如何?(2)所形成的衍射图样中是否还有其它极小重合? 解:(1)单缝衍射极小条件为λθk a =sin依题意有 212λλ= (2)依题意有11sin λθk a = 22sin λθk a =因为212λλ=,所以得所形成的衍射图样中还有其它极小重合的条件为212k k =17-3 有一单缝,缝宽为0.1mm ,在缝后放一焦距为50cm 的汇聚透镜,用波长为546.1nm 的平行光垂直照射单缝,试求位于透镜焦平面处屏上中央明纹的宽度。
解:单缝衍射中央明条纹的宽度为af x λ2=∆代入数据得mm x 461.5101.0101.54610502392=⨯⨯⨯⨯=∆---17-4 用波长为632.8nm 的激光垂直照射单缝时,其夫琅禾费衍射图样第一极小与单缝法线的夹角为50,试求该缝宽。
解:单缝衍射极小的条件λθk a =sin依题意有m a μλ26.70872.0108.6325sin 9=⨯==-17-5 波长为20m 的海面波垂直进入宽50m 的港口。
在港内海面上衍射波的中央波束的角宽是多少?解:单缝衍射极小条件为λθk a =sin依题意有 0115.234.0sin52sin20sin 50===→=--θθ中央波束的角宽为0475.2322=⨯=θ17-6 一单色平行光垂直入射一单缝,其衍射第3级明纹位置恰与波长为600nm 的单色光垂直入射该缝时衍射的第2级明纹位置重合,试求该单色光的波长。






3.5光的衍射一、实验目的(1)观察单缝衍射现象(2)测定单缝衍射的相对光强分布(3)应用单缝衍射的分布规律测定单缝的宽度二、实验仪器GSZ-Ⅱ光学平台(配有光具座、氦氖激光器及电源、狭缝、光电转换器、观察屏、数字式灵敏检流计等)。
三、实验原理(1)光的衍射:光在传播的过程中遇到障碍物会绕过障碍物继续传播,到达沿直线传播所不能到达的区域,并形成明暗条纹。
只有当障碍物的线度和光波的波长可以相比拟时,衍射现象才明显地表现出来。
(2)根据光源和观察屏到障碍物的距离的不同可以把衍射现象分为两大类。
菲涅尔衍射/近场衍射:光源与观察屏之间的距离或光源与障碍物之间的距离是有限的;夫琅禾费衍射/远场衍射:光源到障碍物的距离及观察屏到障碍物之间的距离都为无限大,即平行光入射、平行光出射。
单缝衍射光强分布图四、实验步骤1.观察夫琅禾费单缝衍射现象安排实验光路,调节各光学元件至等高同轴,是激光束垂直照射单缝,调节单缝的宽度和观察屏到单缝的距离使观察屏上出现清晰明显的衍射条纹,然后进行以下操作:(1)改变单缝宽度,观察并记录衍射条纹的变化规律(2)改变单缝到观察屏之间的距离,观察并记录衍射条纹的变化规律(3)移去观察屏,换上光电转换器,是数字是灵敏检流计与之相连。
调节光电转换器的移位螺钉,测出中央极大光强I o和k=∓1,∓2,∓3级的次级大光强=0.047,0.017,0.008。
I k,检验理论结果I kI o(4)观察夫琅禾费圆孔衍射现象。
理论结果表明,夫琅禾费单缝衍射的∓1级次级大光强还不到主极大光强的百分之五。
当数字式灵敏检流计的数字显示为“1”时,表示此时已超出检流计量程,需减小单缝的宽度或者让光电转换器远离单缝。
2.观察菲涅尔单缝衍射现象安排好实验光路,在激光与单缝之间插入一扩束镜使激光束发散后照射单缝产生菲涅尔衍射。
调节单缝宽度和观察屏到单缝的距离使观察屏上出现清晰明显的衍射条纹,然后进行:(1)改变缝宽,观察并记录衍射条纹的变化规律。