计控实验四最少拍控制算法研究

Z
根据题意，输入信号为单位速度输入，即r (t ) = t ，则有：
Φ e ( z ) = (1 − z −1 ) 2
代入式（4-12）求出最小拍控制器为
5.435(1 − 0.5 z −1 )(1 − 0.368z −1 ) D( z ) = (1 − z −1 )(1 + 0.718z −1 )
s ( 0 .5 s + 1)
位速度输入时的最小拍控制器。 解：根据图4-1可求出系统广义被控对象脉冲传递函数
1 − e −Ts 2 ] G( z) = Z[ ⋅ s s (0.5s + 1) 4 = Z [(1 − e −Ts ) 2 ] s ( s + 2) 4 4e −Ts = Z[ 2 ] − Z[ 2 ] s ( s + 2) s ( s + 2) 2 1 1 2 1 1 = Z[ 2 − + ] − Z [e −Ts ( 2 − + )] s s s+2 s s s+2 e − 2T z −1 (1 − z −1 + e 2T z −1 ) = (1 − z −1 )(1 − e − 2T z −1 )
对最小拍控制系统设计的要求是： （1）调节时间最短，即系统跟踪输入信号所需的采样周期数 最少； （2）在采样点处无静差，即对特定的参考输入信号，在达到 稳态后，系统在采样点能精确实现对输入信号的跟踪； （3）设计出来的数字控制器必须是物理上可以实现的； （4）闭环系统必须是稳定的。
一、最小拍闭环脉冲传递函数的确定 首先根据对控制系统性能指标的要求和其他约束条件， Φ (z 构造系统的闭环脉冲传递函数 。) 最小拍控制系统的设计要求是对特定的参考输入信号， 在系统达到稳态后，系统在采样点处静差为零。根据此约束条 件可以构造出系统的误差脉冲传递函数 Φ e (z )。典型计算机控制 系统结构图如图4-1所示。

重庆邮电大学自动化学院计算机控制实验报告学院：自动化学生姓名：魏波专业：电气工程与自动化班级：0830903学号：2009212715最小拍控制系统一、实验目的1、掌握最小拍有纹波控制系统的设计方法。

2、掌握最小拍无纹波控制系统的设计方法。

二、实验设备PC机一台，TD-ACC实验系统一套，i386EX系统板一块三、实验原理及内容典型的最小拍控制系统如图其中D(Z) 为数字调节器， G(Z)为包括零阶保持器在内的广义对象的Z传递函数，Φ (Z)为闭环 Z传递函数， C(Z) 为输出信号的Z传递函数， R(Z) 为输入信号的 Z传递函数。

R为输入， C为输出，计算机对误差E 定时采样按 D(Z) 计算输出控制量 U(Z) 。

图中 K=5。

闭环传递函数1、最小拍有纹波系统设计2、最小拍无纹波设计有纹波系统虽然在采样点上的误差为零，但不能保证采样点之间的误差值为零，因此存在有纹波现象。

无纹波系统设计只要使U（Z）是Z1的有限多项式，则可以保证系统输出无纹波。

四、实验线路图(2)D(Z) 算法采样周期 T=1S，E(Z) 为计算机输入， U(Z) 为输出，有：D(Z)=U(Z)E(Z)=K0 K1Z 1K2Z2K3Z31 P1Z1P2Z 2P3Z 3式中 Ki 与 Pi 取值范围： -0.9999 ～0.9999 ，计算机分别用相邻三个字节存储其 BCD码。

最低字节符号， 00H 为正， 01H为负。

中间字节存前 2 位小数，最高字节存末 2 位小数。

例有系数 0.1234 ，则内存为：地址内容2F00H00H2F01H12H2F02H34H系数存储安排如表5— 1。

表 5—10101H010DH0102H K0010EH P 0103H010FH0104H0110H0105H K10111H P 0106H0112H0107H0113H0108H K20114H P 0109H0115H010AH010BH K3010CH 1 2 3将 D(Z) 式写成差分方程，则有：U K=K0 E K+K1E K-1+K2E K-2+K3 E K-3-P 1U K-1-P2U K-2-P3 U K-3式中 E K～E K-3，误差输入； U K～U K-3，计算机输出。

实验三：最小拍控制系统一、实验目的：1．建立计算机最小拍控制系统的一般概念；2．掌握有纹波最小拍控制器的设计方法3．观察无纹波最小拍控制器的设计方法；4．了解最小拍控制器的优缺点；5．掌握最小拍控制系统的改进方法。

二、实验内容：图1采样周期为T=0.1s1.针对图一所示的计算机控制系统,考虑输入为单位速度信号时，进行计算机控制算法D(Z)设计，编程实现最小拍有纹波系统；num=[5];den=[1,1,5];Gs=tf(num,den)Gz=c2d(Gs,0.1,'zoh')[num1,den1]=c2dm(num,den,1,'zoh')tf2zpk(den1)运行结果：Transfer function:5-----------s^2 + s + 5Transfer function:0.02409 z + 0.0233----------------------z^2 - 1.857 z + 0.9048 Sampling time: 0.1num1 =0 1.2326 0.8288 den1 =1.0000 0.6936 0.3679 ans =-0.3468 + 0.4976i-0.3468 - 0.4976i2.讨论纹波的生成原因，编程实现最小拍有纹波系统；Ts=0.1;Q=2; a=0.5;num=[5];den=[1,1,5];Gs=tf(num,den)Gz=c2d(Gs,0.1,'zoh')z1=tf([1],[1,0],0.1);Qz=1.267*z1*(1+0.9669*z1)*(1-0.598*z1)/(1-a*z1); Qe=1-Qz;Dz=Qz/[Qe*Gz];Qz1=minreal(Dz*Gz/(1+Dz*Gz));t=0:0.1:Q;u=t;plot(0:0.1:Q,u,'r*');hold onyt=lsim(Qz1,u,t,0);plot(0:0.1:Q,yt);3.讨论最小拍系统的特点，采取惯性因子法对最小拍控制器加以改进，并研究惯性因子对系统性能的影响。

计控实验四--最小拍系统设计实验报告||实验名称最小拍系统设计实验课程名称计算机控制技术与系统||实验四 最少拍系统设计实验1、实验目的掌握最少拍系统的设计方法。

2、实验原理框图)(z HG3、实验要求设被控对象为要求：(1)采样时间T=1s ，采用零阶保持器，使用Matlab 求取出广义对象的z 传递函数； (2)设计单位阶跃输入下的最少拍控制器D(z)，给出设计过程； (3)控制系统仿真结果及分析（系统是否稳定？有无纹波？几步跟踪？）； (4)仿真系统对输入信号（斜坡、单位加速度）的灵敏性，观察系统性能变化。

4、实验过程4.1使用Matlab 求取Z 传函利用matlab 语句求取广义对象的Z 传递函数并将其转换为零极点形式，用到的程序如下: T=1; z0=[]; p0=[0 0 -1.252]; k0=2.1;G0=zpk(z0,p0,k0); sysd=c2d(G0,T,'zoh')得到的广义对象的z 传递函数为20.26304(z 2.827)(z 0.19)(z 1)(z 0.2859)++--1,)252.1(1.2)(20=+=T s s s G4.2单位阶跃输入下，理想最小拍系统的设计与仿真典型的输入函数为11(z )(z),q 1,2,3(1z )qA R --==-设闭环脉冲传递函数为(z)Φ，误差表达式设为(z)e Φ，数字控制器为D(z)。

则依据理想最小拍系统的设计原则有11(z)D(z),(z)(1z )(z)(z)1(z)p e F G -Φ=Φ=--Φ，(z)1(z),p q e Φ=-Φ=其中p 表示系统稳定所需要的拍数。

若要使数字控制器形势最简单，阶次最低，取F(z)=1，则11(z)1(z)(1z ),(z)1(1z )p p e --Φ=-Φ=-Φ=--单位阶跃输入r(t)=1对应的z 传递函数为11(z)(1z )R -=-单位阶跃输入对应的q=1，则p=1。

实验四 最少拍控制算法研究一、实验目的1．学习并熟悉最少拍控制器的设计和算法； 2．研究最少拍控制系统输出采样点间纹波的形成； 3．熟悉最少拍无纹波控制系统控制器的设计和实现方法。

二、实验设备1．THBDC-1型 控制理论·计算机控制技术实验平台 2．PCI-1711数据采集卡一块3．PC 机1台(安装软件“VC++”及“THJK_Server ”)三、实验原理1）最小拍系统在采样控制系统中，通常把一个采样周期称作一拍。

在典型输入信号作用下，经过最少拍，使输出量采样时刻的数值能完全跟踪参考输入量的数值，跟踪误差为零的系统称为最少拍系统。

计算机控制系统的方框图为：图4-1 最少拍计算机控制原理方框图根据上述方框图可知，有限拍系统的闭环脉冲传递函数为：)()(1)()()()()(z G z D z G z D z R z C z H +==(4-1) )()(11)()()(1z G z D z R z E z H +==- (4-2) 由(4-1) 、(4-2)解得： )(1)()(1)(z H z H z G z D -⋅= （4-3）首先要使系统的过渡过程在有限拍内结束，显然，这样对系统的闭环脉冲传递函数)(z H 提出了较为苛刻的要求，即其极点应位于z 平面的坐标原点处。

亦即希望系统的脉冲传递函数为101()()k k kF z H z a a z a z z --=+++=（4-4） 式中：F(z)为H(z)的分子多项式，k 为某一整数。

式（4-4）表明H(z)的极点都在z 平面的原点，系统的脉冲响应在经过了有限数k 拍以后就变为零，过渡过程结束。

式（4-4）表明了离散系统中，为了使过渡过程较快地结束应符合的条件。

K 是个有限值，它至少应该是什么数值呢？可以分析一下闭环传递函数H(z)。

将式（4-4）代入D(z)表示式，得)]([)()(1)(1)()(1)(z F z z F z G z H z H z G z D k-⋅=-⋅=（4-5） 如果m 和n 分别为对象和保持器的组合脉冲传递函数G(z)的分子和分母的阶次，l 为式（4-5）中F(z)的阶次，要使D(z)能实现，就应使分母的阶次大于分子的阶次k n m l ≥-+ （4-6）由式（4-6）可见，当0l =时，H(z)的分子0()F z F ==常数，暂态响应的持续节拍数最少。

【例4-1】 设最小拍控制系统如图4-11所示，被控对象的传递函数2()(0.51)G s s s =+，采样周期0.5T s =，试设计在单位速度输入时的最小拍控制器()D z 。

解：系统的广义被控对象脉冲传递函数为 12211211112111122()[](1)[](0.51)(0.51)(1)0.368(10.718)(1)(1)(1)(10.368)TsTTTe G z Z z Z ss s s s e z z ez z z z e z z z --------------==-++-++==----根据题意，输入信号为单位速度输入，即()r t t =，则有12()(1)e z z -Φ=-代入 求出最小拍控制器为11115.435(10.5)(10.368)()(1)(10.718)z z D z z z ------=-+下面对设计出来的最小拍控制器进行分析和校验。

系统的闭环脉冲传递函数为12()2z z z --Φ=-，当输入为单位速度信号时，系统输出序列的z 变换为11212234()()()(2)(1)234TzY z R z z z zz TzTzTz-------=Φ=--=+++即(0)0,(1)0,(2)2,(3)3,y y y T y T ==== 。

输出响应如图4-12所示。

从图中可以看出，当系统为单位速度输入时，经过两拍以后，输出量完全跟踪输入采样值，即()()y k r k =。

但在各采样点之间还是存在一定的误差，即存在一定纹波。

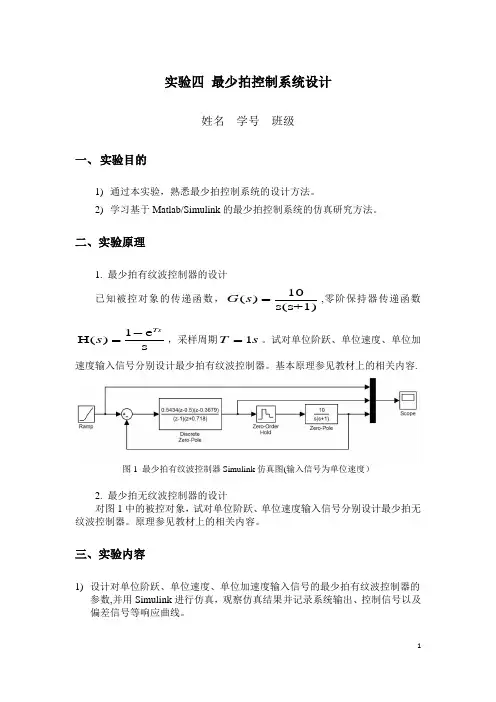
图4-12 单位速度输入时最少拍控制系统输出响应曲线当输入为单位阶跃信号时，系统输出序列的z 变换为12111111()()()(2)21Y z R z z zzzzzzz-------=Φ=-=++++-即(0)0,(1)2,(2)(3)(4)1,y y y y y ===== 。

其输出响应曲线如图4-13所示。

从由图可见，按单位速度输入所设计的最小拍系统，当输入变为单位阶跃信号时，经过两个采样周期，()()y k r k =。

三拍。
Y( z) ? T 2 (0 ?z0 ? 0 ?z? 1 ? 3z? 2 ? 9z? 3 ? 16z? 4 ? ?
2
2020/1/31
10
2）G(z) 为不稳定对象且包含圆外零点
? ? (z)必须包含G(z)中全部圆外零点；
? ? e (z) 必须包含 G(z) 中全部圆外圆上极点；
? ? e (z) 至少应包含 q 个（1 ? z?1 ）因子；
(1 ? z ?1 ) 因式的关于 z? 1 的多项式。
误差传递函数的结构为 ? e (z) ? (1 ? z?1 )M F (z)
2020/1/31
6
取 m(z ? 1)?
z? 1
e (z)R(z) ?
? lim?(1 ? z? 1 ?
z?1 )(1 ?
z?1 )M
2020/1/31
13
例1 被控对象的传递函数为
2.1 G0 (s) ? s2 ( s ? 1.252)
经采样（T=l）和零阶保持，试求其对于单位阶跃输入的最
少拍控制器。
解：（1）广义被控对象 G(z)
G(z) ?
Z
?1 ? ?
?
e s
?
Ts
2.1 ?
?s2
(s
?
1.252)
? ?
?
0.265z? 1(1 ? 2.78z?1 )(1 ? 0.2z? 1 ) (1 ? z? 1 )2 (1 ? 0.286z?1 )
广义被控对象零极点的分布：
圆外极点 无 ，
i? 0
圆外零点 p1 ? ? 2.78 ， j ? 1
延时因子 z?1
r?1
2020输/1/3入1 函数的阶次

实验四 最少拍控制系统设计姓名 学号 班级一、 实验目的1) 通过本实验，熟悉最少拍控制系统的设计方法。

2) 学习基于Matlab/Simulink 的最少拍控制系统的仿真研究方法。

二、实验原理1. 最少拍有纹波控制器的设计 已知被控对象的传递函数，10()s(s+1)G s =,零阶保持器传递函数1e H()sTss -=，采样周期1T s =。

试对单位阶跃、单位速度、单位加速度输入信号分别设计最少拍有纹波控制器。

基本原理参见教材上的相关内容.图1 最少拍有纹波控制器Simulink 仿真图(输入信号为单位速度）2. 最少拍无纹波控制器的设计对图1中的被控对象，试对单位阶跃、单位速度输入信号分别设计最少拍无纹波控制器。

原理参见教材上的相关内容。

三、实验内容1) 设计对单位阶跃、单位速度、单位加速度输入信号的最少拍有纹波控制器的参数,并用Simulink 进行仿真，观察仿真结果并记录系统输出、控制信号以及偏差信号等响应曲线。

根据题意有：有纹波设计如下单位阶跃输入时:响应:单位速度输入时：响应：2)设计对单位阶跃、单位速度输入信号的最少拍无纹波控制器的参数，并用Simulink进行仿真，观察仿真结果并记录系统输出、控制信号以及偏差信号等仿真曲线。

根据题意有：单位阶跃输入时：响应：四、实验报告1)按照实验报告所要求的统一格式，填写实验报告；2)记录控制器参数设计过程、结果、Simulink仿真图和相关响应曲线。

3)根据实验过程和结果进行分析。

能否对单位加速度信号设计无纹波控制器?说明理由。

5.2 最少拍数字控制器的设计原理
r(t) 例 2： e−10T=0.5 T=1 s
—计算机控制技术—
e(t) e(k) D(z) T -
T
1-e-Ts u(t)
s
1 0.1s+1
y(t)
求最少拍控制器D(z)和控制器 1 2 r(t)=1(t) r(t)= 2 t 输出u(k)和系统的输出y(k). −1 1 0.5z 解： (1) R(z)= 1-z-1 G(z)=1-0.5z-1 Φe(z)=1-z-1 Φ(z)=z-1 E(z)=R(z)Φe(z)=1 U(z)=D(z)E(z) -1 -1)z-1 -1+z-2+z-3+· z (1-0.5z =2+z · · D(z)= G(z)(1-z-1) = (1-z-1)0.5z-1 Y(z)=R(z)Φ(z) -1 -2 z -0.5z 1 = 0.5z-1-0.5z-2 · · = -1 z-1=z–1+z-2+z-3+· 1-z
5.2 最少拍数字控制器的设计原理 —计算机控制技术— -1 z-1 0.632z G(z)=1-1.368z-1+0.368z-2 R(z)= (1-z-1)2 (2) Φe(z)=(1-z-1)2 Φ(z)=2z-1-z-2 E(z)=R(z)Φe(z) =z-1 Y(z)=R(z)Φ(z) =2z–2+3z-3+4z-4+· · · -1-z-2 -1+0.368z-2)(2z-1-z-2) 2z (1-1.368z D(z)= G(z)(1-z-1)2 = (1-2z-1+z-2)0.632z-1 2z-1-3.736z-2+2.1z-3-0.368z-4 = 0.632z-1-1.264z-2+0.632z-3 u(k) 3.16 U(z)=D(z)E(z) 2z-2-3.736z-3+2.1z-4-0.368-5 1 = 0.632z-1-1.264z-2+0.632z-3 0 T 2T 3T t =3.16z-1+0.42z-2+z-3+z-4+· · ·

最小拍控制算法研究实验报告
实验报告：最小拍控制算法研究
一、实验目的：
本实验旨在研究最小拍控制算法的原理与实现方法，了解其在不同应用领域的优缺点，并通过实验验证其稳定性和可靠性。

二、实验原理：
最小拍控制算法是一种基于时间周期的控制算法，它通过对任务执行时间进行分析和预测，保证系统能够在规定的时间内完成任务。

该算法以最小的单位时间间隔（即拍）为基础，每个任务被分配到若干个拍中执行。

该算法通过调整拍的长度和数量来保证任务的平衡性和稳定性，从而达到最优控制效果。

三、实验步骤：
1. 设计测试系统并确定测试参数；
2. 编写最小拍控制算法代码，并将其嵌入到测试系统中；
3. 进行实验测试，并记录测试数据；
4. 对测试数据进行分析和处理，得出结论并撰写实验报告。

四、实验结果与讨论：
本实验使用最小拍控制算法对一个简单的测试系统进行了控制，得到了如下实验结果：
1. 最小拍控制算法可以有效地保证系统的稳定性和可靠性，能够在规定的时间内完成任务；
2. 在不同的应用领域中，最小拍控制算法的优缺点各有所表现，
需要结合实际情况进行选择和调整；
3. 最小拍控制算法的代码编写相对较为复杂，需要考虑多个参数和变量之间的关系。

五、实验结论：
本实验研究了最小拍控制算法的原理和应用，并通过实验验证了其稳定性和可靠性。

在不同的应用领域中，该算法具有各自的优缺点，需要结合具体情况进行选择和调整。

总体而言，最小拍控制算法是一种有效的控制算法，可以为各类系统提供稳定和可靠的控制效果。

基于Matlab辅助的“计算机控制技术”教学方法探讨_以“最少拍控制系统”设计为例基于Matlab辅助的“计算机控制技术”教学方法探讨：以“最少拍控制系统”设计为例摘要：计算机控制技术是现代自动化领域的核心内容之一，在这个领域中，掌握合适的教学方法对于学生的学习效果至关重要。

本文以“最少拍控制系统”设计为例，探讨基于Matlab辅助的计算机控制技术教学方法，并通过实践验证了该方法的有效性。

1. 引言计算机控制技术是自动化领域中的重要内容之一，它将计算机与控制系统相结合，实现对各种设备和过程的控制。

在计算机控制技术的教学中，如何提高学生的理论学习和实践能力是一个重要的问题。

本文通过引入Matlab辅助的教学方法，以“最少拍控制系统”设计为例，探讨了有效提高学生学习效果的教学方法。

2. Matlab辅助的教学方法计算机控制技术的理论性较强，学生往往难以理解其中的抽象概念和数学模型。

为了增强学生对理论知识的理解和掌握，可以采用Matlab辅助的教学方法。

Matlab是一种功能强大的数学软件，它能够将抽象的数学模型转化为直观的图形，有助于学生理解和记忆。

在计算机控制技术的教学中，教师可以通过设计一些简单的系统，并用Matlab进行仿真分析，在仿真实验中让学生观察系统的响应特性，并通过实验数据求解出系统参数。

这种实践性强、直观性好的教学方法，可以帮助学生更好地理解和掌握计算机控制技术的知识。

3. “最少拍控制系统”设计为了验证Matlab辅助的教学方法在计算机控制技术教学中的有效性，我们以“最少拍控制系统”设计为例进行了实践。

该系统的主要目标是设计一个控制器，使得系统在给定的最少拍数内稳定。

首先，我们通过Matlab进行仿真分析，得到系统的响应特性。

然后，我们根据系统的数学模型，设计了一个反馈控制器，并进行了仿真实验。

通过实验数据分析，我们得到了系统的最少拍数，并验证了控制器的设计是否有效。

4. 实验结果分析通过实验数据的分析，我们得到了系统的最少拍数为10。

在这里，N使可能情况下的最小正整数。这一传递函数表明闭环系统的脉冲响应在N个采样周期后变为零，从而意味着系统在N拍之内到达稳态。其控制原理如图1：
图1最少拍控制系统原理图
（1）输入信号为单位阶跃信号，设计控制器 ；（2）采样周期T=1s.
4.实验内容与步骤
（1）按系统要求计算 为有纹波控制器和无纹波控制器；
（2）按照系统原理图，在simulink下构造系统结构图模型；取输入信号为单位阶跃信号，设计控制器，观察输入输出波形，打印结果；
（3）观察系统输出波形在采样点以外的波形。
（4）比较有纹波与无纹波系统的区别，分析其原因。
5.实验设计：
（1）最少拍有纹波设计如下
图2有纹波控制设计
（2）最少拍无纹波设计如下：
（3）尝试用M文件实现dalin算法控制
5.实验设计：
6.实验结果：
图3纯滞后系统输出
图4纯滞后系统控制器输出
7.思考与分析：
（1）纯滞后控制系统对阶跃信号有无超调？为什么？
（2）纯滞后控制与PID控制有什么本质区别？消除振铃前后系统输出有什么不同？
(3)了解输入信号对最少拍控制系统的影响及其改进措施。
2.实验设备
(1)硬件环境：
微型计算机一台，P4以上各类微机
(2)软件平台：
操作系统:Windows2000 MATLAB7.0仿真软件
3.实验原理
最少拍控制是一种直接数字设计方法。所谓最少拍控制，就是要求闭环系统对于某种特定的输入在最少个采样周期内达到无静差的稳态，使系统输出值尽快地跟踪期望值的变化。他的闭环z传递函数具有形式
设被控对象为有纯滞后的一阶惯性环节或二阶惯性环节达林算法的设计目标是使整个闭环系统所期望的传递函数该算法控制将调整时间的要求放在次要而超调量小甚至没有放在首位

有时叫做带0阶保持器离散化。 有时叫做带 阶保持器离散化。 阶保持器离散化 前面已经讨论过离散化方法了。 前面已经讨论过离散化方法了。
3
（2）闭环脉冲传递函数
闭环脉冲传递函数
D( z ) G ( Z ) Φ( z ) = 1 + D( z ) G ( Z )
这个闭环传函是根据性能指标要求构造出的（选择的）， 这个闭环传函是根据性能指标要求构造出的（选择的），D(Z) ）， 是要设计的控制器。 是要设计的控制器。 可以求出控制器为： 可以求出控制器为：
i =0 i =1
(4.50 )
数字控制器的直接涉及方法与步骤基本就是这样。 数字控制器的直接涉及方法与步骤基本就是这样。
6
（4）设计步骤归纳
给据性能指标要求和其它约束条件， ① 给据性能指标要求和其它约束条件，构造所要求的闭环脉冲 传函φ(Z) 传函 对被控对象传函G(S)带0阶保持器进行离散化 ② 对被控对象传函 带 阶保持器进行离散化 求出D(Z) ③ 求出 求出u(k) ④ 求出
这时， 这时，闭环脉冲传递函数
Φ(z) =1Φe (z) = 2z z
输出信号Y(z)为 为 输出信号
1
2
Tz1 Y(z) = R(z) Φ(z) = (2z1 z2 ) (1 z1)2 = 2Tz2 + 3Tz3 + 4Tz4 +...
有了E(z),Y(z)，可以求出e(k),y(k)，画出他的时域离散曲线如下 ，可以求出 有了 ， 教材上91页图 页图4-27（b）） 图（教材上 页图 （ ）
系统调节时间
输出Y(Z) 输出
ts=T
1 Y(z) = R(z) Φ(z) = z1 = z1 + z2 + z3 +... (1 z1)

计算机控制系统实验报告班级：测控09-X 学号： XX 姓名 XXX 成绩：实验七 最少拍控制算法的研究一、实验目的1．学习并掌握最少拍控制器的设计和实现方法，并研究最少拍控制系统对三种典型输入的适应性及输出采样点间的纹波。

2．学习并掌握最少拍无纹波控制器的设计和实现方法，并研究输出采样点间的纹波消除以及最少拍无纹波控制系统对三种典型输入的适应性。

二、实验内容1．设计并实现对象具有一个积分环节的二阶系统的最少拍控制，并通过混合仿真实验研究该闭环控制系统对三种典型输入的适应性以及输出采样点间的纹波。

2．设计并实现对象具有一个积分环节的二阶系统的最少拍无纹波控制，并通过混合仿真实验观察，该闭环控制系统输出采样点间纹波的消除，以及系统对三种典型输入的适应性。

三、实验步骤1．设计并连接模拟由一个积分环节和一个惯性环节组成的二阶被控对象的电路，并利用AD μC812构成的数据处理系统完成计算机控制系统的模拟量输入、输出通道的设计和连接。

2．利用上位机的虚拟仪器功能对此模拟二阶被控对象的电路进行测试，分别测取惯性环节的放大倍数、时间常数以及积分环节的积分时间常数。

在上位机完成阶跃输入下最少拍控制计算与实验结果显示、记录。

先完成阶跃输入下最少拍控制器的参数设计和调试，然后再用另外两种典型信号（等速与等加速）作为系统输入，观察系统输出并记录。

3．在上位机完成阶跃输入下最少拍无纹波控制器的计算与实验结果显示、记录。

先完成阶跃输入下最少拍无纹波控制器的参数设计和调试，然后再用另外两种典型信号（等速与等加速）作为系统输入，观察系统输出并记录。

4．对记录的实验结果进行分析，写出实验报告。

四、附录1．被控对象模拟与计算机闭环控制系统的构成 实验系统被控对象的传递函数为1()(1)KG s s T s =+（7－1）它可以用图7.1所示电路来模拟，计算机控制系统的方框图如图7.2所示：最少拍控制的效果对被控对象的参数变化非常敏感，实验中必须测取模拟对象的实际参数。

计算机控制技术--基于Matlab的最少拍控制系统设计学院：计算机科学与技术班级：计科0902班学号：姓名：指导老师：日期： 2012年12月15日一、实验目的：1．学习使用Matlab 设计最少拍控系统的方法； 二、实验工具：X86系统兼容型计算机、MATLAB 软件。

三、实验内容： 1．实验原理最少拍设计，是指系统在典型输入信号（如阶跃信号、速度信号、加速度信号等）作用下，经过最少拍（有限拍）使系统输出的系统稳态误差为零。

因此，最少拍控制系统也称最少拍无差系统或最少拍随动系统，它实质上是时间最优控制系统，系统的性能指标就是系统调节时间最短或尽可能短，即对闭环Z 传递函数要求快速性和准确性。

下面以一个具体实例介绍最少拍系统的设计和仿真。

考虑图1所示的采样数字控制系统，被控对象的脉冲传递函数为210G ()(1)s s s =+图0 最少拍采样数字控制系统设采样周期T=1s ，首先求取广义被控对象的脉冲传递函数： 广义被控对象21112111111110()[](1)11(1)10[](1)110.36793.679(10.718)(1)(10.3679)Ts e G z Z s s s z z z z z z z z z -----------=+=-⨯-+---+=--我们知道，最少拍系统是按照指定的输入形式设计的，输入形式不同，数字控制器也不同。

因此，对三种不同的输入信号分别进行考虑： ① 单位阶跃信号：计算可得到最少拍数字控制器为1111()()1()0.2712(10.3679))()()(1())10.718e z z z z z z D z G z z z ----Φ=Φ=-Φ-==-Φ+检验误差序列：()(1())()1E z z R z =-Φ=由误差的变换函数得知，所设计的系统当k>1后，e （k ）=0就是说，一拍以后，系统输出等于输入，设计正确。

② 单位速度信号：原理同上，我们可以得到：1111()0.5434(10.5)(10.3679)()()(1())(1)(10.718)z z z D z G z z z z ----Φ--==-Φ-+检验误差：1()(1())()E z z R z z -=-Φ=从E(z)看出，按单位速度输入设计的系统，当k 大于等于2之后，即二拍之后，误差e （k ）=0，满足题目要求。

重庆交通大学学生实验报告实验课程名称计算机控制技术 __________________ 开课实验室__________ 304 ____________________学院机电与汽车工程年级2011专业班电气一班学生姓名鑫晟学号621124080111开课时间2013至2014学年第二学期、实验目的了解最少拍控制器参数漂移是对系统稳定性的影响。

二、实验内容被控制对象函数为2.2z J~11 1.2z设计一个单位阶跃输入时的最少拍控制器D(Z)，并仿真分析系统无漂移和有漂移时的系统稳定性。

三、实验设备Matlab软件四、实验步骤与结果分析(1)如果设计时D(Z)和G(z)中的不稳定极点对消，得到控制器的控制为0.45451 1.2z，1 -z J运用matlab软件进行仿真，输入为单位阶跃时，可以得到其仿真图如下:运行得到其输出的图像为:（上图为控制器的输出，下图为系统的输出）可以看出经过了一个周期，系统的输出就达到了稳定，是一个稳定的控制系统（2）当被控制对象的参数发生漂移，变为2.2z‘1 1.3z」时，仿真分析D（Z）为（1）中控制器的输出与系统的输出在此情况下，由于参数的变化闭环系统不再稳定，出现发散的情况（3）按最少拍控制器的设计方法，即闭环误差传递函数中包含被控对象的不稳定极点设计控制器，得到控制器0.0911 -6z J1 -z」其连接图如下所示:仿真可以得到系统的输出如下所示:可以根据输出的图像看出，在经过两个周期以后，系统就达到了稳定(4)当被控制对象的参数发生漂移，变为2.2z‘1 1.3z*时，仿真分析D(Z)为(3)中控制器时系统的输出12可以从其输出的图像看出，在模型有误差的时候，控制器仍能够保持稳定' 这种修正过后的系统在遇到漂移之时处理效果好多了。

能够更加满足设计的要求。

最少拍控制系统实验报告（精选）
本次实验我们设计了一种最少拍控制系统，旨在实现一个简单而稳定的控制系统。

1. 系统结构
系统结构如下图所示：
该系统由一个开关控制器、一个数字控制器（DMC）、一个电机和一个传感器组成。

2. 开关控制器
我们使用一个开关控制器来实现系统的开关操作。

通过控制该开关控制器的开关状态，我们可以决定系统是处于开启状态还是关闭状态。

3. 数字控制器（DMC）
数字控制器（DMC）是实现最少拍控制的核心组件。

我们采用PID控制器来实现控制任务。

PID控制器由比例、积分和微分三个控制元素组成。

比例控制元素处理控制器的当前误差，并根据一定的比例关系输出控制指令；积分控制元素将误差的积分累加到控制器输出中，以增加系统的稳定性和减小未控制的误差；微分控制元素用于响应系统的速度变化，以调整控制器输出并提高系统的响
应速度。

4. 电机和传感器
电机和传感器是系统的执行部分。

电机负责执行控制指令，改变系统状态。

传感器用于监测系统状态，以便反馈给数字控制器。

5. 实验效果
通过实验，我们可以看到该控制系统具有较好的效果。

控制器能够输出稳定的控制指令，通过电机实现系统状态的改变。

传感器及时地反馈系统状态，以便数字控制器做出相应的控制调整。

该最少拍控制系统具有以下优点：
1）系统结构简单明了，易于理解和实现。

2）精度高，能够快速稳定地响应控制指令。

3）系统操作稳定，不易出现异常情况。

本次实验充分展示了我们设计的最少拍控制系统的良好效果，我们相信它能够在现代工业控制领域中得到广泛应用。