当前位置：文档之家 › 计算方法(2)-插值法

计算方法(2)-插值法

  • 格式：ppt
  • 大小：375.50 KB
  • 文档页数：38

下载文档原格式

  / 38

合集下载

计算方法课件：第2次课 计算方法插值

计算方法课件：第2次课 计算方法插值
插值方法 16
2.3.2 Lagrange插值公式
Lagrange插值多项式 令R[x]n+1表示所有的不高于n次的实系数
多项式和零多项式构成的集合，假设函数y=f(x) 的已知值(xi，yi)(yi=f(xi)，xi互异，i=0，1，…，
n)，寻找一个多项式p(x) R[x]n+1，满足：
p(xi)=f(xi)(i=0，1，…，n)
插值问题中的一个非常典型的问题
插值方法 8
2.1 问题的提出(数值预测)
计算函数值
Y
Q：函数关系复杂，没 有解析表达式，或者函数形 式未知。
常见的有：由观测数据
0
(离散数据)计算未观测到的
点的函数值。
X
0
——由观测数据构造一个适当的简单函数近似的代替
要寻求的函数——插值法。
代数插值——简单函数为代数多项式
内存在n+1阶有界导数，则当x [a,b]，必存在一点
ξ(a，b) ，使得
r(x)
f n1( )
(n 1)!
n
(x xk )
k 0
插值方法 25
证明——《数学分析》
误差分析 x偏离插值节点比较远，则误差大，尤
其是外推误差大； 被插函数足够光滑，否则导数过大，用
代数多项式插值不合适。
插值方法 26
谢谢！
插值方法
点x为插值点； 内插——插值点位于插值区间内的插值过程；
外插——插值点位于插值区间外的插值过程，也 叫外推。
插值方法 15
要求： 效率高 精度高 插值函数形式简单——多项式、有理分式。
代数插值法——g(x)=p(x)，为插值多项式 Lagrange插值公式 Aitken插值公式 Newton插值公式

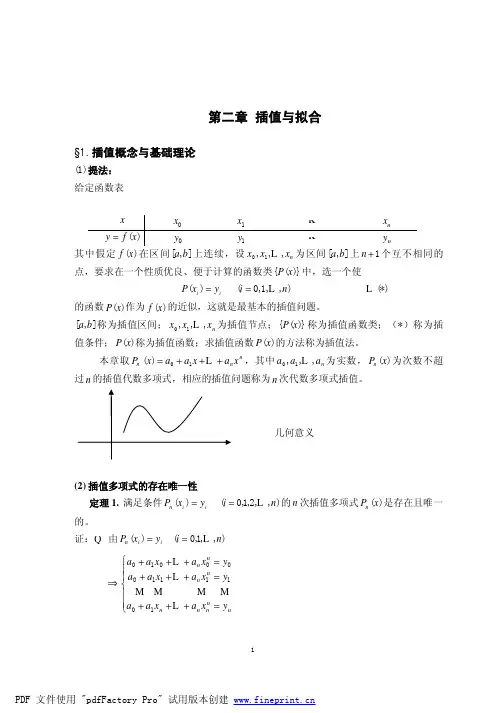
计算方法 插值法

计算方法 插值法

例见 P.74 例 1。 (2) 差商与牛顿基本插值多项式 考虑到拉格朗日插值的缺点：增加新的结点，需重新计算，工作量较大！ 改进的方向：选取形式： a 0 + a1 ( x − x0 ) + a 2 ( x − x0 )( x − x1 ) + L + a n ( x − x0 )( x − x1 ) L ( x − xn −1 ) ； （称之为 n 次牛顿插值多项式） 记 N n ( x) = a 0 + a1 ( x − x0 ) + a 2 ( x − x0 )( x − x1 ) + L + a n ( x − x0 )( x − x1 ) L ( x − x n −1 ) 为了给出 a i 简明计算表达式，引入差商（或均差）概念。 定义 1.
第二章 插值与拟合
§1.插值概念与基础理论
(1) 提法： 给定函数表 x y = f ( x) x0 y0 x1 y1
K K
xn yn
其中假定 f ( x) 在区间 [a, b] 上连续，设 x0 , x1 , L, x n 为区间 [a, b] 上 n + 1 个互不相同的 点，要求在一个性质优良、便于计算的函数类 {P ( x)} 中，选一个使 P ( xi ) = y i (i = 0,1,L, n) L (*) 的函数 P( x) 作为 f ( x) 的近似，这就是最基本的插值问题。 [a, b] 称为插值区间； x0 , x1 , L, x n 为插值节点； {P ( x)} 称为插值函数类；（*）称为插 值条件； P( x) 称为插值函数；求插值函数 P( x) 的方法称为插值法。 本章取 Pn ( x) = a 0 + a1 x + L + a n x n ，其中 a 0 , a1 , L, a n 为实数， Pn ( x) 为次数不超 过 n 的插值代数多项式，相应的插值问题称为 n 次代数多项式插值。

插值法数学计算方法

插值法数学计算方法

插值法数学计算方法插值法是一种数学计算方法，用于在已知数据点的基础上，通过构建一条插值曲线来估计未知数据点的值。

插值法可以应用于各种数学问题中，例如逼近函数、插值多项式、差值等。

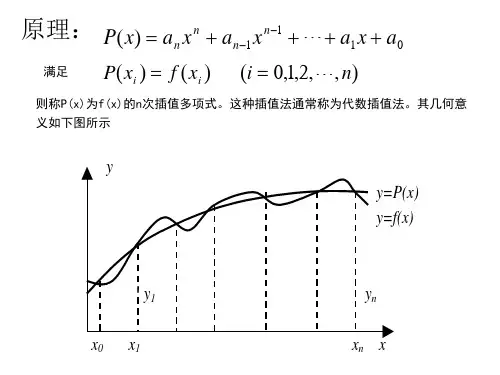
本文将详细介绍插值法的原理和常见的插值方法。

一、插值法的原理插值法的基本思想是通过已知数据点的函数值来构建一个函数表达式，该函数可以通过插值曲线来估计任意点的函数值。

根据已知数据点的数量和分布，插值法可以采用不同的插值方法来构建插值函数。

插值法的原理可以用以下几个步骤来描述：1.收集已知数据点：首先，需要收集一组已知的数据点。

这些数据点可以是实际测量得到的，也可以是其他方式获得的。

2.选择插值方法：根据问题的特性和数据点的分布，选择适合的插值方法。

常见的插值方法包括拉格朗日插值法、牛顿插值法、埃尔米特插值法等。

3.构建插值函数：通过已知数据点，利用选择的插值方法构建插值函数。

这个函数可以拟合已知数据点，并通过插值曲线来估计未知数据点。

4.估计未知数据点：利用构建的插值函数，可以估计任意点的函数值。

通过插值曲线，可以对未知数据点进行预测，获得相应的数值结果。

二、常见的插值方法1.拉格朗日插值法：拉格朗日插值法基于拉格朗日多项式，通过构建一个具有多项式形式的插值函数来逼近已知数据点。

插值函数可以通过拉格朗日基函数计算得到，式子如下：P(x) = ∑[f(xi) * l(x)], i=0 to n其中，P(x)表示插值函数，f(xi)表示已知数据点的函数值，l(x)表示拉格朗日基函数。

2.牛顿插值法：牛顿插值法基于牛顿差商公式，通过构建一个递归的差商表来逼近已知数据点。

插值函数可以通过牛顿插值多项式计算得到，式子如下：P(x) = f(x0) + ∑[(f[x0, x1, ..., xi] * (x - x0) * (x - x1)* ... * (x - xi-1)] , i=1 to n其中，P(x)表示插值函数，f[x0, x1, ..., xi]表示xi对应的差商。

数值计算方法插值法

数值计算方法插值法

f[x1,x2,x3] …
f[x0,x1,x2 ,x3]
例阶2.1差1商求值f(xi)= x3在节点 x=0, 2, 3, 5, 6上的各
解xi :
计算得如下表 f[xi] f[xi,xi+1]
f[xi,xi+1,xi+2 ]
f[xi,xi+1,xi+2 ,xi+2]
00
28
80 4 20
27 8 19 19 4 5
an x0 n an1x0 n1 a1x0 a0 f (x0 )
an x1n
an1
x n1 1
a1x1 a0
f (x1 )
an xn n an1xn n1 a1xn a0 f (xn )
这是惟一一个性关说于明待，定不参论数用何种方法来构a造的0，,n+也a11阶不, 线论性用, 方何an种形式来表示插值多项式,
由线性代数知,任何一个不高于n次的多项式, 都可以表示成函数
1, x x0 , (x x0 )(x x1 ),, (x x0 )(x x1 )(x xn1 )
的线性组合, 也就是说, 可以把满足插值条件 p(xi)=yi (i=0,1,…,n)的n次插值多项式, 写成如下形式
a0 a1(x x0) a2(x x0)(x x1) an (x x0)(x x1)(x xn1)
f[x0 , x1]=
f(x1)- f(x0) x1 – x0
f[x1 , x0]
f(x0)- f(x1) =
x0 – x1
f x0 , x1, x2 f x1, x2 , x0 f x0 , x2 , x1
性质3 若f[x, x0, x1 , …, xk ]是 x 的 m 次多项式, 则 f[x, x0, x1 ,…, xk , xk+1]是 x 的 m-1 次多项式

计算方法插值法(均差与牛顿插值公式)

计算方法插值法(均差与牛顿插值公式)

为f ( x)关于节点 x0 , xk 一阶均差 (差商)
2018/11/7
5
2018/11/7
6
二、均差具有如下性质：
f [ x0 , x1 ,, xk 1 , xk ]

j 0
k
f (x j ) ( x j x0 )( x j x j 1 )(x j x j 1 )( x j xk )
2018/11/7
27
fk fk 1 fk 为f ( x)在 xk 处的二阶向前差分
2
依此类推
m f k m1 f k 1 m1 f k
为f ( x)在 xk 处的m阶向前差分
2018/11/7
28
差分表
xk f k 一阶差分 x0 f 0 x1 f 1 二阶差分 三阶差分 四阶差分
2018/11/7
31
等距节点插值公式
一、牛顿前插公式
2018/11/7
32
2018/11/7
33
二、牛顿插值公式与拉格朗日插值相比
牛顿插值法的优点是计算较简单,尤其是增加 节点时,计算只要增加一项,这是拉格朗日插值 无法比的. 但是牛顿插值仍然没有改变拉格朗日插值的 插值曲线在节点处有尖点，不光滑，插值多 项式在节点处不可导等缺点.
2018/11/7
25
2018/11/7
26
§
2.3.4 差分及其性质
一、差分
fk , 定义3. 设f ( x)在等距节点xk x0 kh 处的函数值为 k 0 ,1, , n , 称
f k f k 1 f k
k 0,1,, n 1
为f ( x)在 xk 处的一阶向前差分

插值法的计算

插值法的计算

20x0年1月1日，甲公司支付价款1 000万元（含交易费用）从上海证券交易所购入A公司同日发行的5年期公司债券，面值1 250万元，票面利率4.72%，于年末支付本年利息（即每年1 250× 4.72%＝59万元），本金最后一次偿还。

合同约定，该债券的发行方在遇到特定情况时可以将债券赎回，且不需要为提前赎回支付额外款项。

甲公司在购买该债券时，预计发行方不会提前赎回。

不考虑所得税、减值损失等因素。

这里20x0年的摊余成本是购买时的1000吗？如果不是那么1000是怎么来的由哪个数字金额调整来的？本人没有会计基础希望内行的朋友解释详细一些，谢谢前4年每年年末收到利息59 万，第5年收到本金+利息= 1250+59=1309万设实际利率为r将未来的收益折成现值：即59/(1+r) + 59/(1+r)^2 + 59/(1+r)^3 + 59/(1+r)^4 + (1250+59)/(1+r)^5 = 1000也可以表示成59(P/A,r,5）+1250(P/S,r,5）=1000解这个方程就要用插值法了，就是假设r为两个值，使等式前段的值一个大于1000，一个小于1000。

例如假设r=9%(a)，则等号前的式子等于1041.9(A)大于1000再设r=11%(b)，则等号前的式子等于959.872(B)小于1000，则这两个假设就符合条件了，再代入公式：(1000-A)/(B-A)=(r-a)/(b-a)得出实际利率r=10%算摊余成本就是期末摊余成本=期初摊余成本+按实际利率算的利息-按票面利率算的应收利息20X0年期末摊余成本= 1000 + 1000*10% - 59 = 1041万20X1年期末摊余成本就是1041+ 104.1-59=1086.1万算至20X4年的时候期末摊余成本应该就等于1250万了设与A1对应的数据是B1，与A2对应的数据是B2，与A对应的数据是B，A介于A1和A2之间，按照（A1-A)/(A1-A2)=(B1-B)/(B1-B2)，计算出A的数值。

计算方法第二章ppt


当方程组的系数矩阵为非奇异 矩阵（即满秩矩阵）时，高斯 消元法可求得唯一解。
列主元高斯消元法
列主元高斯消元法的 基本思想
在高斯消元法的基础上，每次选取列 中绝对值最大的元素作为主元进行消 元，以避免出现小主元导致的误差放 大问题。
列主元高斯消元法的 步骤
首先选取第一列中绝对值最大的元素 作为主元，通过行交换将其移到第一 行第一列位置，然后进行高斯消元。 在后续的消元过程中，每次均选取当 前列中绝对值最大的元素作为主元进 行消元。
100%
数值解法
通过计算机求解常微分方程的近 似解的方法，主要包括欧拉方法 和龙格-库塔方法等。
80%
离散化与步长
将连续的时间或空间域离散化， 取离散点上的函数值作为近似解 ，步长是相邻离散点间的距离。
欧拉方法
显式欧拉法
一种简单的数值解法，通过前 一步的函数值及其导数来推算 下一步的函数值。
隐式欧拉法
通过求解一个非线性方程来得 到下一步的函数值，具有较高 的精度和稳定性。
改进欧拉法
结合显式欧拉法和隐式欧拉法 的优点，提高算法的精度和效 率。
龙格-库塔方法
龙格-库塔法基本思想
自适应步长龙格-库塔法
通过多步计算并利用泰勒级数展开式， 得到更高精度的近似解。
根据误差估计自动调整步长，实现精 度和计算效率的动态平衡。
标准四阶龙格-库塔法
一种常用的高精度数值解法，具有局 部截断误差为$O(h^5)$的优点。
常微分方程数值解法误差分析
局部截断误差
数值解法在单步计算中所产生的误差，可以通过泰勒级数展开式进行估计。
全局误差
数值解法在整个计算过程中所产生的累积误差，与算法稳定性、步长选择等因素有关。

计算方法课件_插值法


P( x) an x an1 x
n
n1
a1 x a0
满足
P( xi ) f ( xi )
(i 0,1,2,, n)
计 则称P(x)为f(x)的n次插值多项式。这种插值法通常 算 称为代数插值法。其几何意义如下图所示 方 法 课 件 y=p(x)
y=f(x)
2016/12/27
算 l0 ( x0 ) 1, l0 ( x1 ) 0 , l0 ( x2 ) 0 方 法 这个问题容易求解。由上式的后两个条件知 : 课 件 x1 , x 2 是 l0 ( x) 的两个零点。于是
1 再由另一条件 l0 ( x0 ) 1 确定系数 c ( x0 x1 )(x0 x2 ) ( x x1 )(x x2 ) 从而导出 l0 ( x) ( x0 x1 )(jkhh x0 x 2 ) 2016/12/27 14
直接由插值条件决定，
y
计 即 a0 , a1 , a 2 满足下面 y0 算 的代数方程组： 方 O x0 法 课 2 a a x a x 0 1 0 2 0 y0 件 该三元一
y=L2(x) y1 x1 y1 x2 y=f(x) x
2 a a x a x 0 1 1 2 1 y1 2 a a x a x 2 2 y2 0 1 2
(i=0,1,2,…,n )
的便于使用的插值多项式P(x),先考察几种简单情形,
线性插值是代数插值的最简单形式。假设给定了函数 近似地代替f(x)。选
x1 的值， f(x)在两个互异的点 x0 ， y0 f ( x0 ), y1 f ( x1 )
,现要求用线性函数 p( x) ax b 择参数a和b, 使 p( xi ) f ( xi )(i 0,1) P(x) 为f(x)的线性插值函数 2016/12/27 jkhh 。

计算方法 第二章插值法_20191105


下面两种办法常用来确定经验函数y=g(x)
（1）插值法
（2）拟合法
根据问题的不同，有时要用插值技术来解决， 有时则应该采用拟合的方法才合理。
（1）插值法的基本思想
已知数据表
xi x1 x2 … xn f(xi) f(x1) f(x2) … f(xn)
求一个经验函数y=g(x)，使g(xi)=f(xi), i=1,…n.
x)
b0
a0 a1 x a2 x2 b1 x b2 x2 b3 x3
n
一般地：F( x) cii( x) i=0
例：F(x) a bx csin x span1, x,sin x,
当插值函数是代数多项式时，插值问题称为代
代 数插值。
数 插
设 Pn(x)=a0+a1x+…+anxn ,
y2
n 次插值多项式 :求次数≤n的多项式Ln(x), 使其满足
Ln(x0)=y0 , Ln(x1)=y1 , ...... , Ln(xn)=yn
..(7)
令 Ln(x)=l0(x)y0 + l1(x)y1 +… +ln(x)yn
求n 次多项式 lj(x) ,(j=0,1,…,n)使其满足条件
容易求得
三角插值：取
spani(
n
x) i=0
a1x a0
=spansin x,cos x,sin 2x,cos 2x, ,sin nx,cos nx
例：取 spansin x,cos x,
F ( x) a sin x bcos x
有理插值：F( x)= Pm ( x) Qn ( x)
例：F (
二次插值 (n=2) 求次数≤2 的多项式L2(x), 使其满足条件 L2(x0)=y0 , L2(x1)=y1 , L2(x2)=y2

计算方法-插值法报告

计算方法报告——插值1.原理简介插值法是利用函数f (x)在某区间中已知的若干点的函数值，作出适当的特定函数，在区间的其他点上用这特定函数的值作为函数f (x)的近似值。

根据算法和插值要求的不同，有多种插值方法。

拉格朗日插值：有平面上点集{（x i,y i）}共n个点，现作函数f(x)图像使其过这n个点P i(x)=∏x−x j x i−x jnj=0 j≠i L n(x)=∑P i(x)×y ini=1则f(x)=L n(x)牛顿插值：同样点集，用不同方法构造插值多项式。

定义差商：f[x0，x1]=f(x0)−f(x1) x0−x1f[x0，x1……x k]=f[x0，x1……x k−1]−f[x1，x2……x k]x0−x k则有：N(x)=f[x0]+∑f[x0，x1……x k](x−x0)(x−x1)…（x−x k−1）nk=1理论上牛顿插值与拉格朗日插值所得插值多项式完全相同，只是不同写法。

2.算法描述分析函数：homework1.C 画图函数：DrawPlot.cpp为简化程序，将Lagrange插值与Newton插值算法作为子函数调用。

子函数Lagrange()中，输入插值点个数n，插值点集x[n]，y[n]，即可得到x点的Lagrange插值函数值L(x)。

同样，Newton()中输入相同信息可得到x点Newton插值函数值N(x)。

主函数main()中，先根据设定选择样点为等距分割还是Chebyshev分割，取得点集point_x[n+1]和point_y[n+1]，取点范围（-1，1）。

再调用子函数分别计算各x[i]点下的真实函数值，牛顿插值函数值，拉格朗日插值函数值及各种误差，在循环结束后将需要的误差L_inf 和L1输出到屏幕。

最后利用root TGraph把计算得到的数组画出函数图像，并存到rootfile 中。

在误差计算中只用了-1~0上的点，画图时扩大范围画到-1~1全部点DrawPlot函数中读取了homework1.C中画的函数图像，将其整合到一起，设置线条颜色及宽度，加上一个图例，重新生成一张图像。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。



2
2
yk1 2

f (xk

h
2
),
y
k

1 2

f (xk

h) 2
21
3.牛顿向后插值公式
Nn (xn

th)

yn

tyn

t(t 1) 2!
2
yn



t(t

1)


(t n!

n

1)

n
yn
(t 0)
插值余项
Rn
(xn

th)

t(t
1) (t (n 1)!
Nn (x0

th)

y0

ty0

t(t 1) 2!
2
y0Leabharlann 插值余项t(t

1)


(t n!

n

1)
n
y0
Rn (x0

th)

t(t
1) (t (n 1)!
n)
h n1
f
(n1) ( ),
(x0 , xn )
20
二.向后差分与牛顿向后插值公式
杂.

根据f(x)函数表或复杂的解析表达式构
造某个简单函数P(x)作为f(x)的近似.
2
2.问题的提法
1)已知条件 设函数y f (x)在区间[a,b]上
连 续, 且 在n 1个不 同点a x0 , x1, , xn b 上 分 别 取 值y0 , y1, , yn
计算方法
第二章 插值法
§1 引言 §2 拉格朗日插值多项式 §3 牛顿插值多项式 §4 分段低次插值 §5 三次样条插值 §6 数值微分
1
§1 引言
一.插值问题的提法
1.插值法的背景及思想

函数f(x)在区间[a,b]上存在且连续,只
知在有限个点的函数值,或函数表达式太复
n n
a0 a1xn an xnn yn
n i1

(xi x j ) 0
i1 j 0
6
§2 拉格朗日插值多项式
一.插值基函数
1.问题的提出
对 节 点xi (i 0,1, , n)中 任 一 点xk (0 k n),作 一n次 多 项 式 lk (x),使 它 在 该 点 值 为1, 在 其 余 点xi 值 为0
Nn (x) a0 a1 (x x0 ) a2 (x x0 )(x x1 ) an (x x0 )(x x1 ) (x xn1 )
一.向前差分与牛顿向前插值公式
1.向前差分定义 步长 设 函 数f (x)在 等 距 节 点xk x0 kh

10.714
11
三.插值余项
1.定义
记Rn (x) f (x) Pn (x),
称 为 插 值 多 项 式Pn (x)的 余 项
2.定理2 设f(x)在区间[a,b]上有直到n+1阶
导数,x0 , x1, , xn 为[a,b]上n+1个互异的节点, Pn (x) 为满足条件 Pn (xi ) f (xi )(i 0,1, , n)
x0 ) (xk
1 xk1 )( xk
xk1) (xk

xn )
lk
(x)

(x x0 ) (x (xk x0 ) (xk

xk1 )( x xk1 ) (x xk1 )( xk xk1 ) (xk
用x0 , x1两 点 作 线 性 插 值, 得y f (x)的 近 似 值y1
y

y1

1 2
f
" (1 )(x

x0 )(x

x1 ),1
(x0 , x1)
用x0
,
x
两
2
点
作
线
性
插
值, 得y

f (x)的 近 似 值y2
y

y2

1 2
f
"(2 )(x

x0 )(x

x2 ),2
取 节 点x0 100 , x2 144 , 近 似 值y2 10.682
y1的 误 差:
115

y1

115 144
121 121
(10.682
10.714 )
0.00835
15
例4 给出f(x)=lnx的数值表
x
0.4
0.5
0.6
0.7
lnx -0.916291 -0.693147 -0.510826 -0.356675
例2 估计例1中的截断误差
解: 线性插值
f (x) x
R1 (x)

1 2
f "( ) 2 (x),
[x0 , x1 ]
抛物插值
f (x) x
R2
(x)

1 3!
f
'''( )3 (x),
[x0 ,
x2 ]
13
四.插值误差的事后估计法
设x0 x x1 x2 , 且f (xi )(i 0,1,2)为 已知
n)
h n1
f
(n1) ( ),
(x0 , xn )
22
例5 从给定的表出发,计算 sin(0.12),sin(0.58)
并估计截断误差.
xk
yk
0.1 0.09983
0.2 0.19867
0.3 0.29552
0.4 0.38942
0.5 0.47943
0.6 0.56464
yk 0.09884 0.09685 0.09390 0.09001 0.08521

x 121 21
l1 ( x)

x x0 x1 x0

x 100 21
2)线性插值多项式
L1 ( x)

y0l0
(x)

y1l1 ( x)

10
x 121 21
11
x
100 21
115

L1
(115)

10

115 121 21

11
115 100 21
其
中a0
,

,
a
为
n
实
数.
2)n次插值多项式
4
求插值多项式的几何意义
5
二.插值多项式的存在唯一性
定理1 若节点 x0 , x1, , xn 互不相同,
则满足插值条件 Pn (xi ) yi (i 0,1, , n)
的n次插值多项式 Pn (x) a0 a1x an xn
an (x x0 )(x x1 ) (x xn1 )
a0
a2
y0

y2

y0

y0 h
(
(x2 x0 )( x2
a1
x2 x0 x1)
)
y1 x1


y2
y0 y0 x0 h
2 y1 y0 2h h
2 y0 2!h 2
的n次插值多项式,则 x [a,b]
有
Rn (x)
f (n1) ( )
(n 1)!

n1
(
x)
n
其中 n1(x) (x xi ), (a,b) 且依赖于x
i0
12
例1 用线性插值和抛物插值求近似值
100 10, 121 11, 144 12,求 115
xk yk
y k
2 yk
3 yk
4 yk
x0 y0
y0
x1 y1
2 y0
y1
3 y0
x2 y2
2 y1
4 y0
y 2
3 y1
x3 y3
2 y2
y3
x4 y4
18
牛顿插值多项式 Nn (xi ) yi (i 0,1, , n)
N n (x) a0 a1 (x x0 ) a1 (x x0 )(x x1 )
]
特例
jk
n 1,线性插值
L1 ( x)

y0

y1 x1

y0 x0
(x

x0 )
9
特例 n 2, 二 次 插 值(抛 物 插 值)
L2 (x)

y0
(x (x0

x1 )( x x2 ) x1 )( x0 x2 )

y1
(x ( x1

x0 )( x x2 ) x0 )( x1 x2 )
2)插值的目的 在一性质优良便于计算的
函 数 类中, 求 一 简 单 函 数P( x), 使 P(xi ) yi (i 0,1, , n)
而 在 其 它 点x xi上, P(x)作 为f (x)的 近 似.
3)相关定义 插值区间、插值节点、插值条件、
插值函数类、插值法
3
3.多项式插值 用代数多项式作插值函数
用线性插值和二次插值求ln0.54近似值
解: 线性插值 取 节 点x0 0.5, x1 0.6,