数字信号处理实验(西电 高西全教材)

数字信号处理实验报告班级：****姓名：郭**学号：*****联系方式：*****西安电子科技大学电子工程学院绪论数字信号处理起源于十八世纪的数学，随着信息科学和计算机技术的迅速发展，数字信号处理的理论与应用得到迅速发展，形成一门极其重要的学科。

当今数字信号处理的理论和方法已经得到长足的发展，成为数字化时代的重要支撑，其在各个学科和技术领域中的应用具有悠久的历史，已经渗透到我们生活和工作的各个方面。

数字信号处理相对于模拟信号处理具有许多优点，比如灵活性好，数字信号处理系统的性能取决于系统参数，这些参数很容易修改，并且数字系统可以分时复用，用一套数字系统可以分是处理多路信号；高精度和高稳定性，数字系统的运算字符有足够高的精度，同时数字系统不会随使用环境的变化而变化，尤其使用了超大规模集成的DSP 芯片，简化了设备，更提高了系统稳定性和可靠性；便于开发和升级，由于软件可以方便传送，复制和升级，系统的性能可以得到不断地改善；功能强，数字信号处理不仅能够完成一维信号的处理，还可以试下安多维信号的处理；便于大规模集成，数字部件具有高度的规范性，对电路参数要求不严格，容易大规模集成和生产。

数字信号处理用途广泛，对其进行一系列学习与研究也是非常必要的。

本次通过对几个典型的数字信号实例分析来进一步学习和验证数字信号理论基础。

实验一主要是产生常见的信号序列和对数字信号进行简单处理，如三点滑动平均算法、调幅广播（AM ）调制高频正弦信号和线性卷积。

实验二则是通过编程算法来了解DFT 的运算原理以及了解快速傅里叶变换FFT 的方法。

实验三是应用IRR 和FIR 滤波器对实际音频信号进行处理。

实验一●实验目的加深对序列基本知识的掌握理解●实验原理与方法1.几种常见的典型序列：0()1,00,0(){()()(),()sin()j n n n n u n x n Aex n a u n a x n A n σωωϕ+≥<====+单位阶跃序列：复指数序列：实指数序列：为实数 正弦序列：2.序列运算的应用：数字信号处理中经常需要将被加性噪声污染的信号中移除噪声，假定信号 s(n)被噪声d(n)所污染，得到了一个含噪声的信号()()()x n s n d n =+。

数字信号处理实验报告实验一：信号、系统及系统响应一、实验目的：(1) 熟悉连续信号经理想采样前后的频谱变化关系，加深对时域采样定理的理解。

(2) 熟悉时域离散系统的时域特性。

(3) 利用卷积方法观察分析系统的时域特性。

(4) 掌握序列傅里叶变换的计算机实现方法，利用序列的傅里叶变换对连续信号、离散信号及系统响应进行频域分析。

二、实验原理与方法：(1) 时域采样。

(2) LTI系统的输入输出关系。

三、实验内容、步骤(1) 认真复习采样理论、离散信号与系统、线性卷积、序列的傅里叶变换及性质等有关内容，阅读本实验原理与方法。

(2) 编制实验用主程序及相应子程序。

①信号产生子程序，用于产生实验中要用到的下列信号序列：a. xa(t)=A*e^-at *sin(Ω0t)u(t)A=444.128;a=50*sqrt(2)*pi;b. 单位脉冲序列：xb(n)=δ(n)c. 矩形序列：xc(n)=RN(n), N=10②系统单位脉冲响应序列产生子程序。

本实验要用到两种FIR系统。

a. ha(n)=R10(n);b. hb(n)=δ(n)+2.5δ(n-1)+2.5δ(n-2)+δ(n-3)③有限长序列线性卷积子程序用于完成两个给定长度的序列的卷积。

可以直接调用MATLAB语言中的卷积函数conv。

conv用于两个有限长度序列的卷积，它假定两个序列都从n=0 开始。

调用格式如下：y=conv (x, h)四、实验内容调通并运行实验程序，完成下述实验内容：①分析采样序列的特性。

a. 取采样频率fs=1 kHz, 即T=1 ms。

b. 改变采样频率，fs=300 Hz，观察|X(ejω)|的变化，并做记录(打印曲线)；进一步降低采样频率，fs=200 Hz，观察频谱混叠是否明显存在，说明原因，并记录(打印)这时的|X(ejω)|曲线。

②时域离散信号、系统和系统响应分析。

a. 观察信号xb(n)和系统hb(n)的时域和频域特性；利用线性卷积求信号xb(n)通过系统hb(n)的响应y(n)，比较所求响应y(n)和hb(n)的时域及频域特性，注意它们之间有无差别，绘图说明，并用所学理论解释所得结果。

数字信号处理第三版高西全实验数字信号处理第三版高西全实验》是一本旨在介绍数字信号处理的实际应用的教材。

本文档旨在概述该教材的目的和内容。

该教材的目的是通过实验教学的方式，帮助学生更好地理解数字信号处理的原理和技术，并将其应用到实际问题中。

它旨在培养学生的实践能力和解决问题的能力，使他们能够熟练地进行数字信号处理的实际操作。

该教材内容包括许多实验，涵盖了数字信号处理的各个方面。

每个实验都介绍了一个特定的概念或技术，并通过实际的操作和实验数据展示了其应用方式和效果。

学生通过完成实验，可以深入了解数字信号处理的各种算法和方法，研究如何使用相关工具和软件进行信号处理，以及如何分析和评估处理结果。

通过研究《数字信号处理第三版高西全实验》，学生将能够掌握数字信号处理的基本概念和技术，并能够独立地应用这些知识解决实际问题。

这将有助于他们在工程、通信、音视频处理等领域中的职业发展，也为进一步深入研究数字信号处理奠定了坚实的基础。

希望该教材能够对学生们的研究和实践有所帮助，使他们能够更好地理解和运用数字信号处理的方法和技术。

实验目标：本实验旨在介绍数字信号的采样和重构过程，并加深对这两个概念的理解。

实验目标：本实验旨在介绍数字信号的采样和重构过程，并加深对这两个概念的理解。

实验步骤：实验步骤：准备实验所需的信号发生器和示波器设备。

设置信号发生器，产生模拟信号，例如正弦波。

调整示波器参数，将模拟信号接入示波器进行显示。

使用采样器采样模拟信号，并记录采样得到的数字信号。

对采样得到的数字信号进行重构，恢复为原始模拟信号。

使用示波器将重构后的信号进行显示，并比较与原始信号的差异。

实验要点：了解采样和重构的基本概念和原理。

熟悉信号发生器和示波器的操作。

掌握采样器的使用方法。

理解数字信号与模拟信号的差异及其影响。

请参考实验指导书中的详细步骤和注意事项进行实验操作，并记录实验数据和结果。

本文档旨在解释《数字信号处理第三版高西全实验》中的实验二内容。

《数字信号处理》第三版，高西全、丁玉美，实验程序清单：实验0实验内容：1、实验用Matlab工具箱函数简介熟悉以下函数的功能、格式（1）abs （2）angle （3）conv （4）filter（5）freqz （6）impz （7）fft （8）ifft（9）plot （10）stem （11）subplot （12）figure2、常用序列的产生及其频谱分析（1）单位脉冲序列及其频谱n=0:50; %定义序列的长度是50x=[1,zeros(1,50)]; %注意：MATLAB中数组下标从1开始%x(1)=1;close all;subplot(3,1,1);stem(x);title('单位冲击信号序列');k=-25:25;X=x*(exp(-j*pi/25)).^(n'*k);magX=abs(X); %绘制x(n)的幅度谱subplot(3,1,2);stem(magX);title('单位冲击信号的幅度谱'); angX=angle(X); %绘制x(n)的相位谱subplot(3,1,3);stem(angX) ; title ('单位冲击信号的相位谱')（2）矩形序列及其频谱n=1:50x=sign(sign(10-n)+1);close all;subplot(3,1,1);stem(x);title(‘矩形序列’);k=-25:25;X=x*(exp(-j*pi/25)).^(n’*k);magX=abs(X); %绘制x(n)的幅度谱subplot(3,1,2);stem(magX);title(‘矩形序列的幅度谱’);angX=angle(X); %绘制x(n)的相位谱sub plot(3,1,3);stem(angX) ; title (‘矩形序列的相位谱’)(3)特定冲击串及其频谱%h2(n)= δ(n)+2.5δ(n-1)+2.5δ(n-2)+δ(n-3)n=1:50; %定义序列的长度是50x=zeros(1,50); %注意：MATLAB中数组下标从1开始x(1)=1;x(2)=2.5;x(3)=2.5;x(4)=1;close all;subplot(3,1,1);stem(x);title(‘特定冲击串’);k=-25:25;X=x*(exp(-j*pi/12.5)).^(n’*k);magX=abs(X); %绘制x(n)的幅度谱subplot(3,1,2);stem(magX);title(‘特定冲击串的幅度谱’);angX=angle(X); %绘制x(n)的相位谱subplot(3,1,3);stem(angX) ; title (‘特定冲击串的相位谱’)（4）采样信号序列及其频谱%x(n)=Ae-anT sin(w0nT)u(nT) （0<=n<=50）;%A=444.128;a=50*sqrt(2.0)*pi; fs=1kHz(T=0.001);w0=50*sqrt(2.0)*pi n=0:50; %定义序列的长度是50A=444.128; %设置信号有关的参数a=50*sqrt(2.0)*pi;T=0.001; %采样率，fs=1kHzw0=50*sqrt(2.0)*pi;x=A*exp(-a*n*T).*sin(w0*n*T); %pi是MATLAB定义的π，信号乘可采用“.*”close all %清除已经绘制的x(n)图形subplot(3,1,1);stem(x); %绘制x(n)的图形title(‘理想采样信号序列’);k=-25:25;W=(pi/12.5)*k;X=x*(exp(-j*pi/12.5)).^(n’*k);magX=abs(X); %绘制x(n)的幅度谱subplot(3,1,2);stem(magX);title(‘理想采样信号序列的幅度谱’);angX=angle(X); %绘制x(n)的相位谱subplot(3,1,3);stem(angX) ; title (‘理想采样信号序列的相位谱’)单位冲击信号的相位谱矩形序列的相位谱特定冲击串特定冲击串的幅度谱特定冲击串的相位谱理想采样信号序列理想采样信号序列的相位谱实验一 系统响应及系统稳定性%====内容1：调用filter解差分方程，由系统对u(n)的响应判断稳定性==== close all;clear allA=[1,-0.9];B=[0.05,0.05]; %系统差分方程系数向量B和Ax1n=[1 1 1 1 1 1 1 1 zeros(1,50)]; %产生信号x1(n)=R8(n)x2n=ones(1,128); %产生信号x2(n)=u(n)hn=impz(B,A,58); %求系统单位脉冲响应h(n)subplot(3,1,1);stem(hn);title('(a) 系统单位脉冲响应h(n)');y1n=filter(B,A,x1n); %求系统对x1(n)的响应y1(n)subplot(3,1,2);stem(y1n);title('(b) 系统对R8(n)的响应y1(n)');y2n=filter(B,A,x2n); %求系统对x2(n)的响应y2(n)subplot(3,1,3);%y='y2(n)';stem(y2n);title('(c) 系统对u(n)的响应y2(n)');box on%===内容2：调用conv函数计算卷积=====x1n=[1 1 1 1 1 1 1 1 ]; %产生信号x1(n)=R8(n)h1n=[ones(1,10) zeros(1,10)];h2n=[1 2.5 2.5 1 zeros(1,10)];y21n=conv(h1n,x1n);y22n=conv(h2n,x1n);figure(2)subplot(2,2,1);stem(h1n); %调用函数stem绘图title('(d) 系统单位脉冲响应h1(n)');box onsubplot(2,2,2);stem(y21n);title('(e) h1(n)与R8(n)的卷积y21(n)');box onsubplot(2,2,3);stem(h2n);title('(f) 系统单位脉冲响应h2(n)');subplot(2,2,4);stem(y22n);title('(g) h2(n)与R8(n)的卷积y22(n)');%====内容3：谐振器分析=======un=ones(1,256); %产生信号u(n)n=0:255;xsin=sin(0.014*n)+sin(0.4*n); %产生正弦信号A=[1,-1.8237,0.9801];B=[1/100.49,0,-1/100.49]; %系统差分方程系数向量B和A y31n=filter(B,A,un); %谐振器对u(n)的响应y31(n)y32n=filter(B,A,xsin); %谐振器对u(n)的响应y31(n)figure(3)subplot(2,1,1);stem(y31n);title('(h) 谐振器对u(n)的响应y31(n)'); subplot(2,1,2);stem(y32n);title('(i) 谐振器对正弦信号的响应y32(n)');(a) 系统单位脉冲响应h(n)(b) 系统对R8(n)的响应y1(n)(f) 系统单位脉冲响应h2(n)(g) h2(n)与R8(n)的卷积y22(n)(h) 谐振器对u(n)的响应y31(n)(i) 谐振器对正弦信号的响应y32(n)实验二时域采样与频域采样1时域采样理论的验证程序清单% 时域采样理论验证程序exp2a.mTp=64/1000; %观察时间Tp=64微秒%产生M长采样序列x(n)% Fs=1000;T=1/Fs;Fs=1000;T=1/Fs;M=Tp*Fs;n=0:M-1;A=444.128;alph=pi*50*2^0.5;omega=pi*50*2^0.5;xnt=A*exp(-alph*n*T).*sin(omega*n*T);Xk= fft(xnt,M); %M点FFT[xnt)]yn='xa(nT)';subplot(3,2,1);stem(xnt);title('(a) Fs=1000Hz');k=0:M-1;fk=k/Tp;subplot(3,2,2);plot(fk,abs(Xk));title('(b) FT[xa(nT)],Fs=1000Hz'); xlabel('f(Hz)');ylabel('幅度');axis([0,Fs,0,1.2*max(abs(Xk))])%================================% Fs=300Hz和Fs=200Hz的程序与上面Fs=1000Hz完全相同。

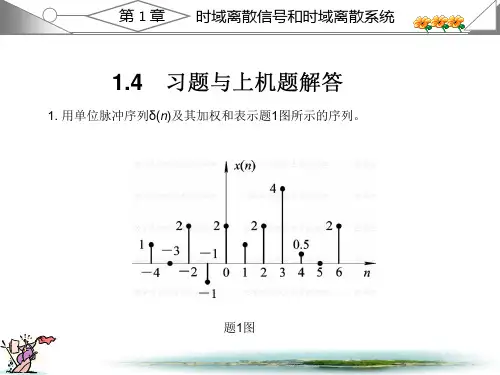
数字信号处理答案高西全第二版【篇一：数字信号处理上机答案(含程序及图片)第三版高西全著】数字信号处理实验一内容一a=0.8;ys=0;a=[1,-0.9];b=[0.05,0.05];xn=[1,zeros(1,50)];x1n=[1 1 1 1 1 1 1 1 zeros(1,50)];x2n=ones(1,128);xi=filtic(b,a,ys); hn=filter(b,a,xn,xi) n=0:length(hn)-1;subplot(2,2,1);stem(n,yn,.)title((a) 系统单位脉冲响应h(n)); xlabel(n);ylabel(hn);y1n=filter(b,a,x1n,xi); n=0:length(y1n)-1;subplot(2,2,2);y=y1(n); stem(n,y1n,.) title((b) 系统对r8(n)的响应y1(n)); xlabel(n);ylabel(yn);y2n=filter(b,a,x2n,xi); n=0:length(y2n)-1;subplot(2,2,4);y=y2(n); stem(n,y2n,.) title((c) 系统对u(n)的响应y2(n)); xlabel(n);ylabel(yn);(a) 系统单位脉冲响应h(n)n(b) 系统对r8(n)的响应y1(n)y1(n)h(n)n(c) 系统对u(n)的响应y2(n)y2(n)n内容二x1n=[1 1 1 1 1 1 1 1 ];h1n=[ones(1,10) zeros(1,10)]; h2n=[1 2.5 2.5 1 zeros(1,10)];y21n=conv(h1n,x1n); y22n=conv(h2n,x1n); m1=length(y21n)-1; m2=length(y22n)-1; n1=0:1:m1; n2=0:1:m2;n11=0:length(h1n)-1; n22=0:length(h2n)-1;subplot(2,2,1); tstem(n11,h1n); title((d) 系统单位脉冲响应h1(n)); xlabel(n);ylabel(h1(n));subplot(2,2,2); stem(n1,y21n,fill); title((e) h1(n)与r8(n)的卷积y21(n)); xlabel(n);ylabel(y21(n));subplot(2,2,3); tstem(n22,h2n); title((f) 系统单位脉冲响应h2(n)); xlabel(n);ylabel(h2(n));subplot(2,2,4); stem(n1,y22n,fill); title((g) h2(n)与r8(n)的卷积y22(n)); xlabel(n);ylabel(y22(n));(d) 系统单位脉冲响应h1(n)(e) h1(n)与r8(n)的卷积y21(n)y21(n)n(f) 系统单位脉冲响应h2(n)h1(n)n(g) h2(n)与r8(n)的卷积y22(n)y22(n)nh2(n)n内容三谐振器对u(n)的响应a=0.8;ys=0;xn=[1,zeros(1,250)];b=[1/100.49,-1/100.49];a=[1,-1.8237,0.9801]; xi=filtic(b,a,ys);yn=filter(b,a,xn,xi) n=0:length(yn)-1;subplot(1,1,1);stem(n,yn,.)谐振器对正弦信号的响应a=0.8;ys=0;xsin=sin(0.014*n)+sin(0.4*n);b=[1/100.49,-1/100.49];a=[1,-1.8237,0.9801]; xi=filtic(b,a,ys);yn=filter(b,a,xsin,xi) n=0:length(yn)-1;subplot(1,1,1);stem(n,yn,.)5010015020025050100150200250数字信号处理实验三实验（1）x1n=[ones(1,4)]; x1k8=fft(x1n,8); x1k16=fft(x1n,16); n=8;f=2/n*(0:n-1); figure(1);f=2/n*(0:n-1);xlabel(\omega/\pi);ylabel(|(e^j^\omega)|);【篇二：数字信号处理课后答案西安电子(高西全丁美玉第三版)】1.2 教材第一章习题解答1. 用单位脉冲序列?(n)及其加权和表示题1图所示的序列。

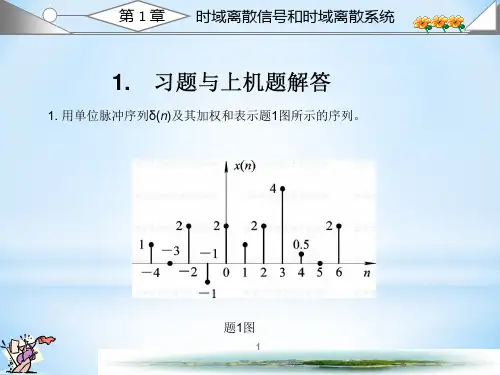
数字信号处理高西全版课后上机实验1. 实验一：系统响应及系统稳定性clcclearx1=[ones(1,8),zeros(1,20)];subplot(321)stem(x1,'.')title('u8(n)');xlabel('n');ylabel('u(n)');x2=ones(1,30);subplot(322)stem(x2,'.')title('u(n)');xlabel('n');ylabel('u(n)');B=[0.05,0.05];A=[1,-0.9];y1=filter(B,A,x1);subplot(323)stem(y1,'.')title('y(n)');xlabel('n');ylabel('y(n)');y2=filter(B,A,x2);subplot(324)stem(y2,'.')title('y(n)');xlabel('n');ylabel('y(n)');x3=[1,zeros(1,30)];subplot(325)stem(x3,'.')title('单位脉冲');xlabel('n');ylabel('u(n)');y3=filter(B,A,x3);subplot(326)stem(y3,'.')title('单位脉冲响应');xlabel('n');ylabel('y(n)');图1 实验(1)波形clcclearx1=[ones(1,8),zeros(1,20)];subplot(321)stem(x1,'.')title('u8(n)');xlabel('n');ylabel('u(n)');h1=[ones(1,10),zeros(1,20)];subplot(322)stem(h1,'.')title('h1(n)');xlabel('n');ylabel('h(n)');h2=[1,2.5,2.5,1,zeros(1,20)];subplot(323)stem(h2,'.')title('h2(n)');xlabel('n');ylabel('h(n)');y1=conv(x1,h1)subplot(324)stem(y1,'.')axis([0,30,0,10])title('y1(n)');xlabel('n');ylabel('y(n)');y2=conv(x1,h2)subplot(325)stem(y2,'.')axis([0,30,0,10])title('y2(n)');xlabel('n');ylabel('y(n)');图2 实验(2)波形clcclearclfx1=ones(1,50);subplot(221)stem(x1,'.')axis([0,50,0,1])title('u(n)');xlabel('n');ylabel('u(n)');A=[1,-1.8237,0.9801];B=[1/100.49,0,-1/100.49];y1=filter(B,A,x1);subplot(223)stem(y1,'.')axis([0,50,-0.05,0.05])title('y(n)');xlabel('n');ylabel('y(n)');n=0:100;x2=sin(0.014*n)+sin(0.4*n);subplot(222)stem(x2,'.')axis([0,100,-1,2])title('x(n)');xlabel('n');ylabel('x(n)');y2=filter(B,A,x2);subplot(224)stem(y2,'.')axis([0,100,-1,1])title('y(n)');xlabel('n');ylabel('y(n)');图3 实验(3)波形2. 实验二：时域采样与频域采样A=444.128;a=50*sqrt(2)*pi;w=50*sqrt(2)*pi;fs1=1000;N1=0.064*fs1;n=0:N1-1;xn1=A.*exp(-a*n/fs1).*sin(w*n/fs1).*(n>=0);subplot(321)stem(xn1,'.')axis([0,55,-10,150])title('x1(n) fs=1kHz');xlabel('n');ylabel('x1(n)');Xk1=fft(xn1,N1);f1=(0:N1-1)/0.064;subplot(322)plot(f1,abs(Xk1/fs1))title('T*FT[x(nT)], Fs=1000Hz');fs2=300;N2=floor(0.064*fs2);n=0:N2-1;xn2=A.*exp(-a*n/fs2).*sin(w*n/fs2).*(n>=0);subplot(323)stem(xn2,'.')axis([0,20,-10,150])title('x2(n)fs=300Hz');xlabel('n');ylabel('x2(n)');Xk2=fft(xn2,N2);f2=(0:N2-1)/0.064;subplot(324)plot(f2,abs(Xk2/fs2))title('T*FT[x(nT)], Fs=300Hz');fs3=200;N3=floor(0.064*fs3);n=0:N3-1;xn3=A.*exp(-a*n/fs3).*sin(w*n/fs3).*(n>=0);subplot(325)stem(xn3,'.')axis([0,15,-10,150])title('x3(n)fs=200Hz');xlabel('n');ylabel('x3(n)');Xk3=fft(xn3,N3)f3=(0:N3-1)/0.064;subplot(326)plot(f3,abs(Xk3/fs3))title('T*FT[x(nT)], Fs=200Hz');图1 实验(1)时域采样代码：n=0:26;xa=1:14;xb=13:-1:1;xn=[xa,xb]; Xk=fft(xn,512);k=0:2/512:2*(1-1/512); subplot(321)plot(k,abs(Xk))axis([0,1,0,200])title('FT[x(n)]')subplot(322)stem(n,xn,'.')title('三角波序列')X32k=fft(xn,32);x32n=ifft(X32k);X16k=X32k(1:2:32);x16n=ifft(X16k,16);k=0:15;subplot(323)stem(k,abs(X16k),'.')title('16点频域采样')axis([0,10,0,200])subplot(324)stem(k,x16n,'.')title('16点IDFT[X16k]')axis([0,30,0,15])k1=0:31;subplot(325)stem(k1,abs(X32k),'.')title('32点频域采样')axis([0,10,0,200])subplot(326)stem(k1,x32n,'.')title('32点IDFT[X32k]')axis([0,30,0,15])运行结果：图2 实验(2)频域采样3. 实验三：用FFT对信号作频谱分析代码：clcclearn1=0:30;x1=[1,1,1,1,zeros(1,27)];n2=0:27;x2=[1:4,4:-1:1,zeros(1,20)];x3=[4:-1:1,1:4,zeros(1,20)];subplot(331)stem(n1,x1,'.')axis([0,10,0,1])title('x1(n)');xlabel('n');ylabel('x1(n)')subplot(332)stem(n2,x2,'.')axis([0,10,0,4])title('x2(n)');xlabel('n');ylabel('x2(n)')subplot(333)stem(n2,x3,'.')axis([0,10,0,4])title('x3(n)');xlabel('n');ylabel('x3(n)')k1=0:1/4:7/4;k2=0:1/8:15/8;X8k1=fft(x1,8);subplot(334)stem(k1,abs(X8k1),'.')title('8点FFT变换')X16k1=fft(x1,16);subplot(337)stem(k2,abs(X16k1),'.')title('16点FFT变换')X8k2=fft(x2,8);subplot(335)stem(k1,abs(X8k2),'.')title('8点FFT变换')X16k2=fft(x2,16);subplot(338)stem(k2,abs(X16k2),'.')title('16点FFT变换')X8k3=fft(x3,8);subplot(336)stem(k1,abs(X8k3),'.')title('8点FFT变换')X16k3=fft(x3,16);subplot(339)stem(k2,abs(X16k3),'.')title('16点FFT变换')运行结果：图1 实验(1)图形代码：clcclearn=0:30;x4=cos(pi/4*n);x5=cos(pi/4*n)+cos(pi/8*n);subplot(321)stem(n,x4,'.')axis([0,30,-1,1])title('x4(n)=cos(pi/4*n)');xlabel('n');ylabel('x4(n)')subplot(322)stem(n,x5,'.')axis([0,30,-2,2])title('x5(n)=cos(pi/4*n+pi/8*n)');xlabel('n');ylabel('x5(n)')k1=0:1/4:7/4;k2=0:1/8:15/8;X8k1=fft(x4,8);subplot(323)stem(k1,abs(X8k1),'.')axis([0,2,0,5])title('8点FFT变换')X16k1=fft(x4,16);subplot(325)stem(k2,abs(X16k1),'.')axis([0,2,0,8])title('16点FFT变换')X8k2=fft(x5,8);subplot(324)stem(k1,abs(X8k2),'.')axis([0,2,0,10])title('8点FFT变换')X16k2=fft(x5,16);subplot(326)stem(k2,abs(X16k2),'.')axis([0,2,0,10])title('16点FFT变换')图2 实验(2)图形clcclearn=1:100;Fs=64;x6=cos(8*pi*n/Fs)+cos(16*pi*n/Fs)+cos(20*pi*n/Fs); N1=16;F1=Fs/N1;k1=-N1/2:N1/2-1;fk1=F1*k1;X16k=fft(x6,16);X16k1=fftshift(X16k)subplot(311)stem(fk1,abs(X16k1),'.')axis([-30,30,0,10])title('变换区间N=16')N2=32;F2=Fs/N2;k2=-N2/2:N2/2-1;fk2=F2*k2;X32k=fft(x6,32);X32k1=fftshift(X32k)subplot(312)stem(fk2,abs(X32k1),'.')axis([-30,30,0,20])title('变换区间N=32')N3=64;F3=Fs/N3;k3=-N3/2:N3/2-1;fk3=F3*k3;X64k=fft(x6,64);X64k1=fftshift(X64k)subplot(313)stem(fk3,abs(X64k1),'.')axis([-30,30,0,40])title('变换区间N=64')图3 实验(3)图形4. 实验四：IIR数字滤波器设计及软件实现function st=mstgN=800;Fs=10000;T=1/Fs;Tp=N*T;t=0:T:(N-1)*T;k=0:N-1;f=k/Tp;fc1=Fs/10;fm1=fc1/10;fc2=Fs/20;fm2=fc2/10;fc3=Fs/40;fm3=fc3/10;xt1=cos(2*pi*fm1*t).*cos(2*pi*fc1*t);xt2=cos(2*pi*fm2*t).*cos(2*pi*fc2*t);xt3=cos(2*pi*fm3*t).*cos(2*pi*fc3*t);st=xt1+xt2+xt3;fxt=fft(st,N);subplot(211)plot(t,st);grid;xlabel('t/s');ylabel('s(t)')axis([0,Tp/8,min(st),max(st)]);title('(a) s(t)的波形')subplot(212)stem(f,abs(fxt)/max(abs(fxt)),'.');grid;title('(b) s(t)的频谱');axis([0,2000,0,1]);end图1 信号产生函数图形%低通N=800;Fs=10000;T=1/Fs;Tp=N*T;t=0:T:(N-1)*T;k=0:N-1;f=k/Tp;fp=280;fs=450;wp=2*fp/Fs;ws=2*fs/Fs;rp=0.1;rs=60;[N,wpo]=ellipord(wp,ws,rp,rs)[B,A]=ellip(N,rp,rs,wpo)[H,W]=freqz(B,A,1000)st=mstg;y1=filter(B,A,st)figure(2)subplot(312)plot(t,y1)title('时域波形')axis([0,Tp,min(y1),max(y1)])subplot(311)plot(W/pi,20*log10(abs(H)/max(abs(H))))title('低通滤波器损耗函数')axis([0,1,-80,10])subplot(313)Y1=fft(y1)stem(f,abs(Y1)/max(abs(Y1)),'.')axis([0,Fs/5,0,1.5])title('幅频特性曲线')%带通N=800Fs=10000;T=1/Fs;Tp=N*T;t=0:T:(N-1)*T;k=0:N-1;f=k/Tp;fp1=440;fpu=560;fs1=275;fsu=900wp=[2*fp1/Fs,2*fpu/Fs];ws=[2*fs1/Fs,2*fsu/Fs];rp=0.1;rs=60;[N,wpo]=ellipord(wp,ws,rp,rs)[B,A]=ellip(N,rp,rs,wpo)[H,W]=freqz(B,A,1000)st=mstg;y1=filter(B,A,st)figure(3)subplot(312)plot(t,y1)title('时域波形')axis([0,Tp,min(y1),max(y1)])subplot(311)plot(W/pi,20*log10(abs(H)/max(abs(H)))) title('带通滤波器损耗函数')axis([0,1,-80,10])subplot(313)Y1=fft(y1)stem(f,abs(Y1)/max(abs(Y1)),'.')axis([0,Fs/5,0,1.5])title('幅频特性曲线')%高通N=800;Fs=10000;T=1/Fs;Tp=N*T;t=0:T:(N-1)*T;k=0:N-1;f=k/Tp;fp=890;fs=600;wp=2*fp/Fs;ws=2*fs/Fs;rp=0.1;rs=60;[N,wpo]=ellipord(wp,ws,rp,rs)[B,A]=ellip(N,rp,rs,wpo,'high')[H,W]=freqz(B,A,1000)y1=filter(B,A,st)figure(4)subplot(311)plot(W/pi,20*log10(abs(H)/max(abs(H))))title('高通滤波器损耗函数')axis([0,1,-80,10])subplot(312)plot(t,y1);title('时域波形')axis([0,Tp,min(y1),max(y1)])subplot(313)Y1=fft(y1)stem(f,abs(Y1)/max(abs(Y1)),'.')axis([0,Fs/5,0,1.5]);title('幅频特性曲线')图2 低通图形图3 带通图形图4 高通图形5. 实验五：FIR数字滤波器设计及软件实现function xt=xtgN=1000;Fs=1000;T=1/Fs;Tp=N*T;t=0:T:(N-1)*T;fc=Fs/10;f0=fc/10;mt=cos(2*pi*f0*t);ct=cos(2*pi*fc*t);xt=mt.*ct;nt=2*rand(1,N)-1;fp=150;fs=200;Rp=0.1;As=70;fb=[fp,fs];m=[0,1];dev=[10^(-As/20),(10^(Rp/20)-1)/(10^(Rp/20)+1)];[n,fo,mo,W]=remezord(fb,m,dev,Fs);hn=remez(n,fo,mo,W);yt=filter(hn,1,10*nt);xt=xt+yt;fst=fft(xt,N);k=0:N-1;f=k/Tp;subplot(211)plot(t,xt);grid;xlabel('t/s');ylabel('x(t)');axis([0,Tp/5,min(xt),max(xt)]);title('(a) 信号加噪声波形') subplot(212)plot(f,abs(fst)/max(abs(fst)));grid;xlabel('f/Hz');ylabel('幅度'); axis([0,Fs/2,0,1.2]);title('(b) 信号加噪声的频谱')end%设计低通滤波器并滤除噪声Fs=1000;N=1000;wp=0.24*pi;ws=0.3*pi;fs=150;fp=120;Wc=(wp+ws)/(2*pi);B=2*pi*(fs-fp)/Fs;Nb=ceil(11*pi/B);hn=fir1(Nb-1,Wc,blackman(Nb));Hw=abs(fft(hn,N))xt=xtg;y=fftfilt(hn,xt,N)f=(0:N-1)*Fs/N;figure(2)subplot(211)plot(f,20*log10(Hw/max(Hw)));title('低通滤波器幅频特性') xlabel('f/Hz');ylabel('幅度');axis([0,Fs/2,-120,10]);subplot(212)plot(f/2000,y);title('滤除噪声后的信号波形')xlabel('t/s');ylabel('yw(t)');图1 信号及其频谱图2 低通滤波器滤除噪声。

数字信号处理课后答案 高西全、丁美玉版1.2 教材第一章习题解答1. 用单位脉冲序列()n δ及其加权和表示题1图所示的序列。

解：()(4)2(2)(1)2()(1)2(2)4(3) 0.5(4)2(6)x n n n n n n n n n n δδδδδδδδδ=+++-+++-+-+-+-+-2. 给定信号：25,41()6,040,n n x n n +-≤≤-⎧⎪=≤≤⎨⎪⎩其它（1）画出()x n 序列的波形，标上各序列的值；（2）试用延迟单位脉冲序列及其加权和表示()x n 序列； （3）令1()2(2)x n x n =-，试画出1()x n 波形； （4）令2()2(2)x n x n =+，试画出2()x n 波形； （5）令3()2(2)x n x n =-，试画出3()x n 波形。

解：（1）x(n)的波形如题2解图（一）所示。

（2）()3(4)(3)(2)3(1)6() 6(1)6(2)6(3)6(4)x n n n n n n n n n n δδδδδδδδδ=-+-+++++++-+-+-+-（3）1()x n 的波形是x(n)的波形右移2位，在乘以2，画出图形如题2解图（二）所示。

（4）2()x n 的波形是x(n)的波形左移2位，在乘以2，画出图形如题2解图（三）所示。

（5）画3()x n 时，先画x(-n)的波形，然后再右移2位，3()x n 波形如题2解图（四）所示。

3. 判断下面的序列是否是周期的，若是周期的，确定其周期。

（1）3()cos()78x n A n ππ=-，A 是常数；（2）1()8()j n x n e π-=。

解：（1）3214,73w w ππ==，这是有理数，因此是周期序列，周期是T=14； （2）12,168w wππ==，这是无理数，因此是非周期序列。

5. 设系统分别用下面的差分方程描述，()x n 与()y n 分别表示系统输入和输出，判断系统是否是线性非时变的。

《数字信号处理》实验报告实验三：用FFT对信号作频谱分析专业网络工程班级 3班学号******xxxx学生姓名 dean任课教师曾蓉辅导教师2018年 4 月 19 日一、实验目的学习用FFT 对连续信号和时域离散信号进行谱分析的方法，了解可能出现的分析误差及其原因，以便正确应用FFT 。

二、实验原理用FFT 对信号作频谱分析是学习数字信号处理的重要内容。

经常需要进行谱分析的信号是模拟信号和时域离散信号。

对信号进行谱分析的重要问题是频谱分辨率D 和分析误差。

频谱分辨率直接和FFT 的变换区间N 有关，因为FFT 能够实现的频率分辨率是 ，因此要求 。

可以根据此式选择FFT 的变换区间N 。

误差主要来自于用FFT 作频谱分析时，得到的是离散谱，而信号（周期信号除外）是连续谱，只有当N 较大时离散谱的包络才能逼近于连续谱，因此N 要适当选择大一些。

周期信号的频谱是离散谱，只有用整数倍周期的长度作FFT ，得到的离散谱才能代表周期信号的频谱。

如果不知道信号周期，可以尽量选择信号的观察时间长一些。

对模拟信号进行谱分析时，首先要按照采样定理将其变成时域离散信号。

如果是模拟周期信号，也应该选取整数倍周期的长度，经过采样后形成周期序列，按照周期序列的谱分析进行。

三、实验内容1）对以下序列进行谱分析。

1423()()1,03()8,470,4,03()3,470,x n R n n n x n n n n n n x n n n n =+≤≤⎧⎪=-≤≤⎨⎪⎩-≤≤⎧⎪=-≤≤⎨⎪⎩其他其他选择FFT 的变换区间N 为8和16 两种情况进行频谱分析。

分别打印其幅频特性曲线。

并进行对比、分析和讨论。

（2）对以下周期序列进行谱分析。

4()cos 4x n nπ=5()cos(/4)cos(/8)x n n n ππ=+选择FFT 的变换区间N 为8和16 两种情况分别对以上序列进行频谱分析。

分别打印其幅频特性曲线。