选 择 排 序 算 法 原 理

完整版)☆排列组合解题技巧归纳总结分类计数原理(加法原理)指完成一件事，有n类办法，在第1类办法中有m1种不同的方法，在第2类办法中有m2种不同的方法。

在第n类办法中有mn种不同的方法，那么完成这件事共有N=m1+m2+。

+mn种不同的方法。

分步计数原理（乘法原理）指完成一件事，需要分成n个步骤，做第1步有m1种不同的方法，做第2步有m2种不同的方法。

做第n步有mn种不同的方法，那么完成这件事共有N=m1×m2×。

×mn种不同的方法。

分类计数原理和分步计数原理的区别在于，分类计数原理方法相互独立，任何一种方法都可以独立地完成这件事；分步计数原理各步相互依存，每步中的方法完成事件的一个阶段，不能完成整个事件。

解决排列组合综合性问题的一般过程如下：1.认真审题弄清要做什么事。

2.确定采取分步还是分类，或是分步与分类同时进行，确定分多少步及多少类。

3.确定每一步或每一类是排列问题(有序)还是组合(无序)问题，元素总数是多少及取出多少个元素。

4.解决排列组合综合性问题，往往类与步交叉，因此必须掌握一些常用的解题策略。

一种常用的解题策略是特殊元素和特殊位置优先策略。

例如，由0,1,2,3,4,5可以组成多少个没有重复数字五位奇数，可以先排末位共有C3^1种方法，然后排首位共有C4^3种方法，最后排其它位置共有A4^1 * 3!种方法，根据分步计数原理得到共有C4^1 * 3^1 * A4^1 * 3.= 288种不同的方法。

另一种常用的解题策略是相邻元素捆绑策略。

例如，7人站成一排，其中甲乙相邻且丙丁相邻，共有多少种不同的排法，可以先将甲乙两元素捆绑成整体并看成一个复合元素，同时丙丁也看成一个复合元素，再与其它元素进行排列，同时对相邻元素内部进行自排。

由分步计数原理可得共有A5^2 * A2^2 = 480种不同的方法。

还有一种常用的解题策略是不相邻问题插空策略。

例如，一个晚会的节目有4个舞蹈、2个相声、3个独唱，舞蹈节目不能连续出场，则节目的出场顺序有多少种，可以先将三种不同的节目分别排列，然后在舞蹈节目之间插入一个相声节目，再在相声节目之间插入一个独唱节目，根据分步计数原理可得共有A4^4 * A2^1 * A3^1 = 种不同的方法。

主要辅助手段：多媒体
作业布置
10-4(2),(4),(5),10-6,
主 要 参考资料
1．《数据结构》，严蔚敏 吴伟民，清华大学出版社；2.数据结构题集（C语言版），
严蔚敏 吴伟民，清华大学出版社；
备注
重点难点
希尔的思想，实现，算法分析
要求掌握知识点和
分析方法
1.概念：排序，主（次）关键字，内部（外部）排序，比较排序算法的技术指标2。插入排序的基本思想；3。直接直接插入排序和希尔的思想，实现，算法分析。
教授思路，采 用 的 教学方法和辅助手段，板书设计，重 点 如 何突出，难点如何解决，师 生 互 动等
难点：堆的调整辅助手段：多媒体
作业布置
10-7,10-8
主 要 参考资料
1．《数据结构》，严蔚敏 吴伟民，清华大学出版社；2.数据结构题集（C语言版），
严蔚敏 吴伟民，清华大学出版社；
备注
章节
10.5归并排序10.6基数排序
讲授主要内容
归并排序 ，基数排序
重点难点
归并排序 ，基数排序的基本思想与算法实现
本章思考题和习题
主 要 参考资料
1．《数据结构》，严蔚敏 吴伟民，清华大学出版社；2.数据结构题集（C语言版），
严蔚敏 吴伟民，清华大学出版社；
备注
章节
10.1概念10.2插入排序
讲授主要内容
1．概念：排序，主（次）关键字，内部（外部）排序，比较排序算法的技术指标2.
插入排序的基本思想；3。直接直接插入排序和希尔的思想，实现，算法分析。
教授思路，采 用 的 教学方法和辅助手段， 板书设计，重 点 如 何突出，难点如何解决，师 生 互 动等
教学思路：

共比较数据2次，交换数据1次。 第3遍：寻找从d(3)到d(4)范围内的最小数据d(k)，即k＝4，将d(3)与d(k)互换数据：
总共比较数据1次，交换数据1次。
显然，通过上述3遍处理，数组d中最小、第2 小、第3小的数据已经分别存储在数组元素d(1)、 d(2)、d(3)中，即数组元素d(1)到d(3)变为有序， 而剩下的d(4)中的数据自然是数组中的最大数据 。因此，通过3遍这样的处理，整个数组内的数据 将是有序的。
第3遍
第4遍
60 58 55 48 43 46
第5遍
60 58 55 48 46 43
A.60、58、48、46、43、55 C.60、58、55、46、43、48
B.60、43、48、46、58、55 D.60、58、55、48、46、43
5. 已知算法1与算法2都是排序算法，可能是冒泡排序或者选择排
1
7
2
9
3
13
4
18
5
55
6
43
7
43
第五趟：从3个元素中选出最小者，将其换入位置5，过程 为：令min_elem表示最小元素（初值为位置5的元素），k 为最小元素的位置序号（初值为5），逐一比较，找出最 小元素及其位置
1
7
2
9
3
13
4
18
5
55
6
43
7
43
位置6的元素最小 交换
1
7
2
9
3
13
4
4个元素共需进行3遍加工处理，总的比较次 数为3＋2＋1＝6次，而总计交换次数每一遍一次 ，共计只有3次。
对于n个元素的数组，用选择算法进行排序时 ，比较次数与冒泡算法相同，但交换的次数比冒 泡排序要少，因此它具有较高的效率。

排列组合的基本原理尊敬的读者：在数学中，排列组合是一种重要的概念，它用于计算可能性和确定事件发生的方式。

本文将介绍排列组合的基本原理，包括排列和组合的定义、计算方法以及应用。

希望通过本文的阐述，您能够更好地理解和运用排列组合的基本原理。

1. 排列的定义和计算方法在数学中，排列指的是从一个集合中选取若干个元素，按照一定顺序排列的方式。

排列通常用P(n,m)表示，其中n为集合的元素个数，m 为选取的元素个数。

排列的计算方法可分为两种情况：1.1 当选取的元素个数m小于或等于集合的元素个数n时，排列的计算公式为：P(n,m) = n! / (n-m)!1.2 当选取的元素个数m大于集合的元素个数n时，排列的计算公式为0，即不存在这种情况。

2. 组合的定义和计算方法组合指的是从一个集合中选取若干个元素，不考虑顺序的方式。

组合通常用C(n,m)表示，其计算方法可分为两种情况：2.1 当选取的元素个数m小于或等于集合的元素个数n时，组合的计算公式为：C(n,m) = n! / (m! * (n-m)!)2.2 当选取的元素个数m大于集合的元素个数n时，组合的计算公式为0，即不存在这种情况。

3. 排列组合的应用排列组合在实际问题中的应用非常广泛，下面举几个例子来说明：3.1 生日排列问题：假设有5个人，每个人的生日在一年中任意选择。

我们可以用排列来计算不考虑年份的情况下，5个人生日的所有可能排列数量。

根据排列的计算公式，可知P(365,5)即为所求。

3.2 钥匙排列问题：某人有5把钥匙，但只有其中一把能打开家门。

每次进门都尝试一把钥匙，直到能够打开为止。

这个过程中，我们可以用排列来计算需要尝试的所有可能方式的数量。

根据排列的计算公式，可知P(5,5)即为所求。

3.3 选课组合问题：某学校的学生需要选择4门选修课，而学校提供了8门选修课供选择。

我们可以用组合来计算学生选择的所有可能组合的数量。

根据组合的计算公式，可知C(8,4)即为所求。

有序和无序排列组合公式好的，以下是为您生成的关于“有序和无序排列组合公式”的文章：咱先来说说啥是有序和无序排列组合公式哈。

打个比方，你去超市买水果，苹果、香蕉、橙子摆在那，你要是规定了先拿苹果再拿香蕉最后拿橙子，这就是有序；要是不管顺序，随便拿，这就是无序。

咱先瞅瞅有序排列，也就是排列公式。

比如说从 5 个不同的东西里选 3 个，按照一定顺序排好，这就可以用排列公式 A(5, 3) 来算。

就像学校组织活动，选 3 个同学分别当主持人、表演节目和后勤服务，这就得考虑顺序，谁先谁后作用可不一样。

再讲讲无序组合，也就是组合公式。

还是那 5 个东西，这次不考虑顺序，只要选出 3 个就行，那就用组合公式 C(5, 3) 。

比如说选 3 个人参加知识竞赛，不管谁在前谁在后，只要选出来就行。

我记得之前给学生讲这个的时候，有个小同学特别可爱。

他瞪着大眼睛问我：“老师，这和我搭积木有啥关系？”我笑着跟他说：“你搭积木的时候，要是规定了先放红色的再放蓝色的，这就是有序；要是随便拿随便放，不讲究顺序，那就是无序呀。

”这小家伙一听，好像恍然大悟了。

在生活中，有序和无序排列组合公式的应用可多了去了。

比如你安排假期出去玩，有 5 个景点，你计划 3 天逛完，每天去一个，这就得用有序排列来算算有多少种安排方法。

要是你只是想挑 3 个景点去，不管先后顺序，那就是无序组合的问题啦。

还有啊，咱过年包饺子，准备了 3 种馅，韭菜鸡蛋、猪肉大葱和虾仁三鲜。

要是规定了第一顿吃韭菜鸡蛋的，第二顿吃猪肉大葱的，第三顿吃虾仁三鲜的，这就是有序；要是不管顺序，反正这三顿就吃这三种馅，这就是无序组合。

再比如说抽奖，从 10 个号码里抽 3 个中奖号码，这就不管顺序，是无序组合。

但要是颁奖，先颁三等奖，再颁二等奖，最后颁一等奖，这就得考虑顺序，是有序排列。

所以说，这有序和无序排列组合公式啊，就藏在咱们生活的角角落落里，等着咱们去发现，去用它们解决问题。

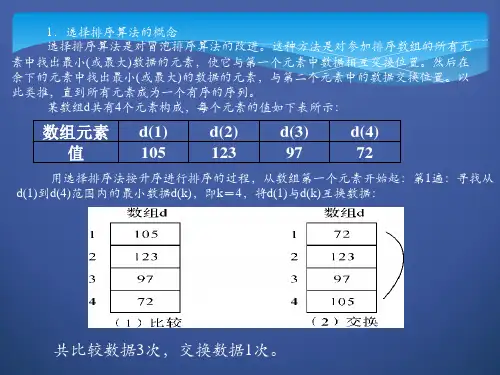
选择排序法的基本思路
选择排序法是一种简单直观的排序算法，基本思路如下：
1. 首先，在序列中找到最小（或最大）的元素，将其放在序列的起始位置。

2. 然后，从剩余的未排序序列中继续寻找最小（或最大）的元素，将其放在已排序序列的末尾。

3. 重复上述步骤，直到所有元素都排好序。

具体步骤如下：
1. 设定一个初始索引为0的位置，表示已排序序列的末尾。

2. 从剩余的未排序序列中，遍历查找最小元素的索引。

将该最小元素与已排序序列的末尾元素交换位置，并更新已排序序列的末尾索引。

3. 重复上述步骤，直到遍历完整个序列。

选择排序的特点是每次只需要找到剩余序列中的最小元素，并进行交换，因此时间复杂度为O(n^2)。

虽然效率较低，但对于小规模的序列来说，它的实现简单且不占用额外的内存空间。

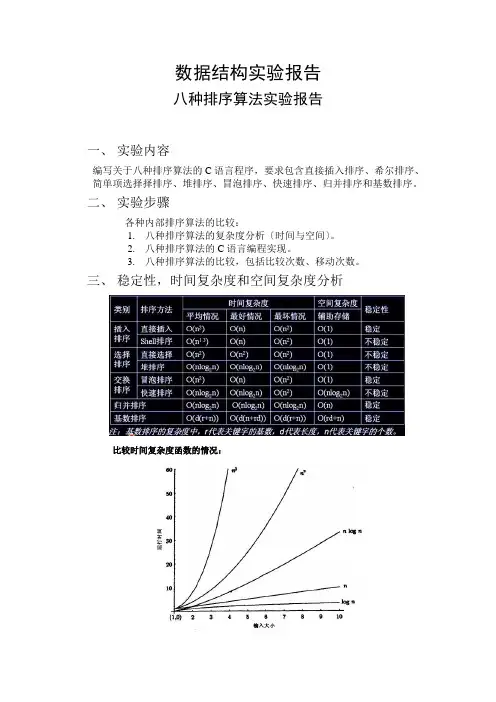
数据结构实验报告八种排序算法实验报告一、实验内容编写关于八种排序算法的C语言程序，要求包含直接插入排序、希尔排序、简单项选择择排序、堆排序、冒泡排序、快速排序、归并排序和基数排序。

二、实验步骤各种内部排序算法的比较：1.八种排序算法的复杂度分析〔时间与空间〕。

2.八种排序算法的C语言编程实现。

3.八种排序算法的比较，包括比较次数、移动次数。

三、稳定性，时间复杂度和空间复杂度分析比较时间复杂度函数的情况：时间复杂度函数O(n)的增长情况所以对n较大的排序记录。

一般的选择都是时间复杂度为O(nlog2n)的排序方法。

时间复杂度来说：(1)平方阶(O(n2))排序各类简单排序:直接插入、直接选择和冒泡排序；(2)线性对数阶(O(nlog2n))排序快速排序、堆排序和归并排序；(3)O(n1+§))排序,§是介于0和1之间的常数。

希尔排序(4)线性阶(O(n))排序基数排序，此外还有桶、箱排序。

说明：当原表有序或基本有序时，直接插入排序和冒泡排序将大大减少比较次数和移动记录的次数，时间复杂度可降至O〔n〕；而快速排序则相反，当原表基本有序时，将蜕化为冒泡排序，时间复杂度提高为O〔n2〕；原表是否有序，对简单项选择择排序、堆排序、归并排序和基数排序的时间复杂度影响不大。

稳定性：排序算法的稳定性:假设待排序的序列中，存在多个具有相同关键字的记录，经过排序，这些记录的相对次序保持不变，则称该算法是稳定的；假设经排序后，记录的相对次序发生了改变，则称该算法是不稳定的。

稳定性的好处：排序算法如果是稳定的，那么从一个键上排序，然后再从另一个键上排序，第一个键排序的结果可以为第二个键排序所用。

基数排序就是这样，先按低位排序，逐次按高位排序，低位相同的元素其顺序再高位也相同时是不会改变的。

另外，如果排序算法稳定，可以防止多余的比较；稳定的排序算法：冒泡排序、插入排序、归并排序和基数排序不是稳定的排序算法：选择排序、快速排序、希尔排序、堆排序四、设计细节排序有内部排序和外部排序，内部排序是数据记录在内存中进行排序，而外部排序是因排序的数据很大，一次不能容纳全部的排序记录，在排序过程中需要访问外存。

a[0]
9 6 17 2 12
9
9
9 6 17
9 6
k
a[1]
2
k
a[2]
j k
6 17 2 12
k 6
j k
17 2 12
第一轮，i=0; k=i; for(j=i+1;j<5;j++) if(a[k]>a[j]) k=j; if(k!=j) {t=a[k];a[k]=a[i];a[i]=t;}
17 9 12
ቤተ መጻሕፍቲ ባይዱ
17 9
17 9 12
a[3]
{t=a[k];a[k]=a[i];a[i]=t;} 第四轮 I=3;k=I;
j
12 12
for(j=i+1;j<5;j++) if(a[k]>a[j])k=j;
a[4]
j
if(k!=i)
{t=a[k];a[k]=a[i];a[i]=t;}
i从0变到3 for(i=0;i<4;i++) 第i轮 k=I;认为第I个数最小， 从下一个数到最后一个数与 a[k]比较， If(a[k]>a[j]) k=j;k就赋值小数 的下标 If(k!=i) {t=a[k];a[k]=a[i];a[i]=t;}既a[k] 与第I个位置上的数交换位 置。
选择法排序(以5个数为例) 基本思路：
第一轮i=0：认为第一个数a[0]最小，把它的下标赋值给k,k=i;(k=0;) 从下一个数(a[1])到最后一个数a[4]与a[k]比较，如果a[k]大于哪个 数，k就赋值哪个数的下标，一轮结束后，k放最小数的下标，则a[k]与 a[0]交换位置。 第二轮i=1;k=i;认为a[1]最小，下标赋给k,将a[k]从下一个数（a[2]） 开始到最后一个数(a[4])比较，找到最小数，把它的下标赋给k，然后 a[k]与a[1]交换位置。 ……5个数比4轮，第i轮认为第i个位置上的数最小（k=i），将a[k]从 下一个数a[i+1]开始到最后一个数一一比较。找出最小数，把下标赋给 k,将a[k]与第i个位置上的数a[i]交换。

１1１1．有.有如如下递归归代代码码 ｓsｏoｌlｖvｅe（(ｔt，, ｎn)）:：
ｉiｆf ｔt＝=１1 ｒrｅeｔtuｕrｒnｎ1１
ｅeｌlｓsｅe ｒrｅeｔtｕurｒnｎ 5５＊* ｓsｏoｌlｖveｅ(ቤተ መጻሕፍቲ ባይዱtｔ-－1ｌ,，nｎ)）ｍmｏodｄ nｎ 则则 ｓsｏoｌｖlｅv（e(２2３3，,２2３3）) 的的结结果果为为（（ ））。。
比比如如 ｉｎiｔn t数数组组【[１1，,1１，,1１,6，,６4，]中４】a中[0 ]ａ,【a[０1】],，a[ａ2【]的１】值，相ａ【等２】，的在值排相序等，时在不排改序变时不其改序变列其，序则列，称则所称用所用的的方方法法
是是稳稳定定的的．.（(插插入入排排序序、、冒冒泡泡排排序序、、二二叉叉树树排排序序、二路归并排序及其他线形排序是稳定的的；;选 择择排排序序、、希希尔尔排排序序、、快快速速排排序序、、堆堆排排序序是是不不稳稳定定的的））．.
ＢB．.系系统统分分配配的的队队列列空空间间溢出
ＣC．系. 系统统分分配配的的链链表表空空间间溢出
ＤD．系. 系统统分分配配的的堆堆空空间间溢溢出
【解析】递归需要使使用用到到系系统统堆堆栈栈空空间间，，如如果果递递归归层层数数过过多多，，导导致致系系统统堆堆栈栈空空间间不不足足。。
４4．以.以下下排排序序方方法法中中，，（（））是是不不稳稳定定的的。。
ＡA１. 1 Ｂ．B.７7Ｃ．C１. ２12 Ｄ．D.２2２2
【解析】程程序序的的运运行行结结果果为为5５２22２mｍｏoｄd ２2３3，，根据费马小定理：∶如如果果是是素素数数，，aａ是是一一
个个整整数数，，那那么么 aａＰp-１1≡＝１1 mｍｏoｄd pｐ，，可可以以得得 5５2２2２mｍｏoｄd 2２３3＝≡１1ｍmｏｄo d２2３3，,结结果果为为1１

数据构造试卷〔一〕三、计算题〔每题6 分，共24分〕1.在如下数组A中链接存储了一个线性表，表头指针为A [0].next，试写出该线性表。

A 0 1 2 3 4 5 6 7data 60 50 78 90 34 40next 3 5 7 2 0 4 12.请画出以下列图的邻接矩阵和邻接表。

3.一个图的顶点集V和边集E分别为：V={1,2,3,4,5,6,7};E={(1,2)3,(1,3)5,(1,4)8,(2,5)10,(2,3)6,(3,4)15,(3,5)12,(3,6)9,(4,6)4,(4,7)20,(5,6)18,(6,7)25};用克鲁斯卡尔算法得到最小生成树，试写出在最小生成树中依次得到的各条边。

4.画出向小根堆中参加数据4, 2, 5, 8, 3时，每参加一个数据后堆的变化。

四、阅读算法〔每题7分，共14分〕1.LinkList mynote(LinkList L){//L是不带头结点的单链表的头指针if(L&&L->next){q=L；L=L－>next；p=L；S1：while(p－>next) p=p－>next；S2：p－>next=q；q－>next=NULL；}return L；}请答复以下问题：〔1〕说明语句S1的功能；〔2〕说明语句组S2的功能；〔3〕设链表表示的线性表为〔a1,a2, …,a n〕,写出算法执行后的返回值所表示的线性表。

2.void ABC(BTNode * BT){if BT {ABC (BT->left);ABC (BT->right);cout<<BT->data<<' ';}}该算法的功能是：五、算法填空〔共8分〕二叉搜索树的查找——递归算法:bool Find(BTreeNode* BST,ElemType& item){if (BST==NULL)return false; //查找失败else {if (item==BST->data){item=BST->data;//查找成功return ___________;}else if(item<BST->data)return Find(______________,item);else return Find(_______________,item);}//if}六、编写算法〔共8分〕统计出单链表HL中结点的值等于给定值X的结点数。

则甲、乙两人不都入选的不同选法种数共有（ D）
A
.C
2 5
A33
B.2C
3 5
A33
C
.A
3 5
D.2C52A33 A53
课堂练习：
5、在如图7x4的方格纸上（每小方格均为正方形） （1）其中有多少个矩形？ （2）其中有多少个正方形？
小结
排列
组合 联系
组合是选择的 结果，排列是 选择后再排序 的结果
方 法 二 ： C 1 5 2 C 3 0 C 9 56 6 6
例5、某医院有内科医生12名，外科医生8名，现要 派5人参加支边医疗队，至少要有1名内科医生和1名 外科医生参加，有多少种选法？
例6：（1）平面内有9个点，其中4个点在一条直线 上，此外没有3个点在一条直线上，过这9个点可确 定多少条直线？可以作多少个三角形？
。
3、要从8名男医生和7名女医生中选5人组成一个医疗队，如果
其中至少有2名男医生和至少有2名女医生，则不同的选法种数
为（ C ）
A.(C8 3C7 2)(C7 3C82)
B .(C 8 3C 7 2)(C 7 3C 8 2)
C.C83C72C73C82
D.C83C72C111
4、从7人中选出3人分别担任学习委员、宣传委员、体育委员，
abd bad dab adb bda dba
acd cad dac
你发现a了dc cda dca 什么b?cd cbd dbc
bdc cdb dcb
不写出所有组合，怎样才能知道组合的种数？
A 求3可 分 两 步 考 虑 ：
求4P
3 4
可分两步考虑：
C 第 一 步 ，3（ 4 ） 个 ； 4

{for (i=1; i<n; i++) /* 对无序记录序列进行n−1趟扫描 */
{ flag = 0; /* 这一趟是否发生交换的标志 */ for (j=1; j<=n-i; j++) /* 这趟扫描的范围是从1到n−i
*/
} if (r[j].key>r[j+1].key) /* 通过temp进行交换 */ { temp = r[j]; r[j] = r[j+1]; r[j+1] = temp; flag = 1;} if (flag == 0) break; /* 若没发生交换，就结束算法 */
11
直接插入排序算法
用一维数组 r 做存储结构， n 表示记录个
数，MAXSIZE是常量并且 MAXSIZE>n。约定n
个记录分别存放在 r[1],r[2],…,r[n] 之中。
直接插入排序算法如下：
2016/6/17
12


void stinsort ( node r[MAXSIZE]， int n) ｛for (i=2； i<=n； i++) /*共进行n-1趟插入*/ ｛r[0]=r[i]；/* r[0]为监视哨*/ j=i-1； while (r[j].key> r[0].key) ｛r[j+1]=r[j]；j--；｝ r[j+1]=r[0]； /*将r[0]即原r[i]记录内容，插到r[j]后一位置*/ ｝ ｝/*sinsort*/
2016/6/17
24
算法思路：
1．先取一个正整数d1(d1 <n)，把全 部记录分成d1 个组，所有距离为d1 的倍数的 记录看成一组，假设d1=4，那么记录共分4组： 第1组：r[1],r[5],r[9],…; 第2组：r[2],r[6],r[10]…; 第3组：r[3],r[7],…; 第4组：r[4],r[8],…;

一、冒泡排序已知一组无‎序数据a[1]、a[2]、……a[n]，需将其按升‎序排列。

首先比较a‎[1]与 a[2]的值，若a[1]大于a[2]则交换两者‎的值，否则不变。

再比较a[2]与a[3]的值，若a[2]大于a[3]则交换两者‎的值，否则不变。

再比较a[3]与a[4]，以此类推，最后比较a‎[n-1]与a[n]的值。

这样处理一‎轮后，a[n]的值一定是‎这组数据中‎最大的。

再对a[1]~a[n- 1]以相同方法‎处理一轮，则a[n-1]的值一定是‎a[1]~a[n-1]中最大的。

再对a[1]~a[n-2]以相同方法‎处理一轮，以此类推。

共处理 n-1轮后a[1]、a[2]、……a[n]就以升序排‎列了。

优点：稳定；缺点：慢，每次只能移‎动相邻两个‎数据。

二、选择排序每一趟从待‎排序的数据‎元素中选出‎最小（或最大）的一个元素‎，顺序放在已‎排好序的数‎列的最后，直到全部待‎排序的数据‎元素排完。

选择排序是‎不稳定的排‎序方法。

n个记录的‎文件的直接‎选择排序可‎经过n-1趟直接选‎择排序得到‎有序结果：①初始状态：无序区为R‎[1..n]，有序区为空‎。

②第1趟排序‎在无序区R‎[1..n]中选出关键‎字最小的记‎录R[k]，将它与无序‎区的第1个‎记录R[1]交换，使R[1..1]和R[2..n]分别变为记‎录个数增加‎1个的新有‎序区和记录‎个数减少1‎个的新无序‎区。

……③第i趟排序‎第i趟排序‎开始时，当前有序区‎和无序区分‎别为R[1..i-1]和R(1≤i≤n-1)。

该趟排序从当前‎无序区中选‎出关键字最‎小的记录 R[k]，将它与无序‎区的第1个‎记录R交换‎，使R[1..i]和R分别变‎为记录个数‎增加1个的‎新有序区和‎记录个数减‎少1个的新‎无序区。

这样，n个记录的‎文件的直接‎选择排序可‎经过n-1趟直接选‎择排序得到‎有序结果。

优点：移动数据的‎次数已知（n-1次）；缺点：比较次数多‎。

排列组合专题二筛选法引言排列组合是数学中常见的概念，可以用于解决诸如选择、排列问题等。

而在排列组合中，筛选法是一种常用的方法，能够帮助我们有效地进行选取和筛选。

本文将介绍排列组合专题二中的筛选法。

筛选法的基本原理筛选法是一种基于逻辑筛选的方法，通过设定条件来选取符合要求的对象。

在排列组合中，筛选法常用于从一个较大的集合中选择出满足特定条件的子集合。

筛选法的步骤1. 确定筛选条件：首先，需要明确所需的筛选条件。

这可以是某些元素的特定属性，或者是满足一定关系的组合。

2. 构建筛选算法：根据筛选条件，构建一个合适的筛选算法。

这可以是一系列的判断语句或循环控制语句，用于按照条件筛选出符合要求的对象。

3. 应用筛选算法：将筛选算法应用到待筛选的集合中。

可以逐个对象进行判断，或者通过循环依次检查每个对象。

4. 输出筛选结果：将符合筛选条件的对象输出为最终的筛选结果。

这可以是一个单一的对象，或者是一个满足条件的子集合。

示例以下是一个简单的排列组合示例，展示了筛选法的应用：给定一个集合 {A, B, C, D, E}，现要从中选取含有两个元素的子集合，且子集合中的元素必须按字母表顺序排列。

1. 确定筛选条件：满足条件的子集合必须含有两个元素，并且元素按字母表顺序排列。

2. 构建筛选算法：构建一个循环控制语句，遍历集合中的每个元素对，并判断是否满足条件。

3. 应用筛选算法：依次检查每个元素对，如果满足条件，则将其加入符合条件的子集合中。

4. 输出筛选结果：最终的筛选结果为 {AB, AC, AD, AE, BC, BD, BE, CD, CE, DE}。

结论筛选法是一种有效的排列组合方法，能够帮助我们按需筛选出满足条件的对象。

通过明确筛选条件、构建筛选算法、应用算法和输出结果，我们可以灵活运用筛选法解决各种排列组合问题。

二项式拓展之：解排列组合问题的五大原则排列、组合是高中数学的重要内容，新教材中概率与统计的增加更突出了排列、组合的重要性．高考对排列组合的考查以两个基本原理——分类加法计数原理和分步乘法计数原理为出发点，侧重检测解题思想和解题技巧，因而对解题策略和思维模式的培养和提炼是平时训练的核心．下面通过具体的例题来解析排列组合问题的解题策略之“五大原则”．一、 分类讨论原则：例1.（2012德州二模）2012年伦敦奥运会某项目参赛领导小组要从甲、乙、丙、丁、戊五名志愿者中选派四人分别从事翻译、导游、礼仪、司机四项不同工作，若其中甲、乙只能从事前三项工作，其余三人均能从事这四项工作，则不同的选派方案共有A ．18种B ．36种C ．48种D ．72种二、 特殊优先原则该原则是指在有限制的排列组合问题中优先考虑特殊元素或特殊位置．例2.（2012烟台二模）甲、乙两人从4门课程中各选修2门，则甲、乙所选的课程中至少有1门相同的选法种数为（用数字作答）＿＿＿答案：30解析：可先求出所有两人各选修2门的种数2424C C =36，再求出两人所选两门都都不同的种数均为2242C C =6，故只至少有1门相同的选法有36－6＝30种。

评注：特殊优先原则是解有限制的排列组合问题的总原则，对有限制的元素和有限制的位置一定要优先考虑．三、先取后排原则该原则充分体现了m m m n m n C A A =·的精神实质，先组合后排列，从而避免了不必要的重复与遗漏．例3.（2009重庆卷理）将4名大学生分配到3个乡镇去当村官，每个乡镇至少一名，则不同的分配方案有 种（用数字作答）．答案：36解析分两步完成：第一步将4名大学生按，2，1，1分成三组，其分法有21142122C C C A ⋅⋅;第二步将分好的三组分配到3个乡镇，其分法有33A 所以满足条件得分配的方案有211342132236C C C A A ⋅⋅⋅= 评注：先取后排原则也是解排列组合问题的总原则，尤其是排列与组合的综合问题．若本例简单分步：先从4名教师中取3名教师分给3所学校有34A 种方法，再将剩下的1名教师分给3所学校有3种选择，则共有34372A =·种分配方案，则有明显重复（如：甲、乙、丙、丁和甲、乙、丁、丙）．因此，处理多元素少位置问题时一般采用先取后排原则．四、正难则反原则若从正面直接解决问题有困难时，则考虑事件的对立事件，从不合题意要求的情况入手，再整体排除．例4.【2012高考真题四川理11】方程22ay b x c =+中的,,{3,2,0,1,2,3}a b c ∈--，且,,a b c 互不相同，在所有这些方程所表示的曲线中，不同的抛物线共有（ ）A 、60条B 、62条C 、71条D 、80条答案：B解析：本题可用排除法，,,{3,2,0,1,2,3}a b c ∈--，6选3全排列为120，这些方程所表示的曲线要是抛物线，则0a ≠且0b ≠,，要减去40225=A ，又22或-=b 和33或-=b 时，方程出现重复，用分步计数原理可计算重复次数为18233=⨯⨯，所以不同的抛物线共有120-40-18=62条.故选B.评注：正难则反原则也是解决排列组合问题的总原则，如果从正面考虑不易突破，一般寻找反面途径．利用正难则反原则的语境有其规律，如当问题中含有“至少”，“最多”等词语时，易用此原则．五、策略针对原则不同类型的排列、组合问题有着不同的应对策略，不同的限制条件要采用不同的解题方法．１．相邻问题捆绑法（整体法），相隔问题插空法例5. 某校高三年级举行一次演讲比赛，共有10位同学参赛，其中一班有3位，二班有2位，其他班有5位．若采用抽签的方式确定他们的演讲顺序，则一班的3位同学恰好被安排到一起（演讲序号相连），而２班的２位同学没有被排在一起的概率为（ ） Ａ．110 Ｂ．120 Ｃ．140 Ｄ．1120解析：10人的全排列数是1010A ，即所有的演讲顺序有1010A 种．符合要求的演讲顺序有两个限制：一班的3位同学相邻，而2班的2位同学不相邻，因此分步完成：①把一班的3位同学看成一个整体，他们自身全排列有33A 种安排；②把这个整体当成1个元素与其他班5个元素一起排列有66A 种安排；③把这6个元素排定后有7个空位（包含两端），从这7个空位中任取2个空位安排2班的2位同学有27A 种排法（这样确保2位同学不相邻）．满足条件的排列共有362367A A A ··种，即所求概率是3623671010120A A A A =··，故选Ｂ． 评注：处理相邻问题和不相邻问题时易采用整体法（确保相邻）和插空法（确保相隔），只是要注意是先整体后插空（相邻与不邻的综合问题）或先排后插（单纯的相隔问题），再就是要注意整体元素的排列顺序问题．2．合理分类直接分步法例6.【2012高考真题陕西理8】两人进行乒乓球比赛，先赢三局着获胜，决出胜负为止，则所有可能出现的情形（各人输赢局次的不同视为不同情形）共有（ ）A. 10种B.15种C. 20种D. 30种答案：C.解析：首先分类计算假如甲赢，比分3：0是1种情况；比分3：1共有3种情况，分别是前3局中（因为第四局肯定要赢），第一或第二或第三局输，其余局数获胜；比分是3：2共有6种情况，就是说前4局2：2，最后一局获胜，前4局中，用排列方法，从4局中选2局获胜，有6种情况.甲一共就1+3+6=10种情况获胜.所以加上乙获胜情况，共有10+10=20种情况.故选C.评注：合理分类与直接分步是两个基本原理———分类加法计数原理和分步乘法计数原理最直接的体现，是解排列组合问题的最原始的方法．诸多排列组合问题总是从合理分类，直接分步得到解决的．3．顺序一定消序法（用除法）例7. 某班新年联欢会原定的5个节目已排成节目单，开演前又增加了两个新节目，如果将这两个节目插入原节目中，那么不同插法的种数为（ ）．Ａ．42 Ｂ．30 Ｃ．20 Ｄ．12解析：新插入两个节目，而原来的5个节目顺序不变，从结果考虑，7个节目的全排列是77A ，而顺序不变的5个节目的全排列是55A ，不变的顺序是总体的551A ，则一共有775542A A =种不同的插入种数，故选A ．评注：某些元素顺序不变的排列用除法解决，即若共有n 个元素，其中m 个元素顺序不变，则其不同的排列数为．当然本题可以这样考虑：最终有7个节目位置，从7个位置中任选2个位置安排新增节目有27A 种方法，其他5个位置按原5个节目的固定顺序排列，因此共有2742A =种不同的插入方法．４．对象相同隔板法例8. （1）高二年级要从3个班级抽取10人参加数学竞赛，每班至少1人，一共有______种不同的安排方法．（2）（2003年荆州市质检卷Ⅱ）10个相同的小球放到3个不同的盒中，每个盒不空，一共有______种不同的放法．解析：两例的实质一样，属于同一模型———对象相同，这类问题处理方式较多，但隔板法简单易操作：10个相同的小球有9个空档（确保盒子不空）．从9个空档中选2个空档放入两块隔板，将小球分成三部分（每一种放档板的放法对应着10个小球分成3部分的分法），每部分一一对应着一个不同的小盒．因此一共有29C 种不同的放法，即2936C =种．而把10个竞赛名额分配给3个班，每班至少1个名额的方法与此一模一样．评注：研究的对象是不加区别的元素时，一般考虑隔板法．这是一个基本的数学模型，由此变形的问题是：10x y z ++=有多少组正整数解？而解法不变．。

解排列组合问题的四大原则排列、组合是高中数学的重要内容，新教材中概率与统计的增加更突出了排列、组合的重要性．高考对排列组合的考查以两个基本原理——分类加法计数原理和分步乘法计数原理为出发点，侧重检测解题思想和解题技巧，因而对解题策略和思维模式的培养和提炼是平时训练的核心．下面通过具体的例题来解析排列组合问题的解题策略之“四大原则”．一、特殊优先原则该原则是指在有限制的排列组合问题中优先考虑特殊元素或特殊位置． 例１ （2003年北京市西城区一模题（文））甲、乙、丙三个同学在课余时间负责一个计算机房的周一至周六的值班工作，每天１人值班，每人值班2天，如果甲同学不值周一的班，则可以排出不同的值班表有（ ）A ．90种B ．89种C ．60种D ．59种解析：特殊元素优先考虑，甲同学不值周一的班，则先考虑甲，分步完成：①从除周一的5天中任取2天安排甲有25C 种；②从剩下的4天中选2天安排乙有24C 种；③仅剩2天安排丙有22C 种．由分步乘法计数原理可得一共有22254260C C C =··种，即选C ．评注：特殊优先原则是解有限制的排列组合问题的总原则，对有限制的元素和有限制的位置一定要优先考虑．二、先取后排原则该原则充分体现了m m m n m n C A A =·的精神实质，先组合后排列，从而避免了不必要的重复与遗漏．例2 （2004年高考全国卷Ⅲ）将4名教师分配到3所中学任教，每所中学至少1名教师，则不同的分配方案共有（ ）．A ．12种B ．24种C ．36种D ．48种解析：先分组再排列：将4名教师分成3组有24C 种分法，再将这三组分配到三所学校有33A 种分法，由分步乘法计数原理知一共有234336C A =·种不同分配方案．评注：先取后排原则也是解排列组合问题的总原则，尤其是排列与组合的综合问题．若本例简单分步：先从4名教师中取3名教师分给3所学校有34A 种方法，再将剩下的1名教师分给3所学校有3种选择，则共有34372A =·种分配方案，则有明显重复（如：甲、乙、丙、丁和甲、乙、丁、丙）．因此，处理多元素少位置问题时一般采用先取后排原则．三、正难则反原则若从正面直接解决问题有困难时，则考虑事件的对立事件，从不合题意要求的情况入手，再整体排除．例3 （2004年北京市春招卷）在100件产品中有6件次品，现从中任取3件产品，至少取到１件次品的不同取法的种数是（ ）A ．12694C CB ．12699C C C ．3310094C C -D ．3310094A C -解析：从100件次品中取3件产品，至少有1件次品的对立事件是取到3件全部是正品，即从94件正品中取3件正品有394C 种取法，所以满足条件的不同取法是3310094C C -，故选C ．如果从正面考虑，则必须分取到1，2，3件次品这三类，没有应用排除法来得简单．而本例最易迷惑人的是B ：12699C C ，即从6件次品中取1件确保了至少有1件次品，再从剩下的99件产品中任取2件即可．事实上这样分步并不相互独立，第一步对第二步有明显影响，设次品为ABCDEF ，正品为甲乙丙丁戊…则12699C C 可以是ＡＢ甲，也可能是ＢＡ甲，因而重复． 评注：正难则反原则也是解决排列组合问题的总原则，如果从正面考虑不易突破，一般寻找反面途径．利用正难则反原则的语境有其规律，如当问题中含有“至少”，“最多”等词语时，易用此原则．四、策略针对原则不同类型的排列、组合问题有着不同的应对策略，不同的限制条件要采用不同的解题方法．1．相邻问题捆绑法（整体法），相隔问题插空法例4 （2004年高考重庆卷（理））某校高三年级举行一次演讲比赛，共有10位同学参赛，其中一班有3位，二班有2位，其他班有5位．若采用抽签的方式确定他们的演讲顺序，则一班的3位同学恰好被安排到一起（演讲序号相连），而2班的2位同学没有被排在一起的概率为（ ）A ．110B ．120C ．140D ．1120解析：10人的全排列数是1010A ，即所有的演讲顺序有1010A 种．符合要求的演讲顺序有两个限制：一班的3位同学相邻，而2班的2位同学不相邻，因此分步完成：①把一班的3位同学看成一个整体，他们自身全排列有33A 种安排；②把这个整体当成1个元素与其他班5个元素一起排列有66A 种安排；③把这6个元素排定后有7个空位（包含两端），从这7个空位中任取2个空位安排2班的2位同学有27A 种排法（这样确保2位同学不相邻）．满足条件的排列共有362367A A A ··种，即所求概率是3623671010120A A A A ··，故选B ． 评注：处理相邻问题和不相邻问题时易采用整体法（确保相邻）和插空法（确保相隔），只是要注意是先整体后插空（相邻与不邻的综合问题）或先排后插（单纯的相隔问题），再就是要注意整体元素的排列顺序问题．2．合理分类直接分步法例5 （2004年高考全国卷Ⅱ）在由数字1，2，3，4，5组成的所有没有重复数字的5位数中，大于23145且小于43521的数共有（ ）个． （ ）A ．56B ．57C ．58D ．60解析：所有大于23145且小于43521的数由以下几类构成：由分类加法计数原理可得，一共有234322343212222158A A A A A ++++++=个，故选C ．评注：合理分类与直接分步是两个基本原理———分类加法计数原理和分步乘法计数原理最直接的体现，是解排列组合问题的最原始的方法．诸多排列组合问题总是从合理分类，直接分步得到解决的．3．顺序一定消序法（用除法）例6 （2003年北京市春招卷）某班新年联欢会原定的5个节目已排成节目单，开演前又增加了两个新节目，如果将这两个节目插入原节目中，那么不同插法的种数为（ ）．A ．42B ．30C ．20D ．12解析：新插入两个节目，而原来的5个节目顺序不变，从结果考虑，7个节目的全排列是77A ，而顺序不变的5个节目的全排列是55A ，不变的顺序是总体的551A ，则一共有775542A A =种不同的插入种数，故选A ． 评注：某些元素顺序不变的排列用除法解决，即若共有n 个元素，其中m 个元素顺序不变，则其不同的排列数为．当然本题可以这样考虑：最终有7个节目位置，从7个位置中任选2个位置安排新增节目有27A 种方法，其他5个位置按原5个节目的固定顺序排列，因此共有2742A =种不同的插入方法．4．对象相同隔板法例7 （1）（2004年湖北省四校联考卷）高二年级要从3个班级抽取10人参加数学竞赛，每班至少1人，一共有______种不同的安排方法．（2）（2003年荆州市质检卷Ⅱ）10个相同的小球放到3个不同的盒中，每个盒不空，一共有______种不同的放法．解析：两例的实质一样，属于同一模型———对象相同，这类问题处理方式较多，但隔板法简单易操作：10个相同的小球有9个空档（确保盒子不空）．从9个空档中选2个空档放入两块隔板，将小球分成三部分（每一种放档板的放法对应着10个小球分成3部分的分法），每部分一一对应着一个不同的小盒．因此一共有29C 种不同的放法，即2936C =种．而把10个竞赛名额分配给3个班，每班至少1个名额的方法与此一模一样．评注：研究的对象是不加区别的元素时，一般考虑隔板法．这是一个基本的数学模型，由此变形的问题是：10++=有多少组正整数解？而解法不变．x y z。

解排列组合问题的四大原则排列、组合是高中数学的重要内容，新教材中概率与统计的增加更突出了排列、组合的重要性．高考对排列组合的考查以两个基本原理——分类加法计数原理和分步乘法计数原理为出发点，侧重检测解题思想和解题技巧，因而对解题策略和思维模式的培养和提炼是平时训练的核心．下面通过具体的例题来解析排列组合问题的解题策略之“四大原则”． 一、特殊优先原则该原则是指在有限制的排列组合问题中优先考虑特殊元素或特殊位置． 例１ （2003年北京市西城区一模题（文））甲、乙、丙三个同学在课余时间负责一个计算机房的周一至周六的值班工作，每天１人值班，每人值班2天，如果甲同学不值周一的班，则可以排出不同的值班表有（ ） A ．90种 B ．89种 C ．60种 D ．59种解析：特殊元素优先考虑，甲同学不值周一的班，则先考虑甲，分步完成：①从除周一的5天中任取2天安排甲有25C 种；②从剩下的4天中选2天安排乙有24C 种；③仅剩2天安排丙有22C 种．由分步乘法计数原理可得一共有22254260C C C =··种，即选C ．评注：特殊优先原则是解有限制的排列组合问题的总原则，对有限制的元素和有限制的位置一定要优先考虑． 二、先取后排原则该原则充分体现了m m mn m n C A A =·的精神实质，先组合后排列，从而避免了不必要的重复与遗漏．例2 （2004年高考全国卷Ⅲ）将4名教师分配到3所中学任教，每所中学至少1名教师，则不同的分配方案共有（ ）． A ．12种 B ．24种 C ．36种 D ．48种解析：先分组再排列：将4名教师分成3组有24C 种分法，再将这三组分配到三所学校有33A 种分法，由分步乘法计数原理知一共有234336C A =·种不同分配方案．评注：先取后排原则也是解排列组合问题的总原则，尤其是排列与组合的综合问题．若本例简单分步：先从4名教师中取3名教师分给3所学校有34A 种方法，再将剩下的1名教师分给3所学校有3种选择，则共有34372A =·种分配方案，则有明显重复（如：甲、乙、丙、丁和甲、乙、丁、丙）．因此，处理多元素少位置问题时一般采用先取后排原则． 三、正难则反原则若从正面直接解决问题有困难时，则考虑事件的对立事件，从不合题意要求的情况入手，再整体排除．例3 （2004年北京市春招卷）在100件产品中有6件次品，现从中任取3件产品，至少取到１件次品的不同取法的种数是（ ）A ．12694C C B ．12699C CC ．3310094C C - D ．3310094A C -解析：从100件次品中取3件产品，至少有1件次品的对立事件是取到3件全部是正品，即从94件正品中取3件正品有394C 种取法，所以满足条件的不同取法是3310094C C -，故选C ．如果从正面考虑，则必须分取到1，2，3件次品这三类，没有应用排除法来得简单．而本例最易迷惑人的是B ：12699C C ，即从6件次品中取1件确保了至少有1件次品，再从剩下的99件产品中任取2件即可．事实上这样分步并不相互独立，第一步对第二步有明显影响，设次品为ABCDEF ，正品为甲乙丙丁戊…则12699C C 可以是ＡＢ甲，也可能是ＢＡ甲，因而重复． 评注：正难则反原则也是解决排列组合问题的总原则，如果从正面考虑不易突破，一般寻找反面途径．利用正难则反原则的语境有其规律，如当问题中含有“至少”，“最多”等词语时，易用此原则． 四、策略针对原则不同类型的排列、组合问题有着不同的应对策略，不同的限制条件要采用不同的解题方法．1．相邻问题捆绑法（整体法），相隔问题插空法例4 （2004年高考重庆卷（理））某校高三年级举行一次演讲比赛，共有。