三角函数单调性

三角函数的单调区间与不等式三角函数是高中数学中重要的概念之一，它在数学和物理等领域有广泛的应用。

而了解三角函数的单调性及其与不等式的关系，对于解题和理解数学概念都极为重要。

本文将详细讨论三角函数的单调区间与不等式的相关内容。

一、正弦函数的单调性与不等式正弦函数是最常见的三角函数之一，其定义域为实数集合R，值域在[-1, 1]之间。

首先我们来研究正弦函数的单调性。

我们知道，正弦函数的一个周期是2π，那么我们可以利用周期性来研究其单调性。

在每个周期内，正弦函数在[0, π/2]、[π/2, π]、[π, 3π/2]、[3π/2, 2π]上的单调性是相同的。

首先来看在[0, π/2]区间内的单调性。

在这个区间内，正弦函数的值是递增的，即sin(x1) < sin(x2)当且仅当0 ≤ x1 < x2 ≤ π/2。

接下来是在[π/2, π]区间内的单调性。

在这个区间内，正弦函数的值是递减的，即sin(x1) > sin(x2)当且仅当π/2 ≤ x1 < x2 ≤ π。

同理，在[π, 3π/2]和[3π/2, 2π]区间内的正弦函数分别是递增和递减的。

根据上述的单调性分析，我们可以利用单调性来解不等式。

比如对于sin(x) > a这样的不等式，我们可以通过分析sin(x)和a的关系，得出x的取值范围。

二、余弦函数的单调性与不等式余弦函数也是一种常见的三角函数，其定义域和值域与正弦函数相同。

我们将讨论余弦函数的单调性及其与不等式的关系。

与正弦函数类似，余弦函数也具有周期性。

在每个周期内，余弦函数在[0, π]、[π, 2π]区间上的单调性是相同的。

在[0, π]区间内，余弦函数的值是递减的，即cos(x1) > cos(x2)当且仅当0 ≤ x1 < x2 ≤ π。

在[π, 2π]区间内，余弦函数的值是递减的，即cos(x1) < cos(x2)当且仅当π ≤ x1 < x2 ≤ 2π。

三角函数单调递增区间公式
如果你想知道三角函数单调递增区间公式是什么，那么你来对地方。

三角函数单调递增区间公式可以帮助我们确定一个函数是单调递增的。

下面就让我们来了解一下它是怎样工作的：
1. 三角函数单调递增区间的基本公式
三角函数单调递增区间的基本公式由两个端点表示，相邻的两组端点
定义一个单调递增的区间。

每一个单调递增的区间的定义如下：
- 如果函数是奇函数，则端点为：(n-1/2)π -- (n+1/2)π；
- 如果函数是偶函数，则端点为：nπ -- (n+1)π。

其中n 为任意整数。

2. 三角函数单调递增区间的更进一步实现
在确定三角函数单调递增区间的时候，如果需要更进一步实现，可以
将相邻两个端点间的值分别记为x1,x2。

然后根据以下公式计算x1、x2：
x1 = nπ + (-1)^n * (1/2)π
x2 = (n+1)π + (-1)^n * (1/2)π
其中n 为任意整数，(-1)^n 是以指数的形式表达的一元二次函数。

3. 三角函数单调递增图象的描绘
通过以上公式，我们可以将三角函数从数学角度上表达出来，然后在图上更加直观的描绘出三角函数的单调递增区间。

在描绘的时候，可以使用两个不同颜色的典型实例线性绘制对应区间。

最后，三角函数单调递增区间公式通过解决关于三角函数诸多函数概念的数学现象，使人们能够更加真实的解答问题。

总之，三角函数单调递增区间的计算主要使用上述的基本公式，此公式可以帮助我们确定一个函数是单调递增的，并且基于此可以更进一步实现更多的概念，从而更加准确地描绘出三角函数单调递增图象。

假期专题辅导系列三-------三角函数的单调性江苏省海安高级中学------罗湘军三角函数的单调性是三角函数的重要性质，在三角函数的各种问题中都能见到单调性的独特应用之处，特别是在比较大小、求三角函数的单调区间，解不等式等方面有着不可替代的作用，下面我们借助于几个例子来进行分析. 一. 典例分析1. 利用三角函数的单调性比较大小 例1 比较下列各组数的大小 （1）33sin(sin),sin(cos)88ππ; (2)13tan4π与17tan5π解析： (1) ∵3cossin 88ππ=,∴330cossin188ππ<<<.而sin y x =在(0,1)内递增,∴33sin(sin )sin(cos)88ππ<.(2) 13tantan 4π= 4π，172tan tan55ππ=， ⎪⎭⎫⎝⎛=<<2,0tan ,5240πππ在x y 内单调递增， 2tantan.45ππ∴<。

点评：比较两个三角函数值的大小常常先将它们化为同名函数，然后将角化为在该函数的同一单调区间内的角．最后利用函数的单调性来比较函数值的大小．2. 利用三角函数的单调性求单调区间 例2 求函数⎪⎭⎫ ⎝⎛-=324sin 21x y π的单调区间.解析:原函数变形为⎪⎭⎫⎝⎛--=432sin 21πx y 令432π-=x u ,则只需求u y sin =的单调区间即可. 2243222sin πππππ+≤-=≤-=k x u k u y 在 (Z k ∈)上单调递增即893833ππππ+≤≤-k x k ,(Z k ∈)上单调递增,u y sin =在2322()2342x k u k k Z πππππ+≤=-≤+∈上单调递减即在)(,8213893Z k k x k ∈+≤≤+ππππ上单调递减故⎪⎭⎫ ⎝⎛-=324sin 21x y π的递减区间为:,893,833⎥⎦⎤⎢⎣⎡+-ππππk k ()k Z ∈ 故原函数递增区间为:)(,8213,893Z k k k ∈⎥⎦⎤⎢⎣⎡++πππ. 点评：研究三角函数的性质时常用整体思想.本题将函数⎪⎭⎫ ⎝⎛-=324sin 21x y π作整体代换,转化为对函数sin y x =的性质的研究.另外,本题也可以画出函数⎪⎭⎫ ⎝⎛-=324sin 21x y π的图象,通过图象来研究性质. 3. 利用三角函数的单调性求值域例3设G 、H 分别为非等边三角形ABC 的重心与外心，A(0，2)，B （0，－2）,且AB GM λ=(λ∈R).（Ⅰ）求点C(x ，y )的轨迹E 的方程；（Ⅱ）过点(2，0)作直线L 与曲线E 交于点M 、N 两点，设ON OM OP +=，是否存在这样的直线L ，使四边形OMPN 是矩形？若存在，求出直线的方程；若不存在，试说明理由.例3.求函数)3cos(2π-=x y 在6π≤x ≤32π范围内的值域。

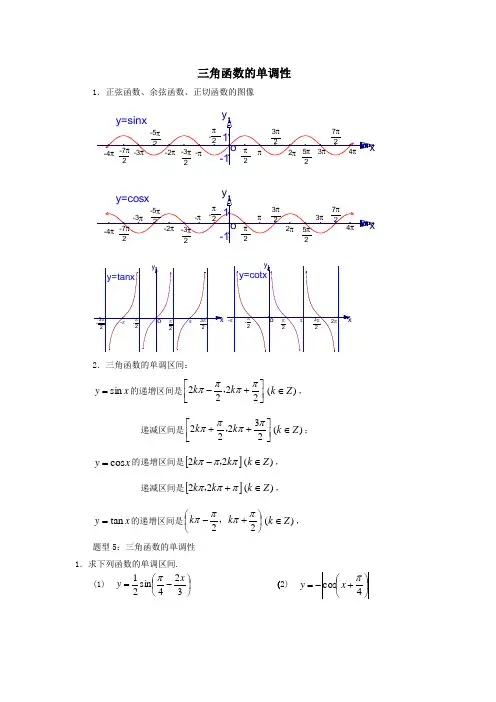
三角函数的单调性1．正弦函数、余弦函数、正切函数的图像2．三角函数的单调区间：x y sin =的递增区间是⎥⎦⎤⎢⎣⎡+-2222ππππk k ，)(Z k ∈，递减区间是⎥⎦⎤⎢⎣⎡++23222ππππk k ，)(Z k ∈； x y cos =的递增区间是[]πππk k 22，-)(Z k ∈，递减区间是[]πππ+k k 22，)(Z k ∈，x y tan =的递增区间是⎪⎭⎫ ⎝⎛+-22ππππk k ，)(Z k ∈，题型5：三角函数的单调性 1．求下列函数的单调区间.(1) ⎪⎭⎫ ⎝⎛-=324sin 21x y π (2) ⎪⎭⎫ ⎝⎛+-=4cos πx y解:(1).原函数变形为⎪⎭⎫⎝⎛--=432sin 21πx y 令432π-=x u ,则只需求u y sin =的单调区间即可.2243222sin πππππ+≤-=≤-=k x u k u y 在 ,(Z k ∈)上 即893833ππππ+≤≤-k x k ,(Z k ∈)上单调递增, u y sin =在)(,23243222Z k k x u k ∈+≤-=≤+πππππ,上 即)(,8213893Z k k x k ∈+≤≤+ππππ,上单调递减 故⎪⎭⎫ ⎝⎛-=324sin 21x y π的递减区间为:,893,833⎥⎦⎤⎢⎣⎡+-ππππk k ()k Z ∈ 递增区间为:)(,8213,893Z k k k ∈⎥⎦⎤⎢⎣⎡++πππ.(2)原函数的增减区间即是函数⎪⎭⎫ ⎝⎛+=4cos πx y 的减增区间,令4π+=x u由函数u y cos =的图象可知:周期π=T 且 u y cos =在,42ππππk x u k ≤+=≤-上,即Z k k x k ∈-≤≤-,443ππππ上递增, 在24ππππ+≤+=≤k x u k 即在Z k k x k ∈+≤≤-,44ππππ上递减故所求的递减区间为⎥⎦⎤⎢⎣⎡--4,43ππππk k ,递增区间为,44k k ππππ⎡⎤-+⎢⎥⎣⎦(Z k ∈) 2．函数y =2sin x的单调增区间是（ ） A ．［2k π－2π，2k π＋2π］（k ∈Z ）B ．［2k π＋2π，2k π＋23π］（k ∈Z ） C ．［2k π－π，2k π］（k ∈Z ） D ．［2k π，2k π＋π］（k ∈Z ）解析：A ；函数y =2x为增函数，因此求函数y =2sin x的单调增区间即求函数y =sin x 的单调增区间。

三角函数单调区间的求法三角函数是数学中十分重要的一类函数，涉及到许多应用，如物理、工程、统计等领域。

在学习三角函数时，掌握它的单调性质是十分必要的。

本文将介绍如何求三角函数的单调区间。

一、正弦函数的单调区间正弦函数的形式为：y=sin(x)，其中x∈[-π/2, π/2]。

在此区间内，正弦函数单调递增。

若x1<x2，则有：sin(x1)<sin(x2)。

在[-π/2, π/2]之外的区间不具有单调性，需要经过化简处理。

二、余弦函数的单调区间余弦函数的形式为：y=cos(x)，其中x∈[0, π]。

在此区间内，余弦函数单调递减。

若x1<x2，则有：cos(x2)<cos(x1)。

在[π, 2π]之外的区间不具有单调性，需要经过化简处理。

三、正切函数的单调区间正切函数的形式为：y=tan(x)，其中x∈(-π/2, π/2)。

在此区间内，正切函数单调递增。

若x1<x2，则有：tan(x1)<tan(x2)。

在(-π/2, π/2)之外的区间不具有单调性，需要经过化简处理。

四、余切函数的单调区间余切函数的形式为：y=cot(x)，其中x∈(0, π)。

在此区间内，余切函数单调递减。

若x1<x2，则有：cot(x2)<cot(x1)。

在(0, π)之外的区间不具有单调性，需要经过化简处理。

五、化简方法若给出的三角函数的区间不具有单调性，可以通过化简将其化为具有单调性的区间。

例如，若要求sin(x)在[π/2, 3π/2]上的单调性，可以先将sin(x)化为cos(x-π/2)，即cos(x-π/2)在[0, π]上的单调性。

同理，若要求cos(x)在[π/2, 3π/2]上的单调性，可以先将cos(x)化为-sin(x-π)，即-sin(x-π)在[0, π]上的单调性。

总之，掌握三角函数的单调性对于正确理解和运用它们是非常重要的。

希望本文能够帮助读者更好地理解和掌握三角函数的单调性。

求三角函数的单调性的基本方法：函数的单调区间的确定，首先要看A 、ω是否为正，sin()y A x k ωϕ=++若ω为负，则先应用诱导公式化为正，然后将ωx +φ看作一个整体，化为最简式，再结合A 的正负，在和两个22,22k x k k z ππππ-≤≤+∈322,22k x k k z ππππ+≤≤+∈区间内分别确定函数的单调增减区间。

1、求函数在区间[-2π，2π]的单调增区间。

)213sin(x y -=π解：⑴利用诱导公式把函数转化为标准函数（）sin(),0,0y A x A ωϕω=+>>的形式：321sin()213sin(ππ--=-=x x y ⑵把标准函数转化为最简函数（）的形式：sin y A x =令，原函数变为123z x π=-1sin()sin 23y x z π=--=-⑶讨论最简函数的单调性：sin y z=-从函数的图像可以看出，的单调增区间为sin y z=-sin y z=-，。

所以，3[2,2]22k k ππππ++Z ∈K 32222K z K ππππ+≤≤+Z∈K 即， πππππ23232122+≤-≤+K x K Z ∈K ∴， ππππ3114354+≤≤+K x K Z∈K ⑷计算k=0,k=±1时的单调增区间：当k=0时，ππ31135≤≤x当k=1时，222333x ππ≤≤当k=-1时，ππ3137-≤≤-x ⑸在要求的区间内[-2π，2π]确定函数的最终单调增区间：因为，所以该函数的单调增区间为[2,2]x ππ∈-和ππ312-≤≤-x ππ235≤≤x 2、求函数在区间[0，π]的单调增区间。

)26sin(2x y -=π解：⑴利用诱导公式把函数转化为标准函数（）sin(),0,0y A x A ωϕω=+>>的形式：sin(2)sin(266y x x ππ=-=--⑵把标准函数转化为最简函数（）的形式：sin y A x =令，原函数变为26z x π=-sin(2)sin 6y x z π=--=-⑶讨论最简函数的单调性：sin y z=-从函数的图像可以看出，的单调增区间为sin y z=-sin y z=-，。