统计学计算题复习完整版

统计学原理复习1（计算题）1．某单位40名职工业务考核成绩分别为:68 89 88 84 86 87 75 73 72 6875 82 97 58 81 54 79 76 95 7671 60 90 65 76 72 76 85 89 9264 57 83 81 78 77 72 61 70 81单位规定:60分以下为不及格，60─70分为及格，70─80分为中,80─90分为良,90─100分为优.要求：（1)将参加考试的职工按考核成绩分为不及格、及格、中、良、优五组并编制一张考核成绩次数分配表;（2）指出分组标志及类型及采用的分组方法；(3）计算本单位职工业务考核平均成绩（4）分析本单位职工业务考核情况.解：(1）（2）分组标志为”成绩”，其类型为"数量标志";分组方法为：变量分组中的开放组距式分组,组限表示方法是重叠组限；（3)本单位职工业务考核平均成绩（4）本单位的职工考核成绩的分布呈两头小，中间大的”正态分布”的形态,说明大多数职工对业务知识的掌握达到了该单位的要求。

2．2004年某月份甲、乙两农贸市场农产品价格和成交量、成交额资料如下：试问哪一个市场农产品的平均价格较高?并说明原因.解：解：先分别计算两个市场的平均价格如下：甲市场平均价格()375.145.5/==∑∑=x m m X（元/斤） 乙市场平均价格325.143.5==∑∑=f xf X （元/斤）说明：两个市场销售单价是相同的，销售总量也是相同的，影响到两个市场平均价格高低不同的原因就在于各种价格的农产品在两个市场的成交量不同.3．某车间有甲、乙两个生产组，甲组平均每个工人的日产量为36件，标准差为9.6件;乙组工人日产量资料如下：要求：⑴计算乙组平均每个工人的日产量和标准差;⑵比较甲、乙两生产小组哪个组的日产量更有代表性？ 解：（1）50.291001345343538251515=⨯+⨯+⨯+⨯==∑∑fxf X （件）986.8)(2=-=∑∑ff X x σ（件） （2）利用标准差系数进行判断:267.0366.9===XV σ甲305.05.29986.8===X V σ乙因为0。

《统计学》复习题一、单选题1．某城市进行工业企业未安装设备普查，个体是( B ）A．工业企业全部未安装设备 B．工业企业每一台未安装设备C．每个工业企业的未安装设备 D．每一个工业企业2．工业企业的设备数，产品产值是（ A ）A．连续变量 B．离散变量C．前者是连续变量,后者是离散变量 D．前者是离散变量,后者是连续变量3．对某班学生按年龄分成16-18岁、19—21岁、22-24岁三组,则24岁是（ A ）A。

最大值 B。

组中值 C. 第三组的上限 D。

第三组的组中值4．一个组的上限与下限之差称为（ D ）A。

组中值B。

组数 C. 全距 D. 组距5．连续变量数列中，其末组为开口组，下限是1000，相邻组的组中值为975，则末组的组中值为( D ）A. 987。

5B. 1000 C。

1025 D. 10506. 在建筑业设备普查中，每个建筑企业是（ B )A. 调查对象B. 填报单位C. 调查单位 D。

调查项目7．向上累计次数表示截止到某一组为止( A ）A．上限以下的累计次数 B．下限以上的累计次数C．各组分布的次数 D．各组分布的频率8。

一组样本数据为3、3、1、5、13、12、11、9、7.这组数据的中位数是（ D ）A.3 B。

13 C.7。

1 D.7 9。

算术平均数、众数和中位数之间的数量关系决定于总体次数的分布状况.在对称的钟形分布中（ A ）A。

算术平均数=中位数=众数 B。

算术平均数〉中位数>众数C。

算术平均数<中位数<众数 D。

中位数>算术平均数。

>众数10．用不考虑顺序的不重复抽样方法,从8个人中抽选3个人，所得样本可能数目的公式为（ B )A． B． C． D．11．某同学的英语成绩为80分，则“成绩”是（ A ）A．品质标志 B．数量标志 C．标志值 D．数量指标12．了解某地区工业企业职工的情况，下列哪个是统计指标( C ）A．该地区每名职工的工资额 B．该地区职工的文化程度C．该地区职工的工资总额 D．该地区职工从事的工种13．对于统计分组设计，下列哪种说法是错误的（ B ）A。

《统计学原理》复习资料（计算部分）一、 编制分配数列（次数分布表） 统计整理公式a) 组距＝上限－下限 b) 组中值＝（上限+下限）÷2c) 缺下限开口组组中值＝上限－1/2邻组组距 d) 缺上限开口组组中值＝下限+1/2邻组组距1．某班40名学生统计学考试成绩分别为：57 89 49 84 86 87 75 73 72 68 75 82 97 81 67 81 54 79 87 95 76 71 60 90 65 76 72 70 86 85 89 89 64 57 83 81 78 87 72 61要求：⑴ 根据上述资料按成绩分成以下几组：60分以下，60~70分，70~80分，80~90分，90~100分，整理编制成分配数列。

⑵ 根据整理后的分配数列，计算学生的平均成绩。

解：分配数列成绩（分） 学生人数（人） 频率（%） 60以下 4 10 60—70 6 15 70—80 12 30 80—90 15 37.5 90—100 3 7.5 合计 40 100平均成绩 55465675128515953307076.754040xf x f⨯+⨯+⨯+⨯+⨯====∑∑（分）或 5510%6515%7530%8537.5%957.5%76.75fx x f=⋅=⨯+⨯+⨯+⨯+⨯=∑∑（分）2．某生产车间40名工人日加工零件数（件）如下：30 26 42 41 36 44 40 37 43 35 37 25 45 29 43 31 36 49 34 47 33 43 38 42 32 25 30 46 29 34 38 46 43 39 35 40 48 33 27 28要求：⑴ 根据以上资料分成如下几组：25~30，30~35，35~40，40~45，45~50，整理编制次数分布表。

⑵ 根据整理后的次数分布表，计算工人的平均日产量。

（作业10P 1） 解：次数分布表日加工零件数（件） 工人数（人）频率（%）25—307 17.5 30—35 8 20 35—40 9 22.5 40—45 10 25 45—50 6 15 合计 40100平均日产量 27.5732.5837.5942.51047.56150037.54040xf x f⨯+⨯+⨯+⨯+⨯====∑∑ 件或 27.517.5%32.520%37.522.5%42.525%47.515%37.5fx x f=⋅=⨯+⨯+⨯+⨯+⨯=∑∑ 件二、 算术平均数和调和平均数的计算 加权算术平均数公式 xfx f=∑∑（常用） fx x f=⋅∑∑（x 代表各组标志值，f 代表各组单位数，ff∑代表各组的比重）加权调和平均数公式 m x m x=∑∑ （x 代表各组标志值，m 代表各组标志总量）分析： m x mx=总产量工人平均劳动生产率（结合题目）总工人人数从公式可以看出，“生产班组”这列资料不参与计算，是多余条件，将其删去。

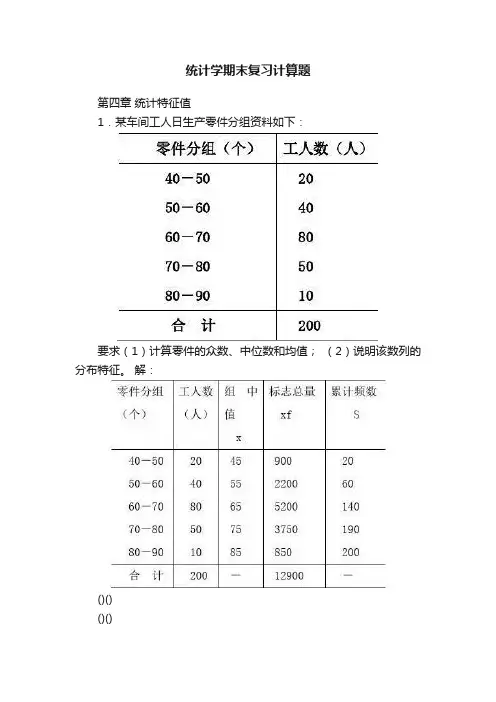
统计学期末复习计算题第四章统计特征值1．某车间工人日生产零件分组资料如下：要求（1）计算零件的众数、中位数和均值；（2）说明该数列的分布特征。

解：()()()())(71.6571.5601050804080408060111个=+=?-+--+=?-+--+=+--i f f f ff f L Mo)(6556010806022006021个=+=?-+=?-+=-i f S NL M mm e)(5.6420012900个===∑∑fxf x因为o e ＜M ＜M x ，所以，该数据分布属于左偏分布。

2．某公司所属三个企业生产同种产品，2002年实际产量、计划完成情况及产品优质品率资料如下：试计算（1）该公司产量计划完成百分比；（2）该公司实际的优质品率。

解：（1）产量计划完成百分比：%95.9320.5325008.02501.11502.1100250150100==++++==∑∑xm m x（2）实际优质品率：%8.9650048425015010098.025096.015095.0100==++?+?+?==∑∑fxf x3．某企业2003年一、二季度生产某产品产量资料如下：要求（1）计算平均等级指标说明二季度比一季度产品质量的变化情况；（2）由于质量变化而给该企业带来的收益（或损失）。

解：（1）平均等级：)(22.15010075050310027501111级=++?+?+?==∑∑fxfx)(5.1100300600100330026001222级=++?+?+?==∑∑fxf x二季度比一季度平均等级下降0.28级。

（2）由于质量下降而带来的损失：)(33.1683501007505080010012507501800111元=++?+?+?==∑∑fpf p)(153510030060010080030012506001800222元=++?+?+?==∑∑fpfp()())(148330100033.16831535212元-=?-=?-∑fp p由于产品质量下降而损失148330元。

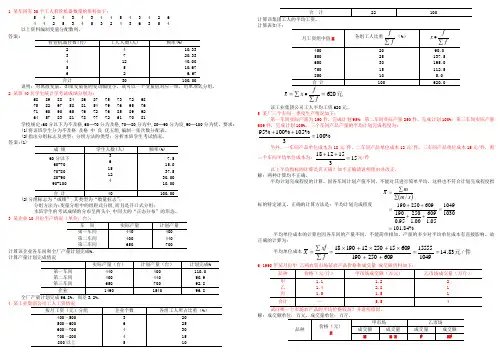
1 某车间有30个工人看管机器数量的资料如下:5 4 2 4 3 4 3 4 4 5 4 3 4 26 4 4 2 5 3 4 5 3 2 4 3 6 3 5 4 以上资料编制变量分配数列。

答案:2 某班40名学生统计学考试成绩分别为:68 89 88 84 86 87 75 73 72 68 75 82 97 58 81 54 79 76 95 76 71 60 90 65 76 72 76 85 89 92 64 57 83 81 78 77 72 61 70 81学校规定:60分以下为不及格,60─70分为及格,70─80分为中,80─90分为良,90─100分为优。

要求: (1)将该班学生分为不及格 及格 中 良 优五组,编制一张次数分配表。

(2)指出分组标志及类型；分组方法的类型；分析本班学生考试情况。

答案:(1)(2)分组方法为:变量分组中的组距式分组,而且是开口式分组；本班学生的考试成绩的分布呈两头小,中间大的“正态分布”的形态。

3 某企业104计算表如下：元620=∑∙∑=fx x 该工业集团公司工人平均工资620元。

5 某厂三个车间一季度生产情况如下：第一车间实际产量为190件，完成计划95%；第二车间实际产量250件，完成计划100%；第三车间实际产量609件，完成计划105%，三个车间产品产量的平均计划完成程度为：%1003%105%100%95=++另外，一车间产品单位成本为18元/件，二车间产品单位成本12元/件，三车间产品单位成本15元/件，则三个车间平均单位成本为：153151218=++元/件以上平均指标的计算是否正确？如不正确请说明理由并改正。

解：两种计算均不正确。

平均计划完成程度的计算，因各车间计划产值不同，不能对其进行简单平均，这样也不符合计划完成程度指标的特定涵义。

正确的计算方法是：平均计划完成程度()%84.1011030104905.160900.125095.0190609250190/==++++=∑∑=x m m X 平均单位成本的计算也因各车间的产量不同，不能简单相加，产量的多少对平均单位成本有直接影响。

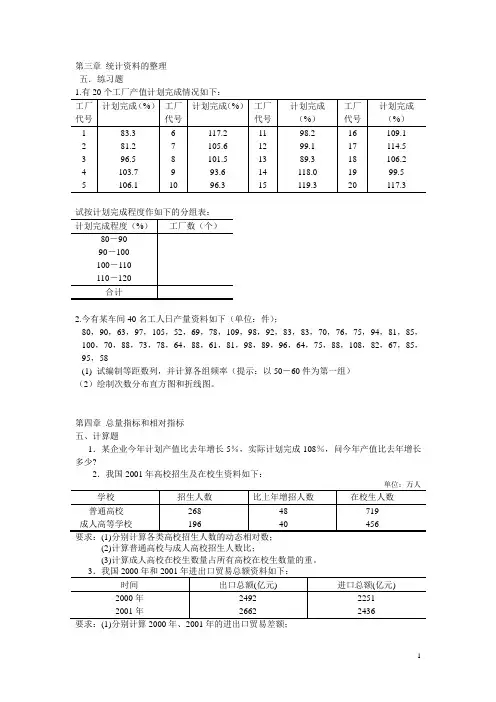
第三章 统计资料的整理 五．练习题试按计划完成程度作如下的分组表：2.今有某车间40名工人日产量资料如下（单位：件）；80，90，63，97，105，52，69，78，109，98，92，83，83，70，76，75，94，81，85，100，70，88，73，78，64，88，61，81，98，89，96，64，75，88，108，82，67，85，95，58(1) 试编制等距数列，并计算各组频率（提示：以50－60件为第一组） （2）绘制次数分布直方图和折线图。

第四章总量指标和相对指标 五、计算题1．某企业今年计划产值比去年增长5％，实际计划完成108％，问今年产值比去年增长多少?2．我国2001年高校招生及在校生资料如下：(2)计算普通高校与成人高校招生人数比；(3)计算成人高校在校生数量占所有高校在校生数量的重。

(2)计算2001年进出口总额比例相对数及出口总额增长速度； (3)分析我国进出口贸易状况。

4．根据下列资料，计算强度相对数的正指标和逆指标，并根据正指标数值分析该地区5．某公司下属三个企业有关资料如下表，试根据指标之间的关系计算并填写表中所缺数第六章 动态数列习题五、计算题1．某公司某年9月末有职工250人，10月上旬的人数变动情况是：10月4日新招聘12名大学生上岗，6日有4名老职工退休离岗，8日有3名青年工人应征入伍，同日又有3名职工辞职离岗，9日招聘7名营销人员上岗。

试计算该公司10月上旬的平均在岗人数。

(2)分别计算该银行2005年第一季度、第二季度和上半年的平均现金库存额。

(2)计算该地区2001—2005年间的平均国民生产总值。

(3)计算2002—2005年间国民生产总值的平均发展速度和平均增长速度。

(2)计算该企业第四季度劳动生产率。

(2)应用最小平方法配合趋势直线，并计算各年的趋势值。

第七章统计指数习题五、计算题1．某市1999年第一季度社会商品零售额为36200万元，第四季度为35650万元，零售物价下跌0．5％，试计算该市社会商品零售额指数、零售价格指数和零售量指数，以及由于零售物价下跌居民少支出的金额。

统计学计算题复习.平均数、中位数和众数的计算和数列特征分析1.算术平均数。

也叫均值，是全部数据的算术平均，是集中趋势的最主要测度值。

主要适用于定距数据和定比数据，但不适用于定类数据和定序数据。

2•众数。

众数是一组数据中出现次数最多的变量值，用M o表示。

主要用于测度定类数据的集中趋势。

由组距式数列确定众数，是先根据出现次数确定众数所在组，然后利用下列公式计算众数的近似值：M o L(f f l) (f f 1)3•中位数。

中位数是一组数据按从小到大排序后，处于中间位置上的变量值，用M e 表示。

主要用于测度定序数据的集中趋势。

由分组数据计算中位数时，先根据公式N确定中位数所在的组，然后用下列公式计算2Ns中位数的近似值：M L ie f m4•众数、中位数和算术平均数的比较(1)X M e M o，数据是正态分布；(2)x<M e VM 0，数据是左偏分布；(3)x>M e>M 0，数据是右偏分布。

例题1:某地区有下列资料：人均月收入(元)户数(人)400以下50400~500 100500~600 450600~700 200700~800 100800~900 60900以上40合计1000要求计算算术平均数、众数、中位数。

（2）说明该数列的分布特征。

.单个总体均值、比例的区间估计的简单随机样本，得出每户农民年平均收入为3210元，标准差为205元。

试求该村每户农民年平均收入和全村年总收入的置信度为95%的置信区间。

例题2:有一大批糖果，现从中随机地取16袋，称得重量(克)如下：506 508 499503 504510 497 512，设袋装糖果的重量服从正态分布，试求总体514 505 493 496 506 502 509 496均值的置信水平为0.95的置信区间•可以根据估计总体均 B.估计总体比例题3: 5.2为调查某市郊区72000户农民家庭中拥有彩电的成数，随机抽取了其中的 400户，结果有92户有彩电，试求总体成数和拥有彩电户数的置信度为95%的置信区间。

1、甲乙两班同时参加《统计学原理》课程的测试，甲班平均成绩为81分，标准差为9.5分，乙班的成绩分组资料如下：按成绩分组学生人数（人）60以下 460~70 1070~80 2580~90 1490~100 2计算乙班学生的平均成绩，并比较甲乙两班，哪个班的平均成绩更有代表性？2、某车间有甲乙两个生产组，甲组平均每个人的日产量为36件，标准差为9.6件，乙组工人产量资料如下：日产量（件）工人数（人）15 1525 3835 3445 13要求：（1）计算乙组平均每个工人的日产量和标准差（2）比较甲乙两生产小组的日产量更有代表性3、某商店1990年各月末商品库存额资料如下：（超级重点题目）月份 1 2 3 4 5 6 8 11 12 库存额60 55 48 43 40 50 45 60 68 又知1月1日商品库存额为63万元，试计算上半年，下半年和全年的平均商品库存额。

4、已知两种商品的销售资料如下：品名单位销售额2002比2001销售量增长（%）2001 2002电视台5000 8880 23自行车辆4500 4200 -7合计9500 13080要求：（1）计算销售量总指标（2）计算由于销售量变动消费者增加或减少的支出金额5、某商店两种商品的销售额和销售价格的变化情况如下：（万元）商品单位销售额1996比1995年销售价格提高（%）1995 1996甲米120 130 10乙件40 36 12要求：（1）计算两件商品销售价格总指标和由于价格变动对销售额的影响绝对值（2）计算销售量总指数，计算由于销售变动消费者增加或减少的支出金额6、某企业上半年产品量与单位成本资料如下：月份产量（千克）单位成本（元）1 2 732 3 723 4 714 3 735 4 696 5 68要求：（1）计算相关系数，说明两个变量相关的密切程度（2）配合回归方程，指出产量每增加1000件时，单位成本平均变动多少？7、根据企业产品销售额（万元）和销售利润率（%）资料计算出如下数据：（重点题目）n=7 ∑x=18090 ∑y=31.1 ∑2x=535500 ∑2y=174.15∑xy=9318要求：（1）确定以利润为因变量的直线回归方程（2）解释式中回归系数的经济含义8、某企业第二季度产品产量与单位成本资料如下：月份产量（千件）单位成本（元）4 3 735 4 696 5 68要求：（1）定量判断产量与单位成本间的相关程度（2）建立直线回归方程，并说明b的经济含义解：（1）所需计算数据见下表：月份产量单位成本45 634 57369 68916 25219276 340合计1221050835因为，，所以产量每增加1000件时，即增加1单位时，单位成本的平均变动是：平均减少2.5元。