第三章—自适应滤波器

自适应滤波器原理
自适应滤波器是一种数字信号处理的方法，它基于信号的统计特性来自动调整滤波器的参数，以适应信号的变化。

其原理可以简要概括如下：
1. 自适应滤波器通过比较输入信号与期望输出信号之间的差异来调整滤波器的参数。

这种差异通常用误差信号来表示，它是输入信号与期望输出信号之间的差。

2. 滤波器的参数调整可分为离散时间和连续时间两种情况。

在离散时间中，滤波器的参数可以通过迭代更新来实现。

其中一个常用的方法是最小均方（LMS）算法，它通过不断调整滤波器的参数，使得误差信号的均方误差最小化。

3. 在连续时间中，自适应滤波器的参数调整可以通过梯度下降法来实现。

梯度下降法基于损失函数的梯度信息，通过更新参数的方向和步长来逐渐降低误差，直到收敛到最优解。

4. 自适应滤波器的应用广泛，特别是在信号处理、通信和控制系统中。

它可以用于去除信号中的杂波、抑制干扰、提升信号的质量等。

常见的应用包括语音降噪、信号恢复和自适应控制等领域。

总之，自适应滤波器通过根据信号的统计特性来调整滤波器的参数，以适应信号的变化。

它是一种有效的信号处理方法，具有广泛的应用前景。

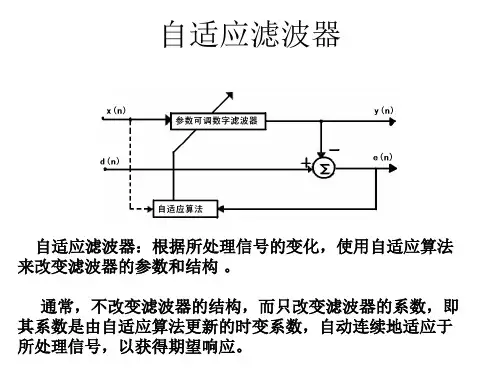
自适应滤波器原理是什么样的自适应滤波器是一种可以根据输入信号的特点自动调整参数的滤波器，其原理基于信号处理领域中的自适应算法。

这种滤波器能够根据输入信号的实时特性来灵活地调整滤波器的参数，以实现更有效的信号处理和数据分析。

自适应滤波器通常用于消除信号中的噪声、增强信号的特定成分或者对特定信号进行分析和识别。

自适应滤波器的基本原理是利用反馈控制的方法，通过不断调整滤波器的参数，使得滤波器的输出信号与期望信号之间的误差最小化。

在实际应用中，自适应滤波器主要包括两个关键部分：滤波器结构和自适应算法。

滤波器结构通常包括输入信号、滤波器系数以及输出信号。

输入信号经过滤波器系数的加权求和后得到输出信号。

自适应滤波器的特点在于其滤波器系数可以根据输入信号的实时特性进行调整，以便更好地适应信号的变化。

不同类型的自适应滤波器有不同的滤波器结构，如最小均方（LMS）滤波器、最小均方误差（LMSE）滤波器等。

自适应算法是实现自适应滤波器的关键，它决定了滤波器参数的调整方式。

常用的自适应算法包括最小均方误差算法（LMS）、最小均方误差算法（LMSE）、最大似然算法等。

这些算法通过对滤波器的误差信号进行分析和计算，不断地更新滤波器的参数，使得滤波器的输出逐渐逼近期望信号。

通过这种方式，自适应滤波器可以有效地处理各种信号，并在信号频谱和动态范围变化时保持较好的性能。

自适应滤波器在许多领域都有着广泛的应用。

在通信领域，自适应滤波器可以用于自动调节语音通信系统中的信道衰落和噪声，提高通信质量和可靠性。

在雷达系统中，自适应滤波器可以用于抑制干扰信号和杂波，提高目标检测的准确性。

此外，自适应滤波器还在生物医学信号处理、金融数据分析等领域有着重要的应用。

总的来说，自适应滤波器是一种能够根据信号特性自动调整参数的滤波器，通过滤除噪声、增强信号或分析信号等方式，实现对信号的有效处理和分析。

其原理基于自适应算法和滤波器结构的相互作用，使得滤波器能够更好地适应信号的变化，具有较强的鲁棒性和适应性。

论文第三章LMS和RLS自适应滤波器的仿真实现与比较自适应滤波器是一种能够根据输入信号的特性自动调整其滤波器性能的滤波器。

LMS（最小均方）和RLS（递归最小二乘）是两种常用的自适应滤波器算法。

本文将对这两种算法进行仿真实现，并对其性能进行比较。

首先，我们实现了LMS自适应滤波器的仿真。

LMS自适应滤波器通过不断调整滤波器系数来最小化预测误差的均方误差。

在仿真中，我们生成了一个包含噪声的信号作为输入信号，并设置了一个期望的滤波器响应。

然后，我们使用LMS算法来自适应调整滤波器的系数，使其逼近期望的响应。

最后，我们比较了实际和期望的滤波器响应，并计算了均方误差。

接下来，我们实现了RLS自适应滤波器的仿真。

RLS自适应滤波器使用递归最小二乘算法来调整滤波器的系数。

在仿真中，我们同样生成了一个包含噪声的输入信号，并设置一个期望的滤波器响应。

然后，我们使用RLS算法来递归地更新滤波器的系数，使其逼近期望的响应。

最后，我们比较了实际和期望的滤波器响应，并计算了均方误差。

在比较LMS和RLS自适应滤波器的性能时，我们主要关注以下几个方面：收敛速度、稳定性和计算复杂度。

收敛速度是指自适应滤波器达到期望的响应所需要的时间。

稳定性是指自适应滤波器在逼近期望的响应时是否会出现不稳定的情况。

计算复杂度是指实现自适应滤波器算法所需要的计算量。

根据我们的仿真结果，我们可以得出以下结论：LMS自适应滤波器的收敛速度较快，但在达到期望的响应后可能会出现振荡的情况，所以在实际应用中需要设置合适的步长参数来平衡收敛速度和稳定性。

RLS自适应滤波器的收敛速度较慢，但在达到期望的响应后相对稳定，不容易出现振荡的情况。

然而，RLS算法的计算复杂度较高，需要大量的计算资源。

总的来说，LMS和RLS自适应滤波器都有各自的优势和劣势。

在实际应用中，我们需要根据具体的需求来选择合适的自适应滤波器算法。

如果追求较快的收敛速度和较低的计算复杂度，可以选择LMS算法；如果追求较稳定的滤波器性能并且有充足的计算资源，可以选择RLS算法。

自适应滤波器设计分析自适应滤波器是一种能够根据输入信号动态调整滤波器参数的滤波器，可以用于信号处理、通信系统、自适应控制等领域。

其主要思想是根据输入信号与期望输出信号之间的差异来调整滤波器的参数，从而实现对输入信号的有效滤波，提高信号质量和系统性能。

1.自适应滤波器的原理：自适应滤波器的原理是基于自适应信号处理的基本思想，即通过不断调整滤波器参数来使得滤波器的输出与期望输出之间的差异最小化。

常见的自适应滤波器算法有最小均方误差（LMS）算法、最小二乘（LS）算法、递归最小二乘（RLS）算法等。

2.自适应滤波器的性能指标：自适应滤波器的性能可以通过误差信号的均方误差来评价，即滤波器输出与期望输出之间的误差的二次平均值。

此外，自适应滤波器的收敛速度也是一个重要的性能指标，即滤波器能够多快地调整到最佳参数值。

3.自适应滤波器的应用：自适应滤波器可以应用于很多领域，比如智能手机中的降噪算法、语音识别系统中的语音增强算法、智能监控系统中的运动检测算法等。

不同应用场景下，自适应滤波器的设计方法和参数设置也会有所不同。

4.自适应滤波器的设计步骤：自适应滤波器的设计一般可以分为以下几个步骤：首先，确定输入信号和期望输出信号；然后，选择适当的自适应滤波器算法和滤波器结构；接着，初始化滤波器参数，并根据输入信号和期望输出信号来不断调整滤波器参数；最后，检验滤波器的性能，并根据需要进行调整和改进。

5.自适应滤波器的优缺点：自适应滤波器的优点是可以根据输入信号的变化来自动调整滤波器参数，从而适应不同的信号环境和系统要求；缺点是需要大量的计算和存储资源，对处理速度要求高，同时，滤波器的性能也会受到系统误差、信号相关性等因素的影响。

在自适应滤波器设计分析中，需要结合具体的应用场景和需求来选择合适的自适应滤波器算法和参数设置，并进行性能评估和调优。

同时，还需要考虑实际系统的计算和存储资源限制，以及对处理速度和滤波器性能的要求。

自适应滤波器c语言实现摘要：一、自适应滤波器简介二、LMS算法原理三、C语言实现自适应LMS算法1.算法流程2.代码实现3.实时处理与优化四、应用案例与效果分析五、总结与展望正文：一、自适应滤波器简介自适应滤波器是一种能够根据输入信号特征自动调整滤波参数的滤波器，广泛应用于信号处理、通信、图像处理等领域。

其中，LMS（Least Mean Squares，最小均方）算法是自适应滤波器中的一种常用算法，以其简单、易实现的特点受到广泛关注。

二、LMS算法原理LMS算法是一种基于Widrow-Hoff思想的在线学习算法，其核心思想是通过最小化误差平方和，不断调整滤波器的参数，使滤波器输出与输入信号尽可能接近。

LMS算法的主要优点是收敛速度快，适应性强，但对噪声敏感。

三、C语言实现自适应LMS算法3.1 算法流程实现自适应LMS算法的过程主要包括以下几个步骤：（1）初始化滤波器参数；（2）输入信号经过滤波器传递函数得到滤波器输出；（3）计算误差信号；（4）更新滤波器参数；（5）重复步骤2-4，直至达到预设迭代次数或满足收敛条件。

3.2 代码实现以下是基于C语言的自适应LMS算法实现框架：```c#include <stdio.h>#include <math.h>// 滤波器系数float alpha, beta;// 滤波器状态float xn[N], yn[N];// 误差信号float error;void lms_filter(float x[], int n, float y[]) {for (int i = 0; i < n; i++) {// 计算滤波器输出yn[i] = beta * yn[i - 1] + alpha * x[i];// 计算误差error = y[i] - yn[i];// 更新滤波器系数beta = beta * (1 - alpha * error);}}```3.3 实时处理与优化在实际应用中，为了提高自适应LMS算法的性能，可以采取以下措施：（1）选择合适的滤波器结构，如FIR、IIR等；（2）调整滤波器系数更新速度，即调整alpha值；（3）采用噪声抑制技术，如噪声整形、卡尔曼滤波等；（4）结合其他自适应算法，如递推最小均方误差（RLS）算法等。

自适应滤波器的设计与实现毕业论文自适应滤波器的设计与实现毕业论文目录第一章前言 (1)1.1 自适应滤波器简介 (1)1.2 选题背景及研究意义 (1)1.3 国外研究发展现状 (2)第二章自适应滤波器的基础理论 (4)2.1 滤波器概述 (4)2.1.1 滤波器简介 (4)2.1.2 滤波器分类 (4)2.1.3 数字滤波器概述 (4)2.2 自适应滤波器基本理论 (7)2.3 自适应滤波器的结构 (9)第三章自适应滤波器递归最小二乘算法 (11)3.1 递归最小二乘算法 (11)3.1.1 递归最小二乘算法简介 (11)3.1.2 正则方程 (11)3.1.3 加权因子和正则化 (16)3.1.4 递归计算 (18)3.2递归最小二乘(RLS)算法的性能分析 (22)第四章基于MATLAB自适应滤波器仿真 (23) 4.1 正弦波去噪实验 (23)4.2 滤波器正则化参数的确定 (28)4.2.1 高信噪比 (28)4.2.2 低信噪比 (31)4.2.3 结论 (33)4.3 输入信号不同对滤波效果的影响 (33)4.3.1 输入信号为周期信号 (33)4.3.2 输入信号为非周期信号 (38)第五章结论与展望 (44)5.1 结论 (44)5.2 对进一步研究的展望 (44)参考文献 (45)致谢 (46)附录 (46)声明 (58)第一章前言1.1自适应滤波器简介自适应滤波器属于现代滤波的畴，它是40年代发展起来的自适应信号处理领域的一个重要应用，自适应信号处理主要是研究结构可变或可调整的系统，可以通过自身与外界的接触来改善自身对信号处理的性能，通常这类系统是时变的非线性系统，可以自动适应信号传输的环境和要求，无须详细的知道信号的结构和实际知识，无须精确设计处理系统本身。

自适应系统的非线性特性主要是由系统对不同的信号环境实现自身参数的调整来确定的。

自适应系统的时变特性主要是由其自适应响应或自适应学习过程来确定的，当自适应过程结束和系统不再进行时，有一类自适应系统可成为线性系统，并称为线性自适应系统，因为这类系统便于设计且易于数学处理，所以实际应用广泛。

自适应滤波器的原理与应用自适应滤波器是一种能够自动调整滤波参数以适应信号特性的信号处理方法。

它广泛应用于通信、声音处理、图像处理等领域。

本文将介绍自适应滤波器的原理和应用，并对其在不同领域中的具体应用进行讨论。

一、自适应滤波器的原理自适应滤波器的原理基于对输入信号进行实时分析和调整滤波参数。

它通过对输入信号和预期输出信号之间的误差进行监测，并根据误差的大小来自动调整滤波器的参数。

具体而言，自适应滤波器主要包括以下几个步骤：1. 信号采样与分析：自适应滤波器首先对输入信号进行采样，并根据采样数据对信号进行分析。

这一步骤旨在了解输入信号的特征和分布情况，为后续的参数调整提供依据。

2. 参数初始化：自适应滤波器在开始时需要对参数进行初始化。

常见的方式是将参数设置为一个初始值，然后在后续的迭代过程中进行调整。

3. 滤波器输出计算：通过对输入信号和滤波器参数进行卷积运算，得到滤波器的输出结果。

这一步骤可以用来与预期输出进行比较，以计算误差。

4. 误差计算与参数调整：根据滤波器输出与预期输出之间的误差，自适应滤波器通过某种算法来调整滤波器的参数，使误差逐渐减小。

常见的算法有最小均方差算法（LMS）和最小误差算法（RLS）等。

5. 参数更新与迭代：通过不断地计算误差和调整参数，自适应滤波器不断迭代，直到达到期望的滤波效果。

二、自适应滤波器的应用1. 语音信号处理：自适应滤波器在语音信号处理中有广泛的应用。

例如，可以利用自适应滤波器对语音信号中的噪声进行实时抑制，提高语音识别和通信质量。

此外，自适应滤波器还可以用于语音增强、回声消除等方面。

2. 图像处理：在图像去噪和增强方面，自适应滤波器也有重要的应用。

通过对图像进行采样和分析，自适应滤波器可以实时调整滤波参数，以去除图像中的噪声并增强图像的细节。

3. 通信系统：在通信系统中，自适应滤波器可以用于抑制多径干扰和自适应均衡。

通过实时调整滤波器参数，可以实现信号的自动补偿和增强。