914740-数字图像处理-第3讲直方图规定化

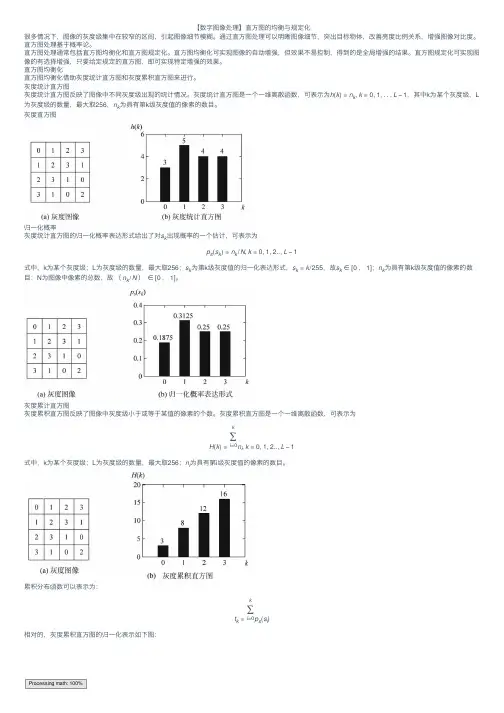
【数字图像处理】直⽅图的均衡与规定化很多情况下，图像的灰度级集中在较窄的区间，引起图像细节模糊。

通过直⽅图处理可以明晰图像细节，突出⽬标物体，改善亮度⽐例关系，增强图像对⽐度。

直⽅图处理基于概率论。

直⽅图处理通常包括直⽅图均衡化和直⽅图规定化。

直⽅图均衡化可实现图像的⾃动增强，但效果不易控制，得到的是全局增强的结果。

直⽅图规定化可实现图像的有选择增强，只要给定规定的直⽅图，即可实现特定增强的效果。

直⽅图均衡化直⽅图均衡化借助灰度统计直⽅图和灰度累积直⽅图来进⾏。

灰度统计直⽅图灰度统计直⽅图反映了图像中不同灰度级出现的统计情况。

灰度统计直⽅图是⼀个⼀维离散函数，可表⽰为h (k )=n k ,k =0,1,...L −1，其中k 为某个灰度级，L 为灰度级的数量，最⼤取256，n k 为具有第k 级灰度值的像素的数⽬。

灰度直⽅图归⼀化概率灰度统计直⽅图的归⼀化概率表达形式给出了对s k 出现概率的⼀个估计，可表⽰为p s (s k )=n k /N ,k =0,1,2..,L −1式中，k 为某个灰度级；L 为灰度级的数量，最⼤取256；s k 为第k 级灰度值的归⼀化表达形式，s k =k /255，故s k ∈[0，1]；n k 为具有第k 级灰度值的像素的数⽬；N 为图像中像素的总数，故（n k /N ）∈[0，1]。

灰度累计直⽅图灰度累积直⽅图反映了图像中灰度级⼩于或等于某值的像素的个数。

灰度累积直⽅图是⼀个⼀维离散函数，可表⽰为H (k )=k ∑i =0n i ,k =0,1,2..,L −1式中，k 为某个灰度级；L 为灰度级的数量，最⼤取256；n i 为具有第i 级灰度值的像素的数⽬。

累积分布函数可以表⽰为：t k =k ∑i =0p s (s i )相对的，灰度累积直⽅图的归⼀化表⽰如下图：Processing math: 100%原理步骤直⽅图均衡化主要⽤于增强动态范围偏⼩的图像的反差。

图像直方图均衡的标准化处理均衡化基本原理：对在图像中像素个数多的灰度值（即对画面其主要作用的灰度值）进行展宽，而对像素个数少的灰度值进行归并，从而达到清晰图像的目的。

代码：img=imread('tim.jpg');figure,imshow(img);[m,n]=size(img); %测量图像尺寸参数h=zeros(1,256) %预创建存放灰度出现概率的向量for k=0:255h(k+1)=length(find(img==k))/(m*n);endfigure,bar(0:255,h,'k') %绘制直方图title('原图像直方图')xlabel('灰度值')ylabel('出现概率')S1=zeros(1,256);for i=1:256for j=1:iS1(i)=h(j)+S1(i); %计算SkendendS2=round(S1*256); %将Sk归到相近级的灰度for i=1:256heq(i)=sum(h(find(S2==i))); %显示均衡化后的直方图endfigure,bar(0:255,heq,'k') %显示灰度变化曲线title('均衡化后的直方图')xlabel('灰度值')ylabel('出现概率')figure,plot(0:255,S2,'r') %显示灰度变化曲线legend('灰度变化曲线')xlabel('原图像灰度级')ylabel('均衡化后灰度级')TR=img;for i=0:255TR(find(img==i))=S2(i+1); %将各个像素归一化后的灰度值付给这个像素endfigure,imshow(TR) %将各个像素归一化后的灰度值赋给这个像素 title('均衡化后图像')imwrite(TR,'tim.jpg');实验效果图：原图像原图像直方图标准化后图像标准化后直方图：灰度变化曲线图像直方图均衡的规定化处理直方图规定化的基本原理：有目的地增强某个灰度区间的图像，即能够人为地修正直方图的形状，使之与期望的形状相匹配。

XX 大学实验报告
（一） 掌握数字图像的直方图规定化处理的算法和方法。

（二） 熟悉数字图像的直方图规定化处理的算法原理。

按照实验内容及参考程序，独立完成此次实验，记下不懂的知识点，查阅资料或者向老 师咨询。

直方图规定化是用于产生处理后有特殊直方图的图像方法。

学院:
专业: 班级: 姓名 实验时间 实验项目名称
实验二：数字图像的直方图规定化处理
令
p r （r ）和Pz （z ）分别为原始图像和期望图像的灰度概率密度函数。

和期望图像均作直方图均衡化处理，应有：
r
s T （r ） 0 p r （r ）dr ，V G （Z ）
对原始图像
z 0
P z
(z )dz ，z
G
1
(V)
由于都是作直方图均衡化处理，所以处理后的原图像的灰度概率密度函数
p S （s ）及理
想图像的灰度概率密度函数 P V （V ）是相等的。

因此，可以用变换后的原始图像灰度级
S
代替上式中的V, 即Z G 1[T （r ）]。

利用此式可以从原始图像得到希望的图像灰度级。

对离散图像，有
P Z (ZJ
虹，V i G (乙)^P z (Z i )， Z i
G 1(S i ) G 1[T(r i )]
n
i 0
综上所述，数字图像的直方图规定化就是将直方图均衡化后的结果映射到期望的理想直 方图上，使图像按人的意愿去变换。

数字图像的直方图规定的算法如下：
（一）将原始图像作直方图均衡化处理， 求出原图像中每一个灰度级 r i 所对应的变
学号 指导教师
实验组 成绩。

数字图像处理实验报告直方图匹配规定化直方图均衡化能够自动增强整个图像的对比度，但它的具体增强效果不容易控制，处理的结果总是得到全局均匀化的直方图。

实际上有时需要变换直方图，使之成为某个特定的形状，从而有选择地增强某个灰度值范围内的对比度。

这时可以采用比较灵活的直方图规定化。

一般来说正确地选择规定化的函数可以获得比直方图均衡化更好的效果。

所谓直方图规定化，就是通过一个灰度映像函数，将原灰度直方图改造成所希望的直方图。

所以，直方图修正的关键就是灰度映像函数。

直方图匹配方法主要有3个步骤（这里设M和N分别为原始图和规定图中的灰度级数，且只考虑N≤M的情况）：(1) 如同均衡化方法中，对原始图的直方图进行灰度均衡化：(2) 规定需要的直方图，并计算能使规定的直方图均衡化的变换：(3) 将第1个步骤得到的变换反转过来，即将原始直方图对应映射到规定的直方图，也就是将所有pf(fi)对应到pu(uj)去。

一、A图直方图规定B图Matlab程序:%直方图规定化clear allA=imread('C:\Users\hp\Desktop\A.tif'); %读入A图像imshow(A) %显示出来title('输入的A图像')%绘制直方图[m,n]=size(A); %测量图像尺寸B=zeros(1,256); %预创建存放灰度出现概率的向量for k=0:255B(k+1)=length(find(A==k))/(m*n); %计算每级灰度出现的概率，将其存入B中相应位置endfigure,bar(0:255,B,'g'); %绘制直方图title('A图像直方图')xlabel('灰度值')ylabel('出现概率')axis([0,260,0,0.015])C=imread('C:\Users\hp\Desktop\B.tif');%读入B图像imshow(C) %显示出来title('输入的B图像')%绘制直方图[m,n]=size(C); %测量图像尺寸D=zeros(1,256); %预创建存放灰度出现概率的向量for k=0:255D(k+1)=length(find(C==k))/(m*n); %计算每级灰度出现的概率，将其存入D中相应位置endfigure,bar(0:255,D,'g'); %绘制直方图title('B图像直方图')xlabel('灰度值')ylabel('出现概率')axis([0,260,0,0.015])S1=zeros(1,256);for i=1:256for j=1:iS1(i)=D(j)+S1(i); %计算B灰度图累计直方图endendcounts=Bfigure,bar(0:255,counts,'r')title('A图像直方图 ')S2=zeros(1,256);for i=1:256for j=1:iS2(i)=counts(j)+S2(i);endend; %"累计"规定化直方图%对比直方图，找到相差最小的灰度级for i=1:256for j=1:255if S1(j)<=S2(i)&S1(j+1)>=S2(i)if abs(S1(j)-S2(i))<=abs(S1(j+1)-S2(i)) T(i)=j;else T(i)=j+1;endendendend%确定变换关系，重组直方图H=zeros(1,256);H(1)=S2(1);for i=2:255if T(i-1)>0for k=(T(i-1)+1):T(i)H(i)=H(i)+D(k);endelse H(i)=0;endendfigure,bar(0:255,H,'g') %显示规定化后的直方图title('A规定B后的直方图')xlabel('灰度值')ylabel('出现概率')axis([0,260,0,0.6])%显示规定图PA=C; %将各个像素归一化后的灰度值赋给这个像素for i=1:mfor j=1:nfor k=2:255if T(k-1)<=C(i,j)&C(i,j)<=T(k)PA(i,j)=k;break;endendendendfigure,imshow(PA) %显示规定化后的图像title('A规定B后图像')imwrite(PA,'guidinghua.bmp');二、用已知直方图规定A图规定灰度为[zeros(1,49),0.3,zeros(1,49),0.1,zeros(1,49),0.2,zeros(1,49),0.1,zeros(1,49 ),0.2,zeros(1,49),0.1]Matlab程序：clear allA=imread('C:\Users\hp\Desktop\B.tif'); %读入A图像imshow(A) %显示出来title('输入的A图像')%绘制直方图[m,n]=size(A); %测量图像尺寸B=zeros(1,256); %预创建存放灰度出现概率的向量for k=0:255B(k+1)=length(find(A==k))/(m*n); %计算每级灰度出现的概率，将其存入B中相应位置endfigure,bar(0:255,B,'g'); %绘制直方图title('A图像直方图')xlabel('灰度值')ylabel('出现概率')axis([0,260,0,0.015])S1=zeros(1,256);for i=1:256for j=1:iS1(i)=B(j)+S1(i); %计算原灰度图累计直方图endendcounts=[zeros(1,49),0.3,zeros(1,49),0.1,zeros(1,49),0.2,zeros(1,49),0.1,zer os(1,49),0.2,zeros(1,49),0.1];%规定化直方图figure,bar(1:300,counts,'r')title('规定化直方图')S2=zeros(1,256);for i=1:256for j=1:iS2(i)=counts(j)+S2(i);endend; %"累计"规定化直方图%对比直方图，找到相差最小的灰度级for i=1:256for j=1:256if S1(j)<=S2(i)&S1(j+1)>=S2(i)if abs(S1(j)-S2(i))<=abs(S1(j+1)-S2(i)) T(i)=j;else T(i)=j+1;endendendend%确定变换关系，重组直方图H=zeros(1,256);H(1)=S2(1);for i=2:256if T(i-1)>0for k=(T(i-1)+1):T(i)H(i)=H(i)+B(k);endelse H(i)=0;endendfigure,bar(0:255,H,'g') %显示规定化后的直方图title('规定化后的直方图')xlabel('灰度值')ylabel('出现概率')axis([0,260,0,0.6])%显示规定图PA=A; %将各个像素归一化后的灰度值赋给这个像素for i=1:mfor j=1:nfor k=2:256if T(k-1)<=A(i,j)&A(i,j)<=T(k)PA(i,j)=k;break;endendendendfigure,imshow(PA) %显示规定化后的图像title('规定化后图像')imwrite(PA,'guidinghua.bmp');。

图像变换是数字图像处理中的一种综合变换，如直方图变换。

使用C语言对位图文件的头信息进行读取，从而对图像进行直方图均衡化处理和灰度变换。

直方图均衡化大多数原始的遥感图像由于其灰度分布集中在较窄的范围内，使图像的细节不够清晰，对比度较低。

为了使图像的灰度范围拉开或使灰度均匀分布，从而增大反差，使图像细节清晰，以达到增强的目的，通常采用直方图均衡化及直方图规定化两种变换。

本文主要介绍直方图均衡化并进行实验。

直方图均衡化的概念直方图均衡化（Histogram Equalization）又称直方图平坦化，实质上是对图像进行非线性拉伸，重新分配图像象元值，使一定灰度范围内象元值的数量大致相等。

这样，原来直方图中间的峰顶部分对比度得到增强，而两侧的谷底部分对比度降低，输出图像的直方图是一个较平的分段直方图：如果输出数据分段值较小的话，会产生粗略分类的视觉效果。

直方图均衡化理论假设灰度级为归一化至范围[0,1]内的连续量，并令Pr (r)表示某给定图像中的灰度级的概率密度函数（PDF），其下标用来区分输入图像和输出图像的PDF。

假设我们对输入灰度级执行如下变换，得到（处理后的）输出灰度级s：S=T(r)=∫0r Pr(w)dw式中w 是积分的哑变量。

可以看出，输出灰度级的概率密度函数是均匀的，即a.当0≤s≤1 时，Ps(s)=1b.当s 为其他时，Ps(s)=0换言之，前述变换生成一幅图像，该图像的灰度级较为均衡化，且覆盖了整个范围[0,1]。

灰度级均衡化处理的最终结果是一幅扩展了动态范围的图像，它具有较高的对比度。

该变换函数只不过是一个累积分布函数（CDF）。

直方图均衡化算法直方图均衡化算法将原图像的直方图改变为在整个灰度范围内基本均匀地分布的形式，由此扩大了像素灰度的动态范围，从而增强了图像的对比度。

直方图均衡化算法步骤为：1) 给出原始图像的所有灰度级k S (k=0,1,…,L-1)。

2) 统计原始图像各灰度级的像素数k n 。

《数字图像处理》实验报告（二）学号：____________ 姓名：__________ 专业：____ 课序号：__________计算机科学与技术学院实验2直方图均衡化一、实验学时：4学时（本部分占实验成绩的40%）二、实验目的：1、理解直方图均衡化的原理及步骤；2、编程实现图像（灰度或彩色）的直方图均衡化。

三、必须学习和掌握的知识点：直方图均衡化是一种快速有效且简便的图像空域增强方法，在图像处理中有着非常重要的意义，因此要求掌握。

四、实验题目：编程实现灰度图像的直方图均衡化处理。

要求给出原始图像的直方图、均衡化图像及其直方图和直方图均衡化时所用的灰度级变换曲线图。

五、思考题：（选做，有加分）实现对灰度图像的直方图规定化处理。

六、实验报告：请按照要求完成下面报告内容并提交源程序、可执行程序文件和实验结果图像。

1、请详细描述本实验的原理：1.直方图均衡化概述图像对比度增强的方法可以分成两类:一类是直接对比度增强方法;另一类是间接对比度增强方法。

直方图拉伸和直方图均衡化是两种最常见的间接对比度增强方法。

直方图拉伸是通过对比度拉伸对直方图进行调整，从而“扩大”前景和背景灰度的差别，以达到增强对比度的目的，这种方法可以利用线性或非线性的方法来实现;直方图均衡化则通过使用累积函数对灰度值进行“调整”以实现对比度的增强。

直方图均衡化的英文名称是Histogram Equalization.直方图均衡化是图像处理领域中利用图像直方图对对比度进行调整的方法。

这种方法通常用来增加许多图像的局部对比度，尤其是当图像的有用数据的对比度相当接近的时候。

通过这种方法，亮度可以更好地在直方图上分布。

这样就可以用于增强局部的对比度而不影响整体的对比度，直方图均衡化通过有效地扩展常用的亮度来实现这种功能。

2基本思想直方图均衡化处理的“中心思想”是把原始图像的灰度直方图从比较集中的某个灰度区间变成在全部灰度范围内的均匀分布。

58表3.3.1所示是以上直方图均衡化的运算步骤和结果（其中第4步的取整表示取方括号中实数的整数部分）。

表3.3.1 直方图均衡化计算列表序号运算步骤和结果1 列出原始图灰度级f，f = 0, 1,…, 7 0 123456 72 列出原始直方图0.020.050.090.120.140.2 0.22 0.163 用式（3.3.4）计算原始累积直方图0.020.070.160.280.420.62 0.84 1.004 取整g = int[(L–1)g f + 0.5]0 0 1 2 3 4 6 75 确定映射对应关系（f→g）0, 1 → 0 2 →13→24→35→ 46 → 67 → 76 计算新直方图0.070.090.120.140.2 0 0.22 0.16由表3.3.1可见，原始直方图的一些不同灰度有可能映射到均衡化直方图的同一个灰度，所以均衡化直方图中实际使用的灰度级数有可能比原始直方图的灰度级数少。

例3.3.3 直方图均衡化效果实例图3.3.5所示是直方图均衡化的一个实例。

图3.3.5（a）和图3.3.5（b）分别为一幅8 bit灰度级的原始图像和它的直方图。

这里原始图像较暗且动态范围较小，反映在直方图上就是其直方图所占据的灰度值范围比较窄且集中在低灰度值一边。

图3.3.5（c）和图3.3.5（d）分别为对原始图进行直方图均衡化得到的结果及其对应的直方图，现在直方图占据了整个图像灰度值所允许的范围。

由于直方图均衡化增加了图像灰度动态范围，所以也增加了图像的对比度，反映在图像上就是图像有较大的反差，许多细节可看得比较清晰了。

但需要注意，直方图均衡化在增强反差的同时也增加了图像的可视粒度，即图像中有许多粗颗粒的像素团出现。

（a）（b）（c）（d）图3.3.5 直方图均衡化实例3.3.2 直方图规定化直方图均衡化的优点是能自动地增强整个图像的对比度，计算过程中没有用户可以调整的参数。