《等式的性质和解方程》练习

等式的性质(一)练习题(共2页)
--本页仅作为文档封面，使用时请直接删除即可--
--内页可以根据需求调整合适字体及大小--
等式的性质（一）练习题
1、填一填。

（1）等式两边同时加上或减去（），等式仍然成立。

这是等式的性质。

（2）使方程左右两边相等的未知数的值，叫做（）。

求方程解的过程叫做（）。

2、在○里填上运算符号，在□里填上合适的数。

（1） x+38=300
解：X+38○□=300○□
X=□
（2）X－64=23
解：X－64○□=23○□
X=□
3、括号里哪个X的值是方程的解请圈起来。

X－16=20 （ X=18 X=36）
+X=11 （ X= X=）
X－6= （ X= X=）
4、解方程并检验。

＋X= X＋=40 X－=
5、根据图中的数量关系列方程并解答。

（1）
X 元 元
（2）有X 吨煤，运走吨，还剩吨。

（3）
原价： X 元
（4）
小军体重千克 小林体重X 千克
6、 想一想，做一做。

已知 X －5=20 ，求 6X+5 的值。

我一共用了元。

促销大酬宾 优惠：420元 现价：4560元 我比你轻12千克。

小学数学五年级上册5.4.1利用等式性质1解方程同步练习一、单选题1．如果方程9+x=17，那么5x-8=()。

A．22B．32C．48D．402．方程x-0.8=2.4与ax=9.6有相同的解，则a的值是（）A．3B．6C．0.3D．0.63．在□里填上1.3，就使方程（）的解是x=6。

A．□×x =7.8B．x＋□=8.1C．x-□=4.44．要使方程x-5.6=11.8的左边只剩下x，等式应（）。

A．左边加上5.6B．两边同时减去5.6C．两边同时加上5.6 5．如果在等式2x=8的左右两边同时加上5，（）。

A．x值仍然等于4B．x值会增加5C．x值会减少5D．x值是原来的5倍6．与方程5x+5=11.5相等的式子是（）。

A．5x=11.5B．x+5=11.5C．5x=11.5-5D．5x=11.5+5二、填空题7．在横线上填上适当的数，使每个方程的解都是x=6。

-x=3.9x÷=1.5×x=7.28．已知4x=y，根据等式的性质，则4x+7=y+；20x=y× 。

9．已知△-x=76，如果方程的解是x=15，那么△=10．如果8x=3x+50，那么8x=50。

11．已知x-a=b，那么x-a+=b+a。

三、计算题12．解方程。

（1）9－x= 78（2）715＋x=1930（3）x－34=5613．解方程（1）x-13=37 （2）x+19=25四、解答题14．列方程求解。

一个数与2.5的差是12.5，求这个数。

15．列方程解决问题。

16．看图列方程解决问题。

五、综合题17．根据等式的性质在横线里填运算符号，在括号里填数。

（1）x+72=100x+72-72=100（）（2）x-36=50x-36+36=50（）（3）x-13=62x-13+13=62（）（4）29+x=4429+x（）=44（）答案解析部分1．【答案】B【解析】【解答】解：9+x=17x=17-9x=8把x=8代入，5x-8=5×8-8=40-8=32。

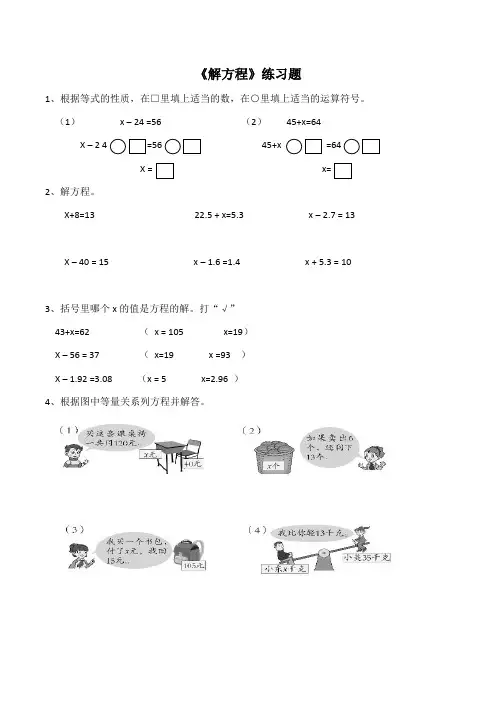
《解方程》练习题1、根据等式的性质，在□里填上适当的数，在○里填上适当的运算符号。

（1）x – 24 =56 （2）45+x=64X –45+x =642、解方程。

X+8=13 22.5 + x=5.3 x – 2.7 = 13 X – 40 = 15 x – 1.6 =1.4 x + 5.3 = 103、括号里哪个x的值是方程的解。

打“√”43+x=62 （x = 105 x=19）X – 56 = 37 （x=19 x =93 ）X – 1.92 =3.08 （x = 5 x=2.96 ）4、根据图中等量关系列方程并解答。

5、在○里填上“＞”、“＜”或“＝”。

（1）当x=12时：5x 70 x÷2 5（2）当x=4时：17x 68 12÷x 7（3）当x=0.2时， 1 x÷0.2（4）当x=88时：x +14 96 x÷4 22（5）当x=1时： 1 7÷x 1.6、判断。

（1）方程2x – 7 =13的解是x = 3。

（）（2）等式两边同时乘或除以相同的数，等式仍然成立。

（）（3）x=0是方程7x=7的解。

（）（4）x=0不可能是方程的解。

（）（5）如果x=7，则61 – x =54. （）7、根据题意列方程解答。

（1）（2）大象的体重是5.76吨，是一头牛体重的4.5倍。

这头牛体重多少吨？（3）一根铁丝长3.5米，第一次剪去一些后，第二次剪去0.15米，这是铁丝比原来短了1.4 米。

第一次剪去多少米？（4）一根铁丝截成两段，甲段是乙段的3倍，比乙段长17米，原来这根铁丝长多少米？（5）已知方程x÷4=100与y – x =80中的x表示的数相等，求x、y各等于多少？附参考答案1、（1）x - 24 +24=56+24，x =80，（2）45+x - 45 =64 - 45，x=192、解方程。

x=5，x=17.2，x=15.7，x=55，x=3，x=4.73、选x的值。

苏教版数学五年级下册试题1.3等式的性质和解方程（二）同步练习（含答案）班级：姓名：等级：一、选择题1．方程2x+1.9=2的解是( )。

A．x=0.5 B．x=5 C．x=0.052．已知3x+7=25，那么6x+1=（）A．22 B．37 C．303．在2.9+x=2.9和2.9x=2.9这两个方程中，x的值（）A．相等B．不相等C．无法比较4．x＝10是下面方程（）的解。

A．5x＋6x＝1.1 B．3x－27＝3 C．x×10＝15．与方程3x+8=68的解相同的是（）A．12x=240 B．8+2x=68 C．15x+x=280二、填空题6．一本书共120页，王老师每天看22页，已经看了x天，还剩（）页。

7．如果3x=12.3，那么x-2.5=（）。

8．看图列方程_____________________9．一个数乘上0.5减去2等于3，这个数为（）。

10．当x=0.5时，4x+3的值是（）．当x=（）时，4x+3=7．11．把方程补完整，并求出方程的解.12.5加上x的3倍等于20，求x．________=20解：x=________12．在○里填上“>”“<”或“=”。

（1）当x=13时，7x○91；（2）当x=0.8时，x÷0.4○0.4；（3）当x=49时，x-25○25；（4）当x=8.6时，48+x○8×7.6。

三、计算题13．解下列方程。

要验算哟!（1）x+2.2=6.3 （2） x÷0.7=0.8 （3） 1.6x=6.4 （4）x-9=10 （5）x-1.8=3 （6） x÷7=0.3 四、看图列方程并解答。

14.15.正方形的周长是10米.求边长是多少米？参考答案1．C2．B3．B4．B5．A6．120－22x7．1.68．x+3x=1209．x＝1010．5 111．12.5+3x 2.512．=；＞；＜；＜13．x=4.1 x=0.56 x=4x=19 x=4.8 x=2.1 检验略14.3x=180 x=6015.4x=10 x=2.5一、现代文阅读1．现代文阅读阅读下文，回答问题。

第三章 一元一次方程3.1.2 等式的性质一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的． 1．根据等式性质，由x =y 可得 A ．4x =y +4B ．cx =cyC ．2x –8=2y +8D ．x c =−y c【答案】B2．已知a =b ，则下列等式不一定成立的是 A ．a –b =0 B ．–5a =–5bC ．ac =bcD ．2a c =2b c【答案】D【解析】A 、a =b 两边都减去b 得，a –b =0，故本选项错误； B 、a =b 两边都乘以–5得，–5a =–5b ，故本选项错误； C 、a =b 两边都乘以c 得，ac =bc ，故本选项错误； D 、c =0时，2a c 与2b c都无意义，故本选项正确． 故选D ．3．下列各对等式，是根据等式的性质进行变形的，其中错误的是 A ．4y –1=5y +2→y =–3B ．2y =4→y =4–2C ．0.5y =–2→y =2×（–2）D ．1–13y =y →3–y =3y 【答案】B【解析】A 、根据等式性质1，4y –1=5y +2两边都减去4y –2，即可得到y =–3，变形正确，故选项错误； B 、根据等式性质2，两边都除以2，即可得到y =4÷2，变形错误，故选项正确；C 、根据等式性质2，0.5y =–2两边都乘以2，即可得到y =2×（–2），变形正确，故选项错误；D 、根据等式性质2，1–13y =y 两边都乘以3，即可得到3–y =3y ，变形正确，故选项错误． 故选B ． 4．如果x =m 是方程12x −m =1的根，那么m 的值是 A ．0B ．2C ．–2D ．–6【答案】C【解析】把x =m 代入方程，得12m –m =1，解得m =–2．故选C ． 5．把方程0.3x=1.2左边的分母化为整数后可得到 A ．3x =1.2 B ．103x =1.2 C ．3x =12D ．103x=12 【答案】B【解析】方程左边的分数分子分母同时乘以10得：103x=1.2．故选B ． 二、填空题：请将答案填在题中横线上． 6．等式的两条性质是：（1）等式两边都__________（或__________）同一个__________或同一个__________，所得的结果仍是等式；（2）等式两边都__________（或__________）同一个__________（__________）所得的结果仍是等式． 【答案】（1）加上，减去，数，字母；（2）乘以，除以不为0的数，或字母7．如果a –3=b –3，那么a =__________，其根据是__________． 【答案】b ，等式性质1【解析】根据等式性质1，等式a –3=b –3的两边同时加3，结果仍相等．因此有（a –3）+3=（b –3）+3，化简得a =b ．8．若方程2x +6=0与关于y 的方程3y +2m =15的解互为相反数，则m =__________．【答案】3三、解答题：解答应写出文字说明、证明过程或演算步骤．9．根据等式的性质解方程：（1）3x+1=7；（2）23x−1=5．【答案】（1）x=2；（2）x=9．【解析】（1）3x+1=7，3x+1–1=7–1，3x÷3=6÷3，x=2；（2）23x−1=5，23x–1+1=5+1，2 3x÷23=6÷23，x=9．10．检验x=5和x=–5是不是方程213x-=x−2的解．【答案】x=5是原方程的解；x=–5不是原方程的解．【解析】把x=5分别代入方程的左边和右边，得左边=2513⨯-=3，右边=5–2=3，∵左边=右边，∴x=5是原方程的解；把x=–5分别代入方程的左边和右边，得左边=25(13)⨯--=–113，右边=–5–2=–7，∵左边≠右边，∴x=–5不是原方程的解．11．小明解关于y的一元一次方程3（y+a）=2y+4，在去括号时，将a漏乘了3，得到方程的解是y=3，请你求出a的值及方程的正确的解．【答案】a的值是1，方程的正解是y=1．学#科网人教版七年级上册期末测试卷一、选择题(每题3分，共30分)1．某天的最高气温是8℃，最低气温是－3℃，那么这天的温差是() A．－3℃B．8℃C．－8℃D．11℃2．下列立体图形中，从上面看能得到正方形的是()3．下列方程是一元一次方程的是()A．x－y＝6 B．x－2＝xC．x2＋3x＝1 D．1＋x＝34．今年某市约有108 000名应届初中毕业生参加中考，108 000用科学记数法表示为() A．0.108×106B．10.8×104C．1.08×106D．1.08×1055．下列计算正确的是()A．3x2－x2＝3 B．3a2＋2a3＝5a5C．3＋x＝3x D．－0.25ab＋14ba＝06．已知ax＝ay，下列各式中一定成立的是() A．x＝y B．ax＋1＝ay－1 C．ax＝－ay D．3－ax＝3－ay7．某商品每件标价为150元，若按标价打8折后，再降价10元销售，仍获利10%，则该商品每件的进价为( ) A ．100元 B ．105元 C ．110元D ．120元8．如果一个角的余角是50°，那么这个角的补角的度数是( ) A ．130° B ．40° C ．90°D ．140°9．如图，C ，D 是线段AB 上的两点，点E 是AC 的中点，点F 是BD 的中点，EF ＝m ，CD ＝n ，则AB 的长是( )A ．m －nB ．m ＋nC ．2m －nD ．2m ＋n10．下列结论：①若a ＋b ＋c ＝0，且abc ≠0，则a ＋c 2b ＝－12；②若a ＋b ＋c ＝0，且a ≠0，则x ＝1一定是方程ax ＋b ＋c ＝0的解； ③若a ＋b ＋c ＝0，且abc ≠0，则abc ＞0； ④若|a |>|b |，则a －ba ＋b>0. 其中正确的结论是( ) A ．①②③ B ．①②④ C ．②③④D ．①②③④二、填空题(每题3分，共24分)11．－⎪⎪⎪⎪⎪⎪－23的相反数是________，－15的倒数的绝对值是________．12．若－13xy 3与2x m －2y n ＋5是同类项，则n m ＝________.13．若关于x 的方程2x ＋a ＝1与方程3x －1＝2x ＋2的解相同，则a 的值为________． 14．一个角的余角为70°28′47″，那么这个角等于____________．15．下列说法：①两点确定一条直线；②两点之间，线段最短；③若∠AOC ＝12∠AOB ，则射线OC 是∠AOB 的平分线；④连接两点之间的线段叫做这两点间的距离；⑤学校在小明家南偏东25°方向上，则小明家在学校北偏西25°方向上，其中正确的有________个．16．在某月的月历上，用一个正方形圈出2×2个数，若所圈4个数的和为44，则这4个日期中左上角的日期数值为________．17．规定一种新运算：a△b＝a·b－2a－b＋1，如3△4＝3×4－2×3－4＋1＝3.请比较大小：(－3)△4________4△(－3)(填“>”“＝”或“<”)．18．如图是小明用火柴棒搭的1条“金鱼”、2条“金鱼”、3条“金鱼”……则搭n条“金鱼”需要火柴棒__________根．三、解答题(19，20题每题8分，21～23题每题6分，26题12分，其余每题10分，共66分) 19．计算：(1)－4＋2×|－3|－(－5)；(2)－3×(－4)＋(－2)3÷(－2)2－(－1)2 018.20．解方程：(1)4－3(2－x)＝5x；(2)x－22－1＝x＋13－x＋86.21．先化简，再求值：2(x2y＋xy)－3(x2y－xy)－4x2y，其中x＝1，y＝－1.22．有理数b在数轴上对应点的位置如图所示，试化简|1－3b|＋2|2＋b|－|3b－2|.23．如图①是一些小正方体所搭立体图形从上面看得到的图形，方格中的数字表示该位置的小正方体的个数．请在如图②所示的方格纸中分别画出这个立体图形从正面看和从左面看得到的图形．24．已知点O是直线AB上的一点，∠COE＝90°，OF是∠AOE的平分线．(1)当点C，E，F在直线AB的同侧时(如图①所示)，试说明∠BOE＝2∠COF.(2)当点C与点E，F在直线AB的两侧时(如图②所示)，(1)中的结论是否仍然成立？请给出你的结论，并说明理由．25．为鼓励居民节约用电，某市电力公司规定了电费分段计算的方法：每月用电不超过100度，按每度电0.50元计算；每月用电超过100度，超出部分按每度电0.65元计算．设每月用电x度．(1)当0≤x≤100时，电费为________元；当x>100时，电费为____________元．(用含x的整式表示)(2)某用户为了解日用电量，记录了9月前几天的电表读数．日期9月1日9月2日9月3日9月4日9月5日9月6日9月7日电表读123130137145153159165 数/度该用户9月的电费约为多少元？(3)该用户采取了节电措施后，10月平均每度电费0.55元，那么该用户10月用电多少度？26．如图，O为数轴的原点，A，B为数轴上的两点，点A表示的数为－30，点B表示的数为100.(1)A，B两点间的距离是________．(2)若点C也是数轴上的点，点C到点B的距离是点C到原点O的距离的3倍，求点C表示的数．(3)若电子蚂蚁P从点B出发，以6个单位长度/s的速度向左运动，同时另一只电子蚂蚁Q恰好从点A出发，以4个单位长度/s的速度向左运动，设两只电子蚂蚁同时运动到了数轴上的点D，那么点D表示的数是多少？(4)若电子蚂蚁P从点B出发，以8个单位长度/s的速度向右运动，同时另一只电子蚂蚁Q恰好从点A出发，以4个单位长度/s的速度向右运动．设数轴上的点N到原点O的距离等于点P到原点O的距离的一半(点N在原点右侧)，有下面两个结论：①ON＋AQ的值不变；②ON－AQ的值不变，请判断哪个结论正确，并求出正确结论的值．(第26题)答案一、1.D 2.A 3.D 4.D 5.D 6.D7．A8.D9.C10.B二、11.23；512.－813.－514．19°31′13″15.316.717．>18.(6n＋2)三、19.解：(1)原式＝－4＋2×3＋5＝－4＋6＋5＝7；(2)原式＝12＋(－8)÷4－1＝12－2－1＝9.20．解：(1)去括号，得4－6＋3x＝5x.移项、合并同类项，得－2x＝2.系数化为1，得x＝－1.(2)去分母，得3(x－2)－6＝2(x＋1)－(x＋8)．去括号，得3x－6－6＝2x＋2－x－8.移项、合并同类项，得2x＝6.系数化为1，得x＝3.21．解：原式＝2x2y＋2xy－3x2y＋3xy－4x2y＝(2x2y－3x2y－4x2y)＋(2xy＋3xy)＝－5x2y＋5xy.当x＝1，y＝－1时，原式＝－5x2y＋5xy＝－5×12×(－1)＋5×1×(－1)＝5－5＝0.22．解：由题图可知－3<b<－2.所以1－3b>0，2＋b<0，3b－2<0.所以原式＝1－3b－2(2＋b)＋(3b－2)＝1－3b－4－2b＋3b－2＝－2b－5.23．解：如图所示．24．解：(1)设∠COF＝α，则∠EOF＝90°－α.因为OF 是∠AOE 的平分线，所以∠AOE ＝2∠EOF ＝2(90°－α)＝180°－2α.所以∠BOE ＝180°－∠AOE ＝180°－(180°－2α)＝2α.所以∠BOE ＝2∠COF .(2)∠BOE ＝2∠COF 仍成立．理由：设∠AOC ＝β，则∠AOE ＝90°－β，又因为OF 是∠AOE 的平分线，所以∠AOF ＝90°－β2.所以∠BOE ＝180°－∠AOE ＝180°－(90°－β)＝90°＋β，∠COF ＝∠AOF ＋∠AOC ＝90°－β2＋β＝12(90°＋β)．所以∠BOE ＝2∠COF .25．解：(1)0.5x ；(0.65x －15)(2)(165－123)÷6×30＝210(度)，210×0.65－15＝121.5(元)．答：该用户9月的电费约为121.5元．(3)设10月的用电量为a 度．根据题意，得0.65a －15＝0.55a ，解得a ＝150.答：该用户10月用电150度．26．解：(1)130(2)若点C 在原点右边，则点C 表示的数为100÷(3＋1)＝25； 若点C 在原点左边，则点C 表示的数为－[100÷(3－1)]＝－50. 故点C 表示的数为－50或25.(3)设从出发到同时运动到点D 经过的时间为t s ，则6t －4t ＝130， 解得t ＝65.65×4＝260，260＋30＝290，所以点D 表示的数为－290.(4)ON －AQ 的值不变．设运动时间为m s，则PO＝100＋8m，AQ＝4m. 由题意知N为PO的中点，得ON＝12PO＝50＋4m，所以ON＋AQ＝50＋4m＋4m＝50＋8m，ON－AQ＝50＋4m－4m＝50.故ON－AQ的值不变，这个值为50.。