第2章 张量分析(清华大学张量分析,你值得拥有)
- 格式:pptx
- 大小:678.01 KB
- 文档页数:39







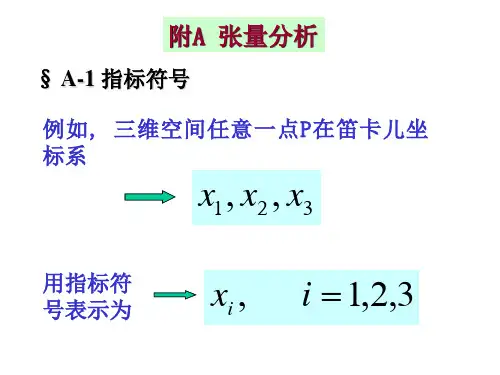

第2章 张量分析§2.1矢量空间、基、基矢1.线性矢量空间设有n 个矢量,1,2,,i i n =a ,它们构成一个集合R ,其中每个矢量i a 称为R 的一个元素。
如()i j i j +≠a a 唯一地确定R 的另一个元素,及i k a (k 为标量)也给定R 内唯一确定的元素,则称R 为线性(矢量)空间。
R 中的零元素记为O ,且具有i ⋅=O a O .2.空间的维数设i α为m 个标量,若能选取i α,使得10mi ii =α=∑a且i α不合为零,则称此m 个矢量线性相关,否则,称为线性无关。
例1 位于同一平面内的两个矢量1a 和2a (如图)是线性无关的,即11220α+α≠a a 若1α和2α为任意值,且不全为零。
例2 位于同一平面内的三个矢量1a ,2a ,3a 是线性相关的,则恒可找到1α,2α,3α(不全为零)使1122330α+α+α=a a a 如图: 21133''=α+αa a a集合R 内线性无关元素的最大个数称为集合或空间的维数。
设R 的维数为n ,则记为n R ,欧氏空间为3R 。
3.空间的基和基元素n R 中任意n 个线性无关元素的全体称为n R 的一个基。
基的每个元素称为基元素,由于n R 的n 确良基元素是线性无关的。
于是n R 内任一个元素r 可表示成基元素的线性组合。
设(1,2,,)i i n =a 为n R 的任选的基,则有:10ni ii ='α≠∑a,i α'为任意的不全为零的标量但总可选取00≠α及i α不全等于零,使得010ni i i =α=α=∑r a或者2a1a21x2x3xi i x =r e110()nnii i i i i ==α=-=ξα∑∑r a a①i αα,00≠ 不全等于零,所以i ξ不全等于零,且为有限值。
② n R 内有无限个基,但只有一个基是独立的,因为n R 内至少只有n 个元素是线性无关的。

张量分析研一 熊焕君 2017.9.281.引论:我们对标量和矢量都非常熟悉。
标量是在空间中没有方向的量,其基本特征是只需要一个数就可以表示,且当坐标系发生转动时这个数保持不变,因此也称其为不变量。
而矢量是个有方向的量,三维空间中矢量需要一组三个数(分量)来表示,其基本特征是当坐标系发生转动时,这三个数按一定规律而变化。
然而在数学物理问题中,还常出现一些更为复杂的量,如描述连续体中一点的应力状态或一个微元体的变形特征等,仅用标量和矢量不足以刻画出他们的性质。
要描述这些量则有必要将标量和矢量的概念加以引申和扩充,即引入新的量——张量。
在概念上,张量和矢量有许多类同之处。
一方面张量也表示某一客观存在的几何量或物理量,显然张量作为一个整体是与描述它所选取的坐标系无关,可像矢量代数那样,用抽象法进行描述;另一方面也可像矢量一样采用坐标法进行描述,此时张量包含有若干个分量元素,各个分量的取值与具体的坐标系相关联。
张量的主要特征是,在坐标系发生变化时,其分量取值遵守着一定的转化定律。
张量方法的核心内容是研究一个复杂的量集坐标转换规律。
我们知道,一个物理定律如果是正确的,就必须不依赖于用来描述它的任何坐标系,张量方法就是既采用坐标系,而又摆脱具体坐标系的影响的不变方法。
于是我们可以在简单的直角坐标系中建立描述某一运动法则的支配方程,如果需要可以用张量方法将其转换到任意一个曲线坐标系中去。
例如对于很大一类边值问题,若选用恰当的曲线坐标系,其边界条件可以简化的表达,那么我们就可以将支配方程用张量方法转化到所采用的坐标系中来,从而使问题的求解容易处理。
2.记号与约定张量是包含有大量分量元素的复杂量集,必须使用适当的记号和约定,才能使其表达形式简化紧凑,从而使分析和讨论有序地进行。
从某种意义上讲,可以说张量是对记号的研究。
所以我们必须熟悉各种约定记号,才能对张量这个工具运用自如。
在张量方法中对一个量的标记采用字母标号法。

一 爱因斯坦求和约定1.1指标变量的集合:n n y y y x x x ,...,,,...,,2121表示为:n j y n i x j i ...,3,2,1,,...,3,2,1,==写在字符右下角的 指标,例如xi 中的i 称为下标。
写在字符右上角的指标,例如yj 中的j 称为上标;使用上标或下标的涵义是不同的。
用作下标或上标的拉丁字母或希腊字母,除非作了说明,一般取从1到n 的所有整数,其中n 称为指标的范围。
1.2求和约定若在一项中,同一个指标字母在上标和下标中重复出现,则表示要对这个指标遍历其范围1,2,3,…n 求和。
这是一个约定,称为求和约定。
例如:333323213123232221211313212111bx A x A x A b x A x A x A bx A x A x A =++=++=++筒写为:ijijbx A =j——哑指标i——自由指标,在每一项中只出现一次,一个公式中必须相同遍历指标的范围求和的重复指标称为“哑标”或“伪标”。
不求和的指标称为自由指标。
1.3 Kronecker-δ符号(克罗内克符号)和置换符号Kronecker-δ符号定义j i ji ij ji ≠=⎩⎨⎧==当当01δδ置换符号ijkijk e e =定义为:⎪⎩⎪⎨⎧-==的任意二个指标任意k j,i,当021)(213,132,3的奇置换3,2,1是k j,i,当112)(123,231,3的偶置换3,2,1是k j,i,当1ijk ijke ei,j,k 的这些排列分别叫做循环排列、逆循环排列和非循环排列。
置换符号主要可用来展开三阶行列式:231231331221233211231231133221332211333231232221131211a a a a a a a a a a a a a a a a a a a a a a a a a a a a ---++==因此有:ijmjimii i i jijAA aa a a a ==++=δδδδδ332211kijjkiijkkjiikjjikijkee e e e e e ==-=-=-=同时有:ijjijij iiiijijijkj ikilkljkijjjiiijijijkjikiie e aa aa a a a aa δδδδδδδδδδδδδδδδδδδ=⋅=++=========++=332211332211331001010100131211232221333231321333222111321321321-=====δδδδδδδδδδδδδδδδδδδδδδδδδδδe e k j i k j i k j i k k k j j j i i i ijk333222111321321321r q p r q p r q p k k k j j j i i i pqr ijke e δδδδδδδδδδδδδδδδδδ⋅=ipp i p i p i p i δδδδδδδδδ==++11332211krkqkpjrjqjpiriqippqrijke e δδδδδδδδδ=jqirjriqjrjqiriqkqrijke e kp δδδδδδδδ-===321321322311332112312213322113312312332211333231232221131211k j i ijkkjiijkaa a e a a a e aa a a a a a a a a a a a a a a a a aaaa a aaa a A ==---++==Kronecker-δ和置换符号符号的关系为:itjsjtiskstkije e δδδδ-=二 张量代数2.1张量的加法(减法)两个同阶、同变异(结构) 的张量可以相加(或相减)。
I.2 符号ij δ与rst e符号ij δ称为“Kronecker delta ”,它的定义是:⎩⎨⎧=01ij δ时当时当j i j i ≠= ()n ,,2,1j ,i = (I.14)定义表明它对指标i 和j 是对称的,即ji ij δδ= (I.15)ij δ的分量集合对应于单位矩阵。
例如,在三维空间中:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡10010001333231232221131211δδδδδδδδδ (I.16) 利用ij δ可以把线元长度平方的公式(I.6)改写成j i ij dx dx dsδ=2(I.17)这里ij δ起了换标的作用,即:如果ij δ符号的两个指标中,有一个和同项中其他因子的指标相重,则可以把该因子的那个重指标替换成ij δ的另一个指标,而ij δ自动消失。
这样:i i jj ji ij dx dx dxdx dxdx ds===δ2类似地有ik jk ij a a =δ;jk ik ij a a =δki kj ij a a =δ;kj ki ij a a =δ (I.18)以及ik jkij δδδ=;il kl jk ij δδδδ= (I.19)所以,ij δ也称为换标符号。
符号rst e 的定义是:⎪⎩⎪⎨⎧-=011rste 个以上指标值相同时中有当为逆序排列时当为正序排列时当2t ,s ,r t ,s ,r t ,s ,r (I.20a) 或)r t )(t s )(s r (21e rst ---=()3,2,1t ,s ,r = (I.20b)其中,正序排列是指(l , 2 . 3 )及其轮流换位得到的(2 . 3 , l )和(3 , 1 , 2 ),逆序排列是指(3 , 2 ,l )及其轮流换位得到的(2 , l , 3 )和(l , 3 , 2 )。
rst e 称为排列符号或置换符号。
它共有27 个元素,其中只有3个元素为1,3个元素为-1 ,其余的元素都是0。