研究生数值分析 样条插值

实验报告：牛顿差值多项式&三次样条问题：在区间[-1,1]上分别取n=10、20用两组等距节点对龙格函数21()25f x x作多项式插值及三次样条插值，对每个n 值，分别画出插值函数及()f x 的图形。

实验目的：通过编程实现牛顿插值方法和三次样条方法，加深对多项式插值的理解。

应用所编程序解决实际算例。

实验要求：1． 认真分析问题，深刻理解相关理论知识并能熟练应用；2． 编写相关程序并进行实验；3． 调试程序，得到最终结果；4． 分析解释实验结果；5． 按照要求完成实验报告。

实验原理：详见《数值分析 第5版》第二章相关内容。

实验内容：（1）牛顿插值多项式1.1 当n=10时：在Matlab 下编写代码完成计算和画图。

结果如下：代码：clear allclcx1=-1:0.2:1;y1=1./(1+25.*x1.^2);n=length(x1);f=y1(:);for j=2:nfor i=n:-1:jf(i)=(f(i)-f(i-1))/(x1(i)-x1(i-j+1));endendsyms F x p ;F(1)=1;p(1)=y1(1);for i=2:nF(i)=F(i-1)*(x-x1(i-1));p(i)=f(i)*F(i);endsyms PP=sum(p);P10=vpa(expand(P),5);x0=-1:0.001:1;y0=subs(P,x,x0);y2=subs(1/(1+25*x^2),x,x0);plot(x0,y0,x0,y2)grid onxlabel('x')ylabel('y')P10即我们所求的牛顿插值多项式，其结果为：P10（x）=-220.94*x^10+494.91*x^8-9.5065e-14*x^7-381.43*x^6-8.504e-14*x^5+123.36*x^4+2.0202e-1 4*x^3-16.855*x^2-6.6594e-16*x+1.0并且这里也能得到该牛顿插值多项式的在[-1，1]上的图形，并和原函数进行对比（见Fig.1）。

第5章 插值与拟合方法插值与拟合方法是用有限个函数值(),(0,1,,)i f x i n =⋅⋅⋅去推断或表示函数()f x 的方法，它在理论数学中提到的不多。

本章主要介绍有关解决这类问题的理论和方法，涉及的内容有多项式插值，分段插值及曲线拟合等。

对应的方法有Lagrange 插值，Newton 插值，Hermite 插值，分段多项式插值和线性最小二乘拟合。

1 实际案例2 问题的描述与基本概念先获得函数（已知或未知）()=在有y f x由表中数据构造一个函数P(x)作为f(x) 的近似函数，去参与有关f (x)的运算。

科学计算中，解决不易求出的未知函数的问题主要采用插值和拟合两种方法。

1）插值问题的描述已知函数()y f x =在[a,b ]上的n +1个互异点nx x x ⋅⋅⋅,,10处的函数值()i i y f x =，求f (x ) 的一个近似函数P (x )，满足()()(0,1,,)i i P x f x i n ==⋅⋅⋅ （5.1）● P (x ) 称为f (x )的一个插值函数; ● f (x ) 称为被插函数;点i x 为插值节点; ● ()()(0,1,,)i i P x f x i n ==⋅⋅⋅称为插值条件; ● ()()()R x f x P x =-称为插值余项。

当插值函数P (x )是多项式时称为代数插值（或多项式插值）。

一个代数插值函数P (x )可写为0()()()mkm k k k P x P x a x a R ===∈∑若它满足插值条件（5.1），则有线性方程组20102000201121112012m m m m m n n m n na a x a x a x y a a x a x a x y a a x a x a x y ⎧+++⋅⋅⋅=⎪+++⋅⋅⋅=⎪⎨⎪⎪+++⋅⋅⋅=⎩ （5.2）当m=n ，它的系数行列式为范德蒙行列式)(1110212110200j i ni j n nnnn nx x x x x x x x x x x D -∏==≤≤≤因为插值节点互异，0D ≠，故线性方程组（5.2）有唯一解，于是有定理 5.1 当插值节点互异时，存在一个满足插值条件()()(0,1,,)i i P x f x i n ==⋅⋅⋅的n 次插值多项式。

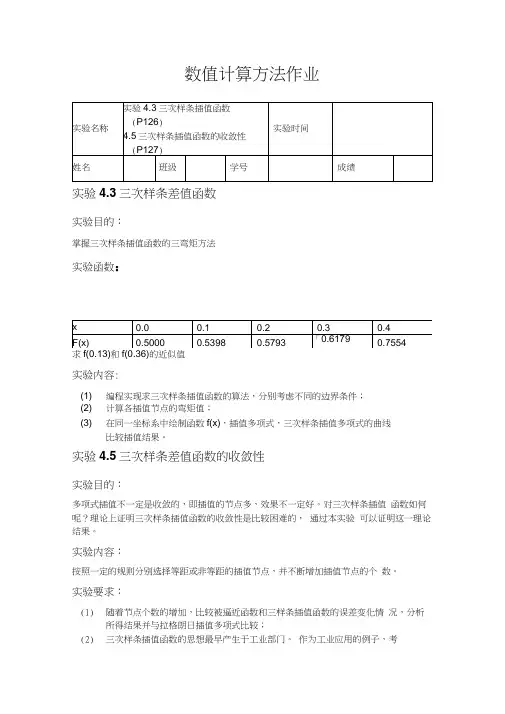
数值计算方法作业实验4.3三次样条差值函数实验目的：掌握三次样条插值函数的三弯矩方法实验函数：求和的近似值实验内容:(1) 编程实现求三次样条插值函数的算法，分别考虑不同的边界条件；(2) 计算各插值节点的弯矩值；(3) 在同一坐标系中绘制函数f(x)，插值多项式，三次样条插值多项式的曲线比较插值结果。

实验4.5三次样条差值函数的收敛性实验目的：多项式插值不一定是收敛的，即插值的节点多，效果不一定好。

对三次样条插值函数如何呢？理论上证明三次样条插值函数的收敛性是比较困难的，通过本实验可以证明这一理论结果。

实验内容：按照一定的规则分别选择等距或非等距的插值节点，并不断增加插值节点的个数。

实验要求：(1)随着节点个数的增加，比较被逼近函数和三样条插值函数的误差变化情况，分析所得结果并与拉格朗日插值多项式比较；(2)三次样条插值函数的思想最早产生于工业部门。

作为工业应用的例子，考虑如下例子：某汽车制造商根据三次样条插值函数设计车门曲线， 其中一 段数据X k 0 1 23 4 5678910y k 0.00.79 1.532.19 2.713.03 3.27 2.89 3.06 3.19 3.29y k0.80.2算法描述:拉格朗日插值：错误！未找到引用源。

n(x _ X ) 其中错误！未找到引用源。

是拉格朗日基函数，其表达式为：h(x)」j=0 (x i- X j )牛顿插值：N n (x) =f (X g ) f[X o ,X i ](X -xO) f[X o ,X i ,X 2〕(X - xO)(x - X i ) •…f[X g ,X i ...X n ] =(f[X i ,X 2,...X n ] - f [ X 。

，为，..人」)/(X . - X g )三样条插值:所谓三次样条插值多项式Sn(x)是一种分段函数，它在节点Xi(a<X0<X1……<Xn<b)分成的每个小区间［x i-i ,x i ］上是三次多项式，其在此区间 上的表达式如下：f[X °,X i ,X 2,...X n ](X -X °)(X -X i )...(X-Xn J )f [X i , X j ]f (X i ) - f (X j ) X i -X jf [X i , X j ,X k]=其中*.f[X j ,X k ] - f[K ,X j ]X k -X iS(x)二 M 3(X i -x) 6h i.Mi (x —Xy )3 . [ y i - y i4 h i (M i - My)6h i h i 6 h ih i M i 4 h i M iy i- 6)( 6*,皿"]因此，只要确定了 Mi 的值，就确定了整个表达式,Mi 的计算方法如下:i 4式中 Mi= S (X i ).则Mi 满足如下n-1个方程:7 M i 」■ 2M i …冷 M i i = di , i =1,2,...n —'1 常用的边界条件有如下几类：(1)给定区间两端点的斜率 m o ,m n ,即s(x 0) = y 0 =m 0,S(x n ) = y n = m n(2) 给定区间两端点的二阶导数 MO ,Mn,即S (XcH y 。

实验报告：牛顿差值多项式&三次样条问题：在区间[-1,1]上分别取n=10、20用两组等距节点对龙格函数21()25f x x作多项式插值及三次样条插值，对每个n 值，分别画出插值函数及()f x 的图形。

实验目的：通过编程实现牛顿插值方法和三次样条方法，加深对多项式插值的理解。

应用所编程序解决实际算例。

实验要求：1． 认真分析问题，深刻理解相关理论知识并能熟练应用； 2． 编写相关程序并进行实验； 3． 调试程序，得到最终结果； 4． 分析解释实验结果； 5． 按照要求完成实验报告。

实验原理：详见《数值分析 第5版》第二章相关内容。

实验内容：（1）牛顿插值多项式1.1 当n=10时：在Matlab 下编写代码完成计算和画图。

结果如下：代码：clear allclcx1=-1:0.2:1;y1=1./(1+25.*x1.^2);n=length(x1);f=y1(:);for j=2:nfor i=n:-1:jf(i)=(f(i)-f(i-1))/(x1(i)-x1(i-j+1));endendsyms F x p;F(1)=1;p(1)=y1(1);for i=2:nF(i)=F(i-1)*(x-x1(i-1));p(i)=f(i)*F(i);endsyms PP=sum(p);P10=vpa(expand(P),5);x0=-1:0.001:1;y0=subs(P,x,x0);y2=subs(1/(1+25*x^2),x,x0);plot(x0,y0,x0,y2)grid onxlabel('x')ylabel('y')P10即我们所求的牛顿插值多项式，其结果为：P10（x）=-220.94*x^10+494.91*x^8-9.5065e-14*x^7-381.43*x^6-8.504e-14*x^5+123.36* x^4+2.0202e-14*x^3-16.855*x^2-6.6594e-16*x+1.0并且这里也能得到该牛顿插值多项式的在[-1，1]上的图形，并和原函数进行对比（见Fig.1）。

第二章 插值法在科学研究与工程技术中，常常遇到这样的问题：由实验或测量得到一批离散样点，要求作出一条通过这些点的光滑曲线，以便满足设计要求或进行加工。

反映在数学上，即已知函数在一些点上的值，寻求它的分析表达式。

此外，一些函数虽有表达式，但因式子复杂，不易计算其值和进行理论分析，也需要构造一个简单函数来近似它。

解决这种问题的方法有两类：一类是给出函数()f x 的一些样点，选定一个便于计算的函数()x ϕ形式，如多项式、分式线性函数及三角多项式等，要求它通过已知样点，由此确定函数()x ϕ作为()f x 的近似，这就是插值法；另一类方法在选定近似函数的形式后，不要求近似函数过已知样点，只要求在某种意义下在这些样点上的总偏差最小。

这类方法称为曲线（数据）拟合法。

设已知区间[,]a b 上的实值函数f 在1n +个相异点[,]i x a b ∈处的函数值(),0,1,,i if f x i n ==，要求构造一个简单函数()x ϕ作为函数()f x 的近似表达式()()f x x ϕ≈使得()(),0,1,,i i i x f x f i n ϕ=== (2-1)这类问题称为插值问题。

称f 为被插值函数；()x ϕ为插值函数；0,,n x x 为插值节点；(2-1)为插值条件。

若插值函数类{()}x ϕ是代数多项式，则相应的插值问题为代数插值。

若{()}x ϕ是三角多项式，则相应的插值问题称为三角插值。

若{()}x ϕ是有理分式，则相应的插值问题称为有理插值。

§1 Lagrange 插值1.1 Lagrange 插值多项式设函数f 在1n +个相异点01,,,n x x x 上的值(),0,1,,i i f f x i n ==是已知的，在次数不超过n 的多项式集合n P 中，求()n L x 使得(),0,1,,n i i L x f n n == (2-2)定理1 存在惟一的多项式n nL P ∈满足插值条件(2-2)。

数值分析中的插值误差控制技巧探讨方向数值分析是应用数学的一个分支，它研究利用数值方法解决数学问题的理论和算法。

其中，插值是数值分析中常用的技术之一，它通过已知数据点来估计未知数据点的值。

然而，插值过程中会引入一定的误差，因此探讨插值误差控制技巧对于优化数值计算过程具有重要意义。

本文将就数值分析中插值误差的控制技巧进行探讨，并介绍一些常用的方法。

一、拉格朗日插值法拉格朗日插值法是插值中常用的一种方法。

它通过已知的n个数据点来构造一个n次多项式，进而估计未知数据点的值。

然而，拉格朗日插值法在一些情况下可能会产生较大的误差。

为了降低插值误差，可以考虑以下几种技巧：1.1 均匀插值节点选择拉格朗日插值法中，节点的选择对插值结果的精度有较大影响。

一种常见的节点选择方式是均匀插值节点，即在插值区间上等距取点。

然而，均匀插值节点在某些函数上可能会产生较大的插值误差。

因此，在实际应用中，可以考虑非均匀插值节点选择，如Chebyshev节点，以减小插值误差。

1.2 引入高次插值多项式拉格朗日插值法是通过构造n次多项式来插值估计。

然而，低次多项式在某些情况下可能无法满足精度要求。

为了降低误差，可以考虑使用高次插值多项式。

通过增加多项式的次数，可以提高插值结果的精度，但也需要注意过高次数可能会引入过拟合问题。

二、牛顿插值法牛顿插值法是另一种常用的插值方法。

与拉格朗日插值法相比，牛顿插值法采用了差商的概念，可以简化计算过程。

然而，在插值过程中，牛顿插值法可能存在一些误差。

为了降低误差，可以考虑以下技巧：2.1 计算插值节点的差商时，采用高阶差商牛顿插值法中，通过计算差商来构建插值多项式。

一般而言，差商越高阶，插值精度越高。

因此，在计算差商时，可以考虑采用高阶差商来提高插值精度。

2.2 选择适当的插值节点与拉格朗日插值法类似，牛顿插值法中节点的选择也对插值结果有一定影响。

在实际应用中，可以根据函数的性质来选择合适的插值节点，以减小插值误差。

数值分析三次样条插值函数【问题】对函数f x =ex, x∈[0,1]构造等距节点的三次样条插值函数，对以下两种类型的样条函数1. 三次自然样条2. 满足S′ 0 =1,S′ 1 =e的样条并计算如下误差：max{ f x1 −S x1 ,i=1,…,N} i−i−i这里xi−1为每个小区间的中点。

对N=10,20,40比较以上两组节点的结果。

讨论你的结果。

【三次样条插值】在每一个区间[t1,t2],…,[tn−1,tn]上，S都是不同的三次多项式，我们把在[ti−1,ti]上表示S的多项式记为Si，从而，S0 x x∈[t0,t1]∈[t1,t2] S x = S1 x x…Sn−1 x x∈[tn−1,tn]通过在节点处函数值、一阶导数和二阶导数的连续性可以得到：Si−1 ti = yi= Si ti 1≤i≤ n−1Si−1′ ti = Si′ tix→ti+limS′′ x =zi=limS′′(x) x→ti−再给定z0和zn 的值就构成了4n个条件，而三次样条插值函数共4n个系数，故可以通过这4n个条件求解三次样条函数的系数，从而求得该三次样条插值函数。

特别的，当z0=zn=0 时称为自然三次样条。

文本预览：一、自然三次样条插值【自然三次样条插值算法】1.由上面的分析可知，求解三次样条函数实际上就是求解一个矩阵：u 1h 1h1u2h2h2u3…v1 z1 v2 z2 z3=v3 … z…hn−2 n−2 vn−2 z vn−1 un−1 n−1ih3…hn−3un−2hn−26…其中hi=ti+1−ti，ui=2(hi+hi−1)，ui=h(yi+1−yi)，vi=bi−bi−1 所以自然三层次样条插值的算法就是在得到端点的函数值，一次导数值和二次导数值，然后根据上述求解矩阵得到v，代入自然三次样条的表达式即可。

2.根据题目中所给出的误差估计，计算在区间中点处的最大误差。

【实验】通过Mathematica编写程序得到如下结果：N=101. 计算得到zi的值为：由此可以得到各个区间的自然三次样条插值函数。

数值分析中的插值方法在数值分析中，插值是一种通过在已知数据点之间估计未知数据点的方法。

它是一种常见的数据处理技术，用于填补数据间的空白，揭示数据间的关联性，或者建立数据模型。

在本文中，我们将讨论数值分析中的几种常见的插值方法。

一、拉格朗日插值拉格朗日插值是一种基于多项式的插值方法。

假设有n个离散数据点，我们想要在这些点之间插值得到未知数据点的值。

拉格朗日插值可以通过构建一个n次多项式来实现。

例如，给定三个数据点(x0, y0)，(x1, y1)，(x2, y2)，我们可以假定插值多项式为：P(x) = y0 * L0(x) + y1 * L1(x) + y2 * L2(x)其中，L0(x)，L1(x)，L2(x)是拉格朗日插值多项式的基函数，由以下公式得到：L0(x) = (x - x1) * (x - x2) / ((x0 - x1) * (x0 - x2))L1(x) = (x - x0) * (x - x2) / ((x1 - x0) * (x1 - x2))L2(x) = (x - x0) * (x - x1) / ((x2 - x0) * (x2 - x1))利用这些基函数，我们可以得到插值多项式P(x)，从而计算出未知点的值。

二、牛顿插值牛顿插值是另一种常见的插值方法，也是基于多项式的。

与拉格朗日插值不同的是，牛顿插值使用了差商的概念来构建插值多项式。

差商是一种表示数据间差异的指标，它可以用于计算插值多项式的系数。

对于n个数据点，差商可以由以下递归公式计算得到：f[x0] = f(x0)f[x0, x1] = (f[x1] - f[x0]) / (x1 - x0)f[x0, x1, ..., xn] = (f[x1, x2, ..., xn] - f[x0, x1, ..., xn-1]) / (xn - x0)基于差商，我们可以得到牛顿插值多项式的表达式：P(x) = f[x0] + f[x0, x1] * (x - x0) + f[x0, x1, x2] * (x - x0) * (x - x1) + ...利用牛顿插值，我们可以通过已知数据点构建插值多项式，进而估计未知点的值。

数值分析常用的插值方法数值分析中常用的插值方法有线性插值、拉格朗日插值、分段线性插值、Newton插值、Hermite插值、样条插值等。

下面将对这些插值方法进行详细介绍。

一、线性插值（linear interpolation）线性插值是最简单的插值方法之一、假设已知函数在两个点上的函数值，通过这两个点之间的直线来估计中间点的函数值。

线性插值公式为：f(x)=f(x0)+(x-x0)*(f(x1)-f(x0))/(x1-x0)其中，f(x)表示要求的插值点的函数值，f(x0)和f(x1)是已知的两个点上的函数值，x0和x1是已知的两个点的横坐标。

二、拉格朗日插值（Lagrange interpolation）拉格朗日插值是一种基于多项式的插值方法。

它通过多个已知点的函数值构造一个多项式，并利用这个多项式来估计其他点的函数值。

拉格朗日插值多项式的一般形式为：f(x) = Σ[f(xi) * Li(x)] (i=0,1,2,...,n)其中，f(x)表示要求的插值点的函数值，f(xi)是已知的多个点的函数值，Li(x)是拉格朗日基函数。

拉格朗日基函数的表达式为：Li(x) = Π[(x-xj)/(xi-xj)] (i≠j，i,j=0,1,2,...,n)三、分段线性插值（piecewise linear interpolation）分段线性插值是一种逐段线性近似函数的方法。

通过将整个插值区间分成多个小段，在每个小段上使用线性插值来估计函数的值。

分段线性插值的过程分为两步：首先确定要插值的点所在的小段，在小段上进行线性插值来估计函数值。

四、Newton插值（Newton interpolation）Newton插值也是一种基于多项式的插值方法。

利用差商的概念来构造插值多项式。

Newton插值多项式的一般形式为：f(x)=f(x0)+(x-x0)*f[x0,x1]+(x-x0)*(x-x1)*f[x0,x1,x2]+...其中，f(x)表示要求的插值点的函数值，f(x0)是已知的一个点的函数值，f[xi,xi+1,...,xi+k]是k阶差商。