当前位置：文档之家 › 第4章 有限差分法-1

第4章 有限差分法-1

  • 格式：ppt
  • 大小：277.50 KB
  • 文档页数：35

下载文档原格式

  / 35

合集下载

第4章_有限差分法.弹性力学

第4章_有限差分法.弹性力学



y xy
0

0
2 1 [(5 7 ) ( 6 8 )] xy 0 4h 2
可见，用差分法解平面 问题，共有两大任务：
一、建立差分方程 将（1-6~8）代入双调和 方程
4 4 4 2 2 2 4 0 4 x x y y
在结点３，x=x0-h, 在结点1, x=x0+h，代入(b) 得：
h2 2 f f f3 f 0 h 2 x 0 2 x 0
h2 2 f f f1 f 0 h 2 x 0 2 x 0
A A
B
(2 5)
从图易看出，式（2－3）右 边的积分式表示A与B之间的x方 向的面力之和；式（2－4）右边 的积分式表示A与B之间的y方向 的面力之和；式（2－5）右边的 积分式表示A与B之间的面力对 于B点的矩。
至此，我们解决了怎样 计算边界上各结点
, , x y
的值的问题。 至于边界外一行虚结点处 的值，则可用边界上
差分公式(１-１)及(１-３)是以相隔2h的两 结点处的函数值来表示中间结点处的一阶导数 值，可称为中点导数公式。 以相邻三结点处的函数值来表示一个端点 处的一阶导数值，可称为端点导数公式。 应当指出：中点导数公式与端点导数公式 相比，精度较高。因为前者反映了结点两边的 函数变化，而后者却只反映了结点一边的函数 变化。因此，我们总是尽可能应用前者，而只 有在无法应用前者时才不得不应用后者。
将式(b),(c)代入，整理得：
B B B A ( x B x A ) ( y B y A ) ( y B y ) p x d s ( x x B ) p y d s (d ) y A A x A A A , , , 为已知， 由式(d)及式(c)可见，设
计算电磁学-第4章-有限差分法

计算电磁学-第4章-有限差分法



同样对微分方程的解y(x)在点(xn,yn)进行泰勒展开
yn1 yn hf ( xn , yn )
1 ' 2 1 '' 3 y ( xn 1 ) y ( xn ) f n h f n h f n h 2! 3!

比较上面两式，只要它们前面项的系数尽可能多的相等，就 保证了截断精度。
1、差分与差商

用差分代替微分，是有限差分法的基本出发点。 这一点由微分原理保证的，当自变量的差分趋于 零时，差分变成微分
f ( x) f ( x h) f ( x)， h x
df f ( x) f ( x) lim dx x 0 x
'
f ( x) f ( x h) f ( x) f ( x) x h
龙格-库塔法

选取α、β、ω系数，使两式项的系数相等
1 fn , 2 f , 3 f , 4 f ,
' n '' n ''' n

如果该关系式能够一直维持到第m阶仍能成立， 但m＋1阶不再成立，就称为m阶龙格-库塔法
cem@
cem@
cem@
cem@
cem@
cem@
cem@
CST粒子仿真

Pierce Gun
ＭＡＧＩＣ
cem@

dy f ( x, y ) dx y x x 0 y0
y( x) y0 f (t , y(t )dt
x0
x
欧拉近似法在函数图上用阶梯的折线代替曲线
f(x) y(x)
yn+1 yn y(x n+1)1) f(n+
有限差分公式

有限差分公式

有限差分公式
有限差分是微分方程解的近似值的一种表示方法，通常用数学表达式
f(x+b)-f(x+a)来表示。

如果将有限差分除以b-a，则可以得到差商。

在微分方程数值解的有限差分方法中，特别是处理边界值问题时，有限差分导数的逼近起着关键的作用。

有限差分通常考虑三种形式：正向差分、反向差分和中心差分。

正向差分是f(x+h)-f(x)，反向差分是f(x)-f(x-h)，中心差分是f(x+h)-f(x-h)。

当h取为1时，正向差分除以h近似于导数。

在数值方法中，有限差分法是一种常用的数值解法，它用差商代替微分方程中的偏导数，从而得到相应的差分方程。

通过解这个差分方程，可以得到微分方程解的近似值。

以上内容仅供参考，如需更多信息，建议查阅数学类书籍或咨询数学专业人士。

传热学60-第四章 导热问题的数值解法

传热学60-第四章 导热问题的数值解法


B (i,j 1)
第四章 导热问题的数值解法 9
根据傅里叶定律， L,R,T ,B各节点向P节点的导热量：
T (i,j 1)
LP RP BP LP
t i 1 , j t i , j ti 1 , j ti , j t i , j 1 t i , j ti , j 1 ti , j
tik 1 tik
的一阶导数采用向前差分，则

tik 1 2tik tik 1 a x 2
第四章 导热问题的数值解法 28
上式移项整理 k k 1 k k ti a ( t i 1 t i 1 ) ( 1 2 a )ti 2 2 x x
x
y 1 y 1 x 1 x 1
(i 1,j )
(i 1,j )
L
R
x
Z方向取单位长度 (i,j 1) B
y
y
第四章 导热问题的数值解法
10
若有内热源， v ,i , j 为P节点所在网格单元的内热源强度
则内热源发热量
在稳态导热下：
v , p v ,i , j x y 1
ti 1, j ti , j y x y 3 1 h(t f ti , j ) xy v ,i , j 0 x 2 2 4
第四章 导热问题的数值解法
19
不规则区域的处理
用阶梯形的折线来模拟真实边界
t2
t1
t2
t2
t2
t2
第四章 导热问题的数值解法 20
第四章 导热问题的数值解法
17
3.
内部角点
内部角点
P(i ,j ) ti ,j
第4章 有限差分法

第4章 有限差分法


可见， 对应于式（4-2）和式（4-3）， 它们 都截断于 hf′(x0)项， 而把 h2项和更高幂次的 项全部略去。 换句话说， 就式（4-2）、 式 （4-3）而言， 略去余数项所引入的误差将 大致和 h 的一次方成正比。
第 4 章
有 限 差 分 法
而对于式（4-4）的一阶中心差商表达式则相当于把相应的泰勒公式
第 4 章
有 限 差 分 法
应用二元函数的泰勒公式，节点 1 的位函数值 u1 可通过 u0 表示为
同理
以 h 和 h1 分别与以上两式相乘，且相加，然后截断于 h 的二次项，便得关 于 的差分表达式为
同理可得
第 4 章
有 限 差 分 法
令 h1 =αh， h2 =βh，代入以上两式，最终再代入给定的泊松方程，即得这类 边界情况所对应的差分计算格式为
第 4 章
有 限 差 分 法
（2） 第三类边界条件的差分离散化 对此，同样需分两种情况讨论。第一种情况是在边界处引入的相应节 点恰好落在边界 L上。 这时，取决于边界 L 在该边界节点处的外法线方向 是否与网格线相重合， 对应有不同的差分离散化结果。 当边界 L 在边界节点 o 处的外法向 n 与网格线相重合时，如图 4-4 所 示，则问题在于如何用差商近似替代法向导数 。 显然， 最简洁的处
3）由所建立的差分格式(即与原定解问题对应的离散数学模型——代数方程 组)，选用合适的代数方程组的解法，编制计算程序，算出待求的离散解。
有限差分法有上述大致固定的处理和计算模式，具有一定的通用性。
第 4 章
有 限 差 分 法
4.2 差分与差商
有限差分法是以差分原理为基础的一种数值计算法。它用离散的函数值 所构成的差商来近似逼近相应的偏导数， 而所谓差商则是基于差分应用的数 值微分表达式。 设一函数 f(x)， 其自变量 x 得到一个很小的增量Δx = h， 则 函数 f(x)的增量 称为函数 f（x）的一阶差分。显然，只要增量 h 很小， 差分Δf与微分 df之间 的差异将很小 。 一阶差分仍是自变量 x 的函数，相类似地按式（4-1）计算一阶差分的差 分， 就得到Δ2f(x)，称之为原始函数 f(x)的二阶差分。 同样， 当 h 很小时， 二阶差分Δ2f(x)逼近于二阶微分d2f。依同理，可以定义更高阶的差分。
第四章 有限差分法及软件PPT课件

第四章 有限差分法及软件PPT课件


状态前，需要若干迭代循环。显式算法的缺点是时步很小，这就意味着
要有大量的时步。因此，对于病态系统——高度非线性问题、大变形、
物理不稳定等，显式算法是最好的。而在模拟线性、小变形问题时，效
率不高。
第四章•第21
页
由于显式有限差分法无需形成总体刚度矩阵，可在每个时步通过
更新结点坐标的方式，将位移增量加到结点坐标上，以材料网格的移 动和变形模拟大变形。这种处理方式称之“拉格朗日算法”，即：在 每步计算过程中，本构方程仍是小变形理论模式，但在经过许多步计 算后，网格移动和变形结果等价于大变形模式。
单元），则忽略对Fi的作用；如果物体处于平衡状态，或处于 稳定的流动（如塑性流动）状态，在该结点处的Fi将视为零。 否则，根据牛顿第二定律的有限差分形式，该结点将被加速：
u . (tt) i
u .i(tt/2)
Fi(t)
t m
（4-25）
第四章•第17 页
式中，上标表示确定相应变量的时刻。对大变形问题，将 (4-25)式再次积分，可确定出新的结点坐标：
t x C
（4-27）
第四章•第22 页
式中，C是波传播的最大速度，典型的是P波Cp：
Cp
K 4G/3
（4-28）
对于单个质量—弹簧单元，稳定解的条件是：
t 2 m k
（4-29）
式中，m是质量，k是弹簧刚度。在一般系统中，包含有各种材料和质 量—弹簧联结成的任意网络，临界时步与系统的最小自然周期Tmin有关：
第四章第四章第第5252页页3个弹性模型各向同性弹性横观各向同性弹性正交各向同性弹性8个弹塑性模型druckerprager模型mohrcoulomb模型应变硬化软化模型遍布节理模型双线性应变硬化软化遍布节理模型修正剑桥模型和胡克布朗模型第四章第四章第第5353页页岩石各向同性的岩石材料胡克布朗模型粘土变形和抗剪强度是体变的函数修正剑桥模型轻胶结的粒状材料在压力作用下导致永久体积减小双屈服面塑性模型层状材料破坏后研究具有非线性材料硬化或软化的层状材料双线性应变硬化软化遍布解理模型松散沉积地层中的开挖具有强度各向异性的层状材料即板岩遍布解理模型破坏后研究失稳过程立柱屈服顶板崩落存在非线性硬化或软化的粒状材料应变硬化软化摩尔库仑模型岩土力学通用模型边坡稳定性分析地下开挖松散或胶结的粒状材料
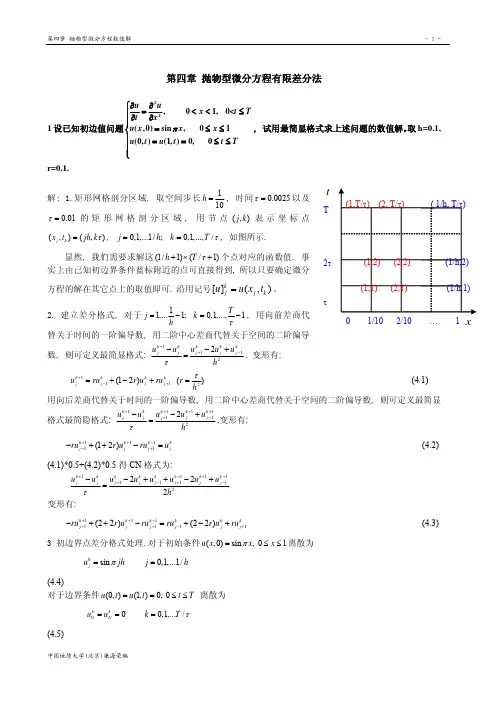
经典偏微分方程课后习题答案

经典偏微分方程课后习题答案

第四章 抛物型微分方程有限差分法1设已知初边值问题22, 01, 0<(,0)sin , 01(0,)(1,)0, 0 u ux t t x u x x x u t u t t T π⎧∂∂=<<⎪∂∂⎪⎪=≤≤⎨⎪==≤≤⎪⎪⎩T ≤, 试用最简显格式求上述问题的数值解。

取h=0.1,r=0.1.0 1/10 2/10 … 1 T 2τ τt解: 1.矩形网格剖分区域. 取空间步长1, 时间2510h =0.00τ=以及0.01τ=的矩形网格剖分区域, 用节点)表示坐标点(,j k (,)(,)j k x t jh k τ=, 0,1,...1/; 0,1,...,/j h k T τ==, 如图所示.显然, 我们需要求解这(1/1)(/1)h T τ+×+个点对应的函数值. 事实上由已知初边界条件蓝标附近的点可直接得到, 所以只要确定微分方程的解在其它点上的取值即可. 沿用记号[]k(,)j j k u x t =。

u 2. 建立差分格式, 对于11,...1; 0,1,...,1Tj k hτ=−=−, 用向前差商代替关于时间的一阶偏导数, 用二阶中心差商代替关于空间的二阶偏导数, 则可定义最简显格式:1122k k k k k1jj j j u u u u u h ++−+=. 变形j τ−−有:1112(12) (k k k kj j j j u ru r u ru r h τ+−+=+−+=(4.1)用向后差商代替关于时间的一阶偏导数, 用二阶中心差商代替关于空间的二阶偏导数, 则可定义最简显格式最简隐格式:111122k k k k k j jj j j u u u u u h τ++++−−+=11+−1kj +,变形有:1111(12) k k k j j j ru r u ru u ++−−−++−= (4.2)(4.1)*0.5+(4.2)*0.5得CN 格式为:111112222k k k k k k k k j jj j j j j j u u u u u u u u h τ+++−+−−++−+=111++−1kj +x x变形有:111111(22)(22) k k k k k j j j j j ru r u ru ru r u ru ++−−+−−++−=+−+ (4.3)3 初边界点差分格式处理.对于初始条件u x (,0)sin , 01=π≤≤h 离散为(4.4)0sin 0,1,...1/j u jh j π==对于边界条件离散为(0,)(1,)0, 0 u t u t t T ==≤≤00 0,1,.../k k N u u k T τ===(4.5)总结: 联立方程(4.1)(4.4)(4.5)得到已知问题的最简显格式差分方程组:11100(12)1 1,...1; 0,1,...,1sin 0,1,...1/0 0,1,.../k k k k j j j j jk k N u ru r u ru T j k h u jh j h u u k T τπτ+−+⎧=+−+⎪⎪=−=−⎪⎨⎪==⎪⎪===⎩ 联立方程(4.2)( 4.4)( 4.5)得到已知问题的最简隐格式差分方程组:1111100(12) 1 1,...1; 0,1,...,1sin 0,1,...1/0 0,1,.../k k k k j j j j jk k N ru r u ru u T j k h u jh j h u u k T τπτ++−−+⎧−++−=⎪⎪=−=−⎪⎨⎪==⎪⎪===⎩ 联立方程(4.3)( 4.4)( 4.5)得到已知问题的CN 格式差分方程组:11111100(22)(22) 1 1,...1; 0,1,...,1sin 0,1,...1/0 0,1,.../k k k k k j j j j j jk k N ru r u ru ru r u ru T j k h u jh j h u u k T τπτ++−−+−⎧−++−=+−+⎪⎪=−=−⎪⎨⎪==⎪⎪===⎩1k j + 4 求解并显示结果利用软件计算(Matlab)如上最简显格式差分方程组.h=1/10;tau=0.0025;T=0.5; r=tau/h^2;M=1/h+1;N=T/tau+1; u=zeros(M,N);for m=1:Mu(m,1)=sin((m-1)*h*pi); endu(1,1:N)=0;u(M,1:N)=0;for n=1:N-1for m=2:M-1u(m,n+1)=r*(u(m+1,n)+u(m-1,n))+(1-2*r)*u(m,n); end end u=u’ 这样我们就计算出不同时刻不同位置k t j x 对应的函数值(,)j k u x t 取tau=0.0025, 即r=0.25绘图, 取tau=0.01, r=1再绘图,如图()图4.2 习题1数值解图示(左r=0.25, 右r=1)2.试构造初边值问题 ()()()()(), 0.51, 0,,0, 0.51,0.5,0, 1,0.51,, 0u u x x x T t x x u x x x u ⎪∂u t t u t t T x ϕ⎧∂∂∂⎛⎞=<<<≤⎜⎟⎪∂∂∂⎝⎠⎪⎪=≤≤⎨⎪==−≤≤⎪∂⎩的显格式，并给出其按最大范数稳定的充分条件。

椭圆型方程的有限差分法

椭圆型方程的有限差分法

第4章 椭圆型方程的有限差分法§2 一维差分格式1、用积分插值法导出逼近微分方程的差分格式。

解：考虑在[a,b]内任一小区间(1)(2)[,]x x ，将上式在此区间上积分得或 (2)(2)(2)(1)(1)(1)(1)(2)()()x x x xx x duW x W x r dx qudx f dx dx-++=⎰⎰⎰（1.1） 其中，()()duW x p x dx= （1.2）特别地，取(1)(2)[,]x x 为对偶单元1/21/2[,]i i x x -+，则 将（1.2）改写成()()du W x dx p x =，再沿1/21/2[,]i i x x -+积分，得11()()ii x i i x W x u u dx p x ---=⎰，利用中矩形公式，得1111/21,[]()ii x i i i ii x i iu u dx W a a h h p x -----≈=⎰（1.3） 又 1/21/21/21/2112,()2i i i i x x i i i i i xx i i h h qudx d u d q x dx h h ++--+++≈=+⎰⎰ （1.4） 1/21/21/21/21112,()2i i i i x x i i i i x x i i u u du r dx b b r x dx dx h h ++--+-+-≈=+⎰⎰ （1.5） 1/21/212()i i x i x i i f x dx h h ϕ+-+=+⎰ （1.6）将（1.3）~（1.5）代入（1.1），即得微分方程的差分格式 如果系数p,q,r 以及右端f 光滑，则可用中矩形公式计算得 2、导出10111000101()()022u u h ha d u h ααϕ--+-+-+=对01()()()p a u a u a αα'-=+的逼近阶。

解：1011011()()x x dx a p p a h p x -⎡⎤===⎢⎥⎣⎦⎰， 记01()()()()Lu a p a u a u a αα'=---， 则逼近阶为2()O h 。

第五版传热学第四章

第五版传热学第四章


3.C＋＋ —— C plus plus，C语言的增强版，目前最常用的应用程序设计 语言，数值计算软件主要使用的语言。
二、常用计算软件
1.MATLAB——矩阵计算软件
matlab软件主界面
2.FLUENT——流体流动通用数值计算软件
3. FLUENT AIRPAK ——人工环境系统分析软件，暖通空调专业和传热学领域必备软件
第四章 导热数值解法基础
本章研究的目的 ——利用计算机求解难以用 分析解求解的导热问题 基本思想 ——把原来在时间、空间坐 标系中连续的物理量的场， 用有限个离散点的值的集合 来代替，通过求解按一定方 法建立起来的关于这些值的 代数方程，来获得离散点 上被求物理量的值。 研究手段——有限差分法
物理问题的数值求解过程
优点——无条件稳定 缺点——不可根据kΔ τ 时刻温度分布直接计算 (k+1)Δ τ 时刻温度分布
ቤተ መጻሕፍቲ ባይዱ
第四节 常用算法语言和计算软件简介
一、常用算法语言
1.FORTRAN语言 ——Formula Translation，数值计算领域所使用的主要语言。
2.C语言 ——将高级语言的基本结构和语句与低级语言的对地址操作结合 起来的应用程序设计语言。


k k k k ti Fo ti 1 ti 1 1 2 Foti


优点——可根据kΔ τ 时刻温度分布直接计算(k+1)Δ τ 时刻温度分布 缺点——选择Δ x和 Δ τ 时必须满足稳定性条件 a a 1 或 1 2 0 2 2 x x 2
第三节 非稳态导热的数值计算
研究对象——一维非稳态导热问题 一、显式差分格式
t 2t a x 2
大学传热学第四章 导热问题的数值解法1

大学传热学第四章 导热问题的数值解法1


对解进行分析
获得物体中的温度分布常常不是工程问题的最终目的，所 得出的温度场可能进一步用于计算热流量或计算设备、零 部件的热应力及热变形等。对于数值计算所获得的温度场 及所需要的一些其他物理量应作仔细的分析，以获得定性 或定量上的一些新的结论。
建立节点方程的泰勒级数展开法
• 函数的泰勒级数展开式为
二维稳态导热内部节点方程式的建立
ydy m,n+1
m-1,n
m,n
x
y
x m,n-1
m+1,n
xdx
y
• 从左面进入微元体的热量
t t
y m1,n
m ,n
x
x
• 从右面进入微元体的热量
t t
y m1,n
m ,n
xdx
x
• 从下面进入微元体的热量
t t
x m,n1
m ,n
y
y
• 从上面进入微元体的热量
t t
x m,n1
m ,n
ydy
y
二维稳态导热内节点方程
• 当物体内没有内热源时，根据能量守恒定律，从各个方向 进入微元体的热量之和为零
0
x
xdx
y
ydy
• 将各热量计算表达式带入，整理后得到
t 1 t t t t
m ,n
4 m1,n
m1,n
m ,n1
y
y
从上面进入微元体的热量
t t
m,n1 m,n x / 2
ydy
y
二维稳态导热平直边界上节点方程
• 当物体内没有内热源时，根据能量守恒定律，从各个方向 进入微元体的热量之和为零
0
m,n
m,n
第4章 有限差分法

第4章 有限差分法


第 4 章
有 限 差 分 法
4.3.2 定解条件的离散化——各类差分计算格式
对于场域边界上给定的三类边界条件（见 1.7 节）， 由于第二类边界条 件可以看作为第三类边界条件的特殊情况，因此，这里只需讨论第一、第三 类边界条件的差分离散化处理。 （1） 第一类边界条件的差分离散化 若如图 4-2 点 M 所示， 划分网格时相应的网格节点恰好落在边界 L 上，则 只要直接把位函数 u| M∈ L = f(rM)的值赋给该对应的边界节点 M 即可。 若划分网格时引入的节点不落在边界 L 上， 则如图 4-3所示， 对于邻近边界的典型节点 o， 由于 h1≠ h2≠ h， 这样， o点及其周围相邻的 1、 2、 3 和 4 点构成一个不对称的星形。此时， 可仿照 4.2 节， 采用泰勒公式进行差分离散化 处理，即能相当精确地导出关于 o 点的差分计 算格式。
截断于 2hf′(x0)项， 略去了 h3项以及更高幂次的项。很明显，三种差商表达 式中以式（4-4）所示的中心差商的截断误差最小，其误差大致和 h 的二次方 成正比。 二阶导数同样可近似为差商的差商，即
这相当于把泰勒公式
截断于 h2f″(x)项， 略去了 h4项以及更高幂次的项，其误差亦大致和 h 的 二次方成正比。
理方法是依据式（4-3）， 这样， 第三类边界条件在此情况下的差分计算 格式为
第 4 章
有 限 差 分 法
当边界 L 在边界节点 o 处的外法向 n 与网格线不重合时，如图 4-5 所 示， 显然有
于是， 关于 o 点的差分计算格式是
第 4 章
有 限 差 分 法
第二种情况是在边界处引入的相应节点不落在边界 L 上， 这时如图 4-6 所示，可在邻近边界的节点 o 上仍按上述方法列出差分计算格式，只是需引 入与节点 o 相关的边界节点 o′，取点 o′处的外法向 n 作为点 o 处的“外法向 n”， 且近似地认为边界条件中给定的函数f1(ro)和 f2(ro)均在点 o′上取值。这 样，将式（4-14）中的 f1(ro)和 f2(ro)改记为 f1(ro′)和f2(ro′)，即得此种情况下关 于 o 点的差分计算格式。

科学计算中的偏微分方程有限差分法-张文生


§4.8 差分格式的收敛性分析---------------------------------------------------------------------170 §4.9 极坐标下：Poission 方程的差分格式 §4.10 用离散 Fourier 变换求解椭圆型问题 第五章 差分方程的求解--------------------------------------------------------------------------184 §5.1 残量校正法 §5.1.1 迭代格式 §5.1.2 收敛性分析 §5.1.3 迭代中止准则 §5.2 基本迭代法--------------------------------------------------------------------------------189 §5.2.1 Jacobi 迭代格式 §5.2.2 Gauss-Seidel 迭代格式 §5.2.3 逐次超松弛迭代格式---------------------------------------------------------------------197 §5.2.4 对称与反对称超松弛迭代格式 §5.2.5 其他迭代形式 §5.3 预条件迭代方法---------------------------------------------------------------------------203 §5.3.1 预条件 Richardson(PR)法 §5.3.2 预条件 Richardson 极小残量(PRMR)法 §5.3.3 预条件 Pdchardson 最速下降(PRSD)法 §5.3.4 共轭梯度(CG)法------------------------------------------------------------------------209 §5.3.5 预条件共轭梯度(PCG)法 §5.3.6 预条件子 §5.4 Krylov 子空间迭代方法--------------------------------------------------------------------21程误差(CGNE)法 §5.4.3 广义共轭残量(GCR)法 §5.4.4 Orthodir 方法---------------------------------------------------------------------------221 §5.4.5 广义极小残量法(GMRES)迭代 §5.4.6 极小残量(MINRES)法 §5.4.7 双共轭梯度(BLCG)法-------------------------------------------------------------------229 §5.4.8 拟极小残量(QMR)法

04有限差分法.ppt

uin n 1 n 1 a n n n ui ui ui 1 ui 1 2 ui 1 2uin uin 1 2h h uin n a n n 1 n n ui ui ui 1 ui 1 2 ui 1 2uin uin 1 或 2h h
n Rj
O t x

2

无条件稳定
2.一维混合问题
u 2u 2 0 t x u x ,0 F x u a, t t u b, t t
0 x b, t 0, 0
对于[a，b]区间的内点，可以构造以上各种格式。 如四点显式
例:驱动腔内的流体流动。
3.网格划分
x h y l xi ih
-----称为步长。
u x, y u i , j
xi , y j i, j
y j jl
4.差分格式 将u在(i,j)附近展成Taylor级数
ui 1, j ui , j ui 1, j ui , j 1 2u 1 3u u h 2 h 2 3 h 3 ... 2 x 3! x x i , j i, j i, j 1 2u 1 3u u h 2 h 2 3 h 3 ... 2 x 3! x x i , j i, j i, j


-----中心差分式
O h 表示具有二阶精度。

2
两Taylor展式相加
2u 1 ui 1, j 2ui , j ui 1, j O h 2 x 2 h2 i, j

传热学-第4章-热传导问题的数值解珐


若步长∆x=∆y，有： ， 若步长
t m ,n = 1 ( 2 t m −1 , n + t m , n + 1 + t m , n −1 + 4 ∆2 x Φ m , n
λ
+
2 ∆ xq w
λ
)
2. 外部角点 控制容积的热平衡为： 控制容积的热平衡为：
∆y tm−1,n − tm,n ∆x tm,n−1 − tm,n ∆x∆y ∆x + ∆y λ +λ + Φ m, n + qw = 0 ∆x 2 2 ∆y 4 2
4. 边界热流密度的三种情况
q （1）绝热边界： w = 0 ）绝热边界：
（2） qw 值不为零：代入给定的 qw 值。 ） 值不为零： （3）对流边界：qw = h(t f ）对流边界： 平直边界节点： 平直边界节点：
2( h∆x
− t m n = 2 t m − 1 , n + t m , n + 1 + t m , n −1 +
第一类边界条件 — 边界温度已知 m-1,n 第二类边界条件 需建立边界节点温度 ∆y 第三类边界条件 的差分方程 n 1. 位于平直边界上的节点
λ∆y
tm−1,n − tm,n ∆x +λ
m m,n+1
qw
m,n m,n-1
∆x
∆x tm,n+1 − tm,n ∆x tm,n−1 − tm,n ∆x∆y +λ + Φm,n + ∆yqw = 0 2 ∆y 2 ∆y 2
若步长∆x=∆y，有： ， 若步长
t m ,n = 1 ( t m −1 , n + t m , n −1 + 2

蒙特卡罗法(新)

第4章有限差分法4.1有限差分法基础4.1.1有限差分法的基本概念4.1.2欧拉近似1. 基本欧拉近似法图4.1欧拉近似法示意图2计算机辅助绘图基础（第4版）2. 用于偏导数的情况4.1.3梯形法则和龙格·库塔法1. 梯形法则计算机辅助绘图基础（第4版） 3图4.2曲边梯形的面积用矩形面积近似图4.3梯形近似示意图2. 龙格·库塔法（Runge Kutta）4计算机辅助绘图基础（第4版）计算机辅助绘图基础（第4版） 54.2二维泊松方程和拉普拉斯方程的有限差分法6计算机辅助绘图基础（第4版）4.2.1建立差分格式图4.4差分网格的结点坐标1. 一阶偏导数计算机辅助绘图基础（第4版）72. 二阶偏导数的差分表达式4.2.2不同介质分界面上连接条件的离散方法和差分格式1. 有不同介质的平面分界的情形图4.5分界面处建立的坐标系8计算机辅助绘图基础（第4版）2. 边界不平行于网格，但是边界无拐点的情形图4.6第一种方法处理对角线边界计算机辅助绘图基础（第4版）9图4.7第二种方法处理对角线边界3. 边界平行于网格，但有拐点的情形图4.8有拐点的平行边界4. 网格成对角线边界时的角形区域边界10计算机辅助绘图基础（第4版）5. 与结点不重合的边界图4.9与网格成对角线的角形区域边界图4.10与结点不重合的边界6. 曲线边界的情形图4.11曲线边界图4.12第二类边界条件4.2.3其他形式的网格及边界条件1. 正三角形六点式2. 六边形三点式3. 正方形九点式图4.13正三角形网格图4.14六边形三点式图4.15正方形九点式4. 直角坐标系拉普拉斯方程的媒质边界的差分格式4.3超松弛迭代法以及有限差分法的误差4.3.1有限差分法求解的一般过程1. 流程图4.16有限差分求解的流程图4.17有限差分求解的框图2. 编程框图3. 举例图4.18例题的分区编号4.3.2超松弛迭代法1. 松弛算法2. 点松弛图4.19点松弛原理图图4.20邻点与原点的松弛关系图4.21第一步的数值关系图4.22点松弛多次后的数值关系3. 增加松弛速度的方法图4.23点松弛、行松弛和块松弛图4.24 15结点块松弛的数值关系4. 逐次超松弛法图4.25收敛因子影响收敛性的变化关系4.3.3有限差分法的收敛性和稳定性4.4轴对称场的差分格式与蒙特卡罗法应用4.4.1轴对称场的差分格式4.4.2蒙特卡罗法应用图4.26轴对称场的差分格式图4.27应用蒙特卡罗法时将封闭区域离散化4.5抛物型和双曲型偏微分方程的有限差分法4.5.1抛物型偏微分方程的有限差分法图4.28解抛物型和双曲型偏微分方程的离散化网格1. 最简单的显式差分格式2. 最简单的隐式格式3. 六点对称格式4. 一般线性抛物型微分方程5. 差分格式的稳定性和收敛性图4.29差分格式的稳定性和收敛性举例4.5.2双曲型偏微分方程的有限差分法1. 显式格式2. 隐式格式。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
o

最简洁的处理方法是依据（4-3），第三类边界条件在此情 况下的差分计算格式为

当边界L在边界节点o处的外法向n与网格线不重合时， 如图4-5所示，显然有

于是，关于o点的差分计算格式是
一般式

第二种情况是在边界处引入的相应节点不落
在边界L上，这时如图4-6所示，

可在邻近边界的节点o上仍按上述方法列出差分 计算格式， 只是需引入与节点o相关的边界节点o’，取点o’处 的外法向n 作为点o处的“外法向n”， 且近似地认为边界条件中给定的函数f1(ro)和f2(ro) 均在点o’上取值。即将式（4-14）中的f1(ro)和 f2(ro)改记为f1(ro’)和f2(ro’)，即得此种情况下关于 O点的差分计算格式。


4.3.2 定解条件的离散化 ——各类差分计算格式

对于场域边界上给定的三类边界条件，第二类边界条 件可以看作为第三类边界条件的特殊情况，因此，只 需讨论第一、第三类边界条件的差分离散化处理。
(1)第一类边界条件的差分离散化 若如图4-２点M所示，划分网格时相应的网格节点 恰好落在边界L上，则只要直接把位函数 u | ML f (rM ) 的值赋给该对应的边界节点M即可。
n
u 0 n
4.3.3 不同媒质分界面上边界条件 的差分计算格式

当给定的边值问题含有多种媒质时，取决于不 同媒质的电磁场特性和不同媒质分界面的几何 形状，将对应有类型繁多的差分计算格式， 仅取两种典型情况进行分析。

(1)分界面与网格线相重合的情况


以二维电场问题为例，
设分界面L’与网络线相重合，如图48所示。


由于差分方程（4-10）、（4-11）中只出现待求函数u在点o(xi, yj) 与其四个相邻点上的值，故通常称为五点差分格式。
为求解给定的边值问题，在完成上述泛定方程的差分格式构造后， 还必须对定解条件——边界条件，以及具体问题中可能存在的衔 接条件（即不同媒质分界面上的边界条件），进行差分离散化处 理。


4.2 差分与差商

有限差分法是以差分原理为基础的一种数值计算方法，它用离散 的函数值所构成的差商来近似逼近相应的偏导数。 差商是基于差分应用的数值微分表达式。 设一函数f(x)，其自变量x有一个很小的增量Dx=h，则函数f(x)的增 量
≈df



称为函数f(x)的一阶差分。 只要增量h很小，差分Df与微分df之间的差异将很小。 一阶差分仍是自变量x的函数

利用网格剖分将定解区域（场域）离散化为网格离散节点的 集合， 应用差分原理，以各离散点上函数的差商来近似替代该点的 偏导数，这样待求的偏微分方程定解问题转化为相应的差分 方程组（代数方程组）问题， 解出各离散点上的待求函数值，即为所求定解问题的离散解， 若再应用插值方法，便可从离散解得到定解问题在整个场域 上的近似解。

应用差分，显然，它可近似地表达为
向前

即有限小的差分Df(x)除以有限小的差分Dx的商，称为差商。

同理，一阶导数f’(x)还可近似表达为
向后

或
中心

式（4-2）、（4-3）、（4-4）分别称为一阶向 前、向后、中心差商。

如图4-1所示，对应于点P的一阶向前、向后、中心差 商，在几何意义上可分别表Байду номын сангаас为弧线PB、AP、AB的 斜率。



对于包括电磁场在内的各种物理场，应用有限差分法 进行数值计算的步骤通常是：

1)采用一定的网格剖分方式离散化场域； 2)基于差分原理的应用，对场域内偏微分方程以及定解条件 进行差分离散化处理（称为构造差分格式）； 3)由所建立的差分格式（代数方程组），选用合适的代数方 程组的解法，编制计算程序，算出待求的离散解。

同理

以h和h1分别与以上两式相乘，且相加，然后截断 u 表达式为 于h的二次项，便得关于的差分
2
x o
2

同理可得

令h1=ah，h2=bh，代入以上两式，最终再代入给 定的泊松方程，即得这类边界情况所对应的差分计 算格式为
(2)第三类边界条件的差分离散化



相类似地，按式（4-1）计算一阶差分的差分， 就得到D2f(x)，称之为原始函数f(x)的二阶差分。

同样，当h很小时，二阶差分D2f(x)逼近于二阶微分 d2f(x)。

依同理，可以定义更高阶的差分。

一阶导数

lim Df ( x)除以无限小的微分 dx lim Dx 即是无限小的微分 df D Dx 0 x 0 的商，

同样需分两种情况讨论。

第一种情况是在边界处引入的相应节点恰好落在边
界L上。

这时，取决于边界L在该边界节点处的外法线方向是否与 网格线相重合，又对应有不同的差分离散化结果。

当边界L在边界节点o处的外法向n与网格线相重合时， 如图4-4所示，则问题在于如何用差商近似替代法向 u 导数 。 n

FDM主要用于静态和准静态问题的求解。

有限差分法与变分法相结合形成有限元法（FEM). 把旋度方程直接转化为差分方程形成时域有限差分法（Finite Difference Time Domain Method, 简称FDTD）


在高频电磁场的传输、辐射、散射和透入等工程问题中应用广泛。

求解由偏微分方程定解问题所构造的数学模型的有限 差分法的基本思想是

4.3.1 偏微分方程的离散化 —五点差分格式

首先需从网格剖分着手决定离散点的分布方式。

原则上，可采用任意的网格剖分方式，但它直接影响所得差 分方程的具体内容，进而影响解题的经济性与计算精度。

为简化问题，通常采用完全有规律的分布方式，这样在每个 离散点上就能得出相同形式的差分方程，有效地提高解题速 度，
(2)分界面对于网格呈对角线形态的情况 此时差分计算格式的推导及其处理方法与上类同，

但为提高差分离散化的逼近度，尚需引入M、N两 个辅助节点（M、N二点分别是线段14 和 23的中 点），如图4-9所示。

对于节点O，如同前所述，当媒质依次代换时，相应的五点 差分格式分别与式（4-16）和（4-17）相同。



对于实际电、磁场问题，如图4-7所示 以通量线（如E线）为边界的第二类齐 次边界条件是常见的一种情况。

这时，边界条件的差分离散化可沿着场域 边界外侧安置一排虚设的网格节点，

显然，对于边界节点o，由于该处 ， 故必然有u1=u3，因此相应于第二类齐次边 界条件 u | L 0 的差分计算格式为

首先，由式（1-66）得出分界面上电位的连续性，即

其次，假设在分界面上自由电荷的面密度s=0，则由式（169）有
以差分格式表示，即为

将ea乘以式（4-16）与eb乘以式（4-17）后相加，代入由式 （4-18）和（4-19）所给定的边界条件，并令K=ea/eb，便得 待求的两种不同媒质分界面上边界条件的差分计算格式为
依据边界上的边界条件，现应有


注意到在以上各式中ua1、ua4、uaM、ub2、ub3、ubN都是虚设 电位值，应用线性插值，它们可由以下方程相互关联：

因此，由实际存在的电位值

可以消去所有虚设电位值，得出关于这类边界条件 的差分计算格式
4.3.4 对称线的差分计算格式

在实际分析电、磁场分布时，经常可观 察到场分布的对称性，因此，在数值计 算中计及场的对称线条件，即可缩小分 析计算的场域，从而在对计算机存贮容 量要求不变的情况下，可获得更为理想 的数值解。 设如图4-10所示，AA’线为二维泊松的对 称线。此时，对位于线上的任一节点O， 由式（4-10），并依据场的对称性，即 有u1=u3，因此相应的差分计算格式为

若划分网格时引入的节点不落在边界 L上，则如图4-3所示，对于邻近边界 的典型节点o，由于h1≠h2≠h，这样， 点及其周围相邻的1、2、3、4点构成 一个不对称的星形。

此时，可仿照4.2节，采用泰勒公式进行 差分离散化处理，即能相当精确地导出 关于o点的差分计算格式。

应用二元函数的泰勒公式，节点1的位置数值u1可 通过u0表示为

依照（4-2）、（4-5），偏导数也可近似地用相应的 差商来表达。

若设定函数u(x, y, z)，当其独立变量x得到一个很小的增量 Dx=h时，则x方向的一阶偏导数可以近似表达为

同样，相应的二阶偏导数可以近似表达为
4.3 差分格式的构造

以二维静态电、磁场泊松方程的第一类边值问题为例。 设具有平行平面场特征的电磁场场域D，如图4-２所示，为一由闭 合边界L所界定的平面域，其定解问题可表述为
且设在媒质ea中位函数ua满足泊松方 程，而在媒质eb中位函数ub满足拉普 拉斯方程。


现若将媒质eb换以媒质ea，则对于o点，据式（4-10）(泊松 方程的差分方程)可得

同理，若将媒质ea换以媒质eb，则对于o点，据式（4-11） (拉普拉斯方程的差分方程)可得

但实际上ua1和ub3是虚设的电位，所以应利用分界面上场量 遵循的边界条件[（1-66）和（1-69）]，把它们从以上两式 中消去－－
它们对应于该点一阶导数的逼近度可分别从以下泰勒 公式的展开式中得知，即由


可见，对应于式（4-2）、（4-3），它们都截断于hf’(x0)项，而把 h2项和更高幂次的项全部略去。 换句话说，就式（4-2）、（4-3）而言，略去余数项所引入的误差 将大致和h的一次方成正比。 而对于式（4-4）的一阶中心差商表达式则相当于把相应的泰勒公 式