第一节 平 面 立 体
平面立体上相邻表面的交线称为棱线。平面立体主要有棱 柱、棱锥等。在投影图上表示平面立体就是把组成立体的平 面和棱线表示出来,然后判断其可见性。看得见的棱线的投影 画成粗实线,看不见的棱线的投影画成虚线。
一、棱柱 棱柱有直棱柱(棱线与底面垂直)和斜棱柱(棱线与底面倾 斜)。 棱柱的顶面和底面是两个形状相同而且互相平行的多边形, 各侧面都是矩形或平行四边形。顶面和底面为正多边形的直 棱柱称为正棱柱。 常见的棱柱有三棱柱、四棱柱、五棱柱和六棱柱等几种。 下面以直三棱柱为例说明其投影特性。
由于N点所在棱面△SAC为侧垂面,可利用该平面在W面上的 积聚投影求得n″,再由n和n″求得(n')。由于N点所属棱面 △SAC的V面投影看不见,所以(n')为不可见。
M点所在平面为一般位置面,可按图3-2a所示过锥顶S和M引 一直线SⅠ,作出SⅠ的有关投影,就可根据点与直线的从属性 质求得点的相应投影。具体作图时,过m'引s'1',由s'1'求作H 面投影s1,再由m'引投影连线交于s1上m点,最后由m'和m求得 m″。
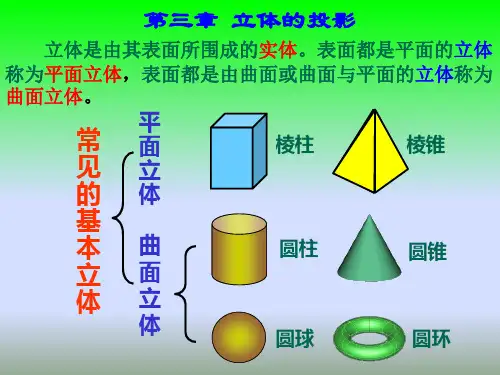
二、棱锥 棱锥的底面为多边形,各侧面为若干具有公共顶点的三角 形。从棱锥顶点到底面的距离称为棱锥高。当棱锥底面为正 多边形、各侧面是全等的等腰三角形时,称为正棱锥。 1.棱锥的三视图 图3-2a所示为正三棱锥的三面投影直观图。该三棱锥的底 面为等边三角形,3个侧面为全等的等腰三角形,假设将其放置 成底面平行于H面,并有一个侧面垂直于W面。
图3-2 正三棱锥的三面投影直观图与三视图
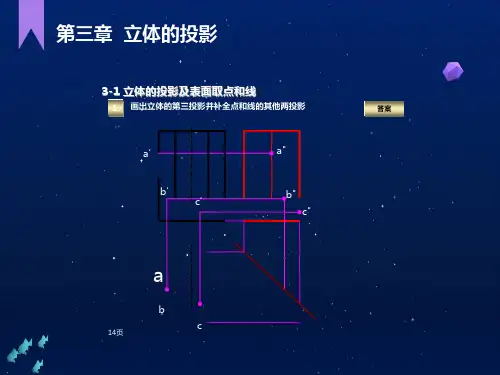
图3-2b所示为该三棱锥的三视图。由于锥底面△ABC为水 平面,所以它的H面投影△abc反映了底面的实形,V面和W面投 影分别积聚成平行X轴和Y轴的直线段a'b'c'和a″(c″)b″, 锥体的后侧面△SAC为侧垂面,它的W面投影积聚为一段斜线 s″a″(c″),它的V面和H面投影为类似形△s'a'c'和△sac, 前者为不可见,后者为可见。左、右两个侧面为一般位置面, 它在3个投影面上的投影均是类似形。