简单多面体的外接球问题

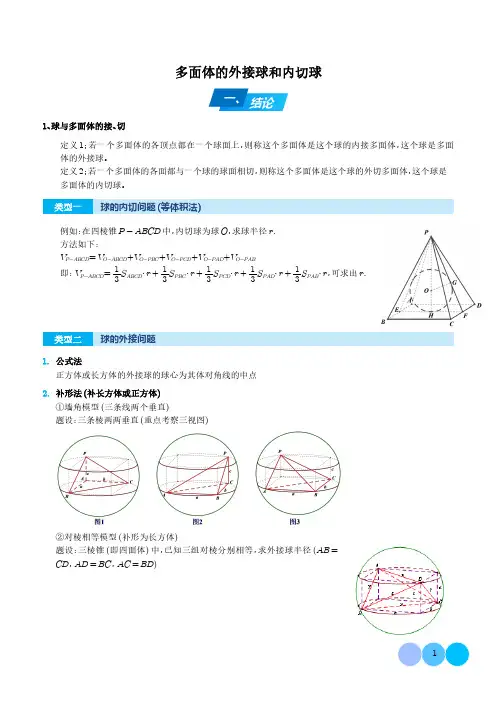
多面体的外接球和内切球一、结论1、球与多面体的接、切定义1；若一个多面体的各顶点都在一个球面上，则称这个多面体是这个球的内接多面体，这个球是多面体的外接球。

定义2；若一个多面体的各面都与一个球的球面相切，则称这个多面体是这个球的外切多面体，这个球是多面体的内切球。

球的内切问题(等体积法)例如：在四棱锥P -ABCD 中，内切球为球O ，求球半径r .方法如下：V P -ABCD =V O -ABCD +V O -PBC +V O -PCD +V O -PAD +V O -PAB即：V P -ABCD =13S ABCD ⋅r +13S PBC ⋅r +13S PCD ⋅r +13S PAD ⋅r +13S PAB ⋅r ，可求出r .球的外接问题1.公式法正方体或长方体的外接球的球心为其体对角线的中点2.补形法(补长方体或正方体)①墙角模型(三条线两个垂直)题设：三条棱两两垂直(重点考察三视图)②对棱相等模型(补形为长方体)题设：三棱锥(即四面体)中，已知三组对棱分别相等，求外接球半径(AB =CD ，AD =BC ，AC =BD )3.单面定球心法(定+算)步骤：①定一个面外接圆圆心：选中一个面如图：在三棱锥P-ABC中，选中底面ΔABC，确定其外接圆圆心O1(正三角形外心就是中心，直角三角形外心在斜边中点上，普通三角形用正弦定理定外心2r=asin A)；②过外心O1做(找)底面ΔABC的垂线，如图中PO1⊥面ABC,则球心一定在直线(注意不一定在线段PO1上)PO1上；③计算求半径R:在直线PO1上任取一点O如图：则OP=OA=R，利用公式OA2=O1A2+OO12可计算出球半径R.4.双面定球心法(两次单面定球心)如图：在三棱锥P-ABC中：①选定底面ΔABC，定ΔABC外接圆圆心O1②选定面ΔPAB，定ΔPAB外接圆圆心O2③分别过O1做面ABC的垂线，和O2做面PAB的垂线，两垂线交点即为外接球球心O.二、典型例题1(2023春·湖南湘潭·高二统考期末)棱长为1的正方体的外接球的表面积为()A.3π4B.3πC.12πD.16π【答案】B【详解】解：易知，正方体的体对角线是其外接球的直径，设外接球的半径为R，则2R=12+12+12=3，故R=3 2．所以S=4πR2=4π×322=3π．故选：B．【反思】本例属于正方体外接球问题，其外接球半径公式可直接记忆.2(2023春·湖南长沙·高三长沙一中校考阶段练习)在四面体PABC中，PA⊥AB，PA⊥AC，∠BAC= 120°，AB=AC=AP=2，则该四面体的外接球的表面积为()A.12πB.16πC.18πD.20π【答案】D【详解】因为PA⊥AB，PA⊥AC，AB∩AC=A,AB,AC⊂平面ABC,所以PA⊥平面ABC.设底面△ABC的外心为G，外接球的球心为O，则OG⊥平面ABC，所以PA⎳OG.设D为PA的中点，因为OP=OA，所以DO⊥PA.因为PA⊥平面ABC，AG⊂平面ABC,所以PA⊥AG，所以OD⎳AG.因此四边形ODAG为平行四边形，所以OG=AD=12PA=1.因为∠BAC=120°，AB=AC=2，所以BC=AB2+AC2-2AB⋅AC cos∠BAC=4+4-2×2×2×-1 2=23,由正弦定理，得2AG=2332=4⇒AG=2.所以该外接球的半径R满足R2=OG2+AG2=5,故该外接球的表面积为S=4πR2=20π.故选:D.【反思】本例属于单面定球心问题①用正弦定理求出ΔABC外心G；②过G做平面ABC的垂线，则外接球球心O在此垂线上；③通过计算算出半径.3(2023秋·湖南娄底·高三校联考期末)《九章算术》是我国古代数学名著，它在几何学中的研究比西方早1000多年．在《九章算术》中，将底面为矩形且一侧棱垂直于底面的四棱锥称为阳马．如图P-ABCD 是阳马，PA⊥平面ABCD，PA=5，AB=3，BC=4．则该阳马的外接球的表面积为()A.1252π3B.50π C.100π D.500π3【答案】B【详解】因PA⊥平面ABCD，AB⊂平面ABCD，AD⊂平面ABCD，则PA⊥AB，PA⊥AD，又因四边形ABCD为矩形，则AB⊥AD.则阳马的外接球与以PA，AB，AD为长宽高的长方体的外接球相同.又PA=5，AB=3，AD=BC=4．则外接球的直径为长方体体对角线，故外接球半径为：R=PA 2+AB 2+AD 22=32+42+522=522，则外接球的表面积为：S =4πR 2=4π⋅504=50π.故选：B【反思】本例属于墙角型模型，通过补形，将原图形补成长方体模型，借助长方体模型求外接球半径.4(2023·全国·高三专题练习)已知菱形ABCD 的各边长为2,∠D =60°．如图所示，将ΔACD 沿AC 折起，使得点D 到达点S 的位置，连接SB ，得到三棱锥S -ABC ，此时SB =3．E 是线段SA 的中点，点F 在三棱锥S -ABC 的外接球上运动，且始终保持EF ⊥AC ，则点F 的轨迹的周长为()A.233π B.433π C.533π D.2213π【答案】C【详解】取AC 中点M ，则AC ⊥BM ,AC ⊥SM ,BM ∩SM =M ，∴AC ⊥平面SMB ，SM =MB =3，又SB =3，∴∠SBM =∠MSB =30°，作EH ⊥AC 于H ，设点F 轨迹所在平面为α，则平面α经过点H 且AC ⊥α，设三棱锥S -ABC 外接球的球心为O ,△SAC ,△BAC 的中心分别为O 1,O 2，易知OO 1⊥平面SAC ,OO 2⊥平面BAC ，且O ,O 1,O 2,M 四点共面，由题可得∠OMO 1=12∠O 1MO 2=60°，O 1M =13SM =33，解Rt △OO 1M ，得OO 1=3O 1M =1，又O 1S =23SM =233，则三棱锥S -ABC 外接球半径r =OO 21+O 1S 2=73，易知O 到平面α的距离d =MH =12，故平面α截外接球所得截面圆的半径为r 1=r 2-d 2=73-14=536，∴截面圆的周长为l =2πr 1=533π，即点F 轨迹的周长为533π．故选：C 【反思】此题典型的双面定球心。

多面体外接球半径常见的5种求法公式法例1 一个六棱柱的底面是正六边形，其侧棱垂直于底面，已知该六棱柱的顶点都在同一个球面上，且该六棱柱的体积为98，底面周长为３，则这个球的体积为 . 解 设正六棱柱的底面边长为x ，高为h，则有263,1,296,8x x x h h =⎧⎧=⎪⎪∴⎨⎨=⎪⎪=⎩⎩ ∴正六棱柱的底面圆的半径12r =，球心到底面的距离2d =.∴外接球的半径1R ==.43V π∴=球. 小结 本题是运用公式222R r d =+求球的半径的，该公式是求球的半径的常用公式. 多面体几何性质法例2 已知各顶点都在同一个球面上的正四棱柱的高为4，体积为16，则这个球的表面积是A.16πB.20πC.24πD.32π解 设正四棱柱的底面边长为x ，外接球的半径为R ，则有2416x =，解得2x =.∴2R R ==∴= .∴这个球的表面积是2424R ππ=.选C.小结 本题是运用“正四棱柱的体对角线的长等于其外接球的直径”这一性质来求解的.补形法例3 若三棱锥的三个侧面两两垂直，则其外接球的表面积是 . 解 据题意可知，该三棱锥的三条侧棱两两垂直，∴把这个三棱锥可以补成一个棱长为.设其外接球的半径为R ，则有()222229R =++=.∴294R =. 故其外接球的表面积249S R ππ==.小结 一般地，若一个三棱锥的三条侧棱两两垂直，且其长度分别为a b c 、、，则就可以将这个三棱锥补成一个长方体，于是长方体的体对角线的长就是该三棱锥的外接球的直径.设其外接球的半径为R，则有2R =.练习1 （2003，四个顶点在同一球面上，则此球的表面积为（ ）3π B. 4πC. D. 6π2（2006年山东高考题）在等腰梯形ABCD 中，AB=2DC=2，0DAB=60∠，E 为AB 的中点，将ADE ∆与BEC ∆分布沿ED 、EC 向上折起，使A B 、重合于点P ，则三棱锥P-DCE 的外接球的体积为（ ）.A. 27B. 2C. 8D. 243 （2008年浙江高考题）已知球O 的面上四点A 、B 、C 、D ，DA ABC ⊥平面，AB BC ⊥，O 的体积等于 .4（2008年安徽高考题）已知点A 、B 、C 、D 在同一个球面上，B BCD A ⊥平面，BC DC ⊥，若6,AB =，则B 、C 两点间的球面距离是 .寻求轴截面圆半径法例4 正四棱锥S ABCD -，点S A B C D 、、、、都在同一球面上，则此球的体积为 .解 设正四棱锥的底面中心为1O ，外接球的球心为O ，如图1所示.∴由球的截面的性质，可得1OO ABCD ⊥平面.又1SO ABCD ⊥平面，∴球心O 必在1SO 所在的直线上. ∴ASC ∆的外接圆就是外接球的一个轴截面圆，外接圆的半径就是外接球的半径.在ASC ∆中，由2SA SC AC ===，得222SA SC AC +=.∴ASC AC ∆∆是以为斜边的Rt . ∴12AC =是外接圆的半径，也是外接球的半径.故43V π=球. 小结 根据题意，我们可以选择最佳角度找出含有正棱锥特征元素的外接球的一个轴截CDAB SO 1图3面圆，于是该圆的半径就是所求的外接球的半径.本题提供的这种思路是探求正棱锥外接球半径的通解通法，该方法的实质就是通过寻找外接球的一个轴截面圆，从而把立体几何问题转化为平面几何问题来研究.这种等价转化的数学思想方法值得我们学习.确定球心位置法例5 在矩形ABCD 中，4,3AB BC ==，沿AC 将矩形ABCD 折成一个直二面角B ACD --，则四面体ABCD 的外接球的体积为A.12512πB.1259πC.1256πD.1253π 解 设矩形对角线的交点为O ，则由矩形对角线互相平分，可知OA OB OC OD ===.∴点O 到四面体的四个顶点A B C D 、、、的距离相等，即点O 为四面体的外接球的球心，如图2所示.∴外接球的半径52R OA ==.故3412536V R ππ==球.选C.外接球内切球问题1. （陕西理•6）一个正三棱锥的四个顶点都在半径为1的球面上，其中底面的三个顶点在该球的一个大圆上，则该正三棱锥的体积是（ ）A ．433 B ．33 C ． 43 D ．123答案 B2. 直三棱柱111ABC A B C -的各顶点都在同一球面上，若12AB AC AA ===,120BAC ∠=︒，则此球的表面积等于 。

常见多面体外接球的有关计算多面体外接球的计算方法多面体是指具有若干个面、边和顶点的几何图形。

而外接球则是指一个球，其球心恰好位于多面体的外部，球面恰好与多面体的顶点相切。

在计算多面体外接球的过程中，我们需要考虑多面体的几何属性以及球的几何属性。

以下是关于多面体外接球计算的方法。

1. 零维多面体（顶点）对于零维多面体，也就是单个顶点，其外接球就是该点本身。

因为只有一个点，所以球心和球面都与该点重合。

2. 一维多面体（线段）对于一维多面体，也就是线段，其外接球是将线段的中点作为球心，并使球面与线段两个端点相切。

3. 二维多面体（三角形、四边形等）对于二维多面体，我们以三角形为例来进行说明。

首先，我们需要计算三角形的垂直平分线，然后求得三条垂直平分线的交点，该交点即为外接球的球心。

球面则通过任意一个顶点与球心的距离来确定。

4. 三维多面体（四面体、正六面体等）对于三维多面体，我们以四面体为例来进行说明。

计算四面体的外接球需要球心和球面两个要素。

首先，我们需要计算四面体的外接圆球，即通过四个顶点所确定的圆球。

然后，我们将四面体的外接圆球的圆心作为外接球的球心，圆球的半径作为外接球的半径。

无论是二维多面体还是三维多面体，计算外接球的主要思路都是找到合适的几何属性来确定球心和球面。

根据不同多面体的特征，我们可以得出相应的计算方法。

需要注意的是，当多面体的顶点过多时，计算外接球可能会变得复杂且耗费较长的时间。

在这种情况下，可以考虑使用计算机辅助的几何软件或算法来进行计算。

综上所述，多面体外接球的计算方法可以根据不同维度的多面体来进行相应的推导和计算。

这些方法可以帮助我们更好地理解和计算多面体的几何性质，并在实际问题中得到应用。

多面体外接球半径常见的5种求法如果一个多面体的各个顶点都在同一个球面上，那么称这个多面体是球的内接多面体，这个球称为多面体的外接球.有关多面体外接球的问题，是立体几何的一个重点，也是高考考查的一个热点.研究多面体的外接球问题，既要运用多面体的知识，又要运用球的知识，并且还要特别注意多面体的有关几何元素与球的半径之间的关系，而多面体外接球半径的求法在解题中往往会起到至关重要的作用. 一、公式法 例1 一个六棱柱的底面是正六边形，其侧棱垂直于底面，已知该六棱柱的顶点都在同一个球面上，且该六棱柱的体积为98，底面周长为3，则这个球的体积为 .解：设正六棱柱的底面边长为x ，高为h ，则有263,1,296,8x x h h =⎧⎧=⎪⎪∴⎨⎨=⎪⎪=⎩⎩ ∴正六棱柱的底面圆的半径12r =，球心到底面的距离d =.∴外接球的半径R= .4π3V ∴=球. 小结：本题是运用公式222R r d =+求球的半径的，该公式是求球的半径的常用公式. 二、多面体几何性质法例2 已知各顶点都在同一个球面上的正四棱柱的高为4，体积为16，则这个球的表面积是（ ）A.16πB.20πC.24πD.32π 解：设正四棱柱的底面边长为x ，外接球的半径为R ，则有2416x =，解得2x =.∴2R R =∴= ∴这个球的表面积是24π24πR =.选C .小结： 本题是运用“正四棱柱的体对角线的长等于其外接球的直径”这一性质来求解的.三、补形法例3 若三棱锥的三个侧面两两垂直，，则其外接球的表面积是 . 解：据题意可知，该三棱锥的三条侧棱两两垂直，∴把这个三棱锥可以补成一个棱于是正方体的外接球就是三棱锥的外接球. 设其外接球的半径为R ，则有()222229R =++=.∴294R =.故其外接球的表面积24π9πS R ==. 小结：一般地，若一个三棱锥的三条侧棱两两垂直，且其长度分别为a b c 、、，则就可以将这个三棱锥补成一个长方体，于是长方体的体对角线的长就是该三棱锥的外接球的直径.设其外接球的半径为R，则有2R .四、寻求轴截面圆半径法例4 正四棱锥S ABCD -的底面边长和S ,A ,B ,C ,D 都在同一球面上，则此球的体积为 . 解：设正四棱锥的底面中心为O 1，外接球的球心为O ，如图3所示.∴由球的截面的性质，可得OO 1⊥平面ABCD .又SO 1⊥平面ABCD ，∴球心O 必在SO 1所在的直线上.∴△ASC 的外接圆就是外接球的一个轴截面圆，外接圆的半径就是外接球的半径. 在△ASC中，由2SA SC AC ===，得222SA SC AC +=.∴△ASC 是以AC 为斜边的Rt △.∴12AC=是外接圆的半径，也是外接球的半径.故4π3V =球. 小结：根据题意，我们可以选择最佳角度找出含有正棱锥特征元素的外接球的一个轴截面圆，于是该圆的半径就是所求的外接球的半径.本题提供的这种思路是探求正棱锥外接球半径的通解通法，该方法的实质就是通过寻找外接球的一个轴截面圆，从而把立体几何问题转化为平面几何问题来研究.这种等价转化的数学思想方法值得我们学习.C D A B S O 1图3五、确定球心位置法例5 在矩形ABCD 中，AB =4,BC =3，沿AC 将矩形ABCD 折成一个直二面角B - AC -D ，则四面体ABCD 的外接球的体积为（ ）CA.12512πB.1259π C.125π6 D.125π3解：设矩形对角线的交点为O ，则由矩形对角线互相平分，可知OA =OB =OC =OD .∴点O 到四面体的四个顶点A 、B 、C 、D 的距离相等，即点O 为四面体的外接球的球心，如图4所示.∴外接球的半径52R OA ==.故34125ππ36V R ==球.选C . 练习：1.一个正三棱锥的四个顶点都在半径为1的球面上，其中底面的三个顶点在该球的一个大圆上，则该正三棱锥的体积是( )C A.33 B.3C.3D.3 2. 一个四面体的所有棱长都为2，四个顶点在同一球面上，则此球的表面积为（ ）A A. 3π B.4π C. 33π D. 6π 3. 在等腰梯形ABCD 中，AB =2DC =2， ∠DAB =60°，E 为AB 的中点，将△ADE 与 △BEC 分别沿ED 、EC 向上折起，使A 、B 重合于点P ，则三棱锥P -DCE 的外接球的体积为（ ） C A.43π B.6π2 C. 6π D. 6π244.已知三棱锥A -BCD 内接于球O ，AB =AD =AC =BD =3,BCD ∠=60°，则球O 的表面积为( )DA.3π2B.2πC.3πD.9π25.已知正三棱锥P -ABC 的主视图和俯视图如图所示，则此三棱锥的外接球的表面积为（ ）DA.4πB.12πC.16π3 D.64π36.已知三棱柱ABC -A B C ''',侧棱AA '⊥底面ABC ，AA '=4，BC 360A ∠=o ,则该三棱柱外接球的表面积为（ ）CA.18πB.19πC.20πD.21π 7.已知直三棱柱ABC -A 1B 1C 1的6个顶点都在球O 的球面上，若AB =3，AC =4，AB ⊥AC ，AA 1=12，则球O 的半径为( )317B.210C.132D.310【答案】C【解析】由球心作面ABC 的垂线，则垂足为BC 中点M .计算AM =52，由垂径定理，OM =6，所以半径R 22513()622+=.8.(2014·全国大纲)正四棱锥的顶点都在同一球面上，若该棱锥的高为4，底面边长为2，则该球的表面积为 ( )A.814π B.16π C.9π D.274π【答案】A9.若三棱锥P -ABC 的最长的棱PA =2，且各面均为直角三角形，则此三棱锥的外接球的体积是 .4π310.在正三棱锥S -ABC 中，M ，N 分别是SC ，BC 的中点，且MN ⊥AM ，若侧棱SA =23，则正三棱锥S -ABC 外接球的表C AO D B图4面积是.【答案】36π【解析】一定要用上隐含条件正三棱锥对棱垂直，又MN∥BS，可得BS⊥SA,BS⊥SC.又AS⊥BC,AS⊥SB得AS⊥SC即SA,SB,SC两两垂直.又因正棱锥SA=SB=SC,所以此三棱锥外接球与补成正方体的外接球相同.所以2R=323g=6，所以R=3.所以正三棱锥S-ABC外接球的表面积是24πR=36π.11. (2015·唐山二模)在三棱锥P-ABC中，△ABC与△PBC都是等边三角形，侧面PBC⊥底面ABC，AB=23，则该三棱锥的外接球的表面积为.【答案】20π12.在菱形ABCD中，A=60°，AB=3,将△ABD沿BD折起到△PBD的位置.若平面PBD⊥平面CBD，则三棱锥P-BCD的外接球体积为.【答案】13.已知四棱锥P-ABCD的三视图如图所示，则此四棱锥外接球的半径为( )A.3B.5C.2D.2【答案】B14. 四棱锥P-ABCD的底面ABCD为矩形,侧面PAD⊥平面ABCD，∠APD=120°，AB=PA=PD=2，则该四棱锥P-ABCD外接球的体积为( )A.32π3B.205π3C.86πD.36【答案】B15. 已知AB是球O的直径，C,D为球面上的两动点，AB⊥CD，若四面体ABCD体积的最大值为9，则球O的表面积为.【答案】36π16. 三棱锥A-BCD的两条棱AB=CD=6，其余各棱长均为5，求三棱锥的内切球半径．【思路分析】法一：内切球球心O到各面的距离相等，如图，可以推断出球心在AB和CD的中点的连线的中点，求出OH即可．法二：先求四面体的体积，再求表面积，利用体积等于表面积和高乘积的13，求出内切球半径．【解析】法一：易知内切球球心O到各面的距离相等．设E、F为CD、AB的中点，则O在EF上且O为EF的中点．在△ABE中，AB=6，AE=BE=4，OH=378．法二：设球心O到各面的距离为R．4×13S△BCD×R=V A-BCD，∵S△BCD=12×6×4=12，V A-BCD=2V C-ABE=67．∴4×13×12R=67.∴R=378．【点评】正多面体与球的切接问题常借助体积求解；也可以由几何图形特征分析出球心的位置，然后解答，考查形式空间想PB CADEF O象能力，逻辑思维能力，是中档题． 【拓展提升】三棱锥A -BCD 的两条棱AB =CD =6，其余各棱长均为5，求三棱锥的外接球的表面积． 17π【解析】补成长方体，如下图，AC D A 1 D 1C 1B 16 5 6 5。

多面体与外接球的三种题型 题型一（直接找直径） 1、在三棱锥S-ABC 中，SA=AC=，SB=，BC=1，则三棱锥S-ABC 的外接球的表面积是 。

2、若三棱锥S-ABC 的所有顶点都在同一个球O 的球面上，SA 面ABC ，SA=，AB=1，AC=2，∠BAC=60°，求球O 的体积。

题型二（作轴截面构造Rt △）1、已知三棱锥S-ABC 的所有顶点都在球O 的球面上，△ABC 是边长为1的正三角形，SC 是球O 的直径，且SC=2，求此棱锥的体积。

2、一个六棱柱的底面是正六边形，其侧棱垂直于底面，已知该六棱柱的顶点都在同一个球面上，且该六棱柱的高为，底面周长为3，则这个球的体积为 。

题型三（补形法）1、若三棱锥的三个侧面两两垂直，且侧棱长均为，则其外接球的表面积为2、一个几何体的三视图如图所示，其中主视图和侧视图是腰长为4的两个全等直角三角形，若该几何体的所有顶点都在同一个球面上，则该球的表面积为 。

3、已知S ，A ，B ，C 是球O 表面上的一点，SA 面ABC ，AB BC ，SA=AB=1，BC=，则球O 的表面积等于 。

23⊥3233⊥⊥24、四棱锥P -ABCD 的三视图如图所示，四棱锥P -ABCD 的五个顶点都在同一个球面上，E ，F 分别是棱AB ，CD 的中点，直线EF 被球面所截的线段长为，则该球的表面积为5、在三棱锥S -ABC 中，SA=BC=2，SB=AC=3，SC=AB=，则该三棱锥外接球的体积是 。

题型四（割补法）1、如图所示的四棱锥P -ABCD 中，底面ABCD 是边长为a的正方形，PD 底面ABCD ，且PD=a ，PA=PA=a ，若在这个四棱锥内放一球，则此球的最大半径是 。

2、已知正四面体的外接球的半径为1，则此正四面体的体积为 。

3、已知三棱锥D -ABC 的顶点都在球O 的球面上，AB=4，BC=3，AB BC ，AD=12，且DA 平面ABC ，则三棱锥A -BOD 的体积是 。

常见多面体外接球的有关计算首先，我们需要了解外接球的定义。

给定一个多面体，外接球是一个球，可以和这个多面体的所有顶点都切线相切。

1.正方体外接球的计算：一个正方体的外接球半径等于边长的一半。

因此，可以通过给定的边长计算出外接球的半径。

2.正六面体外接球的计算：正六面体是一个六个等边三角形构成的多面体。

外接球半径等于正六面体边长的一半。

因此，可以通过给定的边长计算出外接球的半径。

3.正八面体外接球的计算：正八面体是一个八个等边三角形构成的多面体。

外接球半径等于正八面体边长的一半乘以根号2、因此，可以通过给定的边长计算出外接球的半径。

4.正十二面体外接球的计算：正十二面体是一个十二个等边五边形构成的多面体。

外接球半径等于正十二面体边长的一半乘以根号3、因此，可以通过给定的边长计算出外接球的半径。

5.正二十面体外接球的计算：正二十面体是一个二十个等边三角形构成的多面体。

外接球半径等于正二十面体边长的一半乘以根号3乘以根号(5+2√5)除以4、因此，可以通过给定的边长计算出外接球的半径。

对于体积的计算，可以使用外接球的半径和体积公式来计算。

体积公式为：V=(4/3)*π*r³，其中V代表体积，π代表圆周率，r代表外接球的半径。

对于表面积的计算，可以使用外接球的半径和表面积公式来计算。

表面积公式为：S=4*π*r²，其中S代表表面积，π代表圆周率，r代表外接球的半径。

以上是常见多面体外接球的计算方法。

通过这些计算，我们可以得到多面体的外接球的半径、体积和表面积等相关信息。

这些计算方法对于解决与多面体相关的问题和应用非常有用。

确定简单多面体外接球的球心的策略简单多面体外接球问题是立体几何中的难点和重要的考点，此类问题实质是解决球的半径r或确定球心o的位置问题，其中球心的确定是关键.如何确定简单多面体外接球的球心，下面作一些归纳、总结．1 由球的定义确定球心在空间，如果一个定点与一个简单多面体的所有顶点的距离都相等，那么这个定点就是该简单多面体的外接球的球心．由上述性质，可以得到确定简单多面体外接球的球心的如下结论．结论1 正方体或长方体的外接球的球心是其体对角线的中点．结论2 正棱柱的外接球的球心是上下底面中心的连线的中点．结论3 直三棱柱的外接球的球心是上下底面三角形外心的连线的中点．结论4 正棱锥的外接球的球心是在其高上，具体位置可通过计算找到．结论5 若棱锥的顶点可构成共斜边的直角三角形，则公共斜边的中点就是其外接球的球心．例1 （2012年高考辽宁卷·文16）已知点p，a，b，c，d是球o表面上的点，pa⊥平面abcd，四边形abcd是边长为23的正方形.若pa＝26，则△oab的面积为________．图1解析因为外接球球心满足到各个顶点距离相等，直角三角形斜边中点到各个顶点距离相等，故可知pc的中点即为球心o.如图1，在rt△pac中，ac＝26，pc＝43，故r＝23.球心满足oa＝ob＝r＝23，故△oab为等边三角形，所以其面积s＝33．评注（1）球心满足到各个顶点距离相等，故球心常常在某直角三角形的斜边中点处.另外，因为球心与截面圆圆心的连线垂直于截面，故一个球中多个过截面圆圆心的垂线的交点必为球心.（2）此题还可以通过构造长方体找到球心，并获解．例2 （2010年高考全国ⅰ新课标卷·理10）设三棱柱的侧棱垂直于底面，所有棱长都为a，顶点都在同一个球面上，则该球的表面积为（）.a.πa2b.73πa2c.113πa2d.5πa2图2解析设o1，o2分别是正三角形a1b1c1和正三角形abc的中心，又三棱柱abc—a1b1c1是正三棱柱，所以其外接球的球心o是o1o2的中点，如图2，于是其外接球的半径为r＝oo22+ao22＝（a2）2+（23ad）2＝（a2）2+（23×32a）2＝7a212，所以球的表面积为4π·r2＝73πa2，故选b．评注（1）正三棱柱外接球的球心是上下底面正三角形中心的连线的中点.（2）直三棱柱外接球的球心是上下底面三角形外心的连线的中点．2 构造正方体或长方体确定球心长方体或正方体的外接球的球心是在其体对角线的中点处.以下是常见的、基本的几何体补成正方体或长方体的途径与方法．途径1 正四面体、三条侧棱两两垂直的正三棱锥、四个面都是直角三角形的三棱锥都分别可构造正方体．途径2 同一个顶点上的三条棱两两垂直的四面体、相对的棱相等的三棱锥都分别可构造长方体和正方体．途径3 若已知棱锥含有线面垂直关系，则可将棱锥补成长方体或正方体．途径4 若三棱锥的三个侧面两两垂直，则可将三棱锥补成长方体或正方体．例3 （2012年高考辽宁卷·理16）已知正三棱锥p—abc，点p，a，b，c都在半径为3的球面上.若pa，pb，pc两两互相垂直，则球心到截面abc的距离为________．图3解析因为pa，pb，pc两两互相垂直，故正三棱锥p—abc的外接球即是以pa，pb，pc为棱的正方体的外接球，球心是在其体对角线的交点处，如图3，易证op⊥平面abc，所以球心o到截面abc的距离即为球半径r减去正三棱锥p—abc的高.设pa＝a，则（2r）2＝3a2，所以a＝2.设正三棱锥p—abc的高为h，则va—pbc＝vp —abc，即13×12a2·a＝13×34（22）2h，解得h＝233，故球心到截面abc的距离为3－233＝33．评注（1）易知三棱锥o—abc是正三棱锥，求出其高即为所求.（2）构造正方体并找到球心是破解此题的关键．3 由性质确定球心利用球心o与截面圆圆心o1的连线垂直于截面圆及球心o与弦中点的连线垂直于弦的性质，确定球心．例4 三棱锥s—abc中，sa⊥平面abc，sa＝2，△abc是边长为1的正三角形，则其外接球的表面积为________．图4解析设o1是△abc的外心，如图4，则o1a＝o1b＝o1c.过点o1作平面abc的垂线oo1，由此可知直线oo1上任意一点与a，b，c的距离相等，故三棱锥s—abc的外接球的球心在直线oo1上，又要使oa＝os，则o在线段sa的垂直平分线do上，从而三棱锥s—abc的外接球的球心是直线o1o与do的交点．do＝ao1＝23ae＝33，在rt△aod中，ao2＝ad2＋do2＝43，于是s球表＝4π·ao2＝163π．评注（1）一般棱锥的外接球的球心是在经过棱锥的底面多边形的外接圆的圆心且垂直于这个面的直线上.（2）此题也可以通过构造正三棱柱来解答，其球心是两底面三角形中心的连线的中点．。

高三微专题：外接球一、由球的定义确定球心在空间，如果一个定点与一个简单多面体的所有顶点的距离都相等，那么这个定点就是该简单多面体的外接球的球心．简单多面体外接球问题是立体几何中的重点，难点，此类问题实质是①确定球心的位置 ②在Rt △用勾股定理求解外接球半径（其中底面外接圆半径r 可根据正弦定理求得）．二、球体公式1.球表面积S=4π2R 2.球体积公式V=334Rπ三、球体几个结论：（1）长方体，正方体外接球直径=体对角线长 （2）侧棱相等，顶点在底面投影为底面外接圆圆心 （3）直径所对的球周角为90°（大圆的圆周角） （4）正三棱锥对棱互相垂直四、外接球几个常见模型 1.长方体（正方体）模型O例1（2017年新课标Ⅱ)长方体的长，宽，高分别为3,2,1，其顶点都在球O的球面上，则球O的表面积为（）答案：14练习1（2016新课标Ⅱ）体积为8的正方体的顶点都在同一球面上，则该球的表面积为（ ） 答案：12π2.正棱锥（圆锥）模型(侧棱相等，底面为正多边形）球心位置：位于顶点与底面外心连线线段(或延长线）上半径公式：222)(r R h R +-=（R 为外接球半径，r 为底面外接圆半径，h 为棱锥的高，r 可根据正弦定理r Aa2sin = （一边一对角)例2.已知各顶点都在同一个球面上的正四棱锥高为，体积为，则这个球的表面积是____. 【解析】正四棱锥的高为，体积为，易知底面面积为，底面边长为．正四棱锥的外接球的球心在它的高上，记为，，，，在中，，由勾股定理得．所以，球的表面积.练习2．正三棱锥ABC S -中，底面ABC 是边长为3的正三角形，侧棱长为2，则该三棱锥的外接球体积等于 .解析：ABC ∆外接圆的半径为 ，三棱锥ABC S -的直径为3460sin 22==R ，外接球半径32=R ，或1)3(22+-=R R ，32=R ，外接球体积2733233834343πππ=⋅==R V 3. 侧棱与底面垂直锥体（直棱柱，圆柱）(1) 侧棱与底面垂直：球心位置：底面外心正上方，侧棱中垂面交汇处（高的一半处）半径公式：222)2(h r R +=,（R 为外接球半径，r 为底面外接圆半径，h 为棱锥的高，r 可根据正弦定理r Aa2sin = （一边一对角)(2) 直棱柱(圆柱)球心位置：上下底面外心连线中点处公式公式：222)2(h r R +=,（R 为外接球半径，r 为底面外接圆半径，h 为棱锥的高，r 可根据正弦定理r Aa2sin = （一边一对角)例3.在四面体中，ABC SA 平面⊥，,1,2,120====∠︒AB AC SA BAC则该四面体的外接球的表面积为（ ）π11.A π7.B π310.C π340.D 解析：在ABC ∆中，7120cos 2222=⋅⋅-+=BC AB AB AC BC ，7=BC ，ABC ∆的外接球直径为372237sin 2==∠=BAC BC r ， ∴310,)2(2222=+=R SA r R ，340π=S ，选D 练习3（1）直三棱柱的各顶点都在同一球面上，若,，则此球的表面积等于 。