理论力学期中测验-答案
- 格式:pdf
- 大小:205.93 KB
- 文档页数:7
理论力学期中测验2007.12.1年级__________ 学号__________姓名__________ 成绩__________一、挑选题(多选或单选,在准确答案上打 。
每题2分, 共10分)1. 正方体上的六个面各作用有一个平面汇交力系,则该力系自立的平衡方程最多有:_______A:4个;B:6个;C:8个D:12个。
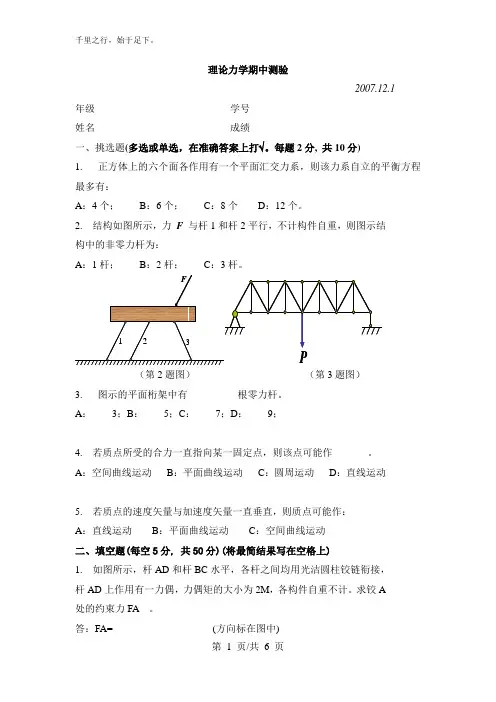
2. 结构如图所示,力F 与杆1和杆2平行,不计构件自重,则图示结构中的非零力杆为:_______A:1杆;B:2杆;C:3杆。
(第2题图)(第3题图)3. 图示的平面桁架中有__________根零力杆。
A:3;B:5;C:7;D:9;4. 若质点所受的合力一直指向某一固定点,则该点可能作_______。
A:空间曲线运动B:平面曲线运动C:圆周运动D:直线运动5. 若质点的速度矢量与加速度矢量一直垂直,则质点可能作:_______A:直线运动B:平面曲线运动C:空间曲线运动二、填空题(每空5分, 共50分)(将最简结果写在空格上)1. 如图所示,杆AD和杆BC水平,各杆之间均用光洁圆柱铰链衔接,杆AD上作用有一力偶,力偶矩的大小为2M,各构件自重不计。
求铰A处的约束力FA 。
答:FA=____________________(方向标在图中)ABCDbbbb2M2. 结构及其受力如图所示,已知均布载荷集度q =20N/m ,力偶矩的大小M =5N ⋅m ,a =1m 。
则CD 杆上C 端所受的约束力的大小为F =____________________ N 。
3. 系统如图所示。
O 1A 杆重为W ,半径为R 的均质圆盘重为W ,杆与水平线的夹角为θ =60︒,OC 铅垂,不计铰链处的摩擦。
无论水平弹簧的拉力有多大,系统都能在图示位置实现自锁。
则杆与圆盘间的最小静滑动摩擦因数 f min=__________。
4. 平面桁架如图所示,该桁架是____________________ (挑选:静定桁架或静不定桁架)。

精选文档理论力学试题及答案一、是非题(每题2分。
正确用√,错误用×,填入括号内。
)1、作用在一个物体上有三个力,当这三个力的作用线汇交于一点时,则此力系必定均衡。
2、力关于一点的矩不因力沿其作用线挪动而改变。
()3、在自然坐标系中,假如速度υ=常数,则加快度α=0。
()4、虚位移是偶想的,极细小的位移,它与时间,主动力以及运动的初始条件没关。
5、设一质点的质量为m,其速度与x轴的夹角为α,则其动量在x轴上的投影为mvx=mvcosa。
二、选择题(每题3分。
请将答案的序号填入划线内。
)1、正立方体的顶角上作用着六个大小相等的力,此力系向任一点简化的结果是。
①主矢等于零,主矩不等于零;②主矢不等于零,主矩也不等于零;③主矢不等于零,主矩等于零;④主矢等于零,主矩也等于零。
2、重P的均质圆柱放在V型槽里,考虑摩擦柱上作用一力偶,其矩为 M时(如图),圆柱处于极限均衡状态。
此时按触点处的法向反力N A与N B的关系为。
①N A=NB;②N A>NB;③N A<NB。
3、边长为L的均质正方形平板,位于铅垂平面内并置于圆滑水平面上,如图示,若给平板一细小扰动,使其从图示位置开始倾倒,平板在倾倒过程中,其质心C点的运动轨迹是。
①半径为L/2的圆弧;②抛物线;③椭圆曲线;④铅垂直线。
4、在图示机构中,A//O2B,杆O2C//O3D,且O1A=20cm,O2C=杆O140cm,CM=MD=30cm,若杆AO1以角速度ω=3rad/s匀速转动,则D点的速度的大小为cm/s,M点的加快度的大小为cm/s2。
①60;②120;③150;④360。
.精选文档5、曲柄OA以匀角速度转动,当系统运动到图示地点(OA//O1B。
AB |OA)时,有V A V B,A B,ωAB 0,AB 0。
①等于;②不等于。
三、填空题(每题5分。
请将简要答案填入划线内。
)1、已知A重100kN,B重25kN,A物与地面间摩擦系数为0.2。

同济大学理论力学期中试题及答案精选文档 TTMS system office room 【TTMS16H-TTMS2A-TTMS8Q8-1.沿长方体的不相交且不平行的棱边作用三个大小相等的力,问边长 a ,b ,c 满足什么条件,该力系才能简化为一个力。
解:向O 点简化:R F '的投影:F F F F F F Rz Ry Rx ='='=',,k F j F i F F R++='∴ [3分] 主矩O M投影:0,,=-=-=Oz Oy Ox M aF M cF bF M()j aF i cF bF M O--=∴ [6分]∵当0=⋅'O R M F时才能合成为力,应有()()[]0=--⋅++j aF i cF bF k F j F i F即()00==-FaF cF bF F 或b=c ,或a=0时,力系才能合成为一个力。
[10分]2. 图示不计自重的水平梁与桁架在B 点铰接。
已知:载荷1F 、F 均与BH 垂直,F 1=8kN ,F=4kN ,M=6m kN ⋅,q=1kN/m ,L=2m 。
试求:(1)支座A 、C 的约束力;(2)杆件1、2、3的内力。
解:(1)取AB 杆为研究对象()∑=0F M B 0212=+-M LF qL AykN 4=Ay F(2)取整体为研究对象()∑=0F M C 02sin 2sin cos 2cos 21112=-⋅-⋅--⋅+⋅++L F L F L F L F L F L F qL M Ay Ax θθθθkN 37.5=Ax F ∑=0x F 0cos 2cos 1=--+θθF F F F Cx Ax0=∑yF 0sin 2sin 1=---+θθF F qL F F Cy Ay kN .F Cx 948=kN 165.F Cy = [6分](3)取D 点为研究对象∑=0x F 01=F [7分](4)取H 点为研究对象∑=0x F 0cos 5=--θF FkN 525-=F [8分](5)取C 点为研究对象∑=0x F 0sin 35=++θF F F CxkN 12.103-=F0=∑y F 0cos 32=++θF F F CykN 90.32=F [10分]3. 曲柄连杆机构在图示位置平衡。

理论力学试题库及答案(通用篇)一、理论力学试题库(通用篇)试题一:已知一质点在平面直角坐标系中的运动方程为 x = 2t² + 3,y = 4t² - t + 1。
求该质点在t = 2s 时的速度和加速度。
试题二:一质点沿圆周运动,其半径为 r,角速度为ω,角加速度为α。
求质点在任意时刻 t 的速度和加速度。
试题三:一质点从静止开始沿直线运动,受到恒力F 的作用。
求质点在任意时刻 t 的速度和位移。
试题四:一质点在平面内做匀速圆周运动,半径为r,角速度为ω。
求质点在任意时刻 t 的速度和加速度。
试题五:一质点在平面内做匀速运动,速度大小为v,方向与水平方向成θ 角。
求质点在任意时刻 t 的位移。
试题六:一质点在重力作用下做自由落体运动,求质点在任意时刻 t 的速度和位移。
试题七:一质点在水平地面上受到一斜向上的拉力F,拉力与水平方向的夹角为θ。
求质点在任意时刻 t 的速度和加速度。
试题八:一质点在平面内做匀速圆周运动,半径为r,角速度为ω。
求质点在任意时刻 t 的切向加速度和法向加速度。
试题九:一质点在平面内做匀速运动,速度大小为v,方向与水平方向成θ 角。
求质点在任意时刻 t 的位移和速度。
试题十:一质点在水平地面上受到一恒力 F 的作用,力与水平方向的夹角为θ。
求质点在任意时刻 t 的速度和位移。
二、答案答案一:t = 2s 时,速度 v = (4t, 8t - 1) = (8, 15) m/s;加速度 a = (8, 8) m/s²。
答案二:质点在任意时刻 t 的速度v = (rω, 0),加速度a = (0, rα)。
答案三:质点在任意时刻 t 的速度 v = (F/m)t,位移 s = (F/m)t²/2。
答案四:质点在任意时刻 t 的速度 v =(rωcos(ωt), rωsin(ωt)),加速度 a = (-rω²sin(ωt), rω²cos(ωt))。


力学 期中考试试题(质点运动学、牛顿运动定律、动能和势能、质点角动量) 答案一、判断题1. √;2. ╳;3. √;4. ╳;5. ╳。
二、选择题1. D ;2. A ;3. B ;4. D ;5. C ;6. D ;7. A ;8. B ;9. C ;10.B 。
三、填空题1. a t =−c ;a n =(b −cc )2R ⁄;c =�b ±√Rc�c ⁄2. a =arctan μ3. 29.6km ∙s −14. v 0=m M ��T mmm m −g�l ; I =m ��T mam −g �l5. ω=4ω0;A =3mr 02ω022⁄四、计算题1. 解 设此时人的头顶在地面的影子位置距离灯柱位置距离为m ′。
由几何关系得,H =ℎ 即, m′=H H−ℎm 上式对时间求二阶导数可得影子顶的加速度a ′=d 2m ′dc =H H −ℎd 2m dc =H H −ℎa 他的头顶在地面上的影子移动的加速度的大小为Ha (H −ℎ)⁄。
2. 解货箱在进入摩擦的台面可分为两个阶段。
首先是部分进入台面,不妨设某一时刻进入该台面的部分长度为m ,此时货箱受到的摩擦力f =μmgm L ⁄;而对于整个箱子都进入台面的情况,箱子受到的摩擦力f =μmg 。
所以货箱在台面滑行的距离s >3L ,摩擦力做功A μ=�f ⃗s 0∙dm ⃗=−�μmgm L dm L 0−�μmgdm s L =12μmgL −μmgμ 由动能定理A μ=E k −E k0可知E k =A μ+E k0=1μmgL −μmgμ+1mv 02 位移至少位移3L ,所以在s =3L 处动能E k ≥0。
则可得,v 0≥�5μgL3. 解设小球运动到x处的速度为v,在接下来的dt时间里面被吸附到小球上的粉尘质量:dm=ρρdm=ρρvdc其中,ρ=πR2是小球的截面积。
以这部分被吸附到小球的粉尘为研究对象,它们在dt时间内由静止到改变为速度v。
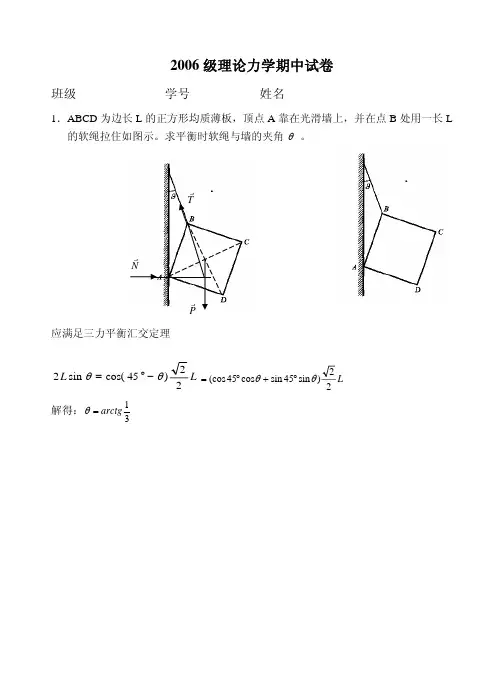
2006级理论力学期中试卷班级 学号 姓名1.ABCD 为边长L 的正方形均质薄板,顶点A 靠在光滑墙上,并在点B 处用一长L 的软绳拉住如图示。
求平衡时软绳与墙的夹角 。
θT r Pr Nr应满足三力平衡汇交定理 L L 22)45cos(sin 2θθ−°=L 22)sin 45sin cos 45(cos θθ°+°= 解得:31arctg =θ2.图示结构中,各杆自重不计。
已知:AB =CD =AD =L =6m ,=5kN /m ,M =18kN ·m ,P =20kN 。
试求A 、D 支座的反力及AC 杆的内力。
B q3.静定水平组合梁如图所示,已知AC=CD=DB=a=2m,CK=b,分布载荷的最大值q=1.960kN/m,重为G=5.880kN的物块E放置在粗糙的斜面上,物块与斜面间的摩擦系数f=0.3,并用细绳跨过定滑轮连接在CB杆的中点D上,不计梁的自重。
试求:(1)物体系统平衡时,b的取值范围;(2)当b=2m时,固定端A处的约束反力及重物E受到的摩擦力。
解:(1)取物块E为研究对象,设其有向下的滑动趋势,受力如图(a)所示,建立坐4.图是平面凸轮机构,已知:,,B O OA 1=1OO AB =s /rad o 2=ω,0=α,图示位置AB 水平,OA AB ⊥,,cm L 15=cm h 10=。
试求图示位置(1)DE 杆上D 点的速度;(2)D 点相对于曲柄OA 的速度。
5.平面机构如图所示。
已知OA杆以匀角速度ω绕O轴转动,与直角三角形板ABC铰接的滑块B被限制在水平轨道中,套筒C与板铰接,其中OA=R,DE穿过套筒C。
在图示位置时,OA杆铅垂,AB与DE平行,φ=30°。
试求该瞬时:(1)滑块B的加速度;(2)DE杆的角速度和角加速度。

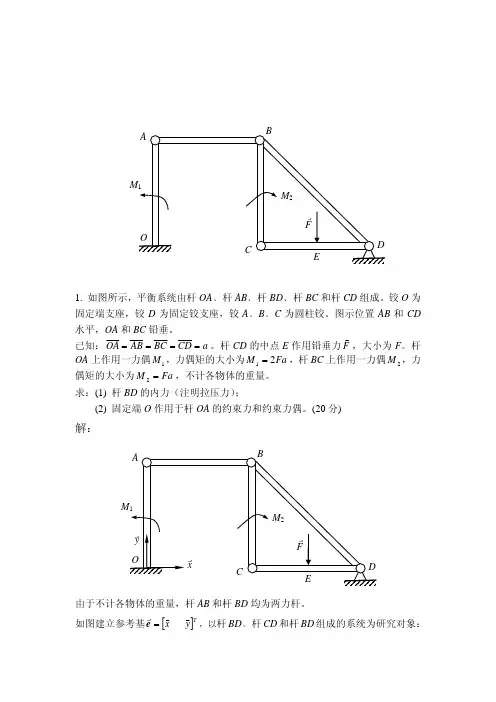
1. 如图所示,平衡系统由杆OA ﹑杆AB ﹑杆BD ﹑杆BC 和杆CD 组成。
铰O 为固定端支座,铰D 为固定铰支座,铰A ﹑B ﹑C 为圆柱铰。
图示位置AB 和CD 水平,OA 和BC 铅垂。
已知:a CD BC AB OA ====。
杆CD 的中点E 作用铅垂力F v,大小为F 。
杆OA 上作用一力偶1M ,力偶矩的大小为Fa M 21=,杆BC 上作用一力偶2M ,力偶矩的大小为Fa M =2,不计各物体的重量。
求:(1) 杆BD 的内力(注明拉压力);(2) 固定端O 作用于杆OA 的约束力和约束力偶。
(20分) 解:由于不计各物体的重量,杆AB 和杆BD 均为两力杆。
如图建立参考基[]Ty x v v r =e , 以杆BD ﹑杆CD 和杆BD 组成的系统为研究对象:0)(1=∑=i n i z D F M v0212=+−a S M aF AB (3分) 解得:2FS AB =(拉力)(1分)以杆BD 为研究对象:0)(1=∑=i n i z C F M v0212=−−M a S a S BD AB (3分)解得:F S BD 22−=(压力)(1分)ABS r BDS rDABS r以杆OA 为研究对象:01=∑=ni ixF,0=+AB x O S F (2分)01=∑=n i iyF,0=y O F (2分)0)(1=∑=i ni z O F M v01=++−O AB M M a S (3分)解得:F F x O 21−=,0=y O F ,Fa M O 23−=(2分)2. 如图所示,梯子由杆OA 和杆AB 组成,铰O 为固定铰支座,铰A 为圆柱铰,杆AB 搁置在地面上,接触点为端点B 。
杆OA 和杆AB 的长度均为l ,图示位置杆OA 和杆AB 的倾角均为60o 。
杆AB 与地面接触点B的静摩擦因数为321=s f 。
人的重量为W ,不计杆OA 和杆AB 的重量。
设梯子始终保持平衡,计算(1) 人到达的最高点P 与点B 的距离x 。


理论力学计考试题及答案一、单项选择题(每题2分,共10分)1. 牛顿第一定律描述的是:A. 物体不受外力作用时的运动状态B. 物体受平衡力作用时的运动状态C. 物体受非平衡力作用时的运动状态D. 物体受任意力作用时的运动状态答案:A2. 动量守恒定律适用于:A. 只有重力作用的系统B. 只有弹力作用的系统C. 只有摩擦力作用的系统D. 任意外力作用的系统答案:D3. 刚体的转动惯量与下列哪个因素无关?A. 质量分布B. 质量大小C. 形状D. 旋转轴的位置答案:C4. 根据能量守恒定律,下列哪种情况不可能发生?A. 机械能守恒B. 机械能增加C. 机械能减少D. 机械能不变答案:B5. 简谐运动的周期与振幅无关,与下列哪个因素有关?A. 质量B. 弹簧常数C. 初始速度D. 初始位移答案:B二、填空题(每题3分,共15分)1. 牛顿第二定律的数学表达式为:\( F = ma \),其中 \( F \) 表示_______,\( m \) 表示_______,\( a \) 表示_______。
答案:力;质量;加速度2. 根据牛顿第三定律,作用力和反作用力大小相等,方向_______,作用在_______。
答案:相反;不同物体上3. 角动量守恒定律适用于_______。
答案:没有外力矩作用的系统4. 刚体的平移运动和旋转运动可以_______。
答案:独立进行5. 根据开普勒第三定律,行星的轨道周期的平方与其轨道半长轴的立方成正比,比例常数与_______有关。
答案:中心天体的质量三、计算题(每题10分,共40分)1. 一质量为2kg的物体在水平面上以3m/s的速度做匀速直线运动,求其动量。
答案:动量 \( p = mv = 2 \times 3 = 6 \) kg·m/s2. 一弹簧的劲度系数为500N/m,若将其拉长2cm,求弹簧的弹性势能。
答案:弹性势能 \( U = \frac{1}{2}kx^2 = \frac{1}{2} \times500 \times (0.02)^2 = 0.5 \) J3. 一质量为5kg的物体从静止开始自由下落,求其在第2秒末的速度。
2008/2009学年第1学期2007交通本科《理论力学(1)》期中考试试卷 课程号:A 卷 考试方式: 闭卷 考试时间: 90分钟1. 如图5-1(a)所示, B ,C 两处为固定铰链 连接,已知 α、Q 和 BD=DA=L ,杆AC 重 量不考虑,试求A ,B 两处的约束反力R A 和 R B (满点15分)。
2.图1所示,五个空 间点力作用于正立方体 的顶点O ,已知各力的 大小分别为F 1、F 2、F 3、 F 4、F 5。
F 4与x 轴的夹 角为α,F 5与z 轴的夹 角为γ。
求此空间力系 合力的大小和方向(满 点15分)。
3.试求图3所示静定 梁在A 、B 、C 三处的 约束反力。
已知AB= BC=2d ,AD=d ,载荷 为W (满点15分)。
解:已知静定梁在AB 段承受载荷,BC 段实际上是假约束——不限制运动,不承受载荷,也没有约束反力。
对所给形式的静定梁与图7-1(b )的形式是等效的。
(1及受力图见图3(b)。
(2)选图示坐标轴,A为简化中心。
(3)列解1矩式平衡方程∑X=02AxR=∑m A (F)=02AM d=∑Y=02AyR d=4.试按如下条件进行分析:(1)开口无底柱状圆筒扣着两个重球,球心为A,B,如图4(a)。
球的单重为W,其半径为r,圆筒自重为Q,内半径为R,r<R <2r,若不计接触面上的摩擦,分析“开口柱状圆筒—钢球”系统翻倒的力学原因以及防止翻倒的原理(满点15分);(2)若上述其它条件不变,只将开口无底柱状圆筒改为有底圆筒,如图4(b),分析“有底柱状圆筒—钢球”系统,是否翻倒的力学原因(满点10分)。
解:(1)①取两球为研究对象,受力图如图4(b): 两球平衡时,有:0,xC D F F F ==∑ 10,2yN FF W ==∑ ()0,2(22)0ADMF F W R r =-=∑D F =②取圆筒为研究对象,受力图如图4(b):根据系统的受力知,无底圆筒有向右倾倒的可能。
《理论力学B》期中考试(总100分)一、选择题(40分,每题4分)1、如图所示,ACD杆与BC杆在C点处用光滑铰链连接,A、B均为固定铰支座。
若以整体为研究对象,以下四个受力图中哪一个是正确。
(C)2、以下四个图所示的力三角形,哪个图表示力矢R是F1和F2两力矢的合力。
(B)3、图示用锥子拔钉子,下面四图所示的作用力中,哪一种是最省力的。
(D)4、以下四种情况(F1=F2=F),哪一种是正确的。
(B)(A)力F1与F2对圆轮的作用是等效的;(B)力F1与F2和M对圆轮的作用是等效的;(C)力F1与F2对圆轮的作用是等效的;(D)力F1与F2对圆轮的作用是等效的;5、已知物块重为P,放在地面上,物块与地面之间有摩擦,其摩擦角为φm=20o,物块受图示Q力的作用,并且P=Q,以下四种情况哪一种说法正确。
(B)(A)o2020(D)o25(C)o25(B)o一定不平衡一定平衡临界平衡一定平衡6、一个点在运动过程中,其速度大小始终保持不变,即v=常量,而全加速度恒为零,即α=0,则点在这一过程中作(C)运动。
(A)匀速曲线(B)变速直线(C)匀速直线(D)变速曲线7、在图示的四连杆机构中,OA以角速度ω绕O轴匀速转动。
当杆OA铅垂时,杆O1B水平,而且O,B、O1在同一水平线上,已知OA=OB=O1B,则该瞬时杆O1B的角速度大小和转向为(B)。
(A )ω(逆时针)(B )ω(顺时针)(C )2ω(顺时针)(D )2ω(逆时针)8、视摩天轮的座舱为刚体,当摩天轮转动时,座舱的运动(C )。
(A )不属于刚体的基本运动(B )是定轴转动(C )是平动(D )复合运动9、甲物体沿一平面直角坐标系x 轴的正向运动,运动方程为x=2+2t ,乙物体沿y 轴的正向运动,运动方程为y=3+2t ,方程中坐标x ,y 以m 计,时间t 以s 计。
当t=1s 时,甲物体相当于乙物体的速度大小为(B )m/s 。
(A )4(B )22(C )2(D )110、圆盘以匀角速度ω绕定轴O 转动,动点M 相对圆盘以匀速v r 沿圆盘直径运动,如图所示。
理论力学期中试卷
1、杆AB的A端置于光滑的水平面上,AB与水平面夹角为300,杆重为P,如图所示。
B处有摩擦,问:摩擦角为时,杆能在此处平衡。
题1图题2图
2、图示悬臂桁架受到大小均为F的三个力作用,则杆1的内力大小为,杆2的内力大小为,杆3的内力大小为。
3、图中,斜面倾角为600,静摩擦因数为f=0.2,一重物W=50N置于斜面上,施加一水平力P使其保持平衡,求力P的大小范围。
题3图题4图
4、构架如图所示,各杆重量不计。
D、C、E、H 均为铰接。
已知:q=50kN/m,M=80kN•m,l=1m,求固定端A和支座B的约束力。
5、大圆环固定不动,其半径R=0.5m,小圆环M 套在杆AB及大圆环上,如图。
当θ=300时,AB 杆转动的角速度ω=2rad/s,试求该瞬时M沿大圆环滑动的速度和M沿AB杆滑动的速度。
Array
题5图。