当前位置：文档之家 › 第九章北航 材料力学 全部课件 习题答案

第九章北航 材料力学 全部课件 习题答案

  • 格式：pdf
  • 大小：551.47 KB
  • 文档页数：11

下载文档原格式

  / 11

合集下载

北航材料力学实验考试题库及答案

北航材料力学实验考试题库及答案

北航材料力学实验考试题库及答案一、选择题（每题5分，共25分）1. 在材料力学实验中，下列哪种材料最适合用于拉伸实验？A. 钢材B. 塑料C. 木材D. 玻璃答案：A2. 以下哪种实验方法可以测量材料的弹性模量？A. 拉伸实验B. 压缩实验C. 扭转实验D. all of the above（以上都对）答案：D3. 在材料力学实验中，以下哪个因素对实验结果影响最小？A. 环境温度B. 试样尺寸B. 试样形状C. 试样材料答案：C4. 以下哪个实验可以用来测量材料的泊松比？A. 拉伸实验B. 压缩实验C. 扭转实验D. 弯曲实验答案：A5. 在材料力学实验中，以下哪种情况不需要进行实验误差分析？A. 实验数据波动较大B. 实验结果与理论值相差较大C. 实验过程中出现异常现象D. 实验结果与预期一致答案：D二、填空题（每题10分，共40分）6. 在拉伸实验中，试样断口附近的应力称为______。

答案：断口应力7. 材料的弹性模量E与泊松比μ之间的关系为：E =____________。

答案：2(1 + μ)8. 在扭转实验中，扭转角φ与扭矩T和长度l的关系为：φ = ____________。

答案：Tl/GI_p9. 在材料力学实验中，以下哪个参数表示材料的强度？__________。

答案：屈服强度或抗拉强度10. 在弯曲实验中，中性轴是指______。

答案：弯曲轴线三、判断题（每题10分，共30分）11. 在材料力学实验中，实验数据波动较大，说明实验结果可信度较低。

（对/错）答案：错12. 在拉伸实验中，试样断口形状对实验结果有较大影响。

（对/错）答案：对13. 在扭转实验中，扭矩与扭转角成正比。

（对/错）答案：对四、简答题（每题15分，共45分）14. 请简述拉伸实验的步骤。

答案：（1）准备试样：根据实验要求，选用适当尺寸和形状的试样；（2）安装试样：将试样安装在拉伸实验机上；（3）加载：按照预定的加载速率对试样进行拉伸；（4）记录数据：观察并记录试样的变形和载荷；（5）卸载：卸载后，观察试样的断口形状和位置；（6）分析数据：计算材料的屈服强度、抗拉强度、弹性模量等参数。

《材料力学》课后习题答案详细

《材料力学》课后习题答案详细

《材料力学》课后习题答案详细在学习《材料力学》这门课程时，课后习题是巩固知识、检验理解程度的重要环节。

一份详细准确的课后习题答案不仅能够帮助我们确认自己的解题思路是否正确，还能进一步加深对知识点的理解和掌握。

材料力学是一门研究材料在各种外力作用下产生的应变、应力、强度、刚度和稳定性的学科。

它对于工程领域的学生来说至关重要，无论是机械工程、土木工程还是航空航天工程等，都离不开材料力学的知识支撑。

对于课后习题的解答，我们首先要明确每个问题所涉及的核心概念和原理。

比如，在研究杆件的拉伸和压缩问题时，需要清楚胡克定律的应用条件和计算公式。

胡克定律指出，在弹性限度内，杆件的伸长或缩短量与所受的拉力或压力成正比。

以一道常见的拉伸习题为例：一根直径为 20mm 的圆杆，受到100kN 的拉力，材料的弹性模量为 200GPa，求杆的伸长量。

解题思路如下：首先，根据圆杆的直径计算出横截面积 A ＝π×（d/2)＾2 ，其中 d 为直径。

然后，根据胡克定律ΔL ＝ FL/EA ，其中F 为拉力，L 为杆长，E 为弹性模量，A 为横截面积，代入已知数据进行计算。

在计算过程中，要注意单位的统一。

拉力的单位通常为牛顿（N），长度的单位要与弹性模量的单位相匹配，面积的单位要为平方米（m²）。

再来看一个关于梁的弯曲问题。

梁在受到横向载荷作用时，会产生弯曲变形。

在解答这类习题时，需要运用到弯矩方程、挠曲线方程等知识。

例如：一简支梁，跨度为 L，承受均布载荷 q，求梁的最大弯矩和最大挠度。

解题时，首先要根据梁的支座情况列出弯矩方程。

然后，通过积分求出挠曲线方程，再根据边界条件确定积分常数。

最后，求出最大弯矩和最大挠度的位置及数值。

在求解过程中，要理解弯矩和挠度的物理意义，以及它们与载荷、梁的几何形状和材料性质之间的关系。

对于扭转问题，要掌握扭矩的计算、切应力的分布规律以及扭转角的计算方法。

比如，一根轴受到扭矩 T 的作用，已知轴的直径和材料的剪切模量，求轴表面的最大切应力和扭转角。

材料力学作业解析（910章）

材料力学作业解析（910章）

材料力学作业解析(910章)材料力学作业解析(第9-1010章章)2013年6月5日第9 章9－1 图示刚性杆AD在B、E两处由弹簧刚度为k的两根弹簧所支承并在FP力作用下保持水平平衡位置。

试簧所支承，并在力作用下保持水平平衡位置试求系统的分叉载荷FPcr。

（提示：假定AB杆在微小倾角时保持平衡）倾角时保持平衡。

）第9 章9－2 图示结构中两根柱子下端固定，上端与一可活动的刚性块固结在一起。

已知l= 3m，直径d= 20mm，柱子轴线之间的间距a= 60mm60。

柱子的材料均为QQ23535钢，E= 200GPa，柱子所受载荷FP的作用线与两柱子等间距，并作用在两柱子所在的平面内。

假设各种情形下欧拉并作用在两柱子所在的平面内假设各种情形下欧拉公式均适用，试求结构的分叉载荷。

第9 章解：本题可能的失稳方式有四种，如图所示。

（a）两杆分别失稳（沿z方向平移，包括单独失稳）（b）两杆作为整体绕y轴失稳（绕y轴转动）（c）两杆作为整体绕z轴失稳（绕z轴转动）（d）两杆共同沿z方向（或沿y方向）平移失稳（沿y方向平移）从刚性块的可能状态出发，进行处理（六自由度）…第9 章9－3 推导两端固支细长压杆的临界载荷公式。

第9 章第9 章第9 章第9 章9－4图示结构中AB为圆截面杆，直径d=80mm，杆BC为正方形截面，边长a=70mm，两杆材料均为Q235钢，E=200GPa，两部分可以各自独立发生屈曲而互不影响。

已知A端固定，B、C为球铰，l=3m，稳定，稳定安全因数=2.5。

试按照细长杆理论确定此结构的许可载荷[FP]。

题中图有问题…第9 章第9 章第9 章9－5图示正方形桁架结构由五根圆钢杆组成，各杆直径均为d=40mm，a40=1m，材料均为Q235钢，1材料均为Q235钢[σ][]=160MPa，160MP[σcr]=0.604[σ]，各杆之间均采用铰链连接。

试：（1）求结构的许可载荷[F求结构的许载荷[P]；]（2）若FP力的方向与图中相反，结构的许可载荷应为多少？第9 章第9 章原题中[σcr]=0.604 [σ]有问题…第9 章9－6如图所示，弹性细长杆AC的长度为l，弯曲刚度EI为常值值，刚性杆刚性杆CB的长度为a，二者通过铰链连接。

材料力学(第四版)第九章

材料力学(第四版)第九章
max
Pl M z max 4 43.3MPa Wz Wz
它比α=150时的斜弯曲最大正应力151.5Mpa小很多。可见， 当 Wy Wz 时，尽管荷载偏离y轴一个不大的角度,也会使梁的 正应显著增加,所以,在工程中应尽量避免发生斜弯曲.
例 ：矩形截面木檩条如图，跨长L=3.3m,受集度为 q=800N/m 的均布力作用， []=12MPa，容许挠度为：L/200 ，E=9GPa， q 试校核此梁的强度和刚度。
Mz My


z
中性轴
y
6.最大正应力及强度条件 在危险截面上作与中性轴平行且与截面只有一个交点的直 线，则这些交点距离中性轴最远。由斜弯曲正应力计算公式可 知，这些交点就是最大正应力作用点。 本例中的矩形截面悬臂梁的最大正应力发生在固定端截面 的a点（最大拉应力）和c点（最大压应力），强度条件为：
max

M z ,max y max Iz M y ,max Wy

M y ,max z max Iy
Mz My
M z ,max Wz


P y

z
中性轴
7.变形计算 斜弯曲的变形计算也可用叠加法。 Py引起的自由端的挠度 Py l 3 P cos l 3
fy 3EI z 3EI z
2.查型钢表得： No.32a工字钢的 Wz 692.2cm3
Wy 70.758cm3
A
C
B x Pz z
P a Py y l P
3.校核梁的正应力强度
max
M z max M y max 151.5MPa 160MPa Wz Wy
所以，梁的正应力强度足够。 附：本题中，若α=00，则梁发生平面弯曲，此时

最新课件-材料力学第九章复杂应力状态强度问题北航 推

最新课件-材料力学第九章复杂应力状态强度问题北航 推

工作应变：
1
1 E
1
-
2
+ 3
单拉极限应力
1u
1 E
1
-
2
+ 3 u
1 E
b
转换为由应力表示的断裂条件
1 - 2 +3 b
强度条件：
1
-
2
+
3
b
n
r2 1 - 2 +3
第二强度理论的 相当应力
• 第一强度理论适用范围：
t,max
c max
Page10
三、 第一、二强度理论综合示图（平面应力状态）
➢ 不论材料处于何种应力状态，只要最大拉应变1达到材 料单向拉伸断裂时的最大拉应变1u，材料即发生断裂。
工作应变：
1
1 E
1
-
2
+ 3
单拉极限应力 1 b , 2 3 0
单拉极限应变
1u
1 E
1
-
2
+ 3 u
b
E
Page 9
二、最大拉应变理论（第二强度理论）
断裂条件： 1 1u
材料力学（I II） 北航 精品课件
北京航空航天大学单辉祖教授编著的《材料力学 (I)》、《材料力学(Ⅱ)》是教育部“高等教育面向 21世纪教学内容和课程体系改革计划”的研究成果， 是面向21世纪课程教材和教育部工科力学“九五” 规划教材，也是普通高等教育“九五”国家级重点 教材 。该教材1999年初版，获2000年度中国高校科 学技术奖（教材类）二等奖，教学改革成果获2001 年度国家级教学成果二等奖、北京市教学成果一等 奖 ；2004年修订出版第2版，修订版已列入“普通 高等学校‘十五’国家教材规划”、高教社“高等 教育百门精品教材”。以材料力学I、II为主教材的 材料力学立体化教学包已作为高等教育出版社的 “名品”向全国推广。

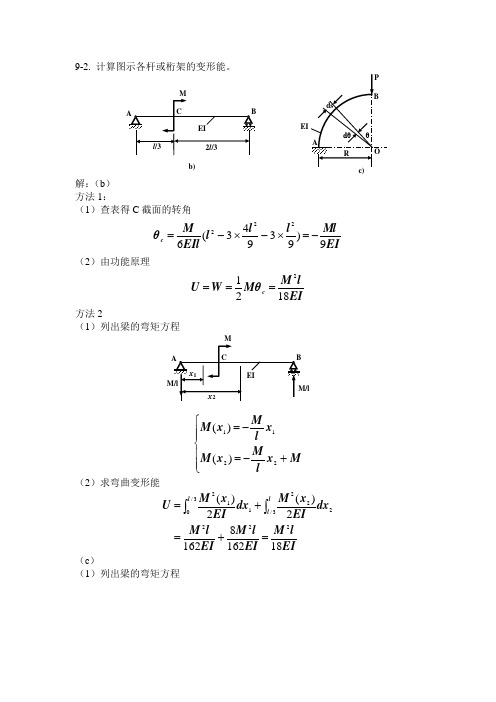
材料力学第九章习题选及其解答

材料力学第九章习题选及其解答

9-2. 计算图示各杆或桁架的变形能。

解：（b ） 方法1：（1）查表得C 截面的转角EIMl l l l EIl M θc 9)93943(6222-=⨯-⨯-=（2）由功能原理EIlM θM W U c 18212=== 方法2（1）列出梁的弯矩方程⎪⎪⎩⎪⎪⎨⎧+-=-=Mx l M x M x lM x M 2211)()( （2）求弯曲变形能EIl M EI l M EI l M dx EI x M dx EI x M U l l l 1816281622)(2)(2223/2223/0112=+=+=⎰⎰ （c ）（1）列出梁的弯矩方程b)θPR θM sin )(-=（2）求弯曲变形能EIR P πdsEI θPR ds EI θM U πl 82)sin (2)(322/022=-==⎰⎰ 9-3. 传动轴的抗弯刚度为EI ，抗扭刚度为GIp 。

皮带拉力T+t=P ，D=2d 。

试计算轴的变形能。

设a=l/4。

解：（1）将外力向轴线简化（2）扭转变形能CD 段发生扭转变形，扭矩为：Pd/2pp GI l d P GI l a Pd U 3232)2()21(2221=+=（3）水平方向弯曲变形能EIl P EI Pl P δP U DH 964821213232=⨯== （4）垂直方向弯曲变形能M(EIl P a EIl Pa EI Pa P δt T U CV 3845)3)(3(21)(213233=⨯+⨯=+= （5）轴的变形能EIl P GI l d P U U U U p 38493233222321+=++=9-4. 试用互等定理求跨度中点C 的挠度，设EI=常量。

解：（a ）（1）将P 力移到C 截面处，如下图（2）由位移互等定理EIPal a EI Pl a θδδf B c 1616221221=⨯=⨯=== 方向向上（b ）（1）将P 力移到C 截面处，如下图（2）由位移互等定理EIPl lEI l P EI l P l θf δδf c c c 4852)2)2((3)2(23231221-=⨯-+-=⨯+===方向向下a)DBb)DB9-8. 试求图示各梁截面B 的挠度和转角。

材料力学答案第9章


通解为
w1 = A1sinkx1 + B1coskx1 +
w2 = A2 sinkx 2 + B2 coskx 2 +
当 x1 = 0，w1 = 0 → B1 = 0 当 x 2 = 0，w2 = 0 → B2 = 0 当 x1 = x2 = 或写成
l F ′ = − w2 ′ ，w1 = w2 = c ，w1 2 c
式中，
k12 =
以上二微分方程的通解为
F F 2 ，k 2 = EI 1 EI 2
w1 = A1sink1 x1 + B1cosk1 x1 + δ w2 = A2 sink 2 x 2 + B2 cosk 2 x 2 + δ
定未知常数的条件为
8
′=0 x1 = 0，w1 = 0，w1 x1 = l ′ = w2 ′ ，w1 = w2，w1 x2 = 0 x2 = l，w2 = δ
3
的扭力矩为
M B = Fϕa
而
ϕ=
注意到 T = M B ，于是得
Tl GI p
F=
即
GI p al
πGd 4 Fcr = = al 32al
由此得（题中给出 F= 42kN ）
GI p
d=
4
32alFcr = πG
4
32 × 0.500 × 0.300 × 42 ×103 m = 0.030m = 30mm π × 79 ×10 9
题 9-10 图 解：该细长压杆的微弯状态如图 9-10 所示。
按图中所取坐标，有
M ( x1 ) =
Fc F x1 − Fw1，M ( x 2 ) = c x 2 − Fw2 2 2

北航材料力学课后习题答案


σ max = 117MPa （在圆孔边缘处）
2-15 图示桁架，承受载荷 F 作用，已知杆的许用应力为[σ ]。若在节点 B 和 C 的
位置保持不变的条件下，试确定使结构重量最轻的α 值（即确定节点 A 的最佳位置）。
解：1.求各杆轴力
题 2-15 图
设杆 AB 和 BC 的轴力分别为 FN1 和 FN2 ，由节点 B 的平衡条件求得
分别为
FN
=
1 2
σmax A
=
1 2
× (100 ×106 Pa) × (0.100m × 0.040m)
=
2.00 ×105 N
=
200kN
Mz
=
FN
(
h 2
−
h )
3
=பைடு நூலகம்
1 6
FN h
=
1 × (200 ×103 N) × (0.100m) 6
= 3.33×103 N ⋅ m
=
3.33kN ⋅ m
2-5 .........................................................................................................................................................2
= 0.2 ×10−3 m 0.100m
= 2.00 ×10−3
rad
α AB
= 0.1×10−3 m = 1.00 ×10−3 0.100m
rad
得 A 点处直角 BAD 的切应变为
γ A = γ BAD = α AD − α AB = 1.00 ×10−3 rad

材料力学作业及练习题参考答案(8、9章)

⑶ 由 max≤[] 有： max＝c,max＝50×103/A＋37.5×103/W≤[] 先按弯曲正应力强度初步选择槽钢型号： 37.5×103/W≤[] W≥37.5×103/[]＝37.5×103/(140×106)＝2.6876×10－4 m3 ＝268.76 cm3 每根槽钢W≥268.76/2＝133.9 cm3 查槽钢表，初选18a#槽钢，其W＝141 cm3，A＝25.669 cm2 再按压缩与弯曲的组合应力进行校核： max＝50×103/A＋37.5×103/W＝50×103/(2×25.669×10－4)＋37.5×103/(2×141×10－6) ＝142.72×106 Pa＞[]＝140 MPa 但 (max－[])/[]＝(142.72－140)/140＝1.9%＜5%，可认为强度条件满足，∴选18a#槽钢。
八章2题： 解：查槽钢表，每根槽钢，A＝25.669 cm2，W＝141 cm3， 则两根槽钢制成的梁：A＝2A＝51.538 cm2， W＝2W＝282 cm3 在B截面左侧的上边缘处： ＝－FN/A＋M/W＝－50×103/(51.538×10－4)＋37.5×103/(282×10－6) ＝123.24×106 Pa， 即在该处为拉应力123.24 MPa ； 在B截面左侧的下边缘处： ＝－FN/A－M/W＝－50×103/(51.538×10－4)－37.5×103/(282×10－6) ＝－142.72×106 Pa， 即在该处为压应力142.72 MPa ； 在B截面右侧的上边缘处： ＝M/W＝37.5×103/(282×10－6)＝132.98×106 Pa， 即在该处为拉应力132.98 MPa ； 在B截面右侧的下边缘处： ＝－M/W＝－37.5×103/(282×10－6)＝－132.98×106 Pa， 即在该处为压应力132.98 MPa。

北京科技大学材料力学课件第九章教材

地面未夯实，局部杆受力大； 横杆之间的距离太大 2.2m>规定值1.7m; 与墙体连接点太少； 安全因数太低：1.11-1.75<规定值3.0。
2006年12月9日，北京市顺义城区北侧减河上一座悬索桥在进 行承重测试时突然坍塌,约50米桥体连同桥上进行测试的10辆满载 煤渣的运输车一起塌下,1名司机和2名检测人员受伤。
对于细长杆，临界应力公式
cr
π2E
2
对于中长杆，由于发生了塑性变形，理论计算比较复 杂，工程中大多采用直线经验公式计算其临界应力，最常 用是直线公式：
cr＝a－b
其中， a 和 b 为与材料有关的常数，单位为MPa。
对于粗短杆，因为不发生屈曲，而只发生屈服(韧性材 料)，故其临界应力即为材料的屈服应力
σp
cr
2E 2
粗短杆
中长杆
细长杆
O
λS
λp
λ
根据临界应力总图中所示之σcr－λ关系，可以确定区分 不同材料三类压杆的柔度极限值λs、 λP 。
令细长杆的临界应力 等于材料的比例极限，得到
＝
P
π 2E
P
对于不同的材料，由于E、σ P 各 不相同， λP 的数值亦不相同。一旦 给定E、 σ P，即可算得λP。
Pcr
Pcr
Pcl/4 l/2 l/4
l 2l l 0.7l
1.0 0.5
2.0
♣ 一端自由，一端固定
♣ 一端铰支，一端固定
P π2EI
cr (l)2
0.7
P π2EI cr (2l)2
P π2EI cr (0.7l)2
欧拉公式的一般形式
Pcr =
2EI (μl)2
1.分析: 哪一根压杆的临 界载荷比较大；
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第四强度理论确定其壁厚。
4
题 9-9 图 解：根据第四强度理论，圆柱形薄壁容器的强度条件为
σ r4
由此得
3 pD [σ ] 4δ
δ
3 pD 3 15106 0.080 m 3.25103 m 3.25 mm 6 4[σ ] 416010
所得 δ D / 20 ，属于薄壁容器，上述计算有效。
σ1 σ 2 0， σ 3 σ
由此可得第三强度理论的相当应力为
1
σ r3 σ1 σ3 σ
(a)
(b)解：对于棱柱体在刚性方模中轴向受压的情况（见题图 b） ，可先取受力微体及坐标如 图 9-4 所示，然后计算其应力。
图 9-4 由图 9-4 可得
σ y σ
根据刚性方模的约束条件，有
9-10 图 a 所示车轮，由轮毂与套于其上的薄钢圈组成。钢圈的内径 d 比轮毂的外径
D 略小，安装时先将钢圈适当加热，以使二者套合，冷却后钢圈即紧套在轮毂上。钢圈的厚度 为，弹性模量为 E，轮毂的刚度很大，分析时可忽略其变形。试求钢圈与轮毂间的相互作用 力，以及钢圈横截面上的初应力。
题 9-10 图 解：在内压 p 作用下（图 b） ，钢圈的周向正应变为
3
式中：足标 b 系指翼缘与腹板的交界点；足标 a 系指上翼缘顶边中点。 3．应力计算及强度校核 三个可能的危险点（ a ， b 和 c ）示如图 9-5。
图 9-5
a 点处的正应力和切应力分别为
σ τ FS S z ( a ) I zt M 7.80 104 N 1.545108 Pa 154.5 MPa Wz 5.0510 4 m 2 130103 1.11510 4 N 1.496107 Pa 14.96 MPa 5 2 7.07 10 0.0137m
题 9-13 图 解：内、外环的受力情况示如图 9-13a 和 b。
7
图 9-13 设铜环的轴力（绝对值）为 FN1 ，钢环的轴力为 FN2 ，由图 c 与 d 所示各半个薄圆环的平 衡条件可得
FN1 FN2
变形协调条件为
pD 2
(a)
ΔD1 ΔD2
物理关系为
(b)
FN1 D E1 A1 F D ΔD2 α2 DΔT N2 E 2 A2 ΔD1 α1 DΔT
Fx 0，πDδ t
得
πD 2 p0 4
pD 4δ 球壁内任一点的应力状态如图 b 所示，由此可得三个主应力依次为 pD σ1 σ 2 σ t ，σ 3 0 4δ σt
9-13
图示组合圆环，内、外环分别用铜与钢制成，已知铜环与钢环的壁厚分别为
与， 交接面的直径为 D， 铜与钢的弹性模量分别为 E1 与 E2， 线胀系数分别为与， 且。 试问当温度升高 T 时，环的周向正应力为何值。
σ 45 τ 3 pD , 8δ σ 45 3 pD τ 8δ
(a) (b)
σ 0 σ x , σ 90 σ t ,
根据广义胡克定律，贴片方向的正应变为
(1 2 ) pD 1 [ x t ] E 4 Eδ 1 1 2(1 ) M (1 )3 pD 45 [ 45 45 ] [ ] E E 8 πD 2 由式(a)可得圆筒所承受的内压为 4 Eδ p ε (1 2 μ) D 0
pD t t E 2E
安装前后，钢圈的直径由 d 变为 D，其周向正应变为
(a)
t
比较式(a)与(b)，得
πD πd D d πd d 2 E ( D d ) Dd
(b)
p
由此得 钢圈横截面上的正应力为
t
pD E ( D d ) 2 d
9-11
第九章 强度理论
9-3
已知脆性材料的许用拉应力[]与泊松比，试根据第一与第二强度理论确定纯剪
切时的许用切应力[ ]。 解：纯剪切时的主应力为
1 3 , 2 0
根据第一强度理论，要求
1 [ ]
即要求
[ ]
由此得切应力的最大许可值即许用切应力为 [ ][ ] 根据第二强度理论，要求
及与轴线成 45° 方位的正应变分别为 0 和 45 ，筒的内径 D、壁厚 、材料的弹性模量 E 与泊 松比 均为已知。试求内压 p 与扭力偶矩 M 之值。
题 9-14 图 解：圆筒壁内任意一点的应力状态如图 9-14 所示。
图 9-14 图中所示各应力分量分别为
x
由此可得
pD pD 2M , t , 2 4 2 πD
可见，该铸铁构件满足强度要求。
9-12
图示圆球形薄壁容器，其内径为 D，壁厚为 ，承受压强为 p 之内压。试证明
壁内任一点处的主应力为 1 2 pD /(4 ), 3 0 。
题 9-12 图 证明：用截面法取该容器的一半（连同内压）示如图 9-12a。
6
图 9-12 由图 a 所示半球的平衡方程
0
σ1 10 MPa，σ2 0，σ3 (5 47.7) MPa 42.7 MPa
2．强度校核 由于该铸铁构件的最大压应力超过最大拉应力，且超过较多，故宜采用最大拉应变理论 对其进行强度校核，即要求
σ r2 σ1 μ(σ2 σ3 ) [σ ]
将上述各主应力值代入上式，得
σ r2 [100.25(42.7)] MPa 20.7 MPa[σ ]
(b)
按照第三强度理论，(a)与(b)两种情况相当应力的比值为
r
σ r3( a ) σ r3(b )

1 μ 1 1 2μ
这表明加刚性方模后对棱柱体的强度有利。
9-5
图示外伸梁，承受载荷 F = 130 kN 作用，许用应力[ ]=170 MPa。试校核梁的强
度。如危险点处于复杂应力状态，采用第三强度理论校核强度。
pD ，σ 2 σ x 0，σ3 σ r 0 2δ
pD 7.5106 0.011 N 8.25107 Pa 82.5 MPa[σ ] 2δ 20.0005m2 计算结果表明，该油管满足强度要求。 σ r3 σ1 σ3
9-9
图示圆柱形容器，受外压 p = 15 MPa 作用。材料的许用应力[]= 160 MPa，试按
r 3 2 2 62.7MPa 125.4MPa
结论：该梁满足强度要求。 4．强度校核 依据第三强度理论，上述三点的相当应力依次为
σ r3( a ) σ1 σ 3 [155.9 ( 1.44)] MPa 157.3 MPa σ r3(b ) [154.4 ( 15.05)] MPa 169.5 MPa σ r3( c ) 2 τ 2 62.7 MPa 125.4 MPa
τ
该点也处于单向与纯剪切组合应力状态，其相当应力为
r 3 139.32 448.22 MPa169.4MPa[ ]
c 点处于纯剪切应力状态，其切应力为
τ
其相当应力为
FS S z ,max I zδ

130103 2.90104 N 6.27 107 Pa 62.7 MPa 5 2 7.07 10 0.0085m
该点处于单向与纯剪切组合应力状态，根据第三强度理论，其相当应力为
r 3 2 4 2 154.52 4 14.962 MPa 157.4MPa [ ]
b 点处的正应力和切应力分别为
3
σ
M yb 7.80 104 (0.140 0.0137)N 1.393108 Pa 139.3 MPa Iz 7.07 105 m 2 FS S z ( b ) I zδ 130103 2.2310 4 N 4.82 107 Pa 48.2 MPa 5 2 7.07 10 0.0085m
将式(c)代入式(b)，得
(c)
(α1 α2 )ΔT
由式(a)可知，
σ FN1 F σ N2 1t 2t E1 A1 E2 A2 E1 E2
(d)
σ1t A1 σ 2t A2，
即
σ1t A2 δ2 σ 2t A1 δ1
σ1t
δ2 σ 2t δ1
(e)
将方程(e)与方程(d)联立求解，得铜环和钢环内的周向正应力依次为
εx
即
1 [σ x μ(σ y σ z )] 0 E
σ x μ(σ y
故有
σx σz
三个主应力依次为
μ σ 1 μ
σ1 σ 2
由此可得其相当应力为
μ σ，σ 3 σ 1 μ
σ r3 σ1 σ3
1 2μ σ 1 μ
2
题 9-5 图 解：1.内力分析 由题图可知， B 截面为危险截面，剪力与弯矩均为最大，其值分别为
FS F 130kN， M Fl2 130103 N 0.600m 7.80104 N m
2．几何性质计算
Iz [
0.122 0.2803 (0.122 0.0085) (0.280 2 0.0137) ]m 4 7.07 105 m 4 12 12 5 7.07 10 Wz m 3 5.05104 m 3 0.140 0.0137 3 S z ( b ) 0.122 0.0137 (0.140 )m 2.23104 m 3 2 S z ( a ) 2 1 S z ,max [2.23104 0.0085 (0.140 0.0137) 2 ]m3 2.90 104 m 3 2
pD 1106 0.200 Pa 5106 Pa 5 MPa 4δ 40.010 pD 1106 0.200 σ tp Pa 10106 Pa 10 MPa 2δ 20.010 σ xp