固体的流态化
- 格式:ppt
- 大小:669.00 KB
- 文档页数:17



一、实验目的1. 观察固体颗粒在流态化过程中的聚式和散式流化现象。
2. 测定床层的堆积密度和空隙率。
3. 测定流体通过颗粒床层时的压降与空塔气速的曲线,并确定临界流化速度。
二、实验原理固体流态化是指固体颗粒在气体或液体介质中,由静止状态逐渐过渡到具有一定流动性的状态。
在此过程中,颗粒的流动速度与气体(或液体)的流速之间存在一定的关系。
当气体(或液体)流速达到某一临界值时,颗粒开始由静止状态转变为流态化状态,此时的流速称为临界流化速度。
三、实验装置1. 实验装置流程:鼓风机→ 气体流量调节阀→ 气体转子流量计→ 温度计→ 气体分布板→ 颗粒床层→ 床层顶部。
2. 实验材料:石英砂、空气或水。
四、实验步骤1. 将石英砂装入床层,轻轻敲打床层,使床层高度均匀一致,并测量首次静床高度。
2. 打开电源,启动风机,调节气体流量,从最小刻度开始,每次增加0.5m³/h,同时记录相应的空气流量、空气温度、床层压降等上行原始数据。
最大气体流量以不把石英砂带出床层为准。
3. 调节气体量从上行的最大流量开始,每次减少0.5m³/h,直至最小流量,记录相应的下行原始实验数据。
4. 测量结束后,关闭电源,再次测量经过流化后的静床高度,比较两次静床高度的变化。
5. 在临界流化点之前,保证床层稳定,避免发生颗粒带出现象。
五、实验数据及处理1. 记录实验数据,包括空气流量、空气温度、床层压降、静床高度等。
2. 绘制压降与空塔气速的曲线。
3. 根据实验数据,确定临界流化速度。
六、实验结果与分析1. 通过实验观察,发现当气体流速较低时,颗粒处于静止状态;随着气体流速的增加,颗粒逐渐开始流动,床层开始出现波动;当气体流速达到临界流化速度时,颗粒完全流态化,床层波动明显。
2. 根据实验数据,绘制压降与空塔气速的曲线,曲线呈非线性关系。
3. 根据曲线,确定临界流化速度为0.4m/s。
七、实验结论1. 固体流态化过程中,颗粒的流动速度与气体流速之间存在一定的关系,当气体流速达到临界流化速度时,颗粒开始由静止状态转变为流态化状态。


固体流态化实验报告一、实验目的。
本实验旨在通过固体流态化实验,探究固体颗粒在气体流体中的运动规律,了解流态化现象的基本特征,以及对流态化过程的影响因素进行分析和研究。
二、实验原理。
固体流态化是指在气体流体作用下,固体颗粒呈现出类似流体的运动状态,其主要原理包括气体流体的作用力和颗粒本身的特性。
气体流体通过固体颗粒时,会产生上升力和阻力,使颗粒呈现出浮力和下沉的运动状态,最终形成流态化现象。
三、实验装置与方法。
本次实验采用了自行设计的固体流态化实验装置,主要包括气源、颗粒料仓、气固分离器、流化床和实验数据采集系统。
实验方法为先将颗粒料充满流化床,然后通过气源将气体通过床层,观察颗粒料的流态化现象,并采集实验数据。
四、实验结果与分析。
经过实验观察和数据采集,我们发现在一定气体流速下,颗粒料开始呈现出流态化现象,颗粒料呈现出了类似流体的运动状态。
通过对实验数据的分析,我们发现气体流速、颗粒料粒径和颗粒料密度是影响固体流态化现象的重要因素。
当气体流速增大时,颗粒料的流态化现象更加明显;颗粒料粒径较小、密度较大时,流态化现象也更加显著。
五、实验结论。
通过本次实验,我们得出了固体流态化现象的一些基本规律,即在气体流体作用下,固体颗粒呈现出流体的运动状态。
同时,我们也发现了影响固体流态化现象的重要因素,为进一步研究和应用固体流态化提供了一定的理论基础。
六、实验总结。
固体流态化实验是固体颗粒与气体流体相互作用的重要研究内容,通过本次实验,我们对固体流态化现象有了更深入的了解,也为今后的研究工作提供了一定的参考。
希望通过我们的努力,能够为固体流态化领域的发展做出更大的贡献。
七、参考文献。
1. 王明,李华. 固体流态化基础与应用. 北京,化学工业出版社,2008.2. 张三,李四. 固体流态化实验技术与应用. 上海,上海科学技术出版社,2010.以上就是本次固体流态化实验的报告内容,谢谢大家的阅读。



4固体流态化实验4.1实验目的(1)掌握测定颗粒静态床层时的静床堆积密度ρb 和空隙率ε的方法; (2)测定流体通过颗粒床层时的压降Δp m 与空塔气速u 的曲线和临界流化速u mf ; 4.2实验原理 4.2.1固定床 1)基本概念当流体以较低的空速u 通过颗粒床层时床层仍处于静止状态,称这种固体颗粒床层为固定床。
床层的静态特性是研究床层动态特性和规律的基础,其主要的特征有静床堆积密度ρb 和空隙率ε两个,它们的定义分别如下:1.静床堆积密度:ρb =M/V,它由静止床层中的固体颗粒的质量M 除以静止床层的体积V 计算而得。
ρb 数值的大小与床层中颗粒的堆积松紧程度有关,因此ρb 在流体通过颗粒床层时不是一个定值,如颗粒床层在最紧与最松两种极限状态时,ρb 就有两种数值,它们的大小在床层最紧与最松时分别测量出相应的床层高度就可以计算得到。
2.静床空隙率ε:ε=1–(ρb /ρs ),它是由颗粒的静床堆积密度ρb 和固体颗粒密度ρs 计算而得。
2)固定床阶段压降Δp m 与空速u 的关系当流体通过固定床的空速较小时,床层的高度基本不变;当流体空速趋于某一临界速度时,颗粒开始松动,床层才略有膨胀。
因此,在此临界速度以前,单位高度的床层的压降(Δp m /L)与空速u 的关系可由欧根公式来表示,并把欧根公式改写成如下形式:m m m d uK d K uL p ψ-+ψ-=∆ρεεμεε322321)1()()1((1) 式(1)中,以实验数据的空速u 为横坐标,以(Δp m /uL )为纵坐标画图得一直线,从直线的斜率中求出欧根系数K 2,从直线的截距中计算出欧根系数K 1。
4.2.2流化床 1)基本概念当流体空速趋近某一临界速度u mf 时,颗粒开始松动,床层略有膨胀,床层高度有所增加;当空速继续加大,此时固体颗粒悬浮在流体中作上下、自转、摇摆等随机运动,好象沸腾的液体在翻腾,此时的颗粒床层称为流化床或沸腾床,临界速度u mf 称为起始流化速度。


固体流态化技术
固体流态化是指固体颗粒在流体(气体或液体)作用下,转变为具有类似流体性质的操作过程,简称流态化。
固体流态化技术是20世纪发展起来的,其最初的应用可追溯至公元16世纪矿石的处理。
第一个涉及流态化的专利是1910年颁发的,第一个工业规模的流态化装置,是用来制造水煤气或发生炉煤气的温克勒气体发生炉,此炉是于19 21年由德国BASF公司开发的。
1942年,埃索公司与凯洛格公司和印第安纳美孚石油公司开发的流态床催化裂化工业装置,建成投入运转;同年,多尔奥列弗公司开发的硫化物矿焙烧的流态化装置建成,并于19 52年应用于硫铁矿焙烧生产二氧化硫。
固体流态化技术在工业上有着广泛的用途,如固体输送、热交换、颗粒混合、干燥、吸附及金属表面涂敷塑料等过程。
催化反应如催化裂化、催化重整、苯酐和醋酸乙烯的生产等;非催化反应如硫铁矿的焙烧,石灰石、白云石的煅烧、水泥生料的烧结等。
随着科技的进步和生产的发展,固体流态化技术的应用将日益广阔。
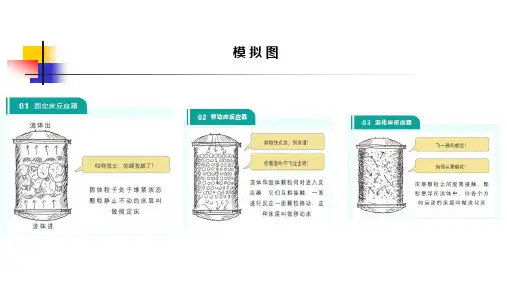
固体流态化实验报告思考题答案(1)什么是固体流态化?流态化技术用于工业有什么优点?答:固体流态化:使颗粒状物料与流动的气体或液体相接触,并在后者的作用下呈现某种类似于流体的状态,这就是固体流态化优点:(1)操作易于实现连续化、自动化(2)床层温度均匀,便于调节和维持所需的温度(3)颗粒之间传热、传质速率高,且流化床与传热壁面间有较高的传热速率(2)流化床的主要特性是什么?答;流化床中的气固运动状态很象沸腾着的液体,并且在许多方面表现出类似于流体的性质(3)流化床的主要特性用于传热有何优答:床层温度均匀,便于调节和维持所需的温度;颗粒之间传热速率高,且流化床与传热壁面间有较高的传热速率(4)什么是散式流化床?答:固体颗粒均匀地分散在流化介质中。
通常两相密度差小的系统趋向于散式流化(5)什么是聚式流化床?答:超过流化所需最小气量的那部分气体以气泡形式通过颗粒层,上升至床层上界面时即行破裂。
所以上界面是以某种频率上、下波动的不稳定界面,床层压降也随之作相应的波动密度差较大的系统趋向于聚式流化(6)散式流化床和聚式流化床有何区别?答:散式流化床中固体颗粒均匀地分散在流化介质中,整个床层均匀;聚式流化床中上界面是以某种频率上、下波动的不稳定界面,床层压降也随之作相应的波动(7)试图示流态化现象的几个阶段,说明临界流态化特点,并在图中标出临界流态化速度答:临界流态化特点:当流速增至临界点时,床层中颗粒开始松动,床层略有膨胀,但颗粒仍不能自由运动。
8)理想流化床可分为哪两个阶段?答:固定床阶段和流化床阶段(9)固定床阶段特点答:当流体速度较低时,流体是穿过静止颗粒之间的空隙而流动,此时,随流速增加,床层压降也增加(10)流化床阶段特点?答:流速升高,刚好全部颗粒悬浮在向上流动的流体中作随机运动,此时颗粒与流体之间的摩擦力恰与其净重力相平衡。
此时,随流速增加,床层压降基本不变,但床层高度逐渐升高。
(11)什么是腾涌现象?答:如果床层高度与直径之比值过大,或气速过高时,大气泡直径长大到与床径相等时。
固体流态化的名词解释1. 引言固体流态化是一种物质在外界作用下从固态向流态转化的过程。
相较于传统的固体和液体状态,固体流态化展现了许多独特的性质和潜力。
本文将对固体流态化进行详细解释,包括其定义、机理、应用和前景。
2. 固体流态化的定义固体流态化,又称为固体颗粒流动或颗粒流动化,是指固态物质在特定条件下,颗粒之间产生流动并表现出类似流体的行为。
这种状态下,固体被视为一个可变形、流动性较高的流体。
3. 流态化机理固体流态化的机理主要涉及颗粒之间的微观相互作用力和流动条件。
通常包括以下几个关键因素:1) 颗粒表面摩擦力:颗粒之间的表面摩擦力越小,流动性越高;2) 颗粒内部结构:颗粒内部的结构和排列方式会影响流动性;3) 外界作用:外界力的引入,如振动、剪切力或液体注入等,可以激发颗粒之间的流动行为;4) 孔隙空间:颗粒之间存在的孔隙空间和通道的形状和大小也会影响固体流态化的程度。
4. 固体流态化的应用固体流态化在许多领域具有重要的应用价值。
以下是几个典型的应用示例:1) 粉末冶金:固体流态化可用于粉末冶金工艺中,以促进粉末的均匀混合以及提高成型的效果;2) 粒子分离和筛选:通过固体颗粒的流态化,可以实现粒子的分离和筛选,广泛用于颗粒物料的分级和分类;3) 化工过程中的颗粒反应器:固体流态化可以使颗粒在反应器中更好地混合并提高反应效率;4) 沉积工艺中的喷涂:固体粉末的流态化可用于金属沉积、涂覆和喷涂工艺中,以获得均匀且致密的表面涂层;5) 滑动摩擦控制:借助固体颗粒的流态化,可以改善材料表面的摩擦性能,实现摩擦的控制和减少磨损。
5. 固体流态化的前景随着科技的发展和对新材料、新工艺的需求增加,固体流态化技术在工业和科学研究中的重要性不断提升。
固体流态化既可以改善传统过程的效率和品质,又可以为新型工艺的开拓提供基础。
同时,固体颗粒流态化也是一个广阔而充满挑战的研究领域,吸引了越来越多的科学家和工程师加入研究队伍。