角的练习题

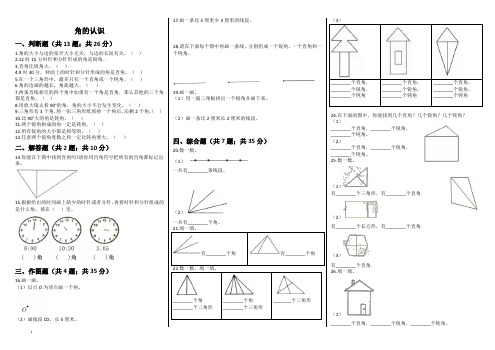
角的认识一、判断题（共13题；共26分）1.角的大小与边的张开大小无关，与边的长短有关。

（）2.12时15分时针和分针形成的角是锐角。

3.直角比锐角大。

（）4.9时30分，钟面上的时针和分针形成的角是直角。

（）5.在一个三角形中，最多只有一个直角或一个钝角。

（）6.角的边画的越长，角就越大。

（）7.两条直线相交的四个角中如果有一个角是直角，那么其他的三个角都是直角。

（）8.用放大镜去看90°的角，角的大小不会发生变化。

（）9.三角形有3个角，将一张三角形纸剪掉一个角后，还剩2个角。

（）10.比90°大的角是钝角。

（）11.两个锐角拼成的角一定是钝角．（）12.所有锐角的大小都是相等的。

（）13.任意两个锐角度数之和一定比钝角要大。

（）二、解答题（共2题；共10分）14.你能在下图中找到直角吗?请你用直角符号把所有的直角都标记出来。

15.根据给出的时间画上缺少的时针或者分针，再看时针和分针组成的是什么角，填在（）里。

三、作图题（共4题；共35分）16.画一画。

（1）以点O为顶点画一个角。

（2）画线段CD，长5厘米。

17.画一条比5厘米少3厘米的线段。

18.请在下面每个图中再画一条线，分别组成一个锐角、一个直角和一个钝角。

19.画一画。

（1）用一副三角板拼出一个锐角并画下来。

（2）画一条比2厘米长2厘米的线段。

四、综合题（共7题；共35分）20.数一数。

（1）一共有________条线段。

（2）一共有________个角。

21.填一填。

有________个角有________个角22.数一数，填一填。

________个角________个三角形________个角________个三角形_______个三角形________个直角，________个锐角，________个钝角________个直角，________个锐角，________个钝角________个直角，________个锐角，________个钝角24.在下面的图中，你能找到几个直角？几个锐角？几个钝角？（1）________个直角，________个锐角，________个钝角。

角练习题及答案LEKIBM standardization office【IBM5AB- LEKIBMK08- LEKIBM2C】角同步训练一、选择题1．下列语句中，正确的是（）A．比直角大的角是钝角 B．比平角小的角是锐角C．钝角的平分线把钝角分为两个锐角 D．钝角与锐角的差一定是锐角2．两个锐角的和（）A．一定是锐角 B．一定是直角C．一定是钝角 D．可能是锐角，可能是直角，也可能是钝角3．在时刻8：30,时钟的时针和分针之间的夹角是（）A．85° B．75°C．70°D．60°4．如果∠A和∠B互为余角，∠B和∠C互为补角，∠A与∠C的和等于120°，那么这三个角分别是（）A．20°，80°，80° B．20°，70°，90°C．30°，60°，90° D．70°，20°，100°5．如果∠α=m°，而∠α既有余角，也有补角，那么n的取值范围是( )A．0°﹤m﹤90° B．m＝90° C．90°﹤m﹤180° D．m＝180°二、填空题6．如图所示，将一副三角板叠放在一起，•使直角的顶点重合于点O，则∠AOC+∠DOB的度数为_____度．7．如果∠α=47°28′，∠α的余角∠β =_____，∠α的补角∠γ=_____，∠γ－∠α=___．8．已知：如图，△ABC中，AB = AC，BD为∠ABC的平分线，∠BDC = 84°，则∠A =____.三、解答题9．如下图所示，已知∠BOD=2∠AOB，OC是∠BOD的平分线，试表示出图中相等的角．10．在飞机飞行时，飞行方向是用飞行路线与实际的南或北方向线之间的夹角大小来表示的．如图，用AN(南北线)与飞行线之间顺时针方向夹角作为飞行方向角．从A到B的飞行方向角为35°，从A到C的飞行方向角为60°，从A到D 的飞行方向角为145°，试求AB与AC之间夹角为多少度AD与AC之间夹角为多少度并画出从A飞出且方向角为105°的飞行线．答案：1．C2．D3．B4．B5．A6．1807．42°32′, 132°32′, 85°4′8．52°9．∠AOB=∠BOC=∠COD，∠AOC=∠BOD10．AB与AC之间夹角为25°，AD与AC之间夹角85°．。

二年级认识角练习题一、选择题1. 角是由两条射线组成的图形，这两条射线的公共端点叫做角的什么？A. 角顶点B. 角的边C. 角的开口D. 角的底2. 下列哪个角不是锐角？A. 30°B. 45°C. 60°C. 90°3. 一个直角的度数是多少？A. 30°B. 45°C. 60°D. 90°4. 一个角的度数大于90°但小于180°，这个角叫做什么？A. 锐角B. 直角C. 钝角D. 平角5. 一个角的度数等于180°，这个角叫做什么？A. 锐角B. 直角C. 钝角D. 平角二、填空题6. 角的度数用符号________表示。

7. 一个角的度数小于90°，这个角叫做________。

8. 一个角的度数等于90°，这个角叫做________。

9. 一个角的度数大于90°但小于180°，这个角叫做________。

10. 一个角的度数等于180°，这个角叫做________。

三、判断题11. 锐角的度数一定小于45°。

（）12. 直角的度数是90°。

（）13. 钝角的度数一定大于90°。

（）14. 平角的度数是180°。

（）15. 一个角的度数大于180°，这个角叫做周角。

（）四、简答题16. 请画出一个锐角，并标出角的顶点和两条边。

17. 请画出一个直角，并标出角的顶点和两条边。

18. 请画出一个钝角，并标出角的顶点和两条边。

19. 请画出一个平角，并标出角的顶点和两条边。

20. 描述一下锐角、直角、钝角和平角的特点。

五、应用题21. 小明在画角，他画了一个角的度数是40°，这个角是什么角？22. 小红在量角器上量得一个角的度数是120°，这个角是什么角？23. 小华在数学课上学习了角的分类，他知道了锐角、直角、钝角和平角，但他忘记了周角的度数，请你告诉他。

角的度量练习题一、选择题1. 以下各角中，度数最小的是：a) 直角b) 钝角c) 锐角d) 平角2. 一个角的度数是110°，那么它的补角度数是：a) 70°b) 90°c) 180°d) 270°3. 两个角互为对角，则它们的和是：a) 90°b) 180°c) 270°d) 360°4. 判断以下各角是否为对角：（需写出“是”或“不是”）a) 35°和145°b) 80°和100°c) 45°和135°d) 30°和180°二、填空题1. 一个角的补角的度数是________。

2. 一个角的补角是________。

3. 直角的对角是________。

4. 锐角的补角数是________。

5. 锐角和钝角的对角互为________。

三、定义题写出下列各种角的定义：1. 锐角：2. 钝角：3. 直角：4. 平角：四、计算题1. 一个角的补角度数是60°，那么它本身的度数是多少？2. 两个角是对角，其中一个角度数是75°，那么另一个角度数是多少？3. 两个角的度数之和是180°，其中一个角度数是80°，那么另一个角度数是多少？4. 两个角互为对角，其中一个角度数是30°，那么另一个角度数是多少？五、应用题1. 甲角是乙角的2倍，乙角是丙角的1.5倍，如果甲角的度数是80°，那么丙角的度数是多少？2. 两个角互为对角，其中一个角度数是x°，那么另一个角度数是多少的表达式？3. 一个角的补角的度数是4倍于它本身的度数，那么这个角的度数是多少？4. 一个直角的对角的度数是多少？六、解答题1. 画出以下各种角并标明度数：a) 45°角b) 90°角c) 135°角d) 锐角e) 钝角2. 父亲说：“我年轻时头发全黑，现在头发有三分之一都是白了。

角的认识练习题角的认识练习题角是几何学中的一个基本概念，也是我们日常生活中经常接触到的一个概念。

正确理解和掌握角的概念对于几何学的学习至关重要。

下面是一些角的认识练习题，帮助我们更好地理解和应用角的概念。

1. 请简要解释什么是角？角是由两条射线（或线段）共享一个端点而形成的图形。

这个共享的端点称为角的顶点，两条射线（或线段）称为角的边。

2. 请判断以下哪些图形中存在角？a) 直线b) 正方形c) 圆d) 三角形答案：b) 正方形和d) 三角形中存在角。

直线和圆并不包含角，因为它们没有边。

3. 请判断以下哪些图形中存在直角？a) 长方形b) 正方形c) 三角形d) 平行四边形答案：a) 长方形和b) 正方形中存在直角。

直角是一个角度为90度的角，长方形和正方形的内角均为90度，因此存在直角。

三角形和平行四边形的内角不一定为90度，所以不一定存在直角。

4. 请判断以下哪些图形中存在锐角？a) 直角三角形b) 钝角三角形c) 等边三角形d) 等腰梯形答案：b) 钝角三角形和d) 等腰梯形中存在锐角。

锐角是指角度小于90度的角。

直角三角形的一个内角为90度，不是锐角；等边三角形的三个内角均为60度，也不是锐角；等腰梯形的内角不一定小于90度，所以不一定存在锐角。

5. 请判断以下哪些图形中存在钝角？a) 直角三角形b) 锐角三角形c) 等边三角形d) 等腰梯形答案：a) 直角三角形和b) 锐角三角形中存在钝角。

钝角是指角度大于90度的角。

直角三角形的一个内角为90度，不是钝角；锐角三角形的所有内角均小于90度，也不是钝角；等边三角形的三个内角均为60度，也不是钝角；等腰梯形的内角不一定大于90度，所以不一定存在钝角。

通过以上练习题，我们对角的概念有了更深入的理解。

角是由两条射线（或线段）共享一个端点而形成的图形，根据角的大小可以分为直角、锐角和钝角。

正确理解和应用角的概念对于几何学的学习和实际问题的解决都具有重要意义。

角的练习题一、选择题1. 一个直角三角形的两个锐角之和是（）。

A. 90°B. 180°C. 360°D. 45°2. 一个圆的周角是（）。

A. 180°B. 360°C. 90°D. 45°3. 一个三角形的内角和是（）。

A. 180°B. 360°C. 90°D. 270°4. 一个等腰三角形的底角相等，如果顶角是70°，那么每个底角的度数是（）。

A. 55°B. 60°C. 70°D. 65°5. 如果一个角是锐角，那么它的度数一定（）。

A. 大于0°小于90°B. 大于90°小于180°C. 大于0°小于180°D. 大于90°小于360°二、填空题1. 一个直角三角形的两条直角边与斜边的夹角是______。

2. 一个等边三角形的每个内角的度数是______。

3. 如果一个角的补角是130°，那么这个角的度数是______。

4. 一个角的余角是40°，那么这个角的度数是______。

5. 一个角的度数是75°，它的余角和补角的和是______。

三、计算题1. 已知一个角的补角是120°，求这个角的度数。

2. 一个三角形的三个内角分别是x°，y°，z°，如果x+y=2z，且x+y+z=180°，求z的度数。

3. 一个等腰三角形的顶角是100°，求它的每个底角的度数。

4. 如果一个角的余角是它的补角的一半，求这个角的度数。

5. 一个圆心角的度数是60°，求它所对的弧长，如果圆的半径是2厘米。

四、简答题1. 描述什么是补角和余角，并给出一个例子。

2. 解释为什么直角三角形的两个锐角之和总是90°。

角的分类练习题一、选择题1. 锐角的度数范围是（）。

A. 0°-90°B. 90°-180°C. 180°-270°D. 270°-360°2. 直角的度数是（）。

A. 30°B. 45°C. 90°D. 180°3. 下列哪个角不是钝角？A. 120°B. 150°C. 90°D. 135°4. 一个角的度数为330°，这个角是（）。

A. 锐角B. 直角C. 钝角D. 周角5. 一个角的度数为360°，这个角是（）。

A. 锐角B. 直角C. 钝角D. 周角二、填空题6. 一个角的度数为15°，这个角是_________。

7. 当一个角的度数大于90°但小于180°时，这个角被称为_________。

8. 一个角的度数为180°，这个角被称为_________。

9. 如果一个角的度数大于270°，那么这个角被称为_________。

10. 一个角的度数为360°，这个角被称为_________。

三、判断题11. 一个角的度数为45°，它是锐角。

（）12. 一个角的度数为270°，它是钝角。

（）13. 一个角的度数为360°，它是周角。

（）14. 一个角的度数为90°，它是直角。

（）15. 一个角的度数为315°，它是锐角。

（）四、简答题16. 请解释什么是锐角，并给出一个锐角的例子。

17. 请解释什么是直角，并说明直角在几何学中的重要性。

18. 请解释什么是钝角，并给出一个钝角的例子。

19. 请解释什么是周角，并说明周角的特点。

20. 请解释什么是平角，并说明平角与直角的关系。

五、计算题21. 如果一个角的度数是45°，另一个角的度数是135°，这两个角的和是多少度？22. 一个角的度数是90°，如果将这个角的度数增加90°，新的角的度数是多少？23. 如果一个角的度数是270°，这个角与一个直角的和是多少度？24. 一个角的度数是360°，这个角与一个锐角的和是多少度？25. 如果一个角的度数是30°，另一个角的度数是这个角的两倍，那么另一个角的度数是多少？六、应用题26. 在一个三角形中，如果两个角的度数分别是40°和60°，求第三个角的度数。

角的度量练习题带答案一、选择题1. 下列哪个角度是锐角？A. 30°B. 90°C. 120°D. 180°2. 下列哪个角度是直角？A. 45°B. 60°C. 90°D. 120°3. 下列哪个角度是钝角？A. 30°B. 60°C. 90°D. 105°4. 一个角的度数是180°，这个角是什么角？A. 锐角B. 直角C. 钝角D. 平角5. 量角器的中心点应与角的哪个部分重合？A. 顶点B. 边C. 角的内部D. 角的外部二、填空题1. 一个角的大小为____度，它是____角。

2. 量角器上的一个小格表示____度。

3. 一个直角的度数是____度。

4. 一个平角的度数是____度。

5. 角的度量单位是____。

三、判断题1. 量角器上的刻度是从0°到180°。

（）2. 两个锐角的和一定是锐角。

（）3. 两个钝角的和一定是钝角。

（）4. 量角时，角的顶点必须与量角器的中心点重合。

（）5. 所有小于90°的角都是锐角。

（）四、画图题1. 画出下列角度的角：（1）30°（2）45°（3）60°（4）90°（5）120°2. 画出下列角的类型：（1）锐角（2）直角（3）钝角（4）平角五、解答题（1）比锐角大，比直角小的角。

（2）比直角大，比平角小的角。

2. 下列角的度数是多少？（1）一个锐角，其度数是45°的一半。

（2）一个钝角，其度数是180°减去一个直角的度数。

3. 在下图中，请用角度表示∠ABC的度数。

（图中未给出具体图形，请自行绘制）六、匹配题请将下列角度与其对应的角度类型匹配：A. 80°B. 100°C. 135°D. 180°1. 锐角2. 钝角3. 直角4. 平角七、简答题1. 解释什么是角的度量，并说明如何使用量角器量角。

认识角练习题在数学的世界里，角是一个非常重要的概念。

为了帮助大家更好地理解和掌握角的知识，下面我们一起来做一些练习题。

一、基础概念1、角是由（）和（）组成的。

答案：一个顶点和两条边。

2、下面的图形中，哪些是角？哪些不是角？（）（）（）（）答案：第一个和第三个是角，第二个和第四个不是角。

第二个图形没有顶点，第四个图形两条边不是直的。

3、一个角有（）个顶点，（）条边。

答案：1 个顶点，2 条边。

二、角的度量1、我们通常用（）来度量角的大小。

答案：量角器。

2、量角时，量角器的中心要与角的（）重合，0 刻度线要与角的（）重合。

答案：顶点重合，一条边重合。

3、角的大小与（）无关，与（）有关。

答案：角的大小与边的长短无关，与两条边张开的大小有关。

三、角的分类1、小于 90 度的角是（）角，等于 90 度的角是（）角，大于 90 度小于 180 度的角是（）角，等于 180 度的角是（）角，等于 360度的角是（）角。

答案：锐角、直角、钝角、平角、周角。

2、一副三角板有（）个直角，（）个锐角。

答案：2 个直角，4 个锐角。

3、用一副三角板可以拼出哪些角？答案：可以拼出 75 度（30 度＋ 45 度）、105 度（60 度＋ 45 度）、120 度（90 度＋ 30 度）、135 度（90 度＋ 45 度）、150 度（90 度＋60 度）。

四、角的计算1、已知∠1 ＝ 30°，∠2 ＝ 40°，求∠3 的度数。

答案：因为三角形内角和为 180 度，所以∠3 ＝ 180 30 40 ＝ 110°。

2、已知一个角是 50 度，它的余角是（）度，它的补角是（）度。

答案：余角是 90 50 ＝ 40 度，补角是 180 50 ＝ 130 度。

3、如图，已知∠AOB ＝120°，∠AOC ＝30°，求∠BOC 的度数。

答案：分两种情况，当 OC 在∠AOB 内部时，∠BOC ＝ 120 30 ＝90°；当 OC 在∠AOB 外部时，∠BOC ＝ 120 ＋ 30 ＝ 150°。

角的度量练习题带答案角的度量是数学中的一个重要概念，它涉及到角度的计算和度量单位。

以下是一些角的度量练习题及其答案，以帮助学生更好地理解和掌握这一概念。

练习题1：一个角的度数是30°，另一个角是它的两倍，求另一个角的度数。

答案：30° × 2 = 60°练习题2：如果一个角的度数是90°，它是一个直角。

那么一个角的度数是45°，它是什么角？答案：45°是一个锐角。

练习题3：一个角的度数是120°，它比直角大多少度？答案：120° - 90° = 30°练习题4：一个角的度数是360°，它是一个周角。

如果将它平均分成4个相等的角，每个角的度数是多少？答案：360° ÷ 4 = 90°练习题5：一个角的度数是180°，它是一个平角。

如果将它平均分成3个相等的角，每个角的度数是多少？答案：180° ÷ 3 = 60°练习题6：一个角的度数是15°，它是一个锐角。

如果将它扩大到原来的3倍，新的角的度数是多少？答案：15° × 3 = 45°练习题7：一个角的度数是150°，它是一个钝角。

如果将它缩小到原来的一半，新的角的度数是多少？答案：150° ÷ 2 = 75°练习题8：如果一个角的度数是75°，它是一个钝角。

那么一个角的度数是75°的三分之一，这个角的度数是多少？答案：75° ÷ 3 = 25°练习题9：一个角的度数是300°，它是一个周角的四分之三。

求这个周角的度数。

答案：300° ÷ (3/4) = 400°练习题10：一个角的度数是40°，另一个角的度数是它的补角。