2010年余姚中学自主招生考试数学试题

2010年余姚中学自主招生考试数学试题一、选择题（本大题共9小题，每小题4分，满分36分）1、 已知一次函数y=ax+b 的图象经过一、二、三象限，且与x 轴交于点（－2，0），则不等式ax > b 的解集为（ ） A. x>2- B. x<2- C. x>2 D. x<2 2、方程组126x y x y ⎧+=⎪⎨+=⎪⎩的解的个数为（ ）A. 1B. 2C. 3D. 4 3、如图，边长为1的正方形ABCD 绕点A 逆时针旋转30︒到正方形AB C D '''，图中阴影部分的面积为（ ）A ．1BC ．1-D ．124、已知二次函数2y ax bx c =++的图象如图所示，则下列6个代数式：ab 、ac 、a b c ++、a b c -+、2a b +、2a b -中，其值为正的式子的个数是（ ） A ．2个B ．3个C ．4个D ．5个5、张阿姨准备在某商场购买一件衣服、一双鞋和一套化妆品，这三件物品的原价和优惠方式如下表所示：请帮张阿姨分析一下，选择一个最省钱的购买方案. 此时，张阿姨购买这三件物品实际所付出的钱的总数为 （ ） A ． 500元 B ． 600元 C ． 700元 D ． 800元 6、如图，⊙O 与Rt △ABC 的斜边AB 相切于点D ，与直角边AC 相交于点E ，且DE ∥BC ．已知AE ＝22，AC ＝32，BC ＝6，则⊙O 的半径是（ ） A ．3B.4C.4 3D.2 3D 'C第12题主视图左视图7、向高为H 的水瓶中注水，注满为止，如果注水量V 与水深h 的函数关系的图象如图所示，那么水瓶的形状是（ ）8、甲、乙、丙3位同学选修课程，从4门课程中，甲选修2门，乙、丙各选修3门，则不同的选修方案共有（ ）A ．36种B ．48种C ．96种D ．192种 9、有依次排列的3个数：3，9，8，对任意相邻的两个数，都用右边的数减去左边的数，所得之差写在这两个数之间，可产生一个新数串：3，6，9，，8，这称为第一次操作；做第二次同样的操作后也可产生一个新数串：3，3，6，3，9，，，9，8，继续依次操作下去，问：从数串3，9，8开始操作第100次以后所产生的那个新数串的所有数之和是多少?（ ）A. 500B.520C.780D. 2000 二、填空题（本大题共6小题，每小题3分，共18分） 10、如果不等式组⎩⎨⎧<->-01a x x 无解，则a 的取值范围是____________．11、小丁、小明、小倩在一起做游戏时，需要确定做游戏的先后顺序.他们约定用“剪子、布、锤子”的方式确定.那么在一个回合中三个人都出“布”的概率是_________． 12、一个几何体，是由许多规格相同的小正方体堆积而成的，其主视图、左视图如图所示，要摆成这样的图形，至少需用______块小正方体 13、若直线b y =（b 为实数）与函数342+-=x x y 的图象至少有三个公共点，则实数b 的取值范围是_________． 14、设直线(1)10kx k y ++-=（k 为正整数）与坐标轴所构成的直角三角形的面积为k S ，则1232008S S S S +++⋅⋅⋅= ．15、如图，一个长方体盒子，一只蚂蚁由A 出发，在盒子的表面上爬到点C 1，已知AB=5cm ，BC=3 cm 1CC =4 cm ，则这只蚂蚁爬行的最短路程是________.A 1B 1C 1D 1ABCD2010年余姚中学自主招生考试数学答题卷姓名一、选择题（本大题共9小题，每小题4分，满分36分）1. 2. 3. 4. 5. 6. 7. 8. 9.二、填空题（本大题共6小题，每小题3分，共18分）10. 11. 12. 13. 14. 15.三、解答题（本大题共5小题，共66分）16（本小题12分）如图，正方形ABCD 的边长为1，点E 是AD 边上的动点，从点A 沿AD 向D 运动．．，以BE 为边，在BE 的上方作正方形BEFG ，连接CG 。

2012年余姚中学自主招生考试数学模拟卷（一）（考试时间90分钟，总分120分）一、选择题(本大题共10小题，每小题4分，共40分，在每一小题给出四个选项中，有且仅有一个选项是符合题目要求．)1．下列命题：①有两边及一边的对角对应相等的两个锐角三角形全等；②有两边及一边的对角对应相等的两个直角三角形全等；③有两边及一边的对角对应相等的两个钝角三角形全等其中正确的说法是（ ）A 、①②B 、②③C 、②D 、①②③2．已知n 是正整数，下列代数式中，哪一个代数式的值可能是某个自然数的平方（ ） A 、2612n n ++ B 、2712n n ++ C 、2812n n ++ D 、 21526n n ++3．从长度分别为1，2，3，4，5的五条线段中，任取三条的不同取法共有n 种，这些取法中， 以取出的三条线段为边可组成的钝角三角形的个数为m, 则nm的值为（ ） A 、101 B 、51 C 、103 D 、52 4．已知关于x 的不等式组230320a x a x +>⎧⎨-≥⎩恰有3个整数解，则a 的取值范围是（ ）A 、23≤a ≤32 B 、43≤a ≤32 C 、43＜a ≤32 D 、43≤a ＜325．已知函数2,0,,0x x y x x -≤⎧=⎨>⎩ ，若4y =，则数x 值为（ ）A 、—4或—2B 、 —4或2C 、—2或4D 、—2或26．某彩电厂家为了打开市场,促进销售,准备对其生产的某种型号的彩电降价销售,在下面四种降价方案中, 当满足a>0,b>0,a≠b 时,降价幅度最小的是( ) A 、 先降价a%,再降价b% B 、 先降价b%,再降价a% C 、先降价2a b +%,再降价2a b+ % D 、一次性降价(a+b)% 7．先阅读，后填空：在逻辑学中：当命题“若 A 则 B ”为真时，A 称为 B 的充分条件；当命题“若 B 则 A ”为真时，A 称为 B 的必要条件；当命题“若 A 则 B ”与“若 B 则 A ”皆为真时，A 是 B 的充分必要条件，同时，B 也是 A 的充分必要条件； 当命题“若 A 则 B ”为真，而“若 B 则 A ”为假时，我们称 A 是 B 的“充分但非必要条件”，B 是A 的“必要但非充分条件”；反之亦然. 命题“a>1”是命题“11a<”的( ) A ．充分必要条件 B ．充分不必要条件 C ．必要不充分条件 D ．既非充分也非必要条件 8．当抛物线c bx ax y ++=2与x 轴两交点及抛物线上一点P 组成以P 为直角顶点的直角三角形时，点P 的纵坐标( )A 、只与a 有关B 、只与b 有关C 、只与c 有关D 、与a 、b 、c 均有关9． 如图1, CD 是RT △ABC 斜边上的高，如图2, 正方形CDEF 是 RT △ABC 的内接正方形，如图3, CD 是△ABC 的角平分线且∠ACB=120°，在图1、图2、图3三个图形中，满足111AC BC CD+=的有（ ）A 、图1、图2B 、图2、图3C 、图1、图3D 、图1、图2、图310． 如图4，直线43y x =与双曲线ky x=（0x >）交于点A ． 将直线43y x =向右平移92个单位后，与双曲线ky x=（0x >） 交于点B ，与x 轴交于点C ，若2=BCAO，则k 的值为（ ） A 、4 B 、8 C 、9 D 、12二、填空题(本大题共7小题，每小题4分，共28分)11．用[x ]表示不大于x 的最大整数，如[4.1]=4，[-2.5]= -3，则方程6x -3[x ]+7=0的解是 . 12.已知a 是方程3210x x +-=的一个实数根，则函数1y ax a =-+的图像不经过第 象限. 13．线段a x y +-=21（1≤x ≤3），当a 的值由-1增加到2时，该线段运动所经过的平面区域的面积为__________________． 14．已知，直线y=34x+4与x 轴，y 轴分别交于A ，B 两点，点C 在y 轴上，若将△ABC 沿AC 折叠，使点B 恰好落在x 轴上的点D 处，则点C 的坐标是 ．15．将一正五边形纸片沿其对称轴对折．旋转放置，做成科学方舟模型．如图所示，该正五边形的边心距OB 长为2，AC 为科学方舟船头A 到船底的距离，则1AC AB += ．ABD图1 图2图3图416． 如图，M 是弧CAB 的中点，MP 垂直弦AB 于P,若弦AC 的长度为x ，线段AP 的长度是x+1，则用含x 的代数式表示线段BP= .17．已知A 为直线y =B 为（1，0）、点C 为（7，0），D 为平面内一点，当以A 、B 、C 、D 为顶点的四边形是有三边相等的等腰梯形时，则点D 的坐标为 .三、解答题(本大题共52分)18. （本题10分） 有一列数123,,,,n a a a a ，满足下列条件：10a =，211a a =+，3211,,1n n a a a a -=+=+ .求证：123,,,,n a a a a 这n 个数的算术平均数不小于12-.19. （本题10分）证明不等式：22222()()()a b c d ac bd ++≥+，并利用此不等式求函数y =20．（本题10分）已知，如图，AB=BM,AC=CN,P 是A 关于BC求证：PA 是∠NPM 的平分线.21．（本题10分）求出所有正整数a,使方程22(21)4(3)0ax a x a +-+-=至少有一个整数根.22．（本题12分）已知点P 是抛物线2y x =上一点，过点M （0，2M ，（1）过点P 作⊙M 的两条切线1l 、2l ，若1l ⊥2l ，求点P 的坐标；（2）若过点Q(2,4)的直线l 与抛物线2y x =只有一个公共点时，求出点M 与直线的距离.P参考答案1．A 提示：对于①可作高，再证全等，②显然成立，对于③可举反例说明不成立.2.D 提示：因为2(3)n +<2612n n ++<2712n n ++<2812n n ++<2(4)n +，所以A 、B 、C 均不成立 而2(5)n +<21526n n ++<2(8)n +，若21526n n ++=2(6)n +，3n=10，n 不为整数； 若21526n n ++=2(7)n +，n=23，21526n n ++=230. 3．B 提示：共10种情况，边长为2，3，5或2，4，5时，组成的三角形为钝角三角形. 4．B 提示：取a =32、43验证. 5.B 提示：若0x ≤，4x -=，4x =-；若0x ＞，24x =，2x =±，0,2x x ∴= ＞. 6.C 提示：设降价前彩电的价格为1,降价后的彩电价格依次为x 1、x 2、x 3、x 4 则x 1=(1-a%)(1-b%)=1-(a+b)%+a%·b%, x 2=(1-b%)(1-a%)=x 1,()()()()241231312324%%1a b % a b %,x 1a b %1a b %a%b%x x ,x x a%b%0,x x x x 111224%.%2a b a b x a b ++⎛⎫⎛⎫=-- ⎪⎪⎝=-+++⎡⎤⎣⎦=-+<-++⎭⎝⎭+⎛⎫- ⎪==-=>∴>=⎝>⎭7.B8． A 提示：P 的纵坐标为1a- 9．B10.D 提示：过A 作AD 垂直x 轴于D ，过B 作BE 垂直于x 轴于E,由题意有△OAD ∽△CBE,设CE=a ，BE=b,故OD=2a ，AD=2b,故A （2a ，2b ）、B （9/2+a ，b ）,故有2b=k/(2a)，b=k/(9/2+a),解得a=3/2,又A 在43y x =上，故b/a=4/3，所以k=4ab=4a ·b/a=12 11.利用x-1＜[x ]≤x ，求得107,33x -<≤-[x ]= 3-或4-，x=81936--或 12.用描点法画出3210x x +-=草图，可知0＜a ＜1，再画出1y ax a =-+草图，可看出函数1y ax a =-+的图像必定不经过第四象限13. 6 14.3(,0)2-或（6，0） 15.设正五边形边长为a ，面积为s ，则111252222s a a AC a AB =⨯⨯⨯=⨯⨯⨯+⨯⨯，得152AC AB += 16.过M 画AB 的平行弦MN 过N 作AB 的垂线交AB 于Q ，易证PQ=x ，QB=AP=x+1，BP=2x+117．分类讨论，11(2、、(1,-、(10,- 18.证明：∵10a =，211a a =+，3211,,1n n a a a a -=+=+ ， ∴22222221211322110,21,21,,21n n n a a a a a a a a a a --==++=++=++ ， ∴222222121211212221n n n a a a a a a a a a n --+++=+++++++- ，∴212(1)122n n a a a a n n ++++=- ≥12-，1n a =-时取等号. 19．证明：∵222222()()()()0(,.) a b c d ac bd da bc ad bc ++-+=-≥=当且仅当时等号成立，∴22222()()() a b c d ac bd ++≥+(,.)ad bc =当且仅当时等号成立 函数y =x 的取值范围为1≤x ≤6，2222222211]]3515y [y 15.y 00y .81x 3.=⨯⨯∴>∴<=++==∴==≤≤由题意知即时等号成立20.提示：易证，点A 、M 、P 在以点B 为圆心的圆上，∴∠APM=12∠ABM ，同理∠APN=12∠ACN ，易证∠CNA=∠BAC=∠AMB,从而∠BNC=∠BMC, 点B 、N 、M 、C 四点共圆，得∠ABM=∠ACN ，从而∠APM=∠APN21.由原方程知x ≠-2，不妨将方程整理成关于a 的一元一次方程2(44)212x x a x ++=+ 得22121(2)x a x +=≥+（因为a 是正整数），则得(4)(2)0x x +-≤，解得42x -≤≤,因此，x 只能 -4，-3，-1，0，1，2.，分别代入a 的表达式，故所求的正整数a 是1，3，6，10.22．（1）易证点P 、M 和两个切点组成的四边形是正方形，从而PM=2，设P 坐标为（2,t t ），则2242(2)2t t +-=，t =P 的坐标为（0，0）、）、（）；（2）若直线l 平行与y 轴，直线l 即x=2，此时点M 与直线l 的距离为2；若直线l 不平行与y 轴，可求得直线l 为44y x =-，易求得点M 与直线l.。

余姚中学2010届高考结果赵捷北京大学法学俞晓婧北京大学工商管理类(自主招生或艺术特长生)毛守迪北京大学地球与空间科学冯一北京大学电子信息科学类周易清华大学生物科学(自主招生或艺术特长生)顾宇炜清华大学材料化学倪雪皎香港中文大学文科基础班曹曼璐复旦大学国际政治陈雅斯复旦大学旅游管理黄玮复旦大学电子信息科学类(自主招生或艺术特长生)王乐乐复旦大学经济学类(自主招生或艺术特长生)黄迪超复旦大学临床医学（8年制本博连读）(自主招生或艺术特长生) 陈梦璐复旦大学新闻传播学类(自主招生或艺术特长生)冯辉复旦大学电子信息科学类郑燕志复旦大学生物科学类陆渝淳上海交通大学公共事业管理(自主招生或艺术特长生)汪岑天一上海交通大学公共事业管理(自主招生或艺术特长生)潘湖杰上海交通大学机械工程及自动化（试点班）(自主招生或艺术特长生) 赵可娜上海交通大学机械类(自主招生或艺术特长生)胡俊杰上海交通大学机械类(自主招生或艺术特长生)徐逸帅上海交通大学工业设计(自主招生或艺术特长生)王齐辉上海交通大学工业设计(自主招生或艺术特长生)张科伟上海交通大学数学与应用数学(自主招生或艺术特长生)蒋垚上海交通大学电气信息类(自主招生或艺术特长生)马雪环上海交通大学生物科学类(自主招生或艺术特长生)陈炉上海交通大学医学院预防医学（五年制）陈涛中国人民大学法学徐天骄中国人民大学国际政治王亚耐中国人民大学新闻传播学类鲁祎思浙江大学社会科学试验班(自主招生或艺术特长生)杨湾湾浙江大学社会科学试验班毛家栋浙江大学人文科学试验班戚圆圆浙江大学人文科学试验班李漂浙江大学人文科学试验班徐佳丽浙江大学人文科学试验班朱意炜浙江大学人文科学试验班熊松波浙江大学工科试验班（工学）(自主招生或艺术特长生)魏迪锋浙江大学工科试验班（工学）(自主招生或艺术特长生)王文权浙江大学理科试验班类史军阳浙江大学工科试验班（工学）陆楠楠浙江大学理科试验班类张叔晗浙江大学工科试验班（工学）陶冠宏浙江大学工科试验班（信息）陈秀灵浙江大学科技与创意设计试验班戚炳炳浙江大学科技与创意设计试验班严祝庆浙江大学医学试验班类金培璐浙江大学社会科学试验班干芸芸浙江大学工科试验班（工学）周能浙江大学社会科学试验班谢鹏程浙江大学理科试验班类胡天耀浙江大学工科试验班（信息）姚津津浙江大学工科试验班（工学）徐凌羿浙江大学工科试验班（工学）吴望冰浙江大学工科试验班（工学）徐镇杰浙江大学医学试验班类罗灵浙江大学工科试验班（工学）吴莎莉浙江大学工科试验班（工学）顾淑霞浙江大学工科试验班（信息）郑焕东浙江大学工科试验班（信息）翁聪叶浙江大学工科试验班（工学）徐彬彬浙江大学工科试验班（信息）茅铭芝浙江大学社会科学试验班毛冠雄浙江大学社会科学试验班吕建忠浙江大学工科试验班（工学）蔡恬恬浙江大学工科试验班（信息）闻人懿浙江大学理科试验班类吴琛浙江大学工科试验班（信息）鲁逸樵浙江大学医学试验班类宋奇波浙江大学人文科学试验班沈卓唯浙江大学医学试验班类周浩烽浙江大学理科试验班类祝伟杰浙江大学工科试验班（信息）罗文科浙江大学人文科学试验班李白璐浙江大学理科试验班类张宇舟浙江大学工科试验班（信息）余思一浙江大学工科试验班（信息）傅文娟浙江大学工科试验班（信息）卢潇磊浙江大学人文科学试验班徐鹏程浙江大学(农科大类) 应用生物科学高淑君浙江大学(农科大类) 应用生物科学陈曼姣浙江大学(农科大类) 应用生物科学周添添浙江大学(农科大类) 应用生物科学黄旭东浙江大学(农科大类) 应用生物科学赵倩浙江大学(农科大类) 应用生物科学陆湛浙江大学(农科大类) 应用生物科学赵颖南京大学临床医学（临床医学、口腔医学、基础医学）谢昊宏西安交通大学经济学类李琪琼西安交通大学公共管理类张瑜澎哈尔滨工业大学计算机科学与技术孙咏雷中国科学技术大学物理学类鲍健中国政法大学国际商务金莺中国医科大学临床医学（七年制）徐周中国医科大学信息管理与信息系统邵暇荔中国医科大学医学影像学章梦艺中国传媒大学法学倪雪韵中央财经大学管理科学唐一波中国劳动关系学院汉语言文学周阳杨对外经济贸易大学西班牙语（经贸方向）陈杰解放军理工大学通信工程金鑫解放军理工大学国防工程与防护王晟琪第二军医大学临床医学夏丽莉首都医科大学预防医学金隆达首都医科大学中药学竺佳晟首都医科大学康复治疗学卢俊晶北京化工大学化学工程与工艺张超杰北京化工大学电子信息工程（电子信息工程、通信工程）应彬权北京科技大学材料科学与工程陈瑶北京语言大学汉语言文学吴佳铭北京协和医学院护理学程智耀北京师范大学-香港浸会大学联合国际学院工商管理（财务学）韩家将南开大学药学黄佳斌天津科技大学材料化学杨启帆天津工业大学工业工程何津太原理工大学农业水利工程宋溢彬太原理工大学材料成型及控制工程陈旭东大连理工大学能源动力类袁征宇大连理工大学软件工程（日语强化）陈焕栋大连理工大学材料类郑学科东北大学机械工程及自动化鲁旻东北大学工程力学卢炳冰东北大学秦皇岛分校会计学许瑶瑶东北财经大学日语（国际商务方向）黄雯春东北财经大学税务茅益青东北师范大学广告学郑泽栋黑龙江中医药大学中医学（针灸推拿）施蓉蓉长春大学汽车服务工程黄雷沈阳工业大学通信工程张雯琳同济大学社会学励泽杰同济大学车辆工程（汽车）郑海滨同济大学电气信息类(自主招生或艺术特长生)杨凯华东理工大学行政管理包磊华东理工大学药物制剂郑严达华东理工大学安全工程姚一鸣华东理工大学广告学邹伟伟华东师范大学俄语方狄华东师范大学统计学石佳檬华东师范大学应用化学陈超然华东师范大学对外汉语袁马荣华东师范大学电子信息科学与技术陈妍竹华东政法大学法学（国际经济法）章思思华东政法大学法学（国际经济法）徐洋华东政法大学法学（民商法律）孙娇润华东政法大学法学（经济法）褚梦洁华东政法大学日语俞旭炜华东政法大学金融学赵越上海大学经济学类(中外合作办学)（金融学）陈洁琼上海大学工商管理类(中外合作办学)（工商管理）韩晨恺上海大学管理科学与工程类杭大威上海大学数学类（数学系）叶青青上海大学应用化学胡超上海大学高分子材料与工程黄杰枫上海大学电子信息工程（电子通信）陈飞翔上海大学自动化（自动化系）姜梦芝上海财经大学电子商务(自主招生或艺术特长生)胡佳乐上海财经大学法学(自主招生或艺术特长生)洪树威上海对外贸易学院国际经济与贸易蒋梦诗上海对外贸易学院会计学（国际会计方向）胡炯炯上海理工大学公共管理类(中外合作办学)（会展经济与管理王建梅上海外国语大学英语陈柯村上海中医药大学中医学（中医方向）徐乐苑上海海事大学经济学类（大类招生）许闻博上海海事大学电子商务冯莹颖上海海洋大学市场营销（国际商务方向）苏荻上海政法学院法学（国际经济法方向）王成城上海应用技术学院机械设计制造及其自动沈捷上海应用技术学院机械设计制造及其自动化施亮东华大学材料类顾天骄东华大学生物工程邵凌霄东华大学艺术设计周旭东东南大学电子科学与技术黄延东南大学材料科学与工程金榜河海大学电气工程及其自动化沈飞舟河海大学工程力学（大禹学院徐芝纶班）(自主招生或艺术蔡聪河海大学英语张弦河海大学水利类（大禹学院强化班）(自主招生或艺术特长叶苇韬江南大学高分子材料与工程邹松波江南大学包装工程张柯挺江南大学教育技术学李文渝南京工业大学电气工程及其自动化宋熊荣南京工业大学应用化学李梦莎南京农业大学农业资源与环境杜阳南京农业大学应用化学郑凯达南京理工大学工业设计应遥瑶南京理工大学热能与动力工程鲁文俊南京航空航天大学飞行器动力工程徐晚昉南京航空航天大学测控技术与仪器毛恒益南京医科大学临床医学谢天草南京信息工程大学汉语言文学（文化创意与设计/高级文秘/文化唐琰挺南京财经大学计算机科学与技术沈华桑苏州大学土建类黄阳洗西交利物浦大学管理科学与工程类(中外合作办学)任韬合肥工业大学电子科学与技术李文文合肥工业大学国际经济与贸易杨柯合肥工业大学电子信息科学与技术李汉宾安徽工程大学信息管理与信息系统林旭挺安徽农业大学设施农业科学与工程应育挺安徽农业大学农业工程类（农业建筑环境与能源工程、农业张翔淮阴师范学院生物技术戚娌娜福州大学电气工程与自动化邵今是厦门大学英语(自主招生或艺术特长生)何润勇厦门大学金融学马洋洋厦门大学生物工程类（含生物工程专业）鲁珊珊厦门大学软件工程（含软件工程、数字媒体艺术专业）叶文明厦门大学物理学类（含物理学专业）周金燕华侨大学国际经济与贸易史杰环华侨大学英语鲁浙杰华侨大学经济学谢琳菲山东大学新闻传播学类傅梦男鲁东大学公共管理类（含旅游管理、公共事业管理）王凯垚山东工商学院工商管理董亚丹山东工商学院物业管理陈斌华中科技大学水利水电工程钱丽琼华中师范大学中国语言文学类（汉语言、对外汉语）高瞻华中农业大学设施农业科学与工程张晶晶华中农业大学林学陈旭桑武汉大学临床医学（五年）应玮武汉大学地理科学（地理科学基地班）马科妮武汉大学药学黄银科武汉理工大学资源环境与城乡规划管理杨亦栋武汉理工大学土木工程严杰韬武汉理工大学热能与动力工程陈石武汉理工大学材料成型及控制工程方敏武汉理工大学法学郑铭垠武汉科技大学车辆工程张湾湾湖北中医药大学医学检验邢天嫣湖北中医药大学中药资源与开发金吉洋湖北第二师范学院英语(师范)王春燕中南大学临床医学与医学技术类魏洋波中南大学电气信息类何佳灏中南大学土建类袁嘉玲中南大学冶金工程（冶金与环境类）姚米娜中南财经政法大学公共事业管理范佳囡中南财经政法大学行政管理陆杰波中南财经政法大学国际商务万俊彦中南财经政法大学法学(自主招生或艺术特长生)舒焕湖南大学英语黄俊泽湖南工业大学电气信息类邹逸广东外语外贸大学社会工作丁洁瑶华南理工大学编辑出版学（新媒体方向）任佩青华南理工大学金融学谢杰伊海南大学行政管理(行政文秘方向)董涵佳西南大学电子科学与技术（含电子科学与技术、自动化翁微盈西南政法大学法学周阳西南交通大学物流工程徐炜杰重庆大学机械设计制造及其自动化蒋凯重庆大学化学工程与工艺张博四川大学药学郑晓炯电子科技大学通信工程何丹丹电子科技大学通信工程陆建平电子科技大学应用物理学陈浙成都理工大学公共事业管理徐柯烽成都中医药大学中西医临床医学胡诗竺广西大学汉语言文学俞烛天云南大学广播电视新闻学倪路长安大学自动化（轨道交通）赵斌西北大学金融学（金融工程）韩樑西北工业大学微电子学胡国权西安电子科技大学机械设计制造及其自动化吕梁西安电子科技大学计算机科学与技术夏启航西安电子科技大学测控技术与仪器张嘉浩西安外国语大学法语邵梦雪西安外国语大学金融学宋雅慧西安建筑科技大学计算机科学与技术黄挺西安科技大学无机非金属材料工程俞清青陕西师范大学生物学基地班钱露陕西师范大学软件工程戴佳栋兰州大学环境科学谢超亦浙江工业大学广播电视新闻学曹潇伟浙江工业大学公共管理类（按大类招生）徐雯晗浙江工业大学广告学陈冲浙江工业大学工商管理类（按大类招生）毛梦颖浙江工业大学工商管理类（按大类招生）王幼丽浙江工业大学建筑学施东东浙江工业大学建筑学张栋浙江工业大学机械工程及自动化茅澍州浙江工业大学机械工程及自动化钟柯松浙江工业大学物理学类（按大类招生）陈博杰浙江工业大学物理学类（按大类招生）翁微军浙江工业大学工业工程韩重赞浙江工业大学工业设计秦蓉蓉浙江工业大学食品质量与安全周云飞浙江工业大学化学类(化学工程与材料类)许晨祥浙江工业大学化学类(化学工程与材料类)楼怡辰浙江工业大学化学类(化学工程与材料类)唐雄锋浙江工业大学法学李莎浙江工业大学环境工程马维浙江工业大学环境科学魏军华浙江工业大学电子信息工程金科清浙江工业大学电气信息类（计算机及软件大类）张梅美浙江工业大学电气信息类（计算机及软件大类）孙佳宁浙江工业大学电气信息类（计算机及软件大类）沈涛浙江工业大学电气信息类（计算机及软件大类）沈灯柯浙江工业大学计算机科学与技术（中外合作办学）毛勇浙江工业大学计算机科学与技术（中外合作办学）朱超浙江工业大学计算机科学与技术（中外合作办学）田青浙江工业大学计算机科学与技术（中外合作办学）陈柯梦浙江工业大学英语平芳炯浙江工业大学教育技术学陈露彬浙江工业大学中药学万惠芳浙江师范大学文科试验班类柯颖浙江师范大学文科试验班类赵燕波浙江师范大学理科试验班类宓锦涛浙江师范大学理科试验班类张佳文浙江师范大学思想政治教育虞琼超浙江师范大学思想政治教育沈文琴浙江师范大学对外汉语闻人淑君浙江师范大学对外汉语宋维维浙江师范大学英语严少波浙江师范大学英语周金环浙江师范大学英语王丹红浙江师范大学英语吕周炳浙江师范大学物理学陆汝焕浙江师范大学化学吴焕杰浙江师范大学化学蔡杰男浙江师范大学历史学顾燕菱浙江师范大学历史学陈晓烨浙江师范大学法学徐芳君浙江师范大学翻译宋佳琪浙江师范大学小学教育张扬洋浙江师范大学科学教育符加侬浙江师范大学科学教育潘畅浙江师范大学国际经济与贸易叶津杨浙江师范大学工商管理类芦金金浙江师范大学工商管理类陈露儿浙江师范大学工商管理类陈丽娜浙江师范大学体育教育(师范)陈佳莉宁波大学人文科学试验班(阳明班)施嫣妮宁波大学人文科学试验班(阳明班)龚科科宁波大学理科试验班(阳明班)汪丽圆宁波大学经济学类（经济与管理类）应畅超宁波大学经济学类（经济与管理类）高丽彬宁波大学经济学类（经济与管理类）周薇宁波大学经济学类（经济与管理类）符栋栋宁波大学经济学类（经济与管理类）潘未庆宁波大学经济学类（经济与管理类）周海泽宁波大学经济学类（经济与管理类）徐光辉宁波大学经济学类（经济与管理类）徐崎特宁波大学工商管理（2+2中加学分互认）吴建萍宁波大学工商管理（2+2中加学分互认）徐前成宁波大学临床医学（医学类）张成开宁波大学临床医学（医学类）李奕润宁波大学临床医学（医学类）黄琢之宁波大学临床医学（医学类）孙滨宁波大学临床医学（医学类）陈科勇宁波大学电子信息科学类（工程技术类）曹张怡宁波大学英语（英语类）何孟菲宁波大学英语（英语类）何津津宁波大学英语（英语类）施烨娜宁波大学日语（日语类）金贝宁波大学日语（辅修英语）董栓泉宁波大学海洋科学类（生物与化学类）黄培培宁波大学法学类（法政文史类）郑奔宁波大学法学类（法政文史类）杨浓浓宁波大学英语(师范)宓泽锋宁波大学地理科学(师范)陈汶锦宁波大学小学教育(师范)高远宁波大学小学教育(师范)禹冰清杭州电子科技大学工商管理类郑箭浦杭州电子科技大学通信工程张正凡杭州电子科技大学软件工程赵焕焕杭州电子科技大学软件工程周海桥杭州电子科技大学数字媒体技术杨杰华杭州电子科技大学数字媒体技术章翔天杭州电子科技大学信息与计算科学施宁焕杭州电子科技大学计算机科学与技术戚青松杭州电子科技大学计算机科学与技术谢欣利杭州电子科技大学法学邵双双杭州电子科技大学英语卢洪芳浙江工商大学金融学吕安佳浙江工商大学金融学陈佳璐浙江工商大学金融学何华渭浙江工商大学金融学陈茂行浙江工商大学会计学劳诚晓浙江工商大学会计学孙焱娜浙江工商大学统计学沈莉莉浙江工商大学统计学毛雅澜浙江工商大学审计学陈佳红浙江工商大学国际经济与贸易张园园浙江工商大学人力资源管理方海芸浙江工商大学物流管理徐云霞浙江工商大学工商管理卢兰芬浙江工商大学工商管理陆颖嘉浙江工商大学工商管理郑璐璐浙江工商大学法学姚骐浙江工商大学法学施亚娜浙江工商大学日语干梦迪浙江工商大学通信工程邵佳莹浙江工商大学食品科学与工程符莎露浙江工商大学食品质量与安全鲁捷超浙江工商大学电子商务袁露婷浙江工商大学市场营销黄佳露浙江工商大学计算机科学与技术谢妮莎浙江工商大学英语董颖浙江工商大学社会工作鲁文桢浙江工商大学环境工程翁晶晶浙江工商大学劳动与社会保障徐未浙江工商大学知识产权姚炬洋浙江工商大学城市管理沈玲佳浙江理工大学国际经济与贸易蒋金杰浙江理工大学土木工程陈烨清浙江理工大学国际经济与贸易王浩杰浙江理工大学机械类（机械设计制造及其自动化、过程装备）张宇萍浙江理工大学信息管理与信息系统陆清清浙江理工大学英语马凯棋浙江理工大学机械类（机械设计制造及其自动化、过程装备）周浙栋浙江理工大学自动化王阳浙江理工大学测控技术与仪器朱泽磊浙江理工大学电气工程及其自动化孙梦霞浙江理工大学应用化学吴欣鸿浙江理工大学计算机科学与技术戚佳楠浙江理工大学法学孟利清浙江理工大学工程管理倪翔宇浙江理工大学风景园林赵柯超温州医学院临床医学黄晨温州医学院临床医学韩赞赞温州医学院临床医学姜泽东温州医学院临床医学万少波温州医学院临床医学张家乐温州医学院临床医学陈海彬温州医学院临床医学周科员温州医学院临床医学胡滢潇温州医学院临床医学张意婷温州医学院临床医学周孜洋温州医学院医学检验丁娇儿温州医学院预防医学吴晓晓温州医学院日语励佶佚温州医学院医学影像学傅孙亚温州医学院护理学陈静丹浙江中医药大学临床医学赵宇浙江中医药大学口腔医学万立峰浙江中医药大学听力学沈楚楚浙江农林大学英语钱佳慧浙江农林大学旅游管理吴超浙江农林大学地理信息系统樊仲琦浙江农林大学统计与信息类赵燊浙江农林大学电子信息类徐嘉扬浙江农林大学电子信息类赵圣杰浙江农林大学电子信息类张峰浙江农林大学电子信息类凌舟洋浙江农林大学农学祝亮亮中国计量学院测控技术与仪器沈林梁中国计量学院食品质量与安全许柯军中国计量学院财务管理朱怡霖中国计量学院计算机科学与技术徐佳颖中国计量学院计算机科学与技术严佳慧中国计量学院知识产权徐佳蓉中国计量学院光电信息工程顾凯翔浙江科技学院机械类（中德联合培养）俞依聪浙江科技学院市场营销余沁珊浙江科技学院建筑学谢锰浙江科技学院通信工程袁炳洋浙江科技学院通信工程王水龙浙江科技学院自动化郑杭燕浙江科技学院自动化孔瀛涛浙江科技学院电子信息工程（含电子信息工程、电子信息科糜特浙江科技学院计算机科学与技术（中澳联合培养）许亦凡浙江财经学院会计学（含ACCA和CGA课程班）陆一航浙江财经学院会计学（含ACCA和CGA课程班）朱逸浙江财经学院国际经济与贸易（含国际贸易、国际商务方向）樊倩莹浙江财经学院国际经济与贸易（含国际贸易、国际商务方向）金培佳浙江财经学院国际经济与贸易（含国际贸易、国际商务方向）马柿丹浙江财经学院国际经济与贸易（含国际贸易、国际商务方向）黄佩佩浙江财经学院金融学（含国际金融、公司金融、货币银行等方向）吴祎雯浙江财经学院金融学（含国际金融、公司金融、货币银行等方向）韩瑾锋浙江财经学院浙江财经学院陈淼苗浙江财经学院财政学(含财经新闻与文秘方向)魏莹莹浙江财经学院工商管理（含企业管理、国际企业管理、房地产经营管理等方向）黄玉洁浙江财经学院审计学章栋静浙江财经学院英语（含经贸、翻译方向）邹浩川浙江财经学院市场营销（营销策划及市场推广方向）蒋爽健浙江海洋学院汉语言文学(师范)徐庆达浙江海洋学院环境工程沈科浙江海洋学院食品科学与工程吕鹏浙江海洋学院计算机科学与技术倪小青浙江传媒学院文化产业管理戎芸浙江传媒学院英语。

余姚中学2010学年度第 二 学 期高一数学期中试卷（实验班）一、选择题（本题10小题,每小题5分,共50分，每小题给出的四个选项中，只有一项是符合题目要求的）1、程序图符号“”可用于( ）A 、输出a=10B 、赋值a=10C 、判断a=10D 、输入a=102、下列函数()f x 中，满足“对任意1x ，2x ∈（0，+∞），当1x <2x 时,都有1()f x 〉2()f x的是 （ ）A ．()f x =1xB 。

()f x =2(1)x -C 。

()f x =x eD ()ln(1)f x x =+3、设,,a b c 为同一平面内具有相同起点的任意三个非零向量，且满足a 与b 不共线,a ⊥c ，∣a ∣=∣c ∣，则∣b •c ∣的值一定等于（ ） A ． 以a ,b 为两边的三角形面积 B 以b ，c 为两边的三角形面积C ．以a ,b 为邻边的平行四边形的面积D 以b ，c 为邻边的平行四边形的面积4、如图，已知六棱锥P ABCDEF -的底面是正六边形，,2PA ABC PA AB ⊥=平面,则下列结论正确的是（ ） Ａ.PB AD ⊥ Ｂ.平面PAB PBC ⊥平面 w 。

w 。

w.k 。

sC. 直线BC ∥平面PAEＤ。

PD ABC ︒直线与平面所成的角为45 5、。

已知函数()f x 是定义在实数集R 上的不恒为零的偶函数，且对任意实数x 都有(1)(1)()xf x x f x +=+，则5(())2f f 的值是（ ）A 。

0 B.12 C 。

1 D.52 w.w 。

w 。

k.s.5.u 。

c 。

o 。

m6、已知一组数据为20、30、40、50、60、60、70，则这组数据的众数、中位数、平均数的大小关系为 （ ）A 、中位数 〉平均数 〉众数B 、众数 >中位数 〉平均数C 、众数 〉平均数 〉中位数D 、平均数 〉众数 〉中位数7、某班有60名学生，学号为1~60号，现从中抽出5位学生参加一项活动，用系统抽样的方法确定的抽样号码可能为( )A ．5，10，15，20，25B ．5，12，31，39,57C ．5，15,25，35，45D ．5，17,29,41，538、如图，一只蚂蚁在边长分别为3,4，5的三角形区域内随机爬行， 则其恰在离三个顶点距离都大于1的地方的概率为（ ）A 、12πB 、1－3πC 、1－6πD 、1－12π9。

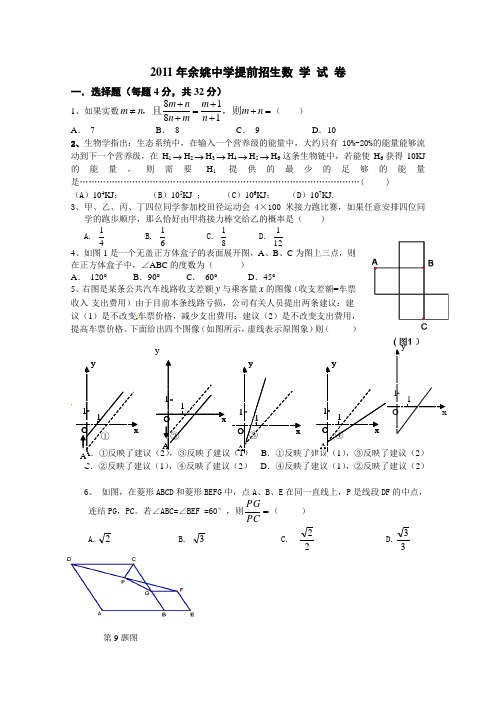
2011年余姚中学提前招生数 学 试 卷一．选择题（每题4分，共32分）1、如果实数8181m n m m n m n n m n ++≠=+=++，且，则（ ） A ． 7 B ． 8 C ． 9 D ．102、生物学指出：生态系统中，在输入一个营养级的能量中，大约只有10%-20%的能量能够流动到下一个营养级，在H 1→H 2→H 3→H 4→H 5→H 6这条生物链中，若能使H 6获得10KJ 的能量，则需要H 1提供的最少的足够的能量是……………………………………………………………………………………( ) （A ）104KJ ； （B ）105KJ ； （C ）106KJ ； （D ）107KJ .3、甲、乙、丙、丁四位同学参加校田径运动会4×100米接力跑比赛，如果任意安排四位同学的跑步顺序，那么恰好由甲将接力棒交给乙的概率是（ ）A. 41B. 61C. 81D. 1214、如图1是一个无盖正方体盒子的表面展开图，A 、B 、C 为图上三点，则在正方体盒子中，∠ABC 的度数为（ ） A ． 120° B ．90° C ． 60° D ．45°5、右图是某条公共汽车线路收支差额y 与乘客量x 的图像（收支差额=车票收入-支出费用）由于目前本条线路亏损，公司有关人员提出两条建议：建议（1）是不改变车票价格，减少支出费用；建议（2）是不改变支出费用，提高车票价格。

下面给出四个图像（如图所示，虚线表示原图象）则（）1），②反映了建议（2）6、 如图，在菱形ABCD 和菱形BEFG 中，点A 、B 、E 在同一直线上，P 是线段DF 的中点，连结PG ，PC 。

若∠ABC=∠BEF =60°，则=PCPG（ ） A.2 B. 3 C. 22 D.33y第9题图7、在高速公路上，从3千米处开始，每隔4千米经过一个限速标志牌，并且从10千米处开始，每隔9千米经过一个速度监控仪，刚好在19千米处第一次同时经过这两种设施，那么，第二次同时经过这两种设施是在（ ）千米处。

余姚中学 高二数学期中试卷一、选择题（本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的） 1.函数x x x y +-=)1(的定义域为 （ ）A .}0|{≥x xB .}1|{≥x xC .}0{}1|{ ≥x xD }10|{≤≤x x 2.阅读如图的程序框图，则输出的S = （ ） A .26 B .35 C .40 D.57 3.设c b a ,,是单位向量，且b a ⊥，则)()(c b c a-⋅-的最小值为（ ）A .2-B .22-C .21- D.1- 4.若)(,)21(20092009102009R x x a x a a x ∈+⋅⋅⋅++=-，则20092009221222a a a +⋅⋅⋅++的值为（ ） A .2 B .0 C .1- D.2-5.从0，1，2，3，4，5这6个数字中任取两个奇数和两个偶数，组成没有重复数字的四位数，则这些四位数的个数为 （ ）A .300B .216C .180 D.1626.在∆ABC 中，若222()tan 3a c b B ac +-=，则角B 的值为 （ ） A .6π B . 3πC .566ππ或 D. 233ππ或7.设y x ,满足约束条件组360200,0x y x y x y --≤⎧⎪-+≥⎨⎪≥≥⎩，若目标函数(0,0)z ax by a b =+>>的最大值为12，则23a b +的最小值为 （ ）A . 256B . 83C . 113D.48.一个篮球运动员投篮一次得3分的概率为a ，得2分的概率为b ，不得分的概率为c (,,(0,1))a b c ∈，已知他投篮一次得分的数学期望为2，(不计其他得分情况)，则ab 的最大值为 （ ）A .16 B . 112 C . 124 D.481 9.已知函数()|lg |f x x =，若0a b <<，且()()f a f b =，则3a b +的取值范围为（ ）A . (23,)+∞B . [23,)+∞C . (4,)+∞ D. [4,)+∞2 0 1 0学年第 一 学 期10.函数2()(0)f x ax bx c a =++≠.对任意非零实数,,,,,a b c m n p ，关于x 的方程2[()]()0m f x nf x p ++=的解集都不可能是 （ ） A .}2,1{ B .}4,1{ C .}4,3,2,1{ D.}64,16,4,1{二．填空题(本大题共7小题，每小题4分，共28分)11.在[0,1]上随机地取两个数,a b ，则这两数的和小于1.2的概率为________12.设某几何体的三视图如下（尺寸的长度单位为米），则该几何体的体积为__________ 13.一个箱子中装有4个白球和3个黑球，一次摸出2个球，则在已知它们的颜色相同的情况下，该颜色是白色的概率为__________（用数字作答）14.如图，已知球O 的面上四点,,,A B C D . DA ⊥平面ABC ，AB BC ⊥,3DA AB BC ===,则球O 的体积等于__________15.如图，用,,,A B C D 四类不同的元件接成系统N .当元件A 正常工作且元件,C D 都正常工作，或者元件A 正常工作且元件B 正常工作，或者元件,,,A B C D 都正常工作时，系统N 正常工作.已知元件,,,A B C D 正常工作的概率依次为2334,,,3445，则系统N正常工作的概率为___________16.若直线y x b =+与曲线234y x x =--恰有一个公共点，则b 的取值范围为_________17.某人有四种颜色的灯泡（每种颜色的灯泡足够多）要在如图所示的6个点111,,,,,A B C A B C 上各装一个灯泡，要求同一条线段的两端的灯泡不同色，则至少用了三种颜色的灯泡的安装方法共有_______种（用数字作答）三．解答题（共5题，第18、19 、20小题14分，第21、22小题15分，共72分） 18.设)(,)21(1010221010R x x a x a x a a x ∈+⋅⋅⋅++=-（1）求展开式的二项式系数的和； （2）求5a 的值；（3）求0246810a a a a a a +++++的值.19.设数列{}n a 满足)(,3333*13221N n na a a a n n ∈=+⋅⋅⋅+++- (1)求数列{}n a 的通项公式； （2）设n nnb a =，求数列{}n b 的前n 项和n S .20.甲、乙两队进行球类比赛，约定先胜3局获胜，比赛结束假设在每局比赛中，甲队获胜的概率为0.6，乙队获胜的概率为0.4，各局比赛相互独立已知第一局比赛已经结束，且甲队获胜（1）求甲队获得这次比赛胜利的概率；（2）设ξ表示从第二局开始到比赛结束所进行的局数，求ξ的分布列和数学期望.21.已知四棱锥P ABCD -的底面为直角梯形，//AB CD ,90DAB ∠=,PA ⊥底面ABCD且112PA AD DC AB ====,M 为PB 中点 （1）证明：平面PAD ⊥平面PCD ; （2）求AB 与平面PAC 所成角； （3）求二面角A MC B --的余弦值21、。

余姚中学2008年自主招生考试数学试题提示：全卷共22道题，满分120分，考试时间90分钟．一、选择题：(本大题共9小题，每小题4分，共36分．在每小题给出的四个选项中，只有一项是符合题目要求的．)．1、“割圆术”是求圆周率的一种算法．公元263年左右，我国一位著名的数学家发现当圆的内接正多边形的边数无限增加时，多边形面积可无限逼近圆面积，即所谓“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣”．请问上述著名数学家为( )A、刘徽B、祖冲之C、杨辉D、秦九昭2、某校食堂有4元、5元、6元三种价格的饭菜供学生们选择(每人限购一份)．三月份销．售该三种价格饭菜的学生比例分别为25％、55％、20％，则该校三月份学生每餐购买饭菜的平均费用是( )．A、4．9元B、4．95元C、5元D、5．05元3、在初中已学过的一次函数、反比例函数和二次函数等函数中，它们的图像与任意一条直线x=a．(a是任意实数)交点的个数为( )．A、必有一个B、一个或两个C、至少一个D、至多一个4、同时掷两个骰予，其中向上的点数之和是5的概率是( )A.1/4 B、1/6 C、1/9 D、1/125、给你一列数：1， l， 2， 6． 24，( )．请你仔细观察这列数的排列规则，然后从四个供选择单选项中选出一个你认为最合理的一项，来填补其中的空缺项，使之符合原数列的排列规律．A、48B、9 6．C、120D、1446、已知．二次函数y=x2-2x+a(a是实数)，当自变量任取x1，x2时，分别与之对应的函数值y l，Y2满足y1>Y2，则x1，x2应满足的关系式是( )A、x l-1<x2-1B、x1-1>x2-1．C、|x1-l|<|x2-1|D、|x1-1|>|x2-1|7、在8个银元中混进了一个大小形状颜色完全一样的假银元，已知7个真银元的重量完全相同，而假银元比真银元稍轻点儿，你用一台天平最少( )次就能找出这枚假银元．A．l B、2． C、3 D、48、如图，P是圆D的直径AB的延长线上的一点，PC与圆D相切于点C，∠A PC的平分线交AC于点Q，则∠PQC=( )．A、30°B、45°C、50°D、60°9、电子计算机中使用二进制，它与十进制的换算关系如下表所示：观察二进制为l 位数、2位数、3位数时，对应的十进制的数，当二进制为6位数时，能表示十进制中的最大数是( )．A 、6 1B 、62．C 、63D 、64二、填空题：(本大题共7小题，每小题3分，共21分．)10、某校去年投资2万元购买实验器材，预计今明两年的投资总额为8万元，若该校这两年．购买的实验器材的投资年平均增长率为x ，则可列方程为ll 、如图，在平行四边形ABCD 中，AE ⊥BC 于E ，AF⊥CD 于F ．∠EAF=45°：且AE+AF=22，则平行四边形ABCD 的周长为 ．12、在一个木制的棱长为3的正方体的表面涂上颜色，将它的棱三等分，然后从等分点把正方体锯开，得到27个棱长为l 的小正方体，将这些小正方体充分混合后，装入口袋，从这个口袋中任意取出一个小正方体，则这个小正方体的表面恰好涂有两面颜色的概率 是13、已知关于x 的一元二次方程x 2+mx+2=0与x 2+2x+m=0有一个公共实数根，则m=14,一个样本为l ，3，2，2，a ，b ，c ．已知这个样本的众数为3，平均数为2，则这个样本的方差=15、如图，在梯形ABCD 中，AB∥DC，DC=2AB=2AD ，BD=6,BC=4，则该梯形的面积S 梯形ABCD = ．16、某计算机用户计划用不超过500元的资金购买单价分别为60元、70元的A 类软件和B 类软件，根据需要A 类软件至少买3片，B 类软件至少买2片，则不同的选购方式共有 种三、解答题：(本大题共6小题，共63分。

浙江省宁波市余姚中学2010年自主招生模拟考试（语文）一、书写（2分）1、请将下面的一段话抄写在答卷的书写格子里。

（要努力做到书写准确、工整、美观）语文，是热爱，是关怀，是追求，是理想，是幻想……生活就是大语文，大语文就是生活。

二、积累与运用（20分）（一）选择题（每小题2分，共12分）2、下列词语中加点的字，读音全部正确的一组是（）A．埋．（mán）怨憧．（chōng）憬气氛．（fēn）龙盘虎踞．（jù）B．绯．（fěi）闻解剖．（pō）癖．好（pǐ）文采斐．（fěi）然C．创．伤（chuàng）矿藏．（zàng）躯壳．（ké）前倨．（jù）后恭D．通缉．（jī）档．（dàng）案豺．（cái）狼飞来横．祸（héng）3、下列词语中没有错别字的一项是（）A．脉搏名信片再接再厉一筹莫展B．气概炒鱿鱼走头无路有恃无恐C．松弛挖墙脚墨守成规唉声叹气D．厮杀渡假村兵荒马乱好高骛远4、依次填入下列各句横线处的词语，最恰当的一组是（）①井冈山、遵义、延安和西柏坡，是中国革命的几处②尽管有的地方“政绩工程”看起来规模宏大，但是由于脱离了实际，弄得劳民伤财，没有使群众受益，加重了群众的负担。

③在灿烂的灯光中，由24名聋哑演员表演的“千手观音”精妙绝伦，人心。

A．胜地不但/反而振奋 B．圣地不但/而且震撼C．胜地不但/而且振奋 D．圣地不但/反而震撼5、下列句中加点的成语使用正确的一句是（）A．初春的校园，篝火晚会上，大家陶醉在这春意阑珊．．．．的氛围中，有的在唱着，有的在跳着，有的在谈着……欢乐围绕在每个人的身边。

B．这次选举，本来他是最有希望的，但由于他近来的所作所为深孚众望．．．．，结果落选了。

C．也许是对故土的深情吧，住在这里的老百姓大都安土重迁．．．．，不愿意搬到别处去。

D ．个别民警认为工作时间饮点酒是小事一桩，就不以为然．．．．，结果因违反公安部颁布的“五条禁令”而受到查处。

2010余姚中学自主招生模拟测试科学试卷考生须知：1．本卷共4大题，34题，考试时间120分钟，满分150分。

2．试卷分为试题卷（共8页）和答题卷（共4页）。

请在答题卷上写上考生姓名、学校、考号。

所有答案写在答题卷上，写在试题卷上无效。

3．可能用到的相对原子质量：H-1 O-16 Mg-24 S-32 C1-35．5 Zn-65 Na-23 C-12 Cu-64 Al-27 N-14一、选择题（本大题有10题，每题3分，共30分，每题只有1个选项正确，多选、错选、不选均得零分。

将选出的答案选项字母填在答题卷的相应空格内）1．同学甲的居住地位于北回归线上，同学乙的居住地位于南回归线上，且两地恰好位于同一经线。

下列有关现象的叙述正确的是：（▲）A．甲同学早上上学之时，正是乙同学下午放学之时B．某天晚上甲同学看到上弦月，乙同学看到的也是上弦月C．某日甲同学看到日食现象，而乙同学在那日晚上看到月食现象D．甲同学居住地处于夏季时，乙同学居住地也处于夏季2．美国医学科研小组采用遗传工程的方法，用一种特殊的"内切酶"，切割了红细胞表面的凝集原，从而实现了血型的转化。

根据这种方法，你认为以下血型转化可以实现的是（▲）A．O型血转化为B型血B．A型血转化为AB型血C．A型血转化为B型血D．A型血转化为O型血3. 一个雨滴从空中由静止开始自由落下一段时间后，突然受到一个水平向右的大小不变的风力作用，则其运动轨迹可能是（不计空气阻力）( )4．如图所示，当滑动变阻器的触片移动时，发现L1变亮了，L2变暗了，那么整个电路中消耗的电功率（▲）A 变大B 变小C 不变D 无法判断5．当人体的皮肤被烧伤时，关于烧伤部位的说法，正确的是（▲）A．若烧伤部分化脓，这是人体的特异性免疫在起作用B．烧伤部位对外界刺激变得迟钝，因为皮肤的神经系统遭到了破坏C．夏天时，烧伤病人更怕热，因为烧伤部位汗腺遭到了破坏D．为了保护烧伤部分，应用多层纱布包扎以免透气6、将KNO3和K2SO4混合物进行分离，有如下操作：①将混合物溶解制成浓溶液；②加热蒸发浓溶液；③冷却溶液；④过滤，移出KNO3晶体；⑤过滤，移出K2SO4晶体。