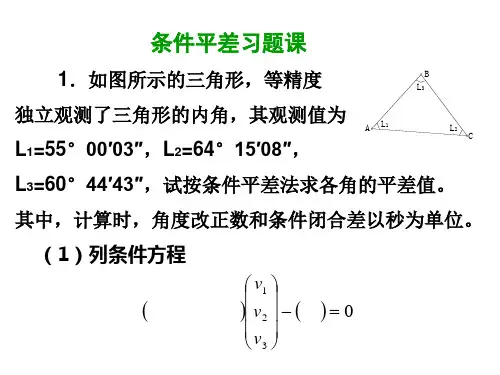
条件平差习题

条件平差习题一、重点内容及难点1. 水准网条件平差● 条件方程列法 ● 权的确定方法2. 边角网条件平差● 条件方程个数确定方法● 条件方程类型：图形条件 极条件 边条件 方位角条件 基线条件3. 条件方程线性化11112ˆ()()()()()()()ˆˆˆˆnn i i ni f f f f f Lf L V V V f L V L L L L =∂∂∂∂=++++=+∂∂∂∂∑● 极条件方程及线性化● 符合三角网条件方程4. 理解条件平差的函数模型和随机模型● 明确必要起算数据、必要观测数据、多余起算数据和多余观测数据的概念； ● 条件平差的出发点：观测值的平差值之间应该存在的函数关系式； ● 随机模型的含义和作用二、公式汇编及条件平差计算步骤1. 根据实际问题，确定出总观测值的个数n 、必要观测值的个数t及多余观测个数r = n – t ，2. 列出条件平差值方程，对其线性化进一步列出改正数条件方程平差值条件方程 ˆ()0F L=改正数条件方程 0=+W AV3. 据具体情况确定观测值的权阵；)(21n p p p diag P =4. 组成法方程式，求出联系数；W NK =1K N W -=-5. 算出观测值改正数和观测值的平差值Lˆ； 1T V P A K -= V L L+=ˆ 6. 检查平差计算的正确性，将平差值L ˆ代入平差值条件方程式，检验平差值是否满足应有的条件关系式；0)ˆ(=LF 7. 计算单位权方差和单位权中误差；rPV V T =20ˆσ8. 列出平差值函数关系式，计算平差值函数及其精度。

对平差值函数全微分，应用广义传播律计算平差值函数的协因数，进一步计算出平差值函数的方差、协方差。

12ˆˆˆˆ(,,,)nf L L L ϕ= ˆˆˆˆTLL Q fQ f ϕϕ= 2ˆˆˆˆ0ˆD Q ϕϕϕϕσ=三、思考题：1.发现误差的必要条件是什么？2. 几何模型的必要元素与什么有关？为什么？3. 测量平差的函数模型和随机模型分别表示哪些量之间的什么关系？4. 什么叫必要起算数据？各类控制网的必要起算数据是如何确定的？5. 条件平差中求解的未知量是什么？能否由条件方程直接求得改正数？6.设某一平差问题的观测个数为n ，必要观测数为t ，若按条件平差法进行平差，其条件方程，法方程及改正数方程的个数各为多少？7. 通常用什么公式将非线性函数模型转化为线性函数模型？ 8. 在条件平差中，能否根据已列出的法方程计算单位权方差？ 9. 条件平差中的精度评定主要是解决哪些方面的问题？四、计算题5.1 有水准网如下图P1点位已知点Hp1=50.002米，P2、P3、P4,为待定点，观测六条线路的线路长度和高差为：S1= 1.0km h1=1.576m，S2=1.5 km h2=2.215m,S3=1.5 km h3=-3.800m,S4=1.0 km h4=0.871m,S5=2.0 km h5=-2.438m,S6= 2.0 km h6=-1.350m。

一、填空。

（每空1分，共22分）1．与的比值称为相对中误差。

2．误差椭圆的三个参数是________、________、_________。

3．闭合导线按条件平差时条件方程式的个数等于___个，分别是____个____________________条件和____对_______________________条件。

4 ．设某平差问题中，观测值个数为n个，必要观测数为t个，若按条件平差，条件方程的个数等于______个，法方程的个数等于_______个。

若按间接平差，误差方程式的个数等于______个，未知数的个数等于______个，法方程的个数等于____个。

5．根据误差传播定律，若某一站观测高差的中误差为2mm，在A、B两点间共观测了4站，则A、B两点间高差的中误差为mm。

6．导线网按条件平差，所列条件方程中的未知数，既有___________的改正数，也有___________的改正数。

7．在水准测量中若已知每公里观测高差的中误差均相等，且又知各水准路线的长度为Si（I=1，2，……n），则观测高差的权可用公式_________求出。

8．偶然误差的特性为：绝对值较小的误差出现的可能性；绝对值相等的正负误差出现的可能性；偶然误差的理论平均值。

1．__________、_________和_________合称为观测条件。

2．水准路线的定权方法有两种：根据_________定权和根据_________定权。

3．由三角形闭合差来计算测角中误差的公式为，称其为菲列罗公式。

4．由不等精度的双观测值之差计算单位权中误差的公式为σ0= ，由等精度的双观测值之差计算观测值中误差的公式为。

5 ．单导线按条件平差时条件方程的个数永远等于个，附合导线中个坐标方位角条件和一对条件，闭合导线中一个条件和对闭合条件。

6．常用的衡量精度的指标有、、、1.独立边角同测网条件方程式的种类，除了具有测角网和测边网的条件式外，还具有反映边角关系的二种条件，它们是和。

平差试卷试卷⼀⼀、简答题（每题5分，共15分）1、何谓系统误差？测量中是如何处理的？2、误差椭圆与误差曲线是否⼀致？如何根据误差椭圆来求任意⽅向位差？3、⾃由⽹平差⽅法有哪些？秩亏⾃由⽹平差中，秩亏数如何确定的？秩亏⾃由⽹平差准则是什么？⼆、填空题（每空3分，共15分）1、常⽤衡量向量的绝对精度指标是（）；常⽤（）作为衡量向量的相对精度指标。

2、设有同精度独⽴观测值12,L L 两个⾓值，且构成函数12sin sin ABL y S L =。

式中AB S 为已知边长，认为⽆误差。

测⾓中误差 1.2σ''=。

则该函数的中误差为（）。

3、已知某待定点观测的测⾓中误差2βσ''=，测边中误差2s mm σ=。

已知点⾄待定点距离为185⽶。

则该点的点位中误差为（）。

4、观测向量[]12TL L L =的权阵为4223LL P ??=,则1L P =( )。

三、下图所⽰测量控制⽹，试按要求完成如下⼯作：1、下图条件平差时，条件式个数？条件式类型？每种类型各建⽴其中⼀个，⾮线性需要线性化。

（10分）2、下图间接平差时，参数个数？误差⽅程个数？类型？每种类型各建⽴⼀个，⾮线性需要线性化。

（10分）四、已知某⼀个待定点的控制⽹中，设该点坐标为参数，采⽤间接平差得到法⽅程为：6.01 3.02 6.00xy --= ??3.02 1.58 3.40xy -++= 已计算得到单位权中误差估值0? 1.2σ''=。

求：（1）该点的误差椭圆参数；（2）该点的点位误差。

（共15分）五、下图所⽰的⽔准⽹中，已知⾼程为135.000A H m =。

⾼差观测数据列于下表中。

试任选⼀种平差法：（1）求待定点⾼程的平差值；（2）求第⼆段⾼差平差值的协因数；（3）求待定点⾼程平差值的中误差。

（共20分）名称 1 2 3 ⾼差观测值（m ） 6.885 6.890 -6.892 ⽔准路线长（km ） 428六、证明：测量平差中根据最⼩⼆乘准则可以求得参数以及观测值的平差值的唯⼀解。

一、填空题（每空2分，共20分）1、最优估计量应具有的性质为 、 和 最优估计量主要针对观测值中仅含 误差而言。

2、间接平差中，未知参数的选取要求满足 、 。

3已知条件平差的法方程为024322421=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡k k ，则PV V T = ，μ= ， 1k p = ，2k p = 。

4、已知某平差问题，观测值个数为79，必要观测量个数为35，则按间接平差进行求解时，误差方程式个数为 ，法方程式个数为 。

5、已知某平差问题观测值个数为50，必要观测量个数为22，若选6个独立参数按具有参数的条件平差进行求解，则函数模型个数为 ，联系数法方程式的个数为 ；若在22个独立参数的基础上，又选了4个非独立参数按具有条件的参数平差进行求解，则函数模型个数为 ，联系数法方程式的个数为 。

6、条件平差中条件方程的个数等于________________,所选参数的个数等于_______________。

7、已知真误差向量1⨯∆n 及其权阵P ，则单位权中误差公式为 ，当权阵P 为 此公式变为中误差公式。

二、计算题（每题2分，共20分）1、条件平差的法方程等价于：A 、0=+W K Q KB 、0=+W Q K WC 、0=+W P K WD 、0=+W P K K答:______2、水准测量中，10km 观测高差值权为8，则5km 高差之权为：A 、2B 、4C 、8D 、16答:______3、已知⎥⎦⎤⎢⎣⎡=∆3112P ，则2L p 为：A 、2B 、3C 、25D 、35答:______4、间接平差中，L Q ˆ为：A 、TA AN 1- B 、A N A T1-C 、T A AN P11--- D 、A N A P T 11---答:______5、观测条件是指:A)产生观测误差的几个主要因素:仪器,观测者,外界条件等的综合B)测量时的几个基本操作:仪器的对中,整平,照准,度盘配置,读数等要素的综合 C)测量时的外界环境:温度,湿度,气压,大气折光……等因素的综合. D)观测时的天气状况与观测点地理状况诸因素的综合答:______ 6、已知观测向量()L L L T=12的协方差阵为D L =--⎛⎝ ⎫⎭⎪3112,若有观测值函数Y 1=2L 1，Y 2=L 1+L 2，则σy y 12等于？(A)1/4 (B)2 (C)1/2 (D)4 答:_____ 7、已知观测向量()L L L T=12的权阵P L =--⎛⎝ ⎫⎭⎪2113,单位权方差σ025=,则观测值L 1的方差σL 12等于:(A)0.4 (B)2.5 (C)3 (D)253答:____ 8、已知测角网如下图,观测了各三角形的内角,判断下列结果,选出正确答案。

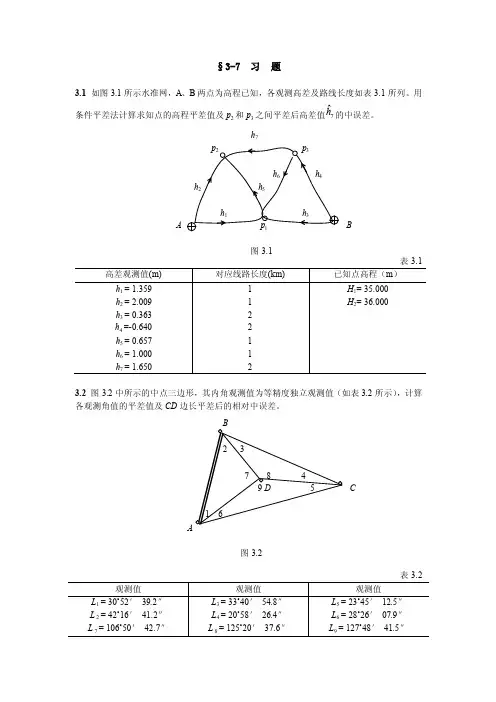
§3-7 习 题3.1 如图3.1所示水准网，A 、B 两点为高程已知，各观测高差及路线长度如表3.1所列。

用条件平差法计算求知点的高程平差值及p 2和p 3之间平差后高差值7ˆh 的中误差。

表3.13.2 图3.2中所示的中点三边形，其内角观测值为等精度独立观测值（如表3.2所示），计算各观测角值的平差值及CD 边长平差后的相对中误差。

表3.23.3 如图3.3所示单一附合导线，起算数据和观测值如表3.3所示，测角中误差为±3″，测边标称精度为±(5+5D )mm ，按条件平差法计算各导线点的坐标平差值，并评定3点平差后的点位精度。

表3.33.4 设某平差问题是按条件平差法进行的，其法方程式为：⎥⎦⎤⎢⎣⎡--42210⎥⎦⎤⎢⎣⎡21k k +⎥⎦⎤⎢⎣⎡66=0试求：（1）单位权中误差0m ；（2）若已知某一平差函数式L f F t ˆ=，并计算得[]p ff /=44，[]p af /=16，[]p bf /=4，试求该平差值函数的权倒数F p /1及其中误差F m 。

3.5 有三角网（如图3.5），其中B 、C 为已知点，A 、D 、E 为待定点，观测角i L （i =1，2，…，10），（1）试写出AD 边的权函数式； （2）设观测值同精度，且E Q LL =，已知方位角BC a 无误差，试求平差后BE a 的权倒数。

3.6 试按条件平差法求证在单一水准路线（如图3.6）中，平差后高程最弱点在水准路线中央。

3.7 已知条件式为0=+W AV ,其中AL W =，观测值协因数阵为1-=P Q LL ，现有函数式)(V L f F T +=，（1） （1） 试求：FF Q ；（2） （2） 试证： V 和F 是互不相关的。

3.8 有独立测边网（如图3.8），边长观测值列于下表。

试按条件平差法求出改正数i S V 以及边长平差值。

（已知E Q S =）。

表3.8。

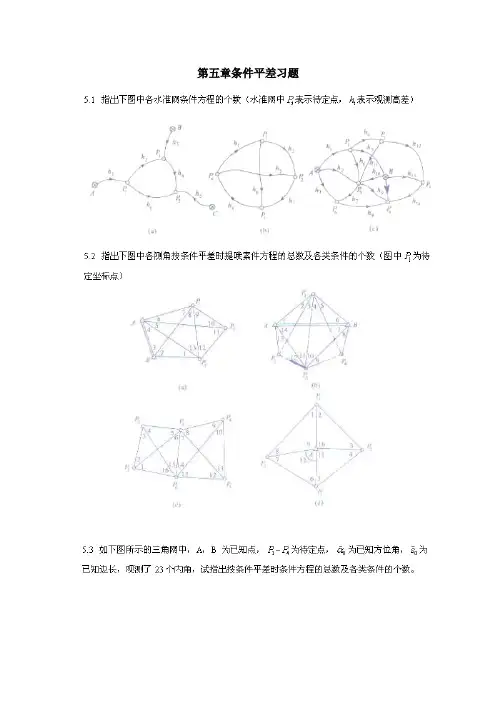
第五章条件平差习题第五章思考题参考答案5.1（a）n=6，t=3，r=3（b）n=6，t=3，r=3（c）n=14，t=5，r=95.2（a）n=13，t=6，r=7共有7个条件方程，其中有5个图形条件，2个极条件。

（b）n=14，t=8，r=6共有6个条件方程，其中有3个图形条件，3个极条件。

（c）n=16，t=8，r=8共有8个条件方程，其中有6个图形条件，2个极条件。

（d）n=12，t=6，r=6共有6个条件方程，其中有4个图形条件，1个圆周条件，1个极条件。

5.3n=23，t=6，r=17共有17个条件方程，其中有9个图形条件，1个圆周条件，1个固定角条件，1个固定边条件，5个极条件。

5.4 （1）n=22，t=9，r=13：7个图形条件，1个圆周条件，2个极条件，2个边长条件，一个基线条件。

（2）12837941314121520111718195610166101119910111213510ˆˆˆ1800ˆˆˆ1800ˆˆˆ1800ˆˆˆ1800ˆˆˆˆ1800ˆˆˆˆ1800ˆˆˆˆ1800ˆˆˆˆˆ1800ˆˆˆsin sin sin L L L L L L L L L L L L L L L L L L L L L L L L L L L L L L L L ++-=++-=++-=++-=+++-=+++-=+++-=++++-=171961116203614184715192211151217121318124ˆsin 1()ˆˆˆˆsin sin sin sin ˆˆˆˆsin sin sin sin 1()ˆˆˆˆsin sin sin sin ˆˆ()ˆˆˆˆsin sin sin sin ˆˆ(ˆˆˆˆsin sin sin sin FG FG L L L L L L L L L L L L L S S S S L L L L S S L L L L ===→=以大地四边形中心为极以中点四边形D 点为极的边长条件1213611891719ˆˆ)ˆˆˆˆsin sin sin sin ˆˆˆˆsin sin sin sin FG AB S S L L L L S S L L L L →=的边长条件（基线条件）5.5 n=8，t=4，r=4；有多种条件方程的列法，其中之一为：1001000100110000120001001104000011014V ⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥-=⎢⎥⎢⎥--⎢⎥⎢⎥---⎣⎦⎣⎦（注意常数项单位为mm ） 5.6 （1）P=3/2，（2）P=15.7 （1）P B =1.6，P C =2.1，P D =2.1，P E =1.6（2）P hCD =1.85.8 []ˆ 2.4998 1.9998 1.3518 1.8515h=2P σ=0.32(mm)5.9 1234561110009100110900101016V V V V V V ⎡⎤⎢⎥⎢⎥-⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥+=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎢⎥⎢⎥⎢⎥⎣⎦ []045452TV mm =---[]ˆ 1.576 2.219 3.7950.867 2.443 1.352T h m =--- 5.10 （1）1ˆ10.3556h m = 2ˆ15.0028h m = 3ˆ20.3556h m = 4ˆ14.5008h m =5ˆ 4.6472h m = 6ˆ 5.8548h m = 7ˆ10.5020h m =（2）±2.2mm。

第五章条件平差§5-1条件平差原理条件平差中求解的未知量是什么?能否由条件方程直接求得5. 1. 02 设某一平差问题的观测个数为n.必要观测数为t，若按条件平差法进行平差，其条件方程、法方程及改正数方程的个数各为多少?5. 试用符号写出按条件平差法平差时，单一附合水准路线中(如图5-1所示)各观测值平差值的表达式。

图5-15. 1. 04 在图5-2中，已知A ,B的高程为Ha = m , Hb=11. 123m,观测高差和线路长度为:图5-2S1=2km,S2=Ikm,S3=,h1=,h2= m,h3= m，求改正数条件方程和各段离差的平差值。

在图5-3的水准网中，A为已知点B、C、D为待定点，已知点高程HA=,观测了5条路线的高差:h1=，h2=0. 821 m，h3=，h4=，h5= m。

各观测路线长度相等，试求:（1）改正数条件方程;(2)各段高差改正数及平差值。

有水准网如图5-4所示，其中A、B、C三点高程未知，现在其间进行了水准测量，测得高差及水准路线长度为h1=1 .335 m，S1=2 km;h2= m，S2=2 km;h3= m，S3=3km。

试按条件平差法求各高差的平差值。

如图 5-5 所示，L1=63°19′40″，=30″；L2=58°25′20″,=20″；L3=301°45′42″，=10″.(1)列出改正数条件方程;(2)试用条件平差法求∠C的平差值(注: ∠C是指内角)。

5-2条件方程5. 对某一平差问题，其条件方程的个数和形式是否惟一?列立条件方程时要注意哪些问题?如何使得一组条件方程彼此线性无关?. 10 指出图5-6中各水准网条件方程的个数(水准网中P i表示待定高程点，h i表示观测高差)。

(a) (b)图5-65. 2. 11指出图5-7中各测角网按条件平差时条件方程的总数及各类条件的个数(图中P i 为待定坐标点)。

误差理论与测量平差(专升本)阶段性作业3试卷总分：100分单选题1. 某一平差问题，有12个同精度观测值，必要观测数t=6，现选取2个独立参数进行平差，应列出的条件方程的个数为_______(4分)(A) 6(B) 8(C) 10(D) 12参考答案：B2. 条件平差中，若令，则= _______ 。

(4分)(A)(B)(C)(D)参考答案：B3. 条件平差中，已知，，则_______。

(4分)(A)(B)(C) 8(D) 4参考答案：A4. 具有参数的条件平差模型中，要求、、满足________。

(4分)(A)(B)(C)(D)参考答案：A5. 条件平差的法方程等价于_______ 。

(4分)(A)(B)(C)(D)参考答案：C6. 在利用条件平差法列测角网的条件方程时，下列哪个条件不属于测角网的基本条件方程的类型_______。

(4分)(A) 图形条件(B) 圆周条件(C) 极条件(D) 余弦条件参考答案：D7. 参数平差中，若系数阵列降秩，则参数解有_______。

(4分)(A) 唯一解(B) 无解(C) 无定解(D) 只有0解参考答案：C8. 若代表必要观测数，r代表多余观测数，n代表总观测数，则条件平差中，误差方程和法方程的个数分别是_______。

(4分)(A) r、r(B) n、t(C) r、t(D) t、r参考答案：A9. 在条件平差法中，对于平差值，闭合差，联系数与改正数的关系描述中，下列式子成立的是_______。

(4分)(A) 、(B) 、(C) 、(D) 、参考答案：C10. 无论平差前定权时单位权中误差怎么选取，条件平差中下列哪组量均不会改变_______。

(4分)(A) 、、(B) 、、(C) 、、(D) 、、参考答案：D判断题11. 若，则。

_____(4分) 正确错误参考答案：错误解题思路：12. 条件平差中，为幂等阵。

_____(4分)正确错误参考答案：正确解题思路：13. 对于同一个平差问题，间接平差和条件平差的结果有可能出现显著差异。

一、填空题：1、观测条件由观测仪器、____________和_____________三部分构成。

2、观测误差按其性质的不同可分为系统误差和偶然误差，其中____________误差在观测或计算过程中可以采用一定的措施消除或削弱，而___________误差在观测结果中必然存在。

3、测量平差的首要任务是经过数据处理，确定观测值的________________，而__________________________________________也是其必不可少的任务。

4、偶然误差的统计规律性是指：界限性、_______性、_______性和_______性。

5、在某相片上量得一距离长为200㎝，其相对中误差为1/3000,则该距离的绝对中误差为_____________________㎝。

6、测量平差是在______________的基础上利用_______________原理进行的。

7、单位权中误差mo、权Pi和中误差mi之间的关系为_______________________。

8、有一四边形导线环，同精度观测其各内角，共观测5组结果，计算出5个闭合差为﹣8″、9″、7″、﹣5″、-7″，则每组观测值之和中误差为____________，每个导线角观测值中误差___________。

（保留一位小数）9、设某角度观测值的协因数为3，则其观测值的权为_________。

10、观测成果的质量高低__________（能、否）反映观测条件的好坏。

11、理论上我们取3倍中误差为极限误差；而等级控制测量因为观测的精度要求比较高，往往规定______倍中误差为极限误差12、衡量精度常用的几种指标有中误差、___________误差和__________误差。

13、精度是指误差分布的________________程度。

14、由三角形闭合差ω计算测角中误差mβ的公式为______________________。

1.1 观测条件是由哪些因素构成的？它与观测结果的质量有什么联系？1.2 测量误差分为哪几类？它们各自是怎样定义的？对观测成果有何影响？ 1.3 何谓多余观测？测量中为什么要进行多余观测？1.4 测量平差的任务是什么？带有系统误差的观测值能否参加平差？2.1 观测量的真值i L ~及真误差i ∆各是怎样定义的？它们与观测值i L 之间有怎样的关系？ 2.2 在相同的观测条件下，大量的偶然误差呈现出什么样的规律性？2.3 偶然误差∆服从什么分布？它的数学期望与方差各是多少？2.4 何谓精度？通常采用哪几种衡量精度的指标？它们各自是怎样定义的？2.5 在相同的观测条件下，对同一个量进行了若干次观测，这些观测值的精度是否相同？在相同的观测条件下所测得的观测值，能否理解为误差小的观测值一定比误差大的观测值的精度高？2.6 为什么通常采用中误差作为衡量精度的标准？它的几何意义是什么？ 2.7 什么是极限误差？它的理论依据是什么？2.8 已知两段距离的长度及其中误差为300.465m ±4.5cm ，660.894m ±4.5cm ，试说明这两个长度的真误差是否相等？它们的最大限差是否相等？它们的精度是否相等？它们的相对精度是否相等。

2.9 有一段距离，其观测值及中误差为345.675m ±15mm ，试估计这个观测值误差的实际可能范围是多少？并求出该观测值的相对中误差？3.1 协方差传播律是用来解决什么问题的？3.2 相关观测值向量1,n X 的协方差阵是怎样定义的？试说明nn xx D ,中各个元素的含义。

当向量1,n X 中的各个分量是两两互相独立时，其协方差阵有什么特点？3.3 已知观测值21,L L 的中误差,21σσσ==协方差012=σ。

设2112-=5+2=L L Y L X ,，Y X T L L Z +==21,，试求X 、Y 、Z 、T 的中误差。

3.4 已知独立观测值21,L L 的中误差为1σ和2σ，试求下列函数的中误差： （1）212L L X -= （2）212121L L L Y +=（3）)sin(/sin 211L L L Z += 3.5 已知观测值向量1,31,21,321,,n n n L L L 及其协方差阵为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡332322131211D D D D D D 对称, 组成函数⎪⎩⎪⎨⎧+=+=+=030201C CL Z B BL Y A AL X式中A,B,C 为系数阵，000C B A ,,为常数阵。

第一章 习题参考答案 1题.略2题.解 (1)222194σσ+（2）2221212219)3(σσL L L +-(3) 222212211212212211211")(cos )sin(sin ")(cos )sin(sin )cos(cos σρσρ⎪⎪⎭⎫ ⎝⎛+++⎪⎪⎭⎫ ⎝⎛++++L L L L L L L L L L L L L 3题. 解TT TLL XY LL YL LL XL B A AD D BAD D AD D ===,,4题.解 设路线总长S 公里，按照测量学上的附合路线计算步骤，则路线闭合差B A h H h h H f -++=21由于是路线中点，故()B A h H h h H f v v -++-===21212121 则线路中点高程()()B A B A B A A A H H h h H H h h H h h H h H v h H H ++⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-=++-=-++-+=-+=2121212121212121ˆ212121111中点设每公里高差观测中误差为0σ，则021)2/(σσσs h h ==按误差传播定律)(16,10425)52/(41)52/(41)2/(41)2/(414141212100212122220202222ˆ21121km S S s s s s h h h h H ≤≤=⋅⨯+⋅⨯=⨯+⨯=+=⎪⎪⎪⎪⎭⎫⎝⎛-⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-=σσσσσσσ中点5.解 设每个测回的中误差为0σ，需要再增加n 个测回，则)2(2028.0,28.020)1(2042.0,42.0200000+±=±=+±=±=n n σσσσ由上式可解出n.即252023202028.042.020222=-⎪⎭⎫ ⎝⎛⨯=-⨯=n 再增加25个测回6题.解[][][][][][][][][]][][][,100010001...,...)...(2121211212122111⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎣⎡⎥⎦⎤==⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎢⎣⎡⎥⎦⎤=+++==p p p p p p p p p P p P p P p Q L L L P p P p P p L p L p L p x n n n p xx n n n n p p pL x][][][][][][p p p p p p p p p p p p p p p nnn⋅⋅++⋅⋅+⋅⋅=1 (1)12221117题。

1.误差来源，测量平差的任务，多余观测的目的。

2.试用公式说明方差协方差阵与协因数阵之间的关系协因数阵与权阵之间的关系在什么情况下它们为对角矩阵若协因数阵为单位阵表示什么意思3.已知随机变量y、z都是观测值L=[L1、L2、L3]T的函数，函数关系如下：2 1 0y L1 4L2 3L3 ”y ，已知Q LL 1 3 2，证明y、z间互不相关。

z 7L1 10L2 16L30 2 44.已知间接平差的模型为V=BX-L,已知观测值的中误差为Q L L，试推导Q V。

5.已知独立观测值L l,L2的中误差为6 1和6 2,试求下列函数的中误差：(1)X L1 2L2(2)Y g L1L226.某平差问题有15个同精度观测值，必要观测数为8,现选取8个参数，且参数之间有2个限制条件。

若按附有限制条件的条件平差法进行平差，应列出多少个条件方程和限制条件方程由其组成的法方程有几个7.在相同条件下，观测两个角度？A=30?00?00?, ?B=75?00?00?，设对?A观测6个测回的权为1,问观测?B 9个测回的权为多少8.在相同观测条件下，应用水准测量测定点A—B—C—D之间的高差，设路线长度分别为S=2km, S=4km, S3=6km,令12km的高差观测值权为单位权观测，设每公里观测高差中误差为，试求各段观测高差之权及单位权中误差。

9.取一长度为d的直线之丈量结果的权为1，则长度为D的直线之丈量结果的权为多少若长度为D的直线丈量了n次，则其算术平均值的权为多少。

10.已知一水准网如下图，其中A B为已知点，观测了8段高差，若设E点高程的平差值与B、E之间高差的平差值为未知参数刃1、刃2，按附有限制条件的条件平差法(概括平差法)进行平差时，必要观测个数为 ____________ ,多余观测个数为 _________ ，一般条件方程个数为 ____________ ，限制条件方程个数为 ___________C11.在已知水准点A B (其搞成无误差)间布设设水准线路，如图所示。

测量平差第五章条件平差习题参考答案测量平差第五章思考题参考答案5.1 （a ）n=6，t=3，r=3（b ）n=6，t=3，r=3（c ）n=14，t=5，r=95.2 （a ）n=13，t=6，r=7共有7个条件方程，其中有5个图形条件，2个极条件。

（b ）n=14，t=8，r=6共有6个条件方程，其中有3个图形条件，3个极条件。

（c ）n=16，t=8，r=8共有8个条件方程，其中有6个图形条件，2个极条件。

（d ）n=12，t=6，r=6共有6个条件方程，其中有4个图形条件，1个圆周条件，1个极条件。

5.3 n=23，t=6，r=17共有17个条件方程，其中有9个图形条件，1个圆周条件，1个固定角条件，1个固定边条件，5个极条件。

5.4 （1）n=22，t=9，r=13：7个图形条件，1个圆周条件，2个极条件，2个边长条件，一个基线条件。

（2）128379413141215201117181956101661011199101112135101800180018001800?1800?1800?18001800???sin sin sin L L L L L L L L L L L L L L L L L L L L L L L L L L L L L L L L ++-=++-=++-=++-=+++-=+++-=+++-=++++-= 171961116203614184715192211151217121318124sin 1()sin sin sin sin sin sin sin sin 1()sin sin sin sin ??()sin sin sin sin ??(sin sin sin sin FG FG L L L L L L L L L L L L L S S S S L L L L S S L L L L ===→=以大地四边形中心为极以中点四边形D 点为极的边长条件1213611891719)sin sin sin sin sin sin sin sin FG AB S S L L L L S S L L L L →=的边长条件（基线条件）5.5 n=8，t=4，r=4；有多种条件方程的列法，其中之一为：1001000100110000120001001104000011014V -??? -=-----（注意常数项单位为mm ） 5.6 （1）P=3/2，（2）P=15.7 （1）P B =1.6，P C =2.1，P D =2.1，P E =1.6（2）P hCD =1.85.8 []? 2.4998 1.9998 1.3518 1.8515h=2P σ=0.32(mm) 5.9 1234561110009100110900101016V V V V V V-+=??--????[]045452TV mm =---[]? 1.576 2.219 3.7950.867 2.443 1.352T h m =--- 5.10 （1）1?10.3556h m = 215.0028h m = 3?20.3556h m = 414.5008h m =5? 4.6472h m = 6? 5.8548h m = 7?10.5020h m = （2）±2.2mm。

平差习题集一、 单项选择1．取一长为d 的直线之丈量结果的权为 1，则长为D 的直线之丈量结果的权D P =（ ）。

a) D d b) d D c) 22D d d) 22dD 2.有一角度测 20 测回，得中误差±0.42 秒，如果要使其中误差为±0.28秒，则还需增加的测回数N=（ ）。

a) 25 b) 20 c) 45 d) 5 3.某平面控制网中一点P ，其协因数阵为：⎢⎣⎡⎥⎦⎤=YY YX XY XX XXQ Q Q Q Q =⎢⎣⎡⎥⎦⎤--5.025.025.05.0 单位权方差20σ =±2.0。

则P 点误差椭圆的方位角 T=（ ）。

a) 90 b) 135 c) 120 d) 454.设L 的权为1，则乘积4L 的权P=（ ）。

a) 1/4 b) 4 c) 1/16 d) 16 5.设⎢⎣⎡⎥⎦⎤21y y ＝⎢⎣⎡⎥⎦⎤⎢⎣⎡⎥⎦⎤--213112x x ；⎢⎣⎡⎥⎦⎤=4113XX D ,设F = y2+ x1，则2F m =（ ）。

a) 9 b) 16 c) 144 d) 36二．填空题1.测量平差遵循的原则为 。

2.条件平差中，利用法方程计算单位权中误差的公式为 。

3.条件方程列立的原则为 、 、 。

4.间接平差的函数模型为 ，随机模型为 。

5.在间接平差中，计算V T PV 有 、 两种方法。

6.在间接平差中, X X Q ˆˆ x xQ ˆˆ，Q LL Q ll 。

7. 水准网的间接平差中，常令 为参数，而平面控制网中常令 为参数。

8.水平角观测中，对某角用测回法等精度观测了3测回，其观测值分别为60°00′00″、60°00′01″、59°59′59″，则该角的最或是值为 ，观测值的中误差为 ，最或是值的中误差为 。

9.测边网的误差方程式为 ，若列此方程，需先行计算出 。

10．若待定点的极大位差和极小位差分别为 3.0dm 、4.0dm ，则该点的点位差为 ；若=135°28′00″，另有AP 方向=180°28′00″，则AP 方向的 值为 ，该方向的位差为 ；若S AP =1km ，则该方向的方位角中误差为 。