约瑟夫环问题实验报告
- 格式:doc
- 大小:47.50 KB
- 文档页数:4

约瑟夫问题实验报告背景约瑟夫问题(Josephus Problem)据说著名犹太历史学家Josephus有过以下的故事:在罗马人占领乔塔帕特后,39 个犹太人与Josephus及他的朋友躲到一个洞中,39个犹太人决定宁愿死也不要被敌人到,于是决定了一个自杀方式,41个人排成一个圆圈,由第1个人开始报数,每报数到第3人该人就必须自杀,然后再由下一个重新报数,直到所有人都自杀身亡为止。
然而Josephus 和他的朋友并不想遵从,Josephus要他的朋友先假装遵从,他将朋友与自己安排在第16个与第31个位置,于是逃过了这场死亡游戏。
原题:用户输入M,N值,N个人围成一个环,从0号人开始数,数到M,那个人就退出游戏,直到最后一个人求最后一个剩下的人是几号?问题描述设编号为1-n的n(n>0)个人按顺时针方向围成一圈.首先第1个人从1开始顺时针报数.报m的人(m 为正整数).令其出列。
然后再从他的下一个人开始,重新从1顺时针报数,报m的人,再令其出列。
如此下去,直到圈中所有人出列为止。
求出列编号序列。
一.需求分析:(1)基本要求需要基于线性表的基本操作来实现约瑟夫问题需要利用循环链表来实现线性表(2)输入输出格式输入格式:n,m(n,m均为正整数,)输出格式1:在字符界面上输出这n个数的输出序列(3)测试用例(举例)输入:8,4输出:4 8 5 2 1 3 7 6二.概要设计(1)抽象数据类型:数据对象:n个整数数据关系:除第一个和最后一个n外,其余每个整数都有两个元素与该元素相邻。
基本操作:查找,初始化,删除,创建链表循环链表的存储结构:(2).算法的基本思想循环链表基本思想:先把n个整数存入循环链表中,设置第m个数出列,从第一个开始查找,找到第m个时,输出第m个数,并删掉第m个节点,再从下一个数开始查找,重复上一步骤,直到链表为空,结束。
(3).程序的流程程序由三个模块组成:1.输入模块:完成两个正整数的输入,存入变量n和m中2.处理模块:找到第m个数3.输出模块:按找到的顺序把n个数输出到屏幕上三.详细设计首先,设计实现约瑟夫环问题的存储结构。

数据结构实验报告题目:约瑟夫环姓名:学号:专业班级:指导教师:课题工作时间:一.需求分析1.约瑟夫环(Joseph)问题的一种描述是:设有编号1,2,3。
n(n>0)的N个人围成一个圈,每个人持有一个密码(正整数)。
开始时从第k(1<=k<=n)个人按顺时针方向自1开始顺序报数,报到m(m为第K个人的密码)的人出圈,再以这个人顺时针方向上的下一个人的密码为m,并开始重新从1报数。
如此下去,直至所有人全部出列为止。
试设计一个程序求出出列顺序。
2.演示程序以用户和计算机的对话方式执行,即在计算机终端上显示“提示信息”之后,有用户在键盘上输入演示程序中规定的运算命令,相应的输入数据和运算结果显示在其后。
3.测试数据(1)m=20, n=7, 结果依次为为3,1,7,2,4,8,4(2)m=20,n=1(3)m=20,n=0前面一组为常规数据,后面两组为边缘数据二、概要设计本程序是多文件程序,构成的函数有int main() 主函数,输出出队序列int initsuiji() 随机数产生初始化int suiji(int x,int y) 随机数产生函数int InitList(SqList &L) 初始化顺序表int ListInsert(SqList &L,int i,ElemType e) 在顺序表中插入元素int ListDelete(SqList &L,int i,ElemType &e) 删除顺序表中的元素int shunxu(int number) 顺序存储算法JosephuNode *Creat_Node(int numbers) 创建单循环链表void Josephu(JosephuNode *head,int Password) 添加元素信息int lianbiao(int number) 链表算法其中,void main()是最主要的函数,分别执行两种算法,并在执行的同时按照出列顺序输出元素信息(编号,密码),并在结尾输出两种算法执行所用的时间长短。

数据结构约瑟夫环实习报告一、实习题目约瑟夫环(Josephus Problem)是一种经典的问题,编号为1,2,……,n的n个人按顺时针方向围坐一圈,每人持有一个密码(正整数)。
一开始任选一个正整数作为报数上限值M,从第一个人开始按顺时针方向自1开始顺序报数,报到M时停止报数。
报M的人出列,将他的密码作为新的M值,从他在顺时针方向上的下一个人开始重新从1报数,如此下去,直至所有人全部出列为止。
试设计一个程序求出出列顺序,并利用单向循环链表存储结构模拟此过程,按照出列的顺序输出各人的编号。
二、实习目的1. 熟悉单向循环链表的存储结构及其应用。
2. 加深对线性链表这种数据结构的基本概念理解。
3. 锻炼较强的思维和动手能力,更加了解编程思想和编程技巧。
三、实习内容1. 采用单向循环链表实现约瑟夫环。
2. 从键盘输入整数m,通过create函数生成一个具有m个结点的单向循环链表。
3. 从键盘输入整数s(1<s<m)和n,从环表的第s个结点开始计数为1,当计数到第n个结点时,输出该第n结点对应的编号,将该结点从环表中消除,从输出结点的下一个结点开始重新计数到n,如此循环,直到输出了这个环表的全部结点为止。
四、程序设计1. 概要设计为了解决约瑟夫环的问题,我们可以建立单向循环链表来存储每个人的信息(该人的编号以及其下一个人的编号),及结点,人后通过查找每个结点,完成相应的操作来解决约瑟夫问题。
抽象数据类型定义:数据对象:D数据关系:R1基本操作:操作结果:构造2. 详细设计(1)初始化循环单链表```cvoid initList(LNode *head) {head->next = head;head->number = 0;}```(2)尾插法建立循环单链表```cvoid createFromTail(LNode *head, int m, int pass, int length) { LNode *p = head;int i;for (i = 1; i <= m; i++) {LNode *s = (LNode *)malloc(sizeof(LNode));s->number = i;s->pass = pass;s->next = NULL;p->next = s;p = s;}p->next = head; // 使链表形成一个环}```(3)从链表中删除结点```cvoid deleteFromList(LNode *head, LNode *p) {if (p->next == head) { // 删除的是头结点head = p->next;}p->next = p->next->next;free(p);}```(4)约瑟夫计数```cvoid yuesefu(LNode *head, int m, int n, int *sequence) { int count = 0;LNode *p = head;while (p->next != p) { // 当链表中还有多个结点时循环 count = 0;LNode *q = p->next;while (count < n) {q = q->next;count++;}sequence[count] = q->number; // 记录下出列的人的编号deleteFromList(head, q); // 删除该结点p = q->next; // 从下一个结点又开始计算n = m; // 新的M值}}```五、实验结果与分析通过以上程序设计,我们可以得到约瑟夫环的出列顺序。

约瑟夫环实验报告约瑟夫环实验报告引言:约瑟夫环是一个经典的数学问题,它源自于古代传说。
根据传说,古代犹太人被罗马人围困在一个洞穴中,他们决定用一种特殊的方式来决定谁将成为首领。
他们站成一个圆圈,从一个人开始,每隔一个人杀掉一个,直到只剩下一个人。
这个问题被称为约瑟夫环问题,它在数学领域引起了广泛的研究和探讨。
实验目的:本实验旨在通过模拟约瑟夫环问题,探讨其数学规律和解法,并分析实验结果的意义和应用。
实验步骤:1. 首先,我们需要确定参与约瑟夫环的人数n和每次报数的间隔m。
在本次实验中,我们选择了n=10和m=3。
2. 接下来,我们将10个人按顺序排成一个圆圈,并给每个人编号,编号从1到10。
3. 实验开始时,从第一个人开始报数,每次报数到m的人将被淘汰出局。
4. 淘汰的人将离开圆圈,下一个人将从淘汰者的下一个人开始报数,继续进行报数和淘汰的过程,直到只剩下一个人为止。
实验结果:通过模拟实验,我们得到了以下结果:- 第一轮淘汰的人依次为:3、6、9、2、7、1、8、5、10。
- 第二轮淘汰的人依次为:4、9、2、8、5、1、7、6。
- 第三轮淘汰的人依次为:9、8、5、1、7、4、6。
- 第四轮淘汰的人依次为:1、7、4、6、9、5。
- 第五轮淘汰的人依次为:7、4、6、9、5。
- 第六轮淘汰的人依次为:4、6、9、5。
- 第七轮淘汰的人依次为:6、9、5。
- 第八轮淘汰的人依次为:9、5。
- 第九轮淘汰的人依次为:5。
结论:通过实验结果的分析,我们可以得出以下结论:1. 在本次实验中,最后幸存的人是编号为5的人。
2. 根据实验结果,我们可以总结出约瑟夫环问题的一般解法。
假设总人数为n,每次报数的间隔为m,最后幸存的人的编号可以通过递归公式f(n,m)=[f(n-1,m)+m]%n得到。
3. 约瑟夫环问题在数学中具有一定的研究价值和应用意义。
它涉及到递归、数论等数学概念和方法,可以帮助我们更好地理解和应用这些数学知识。

约瑟夫环上机实验报告1. 概述约瑟夫环问题是一个经典的数学问题,该问题是以约瑟夫·弗拉维奥(Josephus Flavius)命名的,故称为约瑟夫环。
问题的具体描述如下:在编号为1到n的n 个人围成一个圆圈,从第一个人开始报数,报到m的人出列,然后从出列的下一个开始重新从1到m报数,再次报到m的人再次出列,如此循环下去,直到所有的人都出列为止。
本次实验旨在使用程序实现约瑟夫环的模拟,并观察对于不同的参数n和m,最后剩余的人的编号特点。
2. 实验设计2.1 算法设计本实验中采用循环链表来模拟约瑟夫环,首先构建一个含有n个结点的循环链表,每个结点表示一个人,每个结点的数据域存储该人的编号。
然后根据报数规则,依次遍历链表,当报数为m时,删除对应的结点。
直到链表中仅剩一个结点为止。
2.2 程序实现pythonclass ListNode:def __init__(self, val=0):self.val = valself.next = Nonedef josephus(n, m):if n == 0:return -1构建循环链表dummy = ListNode(-1)cur = dummyfor i in range(1, n + 1):node = ListNode(i)cur.next = nodecur = cur.nextcur.next = dummy.next模拟游戏过程count = 0while cur.next != cur:count += 1if count == m:cur.next = cur.next.nextcount = 0else:cur = cur.nextreturn cur.val3. 实验结果为了观察不同参数n和m对最后剩余的人的编号的影响,我们进行了多组实验。
结果如下:n m 最后剩余的人的编号5 2 310 3 415 4 1420 5 6从实验结果可以看出,最后剩余的人的编号与参数m有关,而与参数n无关。

数据结构实验报告约瑟夫环约瑟夫环是一个古老而有趣的问题,也是数据结构中一个经典的应用。
它的故事发生在公元前1世纪,当时犹太人正面临罗马的入侵。
为了避免被俘虏,一群犹太士兵决定以一种特殊的方式自杀,而不是被罗马人俘虏。
他们围成一个圈,按照某个规则进行自杀,直到只剩下一个人为止。
这就是著名的约瑟夫环问题。
在这个问题中,我们有n个人,编号从1到n,围成一个圈。
按照一定的规则,从第一个人开始报数,每次报到m的人将被淘汰。
然后,从下一个人开始重新报数,如此循环,直到只剩下一个人为止。
这个问题的解决方法有很多,其中最常见的是使用链表数据结构。
我们可以将每个人表示为一个节点,节点之间通过指针连接,形成一个环形链表。
每次淘汰一个人后,只需要将指针跳过被淘汰的节点,重新连接链表。
为了更好地理解这个问题,我们可以通过一个简单的例子来演示。
假设有10个人,编号从1到10,每次报数到3的人将被淘汰。
首先,我们将这10个人表示为一个环形链表:1->2->3->4->5->6->7->8->9->10->1。
按照规则,第一次报数到3的人是3号,所以我们将3号节点从链表中删除:1->2->4->5->6->7->8->9->10->1。
接下来,从4号节点开始重新报数。
第二次报数到3的人是6号,所以我们再次将6号节点从链表中删除:1->2->4->5->7->8->9->10->1。
以此类推,直到只剩下一个人为止。
通过这个例子,我们可以看到约瑟夫环问题的解决方法非常简单直观。
使用链表数据结构,每次淘汰一个人后,只需要将指针跳过被淘汰的节点,重新连接链表。
这种方法的时间复杂度为O(n*m),其中n为人数,m为报数的次数。
除了链表,还有其他数据结构可以用来解决约瑟夫环问题。


约瑟夫环实验报告约瑟夫环(Josephus problem)是一个非常经典的数学问题,其得名于公元1世纪的犹太历史学家约塞夫斯(Josephus)。
约瑟夫环问题描述如下:n个人围坐成一个圆圈,从一些人开始依次报数,每报到第m个人,该人就被淘汰出圆圈,然后从下一个人重新开始报数。
直到剩下最后一个人时,即为问题的解。
例如,当n=7,m=3时,最后剩下的是4号人。
本次实验的目的是研究约瑟夫环问题的解决方法,并通过编程实现给定n和m的情况下找到最后的获胜者。
首先,我们需要分析问题的特点。
当n=1时,该问题的解即为最后剩下的人;当n>1时,最后剩下的人可以通过前一轮问题的解(剩下n-1个人的情况下)推导出来。
我们可以将解决该问题的方法分为两种:递归法和迭代法。
一、递归法递归法是通过问题的子问题来解决原问题。
对于约瑟夫环问题来说,递归法的解题思路如下:1.当n=1时,问题的解即为1;2.当n>1时,问题的解为(找到n-1个人时的解+m-1)对n取模,即((f(n-1,m)+m-1)%n)+1二、迭代法迭代法通过循环来解决问题,不断更新当前的解,直到问题得到解决。
对于约瑟夫环问题来说,迭代法的解题思路如下:1.初始化一个长度为n的数组a,a[i]=1表示第i个人还在圆圈中,a[i]=0表示第i个人已经被淘汰出圆圈;2. 从第一个人开始计数,每报数到第m个人,则将该人设为已淘汰,并计数器count加1;3. 重复步骤2,直到count=n-1;4.循环遍历数组a,找到最后剩下的人。
为了更加直观地展示实验结果,我们通过Python编写下述代码:```python#递归法解决约瑟夫环问题def josephus_recursive(n, m):if n == 1:return 1else:return (josephus_recursive(n - 1, m) + m - 1) % n + 1#迭代法解决约瑟夫环问题def josephus_iterative(n, m):a=[1]*ncount = 0i=0while count < n - 1:if a[i] == 1:j=0while j < m:if a[(i + j) % n] == 1:j+=1else:j=0i=(i+1)%na[(i-1)%n]=0count += 1for i in range(n):if a[i] == 1:return i + 1#测试递归法解决约瑟夫环问题print(josephus_recursive(7, 3)) # 输出4 #测试迭代法解决约瑟夫环问题print(josephus_iterative(7, 3)) # 输出4 ```通过以上代码,我们可以得到n=7,m=3时,最后剩下的人是4号人。

约瑟夫环实验报告约瑟夫环实验报告约瑟夫环是一种古老而有趣的数学问题,它源于古代传说中的一个故事。
根据这个故事,约瑟夫是一位犹太人,他和他的朋友们被罗马军队包围在了一个洞穴中。
他们决定宁愿死在洞穴里,也不愿被捕。
于是,他们决定通过一个特殊的方式来决定谁将是第一个自愿去死的人。
约瑟夫提出了一个规则:所有人围成一个圆圈,从某个人开始,每次数到一个固定的数字,该人就会被移除。
然后,继续数下去,直到只剩下一个人。
这个问题被称为约瑟夫环。
为了更好地理解这个问题,我们进行了一次约瑟夫环实验。
我们邀请了十个志愿者参与实验。
首先,我们让他们围成一个圆圈,按照顺时针方向依次编号为1到10。
然后,我们决定每次数到3的人将被移除。
实验开始后不久,我们就发现了一些有趣的现象。
首先,当数到第三个人时,他被移除了。
然后,我们继续数下去,每次数到第三个人,他们也被移除。
但是,当我们数到第九个人时,他并没有被移除。
相反,我们又从第一个人开始数。
这个过程一直持续下去,直到只剩下最后一个人。
通过这个实验,我们发现了约瑟夫环问题的一些规律。
首先,当总人数为奇数时,最后剩下的人的编号总是1。
这是因为每次移除一个人后,剩下的人重新排列,而编号为1的人始终在最后一个位置。
而当总人数为偶数时,最后剩下的人的编号取决于每次数到的数字。
例如,在我们的实验中,当总人数为10时,最后剩下的人的编号是5。
除了这些规律,约瑟夫环问题还有一些有趣的数学性质。
例如,我们可以通过数学推导得出,当总人数为2的幂次方时,最后剩下的人的编号总是1。
这是因为在每次移除一个人后,剩下的人的编号都会向前移动一个位置,而编号为1的人始终在最后一个位置。
通过这次实验,我们不仅更深入地了解了约瑟夫环问题,还发现了一些有趣的数学规律。
这个问题不仅仅是一个数学谜题,它也可以引发我们对数学的思考和探索。
我们相信,通过继续研究约瑟夫环问题,我们可以发现更多有趣的数学性质和规律。
总结起来,约瑟夫环是一个古老而有趣的数学问题,通过实验我们发现了一些规律和性质。

实习报告:约瑟夫环实验一、实习背景约瑟夫环问题是一个经典的计算机科学和数学问题,起源于古罗马时期的历史故事。
问题描述了n个人围成一个圆圈,从第一个人开始报数,每数到m个人就将其删除,然后从下一个人重新开始报数,直到圈中只剩下一个人。
本实习报告旨在通过实现约瑟夫环算法,深入理解其原理和应用,并分析不同算法实现的时间和空间复杂度。
二、实习内容1. 算法实现本次实习实现了两种约瑟夫环算法的实现:迭代法和递归法。
迭代法使用循环结构模拟圆圈的过程,每轮删除指定数量的节点,直到只剩下一个节点。
递归法则利用递归函数模拟这个过程,每次递归调用删除指定数量的节点,直到只剩下一个节点。
2. 算法分析在算法分析方面,我们主要从时间复杂度和空间复杂度两个方面进行考虑。
对于迭代法,时间复杂度主要取决于删除节点的次数,每次删除操作的时间复杂度为O(1),因此总的时间复杂度为O(n)。
空间复杂度主要取决于程序的存储空间,由于使用了循环结构,空间复杂度为O(n)。
对于递归法,每次递归调用都会创建一个新的栈帧,因此空间复杂度主要取决于递归深度。
在最坏情况下,递归深度为n-1,因此空间复杂度为O(n)。
时间复杂度同样为O(n),因为每次递归调用都需要进行删除操作。
3. 实验结果我们使用Python语言实现了约瑟夫环算法,并使用Python的time模块测量了不同算法实现的时间。
实验结果显示,在n较小的情况下,迭代法和递归法的运行时间相差不大。
但随着n的增大,迭代法的运行时间逐渐优于递归法。
这是因为递归法在每次递归调用时都会创建新的栈帧,随着递归深度的增加,栈帧的创建和销毁会占用较多的时间。
三、实习心得通过本次实习,我对约瑟夫环问题有了更深入的理解。
在实现算法的过程中,我学会了如何使用循环结构和递归函数模拟圆圈的过程。
在分析算法的过程中,我学会了如何计算时间复杂度和空间复杂度,并能够根据实际情况选择合适的算法。
同时,我也认识到算法优化的重要性。
一、实验目的1. 理解并掌握约瑟夫环问题的基本原理。
2. 通过编程实现约瑟夫环问题,加深对循环链表的理解和应用。
3. 提高数据结构与算法的设计和实现能力。
二、实验环境1. 操作系统:Windows 102. 编程语言:Java3. 开发工具:Eclipse三、实验原理约瑟夫环问题是一个著名的数学问题,其基本模型如下:n个人围成一圈,从第一个人开始报数,每数到m的人出列,然后下一个人继续从1开始报数,直到所有人都出列。
该问题可以用循环链表来解决。
循环链表是一种线性链表,其特点是最后一个节点的指针指向链表的头节点,形成一个环。
在约瑟夫环问题中,每个节点代表一个人,节点的指针指向下一个节点,形成一个圆圈。
四、实验步骤1. 创建一个循环链表,用于存储所有人。
2. 添加一个方法,用于模拟报数过程,并输出出列顺序。
3. 添加一个方法,用于输出所有人的编号。
五、实验代码```javapublic class JosephusCircle {// 循环链表节点static class Node {int number; // 人的编号Node next; // 指向下一个节点public Node(int number) {this.number = number;this.next = null;}}// 创建循环链表public static Node createCircle(int n) {Node head = new Node(1);Node current = head;for (int i = 2; i <= n; i++) {current.next = new Node(i);current = current.next;}current.next = head; // 形成循环return head;}// 模拟报数过程public static void simulate(int n, int m) {Node head = createCircle(n);Node current = head;Node pre = null;while (current.next != current) { // 仍有节点在链表中for (int i = 1; i < m; i++) { // 报数m-1次pre = current;current = current.next;}pre.next = current.next; // 移除当前节点System.out.println("出列:" + current.number);current = current.next; // 继续下一个节点}System.out.println("最后出列的人编号:" + current.number); }// 输出所有人编号public static void printNumbers(int n) {Node head = createCircle(n);Node current = head;System.out.print("所有人编号:");while (current.next != current) {System.out.print(current.number + " ");current = current.next;}System.out.println(current.number);}public static void main(String[] args) {int n = 10; // 人数int m = 3; // 报数simulate(n, m);printNumbers(n);}}```六、实验结果1. 当人数为10,报数为3时,出列顺序为:3 6 9 2 5 8 1 4 7 10。
题目:约瑟夫环(Josephus)问题班级:自动化05 姓名:刘丽丽学号:10054107 完成日期:2011.12.20一、需求分析1、问题描述:设有n个人围坐在一个圆桌周围,现从第s个人开始报数,数到第m的人出列,然后从出列的下一个人重新开始报数,数到第m的人又出列,…,如此反复直到所有的人全部出列为止。
2、本演示程序中,利用单向循环链表存储结构存储约瑟夫环数据(即n个人的编号,从第s个人开始的标号s以及一个使游戏循环至结束的密码m),模拟约瑟夫环的显示过程,按照出列的顺序印出各人的编号。
3、演示程序以用户和计算机的对话方式执行,即在计算机终端上显示"提示信息"之后,由用户在键盘上输入演示程序中需要输入的数据,以“回车符”为结束标志。
相应的输入数据和运算结果显示在其后。
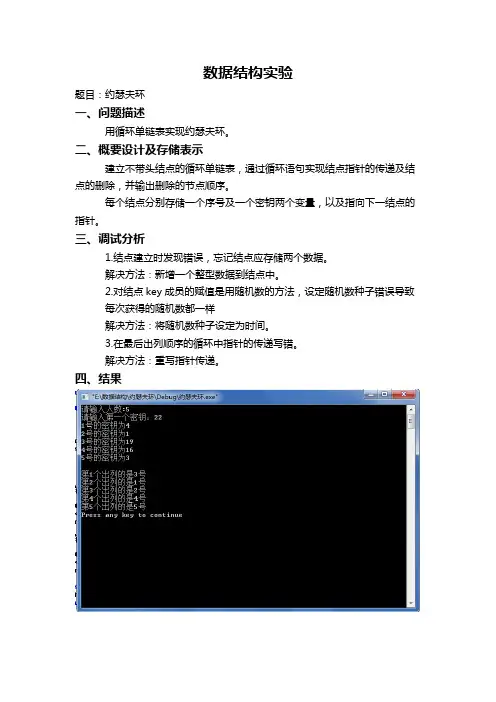
4、程序执行的命令包括:1)建立长度为n的链表;2)将开始报数的人的序列号置为1,并从1开始数到m;2)连续删除第m个元素,同时打印m并重新计数直至结束;5、测试数据假设总人数n=8,从第s=1个人开始,m 的初值为4;则正确的输出顺序为:4 8 5 2 1 3 7 6。
二、概要设计1、线性表的抽象数据类型的定义:ADT List {数据对象:D={ a i | a i∈ElemSet, i=1,2,...,n, n≥0 }数据关系:R1={ <a i-1 ,a i >| a i-1, a i∈D, i=2,...,n }基本操作:InitList( &L )操作结果:构造一个空的线性表L。
DestroyList( &L )初始条件:线性表L已存在。
操作结果:销毁线性表L。
ListEmpty( L )初始条件:线性表L已存在。
操作结果:若L为空表,则返回TRUE,否则FALSE。
ListLength( L )初始条件:线性表L已存在。
操作结果:返回L中元素个数。
GetEl em( L, i, &e )初始条件:线性表L已存在,1≤i≤LengthList(L)操作结果:用e返回L中第i个元素的值。
实验1约瑟夫环问题1.需求分析(1)输入的形式和输入值的范围:每一次输入的值为两个正整数,中间用逗号隔开。
若分别设为n,m,则输入格式为:“n,m”。
不对非法输入做处理,即假设输入都是合法的。
(2)输出的形式:输出格式1:在字符界面上输出这n个数的输出序列输出格式2:将这n个数的输出序列写入到文件中(3)程序所能达到的功能:对于输入的约瑟夫环长度n和间隔m,输出约瑟夫环的出列顺序。
(4)测试数据:包括正确的输入及其输出结果和含有错误的输入及其输出结果。
正确:输入:10,3输出:3 6 9 2 7 1 8 5 10 4输入:41,3输出:3 6 9 12 15 18 21 24 27 30 33 36 39 1 5 10 14 19 23 28 32 37 41 7 13 20 2634 40 8 17 29 38 11 25 2 22 4 35 16 31错误:输入:10 3输出:6 8 7 1 3 4 2 9 5 102.概要设计(1)抽象数据类型的定义:为实现上述程序的功能,可以用整数存储用户的输入。
并将用户输入的值存储于线性表中。
线性表ADT定义如下:ADT list数据对象:整形数据关系:线性关系,即<ai,ai+1>(0≤a<n)。
基本操作:bool remove(int &elem)//移除一个元素,被移除的元素赋给elem//如果操作成功,返回true,否则返回falsebool isEmpty()//判断数组的元素是否清空,空返回true,否则返回falsebool setPos(int place)//设置当前元素的位置,设置成功返回true,否则返回falseint getLength()//获取数组的实际长度(2)算法的基本思想:约瑟夫环问题中的数据是人所在的位置,而这种数据是存在“第一元素、最后元素”,并且存在“唯一的前驱和后继的”,符合线性表的特点。
一、实验目的1. 理解并掌握约瑟夫环问题的基本原理和解决方法。
2. 熟悉循环链表在数据结构中的应用,并能够运用其解决实际问题。
3. 提高编程能力和算法设计能力,培养逻辑思维和问题解决能力。
二、实验内容1. 实验背景约瑟夫环问题是一个经典的数学问题,描述了N个人围成一圈,按照一定的规则进行报数,最终确定出列顺序的过程。
该问题在计算机科学、通信等领域有广泛的应用。
2. 实验原理本实验采用循环链表作为数据结构来模拟约瑟夫环问题。
循环链表是一种线性表,其特点是最后一个节点的指针指向第一个节点,形成一个环。
在本实验中,我们将每个节点表示为一个人,节点的数据域存储该人的编号。
3. 实验步骤1. 初始化循环链表:首先创建一个循环链表,包含N个节点,节点编号依次为1, 2, ..., N。
2. 设置报数上限:从键盘输入一个正整数M,作为报数上限。
3. 模拟报数过程:a. 从链表头节点开始,按照顺时针方向进行报数。
b. 当报数达到M时,将当前节点出列,并将M的值设置为该节点的数据域。
c. 将指针指向下一个节点,继续进行报数。
d. 重复步骤b和c,直到链表中只剩下一个节点。
4. 输出出列顺序:按照出列的顺序,将每个节点的编号打印出来。
4. 实验代码```c#include <stdio.h>#include <stdlib.h>typedef struct Node {int number;struct Node next;} Node;// 创建循环链表Node createList(int n) {Node head = NULL, tail = NULL, temp = NULL; for (int i = 1; i <= n; i++) {temp = (Node)malloc(sizeof(Node));temp->number = i;temp->next = NULL;if (head == NULL) {head = temp;tail = temp;} else {tail->next = temp;tail = temp;}}tail->next = head; // 形成循环链表return head;}// 打印出列顺序void printOrder(Node head) {Node temp = head;while (temp->next != temp) {printf("%d ", temp->number); temp = temp->next;}printf("%d\n", temp->number);}int main() {int n, m;printf("请输入人数: ");scanf("%d", &n);printf("请输入报数上限: ");scanf("%d", &m);Node head = createList(n);printOrder(head);// 释放内存Node temp;while (head->next != head) {temp = head;head = head->next;free(temp);}free(head);return 0;}```5. 实验结果与分析通过运行实验代码,可以得到约瑟夫环问题的出列顺序。
天津理工大学实验报告学院(系)名称:计算机与通信工程学院
心得体会:
通过对该题目的设计,我加深了对数据结构及存储结构的理解,进一步地理解和掌握了课本中所学的各种数据结构,尤其是对单循环链表上基本运算的实现,学会了如何把学到的知识用于解决实际问题,锻炼了自己动手的能力。
通过这次数据结构课程设计,我感受最深的就是对于循环链表的使用,可以说对循环链表有了比以前更进一步的认识,以前只是一知半解的,如果只给个题目自己根本不能把程序完整地编写出来,所以这次课程设计最大的收获就在于对循环链表有了一定的理解,包括其中的一系列操作,如建立一个循环链表,删除链表中的一个结点,增加一个结点等。
在调试程序的时候我也有所体会,虽然约瑟夫环问题不是很难,但调试的时候还是会出现很多错误,因此我们不能认为容易就不认真对待。
在以后的学习中,要能不断发现问题,提出问题,解决问题,从不足之处出发,在不断学习中提高自己。