下载文档原格式
长方体的表面积计算公式长方体是几何学中常见的一个立体图形，它具有六个面，分别为底面、顶面和四个侧面。
要计算长方体的表面积，我们可以使用以下的公式：表面积 = 2(长宽 + 长高 + 宽高)。
在这个公式中，长、宽和高分别代表长方体的三个边长。
通过这个公式，我们可以很容易地计算出长方体的表面积，而不需要进行复杂的几何学运算。
接下来，我们将详细介绍如何使用这个公式来计算长方体的表面积，并且探讨一些与长方体表面积相关的实际问题。
首先，让我们来看一个例子：假设一个长方体的长为5cm，宽为3cm，高为4cm。
我们可以使用上面的公式来计算它的表面积：表面积 = 2(53 + 54 + 34) = 2(15 + 20 + 12) = 2(47) = 94。
因此，这个长方体的表面积为94平方厘米。
通过这个例子，我们可以看到，使用这个公式来计算长方体的表面积非常简单直观。
只需要将长、宽和高代入公式中，然后进行简单的乘法和加法运算，就可以得到长方体的表面积。
除了计算表面积，长方体的表面积还可以帮助我们解决一些实际问题。
例如，在建筑工程中，我们需要计算建筑物的外墙面积，以确定需要多少涂料或者瓷砖。
在包装设计中，我们需要计算包装盒的表面积，以确定需要多少纸张或者包装材料。
在制造业中，我们需要计算产品的表面积，以确定需要多少材料来制造产品。
通过使用长方体的表面积计算公式，我们可以快速准确地解决这些实际问题，从而提高工作效率和减少成本。
此外，长方体的表面积还可以帮助我们理解一些几何学概念。
例如，我们可以通过比较不同长方体的表面积来研究它们的形状和大小。
我们还可以通过改变长、宽和高来探讨表面积的变化规律，从而加深对几何学知识的理解。
总之，长方体的表面积计算公式是一个非常有用的工具，它可以帮助我们计算长方体的表面积，解决实际问题，加深对几何学知识的理解。
希望通过本文的介绍，读者能够更加深入地了解长方体的表面积，并且能够灵活运用这个公式来解决实际问题。
长方体正方体表面积体积公式
长方体和正方体的表面积和体积公式是数学中常用的公式，可以用来计算立体图形的面积和体积。
下面是具体的公式:
长方体表面积公式:S(表面积) = 2(a1a2a3) (其中 a1、a2、a3 分别为长、宽、高)
长方体体积公式:V(体积) = a1a2a3 (其中 a1、a2、a3 分别为长、宽、高)
正方体表面积公式:S(表面积) = 6a2 (其中 a 为正方体的棱长) 正方体体积公式:V(体积) = a3 (其中 a 为正方体的棱长)
其中，a1、a2、a3 分别表示长方体或正方体的一个面的面积，V 表示体积，S 表示表面积，正方体有 6 个面，每个面都是相同的正方形，所以正方体的表面积为 6a2。
长方体和正方体的体积和表面积公式都是用来描述立体图形大
小和形状的公式，可以用来计算立体图形的面积和体积，帮助人们更好地理解和探究数学问题。
长方体和正方体的相关公式1、求长方体的表面积时（6个面）：（长×宽+长×高+宽×高）×22、求长方体的表面积时（5个面）：（长×高+宽×高）×2+长×宽注：这一类题类大致是求：布衣柜、洗衣机或电视机的布罩、抽屉、无盖鱼缸、游泳池、浴池、粉刷房间（记着要扣除门窗的面积）3、求长方体的表面积时（4个面）：（长×高+宽×高）×2注：这类题型通常是求：水管、烟囱、排气管或是在包装盒的四周贴广告等。
4、求特殊长方体（有两个面是正方形）的表面积时（4个面）：长×高（宽）×4或高（宽）×4×长注：这类题型是求：水管、烟囱、排气管或是在包装盒的四周贴广告等。
5、求正方体的表面积（6个面）：边长×边长×66、求正方体的表面积（5个面）：边长×边长×（6-1）注：这类题型通常是求：正方体的鱼缸，就算是题目中没有写无盖，我们也把它看成是5个面，因为鱼缸不可能有盖。
7、长方体的总棱长：（长+宽+高）×4 高=总棱长÷4-（长+宽）长=总棱长÷4-（高+宽）宽=总棱长÷4-（长+高）8、正方体的总棱长：边长×12 边长=总棱长÷12注意：有正方体的题，往往会告诉你总棱长，让你求正方体的表面积，这时我们一定要看清题目，要先求出边长，再求表面积。
※※在做表面积及体积的题时，一定要看情问题中的单位和已知条件的单位，如果不一样，我们可以先计算出结果再换算单位，做到单位统一，还有要注意看清问题，是求总棱长还是求表面积还是求体积。
常考的题有粉刷房间，先求出房间要粉刷的面积，最后再问需要多少涂料。
9、长方体的体积＝长×宽×高正方体的体积＝棱长×棱长×棱长长方体和正方体的体积＝底面积×高高＝体积÷底面积注：把长方体变成正方体的过程中体积不变，表面积改变。
长方体和正方体表面积计算公式长方体和正方体是我们生活中常见的几何体，无论是在建筑、设计、制造还是日常生活中，都有广泛的应用。
在计算长方体和正方体的表面积时，我们需要根据其特定的公式进行计算。
本文将介绍长方体和正方体的表面积计算公式及其应用。
一、长方体表面积计算公式长方体是一种具有六个矩形面的立体几何体，其表面积的计算公式为：长方体表面积 = 2(长×宽 + 长×高 + 宽×高)其中，长、宽、高分别代表长方体的三个边长。
上述公式中，2表示长方体的前后两个面、左右两个面、上下两个面，共六个面，每个面的面积都是长乘宽，因此需要将其相加。
例如，如果一个长方体的长、宽、高分别为3厘米、4厘米、5厘米，则其表面积为：长方体表面积 = 2(3 × 4 + 3 × 5 + 4 × 5) = 2(12 + 15 +20) = 94平方厘米二、正方体表面积计算公式正方体是一种具有六个正方形面的立体几何体，其表面积的计算公式为：正方体表面积 = 6 ×边长其中，边长代表正方体的边长。
上述公式中，6表示正方体有六个面，每个面的面积都是边长的平方，因此需要将其相加。
例如，如果一个正方体的边长为3厘米，则其表面积为：正方体表面积 = 6 × 3 = 6 × 9 = 54平方厘米三、长方体和正方体表面积的应用长方体和正方体的表面积计算公式在实际生活中有广泛的应用。
以下是一些例子：1. 在建筑设计中，建筑师需要计算建筑物的表面积，以确定需要使用的建筑材料的数量和成本。
例如，一个长方体的房间的墙壁和天花板的表面积可以用长方体表面积的公式来计算。
2. 在制造业中，工程师需要计算机器和设备的表面积，以确定需要使用的材料的数量和成本。
例如，一个正方体的箱子的表面积可以用正方体表面积的公式来计算。
3. 在日常生活中，我们可以用长方体和正方体表面积的公式来计算一些日常用品的表面积。
长方体体积和表面积计算公式一、长方体体积计算公式。
1. 公式。
- 长方体体积 = 长×宽×高，用字母表示为V = a× b× h（其中V表示体积，a表示长，b表示宽，h表示高）。
2. 示例。
- 例如一个长方体，长为5厘米，宽为3厘米，高为2厘米。
那么它的体积V = 5×3×2= 30（立方厘米）。
3. 推导过程（简单理解）- 我们可以把长方体看作是由许多个单位小正方体组成的。
长表示沿着一个方向小正方体的个数，宽表示在另一个方向上小正方体的排数，高表示小正方体的层数。
那么总的小正方体个数（也就是长方体的体积）就是长、宽、高这三个数量的乘积。
二、长方体表面积计算公式。
1. 公式。
- 长方体表面积=2×(长×宽 + 长×高+宽×高)，用字母表示为S = 2×(ab + ah+bh)（其中S表示表面积，a表示长，b表示宽，h表示高）。
2. 示例。
- 若长方体长为4厘米，宽为3厘米，高为2厘米。
则表面积S=2×(4×3 +4×2+3×2)- 先计算括号内的值：4×3+4×2 + 3×2=12 + 8+6 = 26（平方厘米）。
- 再乘以2得到表面积S = 2×26 = 52（平方厘米）。
3. 推导过程（简单理解）- 长方体有6个面，相对的面面积相等。
前面和后面的面积都是长×高，左面和右面的面积都是宽×高，上面和下面的面积都是长×宽。
所以表面积就是这六个面的面积之和，也就是2×(长×宽 + 长×高+宽×高)。
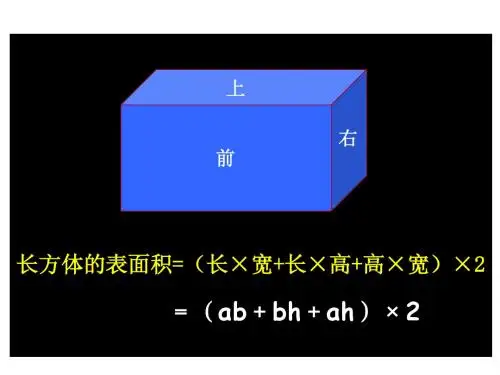
长方体表面积和体积计算公式
长方体是一种常见的几何形状，具有独特的特征和属性。
在数学中，我们经常需要计算长方体的表面积和体积，以便解决各种实际问题。
让我们来看看长方体的表面积计算公式。
长方体的表面积包括所有的外部表面积，即长方体的六个面积之和。
长方体的六个面可以分成三组，每组两个面是相等的。
因此，我们可以使用一个简单的公式来计算长方体的表面积：2×(长×宽 + 长×高 + 宽×高)。
通过这个公式，我们可以轻松计算出长方体的表面积，而无需逐个计算每个面的面积。
接下来，让我们来看看长方体的体积计算公式。
长方体的体积是指长方体所包含的三维空间的大小。
长方体的体积计算公式非常简单，即长×宽×高。
通过这个公式，我们可以很快地计算出长方体的体积，从而帮助我们解决各种涉及空间大小的实际问题。
长方体的表面积和体积计算公式在日常生活和工作中都有着广泛的应用。
比如，当我们需要装载一批长方体形状的物品时，我们可以通过计算长方体的表面积来确定所需的包装材料的数量；当我们需要购买一个长方体形状的容器时，我们可以通过计算长方体的体积来确定容器的大小是否合适。
总的来说，长方体的表面积和体积计算公式是我们在数学中经常会用到的重要知识点。
通过掌握这些公式，我们可以更好地理解长方
体的特征和属性，从而应用到实际问题中去。
希望本文对读者能有所帮助，让大家更加熟练地运用长方体的表面积和体积计算公式。
长方体表面积公式3种
嘿，朋友们！长方体表面积公式有 3 种哦！
第一种公式是：（长×宽+ 长×高+ 宽×高）×2。
比如说有个长方体，长是 5 厘米，宽是 3 厘米，高是 4 厘米，那它的表面积就是（5×3 + 5×4 + 3×4）×2 = (15 + 20 + 12)×2 = (35 + 12)×2 = 94 平方厘米呀，这个
公式是不是很好用呀！
第二种公式呢，就是长×宽×2 + 长×高×2 + 宽×高×2。
就像一个大盒子，长 8 分米，宽 6 分米，高 5 分米，表面积就是8×6×2 + 8×5×2 +
6×5×2 = 96 + 80 + 60 = 236 平方分米，哎呀，一下子就算出来啦！
第三种公式则是底面周长×高 + 长×宽×2。
假设一个长方体底面长方形的长是 7 米，宽是 4 米，高是 6 米，底面周长就是（7 + 4）×2 = 22 米，那表面积就是22×6 + 7×4×2 = 132 + 56 = 188 平方米呢，酷不酷呀！
所以呀，这 3 种长方体表面积公式都很厉害呢，大家学会了吗？是不
是很有趣呀！。
长方体的表面积
（1）前面的面积＝后面的面积＝长×高，
左面的面积＝右边的面积＝宽×高，
上面的面积＝下面的面积＝长×宽。
所以，长方体的表面积＝(前面的面积＋右面的面积＋上面的面积)×2
长方体的表面积＝（长×高＋宽×高＋长×宽）×2
通常我们用字母a表示长，用字母b表示宽，用字母h表示高，用S表示图形的面积。
长方体的表面积是：S＝2（ah＋bh＋ab）。
（2）长方体的表面积=侧面积+底面积×2
侧面积=底面周长×高
长方形的表面积=底面周长×高＋底面积×2
正方体的表面积
正方体的表面积是指围成正方体的6个正方形的面积之和，也就是说，要求一个正方体的表面积，我们只需要求出正方体的一个面的面积，再乘6就可以了。
正方体的表面积＝棱长×棱长×6
通常我们用字母a表示正方体的棱长，用S表示正方体的表面积，所以正方体的表面积是：
S＝6a²。
