相似三角形易错题整理

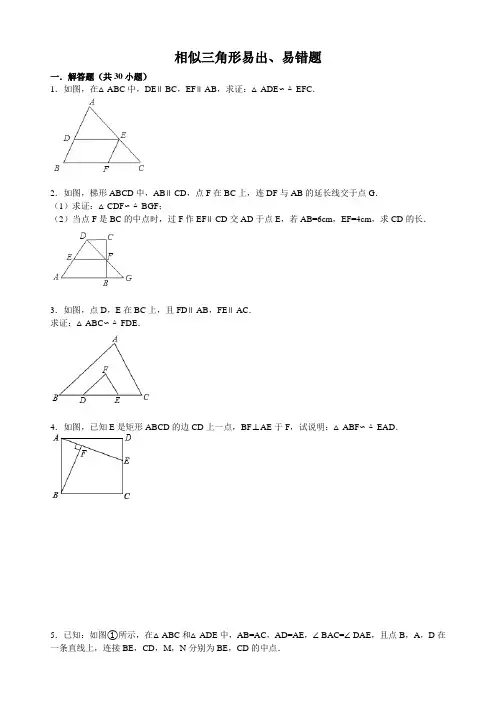
相似三角形易出、易错题一．解答题（共30小题）1．如图，在△ABC中，DE∥BC，EF∥AB，求证：△ADE∽△EFC．2．如图，梯形ABCD中，AB∥CD，点F在BC上，连DF与AB的延长线交于点G．（1）求证：△CDF∽△BGF；（2）当点F是BC的中点时，过F作EF∥CD交AD于点E，若AB=6cm，EF=4cm，求CD的长．3．如图，点D，E在BC上，且FD∥AB，FE∥AC．求证：△ABC∽△FDE．4．如图，已知E是矩形ABCD的边CD上一点，BF⊥AE于F，试说明：△ABF∽△EAD．5．已知：如图①所示，在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE，且点B，A，D在一条直线上，连接BE，CD，M，N分别为BE，CD的中点．（1）求证：①BE=CD；②△AMN是等腰三角形；（2）在图①的基础上，将△ADE绕点A按顺时针方向旋转180°，其他条件不变，得到图②所示的图形．请直接写出（1）中的两个结论是否仍然成立；（3）在（2）的条件下，请你在图②中延长ED交线段BC于点P．求证：△PBD∽△AMN．6．如图，在4×3的正方形方格中，△ABC和△DEF的顶点都在边长为1的小正方形的顶点上．（1）填空：∠ABC=_________°，BC=_________；（2）判断△ABC与△DEC是否相似，并证明你的结论．7．如图，已知矩形ABCD的边长AB=3cm，BC=6cm．某一时刻，动点M从A点出发沿AB方向以1cm/s 的速度向B点匀速运动；同时，动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动，问：（1）经过多少时间，△AMN的面积等于矩形ABCD面积的？（2）是否存在时刻t，使以A，M，N为顶点的三角形与△ACD相似？若存在，求t的值；若不存在，请说明理由．8．如图，在△ABC中，AB=AC=a，M为底边BC上的任意一点，过点M分别作AB、AC的平行线交AC于P，交AB于Q．（1）求四边形AQMP的周长；（2）写出图中的两对相似三角形（不需证明）；（3）M位于BC的什么位置时，四边形AQMP为菱形并证明你的结论．9．已知：P是正方形ABCD的边BC上的点，且BP=3PC，M是CD的中点，试说明：△ADM∽△MCP．10．如图，已知梯形ABCD中，AD∥BC，AD=2，AB=BC=8，CD=10．（1）求梯形ABCD的面积S；（2）动点P从点B出发，以1cm/s的速度，沿B⇒A⇒D⇒C方向，向点C运动；动点Q从点C出发，以1cm/s的速度，沿C⇒D⇒A方向，向点A运动，过点Q作QE⊥BC于点E．若P、Q两点同时出发，当其中一点到达目的地时整个运动随之结束，设运动时间为t秒．问：①当点P在B⇒A上运动时，是否存在这样的t，使得直线PQ将梯形ABCD的周长平分？若存在，请求出t的值；若不存在，请说明理由；②在运动过程中，是否存在这样的t，使得以P、A、D为顶点的三角形与△CQE相似？若存在，请求出所有符合条件的t的值；若不存在，请说明理由；③在运动过程中，是否存在这样的t，使得以P、D、Q为顶点的三角形恰好是以DQ为一腰的等腰三角形？若存在，请求出所有符合条件的t的值；若不存在，请说明理由．11．已知矩形ABCD，长BC=12cm，宽AB=8cm，P、Q分别是AB、BC上运动的两点．若P自点A出发，以1cm/s的速度沿AB方向运动，同时，Q自点B出发以2cm/s的速度沿BC方向运动，问经过几秒，以P、B、Q为顶点的三角形与△BDC相似？12．如图，在△ABC中，AB=10cm，BC=20cm，点P从点A开始沿AB边向B点以2cm/s的速度移动，点Q从点B开始沿BC边向点C以4cm/s的速度移动，如果P、Q分别从A、B同时出发，问经过几秒钟，△PBQ与△ABC相似．13．如图，∠ACB=∠ADC=90°，AC=，AD=2．问当AB的长为多少时，这两个直角三角形相似．14．如图在△ABC中，∠C=90°，BC=8cm，AC=6cm，点Q从B出发，沿BC方向以2cm/s的速度移动，点P从C出发，沿CA方向以1cm/s的速度移动．若Q、P分别同时从B、C出发，试探究经过多少秒后，以点C、P、Q为顶点的三角形与△CBA相似？15．如图所示，梯形ABCD中，AD∥BC，∠A=90°，AB=7，AD=2，BC=3，试在腰AB上确定点P的位置，使得以P，A，D为顶点的三角形与以P，B，C为顶点的三角形相似．16．如图，在矩形ABCD中，AB=15cm，BC=10cm，点P沿AB边从点A开始向B以2cm/s的速度移动；点Q沿DA边从点D开始向点A以1cm/s的速度移动．如果P、Q同时出发，用t（秒）表示移动的时间，那么当t为何值时，以点Q、A、P为顶点的三角形与△ABC相似．17．如图，路灯（P点）距地面8米，身高1.6米的小明从距路灯的底部（O点）20米的A点，沿OA 所在的直线行走14米到B点时，身影的长度是变长了还是变短了？变长或变短了多少米？18．阳光明媚的一天，数学兴趣小组的同学们去测量一棵树的高度（这棵树底部可以到达，顶部不易到达），他们带了以下测量工具：皮尺，标杆，一副三角尺，小平面镜．请你在他们提供的测量工具中选出所需工具，设计一种测量方案．（1）所需的测量工具是：_________；（2）请在下图中画出测量示意图；（3）设树高AB的长度为x，请用所测数据（用小写字母表示）求出x．19．问题背景在某次活动课中，甲、乙、丙三个学习小组于同一时刻在阳光下对校园中一些物体进行了测量．下面是他们通过测量得到的一些信息：甲组：如图1，测得一根直立于平地，长为80cm的竹竿的影长为60cm．乙组：如图2，测得学校旗杆的影长为900cm．丙组：如图3，测得校园景灯（灯罩视为球体，灯杆为圆柱体，其粗细忽略不计）的高度为200cm，影长为156cm．任务要求：（1）请根据甲、乙两组得到的信息计算出学校旗杆的高度；（2）如图3，设太阳光线NH与⊙O相切于点M．请根据甲、丙两组得到的信息，求景灯灯罩的半径．（友情提示：如图3，景灯的影长等于线段NG的影长；需要时可采用等式1562+2082=2602）20．阳光通过窗口照射到室内，在地面上留下2.7m宽的亮区（如图所示），已知亮区到窗口下的墙脚距离EC=8.7m，窗口高AB=1.8m，求窗口底边离地面的高BC．21．如图①，分别以直角三角形ABC三边为直径向外作三个半圆，其面积分别用S1，S2，S3表示，则不难证明S1=S2+S3．（1）如图②，分别以直角三角形ABC三边为边向外作三个正方形，其面积分别用S1，S2，S3表示，那么S1，S2，S3之间有什么关系；（不必证明）（2）如图③，分别以直角三角形ABC三边为边向外作三个正三角形，其面积分别用S1、S2、S3表示，请你确定S1，S2，S3之间的关系并加以证明；（3）若分别以直角三角形ABC三边为边向外作三个一般三角形，其面积分别用S1，S2，S3表示，为使S1，S2，S3之间仍具有与（2）相同的关系，所作三角形应满足什么条件证明你的结论；（4）类比（1），（2），（3）的结论，请你总结出一个更具一般意义的结论．22．已知：如图，△ABC∽△ADE，AB=15，AC=9，BD=5．求AE．23．已知：如图Rt△ABC∽Rt△BDC，若AB=3，AC=4．（1）求BD、CD的长；（2）过B作BE⊥DC于E，求BE的长．24．（1）已知，且3x+4z﹣2y=40，求x，y，z的值；（2）已知：两相似三角形对应高的比为3：10，且这两个三角形的周长差为560cm，求它们的周长．参考答案与试题解析一．解答题（共30小题）1．解答：证明：∵DE∥BC，∴DE∥FC，∴∠AED=∠C．6．如图，在4×3的正方形方格中，△ABC和△DEF的顶点都在边长为1的小正方形的顶点上．（1）填空：∠ABC=135°°，BC=；（2）判断△ABC与△DEC是否相似，并证明你的结论．解答：解：（1）∠ABC=135°，BC=；（2）相似；∵BC=，EC==；∴，；∴；又∠ABC=∠CED=135°，∴△ABC∽△DEC．解：（1）设经过x秒后，△AMN的面积等于矩形ABCD面积的，则有：（6﹣2x）x=×3×6，即x2﹣3x+2=0，（2分）解方程，得x1=1，x2=2，（3分）经检验，可知x1=1，x2=2符合题意，所以经过1秒或2秒后，△AMN的面积等于矩形ABCD面积的．（4分）（2）假设经过t秒时，以A，M，N为顶点的三角形与△ACD相似，由矩形ABCD，可得∠CDA=∠MAN=90°，因此有或（5分）即①，或②（6分）解①，得t=；解②，得t=（7分）经检验，t=或t=都符合题意，所以动点M，N同时出发后，经过秒或秒时，以A，M，N为顶点的三角形与△ACD相似．（8 解：（1）∵AB∥MP，QM∥AC，∴四边形AQMP的周长=AQ+AP+QM+MP=AQ+QB+AP+PC=AB+AC=2a．（2）∵PM∥AB，∴△PCM∽△ACB，∵QM∥AC，∴△BMQ∽△BCA；（3）当点M中BC的中点时，四边形APMQ是菱形，∵点M是BC的中点，AB∥MP，QM∥AC，∴QM，PM是三角形ABC的中位线．∵AB=AC，∴QM=PM=AB=AC．又由（1）知四边形APMQ是平行四边形，∴平行四边形APMQ是菱形．证明：∵正方形ABCD，M为CD中点，∴CM=MD=AD．∵BP=3PC，∴PC=BC=AD=CM．∴．∵∠PCM=∠ADM=90°，∴△MCP∽△ADM．．解解：（1）过D作DH∥AB交BC于H点，∵AD∥BH，DH∥AB，∴四边形ABHD是平行四边形．∴DH=AB=8；BH=AD=2．∴CH=8﹣2=6．∵CD=10，∴DH2+CH2=CD2∴∠DHC=90°．∠B=∠DHC=90°．∴梯形ABCD是直角梯形．∴S ABCD=（AD+BC）AB=×（2+8）×8=40．（2）①∵BP=CQ=t，∴AP=8﹣t，DQ=10﹣t，∵AP+AD+DQ=PB+BC+CQ，∴8﹣t+2+10﹣t=t+8+t．∴t=3＜8．∴当t=3秒时，PQ将梯形ABCD周长平分．②第一种情况：0＜t≤8若△PAD∽△QEC则∠ADP=∠C∴tan∠ADP=tan∠C==∴=，∴t=若△PAD∽△CEQ则∠APD=∠C∴tan∠APD=tan∠C==，∴=∴t=第二种情况：8＜t≤10，P、A、D三点不能组成三角形；第三种情况：10＜t≤12△ADP为钝角三角形与Rt△CQE不相似；∴t=或t=时，△PAD与△CQE相似．③第一种情况：当0≤t≤8时．过Q点作QE⊥BC，QH⊥AB，垂足为E、H．∵AP=8﹣t，AD=2，∴PD==．∵CE=t，QE=t，∴QH=BE=8﹣t，BH=QE=t．∴PH=t﹣t=t．∴PQ==，DQ=10﹣t．Ⅰ：DQ=DP，10﹣t=，解得t=8秒．Ⅱ：DQ=PQ，10﹣t=，化简得：3t2﹣52t+180=0解得：t=，t=＞8（不合题意舍去）∴t=第二种情况：8≤t≤10时．DP=DQ=10﹣t．∴当8≤t＜10时，以DQ为腰的等腰△DPQ恒成立．第三种情况：10＜t≤12时．DP=DQ=t﹣10．∴当10＜t≤12时，以DQ为腰的等腰△DPQ恒成立．综上所述，t=或8≤t＜10或10＜t≤12时，以DQ为腰的等腰△DPQ成立．．解解：设经x秒后，△PBQ∽△BCD，由于∠PBQ=∠BCD=90°，（1）当∠1=∠2时，有：，即；（2）当∠1=∠3时，有：，即，∴经过秒或2秒，△PBQ∽△BCD．．解解：设经过秒后t秒后，△PBQ与△ABC相似，则有AP=2t，BQ=4t，BP=10﹣2t，当△PBQ∽△ABC时，有BP：AB=BQ：BC，即（10﹣2t）：10=4t：20，解得t=2.5（s）（6分）当△QBP∽△ABC时，有BQ：AB=BP：BC，即4t：10=（10﹣2t）：20，解得t=1．所以，经过2.5s或1s时，△PBQ与△ABC相似（10分）．解法二：设ts后，△PBQ与△ABC相似，则有，AP=2t，BQ=4t，BP=10﹣2t分两种情况：（1）当BP与AB对应时，有=，即=，解得t=2.5s（2）当BP与BC对应时，有=，即=，解得t=1s所以经过1s或2.5s时，以P、B、Q三点为顶点的三角形与△ABC相似．．解解：∵AC=，AD=2，∴CD==．要使这两个直角三角形相似，有两种情况：（1）当Rt△ABC∽Rt△ACD时，有=，∴AB==3；（2）当Rt△ACB∽Rt△CDA时，有=，∴AB==3．故当AB的长为3或3时，这两个直角三角形相似．．解解：设经过x秒后，两三角形相似，则CQ=（8﹣2x）cm，CP=xcm，（1分）∵∠C=∠C=90°，∴当或时，两三角形相似．（3分）（1）当时，，∴x=；（4分）（2）当时，，∴x=．（5分）所以，经过秒或秒后，两三角形相似．（6分）．解解：（1）若点A，P，D分别与点B，C，P对应，即△APD∽△BCP，∴=，∴=，∴AP2﹣7AP+6=0，∴AP=1或AP=6，检测：当AP=1时，由BC=3，AD=2，BP=6，∴=，又∵∠A=∠B=90°，∴△APD∽△BCP．当AP=6时，由BC=3，AD=2，BP=1，又∵∠A=∠B=90°，∴△APD∽△BCP．（2）若点A，P，D分别与点B，P，C对应，即△APD∽△BPC．∴=，∴=，∴AP=．检验：当AP=时，由BP=，AD=2，BC=3，∴=，又∵∠A=∠B=90°，∴△APD∽△BPC．因此，点P的位置有三处，即在线段AB距离点A的1、、6处．．解解：以点Q、A、P为顶点的三角形与△ABC相似，①当△ABC∽△PAQ时，，所以，解得：t=6；②当△ABC∽△QAP时，，所以，解得：t=；③当△AQP∽△BAC时，=，即=，所以t=；④当△AQP∽△BCA时，=，即=，所以t=30（舍去）．故当t=6或t=时，以点Q、A、P为顶点的三角形与△ABC相似．．解解：∵∠MAC=∠MOP=90°，∠AMC=∠OMP，∴△MAC∽△MOP．∴，即，解得，MA=5米；同理，由△NBD∽△NOP，可求得NB=1.5米，∴小明的身影变短了5﹣1.5=3.5米．．解解：（1）皮尺，标杆；∴，∴，∴．（7分）．解解：（1）由题意可知：∠BAC=∠EDF=90°，∠BCA=∠EFD．∴△ABC∽△DEF．∴，即，（2分）∴DE=1200（cm）．所以，学校旗杆的高度是12m．（3分）（2）解法一：与①类似得：，即，∴GN=208．（4分）在Rt△NGH中，根据勾股定理得：NH2=1562+2082=2602，∴NH=260．（5分）设⊙O的半径为rcm，连接OM，∵NH切⊙O于M，∴OM⊥NH．（6分）则∠OMN=∠HGN=90°，又∵∠ONM=∠HNG，∴△OMN∽△HGN，∴（7分），又ON=OK+KN=OK+（GN﹣GK）=r+8，∴，解得：r=12．∴景灯灯罩的半径是12cm．（8分）解法二：与①类似得：，即，∴GN=208．（4分）设⊙O的半径为rcm，连接OM，∵NH切⊙O于M，∴OM⊥NH．（5分）则∠OMN=∠HGN=90°，又∵∠ONM=∠HNG，∴△OMN∽△HGN．∴，即，（6分）∴MN=r，又∵ON=OK+KN=OK+（GN﹣GK）=r+8．（7分）在Rt△OMN中，根据勾股定理得：r2+（r）2=（r+8）2即r2﹣9r﹣36=0，解得：r1=12，r2=﹣3（不合题意，舍去），∴景灯灯罩的半径是12cm．（8分）（解解：∵AE∥BD，∴△ECA∽△DCB，∴．∵EC=8.7m，ED=2.7m，∴CD=6m．∵AB=1.8m，∴AC=BC+1.8m，∴，∴BC=4，即窗口底边离地面的高为4m．．解解：设直角三角形ABC的三边BC、CA、AB的长分别为a、b、c，则c2=a2+b2（1）S1=S2+S3；（2）S1=S2+S3．证明如下：显然，S1=，S2=，S3=∴S2+S3==S1；（3）当所作的三个三角形相似时，S1=S2+S3．证明如下：∵所作三个三角形相似∴∴=1∴S1=S2+S3；（4）分别以直角三角形ABC三边为一边向外作相似图形，其面积分别用S1、S2、S3表示，则S1=S2+S3．解：（1）Rt△ABC中，根据勾股定理得：BC==5，∵Rt△ABC∽Rt△BDC，∴==，==，∴BD=，CD=；（2）在Rt△BDC中，S△BDC=BE•CD=BD•BC，∴BE===3．．解解：（1）设=k，那么x=2k，y=3k，z=5k，由于3x+4z﹣2y=40，∴6k+20k﹣6k=40，∴k=2，∴x=4，y=6，z=10．（2）设一个三角形周长为Ccm，则另一个三角形周长为（C+560）cm，则，∴C=240，C+560=800，即它们的周长分别为240cm，800cm．。

（易错题精选）初中数学图形的相似难题汇编含答案(1)一、选择题1．如图，每个小正方形的边长均为1，则下列图形中的三角形（阴影部分）与111A B C ∆相似的是（ ）A ．B ．C ．D ．【答案】B【解析】【分析】 根据相似三角形的判定方法一一判断即可．【详解】解：因为111A B C ∆中有一个角是135°，选项中，有135°角的三角形只有B ，且满足两边成比例夹角相等，故选：B ．【点睛】本题考查相似三角形的性质，解题的关键是学会利用数形结合的思想解决问题，属于中考常考题型．2．如果两个相似正五边形的边长比为1：10，则它们的面积比为（ ）A ．1：2B ．1：5C ．1：100D ．1：10 【答案】C【解析】根据相似多边形的面积比等于相似比的平方，由两个相似正五边形的相似比是1：10，可知它们的面积为1：100．故选：C ．点睛：此题主要考查了相似三角形的性质：相似三角形的面积比等于相似比的平方．3．如图，在Rt △ABC 中，∠ACB ＝90°，∠A ＝60°，AC ＝2，D 是AB 边上一个动点（不与点A 、B 重合），E 是BC 边上一点，且∠CDE ＝30°．设AD ＝x ，BE ＝y ，则下列图象中，能表示y 与x 的函数关系的图象大致是（ ）A ．B ．C ．D ．【答案】C【解析】【分析】 根据题意可得出4,23,AB BC ==4,23,BD x CE y =-=然后判断△CDE ∽△CBD ，继而利用相似三角形的性质可得出y 与x 的关系式，结合选项即可得出答案．【详解】解：∵∠A ＝60°，AC ＝2， ∴4,3,AB BC ==4,23,BD x CE y =-=在△ACD 中，利用余弦定理可得CD 2＝AC 2+AD 2﹣2AC •AD cos ∠A ＝4+x 2﹣2x ， 故可得242CD x x =-+又∵∠CDE ＝∠CBD ＝30°，∠ECD ＝∠DCB （同一个角），∴△CDE ∽△CBD ，即可得,CE CD CD CB= 2223422342yx x x x --+=-+ 故可得： 23343633y x x =-++ 即呈二次函数关系，且开口朝下． 故选C ．【点睛】考查解直角三角形，相似三角形的判定与性质，掌握相似三角形的判定定理与性质定理是4．如图，在ABC ∆中，点D E F 、、分别在边AB AC BC 、、上，// ,//DE BC DF AC ，则下列结论一定正确的是( )A ．DE CE BF AE =B ．AE CE CF BF =C ．AD AB CF AC= D ．DF AD AC AB = 【答案】B【解析】【分析】根据平行线分线段成比例定理，可得B 正确．【详解】解：//DE BC Q ，//DF AC ， ∴AE AD CE BD =，BF BD CF AD =， ∴AE CF CE BF=， 故B 选项正确，选项A 、C 、D 错误，故选：B ．【点睛】本题主要考查平行线分线段成比例，找准对应边是解题的关键．5．如图，点E 是ABCD Y 的边AD 上一点，2DE AE =，连接BE ，交AC 边于点F ，下列结论中错误的是（ ）A ．3BC AE =B ．4AC AF = C ．3BF EF =D ．2BC DE =【解析】【分析】由平行四边形的性质和相似三角形的性质分别判断即可．【详解】解：∵在ABCD Y 中，//AD BC ，AD BC =，∴AEF CBF V :V , ∴AE AF EF CB CF BF ==, ∵2DE AE = ∴332BC DE AE ==，选项A 正确，选项D 错误， ∴133AF AE AE CF CB AE ===，即：3CF AF =， ∴4AC AF =，∴选项B 正确，∴133EF AE AE BF CB AE ===，即：3BF EF =， ∴选项C 正确，故选：D ．【点睛】此题主要考查了平行四边形的性质以及相似三角形的判定与性质，能熟练利用相似三角形对应边成比例是解题关键．6．如图，□ABCD 的对角线AC ，BD 交于点O ，CE 平分∠BCD 交AB 于点E ，交BD 于点F ，且∠ABC ＝60°，AB ＝2BC ，连接OE ．下列结论：①EO ⊥AC ；②S △AOD ＝4S △OCF ；③AC ：BD ＝21：7；④FB 2＝OF •DF ．其中正确的是（ ）A ．①②④B ．①③④C ．②③④D ．①③ 【答案】B【解析】【分析】 ①正确．只要证明EC=EA=BC ，推出∠ACB=90°，再利用三角形中位线定理即可判断． ②错误．想办法证明BF=2OF ，推出S △BOC =3S △OCF 即可判断．③正确．设BC=BE=EC=a ，求出AC ，BD 即可判断．④正确．求出BF ，OF ，DF （用a 表示），通过计算证明即可．【详解】解：∵四边形ABCD 是平行四边形，∴CD ∥AB ，OD=OB ，OA=OC ，∴∠DCB+∠ABC=180°，∵∠ABC=60°，∴∠DCB=120°，∵EC 平分∠DCB ，∴∠ECB=12∠DCB=60°， ∴∠EBC=∠BCE=∠CEB=60°，∴△ECB 是等边三角形，∴EB=BC ，∵AB=2BC ，∴EA=EB=EC ，∴∠ACB=90°，∵OA=OC ，EA=EB ，∴OE ∥BC ，∴∠AOE=∠ACB=90°，∴EO ⊥AC ，故①正确，∵OE ∥BC ，∴△OEF ∽△BCF ，∴12OE OF BC FB == ， ∴OF=13OB ， ∴S △AOD =S △BOC =3S △OCF ，故②错误，设BC=BE=EC=a ，则AB=2a ，3，223(72)a a +， ∴7a ，∴AC ：3a 7217，故③正确，∵OF=137， ∴BF=73a ， ∴BF 2=79a 2，7a•7779⎫=⎪⎪⎝⎭ a 2，∴BF 2=OF•DF ，故④正确，故选：B ．【点睛】此题考查相似三角形的判定和性质，平行四边形的性质，角平分线的定义，解直角三角形，解题的关键是灵活运用所学知识解决问题，学会利用参数解决问题．7．如图，将ABC ∆沿BC 边上的中线AD 平移到A B C '''∆的位置．已知ABC ∆的面积为16，阴影部分三角形的面积9．若1AA '=，则A D '等于（ ）A ．2B ．3C ．4D ．32【答案】B【解析】【分析】 由 S △ABC ＝16、S △A ′EF ＝9且 AD 为 BC 边的中线知 1922A DE A EF S S '∆'∆==，182ABD ABC S S ∆∆== ，根据△DA ′E ∽△DAB 知2A DE ABD S A D AD S ∆∆'⎛⎫=' ⎪⎝⎭，据此求解可得． 【详解】16ABC S ∆=Q 、9A EF S ∆'=，且AD 为BC 边的中线，1922A DE A EF S S ∆∆''∴==，182ABD ABC S S ∆∆==， Q 将ABC ∆沿BC 边上的中线AD 平移得到A B C '''∆，//A E AB ∴'， DA E DAB '∴∆~∆， 则2A DE ABD S A D AD S ∆∆'⎛⎫=' ⎪⎝⎭，即22991816A D A D ⎛⎫== '⎪+⎝⎭'， 解得3A D '=或37A D '=-（舍）， 故选：B ．【点睛】本题主要平移的性质，解题的关键是熟练掌握平移变换的性质与三角形中线的性质、相似三角形的判定与性质等知识点．8．如图，点E是平行四边形ABCD中BC的延长线上的一点，连接AE交CD于F，交BD于M，则图中共有相似三角形(不含全等的三角形)( )对．A．4 B．5 C．6 D．7【答案】B【解析】【分析】由平行四边形的性质可得AD//BC，AB//CD，根据相似三角形的判定方法进行分析，即可得到图中的相似三角形的对数．【详解】∵四边形ABCD是平行四边形，∴AD//BC，AB//CD，∴△ADM∽△EBM，△ADF∽△ECF，△DFM∽△BAM，△EFC∽△EAB，∵∠AFD=∠BAE，∠DAE=∠E，∴△ADF∽△EBA，∴图中共有相似三角形5对，故选：B．【点睛】本题考查平行四边形的性质及相似三角形的判定，平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似；如果两个三角形的两个角分别对应相等（或三个角分别对应相等），那么这两个三角形相似；熟练掌握相似三角形的判定定理是解题关键．9．如图，在四边形ABCD中，BD平分∠ABC，∠BAD=∠BDC=90°，E为BC的中点，AE与BD相交于点F，若BC=4，∠CBD=30°，则DF的长为（）A 235B233C334D435【答案】D【解析】【分析】先利用含30度角的直角三角形的性质求出BD，再利用直角三角形的性质求出DE=BE=2，即：∠BDE=∠ABD，进而判断出DE∥AB，再求出AB=3，即可得出结论．【详解】如图，在Rt△BDC中，BC=4，∠DBC=30°，∴BD=23，连接DE，∵∠BDC=90°，点D是BC中点，∴DE=BE=CE=12BC=2，∵∠DCB=30°，∴∠BDE=∠DBC=30°，∵BD平分∠ABC，∴∠ABD=∠DBC，∴∠ABD=∠BDE，∴DE∥AB，∴△DEF∽△BAF，∴DF DE BF AB＝，在Rt△ABD中，∠ABD=30°，BD=23，∴AB=3，∴23 DFBF＝，∴25 DFBD＝，∴DF=22432355BD=⨯=，故选D．【点睛】此题主要考查了含30度角的直角三角形的性质，相似三角形的判定和性质，角平分线的定义，判断出DE∥是解本题的关键．10．如图，在平面直角坐标系中，已知点A（―3，6）、B（―9，一3），以原点O为位似中心，相似比为，把△ABO缩小，则点A的对应点A′的坐标是（）A．（―1，2）B．（―9，18）C．（―9，18）或（9，―18）D．（―1，2）或（1，―2）【答案】D【解析】【分析】【详解】试题分析：方法一：∵△ABO和△A′B′O关于原点位似，∴△ ABO∽△A′B′O且OA'OA＝13.∴A EAD＝0E0D＝13.∴A′E＝13AD＝2，OE＝13OD＝1.∴A′（－1,2）.同理可得A′′（1,―2）.方法二：∵点A（―3，6）且相似比为13，∴点A的对应点A′的坐标是（―3×13，6×13），∴A′（－1,2）.∵点A′′和点A′（－1,2）关于原点O对称，∴A′′（1,―2）.故答案选D.考点：位似变换.11．如图，在ABC ∆中，,D E 分别是边,AB AC 的中点，ADE ∆和四边形BCED 的面积分别记为12,S S ，那么12S S 的值为（ ）A ．12B ．14C ．13D ．23【答案】C【解析】【分析】根据已知可得到△ADE ∽△ABC ，从而可求得其面积比，则不难求得12S S 的值． 【详解】∵,D E 分别是边,AB AC 的中点，∴DE ∥BC ，∴△ADE ∽△ABC ，∴DE ：BC=1：2， 所以它们的面积比是1：4，所以1211=413S S =-， 故选C ．【点睛】本题考查了三角形的中位线定理和相似三角形的性质：（1）相似三角形周长的比等于相似比；（2）相似三角形面积的比等于相似比的平方；（3）相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比．12．在平面直角坐标系中，已知点E （﹣4，2），F （﹣2，﹣2），以原点O 为位似中心，相似比为，把△EFO 缩小，则点E 的对应点E′的坐标是A ．（﹣2，1）B ．（﹣8，4）C ．（﹣8，4）或（8，﹣4）D ．（﹣2，1）或（2，﹣1）【答案】D【解析】试题分析：根据位似的性质，缩小后的点在原点的同侧，为（-2,1），然后求在另一侧为（2，-1）．故选D考点：位似变换13．如图，点E是矩形ABCD的边AD的中点，且BE⊥AC于点F，则下列结论中错误的是（）A．AF＝12 CFB．∠DCF＝∠DFCC．图中与△AEF相似的三角形共有5个D．tan∠CAD3【答案】D【解析】【分析】由AE=12AD=12BC，又AD∥BC，所以12AE AFBC FC==，故A正确，不符合题意；过D作DM∥BE交AC于N，得到四边形BMDE是平行四边形，求出BM=DE=12BC，得到CN=NF，根据线段的垂直平分线的性质可得结论，故B正确，不符合题意；根据相似三角形的判定即可求解，故C正确，不符合题意；由△BAE∽△ADC，得到CD与AD的大小关系，根据正切函数可求tan∠CAD的值，故D错误，符合题意．【详解】解：A、∵AD∥BC，∴△AEF∽△CBF，∴AEBC＝AFFC，∵AE＝12AD＝12BC，∴AFFC＝12，故A正确，不符合题意；B、过D作DM∥BE交AC于N，∵DE∥BM，BE∥DM，∴四边形BMDE是平行四边形，∴BM ＝DE ＝12BC ， ∴BM ＝CM ，∴CN ＝NF ， ∵BE ⊥AC 于点F ，DM ∥BE ，∴DN ⊥CF ，∴DF ＝DC ，∴∠DCF ＝∠DFC ，故B 正确，不符合题意；C 、图中与△AEF 相似的三角形有△ACD ，△BAF ，△CBF ，△CAB ，△ABE 共有5个，故C 正确，不符合题意．D 、设AD ＝a ，AB ＝b 由△BAE ∽△ADC ，有b a ＝2a ． ∵tan ∠CAD ＝CD AD ＝b a ＝22，故D 错误，符合题意． 故选：D ．【点睛】本题考查了相似三角形的判定和性质，矩形的性质，图形面积的计算，正确的作出辅助线是解题的关键．14．如图，E 是矩形ABCD 中AD 边的中点，BE 交AC 于点,F ABF V 的面积为2，则四边形CDEF 的面积为（）A ．4B ．5C ．6D ．7【答案】B【解析】【分析】设AEF S x =△，根据相似三角形的面积比等于相似比的平方，得出4BCF S x =V ，求出x 即可解答．【详解】解：∵AD ∥BC ，E 是矩形ABCD 中AD 边的中点，∴AEF ~CBF V V ，设AEF S x =△，那么4BCF S x =V ，∵2ABF S =V ， ∴()1x 2422x +=+， 解得：x 1=， ∴325CDEF S x =+=四边形，故选：B.【点睛】此题主要考查相似三角形的相似比与面积比之间的关系，灵活运用关系是解题关键． 15．如图，△AOB 是直角三角形，∠AOB ＝90°，△AOB 的两边分别与函数12,y y x x=-=的图象交于B 、A 两点，则等于（ ）A ．22B ．12C ．14D 3【答案】A【解析】【分析】过点A,B 作AC ⊥x 轴,BD ⊥x 轴,垂足分别为C,D.根据条件得到△ACO ∽△ODB.根据反比例函数比例系数k 的几何意义得出2()S OBD OB S AOC OA ∆=∆＝121＝12利用相似三角形面积比等于相似比的平方得出2OB OA =【详解】 ∵∠AOB ＝90°，∴∠AOC +∠BOD ＝∠AOC +∠CAO ＝90°，∠CAO ＝∠BOD ，∴△ACO ∽△BDO ， ∴2()S OBD OB S AOC OA ∆=∆ , ∵S △AOC ＝12 ×2＝1，S △BOD ＝12×1＝12， ∴2()OB OA ＝121＝12 ， ∴2OB OA =， 故选A ．【点睛】此题考查了反比例函数图象上点的坐标特征和相似三角形的判定与性质，解题关键在于做辅助线，然后得到相似三角形再进行求解16．如图，△ABC 中，∠BAC ＝45°，∠ACB ＝30°，将△ABC 绕点A 顺时针旋转得到△AB 1C 1，当点C 1、B 1、C 三点共线时，旋转角为α，连接BB 1，交AC 于点D ．下列结论：①△AC 1C 为等腰三角形；②△AB 1D ∽△BCD ；③α＝75°；④CA ＝CB 1，其中正确的是（ ）A ．①③④B ．①②④C ．②③④D ．①②③④【答案】B【解析】【分析】 将△ABC 绕点A 顺时针旋转得到△AB 1C 1，得到△ABC ≌△AB 1C 1，根据全等三角形的性质得到AC 1=AC ，于是得到△AC 1C 为等腰三角形；故①正确；根据等腰三角形的性质得到∠C 1=∠ACC 1=30°，由三角形的内角和得到∠C 1AC=120°，得到∠B 1AB=120°，根据等腰三角形的性质得到∠AB 1B=30°=∠ACB ，于是得到△AB 1D ∽△BCD ；故②正确；由旋转角α=120°，故③错误；根据旋转的性质得到∠C 1AB 1=∠BAC=45°，推出∠B 1AC=∠AB 1C ，于是得到CA=CB 1；故④正确．【详解】解：∵将△ABC 绕点A 顺时针旋转得到△AB 1C 1，∴△ABC ≌△AB 1C 1，∴AC 1＝AC ，∴△AC 1C 为等腰三角形；故①正确；∴AC 1＝AC ，∴∠C 1＝∠ACC 1＝30°，∴∠C 1AC ＝120°，∴∠B 1AB ＝120°，∵AB 1＝AB ，∴∠AB 1B ＝30°＝∠ACB ，∵∠ADB 1＝∠BDC ，∴△AB 1D ∽△BCD ；故②正确；∵旋转角为α，∴α＝120°，故③错误；∵∠C 1AB 1＝∠BAC ＝45°，∴∠B 1AC ＝75°，∵∠AB 1C 1＝∠BAC ＝105°，∴∠AB 1C ＝75°，∴∠B 1AC ＝∠AB 1C ，∴CA ＝CB 1；故④正确．故选：B ．【点睛】本题考查了相似三角形的判定和性质，等腰三角形的判定和性质，旋转的性质，正确的识别图形是解题的关键．17．如图，Rt ABO ∆中，90AOB ∠=︒，3AO BO =，点B 在反比例函数2y x =的图象上，OA 交反比例函数()0k y k x=≠的图象于点C ，且2OC CA =，则k 的值为（ ）A ．2-B ．4-C ．6-D ．8-【答案】D【解析】【分析】 过点A 作AD ⊥x 轴，过点C 作CE ⊥x 轴，过点B 作BF ⊥x 轴，利用AA 定理和平行证得△COE ∽△OBF ∽△AOD ，然后根据相似三角形的性质求得21()9BOF OAD S OB S OA ==V V ，24()9COE AOD S OC S OA ==V V ，根据反比例函数比例系数的几何意义求得212BOF S ==V ，从而求得4COE S =V ，从而求得k 的值．【详解】解：过点A 作AD ⊥x 轴，过点C 作CE ⊥x 轴，过点B 作BF ⊥x 轴∴CE ∥AD ，∠CEO=∠BFO=90°∵90AOB ∠=︒∴∠COE+∠FOB=90°，∠ECO+∠COE=90°∴∠ECO=∠FOB∴△COE ∽△OBF ∽△AOD又∵3AO BO =，2OC CA = ∴13OB OA =，23OC OA = ∴21()9BOF OAD S OB S OA ==V V ，24()9COE AOD S OC S OA ==V V ∴4COE BOFS S =V V ∵点B 在反比例函数2y x =的图象上 ∴212BOF S ==V ∴4COE S =V ∴42k =，解得k=±8 又∵反比例函数位于第二象限，∴k=-8故选：D ．【点睛】本题考查反比例函数的性质和相似三角形的判定和性质，正确添加辅助线证明三角形相似，利用数形结合思想解题是关键．18．如图，AB ∥GH ∥CD ，点H 在BC 上，AC 与BD 交于点G ，AB=2，CD=3，则GH 长为（ ）A ．1B ．1.2C ．2D ．2.5 【答案】B【解析】【分析】由AB ∥GH ∥CD 可得：△CGH ∽△CAB 、△BGH ∽△BDC ，进而得：GH CH AB BC =、GH BH CD BC=，然后两式相加即可． 【详解】解：∵AB ∥GH ，∴△CGH ∽△CAB ，∴GH CH AB BC =，即2GH CH BC =①， ∵CD ∥GH ，∴△BGH ∽△BDC ，∴GH BH CD BC =，即3GH BH BC =②， ①+②，得：123GH GH CH BH BC BC +=+=，解得：6 1.25GH ==． 故选：B ．【点睛】本题考查了相似三角形的判定和性质，属于基本题型，熟练掌握相似三角形的判定和性质是解题的关键．19．若△ABC 的每条边长增加各自的50%得△A 'B 'C '，若△ABC 的面积为4，则△A 'B 'C '的面积是（ ）A ．9B ．6C ．5D ．2 【答案】A【解析】【分析】根据两个三角形三边对应成比例，这两个三角形相似判断出两个三角形相似，根据相似三角形的性质即可得到结论．【详解】解：∵△ABC 的每条边长增加各自的50%得△A ′B ′C ′，∴△ABC 与△A ′B ′C ′的三边对应成比例，∴△ABC ∽△A ′B ′C ′， ∴214()150%9ABC A B C S S '''==+V V ， ∵△ABC 的面积为4，则△A'B'C'的面积是9．故选：A ．【点睛】本题考查了相似三角形的性质和判定，熟练掌握相似三角形的判定是解题的关键．20．矩形ABCO 如图摆放，点B 在y 轴上，点C 在反比例函数y k x=(x ＞0)上，OA ＝2，AB ＝4，则k 的值为（ ）A ．4B ．6C ．325D ．425【答案】C 【解析】【分析】 根据矩形的性质得到∠A=∠AOC=90°，OC=AB ，根据勾股定理得到OB 22OA AB =+=5C 作CD ⊥x 轴于D ，根据相似三角形的性质得到CD 855=，OD 45= 求得8545，)于是得到结论． 【详解】解：∵四边形ABCO 是矩形，∴∠A＝∠AOC＝90°，OC＝AB，∵OA＝2，AB＝4，∴过C作CD⊥x轴于D，∴∠CDO＝∠A＝90°，∠COD+∠COB＝∠COB+∠AOB＝90°，∴∠COD＝∠AOB，∴△AOB∽△DOC，∴OB AB OA OC CD OD==，∴2542CD OD==，∴CD85=，OD45=，∴C(45，85)，∴k325 =，故选：C．【点睛】本题考查了反比例函数图象上点的坐标特征，反比例函数的性质，矩形的性质，相似三角形的判定和性质，正确的作出辅助线是解题的关键．。

二、现给出以下四个命题：①等边三角形既是轴对称图形，又是中心对称图形；②相似三角形的面积比等于它们的相似比；③菱形的面积等于两条对角线的积；④三角形的三个内角中至少有一内角不小于60°．其中不正确的命题的个数是（）A、1个B、2个C、3个D、4个考点：等边三角形的性质；三角形内角和定理；菱形的性质；相似三角形的性质。

分析：对四个选项逐个进行判定即可得出结论．解答：解：①依照等边三角形的性质知，等边三角形是轴对称图形，不是中心对称图形，错误；②由相似三角形的性质知相似三角形的面积比等于它们的相似比的平方，错误；③依照菱形的面积公式，错误；④依照三角形内角和定理可知，三角形的三个内角中至少有一内角不小于60°，正确．综合以上分析，不正确的命题包括①②③．应选C．点评：此题要紧考查了等边三角形、相似三角形的性质，菱形的面积公式等内容，范围较广．3、如图，△DEF的边长别离为1，，2，正六边形网格是由24个边长为2的正三角形组成，以这些正三角形的极点为极点画△ABC，使得△ABC∽△DEF．若是相似比=k，那么k的不同的值共有（）A、1个B、2个C、3个D、4个考点：等边三角形的性质；勾股定理的逆定理；相似三角形的性质。

分析：依照题意可得：在正六边形网格找与△DEF相似的三角形；即找三边的比值为1：：2的直角三角形；分析图形可得：共三种情形，相似比别离为：2，2，4；解答：解：∵△DEF的边长别离为1，，2∴△DEF为直角三角形，∠F=30°，∠D=60°依照等边三角形的三线合一，可作三边比为1：：2的三角形∴相似比=k，k可取2，2，4．应选C．点评：此题要紧考查了相似三角形的判定．4、（2020•杭州）若是一个直角三角形的两条边长别离是6和8，另一个与它相似的直角三角形边长别离是3和4及x，那么x的值（）A、只有1个B、可以有2个C、有2个以上，但有限D、有无数个考点：勾股定理；相似三角形的判定与性质。

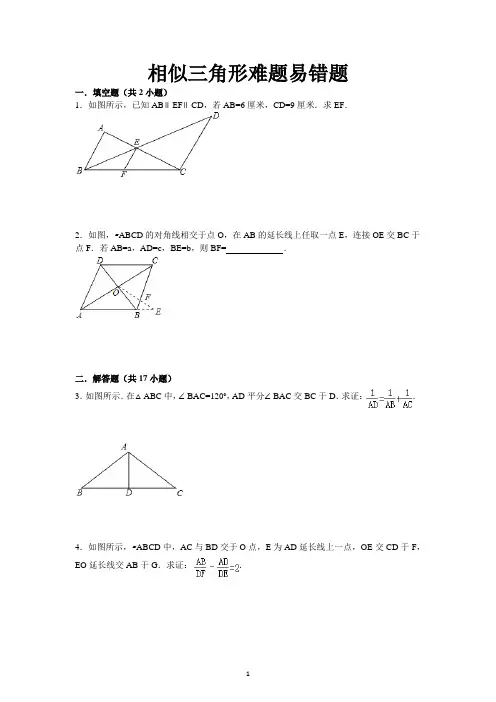
相似三角形难题易错题一．填空题（共2小题）1．如图所示，已知AB∥EF∥CD，若AB=6厘米，CD=9厘米．求EF．2．如图，▱ABCD的对角线相交于点O，在AB的延长线上任取一点E，连接OE交BC于点F．若AB=a，AD=c，BE=b，则BF=_________．二．解答题（共17小题）3．如图所示．在△ABC中，∠BAC=120°，AD平分∠BAC交BC于D．求证：．4．如图所示，▱ABCD中，AC与BD交于O点，E为AD延长线上一点，OE交CD于F，EO延长线交AB于G．求证：．5．一条直线截△ABC的边BC、CA、AB（或它们的延长线）于点D、E、F．求证：．6．如图所示．P为△ABC内一点，过P点作线段DE，FG，HI分别平行于AB，BC和CA，且DE=FG=HI=d，AB=510，BC=450，CA=425．求d．7．如图所示．梯形ABCD中，AD∥BC，BD，AC交于O点，过O的直线分别交AB，CD 于E，F，且EF∥BC．AD=12厘米，BC=20厘米．求EF．8．已知：P为▱ABCD边BC上任意一点，DP交AB的延长线于Q点，求证：．9．如图所示，梯形ABCD中，AD∥BC，MN∥BC，且MN与对角线BD交于O．若AD=DO=a，BC=BO=b，求MN．10．P为△ABC内一点，过P点作DE，FG，IH分别平行于AB，BC，CA（如图所示）．求证：．11．如图所示．在梯形ABCD中，AB∥CD，AB＜CD．一条直线交BA延长线于E，交DC 延长线于J，交AD于F，交BD于G，交AC于H，交BC于I．已知EF=FG=GH=HI=IJ，求DC：AB．12．已知P为△ABC内任意一点，连AP，BP，CP并延长分别交对边于D，E，F．求证：（1）（2）三者中，至少有一个不大于2，也至少有一个不少于2．13．如图所示．在△ABC中，AM是BC边上的中线，AE平分∠BAC，BD⊥AE的延长线于D，且交AM延长线于F．求证：EF∥AB．14．如图所示．P，Q分别是正方形ABCD的边AB，BC上的点，且BP=BQ，BH⊥PC于H．求证：QH⊥DH．15．已知M是Rt△ABC中斜边BC的中点，P、Q分别在AB、AC上，且PM⊥QM．求证：PQ2=PB2+QC2．16．如图所示．在△ABC中，∠ACB=90°，CD⊥AB于D，AE平分∠CAB，CF平分∠BCD．求证：EF∥BC．17．如图所示．在△ABC内有一点P，满足∠APB=∠BPC=∠CPA．若2∠B=∠A+∠C，求证：PB2=PA•PC．（提示：设法证明△PAB∽△PBC．）18．已知：如图，△ABC为等腰直角三角形，D是直角边BC的中点，E在AB上，且AE：EB=2：1．求证：CE⊥AD．19．如图所示，△ABC中，M、N是边BC的三等分点，BE是AC边上的中线，连接AM、AN，分别交BE于F、G，求BF：FG：GE的值．20.在△ABC中，∠A∶∠B∶∠C=1∶2∶4．求证1AB +1AC=1BC提示：要证明如1a +1b=1c几何题的常用方法：①比例法：将原等式变为a+bab=1c或a+ba=bc，故构造成以a+b、b为边且与a、c所在三角形相似的三角形。

2019年九年级数学下册期末复习相似三角形知识点+易错题精选知识概述1.平行线等分线段定理如果一组平行线在一条直线上截得的线段相等，那么在其它直线上截得的线段也相等。

2.平行线分线段成比例定理三条平行线截两条直线，所得的对应线段成比例。

3.相似三角形的定义对应边成比例、对应角相等的两个三角形叫做相似三角形．4.相似三角形的基本性质①相似三角形的对应边成比例、对应角相等．②相似三角形的对应高线的比，对应中线的比和对应角平分线的比都等于相似比。

③相似三角形的周长比等于相似比④面积比等于相似比的平方温馨提示：①全等三角形一定是相似三角形，其相似比k=1．所以全等三角形是相似三角形的特例．其区别在于全等要求对应边相等，而相似要求对应边成比例．②相似比具有顺序性．例如△ABC∽△A′B′C′的对应边的比，即相似比为k，则△A′B′C′∽△ABC的相似比，当且仅当它们全等时，才有k=k′=1．③相似比是一个重要概念，后继学习时出现的频率较高，其实质它是将一个图形放大或缩小的倍数，这一点借助相似三角形可观察得出．5. 相似三角形的判定定理①平行于三角形一边的直线和其他两边或其延长线相交，所得的三角形与原三角形相似；②三边对应成比例的两个三角形相似；③两角对应相等的两个三角形相似；④两边对应成比例且夹角相等的两个三角形相似。

温馨提示：（1）判定三角形相似的几条思路：①条件中若有平行，可采用判定定理1；②条件中若有一对角相等(包括隐含的公共角或对顶角)，可再找一对角相等或找夹边对应成比例；③条件中若有两边对应成比例，可找夹角相等；但是，在选择利用判定定理2时，一对对应角相等必须是成比例两边的夹角对应相等．④条件中若有等腰关系，可找顶角相等或底角相等，也可找腰和底对应成比例。

（2）在综合题中，注意相似知识的灵活运用，并熟练掌握线段代换、等比代换、等量代换技巧的应用，培养综合运用知识的能力。

（3）运用相似的知识解决一些实际问题，要能够在理解题意的基础上，把它转化为纯数学知识的问题，要注意培养当数学建模的思想。

《名校课堂》之相似三角形易错题（一）姓名:_______1、已知 .（1）求的值；（2）如果，求x的值.2、湖南地图出版社首发的竖版《中华人民共和国地图》，将南海诸岛与中国大陆按同比例尺1：6700000表示出来，使读者能够全面、直观地认识我国版图，若在这种地图上量得我国南北的图上距离是82.09厘米，则我国南北的实际距离大约是_______________（结果精确到1千米）3、如果三条线段的长a、b、c满足，那么（a，b，c）叫做“黄金线段组”．黄金线段组中的三条线段（）A．必构成锐角三角形 B．必构成直角三角形 C．必构成钝角三角形 D．不能构成三角形4、如图是两把按不同比例尺进行刻度的尺子，每把尺子的刻度都是均匀的，已知两把尺子在刻度10处是对齐的，且上面尺子在刻度15处与下面的尺子在刻度18处也刚好对齐，则上面尺子的刻度16在下面尺子对应的刻度是（）A．19.4 B．19.5 C．19.6 D．19.75、如图所示，一张矩形纸片ABCD的长AB=acm，宽BC=bcm，E、F分别为AB、CD的中点，这张纸片沿直线EF对折后，矩形AEFD的长与宽之比等于矩形ABCD的长与宽之比，则a：b等于（）：：6、如图，D是BC上一点，E是AB上一点，AD、CE交于点P，且AE：EB=3：2，CP：CE=5：6，那么DB：CD=______．第5题第6题第7题第8题7、如图，在直角坐标系xOy中，A（-4，0），B（0，2），连结AB并延长到C，连结CO，若△COB∽△CAO，则点C的坐标为（）A.:（，）B.（，）C.（，）D.（，）8、如图，P是Rt△ABC的斜边BC上异于B、C的一点，过P点作直线截△ABC，使截得的三角形与△ABC 相似，满足这样条件的直线共有（）A．1条B．2条C．3条D．4条9、一个钢筋三角架三边长分别为20cm,50cm,60cm,现在要做一个和它相似的钢筋三角架,而只有长为30cm和50cm的两根钢筋,要求以其中的一根为一边,从另一根上截两段(允许有余料)作为另两边,则不同的截法有( ) A. 一种 B. 两种 C. 三种 D. 四种或四种以上10、如图，A、B、C、D是⊙O上的四个点，AB=AC，AD交BC于点E，AE=3，ED=4，则AB的长为________．11、如图，∠A=∠B=90°，AB=7，AD=2，BC=3，如果边AB上的点P使得以P，A，D为顶点的三角形和以P，B，C为顶点的三角形相似，则这样的P点共有几个（）A．1 B．2 C．3 D．4第10题第11题第12题12、如图，△ABC中，∠A=78°，AB=4，AC=6．将△ABC沿图示中的虚线剪开，剪下的阴影三角形与原三角形不相似的是（）A B C D13、如果一个直角三角形的两条边长分别是6和8，另一个与它相似的直角三角形边长分别是3和4及x，那么x的值是__________．14、已知直角三角形的两条直角边分别为5cm，12cm，则此直角三角形的重心与外心之间的距离_____．15、如图，△ABC是一张直角三角形彩色纸，AC=15cm，BC=20cm．若将斜边上的高CD 分成n等分，然后裁出（n-1）张宽度相等的长方形纸条．则这（n-1）张纸条的面积和是___cm216、一个等腰直角三角形和一个正方形如图摆放，被分割成了5个部分．①，②，③这三块的面积比依次为1：4：41，那么④，⑤这两块的面积比是______．第15题第16题第17题第18题17、如图，D、E分别是△ABC的边AB、BC上的点，DE∥AC，若S△BDE：S△CDE=1：3，则S△DOE：S△AOC的值为__18、如图，小红作出了边长为1的第1个正三角形△A1 B1 C1 ，算出了正△A1 B1 C1的面积，然后分别取△A1 B1 C1三边的中点A2 B2 C2 ，作出了第二个正三角形A2 B2 C2，算出第2个正A2 B2 C2的面积，用同样的方法作出了第3个正A3 B3 C3，算出第3个正A3 B3 C3的面积，依此方法作下去，由此可得第n次作出的正An Bn Cn的面积是 _______．．19、在比例尺为1：10000的地图上，一块面积为2cm2的区域表示的实际面积是（）A．2000000cm2 B．20000m2 C．4000000m2 D．40000m220、在Rt△ABC，∠ABC=90°，AB=8cm，BC=6cm，G是△ABC的重心，则BG的长为________.21、一块直角三角形木板的一条直角边AB长为1.5m，面积为1.5m 2 ，工人师傅要把它加工成一个面积最大的正方形桌面，请甲、乙两位同学进行设计加工方案，甲设计方案如图1，乙设计方案如图2．你认为哪位同学设计的方案较好？试说明理由．（加工损耗忽略不计，计算结果中可保留分数）22、如图，一天早上，小张正向着教学楼AB走去，他发现教学楼后面有一水塔DC，可过了一会抬头一看：“怎么看不到水塔了？”心里很是纳闷。

相似三角形难题精选模块一：相似三角形中的动点问题如图，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，过点B作射线BB1∥AC．动点D从点A出发沿射线AC方向以每秒5个单位的速度运动，同时动点E从点C 沿射线AC方向以每秒3个单位的速度运动．过点D作DH⊥AB于H，过点E作EF⊥AC交射线BB1于F，G是EF中点，连接DG．设点D运动的时间为t秒．（1）当t为何值时，AD=AB，并求出此时DE的长度；（2）当△DEG与△ACB相似时，求t的值．如图，在△ABC中，ABC＝90°，AB=6m，BC=8m，动点P以2m/s的速度从A 点出发，沿AC向点C移动．同时，动点Q以1m/s的速度从C点出发，沿CB向点B移动．当其中有一点到达终点时，它们都停止移动．设移动的时间为t秒．（1）①当t=2.5s时，求△CPQ的面积；②求△CPQ的面积S（平方米）关于时间t（秒）的函数解析式；（2）在P，Q移动的过程中，当△CPQ为等腰三角形时，求出t的值．如图1，在Rt△ABC中，ACB＝90°，AC＝6，BC＝8，点D在边AB上运动，DE 平分CDB交边BC于点E，EM⊥BD，垂足为M，EN⊥CD，垂足为N．（1）当AD＝CD时，求证：DE∥AC；（2）探究：AD为何值时，△BME与△CNE相似？如图所示，在△ABC中，BA＝BC＝20cm，AC＝30cm，点P从A点出发，沿着AB 以每秒4cm的速度向B点运动；同时点Q从C点出发，沿CA以每秒3cm的速度向A点运动，当P点到达B点时，Q点随之停止运动．设运动的时间为x．（1）当x为何值时，PQ∥BC？（2）△APQ与△CQB能否相似？若能，求出AP的长；若不能，请说明理由.如图，在矩形ABCD中，AB=12cm，BC=6cm，点P沿AB边从A开始向点B以2cm/s 的速度移动；点Q沿DA边从点D开始向点A以1cm/s的速度移动．如果P、Q 同时出发，用t（s）表示移动的时间（0＜t＜6）。

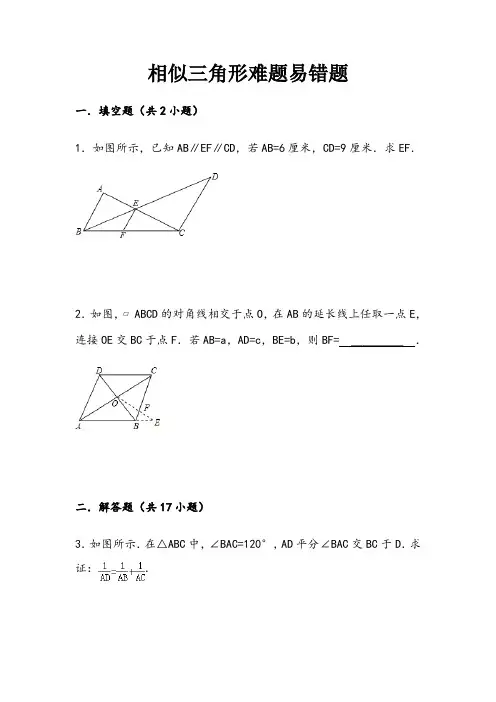
相似三角形难题易错题一．填空题（共2小题）1．如图所示，已知AB∥EF∥CD，若AB=6厘米，CD=9厘米．求EF．2．如图，▱ABCD的对角线相交于点O，在AB的延长线上任取一点E，连接OE交BC于点F．若AB=a，AD=c，BE=b，则BF= _________ ．二．解答题（共17小题）3．如图所示．在△ABC中，∠BAC=120°，AD平分∠BAC交BC于D．求证：．4．如图所示，▱ABCD中，AC与BD交于O点，E为AD延长线上一点，OE交CD于F，EO延长线交AB于G．求证：．5．一条直线截△ABC的边BC、CA、AB（或它们的延长线）于点D、E、F．求证：．6．如图所示．P为△ABC内一点，过P点作线段DE，FG，HI分别平行于AB，BC和CA，且DE=FG=HI=d，AB=510，BC=450，CA=425．求d．7．如图所示．梯形ABCD中，AD∥BC，BD，AC交于O点，过O的直线分别交AB，CD于E，F，且EF∥BC．AD=12厘米，BC=20厘米．求EF．8．已知：P为▱ABCD边BC上任意一点，DP交AB的延长线于Q点，求证：．9．如图所示，梯形ABCD中，AD∥BC，MN∥BC，且MN与对角线BD交于O．若AD=DO=a，BC=BO=b，求MN．10．P为△ABC内一点，过P点作DE，FG，IH分别平行于AB，BC，CA（如图所示）．求证：．11．如图所示．在梯形ABCD中，AB∥CD，AB＜CD．一条直线交BA延长线于E，交DC延长线于J，交AD于F，交BD于G，交AC于H，交BC于I．已知EF=FG=GH=HI=IJ，求DC：AB．12．已知P为△ABC内任意一点，连AP，BP，CP并延长分别交对边于D，E，F．求证：（1）（2）三者中，至少有一个不大于2，也至少有一个不少于2．13．如图所示．在△ABC中，AM是BC边上的中线，AE平分∠BAC，BD⊥AE的延长线于D，且交AM延长线于F．求证：EF∥AB．14．如图所示．P，Q分别是正方形ABCD的边AB，BC上的点，且BP=BQ，BH⊥PC于H．求证：Q H⊥DH．15．已知M是Rt△ABC中斜边BC的中点，P、Q分别在AB、AC上，且PM⊥QM．求证：PQ2=PB2+QC2．16．如图所示．在△ABC中，∠ACB=90°，CD⊥AB于D，AE平分∠CAB，CF平分∠BCD．求证：EF∥BC．17．如图所示．在△ABC内有一点P，满足∠APB=∠BPC=∠CPA．若2∠B=∠A+∠C，求证：PB2=PA•PC．（提示：设法证明△PAB∽△PBC．）18．已知：如图，△ABC为等腰直角三角形，D是直角边BC的中点，E在AB上，且AE：EB=2：1．求证：CE⊥AD．19．如图所示，△ABC中，M、N是边BC的三等分点，BE是AC边上的中线，连接AM、AN，分别交BE于F、G，求BF：FG：GE的值．20.在△ABC中，∠A∶∠B∶∠C=1∶2∶4．求证提示：要证明如几何题的常用方法：①比例法：将原等式变为，故构造成以a+b、b为边且与a、c所在三角形相似的三角形。

（易错题精选）初中数学图形的相似难题汇编附答案一、选择题1．如图，已知ABC ∆和ABD ∆都O e 是的内接三角形，AC 和BD 相交于点E ，则与ADE ∆的相似的三角形是（ ）A ．BCE ∆B ．ABC ∆ C ．ABD ∆ D ．ABE ∆【答案】A【解析】【分析】 根据同弧和等弧所对的圆周角相等， 则AB 弧所对的圆周角BCE BDA ∠=∠，CEB ∠和DEA ∠是对顶角，所以ADE BCE ∆∆∽．【详解】解：BCE BDA ∠=∠Q ，CEB DEA ∠=∠ADE BCE ∴∆∆∽，故选：A ．【点睛】考查相似三角形的判定定理： 两角对应相等的两个三角形相似，关键就是牢记同弧所对的圆周角相等．2．如图所示，在△ABC 中，∠C ＝90°，AB ＝8，CD 是AB 边上的中线，作CD 的中垂线与CD 交于点E ，与BC 交于点F ．若CF ＝x ，tanA ＝y ，则x 与y 之间满足（ ）A ．2244x y+= B ．2244x y -= C ．2288x y -= D ．2288x y+= 【答案】A【解析】【分析】由直角三角形斜边上的中线性质得出CD ＝12AB ＝AD ＝4，由等腰三角形的性质得出∠A ＝∠ACD ，得出tan ∠ACD ＝GE CE＝tan A ＝y ，证明△CEG ∽△FEC ，得出GE CE CE FE ，得出y ＝2FE ，求出y 2＝24FE ，得出24y＝FE 2，再由勾股定理得出FE 2＝CF 2﹣CE 2＝x 2﹣4，即可得出答案．【详解】解：如图所示：∵在△ABC 中，∠C ＝90°，AB ＝8，CD 是AB 边上的中线，∴CD ＝12AB ＝AD ＝4， ∴∠A ＝∠ACD ，∵EF 垂直平分CD ， ∴CE ＝12CD ＝2，∠CEF ＝∠CEG ＝90°， ∴tan ∠ACD ＝GE CE ＝tanA ＝y ， ∵∠ACD+∠FCE ＝∠CFE+∠FCE ＝90°，∴∠ACD ＝∠FCE ，∴△CEG ∽△FEC ， ∴GE CE ＝CE FE， ∴y ＝2FE， ∴y 2＝24FE ， ∴24y＝FE 2， ∵FE 2＝CF 2﹣CE 2＝x 2﹣4， ∴24y＝x 2﹣4， ∴24y+4＝x 2， 故选：A ．【点睛】本题考查了解直角三角形、直角三角形斜边上的中线性质、等腰三角形的性质、相似三角形的判定与性质等知识；熟练掌握直角三角形的性质，证明三角形相似是解题的关键．3．如图，点A在双曲线y═kx（x＞0）上，过点A作AB⊥x轴，垂足为点B，分别以点O和点A为圆心，大于12OA的长为半径作弧，两弧相交于D，E两点，作直线DE交x轴于点C，交y轴于点F（0，2），连接AC．若AC=1，则k的值为（）A．2 B．3225C．435D．2525【答案】B【解析】分析：如图，设OA交CF于K．利用面积法求出OA的长，再利用相似三角形的性质求出AB、OB即可解决问题；详解：如图，设OA交CF于K．由作图可知，CF垂直平分线段OA，∴OC=CA=1，OK=AK，在Rt △OFC 中，CF=22=5OF OC +， ∴AK=OK=25=55， ∴OA=45， 由△FOC ∽△OBA ，可得OF OC CF OB AB OA==， ∴21545OB AB ==，∴OB=85，AB=45， ∴A （85，45）， ∴k=3225． 故选B ．点睛：本题考查作图-复杂作图，反比例函数图象上的点的坐标特征，线段的垂直平分线的性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．4．如图，将ABC ∆沿BC 边上的中线AD 平移到A B C '''∆的位置．已知ABC ∆的面积为16，阴影部分三角形的面积9．若1AA '=，则A D '等于（ ）A ．2B ．3C ．4D ．32【答案】B【解析】【分析】 由 S △ABC ＝16、S △A ′EF ＝9且 AD 为 BC 边的中线知 1922A DE A EF S S '∆'∆==，182ABD ABC S S ∆∆== ，根据△DA ′E ∽△DAB 知2A DE ABDS A D AD S ∆∆'⎛⎫=' ⎪⎝⎭ ，据此求解可得．【详解】16ABC S ∆=Q 、9A EF S ∆'=，且AD 为BC 边的中线， 1922A DE A EF S S∆∆''∴==，182ABD ABC S S ∆∆==， Q 将ABC ∆沿BC 边上的中线AD 平移得到A B C '''∆，//A E AB ∴'， DA E DAB '∴∆~∆，则2A DE ABD S A D AD S ∆∆'⎛⎫=' ⎪⎝⎭，即22991816A D A D ⎛⎫== '⎪+⎝⎭'， 解得3A D '=或37A D '=-（舍）， 故选：B ．【点睛】本题主要平移的性质，解题的关键是熟练掌握平移变换的性质与三角形中线的 性质、相似三角形的判定与性质等知识点．5．如图，在Rt ABC △中，90ACB ∠=︒，CD AB ⊥于点D ，2CD =，1BD =，则AD 的长是（ ）A ．1.B 2C ．2D ．4【答案】D【解析】【分析】 由在Rt △ABC 中，∠ACB=90°，CD ⊥AB ，根据同角的余角相等，可得∠ACD=∠B ，又由∠CDB=∠ACB=90°，可证得△ACD ∽△CBD ，然后利用相似三角形的对应边成比例，即可求得答案．【详解】∵在Rt △ABC 中,∠ACB=90°，CD ⊥AB ，∴∠CDB=∠ACB=90°，∴∠ACD+∠BCD=90°,∠BCD+∠B=90°，∴∠ACD=∠B ，∴△ACD ∽△CBD ，∴=AD CD CD BD， ∵CD=2，BD=1， ∴2=21AD ， ∴AD=4.故选D.【点睛】此题考查相似三角形的判定与性质，解题关键在于证得△ACD ∽△CBD.6．已知正方形ABCD 的边长为5，E 在BC 边上运动，DE 的中点G ，EG 绕E 顺时针旋转90°得EF ，问CE 为多少时A 、C 、F 在一条直线上（ ）A ．35B ．43C ．53D ．34【答案】C【解析】【分析】首先延长BC ，做FN ⊥BC ，构造直角三角形，利用三角形相似的判定，得出Rt △FNE ∽Rt △ECD ，再利用相似比得出1 2.52NE CD ==，运用正方形性质,得出△CNF 是等腰直角三角形，从而求出CE ．【详解】解：过F 作BC 的垂线，交BC 延长线于N 点，∵∠DCE=∠ENF=90°，∠DEC+∠NEF=90°，∠NEF+∠EFN=90°，∴∠DEC=∠EFN ，∴Rt △FNE ∽Rt △ECD ，∵DE 的中点G ，EG 绕E 顺时针旋转90°得EF ，∴两三角形相似比为1：2，∴可以得到CE=2NF ，1 2.52NE CD == ∵AC 平分正方形直角，∴∠NFC=45°，∴△CNF 是等腰直角三角形，∴CN=NF ，∴2255.3323CE NE ==⨯= 故选C ．【点睛】 此题主要考查了旋转的性质与正方形的性质以及相似三角形的判定等知识，求线段的长度经常运用相似三角形的知识解决，同学们应学会这种方法.7．如图，在正方形ABCD 中，3AB =，点M 在CD 的边上，且1DM =，AEM ∆与ADM ∆关于AM 所在直线对称，将ADM ∆按顺时针方向绕点A 旋转90°得到ABF ∆，连接EF ，则cos EFC ∠的值是 （ ）A 171365B 61365C 71525D ．617【答案】A【解析】【分析】 过点E 作//HG AD ，交AB 于H ，交CD 于G ，作EN BC ⊥于N ，首先证明AEH EMG V :V ，则有13EH AE MG EM == ，设MG x =，则3EH x =，1DG AH x ==+， 在Rt AEH V 中利用勾股定理求出x 的值，进而可求,,,EH BN CG EN 的长度，进而可求FN ，再利用勾股定理求出EF 的长度，最后利用cos FN EFC EF∠=即可求解． 【详解】 过点E 作//HG AD ，交AB 于H ，交CD 于G ，作EN BC ⊥于N ，则90AHG MGE ∠=∠=︒，∵四边形ABCD 是正方形，∴3,90AD AB ABC C D ==∠=∠=∠=︒ ，∴四边形AHGD,BHEN,ENCG 都是矩形．由折叠可得，90,3,1AEM D AE AD DM EM ∠=∠=︒====，90AEH MEG EMG MEG ∴∠+∠=∠+∠=︒ ，AEH EMG ∴∠=∠，AEH EMG ∴V :V ，13EH AE MG EM ∴== ． 设MG x =，则3EH x =，1DG AH x ==+在Rt AEH V 中， 222AH EH AE +=Q ，222(1)(3)3x x ∴++= ，解得45x =或1x =-（舍去）， 125EH BN ∴==，65CG CD DG EN =-== ． 1BF DM ==Q 175FN BF BN ∴=+=． 在Rt EFN △ 中，由勾股定理得，2213EF EN FN =+= ，17cos 1365FN EFC EF ∴∠== ． 故选：A ．【点睛】 本题主要考查正方形，矩形的性质，相似三角形的判定及性质，勾股定理，锐角三角函数，能够作出辅助线是解题的关键．8．如图，在平面直角坐标系中，已知点A （―3，6）、B （―9，一3），以原点O 为位似中心，相似比为，把△ABO 缩小，则点A 的对应点A′的坐标是（ ）A ．（―1，2）B ．（―9，18）C ．（―9，18）或（9，―18）D ．（―1，2）或（1，―2）【答案】D 【解析】【分析】【详解】试题分析：方法一：∵△ABO 和△A ′B ′O 关于原点位似，∴△ ABO ∽△A ′B ′O 且OA'OA ＝13.∴A E AD '＝0E 0D ＝13.∴A ′E ＝13AD ＝2，OE ＝13OD ＝1.∴A ′（－1,2）.同理可得A′′（1,―2）. 方法二：∵点A （―3，6）且相似比为13，∴点A 的对应点A′的坐标是（―3×13，6×13），∴A ′（－1,2）. ∵点A′′和点A′（－1,2）关于原点O 对称，∴A ′′（1,―2）.故答案选D.考点：位似变换.9．如图，在△ABC中，∠A＝75°，AB＝6，AC＝8，将△ABC沿图中的虚线剪开，剪下的阴影三角形与原三角形不相似的是（）A．B．C．D．【答案】D【解析】【分析】根据相似三角形的判定定理对各选项进行逐一判定即可．【详解】A、根据平行线截得的三角形与原三角形有两个角相等，故两三角形相似，故本选项错误；B、阴影部分的三角形与原三角形有两个角相等，故两三角形相似，故本选项错误；C、两三角形对应边成比例且夹角相等，故两三角形相似，故本选项错误．D、两三角形的对应边不成比例，故两三角形不相似，故本选项正确；故选：D．【点睛】本题考查了相似三角形的判定，熟练掌握相似三角形的判定定理是解题的关键．10．如图，直角三角形的直角顶点在坐标原点，∠OAB=30°，若点A在反比例函数y=6x（x＞0）的图象上，则经过点B的反比例函数解析式为（）A．y=﹣6xB．y=﹣4xC．y=﹣2xD．y=2x【答案】C 【解析】【分析】直接利用相似三角形的判定与性质得出13BCOAODSS=VV，进而得出S△AOD=3，即可得出答案．【详解】过点B作BC⊥x轴于点C，过点A作AD⊥x轴于点D，∵∠BOA=90°，∴∠BOC+∠AOD=90°，∵∠AOD+∠OAD=90°，∴∠BOC=∠OAD，又∵∠BCO=∠ADO=90°，∴△BCO∽△ODA，∵BOAO=tan30°3∴13BCOAODSS=VV，∵12×AD×DO=12xy=3，∴S△BCO=12×BC×CO=13S△AOD=1，∵经过点B的反比例函数图象在第二象限，故反比例函数解析式为：y=﹣2x．故选C．【点睛】此题主要考查了相似三角形的判定与性质，反比例函数数的几何意义，正确得出S△AOD=2是解题关键．11．把Rt ABC三边的长度都扩大为原来的3倍，则锐角A的余弦值（）A．扩大为原来的3倍B．缩小为原来的13C．扩大为原来的9倍D．不变【答案】D【解析】【分析】根据相似三角形的性质解答．【详解】三边的长度都扩大为原来的3倍，则所得的三角形与原三角形相似，∴锐角A的大小不变，∴锐角A的余弦值不变，故选：D．【点睛】此题考查相似三角形的判定和性质、锐角三角函数的定义，掌握相似三角形的对应角相等是解题的关键．12．在相同时刻，物高与影长成正比，如果高为1米的标杆影长为2米，那么影长为30米的旗杆的高为（）A．20米B．18米C．16米D．15米【答案】D【解析】【分析】在同一时刻物高和影长成正比，即在同一时刻的两个物体，影子，经过物体顶部的太阳光线三者构成的两个直角三角形相似，利用标杆的高：标杆影长=旗杆的高：旗杆的影长，列出方程，求解即可得出旗杆的高度．【详解】解：根据题意解：标杆的高：标杆影长=旗杆的高：旗杆的影长，即1:2=旗杆高：30，∴旗杆的高=130=152⨯米．故选：D．【点睛】本题主要考察的是相似三角形的应用，正确列出方程是解决本题的关键．13．两个相似多边形的面积比是9∶16，其中小多边形的周长为36 cm，则较大多边形的周长为 )A．48 cm B．54 cm C．56 cm D．64 cm【答案】A【解析】试题分析：根据相似多边形对应边之比、周长之比等于相似比，而面积之比等于相似比的平方计算即可．解：两个相似多边形的面积比是9：16，面积比是周长比的平方，则大多边形与小多边形的相似比是4：3．相似多边形周长的比等于相似比，因而设大多边形的周长为x，则有=，解得：x=48．大多边形的周长为48cm．故选A．考点：相似多边形的性质．14．如图，点E是矩形ABCD的边AD的中点，且BE⊥AC于点F，则下列结论中错误的是（）A．AF＝12 CFB．∠DCF＝∠DFCC．图中与△AEF相似的三角形共有5个D．tan∠CAD＝3 2【答案】D 【解析】【分析】由AE=12AD=12BC ，又AD ∥BC ，所以12AE AF BC FC ==，故A 正确，不符合题意； 过D 作DM ∥BE 交AC 于N ，得到四边形BMDE 是平行四边形，求出BM=DE=12BC ，得到CN=NF ，根据线段的垂直平分线的性质可得结论，故B 正确，不符合题意；根据相似三角形的判定即可求解，故C 正确，不符合题意；由△BAE ∽△ADC ，得到CD 与AD 的大小关系，根据正切函数可求tan ∠CAD 的值，故D 错误，符合题意．【详解】解：A 、∵AD ∥BC ，∴△AEF ∽△CBF ， ∴AE BC ＝AF FC， ∵AE ＝12AD ＝12BC ， ∴AF FC ＝12，故A 正确，不符合题意； B 、过D 作DM ∥BE 交AC 于N ，∵DE ∥BM ，BE ∥DM ，∴四边形BMDE 是平行四边形，∴BM ＝DE ＝12BC ， ∴BM ＝CM ，∴CN ＝NF ，∵BE ⊥AC 于点F ，DM ∥BE ，∴DN ⊥CF ，∴DF ＝DC ，∴∠DCF ＝∠DFC ，故B 正确，不符合题意；C 、图中与△AEF 相似的三角形有△ACD ，△BAF ，△CBF ，△CAB ，△ABE 共有5个，故C 正确，不符合题意．D 、设AD ＝a ，AB ＝b 由△BAE ∽△ADC ，有b a ＝2a ．∵tan ∠CAD ＝CD AD ＝b a ，故D 错误，符合题意． 故选：D ．【点睛】本题考查了相似三角形的判定和性质，矩形的性质，图形面积的计算，正确的作出辅助线是解题的关键．15．如图，△ABC中，∠BAC＝45°，∠ACB＝30°，将△ABC绕点A顺时针旋转得到△AB1C1，当点C1、B1、C三点共线时，旋转角为α，连接BB1，交AC于点D．下列结论：①△AC1C 为等腰三角形；②△AB1D∽△BCD；③α＝75°；④CA＝CB1，其中正确的是（）A．①③④B．①②④C．②③④D．①②③④【答案】B【解析】【分析】将△ABC绕点A顺时针旋转得到△AB1C1，得到△ABC≌△AB1C1，根据全等三角形的性质得到AC1=AC，于是得到△AC1C为等腰三角形；故①正确；根据等腰三角形的性质得到∠C1=∠ACC1=30°，由三角形的内角和得到∠C1AC=120°，得到∠B1AB=120°，根据等腰三角形的性质得到∠AB1B=30°=∠ACB，于是得到△AB1D∽△BCD；故②正确；由旋转角α=120°，故③错误；根据旋转的性质得到∠C1AB1=∠BAC=45°，推出∠B1AC=∠AB1C，于是得到CA=CB1；故④正确．【详解】解：∵将△ABC绕点A顺时针旋转得到△AB1C1，∴△ABC≌△AB1C1，∴AC1＝AC，∴△AC1C为等腰三角形；故①正确；∴AC1＝AC，∴∠C1＝∠ACC1＝30°，∴∠C1AC＝120°，∴∠B1AB＝120°，∵AB1＝AB，∴∠AB1B＝30°＝∠ACB，∵∠ADB1＝∠BDC，∴△AB1D∽△BCD；故②正确；∵旋转角为α，∴α＝120°，故③错误；∵∠C 1AB 1＝∠BAC ＝45°，∴∠B 1AC ＝75°，∵∠AB 1C 1＝∠BAC ＝105°，∴∠AB 1C ＝75°，∴∠B 1AC ＝∠AB 1C ，∴CA ＝CB 1；故④正确．故选：B ．【点睛】本题考查了相似三角形的判定和性质，等腰三角形的判定和性质，旋转的性质，正确的识别图形是解题的关键．16．如图，顶角为36o 的等腰三角形，其底边与腰之比等k ，这样的三角形称为黄金三角形，已知腰AB=1，ABC ∆为第一个黄金三角形，BCD ∆为第二个黄金三角形，CDE ∆为第三个黄金三角形以此类推，第2020个黄金三角形的周长（）A ．2018kB ．2019kC ．20182k k + D ．2019(2)k k +【答案】D【解析】【分析】根据相似三角形对应角相等，对应边成比例，求出前几个三角形的周长，进而找出规律：第n 个黄金三角形的周长为k n-1（2+k ），从而得出答案．【详解】解：∵AB=AC=1，∴△ABC 的周长为2+k ；△BCD 的周长为k+k+k 2=k （2+k ）；△CDE 的周长为k 2+k 2+k 3=k 2（2+k ）；依此类推，第2020个黄金三角形的周长为k 2019（2+k ）．故选：D ．【点睛】此题考查黄金分割，相似三角形的性质，找出各个三角形周长之间的关系，得出规律是解题的关键．17．如图，点D是△ABC的边AB上的一点，过点D作BC的平行线交AC于点E，连接BE，过点D作BE的平行线交AC于点F，则下列结论错误的是（）A．AD AEBD EC=B．AF DFAE BE=C．AE AFEC FE=D．DE AFBC FE=【答案】D【解析】【分析】由平行线分线段成比例和相似三角形的性质进行判断.【详解】∵DE//BC，∴AD AEBD EC=，故A正确；∵DF//BE，∴△ADF∽△ABF, ∴AF DFAE BE=，故B正确；∵DF//BE，∴AD AFBD FE=，∵AD AEBD EC=，∴AE AFEC FE=，故C正确；∵DE//BC，∴△ADE∽△ABC,∴DE ADBC AB=，∵DF//BE，∴AF ADAE AB=，∴DE AFBC AE=，故D错误.故选D.【点睛】本题考查平行线分线段成比例性质，相似三角形的性质，由平行线得出比例关系是关键.18．若△ABC的每条边长增加各自的50%得△A'B'C'，若△ABC的面积为4，则△A'B'C'的面积是（）A．9 B．6 C．5 D．2【答案】A【解析】【分析】根据两个三角形三边对应成比例，这两个三角形相似判断出两个三角形相似，根据相似三角形的性质即可得到结论．【详解】解：∵△ABC的每条边长增加各自的50%得△A′B′C′，∴△ABC与△A′B′C′的三边对应成比例，∴△ABC∽△A′B′C′，∴214()150%9ABC A B C S S '''==+V V ， ∵△ABC 的面积为4，则△A'B'C'的面积是9．故选：A ．【点睛】本题考查了相似三角形的性质和判定，熟练掌握相似三角形的判定是解题的关键．19．如图，在ABC ∆中，,D E 分别是边,AB AC 的中点，ADE ∆和四边形BCED 的面积分别记为12,S S ，那么12S S 的值为（ ）A ．12B ．14C ．13D ．23【答案】C【解析】【分析】根据已知可得到△ADE ∽△ABC ，从而可求得其面积比，则不难求得12S S 的值． 【详解】∵,D E 分别是边,AB AC 的中点，∴DE ∥BC ，∴△ADE ∽△ABC ，∴DE ：BC=1：2，所以它们的面积比是1：4，所以1211=413S S =-， 故选C ．【点睛】本题考查了三角形的中位线定理和相似三角形的性质：（1）相似三角形周长的比等于相似比；（2）相似三角形面积的比等于相似比的平方；（3）相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比．20．如图，O 是AC 的中点，将面积为216cm 的菱形ABCD 沿AC 方向平移AO 长度得到菱形OB C D '''，则图中阴影部分的面积是（ ）A ．28cmB ．26cmC ．24cmD ．22cm【答案】C【解析】【分析】 根据题意得，▱ABCD ∽▱OECF ，且AO=OC=12AC ，故四边形OECF 的面积是▱ABCD 面积的14【详解】解：如图，由平移的性质得，▱ABCD ∽▱OECF ，且AO=OC=12AC 故四边形OECF 的面积是▱ABCD 面积14即图中阴影部分的面积为4cm 2．故选：C【点睛】 此题主要考查了相似多边形的性质以及菱形的性质和平移性质的综合运用．关键是 应用相似多边形的性质解答问题.。