SOR迭代_C语言代码

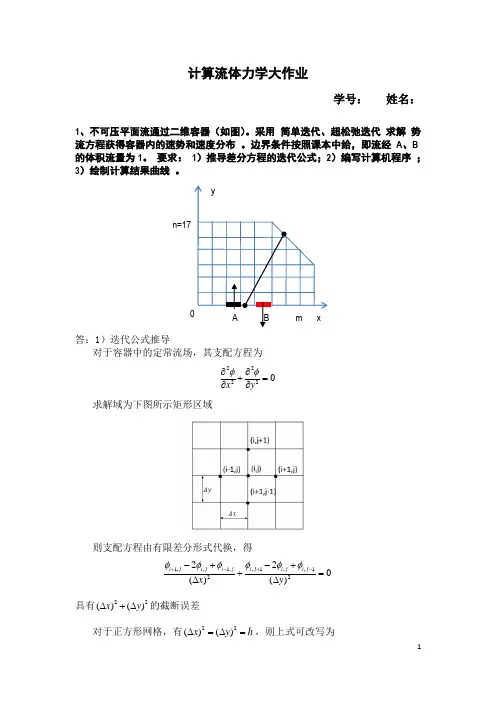
计算流体力学大作业学号： 姓名：1、不可压平面流通过二维容器（如图）。

采用 简单迭代、超松弛迭代 求解 势流方程获得容器内的速势和速度分布 。

边界条件按照课本中给，即流经 A 、B 的体积流量为1。

要求： 1）推导差分方程的迭代公式；2）编写计算机程序 ； 3）绘制计算结果曲线 。

答：1）迭代公式推导对于容器中的定常流场，其支配方程为22220x yφφ∂∂+=∂∂ 求解域为下图所示矩形区域则支配方程由有限差分形式代换，得1,,1,,1,,122220()()i j i j i ji j i j i j x y φφφφφφ+-+--+-++=∆∆具有22()()x y ∆+∆的截断误差对于正方形网格，有22()()x y h ∆=∆=，则上式可改写为n=17,1,1,,1,11()4i j i j i j i j i j φφφφφ+-+-=+++若采用简单迭代公式，即Liebmann 公式，则有(1)()(1)()(1),1,1,,1,11()4n n n n n i j i j i j i j i j φφφφφ++++-+-=+++若采用超松弛迭代，即SOR 公式，则有(1)()()(1)()(1),,1,1,,1,1(1)()4n n n n n n i j i j i j i j i j i j ωφωφφφφφ++++-+-=-++++其中松弛因子12ω<<。

ω最佳值opt ω为opt ω=式中cos(/)cos(/)m n αππ=+，m ，n 分别表示在网格系统中垂直线和水平线的总数。

2）计算机程序本程序采用C 语言编写。

程序源代码如下： #include<stdio.h> #include<math.h> void main() { int m=25,n=17,ilast[17],jlast[25]; int step1,step2; double h=0.25; double psi_j[25][17],psiprv_j,vel_j[25][17],velx_j[25][17],vely_j[25][17]; double psi_c[25][17],psiprv_c,vel_c[25][17],velx_c[25][17],vely_c[25][17]; double Pi,Alpha,Omega,Error; int i,j; for(i=0;i<17;i++) jlast[i]=17; for(i=17;i<m;i++) jlast[i]=17-(i-16); for(j=0;j<9;j++) ilast[j]=25; for(j=9;j<n;j++) ilast[j]=25-(j-8); //数据初始化 for(j=0;j<n;j++) { psi_j[0][j]=1.0; psi_c[0][j]=1.0;}for(i=1;i<m;i++){psi_j[i][jlast[i]-1]=1.0;psi_c[i][jlast[i]-1]=1.0; }for(j=0;j<8;j++){psi_j[m-1][j]=1.0;psi_c[m-1][j]=1.0;}for(i=1;i<m-1;i++){if(i>6 && i<21){psi_j[i][0]=0.0;psi_c[i][0]=0.0;}else{psi_j[i][0]=1.0;psi_c[i][0]=1.0;}}for(i=1;i<m-1;i++){for(j=1;j<jlast[i]-1;j++){psi_j[i][j]=0.5;psi_c[i][j]=0.5;}}//处理右上角数据for(i=0;i<m;i++){for(j=0;j<n;j++){if(j>jlast[i]-1){psi_j[i][j]=0;vel_j[i][j]=3;psi_c[i][j]=0;vel_c[i][j]=3;}}}Pi=4.0*atan(1.0);Alpha=cos(Pi/m)+cos(Pi/n);Omega=(8.0-4*sqrt(4-pow(Alpha,2)))/pow(Alpha,2);//计算速势step1=0;step2=0;//简单迭代while(1){Error=0.0;for(i=1;i<m-1;i++){for(j=1;j<jlast[i]-1;j++){psiprv_j=psi_j[i][j];psi_j[i][j]=(psi_j[i-1][j]+psi_j[i+1][j]+psi_j[i][j-1]+psi_j[i][j+1])/4.0;Error=Error+fabs(psi_j[i][j]-psiprv_j);}}step1++;if(step1>1000)break;if(Error<=0.001)break;}//超松弛迭代while(1){Error=0.0;for(i=1;i<m-1;i++){for(j=1;j<jlast[i]-1;j++){psiprv_c=psi_c[i][j];psi_c[i][j]=(1-Omega)*psi_c[i][j]+Omega*(psi_c[i-1][j]+psi_c[i+1][j]+psi_c[i][j-1]+psi_c[i][j+1])/4.0;Error=Error+fabs(psi_c[i][j]-psiprv_c);}}step2++;if(step2>1000)break;if(Error<=0.001)break;}//计算速度for(i=0;i<m;i++){for(j=0;j<jlast[i];j++){if(j==0){vely_j[i][j]=(-3*psi_j[i][j]+4*psi_j[i][j+1]-psi_j[i][j+2])/2/h;vely_c[i][j]=(-3*psi_c[i][j]+4*psi_c[i][j+1]-psi_c[i][j+2])/2/h;}else if(j==jlast[i]-1){vely_j[i][j]=(psi_j[i][j-2]-4*psi_j[i][j-1]+3*psi_j[i][j])/2/h;vely_c[i][j]=(psi_c[i][j-2]-4*psi_c[i][j-1]+3*psi_c[i][j])/2/h;}else{vely_j[i][j]=(psi_j[i][j+1]-psi_j[i][j-1])/2/h;vely_c[i][j]=(psi_c[i][j+1]-psi_c[i][j-1])/2/h;}}}for(j=0;j<n;j++){for(i=0;i<ilast[j];i++){if(i==0){velx_j[i][j]=(-3*psi_j[i][j]+4*psi_j[i+1][j]-psi_j[i+2][j])/2/h;velx_c[i][j]=(-3*psi_c[i][j]+4*psi_c[i+1][j]-psi_c[i+2][j])/2/h;}else if(i==ilast[j]-1){velx_j[i][j]=(psi_j[i-2][j]-4*psi_j[i-1][j]+3*psi_j[i][j])/2/h;velx_c[i][j]=(psi_c[i-2][j]-4*psi_c[i-1][j]+3*psi_c[i][j])/2/h;}else{velx_j[i][j]=(psi_j[i+1][j]-psi_j[i-1][j])/2/h;velx_c[i][j]=(psi_c[i+1][j]-psi_c[i-1][j])/2/h;}}}for(i=0;i<m;i++){for(j=0;j<jlast[i];j++){vel_j[i][j]=sqrt(pow(velx_j[i][j],2)+pow(vely_j[i][j],2));vel_c[i][j]=sqrt(pow(velx_c[i][j],2)+pow(vely_c[i][j],2));}}//输出结果分布FILE *fp;fp=fopen("f:\\ESL\\YFresult.txt","w");fprintf(fp,"简单迭代结果\n");fprintf(fp,"速度势分布\n");for(j=n-1;j>=0;j--){for(i=0;i<ilast[j];i++){fprintf(fp,"%-10.6f\n",psi_j[i][j]);}}fprintf(fp,"速度分布\n");for(j=n-1;j>=0;j--){for(i=0;i<ilast[j];i++){fprintf(fp,"%-10.6f\n",vel_j[i][j]);}}fprintf(fp,"超松弛迭代结果\n");fprintf(fp,"速度势分布\n");for(j=n-1;j>=0;j--){for(i=0;i<ilast[j];i++){fprintf(fp,"%-10.6f\n",psi_c[i][j]);}}fprintf(fp,"速度分布\n");for(j=n-1;j>=0;j--){for(i=0;i<ilast[j];i++){fprintf(fp,"%-10.6f\n",vel_c[i][j]);}}fclose(fp);//输出tecplot数据FILE *fp1;fp1=fopen("f:\\ESL\\TECPLOT-result.txt","w");fprintf(fp1,"title=erwei grid\n");fprintf(fp1,"variables=x, y, psi_easy, velocity_easy, psi_SOR\n, velocity_SOR\n");fprintf(fp1,"zone t=grid,i=25,j=17,f=point\n");for(j=0;j<n;j++){for(i=0;i<m;i++){fprintf(fp1,"%-10.6f,%-10.6f,%-10.6f,%-10.6f,%-10.6f,%-10.6f\n",i*h,j*h,psi_j[i][j],vel_j[i][j],p si_c[i][j],vel_c[i][j]);}}fclose(fp1);}3）计算结果采用简单迭代，容器内的速势和速度分布速势分布（简单迭代）速度分布（简单迭代）采用超松弛迭代，容器内的速势和速度分布速势分布（SOR ） 速度分布（SOR ）2、用点源（汇）分布在对称轴的源汇模拟流体绕过NACA0012旋称体的二维轴对称势流解。

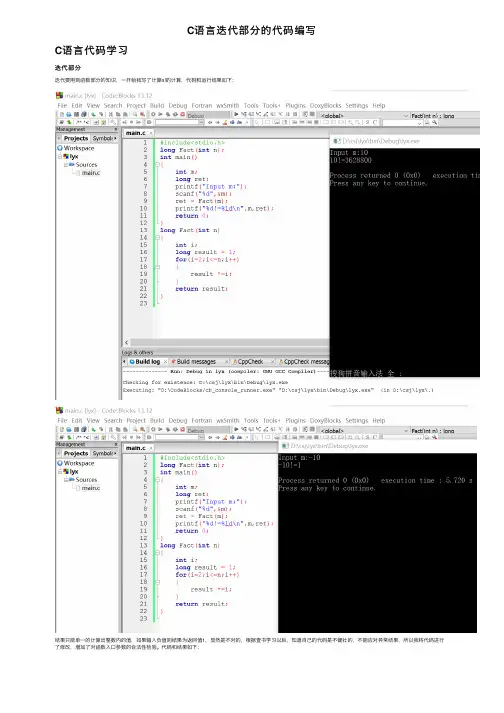
C语⾔迭代部分的代码编写
C语⾔代码学习
迭代部分
迭代要⽤到函数部分的知识，⼀开始我写了计算n!的计算，代码和运⾏结果如下：
结果只能单⼀的计算出整数内的值，如果输⼊负值则结果为返回值1，显然是不对的，根据查书学习以后，知道⾃⼰的代码是不健壮的，不能应对异常结果，所以我将代码进⾏了修改，增加了对函数⼊⼝参数的合法性检验。

代码和结果如下：
图中运⾏的结构好像还不对，-10的结果还是返回值的结果，后来发现主函数没有对函数Fact()返回值的代表异常情况发⽣的特殊值进⾏处理，修改代码以后如下：
迭代循环部分代码编写
编写代码的过程中⼀定要保证代码的完整性，⼀定要能处理⽤户输⼊的任何情况。

!。

SOR迭代法的Matlab程序function [x]=SOR_iterative(A,b)% 用SOR迭代求解线性方程组,矩阵A是方阵x0=zeros(1,length(b)); % 赋初值tol=10^(-2); % 给定误差界N=1000; % 给定最大迭代次数[n,n]=size(A); % 确定矩阵A的阶w=1; % 给定松弛因子k=1;% 迭代过程while k<=Nx(1)=(b(1)-A(1,2:n)*x0(2:n)')/A(1,1);for i=2:nx(i)=(1-w)*x0(i)+w*(b(i)-A(i,1:i-1)*x(1:i-1)'-A(i,i+1:n)*x0(i+1:n)')/A(i,i);endif max(abs(x-x0))<=tolfid = fopen('SOR_iter_result.txt', 'wt');fprintf(fid,'\n********用SOR迭代求解线性方程组的输出结果********\n\n');fprintf(fid,'迭代次数: %d次\n\n',k);fprintf(fid,'x的值\n\n');fprintf(fid, '%12.8f \n', x);break;endk=k+1;x0=x;endif k==N+1fid = fopen('SOR_iter_result.txt', 'wt');fprintf(fid,'\n********用SOR迭代求解线性方程组的输出结果********\n\n');fprintf(fid,'迭代次数: %d次\n\n',k);fprintf(fid,'超过最大迭代次数，求解失败！');fclose(fid);end常微分方程的数值解法实验目的：熟悉在Matlab平台上直接求解常微分方程初值问题试验方法1、利用改进欧拉法解方程：程序内容为：fun=@(x,y)x^(-2)-y/x;h=0.05;X=1:h:2;Y(1)=1;for i=2:21Y(i)=Y(i-1)+h/2*(fun(X(i-1),Y(i-1))+fun(X(i),Y(i-1))+h*fun(X(i-1),Y(i-1))); end;Y运行结果为：Y =Columns 1 through 91.0000 0.9989 0.9957 0.9909 0.9848 0.9778 0.9701 0.9618 0.9530Columns 10 through 180.9440 0.9348 0.9254 0.9160 0.9065 0.8971 0.8876 0.8783 0.8690Columns 19 through 210.8598 0.8508 0.8418真实解的求法为：x=1:0.05:2;y=1./x.*(log(x)+1)y =Columns 1 through 81.0000 0.9988 0.9957 0.9911 0.9853 0.9785 0.9710 0.9630Columns 9 through 160.9546 0.9459 0.9370 0.9279 0.9188 0.9096 0.9004 0.8912Columns 17 through 210.8821 0.8731 0.8641 0.8553 0.8466用四阶R-K算法解常微分方程的程序为：fun=@(x,y)x^(-2)-y/x;h=0.1;X=1:h:2;Y(1)=1;for n=2:11k1=fun(x(n-1),Y(n-1));k2=fun(x(n-1)+h/2,Y(n-1)+h/2*k1);k3=fun(x(n-1)+h/2,Y(n-1)+h/2*k2);k4=fun(x(n-1)+h,Y(n-1)+h*k3);Y(n)=Y(n-1)+h/6*(k1+2*k2+2*k3+k4)end;Y运行后了结果为：Y =Columns 1 through 91.0000 0.9957 0.9853 0.9710 0.9546 0.9370 0.9188 0.9004 0.8821Columns 10 through 110.8641 0.8466真实解的求法为：x=1:0.1:2;y=1./x.*(log(x)+1)y =Columns 1 through 91.0000 0.9957 0.9853 0.9710 0.9546 0.9370 0.9188 0.9004 0.8821Columns 10 through 110.8641 0.8466可见其精确度至少已达到0.0012、MATLAB中数值解法“ode45”为：[x1,y1] = ode45(@(x,y)x^(-2)-y/x,[1,2],y0);符号解法“dsolve”求解为：dsolve('Dy=x^(-2)-y/x','y(1) = 1','x')ans =(log(x)+1)/x画出两种算法的图形位：[x1,y1] = ode45(@(x,y)x^(-2)-y/x,[1,2],1);fplot('(log(x)+1)/x',[1,2]);hold on, plot(x1,y1,'ro');数值算法同解析算法几乎完全吻合。

西京学院数学软件实验任务书实验四实验报告一、实验名称：线性方程组的J-迭代，GS-迭代，SOR-迭代。

二、实验目的：熟悉线性方程组的J-迭代，GS-迭代，SOR-迭代，SSOR-迭代方法，编程实现雅可比方法和高斯-赛德尔方法求解非线性方程组12123123521064182514x x x x x x x x +=⎧⎪++=⎨⎪++=-⎩的根，提高matlab 编程能力。

三、实验要求：已知线性方程矩阵，利用迭代思想编程求解线性方程组的解。

四、实验原理：1、雅可比迭代法（J-迭代法）：线性方程组b X A =*，可以转变为：迭代公式(0)(1)()k 0,1,2,....k k J XXB X f +⎧⎪⎨=+=⎪⎩ 其中b M f U L M A M I B J 111),(---=+=-=，称J B 为求解b X A =*的雅可比迭代法的迭代矩阵。

以下给出雅可比迭代的分量计算公式，令),....,()()(2)(1)(k n k k k X X X X =，由雅可比迭代公式有b XU L MXk k ++=+)()1()(，既有i ni j k i iji j k iij k iij b X aXa X a +--=∑∑+=-=+1)(11)()1(，于是，解b X A =*的雅可比迭代法的计算公式为⎪⎩⎪⎨⎧--==∑∑-=+=+)(1),....,(111)()()1()0()0(2)0(1)0(i j n i j k j ij k j ij i ii k iTn X a X a b a X X X X X 2、 高斯-赛德尔迭代法（GS-迭代法）：GS-迭代法可以看作是雅可比迭代法的一种改进，给出了迭代公式：⎪⎩⎪⎨⎧--==∑∑-=+=+++)(1),....,(111)1()1()1()0()0(2)0(1)0(i j n i j k j ij k j ij i ii k iTn X a X a b a X X X X X 其余部分与雅克比迭代类似。

C语⾔复习---迭代法，⽜顿迭代法，⼆分法求根⼀：⽤迭代法求 x=√a。

求平⽅根的迭代公式为：X(n+1)= (Xn+a/Xn) /2。

#define _CRT_SECURE_NO_WARNINGS#include <stdio.h>#include <stdlib.h>#include <math.h>int main(){double x1, x2;float a;scanf("%f", &a);x2 = 1.0;do{x1 = x2;x2 = (x1 + a / x1) / 2;} while (fabs(x1-x2)>pow(10,-5));printf("value:%lf", x2);system("pause");return0;}⼆：⽤求⽅程在1.5附近的根（2x3-4x2+3x-6=0）例：⽅程求根⽜顿迭代法求⽅程 f(x)=x3+x2-3x-3=0在1.5附近的根f(x)=x^3+x^2-3x-3f'(x)=3x^2+2x-3x(n+1)=xn-f(xn)/f'(xn)令x1=1.5x2=1.777778x3=1.733361x4=1.732052x5=1.732051x6=1.732051如果精确到0.000001,则x=1.732051准确值=根号3重要公式#include <stdio.h>#include <stdlib.h>#include <math.h>int main(){double x1=0, x2;double fx1, fx2;x2 = 1.5;while (fabs(x1 - x2)>=1e-6){x1 = x2;fx1 = 2 * x1*x1*x1 - 4 * x1*x1 + 3 * x1 - 6; //f(xn)fx2 = 6 * x1*x1 - 8 * x1 + 3; //f(xn)'x2 = x1 - fx1 / fx2;}printf("value:%lf", x2);system("pause");return0;}三：⼆分法求⽅程的根给定精确度ξ,⽤⼆分法求函数f(x)零点近似值的步骤如下:1确定区间[a,b],验证f(a)·f(b)<0（这是前提，选取的区间必须满⾜这个条件）,给定精确度ξ. 2求区间(a,b)的中点c.3计算f(c).(1) 若f(c)=0,则c就是函数的零点;(2) 若f(a)·f(c)<0,则令b=c;(3) 若f(c)·f(b)<0,则令a=c.(4) 判断是否达到精确度ξ:即若|a-b|<ξ,则得到零点近似值a(或b),否则重复2-4.#include <stdio.h>#include <stdlib.h>#include <math.h>double fx(double x){return2 * x*x*x - 4 * x*x + 3 * x - 6;}int main(){double x1 , x2;double fx1, fx2;double e = 1e-6;do{printf("enter (x1,x2):\n");scanf("%lf", &x1);scanf("%lf", &x2);if (x1>x2){double temp = x1;x1 = x2;x2 = temp;}fx1 = fx(x1);fx2 = fx(x2);} while (fx1*fx2>0);if (fabs(fx1) < e)printf("solution1:%lf\n", x1);else if (fabs(fx2) < e)printf("solution2:%lf\n", x2);else{while (fabs(x1 - x2) >= e){double mid = (x1 + x2) / 2;if (fx(mid)*fx2 < 0)x1 = mid;elsex2 = mid;}printf("solution3:%lf", x2);}system("pause");return0;}。

数值分析Python 实现系列——⼆、逐次超松弛迭代法（SOR ）⼆、超松弛迭代法(SOR)1.原理:回顾:在⼀般情况下 : 收敛过慢甚⾄不收敛的B 与f ,经过对系数矩阵A 分裂成A =M −N 的形式, 使得迭代公式变为: x k +1=(I −M −1)Ax k +M −1f 雅克⽐迭代法选取 : 现将A 如下分解A =D −L −U ,D 为对⾓阵,L 为下三⾓阵,U 为上三⾓阵,取M ≡D ,取N ≡L +U ,在这⼀章中我们选取下三⾓矩阵M =1ω(D −ωL ),ω>0,其中ω为松弛因⼦,我们可以发现当ω为1时,M =D −L ,正是⾼思-赛德尔迭代法,下⾯推导迭代公式:x k +1=I −M −1A x k +M −1bx k +1=I −ω(D −ωL )−1A x k +ω(D −ωL )−1bx k +1=(D −ωL )−1((1−ω)D +ωU )x k +ω(D −ωL )−1b推导完毕,我们较为常⽤的是下式:(D −ωL )x k +1=((1−ω)D +ωU )x k +ωb以及:x (0)=(x (0)1,...,x (0)n )T ,x (k +1)i =x (k +)i +Δx i Δx i =ωb i −i −1∑j =1a ij x (k +1)j −n ∑j =1a ij x (k )j a ii i =1,2,...,n ,k =0,1,...,ω为松弛因⼦当ω>1时为超松弛迭代,当ω<1时为低松弛迭代迭代终⽌条件:max 1≤i ≤n |Δx i |=max1≤i ≤n |x (k +1)i −x (k )i |<ε,下⾯我们试试⽤Python 实现这⼀功能.2.实现:import numpy as npimport matplotlib.pyplot as pltMAX = 110 # 遍历最⼤次数A = np.array([[-4, 1, 1, 1], [1, -4, 1, 1], [1, 1, -4, 1], [1, 1, 1, -4]])b = np.array([[1], [1], [1], [1]]) # 注意这⾥取列向量omega_list = [1 + 0.005 * i for i in range(100)] # 取到不同的omega 值,观察趋势length = len(A)count = [] # 记录遍历的次数for omega in omega_list: # 遍历每⼀个omega 值times = 0x_0 = np.zeros((length, 1))x_hold = x_0 + np.ones((length, 1))while (np.linalg.norm(x_hold - x_0, ord=2) >= 10 ** (-5)) and (times <= MAX):# 遍历停⽌条件以k+1次与k 次迭代的向量差的⼆范数以及遍历最⼤次数为标准x_hold = x_0.copy() # 这⾥不要⽤赋值,要⽤copyx_new = x_0.copy()for i in range(length):# 根据迭代公式迭代x_new[i][0] = x_0[i][0] + omega * (b[i][0] - sum([A[i][j] * x_new[j][0] for j in range(i)]) - sum([A[i][j] * x_0[j][0] for j in range(i, length)])) / A[i][i]x_0 = x_new.copy()times += 1count.append(times)plt.plot(omega_list, count) # 观察omega 与迭代次数的关系plt.show()思路:1.遍历设限:第⼀种是到达精度,到达精度停⽌迭代,第⼆种是到达规定最⼤次数,这个可以⾃⼰设定.2.在根据迭代公式改变各个向量分量时,要注意遍历范围.结果:{。

课题三解线性方程组的迭代法实验目标：分别采用Jacobi迭代法，Gauss-Seidel迭代法和SOR迭代法求解线性方程组。

Jocabi迭代法：#include<iostream>#include<math.h>using namespace std;int i,j,k; //计数器int M = 2000;int Array(double ***Arr, int n){double **p;int i;p=(double **)malloc(n*sizeof(double *));if(!p)return 0;for(i=0;i<n;i++){p[i]=(double *)malloc(n*sizeof(double));if(!p[i])return 0;}*Arr=p;return 1;}void main(){double eps ;cout<<"默认最多迭代次数为2000次"<<endl<<"迭代精度为：";cin>>eps;double **matrix;int n;cout<<"矩阵大小为：";cin>>n;double *X;X= new double[n];double *Y;Y= new double[n];double *G;G= new double[n];for(i=0;i<n;i++){Y[i]=0;}if(!Array(&matrix,n))cout<<"内存分配失败！";elsecout<<"请输入矩阵:"<<endl;for( i=0;i<n;i++){for( j=0;j<n;j++){cin>>matrix[i][j];}}cout<<"请输入右端项："<<endl;double *B;B = new double[n];for(i=0;i<n;i++){cin>>B[i];}for (i = 0 ;i< n;i++){if (fabs(matrix[i][i]) < eps){cout <<"打印失败"<<endl;return;}double T = matrix[i][i];for ( j = 0 ; j< n;j++){matrix[i][j] = -matrix[i][j]/T;}matrix[i][i] = 0;G[i] = B[i]/T;}int counter = 0;while (counter < M){for (i = 0;i < n; i++){double temp = 0;for (j = 0;j<n; j++){temp = temp + matrix[i][j]*Y[j];}X[i] = G[i] + temp;}double temp = 0;for (i = 0 ;i< n ; i++){temp = temp + fabs(X[i] - Y[i]);}if (temp <= eps)break;else{for( i = 0; i < n ;i++){Y[i] = X[i];}}counter++;}cout << "迭代次数为："<<counter<<"次。

牛顿迭代法c++代码牛顿迭代法是一种数值计算方法，用于求解非线性方程的根。

它是通过不断迭代逼近的方式来逐步逼近方程的根。

在数学上，给定一个函数f(x)，我们希望找到一个近似的解x*，使得f(x*)=0。

牛顿迭代法的基本思想是利用切线逼近函数曲线，求得切线与x轴的交点，将该交点作为新的近似解，不断迭代直到满足精度要求。

牛顿迭代法的迭代公式为：x_n+1 = x_n - f(x_n)/f'(x_n)。

下面是一个用C++实现牛顿迭代法的示例代码：```cpp#include <iostream>#include <cmath>double f(double x) {return x*x - 2; // 求解方程x^2 - 2 = 0}double f_derivative(double x) {return 2*x; // 方程f(x) = x^2 - 2的导数为2x}double newton_method(double x0, double epsilon, intmax_iterations) {double x = x0;int iteration = 0;while (iteration < max_iterations) {double fx = f(x);double f_derivative_x = f_derivative(x);if (std::abs(fx) < epsilon) {std::cout << "Found solution: x = " << x << std::endl;return x;}if (std::abs(f_derivative_x) < epsilon) {std::cout << "Derivative is close to zero. Exiting." << std::endl;return std::numeric_limits<double>::quiet_NaN(); // 返回NaN表示迭代失败}x = x - fx/f_derivative_x;++iteration;}std::cout << "Maximum iterations reached. Exiting." << std::endl;return std::numeric_limits<double>::quiet_NaN(); // 返回NaN 表示迭代失败}int main() {double x0 = 1.0; // 初始值double epsilon = 1e-6; // 精度要求int max_iterations = 1000; // 最大迭代次数double root = newton_method(x0, epsilon, max_iterations);return 0;}```以上代码中，我们定义了两个函数f(x)和f_derivative(x)，分别表示了要求解的非线性方程和该方程的导数。

c语言多项式迭代多项式迭代通常是指通过迭代的方式求解多项式的值。

在C语言中，可以使用循环结构来实现多项式的迭代。

假设我们有一个多项式f(x) = ax^3 + bx^2 + cx + d，我们可以通过以下代码实现多项式的迭代：```cinclude <>int main() {double a, b, c, d, x, y;int n;printf("请输入多项式的系数a, b, c, d：");scanf("%lf %lf %lf %lf", &a, &b, &c, &d);printf("请输入x的值：");scanf("%lf", &x);printf("请输入迭代的次数n：");scanf("%d", &n);y = a x x x + b x x + c x + d; // 计算多项式的初始值for (int i = 1; i <= n; i++) {y = a y y y + b y y + c y + d; // 迭代计算多项式的值}printf("迭代%d次后，多项式f(x)的值为：%lf\n", n, y);return 0;}```在上述代码中，我们首先从用户输入中获取多项式的系数a、b、c、d以及x的值和迭代的次数n。

然后，我们计算多项式的初始值y，并使用循环结构进行n次迭代计算，每次迭代都使用上一次计算得到的y值来计算新的y 值。

最后，我们输出迭代n次后多项式的值。

方程组迭代法实现在数值分析课程中，有许多诸如迭代之类的计算方法，可以非常有效通过求迭代近似解决许多无法求，或很难求精确解的问题。

但这类方法往往有着非常巨大的计算量，并不适合通过人力自行解决，所以我便打算自己编写一个程序，可以实现三种求方程组解的迭代法。

另外，由于SOR 法会有寻找最佳的w 值的需求，所以也一并实现了寻找SOR 法的最佳w 。

在编写程序之前，应对三种方法的迭代过程充分了解。

雅可比迭代法：()()()112213311112212233222212211()1n n n n n n n n nn n n nn x a x a x a x b a x a x a x a x b a II x a x a x a x b a ⎧=----+⎪⎪⎪=----+⎪⎨⎪⎪⎪=---+⎪⎩高斯-赛德尔法：()()()(1)()()()11221331111(1)(1)()()22112332222(1)(1)(1)(1)()()1122,11,11(1)(1)1221111k k k k n n k k k k n n k k k k k k i i i i i i i i i in n i ii k k n n n n nn x a x a x a x b a x a x a x a x b a x a x a x a x a x a x b a x a x a x a +++++++--++++=----+=----+=-------+=--()(1)(1)()k k nn n n IV a x b ++⎧⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪--+⎪⎩SOR 法：(1)()k k w X L X f+=+根据以上的迭代法的思想，设计了程序，运行界面如下：该程序在使用过程中对用户进行引导，用户可自行选择方法，并输入方程组，程序为用户提供解答，并给出迭代次数。

如图所示，其中高斯赛德尔法输入了课本第六章的例题中1.2式，而SOR法则是课本第六章习题的第八题，并且还发现课本第八题的答案有误，经我人工检验后，上述程序中的解才是正确答案。

迭代法迭代法也称辗转法，是一种不断用变量的旧值递推新值的过程,跟迭代法相对应的是直接法（或者称为一次解法），即一次性解决问题。

迭代法又分为精确迭代和近似迭代。

“二分法”和“牛顿迭代法”属于近似迭代法。

迭代算法是用计算机解决问题的一种基本方法。

它利用计算机运算速度快、适合做重复性操作的特点，让计算机对一组指令（或一定步骤）进行重复执行，在每次执行这组指令（或这些步骤）时，都从变量的原值推出它的一个新值。

利用迭代算法解决问题，需要做好以下三个方面的工作：一、确定迭代变量。

在可以用迭代算法解决的问题中，至少存在一个直接或间接地不断由旧值递推出新值的变量，这个变量就是迭代变量。

二、建立迭代关系式。

所谓迭代关系式，指如何从变量的前一个值推出其下一个值的公式（或关系）。

迭代关系式的建立是解决迭代问题的关键，通常可以使用递推或倒推的方法来完成。

三、对迭代过程进行控制。

在什么时候结束迭代过程？这是编写迭代程序必须考虑的问题。

不能让迭代过程无休止地重复执行下去。

迭代过程的控制通常可分为两种情况：一种是所需的迭代次数是个确定的值，可以计算出来；另一种是所需的迭代次数无法确定。

对于前一种情况，可以构建一个固定次数的循环来实现对迭代过程的控制；对于后一种情况，需要进一步分析出用来结束迭代过程的条件。

例 1 ：一个饲养场引进一只刚出生的新品种兔子，这种兔子从出生的下一个月开始，每月新生一只兔子，新生的兔子也如此繁殖。

如果所有的兔子都不死去，问到第12 个月时，该饲养场共有兔子多少只？分析：这是一个典型的递推问题。

我们不妨假设第 1 个月时兔子的只数为u 1 ，第 2 个月时兔子的只数为u 2 ，第 3 个月时兔子的只数为u 3 ，……根据题意，“这种兔子从出生的下一个月开始，每月新生一只兔子”，则有u 1 ＝ 1 ，u 2 ＝u 1 ＋u 1 ×1 ＝ 2 ，u 3 ＝u 2 ＋u 2 ×1＝ 4 ，……根据这个规律，可以归纳出下面的递推公式：u n ＝u n － 1 × 2 (n ≥ 2)对应u n 和u n － 1 ，定义两个迭代变量y 和x ，可将上面的递推公式转换成如下迭代关系：y=x*2x=y让计算机对这个迭代关系重复执行11 次，就可以算出第12 个月时的兔子数。

一、数值求解如下正方形域上的Poisson 方程边值问二、2222(,)2,0,1(0,)(1,)(1),01(,0)(,1)0,01u u f x y x y x y u y u y y y y u x u x x ⎧⎛⎫∂∂-+==<<⎪ ⎪∂∂⎪⎝⎭⎨==-≤≤⎪⎪==≤≤⎩二、用椭圆型第一边值问题的五点差分格式得到线性方程组为2,1,1,,1,10,1,,0,141,?,?,?,?0,1i j i j i j i j i j ijj N j i i N u u u u u h f i j N u u u u i j N -+-+++----=≤≤====≤≤+，写成矩阵形式Au=f 。

其中 三、基本原理程序步骤：所有的步骤基本一致 1． 设置u ，n ，并给u ，n 赋初值； 2． While 语句循环，到的6步 3． Up 我第K 次迭代的值； 4． 分别进行计算，sum=0; 例如:Jacobi :sun= sum+A(i,j)*Ub; SOR 和Gauss_Seidel= sum+A(i,j)*u; 各自进行相应的下不运算。

5． 计算|Up-u|<ep 的绝对值，判断是否停机 6． 如果小于规定误差，迭代终止； 7． 输出结果u 和迭代次数k8． 在块的迭代中调用了追赶法的求解子程序zg ，在SOR 设计了A 得自动生成子程序creat_matix.1122N N v b v b u f v b ⎛⎫⎛⎫ ⎪ ⎪ ⎪⎪== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭4114114ii A -⎛⎫ ⎪- ⎪= ⎪- ⎪-⎝⎭11,12,1,121,22,2,21,2,,2211,12,1,121,22,2,221,2,,(,,...,),(,,...,),......,(,,...,)(,,...,)?,(,,...,)?,......,(,,...,)?1,999,0.10.011T T N N TN N N N N T T N N T N N N N N v u u u v u u u v u u u b h f f f b h f f f b h f f f h N h N ====+=+=+===+取或则或,2,,1,2,...,i j f i j N==1122NN A I I A A I IA -⎛⎫ ⎪-⎪= ⎪- ⎪-⎝⎭四、编写求解线性方程组Au=f的算法程序，用下列方法编程计算，并比较计算速度。