《距离》阅读及答案

部编版五年级语文上册《阅读理解》专项练习题（含答案）他落榜了！一千二百年前。

榜纸那么长那么大，可就是没有他的名字。

竟单单容不下他的名字“张继”那两个字。

考中的人，姓名一笔一画写在榜单上，天下皆知。

奇怪的是，在他的感觉里，考不上才更是天下皆知，这使他羞惭沮丧。

离开京城吧！议好了价，他踏上小舟。

本来预期的情节不是这样的，本来也许有插花游街，马蹄轻疾的风流，有衣锦还乡袍笏加身的荣耀。

然而寒窗十年，虽有他的悬梁刺股，琼林宴上，却没有他的一角席次。

船行似风。

江枫如火。

这天黄昏，船来到了苏州。

但，这美丽的古城，对张继而言，也无非是一个触动愁情的地方。

如果说白天有什么该做的事，对一个读书人而言，就是读书吧！夜晚呢？在这样一个忧伤的夜晚，在异乡的江畔，在秋冷雁高的季节，容许落魄的士子放肆他的忧伤。

江水，可以无限度地收纳古往今来一切不顺遂之人的泪水。

江水睡了，船睡了，船家睡了，岸上的人也睡了。

唯有他，张继，醒着，夜愈深，愈清醒，清醒如败叶落尽的枯树，似梁燕飞去的空巢。

月亮西斜了，一副意兴阑珊的样子。

有鸟啼粗嘎嘶哑，是乌鸦。

那月亮被它叫得更暗淡了。

江岸上，想已霜结千草。

夜空里，星子亦如清霜。

在须角的眉梢，他感觉，似乎也森然生凉。

……——摘自张晓风《不朽的失眠》拓展资料：张继于“天宝十二年（753）礼部侍郎杨浚下及第”，也就是说考取了进士。

天宝十四年（755）一月爆发了安史之乱，天宝十五年（756）六月，唐玄宗仓皇奔蜀。

因为当时江南政局比较安定，所以不少文士纷纷逃到今江苏、浙江一带避乱，其中也包括张继。

一个秋天的夜晚，诗人泊舟苏州城外的枫桥。

江南水乡秋夜幽美的景色，吸引着这位怀着旅愁的客子，使他领略到一种情味隽永的诗意美，写下了这首意境清远的小诗。

此诗精确而细腻地描述了一个客船夜泊者对江南深秋夜景的观察和感受，勾画了月落乌啼、霜天寒夜、江枫渔火、孤舟客子等景象，有景有情有声有色。

此外，这首诗也将作者羁旅之思，家国之忧，以及身处乱世尚无归宿的顾虑充分地表现出来，是写愁的代表作。

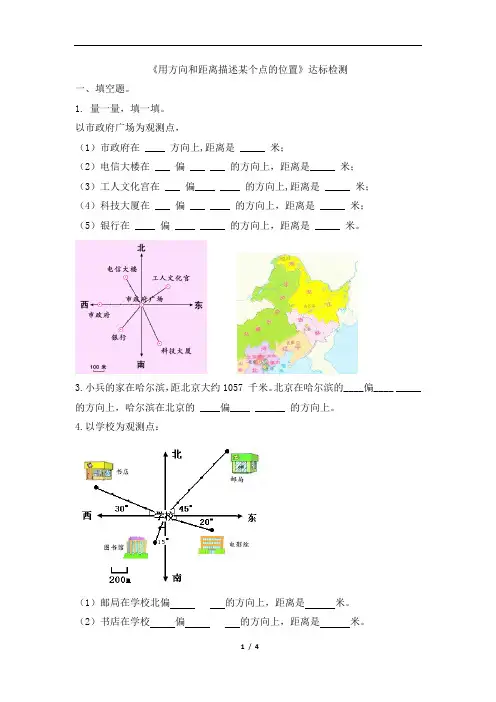
《用方向和距离描述某个点的位置》达标检测一、填空题。

1. 量一量，填一填。

以市政府广场为观测点，（1）市政府在 ____ 方向上,距离是 _____ 米；（2）电信大楼在 ___ 偏 ___ ___ 的方向上，距离是_____ 米；（3）工人文化宫在 ___ 偏____ ____ 的方向上,距离是 _____ 米；（4）科技大厦在 ___ 偏 ___ ____ 的方向上，距离是 _____ 米；（5）银行在 ____ 偏 ____ _____ 的方向上，距离是 _____ 米。

3.小兵的家在哈尔滨，距北京大约1057 千米。

北京在哈尔滨的____偏____ _____的方向上，哈尔滨在北京的 ____偏____ ______ 的方向上。

4.以学校为观测点：（1）邮局在学校北偏的方向上，距离是米。

（2）书店在学校偏的方向上，距离是米。

（3）图书馆在学校偏的方向上，距离是米。

（4）电影院在学校偏的方向上，距离是米。

5.以灯塔为观察点：（1）A岛在偏的方向上，距离是千米；（2）B岛在偏的方向上，距离是千米。

二、用心选一选。

1.北偏西30°，还可以说成（）。

A.南偏西30°B.西偏北30°C.西偏北60°2.如下图：（1）小强看小林在（）。

A.北偏东50°B.东偏北50°C.西偏南40°（2）小林看小强在（）。

A.北偏东50°B.东偏北50°C.西偏南40°3.如下图：（1）以超市为观察点，商场在（）。

A.正南方B.正西方C.正东方（2）以超市为观察点，学校在（）。

A.东偏南30°B. 南偏东30°C.西偏北30°（3）从绿苑小区出发，走（）站就到学校了。

A.3B.4C.54.山东省在北京市的（）。

A.西偏南方向B.东偏南方向C.西偏北方向《用方向和距离描述某个点的位置》达标检测参考答案一、1.（1）正西 400（2）北西 30° 300（3）北东 55° 300（4）南东 25° 400（5）南西40° 3003.西南 45°东北 45°4.（1）东 45° 1000（2）西北 30° 800（3）南西 15° 400（4）东南 20° 6005.（1）北东 3（2）西南 4二、1.C2.（1）A （2）C3.（1）B（2）A（3）D4.B。

九年级语文上册第一单元名著导读《艾青诗选》练习题（含答案）九年级语文上册第一单元名著导读《艾青诗选》练习题1．下面这段节选出自于艾青的哪首长诗？抒发了作者怎样的怀念？大堰河，深爱着她的乳儿/在年节里，为了他，忙着切那冬米的糖/为了他，常悄悄地走到村边的她的家里去/为了他，走到她的身边叫一声“妈"/大堰河，把他的画的大红大绿的关云长贴在灶边的墙上/大堰河，会对他的邻居夸口赞美她的乳儿/大堰河曾做了一个不能对人说的梦/在梦里，她吃着她的乳儿的婚酒，坐在辉煌的结彩的堂上/而她的娇美的媳妇亲切的叫她“婆婆”……2．《大堰河——我的保姆》是艾青的成名之作，这首诗感情真挚深切。

请结合这首诗的内容说说这首诗给你带来哪些情感体验。

3．阅读《艾青诗选》节选片断，回答问题：（甲）你住在哪里？/我住在万年的深山里/我住在万年的岩石里/你的年纪——/我的年纪比山的更大/比岩石的更大/你从什么时候沉默的？/从恐龙统治了森林的年代/从地壳第一次震动的年代/你已死在过深的怨愤里了么？/死？不，不，我还活着——/请给我以火，给我以火！（乙）我带着金黄的花束，我带着林间的香气，我带着亮光和温暖，我带着满身的露水快起来，快起来快从枕头里抬起头来，睁开你的被睫毛盖着的眼，让你的眼看见我的到来。

(1)（乙）段中的“我"是指代什么？(2)这两首诗分别作于1937年和1942年，正是中华民族处于危急存亡的关头。

请结合时代背景谈谈诗人歌咏了什么精神？4．作家聂华苓说：“艾青的诗，好在那雄浑的力量，直截了当的语言，强烈鲜明的意象。

”请结合艾青诗作，任选一个角度，谈谈你对艾青诗歌特色的理解。

5．《艾青诗选》中的《吹号者》写于1939年，请结合《吹号者》节选内容，说说《吹号者》一诗中“号声"的意蕴。

在震撼天地的冲杀声里，/在决不回头的一致的步伐里，/在狂流般奔涌着的人群里，/在紧密的连续的爆炸声里，/我们的吹号者/以生命所给与他的鼓舞，/一面奔跑，一面吹出了那短促的，急迫的，激昂的，/在死亡之前决不中止的冲锋号，/那声音高过了一切，/又比一切都美丽，……/他被一颗旋转过他的心胸的子弹打中了！/他寂然地倒下去/没有一个人曾看见他倒下去，/他倒在那直到最后一刻/都深深地爱着的土地上，/然而，他的手却依然紧紧地握着那号角；/听啊，/那号角好像依然在响……6．请根据阅读积累，在下面表格的横线处填写相应人物姓名。

2022-2023学年七年级数学上册第三章《整式及其加减》测试卷一、单选题1．填在下面各正方形中的四个数之间都有一定的规律，按此规律可得到+++a b c d 的值为（）A ．355B ．356C ．435D ．4362．若单项式25m x y +-与单项式2136n y x -的和仍为单项式，则2m n -的值为（）A ．6B ．1C ．3D ．1-3．已知一个多项式与239x x +的和等于2341x x +-，则这个多项式是（）A ．51x --B ．51x +C ．131x --D ．131x +4．下列结论正确的个数是（）①2-不是单项式②多项式3527x y xy --是三次三项式③232π3a b c的系数是23，次数是6④233m n -的次数为4A ．0个B ．1个C ．2个D ．3个5．多项式23211332x y xy -+的次数为（）A ．5B ．3C ．7D ．86．已知53x y -=-，则55x y -+的值为（）A ．0B ．2C ．5D ．87．一本笔记本的原价为a 元，降价后每本比原来便宜了b 元，小明买了4本这样的笔记本，则他一共花费了（）A ．()44a b -元B ．()4a b -元C ．()4a b -元D ．4b 元8．按如图所示的运算程序，当输入3x =，6y =时，输出的结果为（）A ．1B ．6C ．45D ．819．若()22m -与3n +互为相反数，则m n 的值是（）A ．8-B ．8C ．9-D ．910．当=1x -时，3238ax bx -+的值为18，则1282b a -+的值为（）A ．40B ．42C ．46D ．56二、填空题11．在式子1x，1x y ++，2022，a -，23x y -，13x +中，整式的个数是______个．12．已知520a b ++-=，则27a b -+的值为___________13．a ，b 两数平方的和除以3的商可以表示为______．14．已知有理数a 、b 、c 满足1,2,3a b c ===，且a b c a b c +-=+-，则a b c ++=__________．15．如关于x ，y 的多项式2347514x y mxy y xy +-+化简后不含二次项，则m =______．16．已知关于x 的多项式||2(4)31m m x x ---+是二次三项式，则m =________，当=1x -时，该多项式的值为________．17．对于任何有理数，我们规定符号a b cd的意义是a b ad bc c d =-，如121423234=⨯-⨯=-，当23(1)0x y -++=时，2221x y x --值为______．18．规定：()3f x x =-，()2g y y =+，例如()2235f -=--=，()2220g -=-+=．则式子()()11f x g x -++的最小值是__________．三、解答题19．已知()2230a b -++=，求代数式2222332232a b ab ab a b ab ab ⎡⎤⎛⎫---++ ⎪⎢⎥⎝⎭⎣⎦的值．20．已知代数式2=2+3+21A x xy y -，22B x xy x -=++．(1)当=1x -，2y =时，求2A B -的值；(2)若2A B -的值与x 的取值无关，求y 的值．21．某超市销售茶壶、茶杯，每只茶壶定价20元，每只茶杯定价4元．今年“双十一”期间开展促销活动，向顾客提供两种优惠方案：方案一：每买一只茶壶就赠一只茶杯；方案二：茶壶和茶杯都按定价的90%付款．某顾客计划到这家超市购买6只茶壶和x 只茶杯茶（杯数多于6只）．(1)用含x 的代数式分别表示方案一与方案二各需付款多少元？(2)当25x =时，若规定每位顾客只能在以上两种方案中任选一种，请通过计算说明该顾客选择上面两种购买方案中哪一种更省钱？22．某超市新进了一批百香果，进价为每斤8元，为了合理定价，在前五天试行机动价格，售出时每斤以10元为标准，超出10元的部分记为正，不足10元的部分记为负，超市记录的前五天百香果的销售单价和销售数量如下表所示，第1天第2天第3天第4天第5天销售单价（元）1+2-3+1-2+销售数量（斤）2035103015(1)前5天售卖中，单价最高的是第___________天；单价最高的一天比单价最低的一天多___________元；(2)求前5天售出百香果的总利润；(3)该超市为了促销这种百香果，决定推出一种优惠方案：购买不超过6斤百香果，每斤12元，超出6斤的部分，每斤9.6元．若嘉嘉在该超市买(6)x x >斤百香果，用含x 的式子表示嘉嘉的付款金额．23．为了节约用水，某自来水公司采取以下收费方法：若每户每月用水不超过10吨，则每吨水收费2.6元；若每户每月用水超过10吨，则超过的部分按每吨3元收费．8月份李老师家里用水a 吨(10a >)．(1)请用含a 的代数式表示李老师8月份应交的水费．(2)当13a =时，求李老师8月份应交水费多少元？24．已知若a b 、互为相反数，、c d 互为倒数，m 的绝对值为2022．(1)直接写出a b +，cd ，m 的值；(2)求a bm cd m+++的值．25．已知多项式2134331m x y x y x +-+--是五次四项式，单项式333n m x y z -与该多项式的次数相同．（1）求m 、n 的值．（2）若2|1|(2)0x y -+-=，求这个多项式的值．26．阅读下面的材料，完成相关的问题．在学习绝对值时，我们已经知道绝对值的几何含义，如|5-1|表示5，1在数轴上对应的两点之间的距离；|5+1|=|5-（-1）|，所以|5+1|表示5，-1在数轴上对应的两点之间的距离；|5|=|5-0|，所以|5|表示5在数轴上对应的点到原点的距离．一般地，点A 、B 在数轴上分别表示数m ，n ，那么点m ，n 之间的距离等于|m -n |．（1）利用数轴探究：①若点P 表示数2，则在同一数轴上到点P 的距离为5个单位长度的点表示的数是；②|x +3|+|x -2|有最值（填“大”或“小”），此时整数x 的值为；（2）若点M 、N 、P 是数轴上的三点，点M 表示的数为4，点N 表示的数为-2，动点P 表示的数为x ．若12PM PN +=，则x 的值为；（3）已知多项式32235x y xy --的常数项是a ，次数是b ，a 、b 两数在数轴上所对应的点分别为A 、B ，若点A ，点B 同时沿数轴正方向运动，点A 的速度是点B 的3倍，且2秒后，使点B 到原点的距离是点A 到原点的距离的2倍，求点B 的速度．27．为了加强公民的节水意识，合理利用水资源，某市采用价格调控的手段达到节水的目的，该市自来水收费的价目表如表（注：水费按一个月结算一次）：请根据价目表的内容解答下列问题：每月用水量（m 3）单价（元/m 3）不超出26m 3的部分3超出26m 3不超出34m 3的部分4超出34m 3的部分7(1)填空：若该户居民1月份用水20立方米，则应收水费元；若该户2月份用水30立方米，则应收水费元；(2)若该户居民3月份用水x 立方米（其中2634x £＜），则应收水费多少元？（结果用含x 的代数式表示）(3)若该户居民3月份用水a 立方米（其中34a ＞），则应收水费多少元？（结果用含a 的代数式表示）28．在解决数学问题的过程中，我们常用到“分类讨论”的数学思想，下面是运用分类讨论的数学思想解决问题的过程，请仔细阅读，并解答题目后提出的【探究】．【提出问题】两个不为0的有理数a ，b 满足a ，b 同号，求a a b b+的值．【解决问题】解：由a 、b 同号且都不为0可知a 、b 有两种可能：①a 、b 都是正数：②a 、b 都是负数．①若a 、b 都是正数，即0a >，0b >，有a a =及b b =，则112aa bba b++==+=；②若a 、b 都是负数，即0a <，0b <，有a a =-及b b =-，()()()()112a b a b a b a b--+=+=-+-=-；所以a a bb+的值为2或2-．【探究】请根据上面的解题思路解答下面的问题：(1)已知3a =且7b =，且a b <，求a b +的值．(2)两个不为0的有理数a ，b 满足a ，b 异号，求a a b b+的值．(3)若0abc >，则||||||a b c a b c++的值可能是多少？参考答案：1．D2．D3．A4．B5．A6．D7．A8．A9．D10．B11．512．-513．223a b +14．4-或0或615．2-16．4-4-17．28-18．719．解：2222332232a b ab ab a b ab ab⎡⎤⎛⎫---++ ⎪⎢⎥⎝⎭⎣⎦()222232233a b ab ab a b ab ab =--+++222232233a b ab ab a b ab ab =-+--+2ab ab =+，∵()2230a b -++=，()22030a b -≥+≥，，∴()22030a b -=+=，，∴2030a b -=+=，，∴23a b ==-，，∴原式()()2232318612=⨯-+⨯-=-=．20．（1）解：由题意可得，22223212(2)A B x xy y x xy x -=++---++2223212224x xy y x xy x =++--+--5225xy x y =-+-，当=1x -，2y =时，252255(1)22(1)225102459A B xy x y -=-+-=⨯-⨯-⨯-+⨯-=-++-=-；（2）解：由题意可得，2(52)25A B x y y -=-+-，∵2A B -的值与x 的取值无关，∴520y -=，解得：25y =；21．（1）解：某顾客计划到这家超市购买6只茶壶和x 只茶杯（茶杯数多于6只），根据题意可得：方案一：()()62046496x x ⨯+-=+元；方案二：()()620490% 3.6108x x ⨯+⨯=+元；（2）当25x =时，方案一需付款42596196⨯+=（元），方案二需付款3.625108198⨯+=（元），∵196198<，∴选择方案一更省钱．22．、（1）解：∵+3+2+1>1>2>>--，∴前5天售卖中，单价最高的是第3天；∵+3(2)=5--∴价最高的一天比单价最低的一天多5元，故答案为：3，5；（2）解：以10元为标准每斤百香果所获的利润为108=2-（元），前5天售出百香果的总利润为：20(12)35(22)10(32)30(12)15(22)⨯++⨯-++⨯++⨯-++⨯+=203350105301154⨯+⨯+⨯+⨯+⨯=200（元），答：前5天售出百香果的总利润为200元；（3）解：根据题意得，()()1269.669.614.4x x ⨯+-=+元，即嘉嘉在该超市买(6)x x >斤百香果，付款金额为()9.614.4x +元．23．、（1）()26310a +-（2）当13a =时())26310(35a +-=元24．（1）解： a b 、互为相反数，、c d 互为倒数，m 的绝对值为2022，012022a b cd m ∴+===±，，；（2）解：当2022m =时，02022120232022a b m cd m +++=++=，当2022m =-时，02022120212022a b m cd m +++=-++=--，∴a bm cd m+++的值为2023或2021-．25．、解：（1）∵多项式2134331m x y x y x +-+--是五次四项式，∴13m +=，解得2m =，∵单项式333n m x y z -与该多项式的次数相同，∴3315n m +-+=，即33215n +-+=，解得1n =，∴2m =，1n =；（2）∵2|1|(2)0x y -+-=，∴10x -=，20y -=，∴1x =，2y =，由（1）得这个多项式为：2334331x y x y x -+--，∴2334331x y x y x -+--＝233431212311-⨯⨯+⨯-⨯-＝24231-+--＝26-，所以这个多项式的值为26-．26．、解：（1）①设在同一数轴上到点P 的距离为5个单位长度的点表示的数是x ，由题意得：25x -=，∴25x -=±，∴3x =-或7x =，故答案为：-3或7；②当2x >时，3232215x x x x x ++-=++-=+>；当3x <-时，()()3232215x x x x x ++-=-+--=-->；当32x -≤≤时，()32325x x x x ++-=+--=；∴32x x ++-有最小值，此时32x -≤≤；故答案为：小，32x -≤≤；（2）∵点M 、N 、P 是数轴上的三点，点M 表示的数为4，点N 表示的数为-2，动点P 表示的数为x ，∴4PM x =-，2PN x =+，∵12PM PN +=，∴4212x x -++=，当>4x 时，42422212x x x x x -++=-++=-=，解得7x =；当<2x -时，()()42422212x x x x x -++=---+=-+=，解得5x =-；当24x -≤≤时，()()4242612x x x x -++=--++=≠；∴综上所述，5x =-或7x =，故答案为：-5或7；（3）∵多项式32235x y xy --的常数项是a ，次数是b ，∴53a b =-⎧⎨=⎩，设B 的运动速度为v ，则A 的运动速度为3v ，则2s 后A 表示的数为56v -+，B 表示的数为32v +，∴B 到原点的距离32v =+，A 到原点的距离为56v -+，∵2秒后，使点B 到原点的距离是点A 到原点的距离的2倍，∴32=256v v +-+，解得12v =或1310v =．27．（1）∵2026<∴用水20立方米，则应收水费为20360⨯=元；∵263034<<∴用水30立方米，则应收水费为()2633026494⨯+-⨯=元；故答案为：60；94．（2）依题意得：应收水费为326426x ´+´-（）426x -=（）元．故应收水费426x -（）元；（3）依题意得：应收水费为32643426734a ´+´-+-（）（）7128a -=（）元．故应收水费7128a -（）元．28．（1）解：∵3a =，7b =，∴3a =或3-，7b =或7-，∵a b <，∴3a =，7b =或3a =-，7b =，当3a =，7b =时3710a b +=+=，当3a =-，7b =时374a b +=-+=，综上，a b +的值10或4；（2）解：由a 、b 异号，可知：①0a >，0b <；②a<0，0b >，当0a >，0b <时，110a ba b +=-=；当a<0，0b >时，110a ba b+=-+=，综上，a ab b+的值为0；（3）解：由题意得：a ，b ，c 三个有理数都为正数或其中一个为正数，另两个为负数．①当a ，b ，c 都是正数，即0a >，0b >，0c >时，则：||||||1113a b c a b ca b c a b c++=+=++=；②当a ，b ，c 有一个为正数，另两个为负数时，设0a >，0b <，0c <，则：||||||1111a b c a b c a b c a b c --++=++=--=-所以：||||||a b c a b c++的值为3或1-．。

1 负数的初步认识项目 内 容1.在下列生活现象中填出相反的情况。

(1)六(1)班上学期转来3人,本学期( )2人。

(2)张阿姨做生意,2月份( )1500元,3月份亏损200元。

2.认识相反意义的量。

零上16℃用16℃表示,零下16℃用( )表示。

3.认识正、负数。

存折中“支出(-)或存入(+)”一栏有2000、-500这两个数据,它们分别表示( )、( )。

4.正、负数的读、写。

-38读作( ) +6.3读作( ) 5.通过预习,我知道了像-16,-500,-38,-0.4,…这样的数叫做( );+16,+20,38,+6.3,…这样的数叫做( )。

正数前面可以加“+”号,也可以( ),但是“-”( )省去。

6.( )既不是正数,也不是负数。

7.哪些是正数?哪些是负数?-6 1.5+27 0 -5.2 -34 +328.通常,我们规定海平面的海拔高度为0m 。

珠穆朗玛峰的海拔高度为( )m,吐鲁番盆地的海拔高度约为( )m 。

温馨 提示知识准备:整数、分数、小数等数的相关知识。

参考答案1.(1)转走(2)盈利 2.-16℃3.存入2000元支出500元4.负八分之三正六点三5.负数正数省略不能6.0+327.正数:1.5 +27负数:-6 -5.2 -348.8844.43 -1552负数的大小比较项目内容1.+2.1读作( ) -6读作( )2.某日傍晚,黄山的气温由上午的零上2摄氏度下降了7摄氏度,这天傍晚黄山的气温是多少摄氏度?3.在直线上,以0为分界线,右边的数是( ),左边的数是( ),所有的数都可以用( )上的点来表示。

4.比较数的大小。

下面是未来一周每天的最低气温情况,请你比较它们的大小。

-8( )-6( )-4( )-3( )-2( )0( )25.通过预习,我知道了在直线上可以表示出正数、0和负数,0右边的数是( )数,左边的数是( )数。

负数都比0( ),正数都比0( )。

名著导读《星星离我们有多远》导读与练习【作者简介】卞毓麟(1943— )，1965年南京大学天文系毕业。

现为中国科学院北京天文台教授，中国天文学会常务理事，天文学名词审定委员会主任，中国科普作家协会会员，上海科技教育出版社版权部主任，上海天文学会副理事长，中国科普作协翻译工作委员会副主任。

卞毓麟从事科普创作20多年，参与编著、翻译的科普图书有70余种，发表的科普文章约400篇，累计字数400余万。

他的读者从刚识字的娃娃到非本行的科学家都有，他的科普佳作不仅熔科学性趣味性于一炉，且极富人文色彩，如《恐龙·陨石及社会文明》《“水调歌头·明月几时有”科学注》《莎士比亚外篇》《叫三声夸克》等，无不描绘着科学与文化一个个闪光的交点。

他曾多次获得表彰，中国科普作家协会表彰他为“建国以来，特别是科普作协成立以来成绩突出的科普作家”；在1996年的全国科普工作会议上，他又被授予“全国先进科普工作者”的称号。

【作品概述】《星星离我们有多远》是科普作家卞毓麟创作的科普著作。

全书包含“序曲”“尾声”共十一篇。

序曲：从郭沫若的诗歌《天上的街市》和“牛郎织女”的神话传说引入，简要介绍星座的概念、划分与命名的有关知识。

大地的尺寸西方科学家在研究星星的距离的过程中，首先弄懂了地球是圆形的，并且初步测出了地球的周长；接着中国唐代科学家第一次进行了子午线的实测工作；后来的科学家们利用三角网，测定出了子午线的长度，更精确地测出了地球的形状。

明月何处有公元前3世纪小亚细亚的阿里斯塔克初步推算出了月球的大小，指出地球不是字宙中最大的天体，古希腊的天文学家伊巴谷初步测量出了月球到地球的距离；法国天文学家拉卡伊和他的学生拉朗德利用三角法测量出了月亮到地球的距离；后来的科学家先用雷达，再用激光精确地测量出了月亮到地球的距离。

太阳离我们多远德国天文学家开普勒在研究中发现了行星运动的三大定律；接着介绍“视差”的概念，意大利天文家卡西尼领导筹建了巴黎天文台，并测量出了火星视差；后来哈雷，潘格雷、恩克等天文学家利用“金星凌日”的机会测定了大阳视差。

⾼考语⽂北京卷《海棠花》阅读答案⾼考语⽂北京卷《海棠花》阅读答案 海棠花 季羡林 ①早晨到研究所去的路上，抬头看到⼈家的园⼦⾥正开着海棠花，缤纷烂漫地开成⼀团。

这使我想到⾃⼰故乡院⼦⾥的那两棵海棠花，现在想也正是开花的时候了。

②我虽然喜欢海棠花，但却似乎与海棠花⽆缘。

⾃家院⼦⾥虽然就有两棵，但是要到记忆⾥去搜寻开花时的情景，却只能搜到很少⼏个断⽚。

记忆中最深刻的是⼀个黄昏，在家南边⼀个⾼崖上游玩，向北看，看到⼀⽚屋顶，其中纵横穿插着⼀条条的空隙，是街道。

虽然也可以幻想出⼀⽚海浪，但究竟单调得很。

可是在这⼀⽚单调的房顶中却地看到⼀树花的尖顶，绚烂得像是西天的晚。

当时我真有说不出的⾼兴，其中还夹杂着⼀点⼉渴望，渴望⾃⼰能够⾛到这树下去看上⼀看。

于是我就按着这⼀条条的空隙数起来，终于发现，那就是⾃⼰家⾥那两棵海棠树。

我⽴刻跑下崖头，回到家⾥，站在海棠树下，⼀直站到淡红的花团渐渐消逝到黄昏⾥去，只朦胧留下⼀⽚淡⽩。

③但是这样的情景只有过⼀次，其余的春天我都是在北京度过的。

北京是古⽼的都城，尽有许多机会可以作赏花的韵事，但是⾃⼰却很少有这福⽓。

我只到中⼭公园去看过芍药，到颐和园去看过⼀次⽟兰。

⾄于海棠，不但是很少看到，连因海棠⽽出名的寺院似乎也没有听说过。

北京的春天是⾮常短的，短到⼏乎没有。

最初还是残冬，可是接连吹上⼏天⼤风，再⼀看树⽊都长出了嫩绿的叶⼦，已经是夏天了。

④夏天⼀来，我就⼜回到故乡去。

院⼦⾥的两棵海棠已经密密层层地盖满了⼤叶⼦，很难令⼈回忆起这上⾯曾经开过团团滚滚的花。

晚上吃过饭后，就搬了椅⼦坐在海棠树下乘凉，从叶⼦的空隙处看到灰⾊的天空，上⾯嵌着⼀颗⼀颗的星。

这时候，⾃⼰往往什么都不想，只让睡意轻轻地压上眉头。

等到果真睡去半夜⾥再醒来的时候，往往听到海棠叶⼦窸窸窣窣地直响，知道外⾯下⾬了。

⑤似乎这样的夏天也没有能过⼏个。

六年前的`秋天，当海棠树的叶⼦渐渐地转成淡黄的时候，我离开故乡，来到了德国。

一、解答题1．阅读下面材料：在数轴上6与1-所对的两点之间的距离：6(1)7--=； 在数轴上2-与3所对的两点之间的距离：235--=；在数轴上8-与4-所对的两点之间的距离：(8)(4)4---=；在数轴上点A 、B 分别表示数a 、b ，则A 、B 两点之间的距离AB a b b a =-=-． 回答下列问题：（1）数轴上表示2-和5-的两点之间的距离是_______；数轴上表示数x 和3的两点之间的距离表示为_______；数轴上表示数_______和_______的两点之间的距离表示为2x +；（2）七年级研究性学习小组在数学老师指导下，对式子23x x ++-进行探究： ①请你在草稿纸上画出数轴，当表示数x 的点在2-与3之间移动时，32x x -++的值总是一个固定的值为：_______．②请你在草稿纸上画出数轴，要使327x x -++=，数轴上表示点的数x =_______．解析：（1）3；|x−3|；x ，-2；（2）5；−3或4．【分析】（1）根据题意找出数轴上任意点间的距离的计算公式，然后进行计算即可；（2）①先化简绝对值，然后合并同类项即可；②分为x ＞3和x ＜−2两种情况讨论．【详解】解：（1）数轴上表示−2和−5的两点之间的距离为：|−2−（−5）|=3；数轴上表示数x 和3的两点之间的距离为：|x−3|；数轴上表示数x 和−2的两点之间的距离表示为：|x ＋2|；故答案为：3，|x−3|，x ，-2；（2）①当x 在-2和3之间移动时，|x ＋2|＋|x−3|=x ＋2＋3−x=5；②当x ＞3时，x−3＋x ＋2=7，解得：x=4，当x ＜−2时，3−x−x−2＝7．解得x=−3，∴x=−3或x=4．故答案为：5；−3或4．【点睛】本题主要考查的是绝对值的定义和化简，根据题意找出数轴上任意两点之间的距离公式是解题的关键．2．（1）在图所示的数轴上标出以下各数：52- ，-5.5，-2，+5， 132 （2）比较以上各数的大小，用“＜”号连接起来； （3) 若点A 对应 5.5-，点B 对应132，请计算点A 与点B 之间的距离．解析：（1）画图见解析；（2） 5.5-＜52-＜2-＜132＜+5；（3）9. 【分析】（1）先画数轴，根据数轴上原点左边的为负数，原点右边的为正数，在数轴上描出对应各数的点即可得到答案；（2）根据数轴上的数，右边的数大于左边的数，直接用“＜”连接即可得到答案；（3）数轴上点A 与点B 对应的数分别为,a b ，则AB a b =-或b a -，根据以上结论代入数据直接计算即可得到答案．【详解】解：（1）如图，在数轴上表示各数如下：（2）因为数轴上的数，右边的数总大于左边的数：所以按从小到大排列各数为：5.5-＜52-＜2-＜132＜+5 （3）因为：A 表示 5.5-，B 表示132， 所以：点A 与点B 之间的距离为： ()13 5.5 3.5 5.599.2AB =--=+== 【点睛】本题考查的是利用数轴上的点表示有理数，利用数轴比较有理数的大小，数轴上两点之间的距离，绝对值的含义，掌握以上知识是解题的关键．3．给出四个数：3,4--,2,6，计算“24点”，请列出四个符合要求的不同算式． （可运用加、减、乘、除、乘方运算，可用括号；注意：例如4(123)24⨯++=与(213)424++⨯=只是顺序不同，属同一个算式．）算式1：_________________；算式2_______________；算式3：_________________；算式4_______________；解析：()()342624,-⨯-+⨯=()()342624,-⨯-+-=()()643224,⨯-⨯-+=()()()()43624624.-⨯--÷=-⨯-=【分析】由241212,=+ 可得()342624,-⨯-+⨯=由()2438=-⨯-，可得()()342624,-⨯-+-=由()24124,=-⨯- 可得()()643224,⨯-⨯-+=由()2446=-⨯-，可得()()()()43624624-⨯--÷=-⨯-=，从而可得答案．【详解】解：算式1：()()3426121224,-⨯-+⨯=+=算式2：()()()()34263824,-⨯-+-=-⨯-=算式3：()()()()643224124,⨯-⨯-+=-⨯-=算式4：()()()()()()43624334624,-⨯--÷=-⨯--=-⨯-=故答案为：()()342624,-⨯-+⨯=()()342624,-⨯-+-=()()643224,⨯-⨯-+=()()()()43624624.-⨯--÷=-⨯-=【点睛】本题考查有理数的混合运算，解答本题的关键是明确有理数混合运算的计算方法，注意本题答案不唯一，这是一道开放性的题目，同时考查了学生的逆向思维．4．计算：（1）412115(2)5⎡⎤⎛⎫----⨯-÷- ⎪⎢⎥⎝⎭⎣⎦（2）1111243812⎛⎫÷-+- ⎪⎝⎭（要求简便方法计算） 解析：（1）-21；（2）17-【分析】 （1）先进行幂的运算，再算括号里面的，去括号应注意括号前的负号，再算加减． （2）除数和被除数同时乘24可得1111243812⎡⎤⎛⎫÷⨯-+- ⎪⎢⎥⎝⎭⎣⎦再算括号里的可得出答案． 【详解】解：（1）原式＝﹣16﹣[-11+1]÷(-2)＝﹣16-5=-21；（2）原式＝1111243812⎡⎤⎛⎫÷⨯-+- ⎪⎢⎥⎝⎭⎣⎦＝[]1832÷-+-1(7)=÷- =17- 【点睛】本题考查的是有理数的加减、乘除以及乘方的运算，熟练掌握运算法则是解题的关键． 5．计算：（1）()4235524757123⎛⎫÷--⨯-÷- ⎪⎝⎭； （2）()3218223427⎛⎫-⨯+-⨯- ⎪⎝⎭． 解析：（1）0；（2）1-．【分析】（1）原式先把除法转换为乘法，再逆用乘法分配律进行计算即可得到答案；（2）原式先计算乘方运算，再计算乘法运算，最后算加减运算即可求出值．【详解】解：（1）()4235524757123⎛⎫÷--⨯-÷- ⎪⎝⎭ 45355171271234⎛⎫=⨯--⨯+⨯ ⎪⎝⎭ 4535571271212=-⨯-⨯+ 43517712⎛⎫=--+⨯ ⎪⎝⎭ 5012=⨯ 0=； （2）()3218223427⎛⎫-⨯+-⨯- ⎪⎝⎭ ()98427427⎛⎫-⨯+-⨯- ⎝=⎪⎭98=-+1=-．【点睛】此题主要考查了有理数的混合运算，熟练掌握运算法则是解答此题的关键．6．321032(2)(3)5-÷---⨯解析：﹣31．【分析】根据有理数的混合运算法则计算即可．【详解】解：321032(2)(3)5-÷---⨯=10－32÷（﹣8）－9×5=10－（﹣4）－45=10+4－45=14－45=﹣31．【点睛】此题主要考察了有理数的混合运算，解题关键是掌握有理数混合运算法则．7．计算：（1）()213433⎛⎫---+-+ ⎪⎝⎭； （2）()()202011232---+-+． 解析：（1）-6；（2）132- 【分析】（1）先化为省略括号的形式，将整数及分数分别相加，再计算加法；（2）先计算乘方，同时计算绝对值及去括号，再计算加减法．【详解】（1）解：原式=213433-+-+ ()213433⎛⎫=--++ ⎪⎝⎭71=-+6=-；（2）解：原式=11232--+=142- =132-．【点睛】此题考查有理数的混合运算，掌握有理数加减混合运算法则及有理数乘方运算法则是解题8．计算：（1）()222112136⎡⎤⎛⎫⎛⎫-+---÷- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦（2）131121346⎛⎫-⨯-+ ⎪⎝⎭解析：（1）1；（2）9-【分析】（1）先算括号里面的，再算括号外面的即可；（2）根据乘法分配律计算即可；【详解】（1）()222112136⎡⎤⎛⎫⎛⎫-+---÷- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦， 11463⎡⎤=-+-⨯⎢⎥⎣⎦， 121=-+=；（2）131121346⎛⎫-⨯-+ ⎪⎝⎭， ()()()431121212346=-⨯--⨯+-⨯， 16929=-+-=-；【点睛】 本题主要考查了有理数的混合运算，准确计算是解题的关键．9．以1厘米为1个单位长度用直尺画数轴时，数轴上互为相反数的点A 和点B 刚好对着直尺上的刻度2和刻度8．（1）写出点A 和点B 表示的数；（2）写出在点B 左侧，并与点B 距离为9.5厘米的直尺左端点C 表示的数；（3）若直尺长度为a 厘米，移动直尺，使得直尺的长边CD 的中点与数轴上的点A 重合，求此时左端点C 表示的数．解析：（1）点A 表示的数是-3，点B 表示的数是3；（2）点C 表示的数是-6.5；（3）3-0.5a【分析】（1）根据AB=8-2=6，点A 和点B 表示的数是互为相反数，即可得到结果；（2）利用点B 表示的数3减去9.5即可得到答案；（3）利用中点表示的数向左移动0.5a 个单位计算即可．（1）∵AB=8-2=6，点A 和点B 表示的数是互为相反数，∴点A 表示的数是-3，点B 表示的数是3；（2）点C 表示的数是：3-9.5=-6.5；（3）∵直尺长度为a 厘米，直尺中点表示的数是-3，∴直尺此时左端点C 表示的数-3-0.5a ．【点睛】此题考查利用数轴表示数，数轴上两点之间的距离，数轴上点移动的规律，熟记数轴上点移动的规律进行计算是解题的关键．10．定义：数轴上给定不重合两点A ，B ，若数轴上存在一点M ，使得点M 到点A 的距离等于点M 到点B 的距离，则称点M 为点A 与点B 的“平衡点”．请解答下列问题：（1）若点A 表示的数为－3，点B 表示的数为1，点M 为点A 与点B 的“平衡点”，则点M 表示的数为_______；（2）若点A 表示的数为－3，点A 与点B 的“平衡点”M 表示的数为1，则点B 表示的数为________；（3）点A 表示的数为－5，点C ，D 表示的数分别是－3，－1，点O 为数轴原点，点B 为线段CD 上一点．①设点M 表示的数为m ，若点M 可以为点A 与点B 的“平衡点”，则m 的取值范围是________；②当点A 以每秒1个单位长度的速度向正半轴方向移动时，点C 同时以每秒3个单位长度的速度向正半轴方向移动．设移动的时间为t （0t >）秒，求t 的取值范围，使得点O 可以为点A 与点B 的“平衡点”．解析：（1）－1；（2）5；（3）①43t -≤≤-；②26t ≤≤且 5t ≠【分析】（1）根据平衡点的定义进行解答即可；（2）根据平衡点的定义进行解答即可；（3）①先得出点B 的范围，再得出m 的取值范围即可；②根据点A 和点C 移动的距离，求得点A 、C 表示的数，再由平衡点的定义得出答案即可．【详解】解：（1）（1）点M 表示的数=312-+=−1； 故答案为：−1；（2）点B 表示的数=1×2−（−3）=5；故答案为：5；（3）①设点B 表示的数为b ，则31b -≤≤-，∵点A 表示的数为－5，点M 可以为点A 与点B 的“平衡点”，∴m 的取值范围为：43m -≤≤-，故答案为：43m -≤≤-；②由题意得：点A 表示的数为5t -，点C 表示的数为33t -，∵点O 为点A 与点B 的平衡点，∴点B 表示的数为：5t -，∵点B 在线段CD 上，当点B 与点C 相遇时，2t =，当点B 与点D 相遇时，6t =，∴26t ≤≤，且 5t ≠，综上所述，当26t ≤≤且 5t ≠时，点O 可以为点A 与点B 的“平衡点”．【点睛】本题考查了实数与数轴，掌握数轴上点的表示方法，以及两点的中点表示方法是解题的关键．11．小李坚持跑步锻炼身体，他以30分钟为基准，将连续七天的跑步时间（单位：分钟）记录如下：10，-8，12，-6，11，14，-3（超过30分钟的部分记为“+”，不足30分钟的部分记为“-”）（1）小李跑步时间最长的一天比最短的一天多跑几分钟？（2）若小李跑步的平均速度为每分钟0.1千米，请你计算这七天他共跑了多少千米？ 解析：（1）22分钟；（2）24千米．【分析】(1)时间差=标准差的最大值-标准差的最小值；(2)先计算出一周的总运动时间，利用路程，速度，时间的关系计算即可.【详解】（1）()14822--=（分钟）．故小李跑步时间最长的一天比最短的一天多跑22分钟．（2）()30710812611143240⨯+-+-++-=（分钟），0.124024⨯=（千米）．故这七天他共跑了24千米．【点睛】本题考查了有理数的混合运算，熟练运用标准差计算时间差，标准时间计算总时间是解题的关键.12．计算（1）3124623⎛⎫⎛⎫-÷-+⨯- ⎪ ⎪⎝⎭⎝⎭（2）()()34011 1.950.50|5|5---+-⨯⨯--+．解析：（1）14；（2）0【分析】（1）先计算乘法和除法，再计算加法；（2）分别计算乘方、乘法和绝对值，再计算加法和减法．【详解】解：（1）原式=2124633⎛⎫⎛⎫-⨯-+⨯- ⎪ ⎪⎝⎭⎝⎭()162=+-14=；（2）原式011055=-++-+=0．【点睛】本题考查有理数的混合运算．（1）中注意要先把除法化为乘法再计算；（2）中注意多个有理数相乘时，只要有一个因数为0，那么积就为0．13．某农户家准备出售10袋大米，称得质量如下：（单位：千克）182，180，175，173，182，185，183，181，180，183（1）填空：以180千克作为基准数，可用正、负数表示这10袋大米的质量与180的差为 ；（2）试计算这10袋大米的总质量是多少千克？解析：（1）＋2，0，−5，-7，＋2，＋5，＋3，＋1，0，+3；（2）1804千克【分析】（1）规定超出基准数为正数，则不足部分用负数表示，即可；（2）把第（1）题10个数相加，再加上180×10，即可．【详解】（1）以180千克为基准数，超过180千克的记作正数，低于180千克的记作负数，那么各袋大米的质量分别为：＋2，0，−5，-7，＋2，＋5，＋3，＋1，0，+3，故答案是：＋2，0，−5，-7，＋2，＋5，＋3，＋1，0，+3；（2）(＋2+0−5-7＋2＋5＋3＋1+0+3)+ 180×10=1804（千克），答：这10袋大米的总质量是1804千克．【点睛】本题主要考查正负数的意义以及有理数的加减法的实际应用，熟练掌握有理数的加减法运算法则，是解题的关键．14．计算（1）18()5(0.25)4+----（2）2﹣412()(63)7921-+⨯- （3）1373015-⨯ （4）22220103213()2(1)43⎡⎤--⨯-⨯--÷-⎢⎥⎣⎦． 解析：（1）3；（2）37；（3）﹣236；（4）72【分析】（1）本式为简单的有理数加减运算，从左到右先将分数进行计算，再从左到右计算即可．（2）按照有理数混合运算的顺序，利用乘法分配律直接去括号，再进行运算． （3）将﹣71315分解为﹣7﹣1315，再利用乘方分配律进行计算即可． （4）分别根据有理数的乘方计算出各数，再根据实数混合运算的法则进行计算即可．【详解】解：（1）18()5(0.25)4+---- ＝118544--+ ＝3；（2）2﹣412()(63)7921-+⨯- ＝4122(63)(63)(63)7921⎡⎤-⨯--⨯-+⨯-⎢⎥⎣⎦ ＝2﹣（﹣36+7﹣6），＝2﹣（﹣35）＝37；（3）1373015-⨯ ＝﹣7×30+（﹣1315）×30 ＝﹣210﹣26=﹣236；（4）22220103213()2(1)43⎡⎤--⨯-⨯--÷-⎢⎥⎣⎦ ＝341(92)149--⨯-⨯-÷ ＝912-+＝72． 【点睛】此题考查了有理数的混合运算注意：要正确掌握运算顺序，即乘方运算（和以后学习的开方运算）叫做三级运算；乘法和除法叫做二级运算；加法和减法叫做一级运算．在混合运算中要特别注意运算顺序：先三级，后二级，再一级；有括号的先算括号里面的；同级运算按从左到右的顺序．15．计算：－32＋2×（－1）3－（－9）÷213⎛⎫ ⎪⎝⎭解析：70【分析】先计算乘方，然后计算乘除，再计算加减，即可得到答案． 【详解】解：原式=92(1)(9)9-+⨯---⨯ =9281--+ =70． 【点睛】本题考查了有理数的混合运算，解题的关键是熟练掌握运算法则进行解题． 16．计算： （1）()11270.754⎛⎫--+-+ ⎪⎝⎭； （2）()()202023111242144⎛⎫-++-⨯--⨯- ⎪⎝⎭； 解析：（1）6；（2）11． 【分析】（1）先变成省略括号和形式，同时把小数化分数，把分数相加，同号相加，最后异号相加即可；（2）先算乘方，去绝对值和带分数化假分数，再计算乘法，最后计算加减法即可． 【详解】 解：（1）()11270.754⎛⎫--+-+ ⎪⎝⎭， =1312744+-+， =1217+-， =13-7， =6；（2）()()202023111242144⎛⎫-++-⨯--⨯- ⎪⎝⎭， =()351124444⎛⎫++⨯--⨯- ⎪⎝⎭=11235++- =11． 【点睛】本题考查含有乘方的有理数混合，掌握有理数混合运算的法则，解答的关键是熟练掌握运算法则和运算顺序． 17．计算 （1） ()375244128⎛⎫---⨯- ⎪⎝⎭（2） ()212382455-+--÷-⨯解析：（1）47；（2）4925【分析】（1）根据乘法分配律，求出算式的值是多少即可；（2）先计算乘方及绝对值运算，再计算乘除法运算，最后算加减运算即可求出值． 【详解】 解： ()375244128⎛⎫---⨯- ⎪⎝⎭ ＝18+14＋15 ＝47（2）()212|38|2455-+--÷-⨯＝11452455⎛⎫-+-⨯-⨯ ⎪⎝⎭＝24125+4925=【点睛】此题主要考查了有理数的混合运算，要熟练掌握，注意明确有理数混合运算顺序：先算乘方，再算乘除，最后算加减；同级运算，应按从左到右的顺序进行计算；如果有括号，要先做括号内的运算．18．设0a >，x ，y 为有理数，定义新运算：||a x a x =⨯※．如323|2|6=⨯=※，()414|1|a a -=⨯-※．（1）计算20210※和()20212-※的值． （2）若0y <，化简()23y -※．（3）请直接写出一组,,a x y 的具体值，说明()a x y a x a y +=+※※※不成立． 解析：（1）0；4042；(2)6y -；（3）1a =，2x =，3y =-（答案不唯一） 【分析】(1)根据题意※表示前面的数与后面数的绝对值的积，直接代入数据求解计算； (2)有y<0，得到y 为负数，进而得到-3y 为正数，去绝对值后等于本身-3y ，再代入数据求解即可；(3)按照题意要求写一组具体的,,a x y 的值再验算即可． 【详解】解：(1)根据题意得:202102021|0|0=⨯=※；()202122021|2|4042-=⨯-=※；(2)因为0y <， 所以30y ->，所以()()232|3|236y y y y -=⨯-=⨯-=-※； (3)由题意，当,,a x y 分别取1a =，2x =，3y =-时，此时()2311※※(-1)=1-=，而11※2※(-3)=2+3=5+，所以，()a x y a x a y +=+※※※不成立． 【点睛】本题是新定义题型，按照题目中给定的运算要求和顺序进行求解即可． 19．计算：（﹣1）2014＋15×（﹣5）＋8 解析：8 【分析】先算乘方，再算乘法，最后算加法，由此顺序计算即可． 【详解】 原式＝1＋15×（﹣5）＋8＝1﹣1＋8=8． 【点睛】此题考查有理数的混合运算，注意运算的顺序与符号的判定． 20．计算： （1）6÷（－3）×（－32） （2）－32×29-＋（－1）2019－5÷（－54） 解析：（1）3；（2）1． 【分析】（1）根据有理数的乘除混合运算法则计算即可； （2）根据有理数的混合运算法则计算即可． 【详解】解：（1）原式=6×1-3⎛⎫⎪⎝⎭ ×（－32）=3；（2）原式=－9×29＋（－1）－5×4-5⎛⎫ ⎪⎝⎭=-2-1+4 =1． 【点睛】本题考查有理数的混合运算，解答本题的关键是明确有理数混合运算的计算方法．21．计算：（1）()()34287⨯-+-÷； （2）()223232-+---． 解析：（1）16-；（2）6． 【分析】（1）先算乘除，后算加法即可；（2）原式先计算乘方运算，再化简绝对值，最后算加减运算即可求出值． 【详解】（1）原式12416=--=- （2）原式34926=-+-= 【点睛】此题考查了有理数的混合运算，熟练掌握运算法则是解本题的关键． 22．计算：（1）45(30)(13)+---；（2）32128(2)4-÷-⨯-． 解析：（1）28；（2）-2 【分析】（1）有理数的加减混合运算，从左往右依次计算即可；（2）有理数的混合运算，先算乘方，然后算乘除，最后算加减，有小括号先算小括号里面的． 【详解】解：（1）45(30)(13)+--- =4530+13- =15+13 =28（2）32128(2)4-÷-⨯- =18844-÷-⨯ =11-- =-2． 【点睛】本题考查有理数的混合运算，掌握运算顺序和计算法则正确计算是解题关键． 23．计算： （1）31113+(0.25)(4)3444---+--（2）31(2)93--÷（3）1125100466()46311-⨯-⨯-⨯ 解析：（1）21；（2）-35；（3）-392 【分析】（1）有理数加减混合运算，从左到右以此计算，有小括号先算小括号里面的，可以使用加减交换律和结合律使得计算简便；（2）有理数的混合运算，先算乘方，然后算乘除，最后算加减； （3）有理数的混合运算，可以使用乘法分配律使得计算简便． 【详解】 解：（1）31113+(0.25)(4)3444---+-- =311113+434444-+ =3111(13+4)(3)4444+-=183+ =21（2）31(2)93--÷=893--⨯ =827-- =35-（3）1125100466()46311-⨯-⨯-⨯ =11101004664633⎛⎫⎛⎫--⨯-⨯- ⎪ ⎪⎝⎭⎝⎭=11101004466664633+-⨯-⨯-⨯⨯ =40011120+---=392- 【点睛】本题考查有理数的混合运算，掌握运算顺序和计算法则正确计算是解题关键． 24．计算下列各题： （1）（14﹣13﹣1）×（﹣12）； （2）（﹣2）3+（﹣3）×[（﹣4）2﹣6]． 解析：（1）13；（2）-38【分析】（1）根据乘法分配律可以解答本题；（2）根据有理数的乘方、有理数的乘法和加减法可以解答本题．【详解】解：（1）（14﹣13﹣1）×（﹣12）＝14×（﹣12）﹣13×（﹣12）﹣1×（﹣12）＝（﹣3）+4+12＝13；（2）（﹣2）3+（﹣3）×[（﹣4）2﹣6]＝（﹣8）+（﹣3）×（16﹣6）＝（﹣8）+（﹣3）×10＝（﹣8）+（﹣30）＝﹣38．【点睛】本题考查有理数的混合计算，掌握有理数混合运算的顺序，会利用简便运算简化运算是解题关键．25．计算：（1）2×（-3）3-4×（-3）（2）-22÷（12-13）×（-58）解析：（1）-42；（2）15【分析】（1）先算乘方、乘法，再算加减法即可；（2）先算括号和乘方，再算乘除即可．【详解】（1）原式 =2(27)12⨯-+=-54+12= 42-．（2）原式 =15 4()68 -÷⨯-=5 468⨯⨯=15．【点睛】本题考查了有理数的运算，掌握运算法则及运算顺序是关键．26．某路公交车从起点经过A，B，C，D站到达终点，一路上下乘客如下表所示．（用正数表示上车的人数，负数表示下车的人数））到终点下车还有多少人；（2）车行驶在____站至___ 站之间时，车上的乘客最多；（3）若每人乘坐一站需买票0.5元，问该车出车一次能收入多少钱？列式计算．解析：（1）30；（2）B，C；（3）71.5元．【分析】（1）根据正负数的意义，上车为正数，下车为负数，求出A、B、C、D站以及终点站的人数，即可得解；（2）根据（1）的计算解答即可；（3）根据各站之间的人数，乘票价0.5元，然后计算即可得解．【详解】解：（1）根据题意可得：到终点前，车上有16+15-3+12-4+7-10+8-11=30，即30人；故到终点下车还有30人．故答案为：30；（2）根据图表：A站人数为：16+15-3=28（人）B站人数为：28+12-4=36（人）C站人数为：36+7-10=33（人）D站人数为：33+8-11=30（人）易知B和C之间人数最多．故答案为：B；C；（3）根据题意：（16+28+36+33+30）×0.5=71.5（元）．答：该出车一次能收入71.5元．【点睛】本题考查了正数和负数，有理数的混合运算，读懂图表信息，求出各站点上的人数是解题的关键．27．已知：b是最小的正整数，且a、b满足（c－5）2＋|a＋b|＝ 0请回答问题：（1）请直接写出a、b、c的值：a＝，b＝，c＝，（2）数轴上a，b，c所对应的点分别为A，B，C，则B，C两点间的距离为；（3）在（2）的条件下，点A、B、C开始在数轴上运动，若点A以每秒1个单位长度的速度向左运动，同时，点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动，设运动了t秒，①此时A表示的数为；此时B表示的数为；此时C表示的数为；②若点B与点C之间的距离表示为BC，点A与点B之间的距离表示为AB．请问：BC－AB的值是否随着时间t的变化而改变？若变化，请说明理由；若不变，请求其值．解析：（1）-1；1；5；（2）4；（3）①-1-t ；1+2t ；5+5t ；②BC -AB 的值为2，不随着时间t 的变化而改变． 【分析】（1）先根据b 是最小的正整数，求出b ，再根据c 2＋|a +b |=0，即可求出a 、c ； （2）由（1）得B 和C 的值，通过数轴可得出B 、C 的距离；（3）①在（2）的条件下，通过运动速度和运动时间可表示出A 、B 、C ； ②先求出BC =3t +4，AB =3t +2，从而得出BC -AB =2． 【详解】解：（1）∵b 是最小的正整数， ∴b =1．∵（c -5）2+|a +b |=0， ∴a =-1，c =5； 故答案为：-1；1；5；（2）由（1）知，b =1，c =5，b 、c 在数轴上所对应的点分别为B 、C ， B 、C 两点间的距离为4；（3）①点A 以每秒1个单位长度的速度向左运动，运动了t 秒，此时A 表示的数为-1-t ； 点B 以每秒2个单位长度向右运动，运动了t 秒，此时B 表示的数为1+2t ； 点C 以5个单位长度的速度向右运动，运动了t 秒，此时C 表示的数为5+5t ． ②BC -AB 的值不随着时间t 的变化而改变，其值是2，理由如下：∵点A 都以每秒1个单位的速度向左运动，点B 和点C 分别以每秒2个单位长度和5个单位长度的速度向右运动，∴BC =5+5t –(1+2t )=3t +4，AB =1+2t –(-1-t )=3t +2， ∴BC -AB =（3t +4）-（3t +2）=2． 【点睛】本题考查了数轴与绝对值，通过数轴把数和点对应起来，也就是把“数”和“形”结合起来，二者互相补充，相辅相成，把很多复杂的问题转化为简单的问题，在学习中要注意培养数形结合的数学思想． 28．计算：（1）4222(37)2(1)-+--⨯-； （2）157(36)2912⎛⎫-+⨯- ⎪⎝⎭．解析：（1）-2；（2）-19 【分析】（1）先括号里，再计算乘方、乘法，最后相加减即可； （2）利用乘法的分配率进行计算． 【详解】（1）4222(37)2(1)-+--⨯-=16162-+-=-2；（2）157(36) 2912⎛⎫-+⨯-⎪⎝⎭=157(36)(36)(36) 2912⨯--⨯-+⨯-=－18+20－21=-19【点睛】考查了有理数的混合运算，要熟练掌握，注意明确有理数混合运算顺序：先算乘方，再算乘除，最后算加减；同级运算，应按从左到右的顺序进行计算；如果有括号，要先做括号内的运算．29．体育课上全班男生进行了百米测试，达标成绩为14秒，下面是第一小组8名男生的成绩记录，其中“+”表示成绩大于14秒，“－”表示成绩小于14秒．解析：9秒．【分析】根据平均成绩的计算方法，先列式计算表格中所有数据的平均数，再加上标准成绩即可得出结果．【详解】解：1.20.7010.30.20.30.50.18-++--+++=-（秒）140.113.9-=（秒）．答：这个小组8名男生的平均成绩是13.9秒．【点睛】此题考查了有理数的混合运算的实际应用，正确理解题目中正数和负数的含义是列式计算的关键．30．赣州享有“世界橙乡”的美誉，中华名果赣南脐橙热销世界各地．刚大学毕业的小明把自家的脐橙产品放到了网上售卖，他原计划每天卖100kg脐橙，但由于种种原因，实际每天的销售量与计划量相比有出入，下表是某周的销售情况（超额记为正，不足记为负．单位：kg）．）根据记录的数据可知前三天共卖出kg（2）根据记录的数据可知销售量最多的一天比销售量最少的一天多销售kg；（3）若脐橙按4.5元/kg出售，且小明需为买家支付运费（平均0.5元/kg），则小明本周一共赚了多少元？解析：（1）296；（2）29；（3）2868元【分析】（1）将前三天的销售量相加即可；（2）根据表格销量最多的一天为周六，最少的一天为周五，用周六的销量减去周五的销量即可得到答案；（3）先计算出本周的总销量，再乘以每千克的利润即可．【详解】（1）4－3－5＋300=296（kg），故答案为：296；（2）（＋21）－（－8）=29（kg），故答案为：29；（3）4－3－5＋14－8＋21－6=17（kg），17＋100×7=717（kg），717×（4.5－0.5）=2868（元），小明本周一共赚了2868元．【点睛】此题考查正负数的实际应用，有理数混合运算的实际应用，正确理解表格意义列式计算是解题的关键．。

《程氏爱鸟》阅读答案及翻译文言文阅读题程氏爱鸟吾昔少年时，所居书室前，有竹柏杂花，丛生满庭，众鸟巢其上。

武阳君1恶杀生，儿童婢仆，皆不得捕取鸟雀。

数年间，皆巢于低枝，其鷇2可俯而窥也。

又有桐花凤四五百，翔集其间，此皆鸟羽毛至为珍异难见，而能驯扰，殊不畏人，闾里间见之，以为异事。

此无他，不忮3之诚，信于异类也。

有野老言：鸟雀巢去人太远，则其子有蛇、鼠、狐狸、鸱、鸢之扰。

人既不杀，则自近人者，欲免此患也。

由是观之，异时鸟雀巢不敢近人者，以人甚于蛇、鼠之类也。

（选自苏轼《东坡杂记》）【注释】 1 .武阳君：苏轼的母亲。

2. 鷇kou：初生的小鸟。

3. 忮zhi：凶狠。

1.解释下列加点词语在句中的意思。

（2分）（1）信于异类也（）（2）去人太远（）2.把文中画线句子翻译成现代汉语。

（3分）此皆鸟羽毛至为珍异难见，而能驯扰，殊不畏人3.联系上下文，众鸟皆巢于低枝的原因是什么？（2分）4.选文最后异时鸟雀巢不敢近人者，以人甚于蛇、鼠之类也一句引发了你怎样的思考？（3分）参考答案：语文网1.（1）使信任(2)距离，离2. 这种鸟的羽毛是最为珍贵很难得见得到的，但（这种鸟）却能很驯服不受干扰（地待在那儿），而且也不怕人。

3.因为我的母亲对杀生的行为很痛恨，嘱咐家里的小孩、奴婢及仆人，都不能捕捉鸟雀。

或：因为（主人）对待这些鸟雀的诚心，对待这些不同于人类的动物一直守信用。

4.例：人类不能以自然之长的居高心态来欺压其它动物，要与其它动物相互信任，和谐共处，不能以恶毒的方式或态度来伤害其它动物。

翻译：我在少年的时候,所居住的书房前,种有翠竹松柏以及一些花草,郁郁葱葱地长满在庭院里,许多鸟在上面筑巢。

我的母亲对杀生的行为很痛恨，嘱咐家里的小孩、奴婢及仆人，都不能捕捉鸟雀。

几年的时间下来，鸟雀们都将巢建在花木的低枝上，鸟巢里孵的小鸟低下头去都可以偷偷地看得到。

还有一种叫桐花凤的鸟也有四五百只，飞翔在院子里，这种鸟的羽毛是最为珍贵很难得见得到的，但（这种鸟）却能很驯服不受干扰（地待在那儿），而且也不怕人。