采用小波变换实现图像压缩编码
- 格式:doc
- 大小:1.11 MB
- 文档页数:25

研究基于小波变换的图像压缩摘要图像压缩的关键技术是图像数据转换,转换后的数据进行数据量化和数据熵编码。
基于小波变换的图像压缩是一种常见的图像压缩方法,本篇论文使用小波变换、多分辨率分析及不同规模的量化和编码实现图像压缩。
在相同的条件下,本文采用两种不同的方法,第一种方法保留低频和放弃高频,第二种方法是阈值方法来实现图像压缩。
关键词:关键词——小波变换;小波图像系数;量化;编码1.引言图像压缩是指损失一部分比特率的技术或无损还原原始图像信息。
在信息理论中,它的有效性,源编码的问题,即通过移除冗余即不必要的信息来实现这一目标。
压缩的图像信息有两个方法,模拟和数字,因为数字压缩方法有大幅减少比特数量的优势,绝大多数的系统使用数字压缩方法。
信号分析及处理的常用方法是傅里叶变换(FT),而且最广泛的分析工具应用于图像处理,但由于傅里叶变换不能满足局部的时间域和频率域的特点,小波变换具有傅立叶变换没有的两个特征,同时小波变换系数相同的空间位置描述在不同的尺度上有相似性,使得小波变换能进行量化编码。
近年来,使用基于小波变换的图像压缩已取得了很大的进步,也变换算法充分利用小波系数的特性。
2.图像压缩编码的基本原理图像编码研究侧重于如何压缩图像数据信息,允许一定程度的失真条件下的还原图像(包括主观视觉效果),称为图像压缩编码。
然后使图像信号的信号源通过系统PCM编码器由线性PCM编码,压缩编码器压缩图像数据,然后摆脱码字的冗余数据。
图像压缩编码的基本原理是图1。
图1 图像压缩编码的基本框图因此,图像编码是使用统计特性的固有效果和视觉特征,从原始图像中提取有效信息,信息压缩编码和删除一些无用的冗余信息,从而允许高效传输的数字图像或数字存储。
图像恢复时,恢复图像的不完全与原始图像相同,保留有效信息的图像。
3.小波分析的基本理论小波变换具有良好的定位时间和频域的特征,充分利用非均匀分布的分辨率,对于高频信号,使用时域的小时间窗口,进行低频信号分析,使用一个大的时间窗口。



小波变换在数字图像处理中的应用数字图像处理是一门跨学科的科学,它涉及到数学、计算机科学、物理学等多个领域。
其中,小波变换是数字图像处理中一种非常重要的技术,它在图像去噪、边缘检测、压缩编码等方面都有广泛的应用。
一、小波变换的基本概念小波变换(Wavelet Transform)是一种信号处理技术,它是通过对信号进行分解和重构来描述信号的局部特征。
与傅里叶变换不同,小波变换可以对信号的高频部分和低频部分进行细致的分析。
小波变换的基本思想是将信号分解成不同频率的小波基函数,并利用这些基函数来描述信号的局部特征。
这里的小波基函数是满足正交归一性和母小波的语法结构,它可以用不同的参数来描述不同的频率和尺度。
常用的小波函数包括Haar小波、Daubechies小波、Symlets小波等。
二、1. 图像去噪图像噪声是数字图像处理中普遍存在的问题,它会影响图像的视觉效果和后续处理结果。
小波变换可以对图像进行频域分析,在不同频率和尺度上对信号进行分解和重构,从而去除图像中的噪声。
例如,可以采用离散小波变换对图像进行处理,利用小波基函数的多尺度特性来分解图像,然后通过阈值去噪的方法来去除噪声。
在这个过程中,可以根据具体的应用需求选择不同的小波基函数和去噪方法。
2. 图像边缘检测图像中的边缘是图像中非常重要的信息,它可以用来描述图像中不同物体的边界。
小波边缘检测可以通过对图像的小波变换进行处理,提取出不同尺度的边缘信息,从而实现图像的边缘检测。
例如,可以利用Gabor小波函数来进行图像边缘检测,将图像分解为不同尺度和方向上的小波系数,然后通过计算其幅度和相位来提取边缘信息。
这个过程可以实现图像的边缘检测,并具有良好的鲁棒性和灵敏度。
3. 图像压缩编码数字图像的压缩编码是数字图像处理中广泛应用的技术,它可以减少存储和传输的开销,并提高图像的传输效率。
小波变换也可以应用于图像的压缩编码中,通过小波分解和量化来实现图像压缩。

收稿日期:2017-06-07 修回日期:2017-10-10 网络出版时间:2018-02-08基金项目:国家自然科学基金(61502211)作者简介:詹 为(1992-),女,硕士研究生,研究方向为图像处理;段先华,教授,博士,研究方向为电子对抗㊁图像处理㊁模式识别等;於跃成,副教授,博士,研究方向为机器学习㊁数据挖掘㊁模式识别等㊂网络出版地址:http :// /kcms /detail /61.1450.TP.20180207.1913.074.html基于小波变换的图像压缩编码方法研究詹 为,段先华,於跃成(江苏科技大学计算机学院,江苏镇江212003)摘 要:嵌入式零树小波(EZW )是一种非常有效的基于离散小波变换的图像编码算法,可以实现渐进编解码,具有较好的图像恢复质量㊂在研究嵌入式零树小波编码算法及原理的基础上,针对其对系数重复扫描而带来的计算量与编码比特数的增加,以及扫描过程中出现的大量零数根而导致的算法复杂度增加等不足,提出一种将改进的EZW 算法与霍夫曼编码方法相结合的图像压缩编码方法㊂首先通过扩充编码符号改变扫描方式,来实现零树结构的快速判断,避免连续出现零数根㊂然后将改进的算法与霍夫曼编码联合编码来代替算术编码方法使其更简单㊂最后,在Matlab 中模拟仿真,将改进算法与原算法进行比较分析㊂实验结果表明,与独立的EZW 算法相比,改进算法不仅增加了编码效率,同时也提高了峰值信噪比(PSNR ),证明了改进算法的有效可行性㊂关键词:图像压缩;离散小波变换;霍夫曼编码;嵌入式零数小波中图分类号:TP 391.41 文献标识码:A 文章编号:1673-629X (2018)06-0021-05doi :10.3969/j.issn.1673-629X.2018.06.005Research on Image Compression Coding Method Based onWavelet TransformZHAN Wei ,DUAN Xian -hua ,YU Yue -cheng(School of Computer Science and Engineering ,Jiangsu University of Science and Technology ,Zhenjiang 212003,China )Abstract :Embedded zerotree wavelet (EZW )is a kind of very effective image coding algorithm based on discrete wavelet transform ,which can achieve progressive code with a good quality of image recovery.In the research of embedded zero tree wavelet coding algo⁃rithm ,there exist deficiency that repeated scanning of coefficient would increase the amount of calculation and the coding bits number ,furthermore during the scanning process a large number of zero would result in high -order complexity.For this ,we propose an improved EZW algorithm of image compression coding combing Huffman coding.First of all ,it expands encoding dictionary to change scanning way ,implementing the quick determination of the zero tree structures ,avoiding continuous zero root.Then it is combined with the Huff⁃man code to replace the arithmetic coding method to make it simpler.Finally ,we compare the original algorithm with the proposed algo⁃rithm in the simulation with Matlab.The experiments show that in comparison to the independent EZW algorithm ,the proposed algorithm not only increases the coding efficiency ,but also improves the peak signal -to -noise ratio (PSNR ),which proves its feasibility.Key words :image compression ;discrete wavelet transform ;Huffman coding ;EZW0 引 言信息时代带来了 信息爆炸”,导致了数据爆炸性增加㊂因此,不管数据传输或数据存储,高效数据压缩是必要的,例如,在遥感技术领域,各种空间探头必须使用压缩技术将巨大的数据信息发送回地面㊂然而,随着现代信息通信在商业社会中的需求日益增长,图像通信和通信网络的容量之间的矛盾越来越突出,特别是大量的数字图像数据难以传输存储㊂并且在获得和使用图像信息时也造成了很多困难,成为图像通信发展中的 瓶颈”问题㊂为了解决这些问题,越来越多的学者致力于图像压缩的研究㊂传统的基于块的变换,通过块运动估计和补偿技术来消除多余图像部分的离散余弦变换(DCT )压缩方法在低码率时恢复图像会出现明显的方块效应[1-3],这将在一定程度上影第28卷 第6期2018年6月 计算机技术与发展COMPUTER TECHNOLOGY AND DEVELOPMENT Vol.28 No.6June 2018响图像的恢复质量㊂针对这一问题,近年来基于小波变换的图像压缩方法逐渐成为其研究热点㊂近年来,基于小波的图像压缩算法与嵌入式比特流相继提出,如嵌入式零树小波压缩(EZW)算法㊁集合分层树(SPIHT)算法㊁嵌入式块编码与优化截断(EBCOT)算法和自适应扫描小波差分减少(ASW⁃DR)等等㊂其中,EZW[4]是一种简单有效的图像压缩算法,由Shapiro于1993年提出㊂EZW算法适应不同尺度层在小波域中的幅度相关性预测和排序,可以消除像素之间的相关性,同时可以在不同的分辨率下保持精细的结构㊂所以EZW可以实现一些重要系数的渐进编码和有效压缩㊂虽然EZW算法现在被认为对于小波图像编码方法更有效,但仍存在不足之处㊂例如:EZW的编码思想是通过不断扫描小波变换后的图像,以生成更多的零树来对图像进行编码㊂扫描过程中为了判断小波系数是零树根还是孤零,需要对系数进行重复扫描;由于EZW算法中的 零树结构”思想,在实际的编码过程中,生成的零树根越多,用以表示图像的数据量便会越少㊂而多棵零数根将会导致零树根大量存在编码流中;编码产生的四种符号中,每一种符号出现的机率也是不相等的㊂出现机率最高的是零树根,占有的比率达到百分之五十以上,而且它的连续性也很强㊂另外三种符号出现的机率不是很高且连续性也不是很强㊂上述问题会导致编码符号流中存在大量冗余,使得压缩编码时间变长,从而降低图像的编码效率㊂基于此,提出了一种改进算法㊂首先通过扩充编码符号改进扫描方式,能够实现零树结构的快速判断,然后将改进算法用霍夫曼编码代替算术编码方法使其更简单㊂1 基于小波变换的图像压缩1.1 数字图像中的小波变换在图像处理中应用的小波变换是二维小波变换,定义为:WT f(a,b1,b2)=1a∬f(x1,x2)ψ(x1-b1a,x2-b2a)d x1d x2(1)其逆变换如下:f(x1,x2)=1Cψ∫+¥0∬WT(a,b1,b2)ψ(x1-b1a,x2-b2a)d b1b2(2)其中,f(x1,x2)表示空间L2(R)中的一个二维信号,变量x1,x2分别表示信号的水平坐标和垂直坐标;ψ(x1,x2)表示由此信号构造的小波基;ψ(x1-b1a, x2-b2a)表示函数扩大或缩小的范围;Cψ表示为:Cψ=14π2∬ψ(w1,w2)2w1+w2d w1d w2(3)其中,ψ(w1,w2)是ψ(x,y)的二维Fourier变换㊂数字图像中采用的是二维离散小波变换㊂在选择小波基的基础上,将图像分解成许多不同的尺度㊁方向,小波变换后空间域子带图像发生变化,二维小波变换可以看成行和列两个方向的一维小波变换㊂对于一幅原始图像,先对其行作小波变换,行变换结束后,再对其进行列小波变换㊂根据这个算法,在小波变换后分解为四个子系统的图像:LL表示特征的原始图像,包含原始图像的基本内容;LH㊁HL和HH是垂直㊁水平和高频特性的对角分量向右倾斜,分别包含边缘㊁纹理和轮廓等垂直㊁水平和对角线方向的图像数据㊂这里LL子带包含图像的大多数数据,然后对小波变换的一级低频子带重复以上变换,直到达到所需要的分辨率为止[5-6]㊂一级分解后继续分解的过程叫做多分辨率分析,即多级小波分解的概念,形成小波的多级变换㊂1.2 小波变换图像压缩步骤基于小波变换的图像压缩编解码框图如图1所示㊂其中,整幅图像首先通过小波变换,然后实际编码应用于完整的小波系数㊂小波是有损压缩技术之一,一般有三个过程:(1)变换:将变换后的数据变换为小波系数矩阵㊂(2)量化:小波系数被量化为有限的字母表,这一步不是可逆的㊂(3)编码:量化之后得到的符号被进一步压缩为最小化比特率㊂图1 图像编码框图1.3 基于小波变换的图像压缩编码相比较离散余弦变换,基于小波变换的图像压缩能够更好地实现较高的压缩比和较理想的图像恢复质量㊂而嵌入零树小波图像编码㊁分层小波树集分割算法和优化截断点嵌入块编码算法则是目前比较经典的小波图像编码算法[7]㊂文中将围绕EZW算法展开㊂1.4 嵌入式零树小波编码算法一般来说,在小波图像压缩过程中量化是其中最关键的部分,它将图像小波系数很好地组织起来实现㊃22㊃ 计算机技术与发展 第28卷有效压缩㊂小波零树编码主要采用小波特征系数,很好地实现了嵌入式图像编码㊂其编码思想是不断扫描变换图像,生成更多的零树到图像代码[8]㊂其算法步骤可执行如下:(1)确定初始阈值T0㊂T0=2⌊log2(MAX(X i))」(4)其中,X i表示小波变换分解到第i级时的系数,之后每扫描一次,阈值减少一半㊂(2)主扫描㊂第n(n=1,2, ,L)次扫描时,算法按照顺序将小波分解系数与阈值T i-1依次进行比较,已处理的系数由以下输出符号表示:零树根(T),孤立零(Z),正重要系数(P)和负重要系数(N)㊂其表示分别为P:当前系数为正且绝对值大于阈值;N:当前系数为负且绝对值大于阈值; T:当前系数绝对值小于0为不重要系数且所有子孙系数都为不重要系数;Z:当前系数值不重要,但是至少有一个儿子系数重要㊂通过四个符号,扫描小波系数,并判断小波系数,并将相应的符号放入符号表中㊂也就是说在扫描过程中,用一个主扫描表记录这些输出符号㊂为防止下次主扫描时重复编码,在第n次扫描结束后,将输出符号为P或N的系数的位置加标记或将这些系数置0㊂(3)辅扫描㊂对于主扫描后的重要系数做细化编码㊂对主扫描表进行顺序扫描,对其中输出符号为P或N的小波系数进行量化㊂在量化系数之前要构造量化器㊂量化器的输入间隔为[T n-1,2T n-1),将其等分为两个量化区间[T n-1,1.5T n-1),[1.5T n-1,2T n-1),若小波系数属于前一区间,则输出量化符号 0”,重构值为1.25 Tn-1,否则输出量化符号为 1”,重构值为1.75T n-1㊂输出的符号 0”㊁ 1”由一个辅扫描表记录㊂(4)重新排序,其目的为与设置第n+1次扫描所用的量化间隔,以提高解码精度㊂(5)输出编码信息㊂(6)重复上述步骤,直到满足所需的比特率编码停止为止㊂2 嵌入式零数小波图像压缩编码算法改进方案2.1 EZW算法存在的不足EZW的编码思想是通过不断扫描小波系数,以生成更多的零树来对图像实现编码,经研究发现该算法存在下列问题[9-15]:(1)存在重复扫描,不仅浪费了时间和空间,而且影响了效率㊂(2)逐次逼近量化过程中,产生了多棵零树,不仅增加了编码的比特数,同时也增加了编码工作计算量㊂(3)编码产生的四种符号中,每一种符号出现的机率也是不相等的㊂出现机率最高的是零树根,占有的比率达到百分之五十以上,而且它的连续性很强㊂另外三种符号出现的机率不高,连续性也不强,这将会出现大量连续的零数根㊂因此不仅浪费了时间,同时也影响了图像的编码效率和压缩比率㊂若采用原EZW算法的扫描方式和编码方法,算法的复杂度会增加且会产生编码冗余㊂2.2 改进的算法思想针对其不足,提出了以下改进方案㊂(1)采用扩充编码符号的方法进行改进,用6个标志位代替EZW算法中的4个标志位对小波系数进行量化,以实现零树结构的快速判断㊂由于在图像的分解过程中,会产生大量的能量,其中大部分会聚集在低频子带中㊂这就导致了低频子带的系数远远大于其余的子带,因此会产生更多的零树㊂而且在编码时重要系数的后面依旧会产生很多零树根,因此在扫描低频子带LL时,若一个系数为正重要系数,则继续对其子孙系数进行判断,若子孙中至少含有一个重要系数则标记为P n,若不含重要系数则标记为P;若一个系数为负重要系数,则继续对其子孙系数进行扫描判断,若子孙中至少含有一个重要系数则标记为N n,若不含重要系数则标记为N,并对子孙系数进行标记,在该阈值下跳过不扫描㊂通过这种方式,减少了对重要系数的扫描,提高了效率㊂(2)改进后,用霍夫曼编码代替原来的算数编码㊂算术编码采用不同的概率分布模型进行编码,相比较霍夫曼编码,大大增加了算法的复杂度㊂上述提到EZW编码算中会出现大量的零数根,各个符号出现的机率不同,而霍夫曼编码会统计每个频率符号,按照大小的频率和二叉树的重新形成排序,并获得所有的符号代码㊂因为霍夫曼代码是不等长的编码,短码表示高概率,而长码表示低概率,从而实现压缩的目的㊂此外,霍夫曼编码是一个无损编码方法,理论上不影响图像恢复㊂主扫描编码后标志位符号的这种特点正好符合霍夫曼编码的特点㊂采用霍夫曼编码不但可以减少编码所需要的比特数,而且还可以降低算法的复杂度㊂2.3 改进的图像编码流程改进编码算法就是根据其EZW算法特性,通过扩充编码符号改变扫描顺序,并根据霍夫曼编码特性,结合霍夫曼编码来提高图像的压缩性能㊂改进算法的具体实现步骤可以总结如下:输入一幅原始图像,先对其进行小波变换,然后主扫描,产生用以记录重要系数位置信息的小波系数符号表;其次是副扫描,产生记录㊃32㊃ 第6期 詹 为等:基于小波变换的图像压缩编码方法研究重要系数量化情况的小波系数量化表㊂每扫描完一次,都会将主扫描形成的主表与副扫描表中的量化值先后分别进行霍夫曼无损编码,形成的码流就是某个量化步长下的零树方式的编码码流,通过解码这个码流就可以得到输入图像的重构恢复图像㊂每完成一次编码,阈值就会减半,然后进行重复扫描,熵编码,直到达到设定的比特率或其所需要的精度㊂改进的嵌入式零树小波变换编码流程如图2所示㊂图2 改进的嵌入式零树小波变换编码流程具体仿真过程如下:(1)读取原始图像的信息,通过函数X =imread ('cameraman.bmp ')读取图像㊂(2)使用哈尔小波变换二维矩阵,de _x =haardec (X )㊂(3)得到变换后的矩阵,使用改进的EZW 对转换后的矩阵进行编码,由ezw _encode (de _x ,10)函数实现㊂(4)将改进的EZW 与霍夫曼编码相结合,该实现功能由函数huffman (DD )实现㊂(5)由函数ihuffman (encode _x ,h ,sortindex )来实现解码㊂(6)通过函数ezw _decode 实现符号解码,解码成之前矩阵中对应的像素值,将矩阵转换为图像㊂3 实验结果及分析为了验证改进后的嵌入式零数小波算法的有效性,利用MATLAB 仿真软件进行实验,并与原EZW 算法进行对比,以证明该算法的可行性㊂3.1 图像质量评估测度在图像编码系统中,常用峰值信噪比(peak signal to noise ratio ,PSNR )来衡量其性能㊂MSE =1MN ∑M -1m =0∑N -1n =0=x m ,()n -x ~m ,()n 2 (5)PSNR =10log 102552MSN(6)其中,MSN 为均方误差;x (m ,n )为原始图像像素值;x ~(m ,n )为解压缩之后的像素值[16]㊂3.2 EZW 与改进的EZW 的对比选用大小为256*256的3幅灰度图像Camera⁃man ㊁Lena ㊁Pepper 作为测试对象进行实验㊂对原始图像进行3级分解㊂在阈值为32时,与传统的EZW 算法进行对比,如图3所示㊂表1与表2为性能分析实验数据对比㊂图3 改进的EZW 与EZW 算法重构对照比较表1 阈值32下所需的编码位数图像EZW 算法(位)改进的EZW 算法(位)节省(位)Cameraman 23994218282166Lena 24001218212180Pepper23983217992184 从表1可以看出,用改进的编码方式进行编码后,减少了传输或存储所需的编码符号流所需的位数,避免了符号冗余,可有效提高图像的压缩比和编码效率,降低算法复杂度㊂表2 不同比特率下PSNR 比较比特率/(b ㊃p -1)CameramanLena Pepper PSNR /dB PSNR /dB PSNR /dB EZW 改进算法EZW 改进算法EZW 改进算法0.1522.3423.8423.2324.1222.5123.120.2527.6630.0228.4329.3428.3229.430.3531.4833.4232.2133.0932.1333.210.4535.3036.8936.9038.0235.7336.430.5537.5439.0138.4340.3237.8138.760.6539.4440.8240.8941.8339.4341.010.7541.1742.7341.4343.0941.1242.980.8542.8044.3743.8446.3243.5945.120.9543.9546.9947.9948.9346.8947.541.0546.3248.5349.0150.8648.2149.79㊃42㊃ 计算机技术与发展 第28卷 从表2看到,在相同比特率下,改进算法的峰值信噪比略高,也即重构图像的质量有了相应提高㊂图4为其在不同比特率下的峰值信噪比折线图㊂通过对改进EZW 算法与原EZW 算法进行仿真实验,将实验得到的数据㊁图像进行比较,可以看出无论是在峰值信噪比㊁编码所需位数还是人眼的主观评价上,改进算法都较原始EZW 算法略有提高,有效可行㊂4摇结束语针对EZW 算法的不足,给出了具体的改进措施:扩充编码符号;将改进的EZW 编码与霍夫曼组合来提高图像编码效率㊂实验结果表明,改进算法与原算法相比较,不仅其图像的峰值信噪比有所提高,而且避免了产生大量冗余比特流,提高了图像编码效率㊂改进算法在主观视觉和客观数据方面均优于EZW ㊂因此,该算法是有效可行的㊂文中研究处理的只是灰度图像,而未考虑彩色图像和视频图像,因此对彩色图像与视频进行高效的压缩是今后研究的主要方向㊂同时,由于小波分析中小波基的多样性和灵活性,使其在不同应用领域的特殊性研究具有实用性㊂此外,文中只是在软件上实现,即利用Matlab 仿真软件在PC 机上实现,这样对系统执行的速度有一定的限制,制约了整个系统的编码速度,可以考虑在硬件如DSP 上实现,这样能够提高整个系统的性能㊂参考文献:[1] 朱 虹.数字图像技术与应用[M ].北京:机械工业出版社,2011.[2] PARMAR H M ,SCHOLAR P parison of DCT andwavelet based image compression techniques [J ].Internation⁃al Journal of Engineering Development and Research ,2014,2(1):664-669.[3] 孙一惟.基于小波变换和DCT 的图像压缩系统设计与实现[D ].长春:吉林大学,2016.[4] RAID A M ,KHEDR W M ,EL -DOSUKY M A ,et al.Imagecompression using embedded zerotree wavelet [J ].Signal &Image Processing ,2014,5(6):33-39.[5] GOLDBERG M A ,PIVOVAROV M ,MAYO -SMITH WW ,et al.Application of wavelet compression to digitized ra⁃diographs [J ].American Journal of Roentgenology ,1994,163(2):463-468.[6] ZHANG Ning ,ZHU Jinfu.Study on image compression andfusion based on the wavelet transform technology [J ].Inter⁃national Journal on Smart Sensing &Intelligent Systems ,2015,8(1):480-496.[7] 刘 敬.基于小波变换的图像压缩算法研究[D ].重庆:重庆大学,2012.[8] 林 行.基于零树小波的静止图像压缩算法的研究[D ].沈阳:沈阳工业大学,2014.[9] XIE Xin ,XU Yin ,LIU Qing ,et al.A study on fast SIFT im⁃age mosaic algorithm based on compressed sensing and wavelet transform [J ].Journal of Ambient Intelligence and Humanized Computing ,2015,6(6):835-843.[10]LI Gongxin ,WANG Wenxue ,WANG Yuechao ,et al.Nano -manipulation based on real -time compressive tracking [J ].IEEE Transactions on Nanotechnology ,2015,14(5):837-846.[11]张德干,康学净,王京辉.一种新的图像压缩编码算法[J ].光电子㊃激光,2012,23(6):1173-1180.[12]CHENG K J ,DILL J.Lossless to lossy dual -tree BEZWcompression for hyperspectral images [J ].IEEE Transactionson Geoscience and Remote Sensing ,2014,52(9):5765-5770.[13]田杰华,顾晓东,汪源源.利用人眼视觉特性的低比特率小波图像压缩[J ].仪器仪表学报,2010,31(11):2515-2520.[14]陈平平,谭定英,刘秀峰.一种改进的小波变换图像压缩算法[J ].计算机工程与应用,2012,48(14):175-179.[15]郑侃侃.低码率低复杂度图像/视频编码技术研究[D ].上海:上海交通大学,2015.[16]刘书琴,毋立芳,宫 玉,等.图像质量评价综述[J ].中国科技论文在线,2011,6(7):501-506.㊃52㊃ 第6期 詹 为等:基于小波变换的图像压缩编码方法研究。




基于小波变换的图像压缩技术近年来,随着数字图像在生活中的广泛应用,对图像数据的存储和传输需求也越来越大。
然而,图像数据的存储和传输都需要大量的存储空间和传输带宽,对于一些容量有限、带宽不足或网络受限等场景,就需要对图像进行压缩。
而小波变换技术作为一种高效的图像压缩方法,已经在实际应用中得到广泛运用。
1. 小波变换的原理小波变换是利用数学中的小波基函数对信号进行变换的一种新的方法。
其基本思想是利用小波基函数将信号分解为不同的尺度和频率下的子信号,从而实现对信号的压缩和重构。
小波变换的主要优点在于它能够捕捉信号中的瞬时变化和局部特征,并能够实现对信号的多尺度和多频带的分析。
2. 小波变换在图像压缩中的应用在图像压缩中,小波变换主要用于图像的离散小波变换(DWT)。
其原理是先将图像分解成多个尺度和频率下的子图像,再根据不同的重要性程度进行量化和编码,最后再通过反离散小波变换(IDWT)重构出原始图像。
对于高频部分的系数,可以通过丢弃一定的系数数据来实现图像的压缩。
3. 小波变换的优势和不足小波变换作为一种高效的图像压缩方法,相较于其它图像压缩方法,具有以下优点:(1)小波变换能够对图像进行多尺度和多频带的分析,从而更好地保留了图像的空间分辨率和频率特征。
(2)小波变换通过选择不同的小波基函数,能够很好地适应各种类型的信号。
(3)小波变换通过对高频分量的系数进行丢弃,可以实现较高的压缩比。
尽管小波变换在图像压缩中具有较高的效率和优势,但也存在一些不足之处。
例如:(1)小波变换本身需要大量的计算,并且需要一定的优化和加速,才能实现实时的图像传输和处理。
(2)小波变换的局部特征使得其对整个图像的处理是非常局限的,因此需要结合其它的算法和方法,才能实现更加全面的图像处理和分析。
4. 结语小波变换作为一种高效的图像压缩方法,在实际应用中得到了广泛的应用和研究。
通过分析其原理和应用特点,我们可以看出小波变换在图像处理、分析和传输中具有较高的效率和优势。

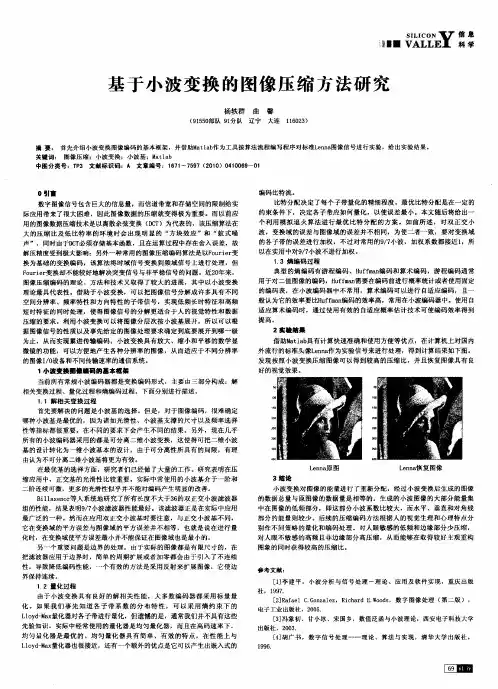
总第171期2008年第9期舰船电子工程Ship Electronic Enginee ring Vol.28No.9161 基于小波变换图像压缩软件的实现3张培珍1) 杨根源2) 平殿发1) 徐圣良1)(海军航空工程学院研究生管理大队1) 烟台 264001)(海军航空工程学院指挥系2) 烟台 264001)摘 要 针对传统小波变换过程复杂的缺点和S PIH T 算法编码过程重复运算、存储量大的问题,提出一种改进的图像压缩编码方法。
通过设计软件实现了静态影像的压缩编码。
关键词 小波变换;图像压缩编码中图分类号 TN919.81Realization of I mage Comp ression Soft wareBased on Wavelet Tra nsf or mZ ha ng Peizhen 1) Ya ng Ge nyuan 2) Ping Dia nf a 1) X u She ngliang 1)(Depa rtment of Graduate Manage ment ,NA EI 1),Y a ntai 264001)(Depart me nt of Comma nd ,NA EI 2),Y antai 264001)Abs tra ct In view of t he proble ms of complicated co nvolution proce ss of wavelet tra ns fo rm ,repeated calc ula tions and a large of needed me morie s of S PIH T algorithm.An imp roved met hod that use s wavelet t ransform for image compre ssio n is pre sented.visual C ++ 6.0is used a s a progra mming platf orm ,a nd a demo system of static image compression is realized.Ke y w ords wa velet t ransform ,image compre ssion coded Class N umber TN919.811 引言随着现代通信应用和计算机技术的迅速发展,图像压缩技术仍然是当今研究的一个重要课题[1~3]。
832008年第02期,第41卷 通 信 技 术 Vol.41,No.02,2008总第194期 Communications Technology No.194,Totally收稿日期:2007-10-23。
作者简介:郑 伟(1972-),女,副教授,博士,主要研究方向为图像处理;崔跃利(1982-),男,硕士研究生,主要研究方向为图像压缩;王芳(1980-),女,助教,主要研究方向为图像压缩。
基于小波变换的图像压缩编码研究综述郑 伟, 崔跃利, 王 芳(河北大学 电子信息工程学院,河北 保定 071002)【摘 要】图像压缩是指以尽量少的比特数代表原来图像的技术。
小波变换由于在时域和频域同时具有局域化特性, 弥补了DCT变换的不足,其多分辨率特性还便于与人眼视觉特性相结合。
小波图像编码还便于与其它新兴图像编码方法相结合,成为当前研究热点。
文中介绍了小波变换的基本理论,讨论了小波图像压缩研究现状和进展,并指出存在的主要问题,最后展望小波图像压缩编码的发展前景。
【关键词】图像压缩;小波变换;小波基;分形编码【中图分类号】TP391 【文献标识码】A 【文章编号】1002-0802(2008)02-0083-03A Review of Image Compression Coding Based on Wavelet TransformZHENG Wei , CUI Yue-li , WANG Fang(College of Electronic and Information Engineering, Hebei University, Baoding Hebei 071002, China)【Abstract】Image compression is a technology which uses as few as possible bits to represent the original image. As wavelet transform has local characteristics on the time and frequency domain, it makes up the deficiency of DCT. Moreover, its multi-resolution characteristics can easily associate with the human visual system (HVS). Wavelet-based image compression is prone to combining with new image coding methods. It has already become the research hotspots at present. This paper introduces wavelets theory, and discusses the research and progress of wavelet-based image compression, and then points out the main problems. Finally, it looks forward to its future development. 【Key words】image compression; wavelet transform; wavelet base; fractal coding0 引言随着多媒体技术及网络迅速发展,图像压缩在多媒体信息的传输和存储中显得越来越重要。
小波变换在图像处理中的应用引言图像处理是计算机科学领域中的一个重要研究方向,它涉及到对图像的获取、分析、处理和显示等多个方面。
而小波变换作为一种有效的信号处理工具,已经被广泛应用于图像处理中,其具有较好的时频局部性和多尺度分析能力。
本文将探讨小波变换在图像处理中的应用,并重点介绍其在图像压缩、图像增强和图像恢复等方面的具体应用。
一、小波变换在图像压缩中的应用图像压缩是指通过对图像数据进行编码和解码,以减少图像数据的存储空间和传输带宽。
小波变换作为一种多尺度分析工具,能够将图像信息分解为不同频率和不同分辨率的子带,从而实现对图像的有效压缩。
通过小波变换,可以将图像中的高频细节信息和低频基本结构信息分离出来,然后根据实际需求选择保留或舍弃相应的子带,以达到图像压缩的目的。
小波变换在图像压缩中的应用已经成为了现代图像压缩标准中的重要组成部分,例如JPEG2000标准就采用了小波变换进行图像编码和解码。
二、小波变换在图像增强中的应用图像增强是指通过对图像进行处理,以改善图像的质量、增强图像的细节和对比度等。
小波变换作为一种时频局部化的分析工具,能够提取出图像中的不同频率和不同方向的特征信息,从而实现对图像的增强。
通过小波变换,可以对图像进行去噪、锐化、边缘提取等操作,以增强图像的细节和对比度。
此外,小波变换还可以用于图像的颜色增强和色彩平衡等方面,从而实现对图像色彩的改善。
小波变换在图像增强中的应用已经被广泛应用于医学影像、卫星遥感图像等领域。
三、小波变换在图像恢复中的应用图像恢复是指通过对损坏或失真的图像进行处理,以恢复原始图像的过程。
小波变换作为一种多尺度分析工具,能够提取出图像中的不同频率和不同分辨率的信息,从而实现对图像的恢复。
通过小波变换,可以对图像进行去噪、补全、修复等操作,以恢复图像的细节和结构。
此外,小波变换还可以用于图像的运动估计和图像的超分辨率重建等方面,从而实现对图像的更好的恢复效果。
基于小波变换图像压缩编码研究的现状与发展摘要:本中介绍了小波变换的基本理论,讨论了小波图像压缩研究现状和进展,特别就目前小波图像编码与其它新兴图像编码方法相结合研究热的点作了初步探讨,最后展望小波图像压缩编码的发展前景。
关键词:小波变换图像压缩小波基小波变换是20世纪80年代后期发展起来的一种新的信息处理方法,解决了很多傅里叶变换不能解决的问题。
小波变换由于在时域和频域同时具有局域化特性,弥补了DCT变换的不足,可以把图像信息定位到任何精度级上,以实现根据图像信息重要性进行优先编码、传输,并且其多分辨率特性便于与人眼视觉特性相结合,小波变换图像编码压缩成为当前研究热点。
小波变换与其它编码方法相结合成为图像压缩算法的发展趋势。
1 小波变换压缩编码的理论小波变换的基本思想是用一组小波或基函数表示一个函数或信号。
若,将任意的连续函数在小波基下进行展开,称这种展开为函数的连续小波变换(Continue WaveletTransform,简记为CWT),其表达式为:(3)在对图像进行分析、处理的应用中,我们主要采用离散小波变换(DWT),一般选取,此时称DWT为多分辨率分析。
S.Mallat首先将多分辨率分析用于图像数据的压缩,并给出了信号分解与合成的塔式快速小波变换算法,该算法的出现使小波分析方法在信号处理领域真正得以实用化。
2 小波变换图像压缩编码基本原理1989年,Mallat提出了小波变换多分辨率分析的概念,并给出了用于信号分析和重构的Mallat塔式算法[1]。
所谓Mallat塔式算法,就是将一幅图像经过小波变换分解为一系列不同尺度、方向、空间域上局部变化的子带图像。
一幅图像经过一次小波变换后产生4个子带图像:LL代表原图像近似分量,反映原图像的基本特性;HL、LH和HH分别表示水平、垂直和对角线的高频分量,反映图像信号水平方向、垂直方向与对角线方向的边缘、纹理和轮廓等。
其中,LL子带集中了图像的绝大部分信息,以后的小波变换都是在上一级变换产生的低频子带(LL)的基础上再进行小波变换。
基于小波变换的图像压缩方法研究摘要在当今社会,由于图像采集设备的广泛应用以及采集分辨率的逐步提高,图像数据呈指数增长,为了能够充分的利用图像数据,对图像和视频数据进行压缩成为亟待解决的问题并且成为图像处理领域研究的一个热点问题。
而小波变换因其优秀的时-频局部性特征和与人眼视觉系统多通道相吻合的多分辨率分解特性,在图像压缩领域得到了较为广泛的应用,基于小波变换的图像压缩编码算法成为了图像压缩领域中的一个最重要的分支,对其进行的研究和改进无疑是一项相对重要的任务和研究热点。
本文首先介绍小波分析及其性质,对尺度函数、小波母函数、多分辨分析等进行分析。
然后根据近些年发表的学术文章,分析并整理了第二代小波变换的理论与实现方法,分析了第二代小波变换的优点及这些优点在图像压缩中的应用。
还分析了图像小波变换后小波系数的特征,讨论了优化小波系数的小波基选择问题。
最后阐述了当前热门的EZW编码算法和SPIHT编码算法。
关键词:小波变换图像压缩小波基 EZW编码算法SPIHT 编码算法The research of image compression based on WaveletTransformAbstractWith the wide application of image acquisition device and the improvement of acquisition resolution, image data are growing rapidly. In order to utilize the image data effectively, the compression of image and video has become an urgent problem and has become a research hotpot in multimedia technology field. The wavelet transform technology becomes widely used in image compression fieldsfor its good time-frequency partial characteristic and wavelet multi-resolution characteristic matching well with the multichannel model of HVS. The image compression method based on wavelet transform has become an important branch of image compression,study and improve the algorithms of image compression based on wavelet is not only an important task but also a research hot.The thesis introduces the basic concepts of wavelet transform andmultiresolution analysis.Have analyzed and systemically summarized principles and realizing methods of the second generation wavelet, have analyzed advantages of the second generation wavelet transform and their applications in image compression. Characteristics of wavelet coefficients after wavelet transform are analyzed, discussed the optimal wavelet coefficients ofthe wavelet base selection problem. Finally elaborated the current popular EZW coding and SPIHT coding algorithm.Keywords:Wavelet transform Image compression Wavelet EZW coding algorithm SPIHT coding algorithm目录1绪论1.1 引言1.2小波的定义1.3小波的发展历史1.4图像压缩的基本方法及现状2 第一代小波分析的基本理论2.1第一代小波的性质与特点2.2 连续小波变换2.3 离散小波变换2.4 二维小波3 第二代小波分析的基本理论3.1 提升算法的基本方法3.2 Lazy提升3.3提升算法的过程3.4提升变换与第一代小波变换的比较4 基于小波变换的图像压缩方法4.1 图像压缩中小波基的选择问题4.2 EZW编码方法4.2.1 EZW编码方法的基本思想4.2.2 EZW算法实现的一般步骤4.3 SPIHT编码方法4.3.1 SPIHT编码方法的原理4.3.2 SPIHT算法的实现过程4.4 实验结果及结论5 总结与展望1绪论1.1引言科学研究表明,在人类从外界获取的信息中,有80%以上是来自视觉感知的。
目录第一章前言 (1)1.1图像压缩的必要性 (1)1.2图像压缩原理 (1)1.3小波变换编码的发展现状 (1)1.4论文内容结构 (2)第二章小波变换的基本理论 (3)2.1 连续小波变换 (3)2.2 离散小波变换 (4)2.3小波包分析 (5)第三章用Matlab实现具体图像的压缩编码 (9)3.1 基于小波变换的图像局部压缩 (9)3. 2 利用二维小波变换进行图像压缩 (11)3. 3 基于小波包变换的图像压缩 (16)第四章对小波变换图像压缩编码的总结和展望 (19)第五章结束语 (20)参考文献: (21)致谢 (22)摘要:随着多媒体通信和计算机通信网的快速发展,图像传输已成为重要的通信内容,无论是图像数据的传输还是存储,都要求对图像数据进行压缩,以减少图像通信的数据量和图像存储的空间。
根据目前网络多媒体通信技术的现状和发展趋势,在将来相当长的一段时间内,数字化的媒体数据以压缩形式存储和传输势在必行。
基于小波变换的图像压缩技术采用多尺度分析, 因此可根据各自的重要程度对不同层次的系数进行不同的处理,图像经小波变换后,并没有实现压缩,只是对整幅图像的能量进行了重新分配。
事实上,变换后的图像具有更宽的范围,但是宽范围的大数据被集中在一个小区域内,而在很大的区域中数据的动态范围很小。
小波变换编码就是在小波变换的基础上,利用小波变换的这些特性,采用适当的方法组织变换后的小波系数,实现图像的高效压缩的。
关键词:小波分析;图像压缩;MATLABABSTRACT:As multimedia communications and the rapid development of computer communication network, the image transfer has become an important content of the communication, either transmission or storage of image data, the image data are required to be compressed to reduce the image data amount of communication and an image memory space . According to the current network multimedia communication technology status and development trend in the future for a long period of time, the digitized media data stored and transmitted in compressed form is imperative.Wavelet-based image compression technology uses multi-scale analysis, it can be according to their degree of importance on different levels for different coefficients processing, image by wavelet transform, and did not achieve compression, but the energy of the whole image has been re-assignment. In fact, the converted image has a wider range, but a wide range of large data is concentrated in a small area, while a large dynamic range of the data area is small. Wavelet transform coding is based on the wavelet transform, wavelet transform these characteristics, using appropriate methods organization transformed wavelet coefficients, to achieve efficient image compression.Key words: Wavelet Transform;Image Compression;MATLAB第一章前言1.1图像压缩的必要性图像数字化后,其数据量非常庞大,例如,对于640*480像素的彩色图像,如果每个像素的位深度为24,即24bit/像素,按照30帧/s的速度进行播放,则一张650M的光盘只能存储大约24s左右的播放画面。
当前随着多媒体通信和计算机通信网的快速发展,图像传输已成为重要的通信内容,无论是图像数据的传输还是存储,都要求对图像数据进行压缩,以减少图像通信的数据量和图像存储的空间。
根据目前网络多媒体通信技术的现状和发展趋势,在将来相当长的一段时间内,数字化的媒体数据以压缩形式存储和传输将势在必行。
在多媒体计算机系统,电子出版,视频会议,数字图书馆等众多领域数字图像都有着广泛的应用。
然而,大数据量的图像,使存储成本变高,而现在的网络环境不能满足多媒体通信的需求。
在此背景下,图像编码理论迅速发展了起来,并且越来越受到广泛的关注。
1.2图像压缩原理对于给定的任何图像,图像都能分解成一个轮廓信号(低频子图)和水平、垂直、对角线三个方向上的细节信号(高频子图),相应的轮廓信号又可以进一步分解。
而图像的主要能量部分是低频部分,而且人眼视觉系统对低频部分更为敏感,所以可以对低频部分进行低压缩比,对高频部分相应采用较高压缩比,最终再将所有的分量进行图像重构,重构后的图像即是预期压缩处理后的图像。
1.3小波变换编码的发展现状小波分析诞生于20世纪80年代, 被认为是调和分析即现代Fourier分析发展的一个崭新阶段。
众多高新技术以数学为基础,而小波分析被誉为“数学显微镜”,这就决定了它在高科技研究领域重要的地位。
目前, 它在模式识别、图像处理、语音处理、故障诊断、地球物理勘探、分形理论、空气动力学与流体力学上的应用都得到了广泛深入的研究,甚至在金融、证券、股票等社会科学方面都有小波分析的应用研究。
在传统的傅立叶分析中,信号完全是在频域展开的,不包含任何时频的信息,这对于某些应用来说是很恰当的,因为信号的频率的信息对其是非常重要的。
但其丢弃的时域信息可能对某些应用同样非常重要,所以人们对傅立叶分析进行了推广,提出了很多能表征时域和频域信息的信号分析方法,如短时傅立叶变换,Gabor变换,时频分析,小波变换等。
其中短时傅立叶变换是在傅立叶分析基础上引入时域信息的最初尝试,其基本假定在于在一定的时间窗内信号是平稳的,那么通过分割时间窗,在每个时间窗内把信号展开到频域就可以获得局部的频域信息,但是它的时域区分度只能依赖于大小不变的时间窗,对某些瞬态信号来说还是粒度太大。
换言之,短时傅立叶分析只能在一个分辨率上进行。
所以对很多应用来说不够精确,存在很大的缺陷。
而小波分析则克服了短时傅立叶变换在单分辨率上的缺陷,具有多分辨率分析的特点,在时域和频域都有表征信号局部信息的能力,时间窗和频率窗都可以根据信号的具体形态动态调整,在一般情况下,在低频部分(信号较平稳)可以采用较低的时间分辨率,而提高频率的分辨率,在高频情况下(频率变化不大)可以用较低的频率分辨率来换取精确的时间定位。
1.4论文内容结构本文首先介绍了小波变换的基本理论,包括连续小波变换,离散小波变换和小波基。
然后用MATLAB实现具体图像的压缩编码,包括基于小波变换的图像局部压缩,利用二维小波变换进行图像压缩,基于小波包变换的图像压缩。
第二章 小波变换的基本理论2.1 连续小波变换定义:设)()(2R L t ∈ψ,其Fourier Transform 为)(ˆωψ,当)(ˆωψ满足条件时, ∞<=⎰R d C ωωωψψ2)(ˆ (2-1) 我们称)(t ψ为一个基本小波(或者母小波)。
)(1)(,ab t a t b a -=ψψ 0;,≠∈a R b a (2-2) 将母函数)(t ψ 伸缩和平移后获得一个小波序列。
其中a 为伸缩因子,b 为平移因子。
对于任意的函数)()(2R L t f ∈的连续小波变换为dt ab t t f af b a W R b a f )()(,),(2/1,->==<⎰-ψψ (2-3) 其逆变换(重构公式)为⎰⎰∞∞-∞∞--=dadb a b t b a W a C t f f )(),(11)(2ψψ (2-4)∞<⎰∞∞-dt t )(ψ (2-5))(ˆωψ是一个连续函数。
在原点)(ˆωψ必须等于0,即 0)()0(ˆ==⎰∞∞-dt t ψψ (2-6) 既满足逆变换条件式,又满足(2-7)式子稳定性条件的小波)(t ψ的Fourier Transform ,可以实现信号重构在数值上的稳定:∑∞∞--≤≤B A j 2)2(ˆωψ(2-7)式中。
2.2 离散小波变换连续小波变换中的尺度伸缩参数和平移参数都是连续变化的实数,在应用中需要计算连续积分,在处理数字信号时很不方便,因此连续小波变换),(b a W f 只用于理论分析与论证。
在实际数值计算中常采用离散形式,即离散小波变换(DWT )。
离散形式都是针对连续的尺度参数a 和连续平移参数b 的。
而不是针对时间变量t 的。
这一点与我们以前习惯的时间离散化不同。
在连续小波)(,t b a ψ中,考虑函数:)()(2/1,ab t a t b a -=-ψψ 这里R b ∈,+∈R a ,且0≠a ,ψ是容许的,为方便起见,在离散化中,总限制a 只取正值,这样相容性条件就变为∞<=⎰∞ωωωψψd C 0)(ˆ (2-8) 通常,把连续小波变换中尺度参数a 和平移参数b 的离散公式分别取作j a a 0=,这里Z j ∈,扩展步长10≠a 是固定值,假定10>a 。
所以相应的离散小波函数)(,t k j ψ就可以写成: )()()(002/00002/0,kb t a a a b ka t a t j j j j j k j -=-=---ψψψ (2-9) 离散形式小波变换系数为:>=<=⎰∞∞-k j k j k j f dt t t f C ,*,,,)()(ψψ (2-10) 它的重构公式是:∑∑∞∞-∞∞-=)()(,,t C C t f k j k j ψ (2-11)C 是一个常数,它与信号无关的。