大学物理东南大学.ppt

格式：ppt
大小：1.24 MB
文档页数：24

下载文档原格式

大学物理PPT完整全套教学课件pptx

非弹性碰撞
碰撞后系统动能不守恒，部分机械能转化为内能，损失了机械能。如湿纸或橡皮泥的碰撞等。
完全非弹性碰撞
碰撞后两物体粘在一起运动，动能损失最大，机械能损失也最大。
能量守恒定律
定律表述
自然界中的一切物质都具有能量，能量既不能创造也不能消灭，而只能从一种形式转换成另一种形式，从一个物体传递到另一个物体；在转化和传递过程中能量的总量保持不变。
大学物理的学习方法和要求
掌握基本概念和基本规律
注重实验和实践
学习大学物理首先要掌握基本概念和基本规律，理解它们的物理意义和适用范围。
大学物理实验是学习物理学的重要环节，通过实验可以加深对物理概念和规律的理解，培养实验技能和动手能力。
培养物理思维
拓宽知识面
学习大学物理要注重培养物理思维，即运用物理学的方法和观点去分析和解决问题的能力。
热力学第二定律的表述及实质
表述
实质
应用
热力学第二定律有多种表述方式，其中最著名的是开尔文表述和克劳修斯表述。开尔文表述指出，不可能从单一热源吸取热量，使之完全变为有用功而不产生其他影响。克劳修斯表述指出，热量不可能自发地从低温物体传到高温物体而不引起其他变化。
热力学第二定律的实质是揭示了自然界中一切与热现象有关的宏观过程都具有方向性，即不可逆性。这种方向性是由系统内部的微观状态数目的变化所决定的，也就是由系统的熵增原理所决定的。
循环过程卡诺循环
01
02
定义
工作原理
卡诺循环是一种理想的可逆循环，由两个等温过程和两个绝热过程组成。它是热力学第二定律的出发点，也是热机效率的理论极限。
卡诺循环通过高温热源吸收热量，在低温热源放出热量，并对外作功。其效率只与高温热源和低温热源的温度有关，而与工作物质无关。

大学物理东南大学PPT课件

y N o
mg
y
由 Fyt mv y mv 0 y Py P0 y
(N mg )t 0 (m 2 gh )
N
N mg m 2gh
t
o mg
t 1s时, N 600 600 1200 N 2mg
t 0.1s时, N 600 6000 6600 N 11mg
可以看出当物体状态变化相同量，力
§1.质点和质点系的动量定理 / 一、Newton第二定律的原始形式
二、冲量
力对时间的累积效应。例如：撑杆跳运动员从横杆跃过,
落在海棉垫子上不会摔伤，
如果不是海棉垫子，而是大理石板，又会如何呢？
§1.质点和质点系的动量定理 / 二、冲量
又如汽车从静止开始运动，加速到 20m/s如果牵引力大，所用时间短，如果牵引力小所用的时间就长。
§1.质点和质点系的动量定理 / 四、质点的动量定理
②. 平均冲力的计算由：
F
t
t0
Fdt
t t0
I t t0
P P0 t t0
③.F 为合外力，不是某一个外力。
④.动量定理的分量式：
Ix
t
t0
Fxdt Fx t mv x mv 0x Px P0x
Iy
t
t0
Fydt Fyt mv y mv 0 y Py P0 y
m1v1
m1v10
f12
t
t0
(
F2
f21 )dt
m 2v2
m 2v20
f21
考虑质点组成的系统两式求和：
m2
v20 v2
F2
§1.质点和质点系的动量定理 / 五、质点系的动量定理
t

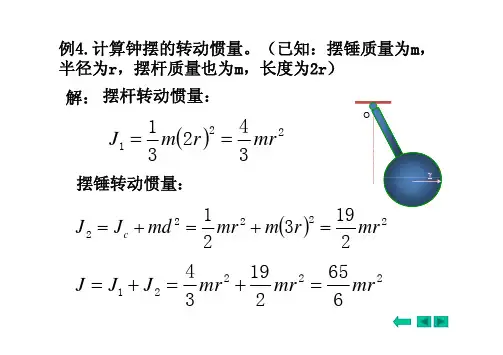
东南大学大学物理课件4-2

设小虫爬到p点
r p

例2.质量为M，半径为R的转台，可绕中心轴转动。转台与轴间摩擦不计，设质量为m的人站在台边缘。初始时人、台都静止。若人相对台匀速率沿边缘行走一周，问：相对地面，人和台各转过多少角度？ 2 解：人： J mR 设对地的角速度 1 台： J MR2 设对地的角速度
四转动定律的应用基本方法和步骤分析力，确定外力矩
列出转动定律和牛顿定律方程
列出线量和角量之间的关系式求解联立方程
例1 半径为r的定滑轮绕转轴的转动惯量为J，两边分别悬挂质量为m1和m 2的物体A、B，A置于倾角为的斜面上，它和斜面间的摩擦因数为，B向下作加速运动时，求⑴其下落加速度的大小；⑵滑轮两边的张力。（绳的质量及伸长均不计，绳与滑轮间无滑动，滑轮轴光滑） a1 解： m
mg 外力矩 M mgr cos dJ dr 1 2 dL d dJ 2 2mr M ( J ) J ml mr dt dt dt dt dt 12 dr 12v0 7l g dr g mgrcos 2mr v cos t cos( t) dt dt 2 24v0 7l
2
§4-6 刚体进动（旋进）
高速旋转的物体，其自转轴绕另一个轴转动的现象。设陀螺质量为m，以角速度自转重力对固定点o的力矩：
M r mg
M mgrsin

L
绕自身轴转动的角动量：
ˆ L Jr 0
L J
O

c
r
角动量定理的微分式：
L
r 和 v 组成的平面。
0

→
r
mv
2. 质点的角动量定理 d (mv ) 质点m，所受合力 F ， F —动量定理

大学物理ppt课件完整版

03
计算机模拟和仿真
利用计算机进行数值模拟和仿真实验，验证理论预测和实验结果。
2024/1/25
5
物理学的发展历史
01
02
03
古代物理学
以自然哲学为主要形式，探讨自然现象的本质和规律，如古希腊的自然哲学。
2024/1/25
经典物理学
以牛顿力学、电磁学等为代表，建立了完整的经典物理理论体系。
固体的电子论
介绍了能带理论、金属电子论、半导体电子论等。
30
核物理和粒子物理基础
原子核的基本性质
包括核力、核子、同位素等基本概念。
放射性衰变
阐述了α衰变、β衰变、γ衰变等放射性衰变过程及其规律。
粒子物理简介
介绍了基本粒子、相互作用、粒子加速器等基本概念。
2024/1/25
31
THANKS
感谢观看
19
恒定电流的电场和磁场
恒定电流：电流大小和方向均不随时间变化的电流。
2024/1/25
毕奥-萨伐尔定律：计算电流元在空间任一点产生的磁场。
奥斯特-马可尼定律：描述电流产生磁场的规律。
磁场的高斯定理和安培环路定理：揭示磁场的基本性质。
20
电磁感应
法拉第电磁感应定律
描述变化的磁场产生感应电动势的规律。
01
又称惯性定律，表明物体在不受外力作用时，将保持静止状态
或匀速直线运动状态。
牛顿第二定律
02
又称动量定律，表明物体加速度与作用力成正比，与物体质量
成反比。
牛顿第三定律
03
又称作用与反作用定律，表明两个物体间的作用力和反作用力
总是大小相等、方向相反、作用在同一直线上。

东南大学物理课件第3章

v1,v2为相对于地面参考系速度,设都沿x轴正方向
解
v1 v2 v'
(m1 m2 )v m1v1 m2 v2
m1 v2 v v' 2.17103 m s 1 m1 m2
v1 3. 1710 m s
3 1
动量守恒定理中各物体的动量必须都相应于同一惯性参考系而言
38.
例3 设有一质量为2m的弹丸, 从地面斜抛出去, 2m 它飞行在最高点 m m 处爆炸成质量相 x O xC C 等的两个碎片，其中一个竖直自由下落，另一个水平抛出，它们同时落地．问第二个碎片落地点在何处?
dv dm F m u dt dt
dm dm dt dt
dv dm' F m u dt dt
设火箭高空飞行时
dv dm m u dt dt
F 0 则
v
m dm v0 dv u m0 m
火箭的推力
m 选取 v 的方向为正向 v v0 u ln m0 m0 v v0 u ln m 为起始时刻 t 0 火箭的质量 m0 m 为时刻 t 火箭的质量 m0 N 称为质量比式中 m
y
s v
z'
s ' v ' v
y'
2
m2
m1
z
o
o'
v1
x x'
[例2] 一长为l 均匀柔软绳子，其单位长度的质量为，将其卷堆成一堆放在地面上，若手握绳一端，以匀速 v 将其上提，当绳一端被提到离地面高度为 y 时，求手的提力。
F
v
y

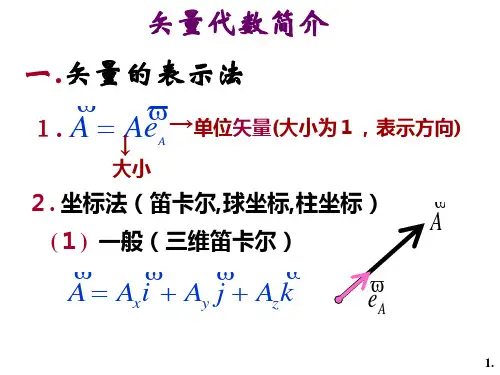
东南大学物理课件第1章

dr dr dt dt
例1(书)
设质点的运动方程为
r(t) x(t)i y(t) j ,
其中
x(t ) 1.0t 2.0，
y(t ) 0.25t 2.0，
2
式中x，y的单位为m(米)， t 的单位为s(秒)，
（1）求 t 3 s 时的速度．（2）作出质点的运动轨迹图．
求导积分
v(t )
求导积分
a (t )
[例3](书)有一个球体在某液体中竖直下落, 其初速度 v0 10 j ，它在液体中的加速度为 a 1.0vj 问： (1)经过多少时间后可以认为小球已停止运动；(2) 此球体在停止运动前经历的路程有多长？
分析：
a. 本题属第二类问题，已知a 和初始条件求其他 b. 积分中“技术”问题
y/m
t 4s
t 2 s 4
t0
2 4
t 2s
x/m
6
[例2 ] 如图A、B 两物体由一长为 l 的刚性细杆相连，A、B 两物体可在光滑轨道上滑行, 如物体 A以恒定的速率 v 向左滑行, 当 60 时, 物体B的速率为多少？
分析：
a. 建立恰当坐标系 dx dy b. 速度定义 vx , v y dt dt c. 找出 x、y 间满足的函数关系式。即 x 2+y 2=l 2=常数
已知：x(t ) 1.0t 2.0，y(t ) 0.25t 2 2.0，解 (1) 由题意可得
t 3 s 时速度为 v 1.0i 1.5 j
1
dx dy vx 1.0， vy 0.5t dt dt
速度 v的值 v 1.8m s ，它与 x轴之间的夹角

东南大学物理课件第4章

dM ydF M dM
11.
令大气压为 p0 ，则 p p0 g (h y)
dF PdA [ p0 g (h y)]Ldy
F [ p0 g (h y)]Ldy 0 y 1 2 p0 Lh gLh 2
代入数据，得
h y
10
h
ω
M J
J （类比 F ma )
刚体定轴转动的角加速度与它所受的合外力矩成正比，比例系数称转动惯量.
12.
三. 转动惯量
1. 概念 —— 转动惯性的量度相关因素：质量、质量分布（几何形状）、转轴
J 的意义：描述转动中惯性大小的物理量 .
同样的力矩作用于两个绕定轴转动的不同刚体, J大的刚体获得的小,即角速度改变得慢, 也就是保持原有转动状态的惯性大.
dA
dy
F 5.9110 N
O
x
L
dF [ p0 g (h y)]Ldy dF 对通过点Q的轴的力矩 dM ydF
M y[ p0 g p0 Lh gLh 2 6
h
dF
h
dy
y O Q
代入数据，得：
质点运动
刚体的一般运动可看作：随质心的平动
+
绕质心的转动
的合成
二. 研究方法 ( 定轴转动 )
(1) 每一质点均作圆周运动，圆面为转动平面；
(2) 任一质点运动 , , 均相同，但 v, a 不同；
(3) 运动描述仅需一个角坐标． z
1. 只研究一个平面 ( 参考平面 ) 2. 只以角量( 如 M ,θ,ω,α… )
1 2 2
1 2 2
5.

东南大学大学物理课件4-3

设小虫爬到p点
r p

例2.质量为M，半径为R的转台，可绕中心轴转动。转台与轴间摩擦不计，设质量为m的人站在台边缘。初始时人、台都静止。若人相对台匀速率沿边缘行走一周，问：相对地面，人和台各转过多少角度？解： J mR2 设对地的角速度人：台： 1 MR 2 设对地的角速度 J
光滑平面上一轻质弹簧劲度系数为k一端固定另一端系一质量为m?的滑块最初滑块静止时弹簧呈自然长度lo今一质量为m的子弹以速度vo沿水平方向并垂直于弹簧轴线射向滑块且留在其中滑块在水平面内滑动当弹簧被拉伸至长度l时求滑块速度的大小和方向
例1.质量很小,长度为 l 的细杆,可绕过中心O并与纸面垂直的轴在竖直面内转动,杆静止于水平位置时,一只小虫以速率v0垂直落在距O点 l 4处,并背离O向细杆 A段爬行,设小虫和杆质量均为m,欲使细杆以恒定角速度转动,小虫应以多大速率向细杆端点爬行。解：重力冲量矩可忽略，碰撞前后角动量守恒 vO 12v0 A l 4 l 1 l 2 2 · m v0 m l m( ) 7l 4 12 4 O ·
M C J C
Fy maCy
可以证明，定轴转动定律在此仍适用
车轮的纯滚动
R A
B
RB
RA
RB
vC
A
RG
G
车轮中心前进的距离与绕质心转过的角度的关系则
x R vc R
ac R
车轮上任意一点的速度
v vC r
vG vC r 0
2
§4-6 刚体进动（旋进）
高速旋转的物体，其自转轴绕另一个轴转动的现象。设陀螺质量为m，以角速度自转
重力对固定点o的力矩：

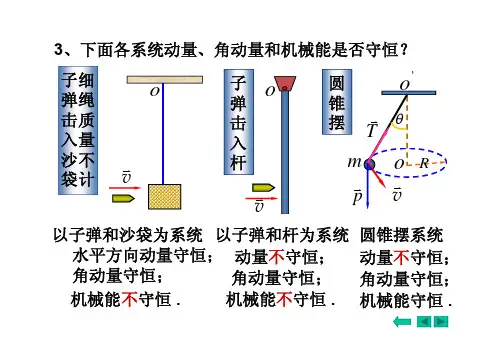
东南大学大学物理课件5-1

dy 0 y
y a x

P
dEˊ
x
dE
dy
dy dE er er 1 2 oa 2 ( x 2 y 2 ) 2
0
Ey dEy 0
xdy E x dE x dE cos 2 2 2 x y 2 0 0
2
讨论：无限长带电直线： 1 = 0， 2 =
y P a o
E
Ey Ex 0 E 2 oa
1
2 x
例5.求无限大均匀带电平面的场强（面电荷密度）。解：平面可看作许多与z轴平 y 行无限长均匀带电细棒组成.
无限长带电细棒 E 2 oa dq ldy dq l z
e12
r12
§5–3 电场强度
一电场库仑定律给出了两个点电荷相互作用的定量关系问题：相互作用是如何传递的？超距作用？近距？电场：一种特殊物质。静电场：静止电荷所产生的电场。电场的两个重要性质：力学性质：电荷在电场中要受到电场力的作用。 — 引出电场强度能量性质：电场力对电荷有作功的本领。 —引出电势
• 带电油滴滴入匀强电场
F电 F重
qE
油空
( ）gV 油空
19
q 8.026 10
C
q ne
使油滴带不同电量，重复测量得油滴所带电量总是一个最小电量e 的整数倍直接证实了电荷的量子性 1986年e的推荐值为
19 e 1.60217733(46) 10 库仑
x
例3.均匀带电圆板，半径为R，电荷面密度为。求轴线上任一点P的电场强度。 dr 解：利用带电圆环场强公式

东南大学理论力学之动力学教学PPT

得
2.
质点系的动量矩定理
(e) dLO M O ( Fi ) dt
称为质点系的动量矩定理:质点系对某定点O 的动量矩对时间的导数,等于作用于质点系的外力对于同一点的矩的矢量和.
投影式:
(e) dLx M x ( Fi ) dt
dLy dt (e) M y ( Fi )
在活塞上作用一恒力F .
不计摩擦及滑块B的质
量,求:作用在曲柄轴A处的最大水平约束力Fx .
解:如图所示
m1 m2 aCx Fx F
1 r xC m1 cos m2 r cos b 2 m1 m2 d 2 xC r 2 m1 aCx 2 m2 cos t dt m1 m2 2
对轴的动量矩
Lz M z (mi vi )
n i 1
[ LO ]z Lz LO Lx i Ly j Lz k 即（1）刚体平移.可将全部质量集中于质心, 作为一个质点来计算. LO M O (mvC ) , Lz M z (mvC )
(e) dLz M z ( Fi ) dt
内力不能改变质点系的动量矩.
例12-1 已知： R, J , M , , m ,小车不计摩擦.
求小车的加速度 a .
解:
LO J m v R
( M Oe) M mg sin R
d [ J mvR] M mg sin R dt
第十章质点动力学的基本方程
§10-1
动力学的基本定律
第一定律 (惯性定律):
不受力作用的质点，将保持静止或作匀速直线运动。
第二定律 ma F P mg , g 9.8 m 重力

东南大学大学物理课件第一章

r dr ds v v
当 t0时：
z 四加速度 —反映速度的变化 v t 2 1 t 2 v1 v v2 2 平均加速度 a m s o t t y v1 方向：为速度增量的方向 x v 2 v dv d r 2 a m s 瞬时加速度： lim 2 v2 t dt dt t 0
• 提醒
– 培养良好学习习惯——及时复习、及时总结； – 抓住基本概念、内容和基本解题方法； – 课内与课外相结合、教材与参考书相结合； – 适合你的是最好的——量力而行，不要跟风； – 教与学要经常沟通，互相适应，教学相长；
教材和参考书目
• 教材：《物理学》（笫五版）马文蔚高等教育出版社 2006年 • 参考书：
• 5．学习物理学的困难 • 1）物理学内容广泛：涵盖力学、热学、光学、电磁学等领域； • 2）时空跨度大：从经典到近代，从宏观到微观和宇观； • 3）方法变化大：从中学的常量问题到应用矢量和微积分处理复杂的变量问题。
• 注意中学物理与大学物理的区别
– 研究对象与数学工具的变更； – 理论体系更为系统； – 认知方法和授课方式的变更。
• 1. 大学物理学教程吴锡珑主编，高等教育出版社 • 2. 普通物理学（第五版），程守诛江之泳主编，高等教育出版社 • 3. 大学物理学（第二版）张三慧主编，清华大学出版社
一、矢量代数的基本知识
标量：只有大小，例如：质量、长度、时间、密度、能量、温度等。矢量：既有大小又有方向，并有一定的运算规则，例如：位移、速度、加速度、角速度、电场强度等。 1、矢量的几种表示方式：几何表示 — — 有指向的线段。解析表示（直角坐标系）

东南大学物理系半导体物理课程总结.ppt

• 在晶体能带理论中，E(k) Ec(0) 2k 2
2m *
En(k)=En(-k)
dE(k) dE(k)
dk
dk
• 同一能带中，k和-k态具有大小相同、方向相反的速度
v(k) = -v(-k)
E
k v
k
满带电子不导电
• 在一个完全被电子充满的能带中，每一个电子带一定的电流-qv,
J evj =0
– 电子在外力作用下运动时，同时还和半导体内部原子、电子相互作用，电子的加速度应该是
半导体内部势场和外电场作用的综合效果。
• 引进有效质量的意义：
– 概况了半导体内部势场的作用。
– 有效质量可以直接由实验确定。
–
半导体的电导率，迁移率等都与有效质量相关 13
§1.4本征半导体的导电机构空穴
满带电子不导电
• 杂质
–与组成晶体材料的元素不同的其他化学元素
❖ 形成原因
▪ 原材料纯度不够 ▪ 制作过程中有玷污 ▪ 人为的掺入
• 分类(1)：按杂质原子在晶格中所处位置分
– 间隙式杂质
• 杂质原子位于晶格原子的间隙位置 • 要求杂质原子比较小
Electron States and Relating Bonds in Semiconductors
重点:
• 电子的共有化运动
• 导带、价带与禁带
晶体的能带电子共有化运动
原子组成晶体后，由于电子壳层的交叠，电子不再局限在某一个原子上，可以由一个原子转移到相邻的原子中去，可以在整个晶体中运动。称为电子的共有化运动。
则 j (e)v(k) k k0
k1
k
(e)v(k) (e)v(k0 )

大学物理学复习题(第五版)东南大学精品PPT课件

v v 0 2 t 2 i 1 t j 2 2 t 2 2 i 1 t 2 2 j
r
t
dr vdt
r2t32ti6t22t j
0
0
3
6．质量为m的小球在水中受的浮力为常力F,当它静止
开始沉降时,受到水的沾滞阻力为 f =ku(k为常数),求小球
在水中竖直沉降的速度u与时间t的关系。
m1 k m2
在整个过程中，系统的机械能、动量守恒
12m1u12 12m2u22 12kxx02
m1u1m2u2 0
14.质量为0.05kg的小块物体，置于一光滑水平桌面上．有一绳一端连接此物，另一端穿过桌面中心的小孔（如图所示）．该物体原以3rad/s的角速度在距孔0.2m 的圆周上转动．今将绳从小孔缓慢往下拉，使该物体之
质点切向加速度______
d8t26t(S)I dt 8t26tdt 8t3 3t2
dt
0
0
3
a R
399SI a390SI
8．一物体质量为10kg，受到方向不变的力 F4 06t0 SI
的作用，，若物体的初速度大小为10m/s ，方向与力同
向，则在3s末物体速度的大小等于
．
3
3
在杆中时的角速度多大？2)杆在碰撞后的最大偏角? 3)在最大偏角时的角加速度
解: 子弹射入过程中,子弹-杆系统受合外力矩为零
角动量守恒: mu0d(1 3M2Lm2d)
M32Lmu30m d d2
uu uu 2 1 p m 2 1 0
T
I F dt IGmgT2mjg 0
I合力 ITIGp0
ITIG2mjg
F n
mg
y
11．如图所示，小球质量为m，挂在轻弹簧的一端（弹簧的劲度系数为k，弹簧的原长l0 ）另一端固定。先将弹簧放在水平位置，并保持原长，然后释放。已知摆到竖直位置时小球的速度为 v ，则此时弹簧长度l为________ 。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

用效果相同，用 F~t 图表示，曲线下面积，用与之相同的矩形面积来代替。三、动量
F
F o
t0
t
t
我们常用速度来表示物体的运动状态，速度是否能全面反映物体的运动状态？例如：用速度相同的乒乓球和钢球去冲击玻璃。
§1.质点和质点系的动量定理 / 三、动量
用动量来描写物体运动状态
１.动量定义：
( Fi外 )dt P P0 P
质点系的动量定理：合外力的冲量等于质点系动量的增量。
§1.质点和质点系的动量定理 / 五、质点系的动量定理
t t0
注意几点
1.内力不会改变系统的动量，只有外力可改变系统的动量。
I F (t t0 ) Ft
2、F~t图在F~ t 图曲线下的面积为冲量。 F 曲线下的面积为：
S F (t t0 ) Ft
o
F
t0
t
t
§1.质点和质点系的动量定理 / 二、冲量
3. 明确几点 1.冲量是矢量，其方向为合外力的方向。 2.冲量的单位：牛顿 ·秒，N· s 4 . 变力的冲量在很多的实际问题中，物体受到的力是随时间变化的，如பைடு நூலகம்棒球时，棒与球之间的作用力是随时间变化的。
§1.质点和质点系的动量定理 / 二、冲量
F F~t图曲线下的面积为冲量。由高等数学中计 Fi 算曲线下的面积方法，将曲线下 o t0 t 的面积分割成无数多的矩形面积，再求和： n t S lim Fi t t Fdt t 0
i 1
0
t
t
为变力的冲量，即
I Fdt
考虑质点组成的系统两式求和：
t t0
f21
m2 v20 v2 F2
§1.质点和质点系的动量定理 / 五、质点系的动量定理
( Fi外 fi内 )dt mivi mivi 0
f12与f21为一对作用力和反作用力,
f12 f21
t t0
fi内 0 即系统的内力矢量合为 0。令P mivi Pi 为系统的动量矢量合，
第一节质点与质点系的动量定理
一、Newton第二定律的原始形式
由Newton第二定律，得 dv d (mv ) F ma m dt dt Newton把质点的质量与其运动速度之积定义为动量，即
p mv dp F dt
这就是Newton第二定律的原始形式
2
t1
上式中，等式左边的量是过程量，有边的量是状态量的变化，这一关系—力的时间累积效应具有重要的意义和应用价值。为此，特别定义物理量来表示上式的左、右两边。
§1.质点和质点系的动量定理 / 一、Newton第二定律的原始形
二、冲量力对时间的累积效应。
例如：撑杆跳运动员从横杆跃过, 落在海棉垫子上不会摔伤，如果不是海棉垫子，而是大理石板，又会如何呢？
§1.质点和质点系的动量定理 / 二、冲量
又如汽车从静止开始运动，加速到 20m/s如果牵引力大，所用时间短，如果牵引力小所用的时间就长。
可以看出，当物体的状态变化一定时，作用力越大，时间越短；作用力越小，时间越长。
§1.质点和质点系的动量定理 / 二、冲量
1、恒力的冲量力与力的作用时间的乘积为恒力的冲量。
P mv
单位：千克· 米/秒,
kg· m/s
2.动量与冲量的区别： ①.动量是状态量；冲量是过程量，
②.动量方向为物体运动速度方向；冲量方向为力的作用时间内动量变化的方向。
§1.质点和质点系的动量定理 / 三、动量
四、质点的动量定理当作用在物体上的外力变化很快时，计算物体受到的冲量比较困难，但外力作用在物体上一段时间后会改变物体的运动状态，质点的动量定理建立起过程量冲量与状态量动量之间的关系。 1.质点的动量定理由牛顿第二定律
动量定理的应用
§1.质点和质点系的动量定理 / 四、质点的动量定理
五、质点系的动量定理
两个质点组成的质点系，对两个质点分别应用质点的动量定理： t t ( F1 f12 )dt m1v1 m1v10
0
v10 v1 m1
f12
F1
( F2 f21 )dt m2v2 m2v20
在经典力学范围内，m=constant, 与F=ma 等价，但在高速运动情况下，Newton第二定律的原始形式才成立。
§1.质点和质点系的动量定理 / 一、Newton第二定律的原始形
由Newton第二定律，有 Fdt d (mv ) t Fdt mv2 mv1
I x Fx dt Fx t mvx mv0 x Px P0 x I y Fydt Fy t mvy mv0 y Py P0 y
t t0
t t0
⑤.冲量的方向与动量增量的方向一致。
§1.质点和质点系的动量定理 / 四、质点的动量定理
播放教学片VCD1
①. 计算物体冲量时，无须确定各个外力，只须知道质点始末两态的动量的变化即可。
§1.质点和质点系的动量定理 / 四、质点的动量定理
②. 平均冲力的计算由： t t Fdt I P P0 F t t0 t t0 t t0
0
③.F 为合外力，不是某一个外力。 ④.动量定理的分量式：
dv d(mv) dP F ma m dt dt dt
§1.质点和质点系的动量定理 / 四、质点的动量定理
由变力的冲量： I Fdt dP P t 有 I t dt P dP P P0 dt I mv mv0 P 即
0
t t0
0
质点动量定理：质点所受的合外力冲量，等于质点动量的增量。 2. 明确几点
t t0
§1.质点和质点系的动量定理 / 二、冲量
5、平均冲力
由于力是随时间变化的，当变化较快时，力的瞬时值很难确定，用一平均的力代替该过程中的变力，用平均力F表示：
I Fdt Ft
t t0
F
t t0
Fdt
t t0
I t t0
平均力的作用效果与这段时间内变力的作
§1.质点和质点系的动量定理 / 二、冲量