当前位置：文档之家 › 马尔可夫信源

马尔可夫信源

  • 格式：ppt
  • 大小：1.35 MB
  • 文档页数：21

下载文档原格式

  / 21

合集下载

马尔可夫信源

马尔可夫信源
设信源所处的状态为：S E E1, E2 ,, EJ



信源每个状态下可能输出的符号： X A a1 , a2 ,, aq
每一时刻信源发出一个符号后，所处的状态发生转移 信源输出的随机符号序列为： x1，x2 ,, xl 1, xl ,
, sl 1 , sl , 信源所处的随机状态序列为： s1，s2，
2. 6 马尔可夫信源


2.6.2(2)M阶马尔可夫信源的信息熵
时齐的、遍历的M阶马尔可夫信源的熵
H H m 1 Q Ei H X akm P akm1 | ak1 ak2 akm
k1 1 k2 1 km 1 km1
设在第L时刻信源处于状态 E i 时，输出符号 ak 的概率给定为：
P xl ak | sl Ei

另外，假设在第 l 1 时刻信源处于Ei状态，下一时刻转移到Ej 状态的转移概率为： P {sl E j | sl 1 Ei ) ij (l ) P 称此信源的随机状态服从马尔可夫链
电子信息工程学院
信息论
2. 6 马尔可夫信源
若当这些概率和时刻L无关，既满足

P( xl ak | sl Ei ) P ak | Ei
Pij P E j | Ei

则成为时齐的或齐次的。此时，信源的状态序列服从时齐马 尔可夫链。
若时齐马尔可夫链对一切 Ei , E j存在不依赖于Ei 的极限
p(0 / 01) p(1 / 01) p(0 / 10) p(1 / 10) 0.5
确定该马氏源的状态，写出状态转移矩阵，画出信源的状态转移 图。
电子信息工程学院

第二章-信息论基本概念（3）

第二章-信息论基本概念（3）

H ( X m1 / X1 X 2 X m )
这表明：m阶马尔可夫信源的极限熵H 就等于m阶条件熵，记为H m 1
akm )
设状态 Ei (ak1 ak2 akm ),信源处于状态Ei时，再发出下一个符号akm1
此时，符号序列 (ak2 ak3 a ) km1 就组成了新的信源状态
Ej (ak2 ak3 a ) km1 ，这时信源所处的状态由 Ei 转移到 Ej
状态转移图(香农线图)
0:0.5 E1
1:0.5 E3
1
0:0.6
E2
1:0.4
【注】E1、E2、E3是三种状态，箭头是指从一个状态转移到另
一个状态，旁边的数字代表发出的某符号和条件概率p(ak/Ei) 。 这就是香农提出的马尔可夫状态转移图，也叫香农线图。
二、马尔可夫信源
若信源输出的符号和信源所处的状态满足以下两个条 件，则称为马尔可夫信源：
a1 a2
p(sl
E2
/ xl
a3
sl1 E1 ) 0 sl1 E1 ) 1 sl1 E1 ) 1 sl1 E1 ) 0
可求得状态的一步转移概率：
1
2
1 4
0
1 4
0
0
1 2
1 2
0
0
p(E j
/
Ei
)
0
3
1
0
0
44
0
0
0
0
1
0
0
0
3 4
1 4
此信源满足马尔可夫的 两个条件，所以是马尔可夫 信源，并且是齐次马尔可夫 信源。
对于这个随机序列，若有：
p(xn Sin | xn1 Sin1 ,..., x1 Si1 ) p(xn Sin | xn1 S ) in1

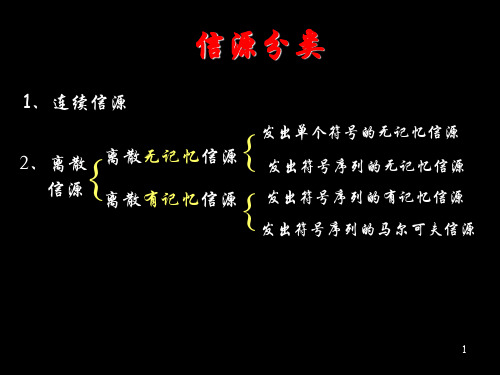
马尔科夫信源课件

马尔科夫信源课件

马尔科夫信源在物联网中的应用前景
1 2
物联网通信
探讨马尔科夫信源在物联网通信中的应用前景， 分析其在物联网通信中的优势和局限性。
低功耗设计
研究如何在保证性能的同时降低马尔科夫信源的 功耗，以满足物联网设备低功耗的需求。
3
跨领域应用
探讨马尔科夫信源在其他领域的应用前景，如生 物信息学、医学影像处理等，分析其在这些领域 的适用性和优势。
进行计算。
应用
03
状态转移概率是马尔科夫信源的重要参数，用于描述信源的动
态特性，是进行信息编码和数据压缩的重要依据。
平稳状态分布
01
定义
平稳状态分布是指马尔科夫信源在无限长时间内的状态概率分布。
02
计算方法
平稳状态分布可以通过迭代计算得到，也可以通过数学模型进行推导。
03
应用
平稳状态分布是马尔科夫信源的重要参数，用于描述信源的统计特性，
如果马尔科夫链的状态转移是稳定的，那么信源的统计特性就可以被视为具有长期一致性，从而在编 码时可以利用这些信息来提高压缩效率。相反，如果状态转移是不稳定的，那么信源的统计特性就可 能具有较大的波动，需要采用不同的编码策略来处理。
03 马尔科夫信源的编码与解码
CHAPTER
编码原理
统计特性
马尔科夫信源的编码原理基于信源的统计特性，通过对概率较大符号的压缩，以及对概率较小符号的冗余编码，实现 数据压缩。
计算复杂度
编码与解码过程中的计算复杂度也是衡量效率的重要因素，计算复 杂度越低，表示实现越简单，效率越高。
04 马尔科夫信源的应用场景
CHAPTER
自然语言处理
语言模型
马尔科夫链蒙特卡洛方法可以用于构 建语言模型，通过训练大量文本数据 ，预测给定前一个词的情况下下一个 词的概率分布。

第2章_2.7马尔可夫信源

第2章_2.7马尔可夫信源

在状态E2时， 以0.8的概率发出符号 1，状态仍然为 E2； 以0.2的概率发出符号 0，状态转移到 E1
19
马尔可夫信源－状态转移图
为什么马尔可夫信源是非平稳的信源： 初始概率为： p(0) p(1) 0.5 进入 E1 或 E 2 两个状态。之后无论在哪个状态， 下一个输出的符号有80％的可能性是1，转移 到 E 2 ，有20％的可能性是0，转移到 E1 ，所以 p(0) 0.2; p(1) 0.8 ，与初始概率不同， 不满足平稳信源的定义 。
jE
iE
6
1,...,k步转移概率
定义k步转移概率为
(k ) pij (m) P{Sm k j | Sm i}
i, j E
它表示在时刻m时，Xm的状态为i的条件下， 经过k步转移到达状态j的概率。 性质：
(k ) 1、pij (m) 0
i, j E iE
2、 pij( k ) (m) 1
21
m阶马尔可夫信源
m阶马尔可夫信源：在任何时刻l，输出 分量的概率分布只与前面m个分量的输出有 关。
可以把前面m个分量组成的序列做为l时 刻信源所处的状态 。
如果信源的符号集是 A a1
m q 则信源的状态共有个
a2 aq
22
m阶马尔可夫信源
例2.9 二元二阶马尔可夫信源。二元指信源 可能的输出有2种取值，如0，1； 马尔可夫信源共有个 q m 2 2 4 状态， 前两个分量可能取值的排列
E0 E1 E2 ，其中设为 该马尔可夫信源有三个状态： E0 初始状态，初始概率为 p(0) p(1) 0.5 ，等概率的 转移到 E1和E2 这两个状态
18
马尔可夫信源－状态转移图

马尔科夫信源

马尔科夫信源
x3 0 1 00 0.4 0.6 01 0.2 0.8 10 0.3 0.7 11 0.4 0.6

• 从第四单位时间开始，随机变量Xi只与前面二 个单位时间的随机变量Xi-2Xi-1有依赖关系: p(xi| xi-1 xi-2…x2 x1) = p(xi| xi-1 xi-2) (i＞3) 且 p(xi| xi-1 xi-2) = p(x3| x2x1) (i＞3) 求：⑴信源状态转移情况和相应概率； ⑵画出完整的二阶马尔可夫信源状态转移图； ⑶求平稳分布概率； （4）马尔科夫信源达到稳定后，0和1的分布 概率。
s1 00; s2 01; s3 10; s4 11
由于信源只可能发出0或者1，所以信源下一时刻只 可能转移到其中的两种状态之一。如目前所处状态 为00，那么下一时刻信源只可转移到00或者01。而不 12 会转到10或者11状态。
p( s1 | s1 ) p( s4 | s4 ) 0.8, p( s3 | s2 ) p( s1 | s3 ) p( s4 | s2 ) p( s4 | s2 ) p( s2 | s3 ) 0.5; p( s2 | s1 ) p( s3 | s4 ) 0.2
区 别
p11 p1n P p( x j | si ) pQ1 pQn
7
马尔可夫信源
• 状态转移图
–齐次马尔可夫链可以用其 状态转移图(香农线图)表示 –每个圆圈代表一种状态 –状态之间的有向线代表某 一状态向另一状态的转移 –有向线一侧的符号和数字 分别代表发出的符号和条 件概率
• 解: • 设信源开始处于s0状态,并以 等概率发出符号0和1,分别 到达状态s1和s2 : s0 • 若处于s1 ,以0.3和0.7的概率 发出0和1到达s3和s4 • 若处于s2,以0.4和0.6的概率 发出0和1到达s5和s6

信息论马尔科夫信源

信息论马尔科夫信源

x
xk N ) log p(
xk N
xk N m xk N 1
)}
p( xk1 xkm1 )
xk1 xkm
)
H(
X m1
X1 X m
) H m1
p( xkm1 / xk1 xk2 xkm ) p( xk / si ) p( s j / si ) H H m1 p( si ) p( s j / si ) log 2 p( s j / si )
输出状态序列：S1S2 Sl 1Sl
1
2
某时刻输出符号仅与此刻信源所处的状态有关；
某时刻所处状态由当前输出符号和前一时刻信源状态 唯一确定。
设l时刻信源处于si , 输出xk
pl (
pl (
xk
si
si
) p(
X l xk
Sl si
)
)
sj
) p(
Sl s j
Sl 1 si
则由信源输出符号的条件概率
p( xim1 / xi1 xi2 ... xim )
可以确定状态转移概率p(sj/si)，i，j∈{1,2,…,nm} 马尔可夫信源的状态空间
s1...si ...s j ...sn m p( s / s ) j i
例：设一个二元一阶马尔可夫信源，信源符号集为 X={0,1}，信源输出符号的条件概率为 p(0/0)=0.25，p(0/1)=0.50，p(1/0)=0.75，p(0/1)=0.50， 求状态转移概率。 解：由于信源符号数n=2，因此二进制一阶信源仅有2个状 态：s1=0，s2=1。由条件概率求得信源状态转移概率为 p(s1/s1)=0.25，p(s1/s2)=0.50，p(s2/s1)=0.75，p(s2/s2)=0.50

3.4_马尔可夫信源

信息论与编码技术电子信息工程专业主讲：孙静机械电子工程系3.4 马尔可夫信源离散信源中有一类特殊的信源，其信源输出的符号序列中符号之间的依赖关系是有限的，并且满足马尔可夫链的性质，因此可用马尔可夫链来处理。

任何时刻信源符号发生的概率只与前面已经发生过的若干个符号有关，而与更前面的符号无关。

3.5.2课上要求：课本P641.【定义】若离散平稳信源在某时刻发出的符号仅与在此之前发出的有限个符号有关，而与更早些时刻发出的符号无关，这类信源称为马尔可夫（MovKov）信源。

2.【数学描述】如果随机变量序列X 中的任一时刻(n +1)的随机变量X n +1只依赖于前面已经发生的n 个随机变量X 1X 2…X n ，与更前面的随机变量无关，则称这种信源为n 阶马尔可夫信源。

其概率分布表示为：)|()|(21211221n i i i i i i i i n i i x x x x p x x x x x x x x p ---++---=3.【特殊说明】①n阶马尔可夫信源只与前面发出的n个符号有关，即关联长度为n+1。

②当n=1时，即任何时刻信源符号发生的概率只与前面一个符号有关，则称为一阶马尔可夫信源。

二、相关概念1.状态【定义】把排在指定符号前面与它相关联的n个符号定义为该符号的状态。

【数目】n阶马尔可夫信源可以有q n种不同的状态。

当前时刻输出的符号1.状态【举例】序列的状态是由信源的符号构成的。

•比如二元二阶马尔可夫信源有四个状态：{0，1} {00，01，10，11}前一时刻输出的符号2.状态转移设离散平稳有记忆信源的状态集为S={S1,S2,…,S J}，在每一状态下输出的符,a2,…,a q}，并认为每一时刻号X∈A={a1，当信源发出一个符号后，信源所处的状态将会发生转移。

【注意】本课程只研究时齐马尔可夫信源，即状态转移过程与时间无关。

1.前提假设信源输出符号序列为：x 1, x 2, … , x l -1, x l , …。

马尔可夫信源和剩余度


BUPT Press
举例
BUPT Press
BUPT Press
BUPT Press
信源熵的相对率

H H0
信源的剩余度（冗余度）
1 1
H H0 1 H log q
英文的冗余度
1
1.4 0.71 4.76
信息变差
BUPT Press
BUPT Press
BUPT Press
BUPT Press

3.3.3
马尔可夫信源
马尔可夫信源是一类相对简单的有记忆信源，信源在 某一时刻发出某一符号的概率除与该符号有关外，只 与此前发出的有限个符号有关。
BUPT Press
3.3.3
马尔可夫信源
我们把前面若干个符号看作 一个状态，可以认为信源在 某一时刻发出某一符号的概 率除了与该符号有关外，只 与该时刻信源所处的状态有 关，而与过去的状态无关。 信源发出一个符号后，信源 所处的状态即发生改变，这 些状态的变化组成了马氏链。
BUPT Press
BUPT Press
BUPT Press
BUPT Press
BUPT Press
例
BUPT Press
BUPT Press
BUPT Press
一步转移概率矩阵
BUPT Press
BUPT Press
m阶马尔可夫信源的条件概率
m阶马尔可夫信源的极限熵
BUPT Press
BUPT Press
BUPT Press
BUPT Press
例3.5 设有一个二元2阶马尔可夫信源，其信源符号集为
BUPT Press
解得 计算极限熵
BUPT Press

ch06马尔可夫信源


Review of the last lecture
问题2&3:
• H(X)/矢量熵= H(X1X2…XN-1XN)/联合熵表示平均发一个消息 （由N个符号组成）提供的信息量。 • 平均符号熵：信源平均每发一个符号提供的信息量为
H N (X ) =
1 N
H (X1X 2 … X N )
• 极限熵：当N→∞时，平均符号熵取极限值称之为极限熵 或极限信息量。用H∞表示，即
• 这里利用了m阶马尔可夫信源“有限记忆长度”的根本特 性，使无限大参数N变为有限值m，把求极限熵的问题变 成了一个求m阶条件熵的问题。 • 状态一步转移概率p(ej /ei)是给定或测定的。求解Hm+1条件 熵的关键就是要得到p(ei)(i=1,2,…,nm) 。 p(ei)是马尔可夫 信源稳定后(N→∞)各状态的极限概率。 • 有限状态的马尔可夫链：状态空间的状态是有限的。 • 可列状态的马尔可夫链：状态空间I是{0,±1,±2,…}。
k =1
由图中看出： P( S = e / X = x , S = e ) = 0 ⎧ l 2 l 1 l −1 1
⎪ P( S = e / X = x , S = e ) = 1 l 1 l 1 l −1 1 ⎪ ⎪ ⎨ P( S l = e2 / X l = x2 , S l −1 = e1 ) = 1 ⎪ P( S = e / X = x , S = e ) = 0 l 3 l 2 l −1 1 ⎪ ⎪ ⎩
H ∞ = lim
N →∞
1 N
H (X1X 2 … X N )
Review of the last lecture
• 极限熵的存在性：当离散有记忆信源是平稳信源时，从 数学上可以证明，极限熵是存在的，且等于关联长度 N→∞时，条件熵H(XN/X1X2…XN-1)的极限值，即

2-6 第2章 2.2.4-5 马尔可夫信源


信源输出的随机符号序列为X1 X 2 X l , X l X ( x1 , x2 , xn ), l 1, 2, 信源所处的状态序列为S1S 2 Sl , Sl S (e1 , e2 , eJ ), l 1, 2,
3
马尔可夫信源定义
定义 若信源输出的 符号序列 和 状态序列 满足下述条件则称此信源为马尔可夫信源 1、某一时刻l 信源的输出仅与信源的当前状态有关，即 p ( X l xk Sl e j , X l 1 xk1 , Sl 1 ei ,) p ( X l xk Sl e j ) 其中，xk、xk1 A；ei、e j S 2、信源的状态只由当前的输出符号和前一时刻信源状态 唯一确定，即 1 p ( Sl ei X l xk , Sl 1 e j ) 0
6
马尔可夫链状态转移图-例题
通常我们用马尔可夫 链的状态转移图来描 述马尔可夫信源。
例 一个二进制一阶马尔可夫信源， 信源符号集为X {0,1}， 条件概率为 p (0 0) 0.25, p(0 1) 0.5, p (1 0) 0.75, p(1 1) 0.5, q 2, m 1, 所以e1 0, e 2 1.
i j
其中p (e j )是马尔可夫链的平稳分布。 p (e j )为极限概率，满足方程组 p (e j ) p (ei ) p (e j / ei ) Nhomakorabeai 1 nm
( j 1, 2,..., n m )
及条件 p (e j ) 0,
p (e
j 1
nm
j
) 1
15
计算此马尔可夫信源熵-例题
N
H ( X m1 X 1 , X 2 ,, X m ) H m1 即m阶马尔可夫信源的极限 熵等于m阶条件熵。 13
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

a a k1 k2
aq
akm
)

(k1, k2, , km , km1 1, 2, , q)
并满足
0 P(akm1 | a a k1 k2 akm ) 1 且
q
P(akm1 | a a k1 k2
km1 1
akm ) 1
(k1, k2, , km, km1 1, 2, , q)
设在第L时刻信源处于状态 Ei 时，输出符号 ak 的概率给定为：
P xl ak | sl Ei
另外，假设在第 l 1 时刻信源处于Ei状态，下一时刻转移到Ej
状态的转移概率为： Pij (l ) P{sl E j | sl1 Ei )
称此信源的随机状态服从马尔可夫链
这种信源的状态序列在数学模型上可以作为时齐马尔可夫 链来处理。因而可用马尔可夫链的状态转移图来描述信源。
马尔可夫链的状态转移图：每个圆圈代表一种状态，状态 之间的有向线代表某一状态向另一状态转移。有向线一侧 的符号和数字分别代表发出的符号和条件概率。
电子信息工程学院
信息论
2. 6 马尔可夫信源
信息论
2. 6 马尔可夫信源
注：条件②表明，若信源处于某一状态 Ei ，当它输出一个 符号后，所处的状态就变了，一定从状态Ei 转移到另一状 态。显然，状态的转移依赖于输出的信源符号，因此任何 时刻信源处于什么状态完全由前一时刻的状态和输出的符 号决定。
这种信源的状态序列在数学模型上可以作为时齐马尔可夫 链来处理。因而可用马尔可夫链的状态转移图来描述信源。
(1)P( xl ak | sl Ei , xl1 ak1, sl1 E j , )
P(xl ak | sl Ei )
(2)P(sl E j | xl ak sl 1 Ei )
0 1
Ei , E j E ak A
电子信息工程学院
2.6.1(2) m阶马尔可夫信源定义
m阶马尔可夫信源符号集共有q个符号，则信源共有 qm 个 不同状态，对应于 qm 个长度为m的不同符号序列。
定义 m阶有记忆离散信源的数学模型可由一组信源符号集
和一组条件概率确定：X

P


a1, a2 , , 源自P(akm1| 号序列 a a k2 k3 akm1 组成了新的信源状态E j a a k2 k3 ， akm1 E
信源所处的状态也由 Ei 转移到E j 。
电子信息工程学院
信息论 2. 6 马尔可夫信源
[例2-9] 给定二元二阶马氏源，符号集A:{0,1}，符号转移概率分 别为:
p(0 / 00) p(1/11) 0.8
马尔可夫链的状态转移图：每个圆圈代表一种状态，状态 之间的有向线代表某一状态向另一状态转移。有向线一侧 的符号和数字分别代表发出的符号和条件概率。
电子信息工程学院
信息论
2. 6 马尔可夫信源
注：条件②表明，若信源处于某一状态 Ei ，当它输出一个 符号后，所处的状态就变了，一定从状态Ei 转移到另一状 态。显然，状态的转移依赖于输出的信源符号，因此任何 时刻信源处于什么状态完全由前一时刻的状态和输出的符 号决定。
M=1时，称为一阶马尔可夫信源。
电子信息工程学院
信息论
2. 6 马尔可夫信源
m 阶马尔可夫信源在任何时刻L，符号发生概率只于前M个
符号有关，所以可设状态Ei a a k1 k2 akm 。由于 k1, k2 , , km 均可 取1, 2, , q ,的信源状态集 E E1, E2, , EJ , J qm, 则已知的
条件概率可变换成下式。
P a | a a km1 k1 k2 akm P akm1 | Ei P ak | Ei
k 1, 2, , q;i 1, 2, , J
条件概率 P akm1 | Ei 则表示任何L时刻信源处在状态Ei 时输出符 号akm1 的概率。而akm1 可以取 a1, a2 , , aq 之一，所以可以简化 成 ak 表示。而且当在 L时刻，信源输出符号 akm1 后，由符
符号转移概率与状态转移概率的对应如下：
p(0 / 01) p(s2 / s1) p(1/ 01) p(s3 / s1) 0.5
p(0 /10) p(s0 / s2 ) p(1/10) p(s3 / s2 ) 0.5


lim
N
Pij

Pj
，且满足
Pj
0; Pj
Pij ; Pj
i0
j
1
则称其具有遍历性，Pj 称为
平稳分布，其中Pj 为该马尔可夫链的初始分布。
电子信息工程学院
信息论
2. 6 马尔可夫信源
2.6.1(1) 马尔可夫信源定义
马尔可信源的输出的符号序列和信源所处的状态满 足下列两个条件：
信息论
2. 6 马尔可夫信源
设信源所处的状态为：S E E1, E2, , EJ
信源每个状态下可能输出的符号： X A a1,a2, ,aq
每一时刻信源发出一个符号后，所处的状态发生转移
信源输出的随机符号序列为： x1，x2, , xl1, xl ,
信源所处的随机状态序列为： s1，s2， , sl1, sl ,
p(1/ 00) p(0 /11) 0.2, p(0 / 01) p(1/ 01) p(0 /10) p(1/10) 0.5
确定该马氏源的状态，写出状态转移矩阵，画出信源的状态转移 图。
电子信息工程学院
信息论 2. 6 马尔可夫信源
解:信源状态序列：
A2 {s0 00, s1 01, s2 10, s3 11}
电子信息工程学院
信息论
2. 6 马尔可夫信源
若当这些概率和时刻L无关，既满足
P(xl ak | sl Ei ) Pak | Ei
Pij P Ej | Ei
则成为时齐的或齐次的。此时，信源的状态序列服从时齐马 尔可夫链。
若时齐马尔可夫链对一切 Ei , E j存在不依赖于Ei 的极限