纯Excel公式坐标反算程序(固定起算点)
- 格式:xls
- 大小:41.00 KB
- 文档页数:3

在Excel中,可以使用以下公式来计算道路坐标:
计算两点间的距离:
使用距离公式:D = sqrt((x2-x1)^2 + (y2-y1)^2)。
其中,x1、y1是第一个点的坐标,x2、y2是第二个点的坐标。
计算直线距离(两点间的最短距离):
使用直线距离公式:D = abs(y2-y1) + abs(x2-x1)。
计算斜率:
使用斜率公式:m = (y2-y1) / (x2-x1)。
计算角度:
使用角度公式:θ = arctan(m)。
其中,arctan是反正切函数,m是斜率。
计算坐标变换(平移和旋转):
使用平移公式:x' = x + tx,y' = y + ty。
其中,tx和ty是平移量。
使用旋转公式:x' = x * cos(θ) - y * sin(θ),y' = x * sin(θ) + y * cos(θ)。
其中,cos和sin是余弦和正弦函数,θ是旋转角度。
这些公式可以根据具体需求进行组合和调整,以计算道路坐标和其他相关参数。
请注意,这些公式假设坐标系为笛卡尔坐标系,并且输入的坐标值是实数。
如果使用其他坐标系或涉及复数计算,可能需要使用不同的公式或函数。


坐标方位角EXCEL计算公式
一:坐标形式:
坐标点的坐标形式有两种,分别为空间坐标(XYZ)和地面坐标(XY)。
空间坐标(XYZ),即X、Y和Z三个方向上的坐标值,其中X为从原点到当前点之间的直线距离,Y和Z分别为X的垂直方向距离,常用来表示空间点的位置。
地面坐标(XY),即基准平面上的X和Y的坐标值,X和Y分别为基准平面的两个方向的距离,常用来表示地面上的位置。
二、坐标方位角的计算:
Azimuth=ArcTan[(X2-X1)/(Y2-Y1)]
其中,ArcTan为反正切函数,ArcTan[(X2-X1)/(Y2-Y1)]是从点
(X1,Y1)指向点(X2,Y2)的正切值。
计算公式在excel中的表达式为:
=ATAN2(Y2-Y1,X2-X1)
计算结果即为两点之间的坐标方位角。
三、两点之间的真空方位角:
真空方位角(Geodetic Azimuth),也就是从一个点指向另一点的“直线”方位角,是指一点与另一点之间的空间方向的夹角,可以用两个点的经纬度坐标来表示,可以用如下公式计算:
Geodetic Azimuth=ArcTan[(cosφ2cosΔλ)/(sinφ2-sinφ1)]其中,ArcTan为反正切函数。

坐标正算、反算计算方法及在Excel 中的VBA 编程测量中经常需要将某点相对坐标系坐标转换成线路的里程、偏距,或根据线路某一里程偏距计算出对应的相对坐标系坐标,为寻求一种快速简单高效的计算方法,本文对线路正算反算的原理进行了阐述,并结合Excel VBA 编程,将编程和Excel 的拖拽的功能相结合,编制出实用计算表,特别适用于需要大量计算边桩、围护桩的情况。
关键词:坐标方位角坐标正算坐标反算 V AB 编程循环迭代直接算法一、坐标方位角的反算1.坐标方位角反算如图1所示,已知点A 、B 的坐标,求直线AB坐标方位角α。
图1坐标方位角反算直线AB 之间的坐标增量:AB B AAB B Ax x x y y y ∆=−∆=−当0,0AB AB x y ∆>∆>时,角α位于第一象限角:arctan ABABy x α∆=∆当0,0AB AB x y ∆<∆>时,角α位于第二象限角:arctan 180AB ABy x α∆=+°∆当0,0AB AB x y ∆<∆<时,角α位于第三象限角:arctan 180AB ABy x α∆=+°∆当0,0AB AB x y ∆>∆<时,角α位于第二象限角:arctan360AB AB y x α∆=+°∆2.坐标方位角反算的VBA 编程可用VBA 将上述过程定义为一个名为angel()的函数,代码如下:Function angel(x0As Double, y0 As Double, x1 As Double, y1 As Double) As Double dx = x1- x0dy = y1- y0If dx > 0 And dy > 0 Thenangel = Atn(dy / dx)End IfIf dx < 0 And dy > 0 Thenangel = Atn(dy / dx) + 3.14159265358979End IfIf dx < 0 And dy < 0 Thenangel = Atn(dy / dx) + 3.14159265358979End IfIf dx > 0 And dy < 0 Thenangel = Atn(dy / dx) + 3.14159265358979 * 2End IfEnd Function二、直线段坐标正算与反算1.直线段正算图2直线段计算已知HZ 点坐标(x1,y1)、里程N HZ ,ZH 点坐标(x2,y2),正算时已知P 点对应的中桩里程Np 和偏距e (规定沿着线路前进方向,左边偏距为负,右边偏距为正),Np>N HZ ,求P 点对应的坐标。
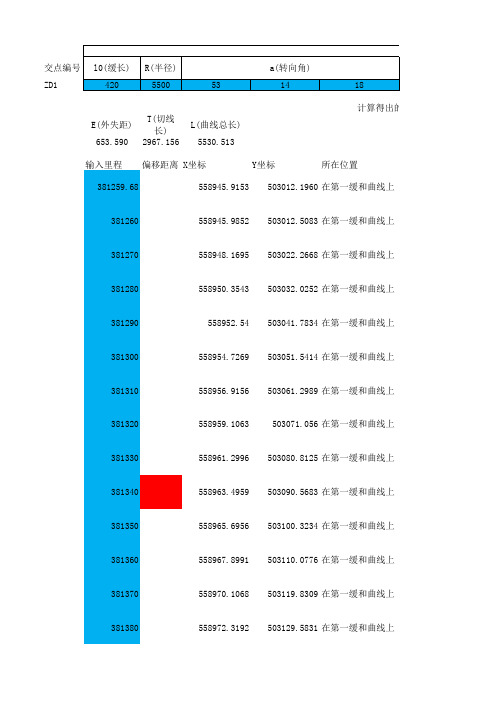
交点编号ZD1计算得出的数E(外失距)T(切线长)L(曲线总长)653.5902967.1565530.513输入里程偏移距离X坐标Y坐标所在位置381259.68558945.9153503012.1960在第一缓和曲线上381260558945.9852503012.5083在第一缓和曲线上381270558948.1695503022.2668在第一缓和曲线上381280558950.3543503032.0252在第一缓和曲线上381290558952.54503041.7834在第一缓和曲线上381300558954.7269503051.5414在第一缓和曲线上381310558956.9156503061.2989在第一缓和曲线上381320558959.1063503071.056在第一缓和曲线上381330558961.2996503080.8125在第一缓和曲线上381340558963.4959503090.5683在第一缓和曲线上381350558965.6956503100.3234在第一缓和曲线上381360558967.8991503110.0776在第一缓和曲线上381370558970.1068503119.8309在第一缓和曲线上381380558972.3192503129.5831在第一缓和曲线上381390558974.5367503139.3341在第一缓和曲线上381400558976.7596503149.0839在第一缓和曲线上381410558978.9885503158.8323在第一缓和曲线上381420558981.2238503168.5793在第一缓和曲线上381430558983.4658503178.3248在第一缓和曲线上381440558985.7149503188.0685在第一缓和曲线上381450558987.9717503197.8105在第一缓和曲线上381460558990.2365503207.5507在第一缓和曲线上381470558992.5098503217.2889在第一缓和曲线上381480558994.7919503227.025在第一缓和曲线上381490558997.0833503236.7589在第一缓和曲线上381500558999.3844503246.4906在第一缓和曲线上381510559001.6957503256.2198在第一缓和曲线上381520559004.0174503265.9466在第一缓和曲线上381530559006.3502503275.6707在第一缓和曲线上381540559008.6943503285.392在第一缓和曲线上381550559011.0502503295.1106在第一缓和曲线上381560559013.4183503304.8261在第一缓和曲线上381570559015.7991503314.5386在第一缓和曲线上381580559018.1929503324.2478在第一缓和曲线上381590559020.6001503333.9538在第一缓和曲线上381600559023.021*******.6563在第一缓和曲线上381610559025.4567503353.3552在第一缓和曲线上381620559027.9068503363.0504在第一缓和曲线上381630559030.3721503372.7417在第一缓和曲线上381640559032.852*******.4291在第一缓和曲线上381650559035.3496503392.1124在第一缓和曲线上381660559037.8627503401.7915在第一缓和曲线上381670559040.3925503411.4662在第一缓和曲线上381679.68559042.8578503420.827在圆曲线上381680559042.9395503421.1364在圆曲线上381700559048.0862503440.4628在圆曲线上381720559053.3031503459.7704在圆曲线上381740559058.5902503479.0589在圆曲线上381760559063.9474503498.3281在圆曲线上381780559069.3747503517.5776在圆曲线上381800559074.8719503536.8073在圆曲线上381820559080.4389503556.0168在圆曲线上381840559086.0758503575.206在圆曲线上381860559091.7825503594.3746在圆曲线上381880559097.5588503613.5223在圆曲线上381900559103.4047503632.6488在圆曲线上381920559109.3201503651.754在圆曲线上381940559115.305503670.8375在圆曲线上381960559121.3591503689.8992在圆曲线上381980559127.4826503708.9387在圆曲线上382000559133.6753503727.9558在圆曲线上382020559139.9371503746.9502在圆曲线上382040559146.2679503765.9218在圆曲线上382060559152.6676503784.8702在圆曲线上382080559159.1363503803.7953在圆曲线上382100559165.6736503822.6966在圆曲线上382120559172.2797503841.5741在圆曲线上382140559178.9544503860.4274在圆曲线上382160559185.6976503879.2564在圆曲线上382180559192.5092503898.0607在圆曲线上382200559199.3892503916.8401在圆曲线上382220559206.3374503935.5943在圆曲线上382240559213.3537503954.3232在圆曲线上382260559220.4381503973.0264在圆曲线上382280559227.5905503991.7038在圆曲线上382300559234.8107504010.355在圆曲线上382320559242.0987504028.9798在圆曲线上382340559249.4544504047.578在圆曲线上382360559256.8777504066.1494在圆曲线上382380559264.3685504084.6936在圆曲线上382400559271.9266504103.2104在圆曲线上382420559279.552504121.6997在圆曲线上382440559287.2446504140.1611在圆曲线上382460559295.0043504158.5944在圆曲线上382480559302.831504176.9994在圆曲线上382500559310.7245504195.3757在圆曲线上382520559318.6849504213.7233在圆曲线上382540559326.7118504232.0418在圆曲线上382560559334.8054504250.331在圆曲线上382580559342.9654504268.5906在圆曲线上382600559351.1917504286.8204在圆曲线上382620559359.4843504305.0202在圆曲线上382640559367.843504323.1898在圆曲线上382660559376.2677504341.3288在圆曲线上382680559384.7583504359.437在圆曲线上382700559393.3147504377.5143在圆曲线上382720559401.9368504395.5603在圆曲线上384850560668.0166506091.886在圆曲线上384851560668.7578506092.5573在圆曲线上382740559410.6245504413.5749在圆曲线上382760559419.3776504431.5577在圆曲线上382780559428.196504449.5086在圆曲线上382800559437.0797504467.4273在圆曲线上382820559446.028*******.3136在圆曲线上382840559455.0422504503.1673在圆曲线上382860559464.1208504520.988在圆曲线上382880559473.2641504538.7756在圆曲线上382900559482.4721504556.5298在圆曲线上382920559491.7445504574.2505在圆曲线上382940559501.0814504591.9373在圆曲线上382960559510.4825504609.59在圆曲线上385087.095560847.1194506247.2164在圆曲线上382980559519.9477504627.2084在圆曲线上383000559529.4769504644.7923在圆曲线上383020559539.07504662.3415在圆曲线上383040559548.7269504679.8556在圆曲线上383060559558.4474504697.3345在圆曲线上383080559568.2313504714.7779在圆曲线上383100559578.0787504732.1857在圆曲线上383120559587.9893504749.5575在圆曲线上383140559597.963504766.8931在圆曲线上383160559607.9996504784.1924在圆曲线上383180559618.0991504801.4551在圆曲线上383200559628.2613504818.6809在圆曲线上383220559638.4861504835.8697在圆曲线上383240559648.7733504853.0211在圆曲线上383260559659.1228504870.1351在圆曲线上383280559669.5345504887.2113在圆曲线上383300559680.0082504904.2495在圆曲线上383320559690.5438504921.2495在圆曲线上383340559701.1411504938.2111在圆曲线上383360559711.8001504955.1341在圆曲线上383380559722.5205504972.0182在圆曲线上383400559733.3022504988.8632在圆曲线上383420559744.1451505005.6688在圆曲线上383440559755.0491505022.435在圆曲线上383460559766.014505039.1613在圆曲线上383480559777.0396505055.8477在圆曲线上383500559788.1258505072.4939在圆曲线上383520559799.2725505089.0997在圆曲线上383540559810.4794505105.6648在圆曲线上383560559821.7466505122.189在圆曲线上383580559833.0737505138.6722在圆曲线上383600559844.4608505155.1141在圆曲线上383620559855.9075505171.5145在圆曲线上383640559867.4138505187.8731在圆曲线上383660559878.9795505204.1898在圆曲线上383680559890.6045505220.4643在圆曲线上383700559902.2885505236.6964在圆曲线上383720559914.0315505252.8859在圆曲线上383740559925.8334505269.0327在圆曲线上383760559937.6938505285.1364在圆曲线上383780559949.6127505301.1968在圆曲线上383800559961.59505317.2139在圆曲线上383820559973.6254505333.1872在圆曲线上383840559985.7188505349.1167在圆曲线上383860559997.8701505365.0021在圆曲线上383880560010.079505380.8433在圆曲线上383900560022.3455505396.6399在圆曲线上383920560034.6693505412.3918在圆曲线上383940560047.0504505428.0988在圆曲线上383960560059.4884505443.7607在圆曲线上383980560071.9834505459.3772在圆曲线上384000560084.535505474.9482在圆曲线上384020560097.1432505490.4734在圆曲线上384040560109.8077505505.9527在圆曲线上384060560122.5285505521.3859在圆曲线上384080560135.3053505536.7727在圆曲线上进口384082560136.586505538.3088在圆曲线上384100560148.1379505552.1129在圆曲线上384120560161.0263505567.4063在圆曲线上384140560173.9702505582.6528在圆曲线上384160560186.9694505597.8522在圆曲线上384180560200.023*******.0041在圆曲线上384200560213.1333505628.1085在圆曲线上384220560226.2976505643.1651在圆曲线上384240560239.5165505658.1737在圆曲线上384260560252.7899505673.1342在圆曲线上384280560266.1177505688.0463在圆曲线上384300560279.4995505702.9098在圆曲线上384320560292.9354505717.7246在圆曲线上384340560306.425505732.4905在圆曲线上384360560319.9682505747.2071在圆曲线上386370.194561920.5846506944.755在第二缓和曲线上386380561929.3769506949.097在第二缓和曲线上386390561938.3509506953.5091在第二缓和曲线上386400561947.3326506957.9057在第二缓和曲线上386410561956.3217506962.2871在第二缓和曲线上386420561965.318506966.6536在第二缓和曲线上386430561974.3212506971.0058在第二缓和曲线上386440561983.3313506975.3439在第二缓和曲线上386450561992.3479506979.6683在第二缓和曲线上386460562001.3708506983.9795在第二缓和曲线上386470562010.3999506988.2777在第二缓和曲线上386480562019.435506992.5635在第二缓和曲线上386490562028.4758506996.8371在第二缓和曲线上386500562037.5222507001.0989在第二缓和曲线上386510562046.5739507005.3494在第二缓和曲线上386520562055.6307507009.5889在第二缓和曲线上386530562064.6926507013.8178在第二缓和曲线上386540562073.7591507018.0365在第二缓和曲线上386550562082.8303507022.2454在第二缓和曲线上386560562091.9058507026.4448在第二缓和曲线上386570562100.9854507030.6352在第二缓和曲线上386580562110.0691507034.8169在第二缓和曲线上386590562119.1566507038.9904在第二缓和曲线上386600562128.2477507043.156在第二缓和曲线上386610562137.3422507047.3141在第二缓和曲线上386620562146.4399507051.4651在第二缓和曲线上386630562155.5407507055.6094在第二缓和曲线上386640562164.6444507059.7474在第二缓和曲线上386650562173.7508507063.8795在第二缓和曲线上386660562182.8597507068.006在第二缓和曲线上386670562191.9709507072.1274在第二缓和曲线上386680562201.0842507076.2441在第二缓和曲线上386690562210.1995507080.3564在第二缓和曲线上386700562219.3166507084.4648在第二缓和曲线上386710562228.4353507088.5696在第二缓和曲线上386720562237.5554507092.6712在第二缓和曲线上386730562246.6768507096.7701在第二缓和曲线上386740562255.7992507100.8666在第二缓和曲线上386750562264.9226507104.9611在第二缓和曲线上386760562274.0466507109.054在第二缓和曲线上386770562283.1712507113.1457在第二缓和曲线上386780562292.2961507117.2367在第二缓和曲线上386790562301.4212507121.3272在第二缓和曲线上386790.194562301.5982507121.4065里程大于第二曲线终点出的数据77.38323998X,YZH点558945.915262433,503012.196005598558945.985159621,503012.508278528558948.169524053,503022.266790301558950.354324447,503032.025204476558952.539983235,503041.783426423558954.726922822,503051.541361401558956.915565577,503061.298914505558959.106333821,503071.055990605558961.299649809,503080.812494298558963.495935725,503090.568329848558965.695613664,503100.323401136558967.899105623,503110.0776116558970.106833485,503119.830864183558972.319219007,503129.58306128558974.536683812,503139.33410468558976.759649366,503149.083895513558978.988536976,503158.832334194558981.223767767,503168.579320371558983.465762675,503178.324752868558985.714942431,503188.068529631558987.971727545,503197.810547675558990.236538297,503207.550703026558992.509794716,503217.288890671558994.791916572,503227.025004501558997.083323356,503236.758937257558999.384434271,503246.490580475559001.695668208,503256.219824436559004.017443738,503265.946558106559006.350179094,503275.670669084559008.694292153,503285.39204355559011.050200422,503295.110566211559013.418321019,503304.826120244559015.799070658,503314.538587243559018.192865629,503324.247847169559020.600121785,503333.953778293559023.021254516,503343.656257141559025.456678739,503353.355158447559027.906808873,503363.05035509559030.372058821,503372.741718051559032.852841953,503382.429116352559035.349571081,503392.112417007559037.862658444,503401.791484967559040.392515682,503411.466183069 HY点559042.857778326,503420.826997207559042.939545997,503421.136377572 559048.086221484,503440.462817768 559053.303140754,503459.770415044 559058.590234822,503479.058914092 559063.947433775,503498.32805986 559069.374666776,503517.577597547 559074.871862058,503536.807272616 559080.438946933,503556.01683079 559086.075847786,503575.206018058 559091.782490078,503594.374580679 559097.558798352,503613.522265186 559103.404696225,503632.648818385 559109.320106397,503651.753987364 559115.304950647,503670.837519493 559121.359149838,503689.899162429 559127.482623913,503708.938664115 559133.675291902,503727.955772792 559139.937071917,503746.950236992 559146.267881159,503765.921805551 559152.667635915,503784.870227604 559159.136251559,503803.795252594 559165.673642557,503822.696630273 559172.279722463,503841.574110706 559178.954403924,503860.427444274 559185.697598682,503879.256381676 559192.509217568,503898.060673936 559199.389170513,503916.8400724 559206.337366542,503935.594328749 559213.353713778,503954.32319499 559220.438119443,503973.026423471 559227.590489859,503991.703766876 559234.810730449,504010.354978232 559242.09874574,504028.979810912 559249.45443936,504047.578018637 559256.877714045,504066.149355481 559264.368471636,504084.693575873 559271.926613081,504103.2104346 559279.552038439,504121.699686812 559287.244646877,504140.161088022 559295.004336674,504158.594394114 559302.831005224,504176.999361341 559310.724549034,504195.375746333 559318.684863726,504213.723306095 559326.71184404,504232.041798016 559334.805383834,504250.330979869 559342.965376087,504268.590609812 559351.191712897,504286.820446397 559359.484285487,504305.020248568 559367.842984203,504323.189775667 559376.267698517,504341.328787436 559384.758317027,504359.437044021 559393.314727463,504377.514305973 559401.93681668,504395.560334255 560668.016616769,506091.886043581560668.757845184,506092.557296464559410.624470668,504413.574890242559419.377574549,504431.557735726559428.19601258,504449.508632916559437.079668153,504467.427344445559446.028423798,504485.313633374559455.042161186,504503.167263188559464.120761126,504520.987997807559473.26410357,504538.775601585559482.472067616,504556.529839315559491.744531505,504574.250476229559501.081372626,504591.937278006559510.482467517,504609.590010772 QZ点560847.119439937,506247.216378716559519.947691866,504627.2084411559529.476920514,504644.792336022559539.070027453,504662.341463022559548.726885834,504679.855590047559558.447367962,504697.334485505559568.231345303,504714.77791827559578.07868848,504732.185657686559587.989267283,504749.557473568559597.962950661,504766.893136206559607.999606732,504784.192416368559618.09910278,504801.455085304559628.261305258,504818.680914748559638.486079789,504835.869676921559648.773291171,504853.021144532559659.122803373,504870.135090786559669.534479544,504887.211289384559680.008182008,504904.249514524559690.543772271,504921.249540908559701.141111018,504938.211143742559711.80005812,504955.134098741559722.520472632,504972.018182131559733.302212798,504988.863170651559744.145136048,505005.668841557559755.049099005,505022.434972628559766.013957484,505039.16134216559777.039566497,505055.847728981559788.12578025,505072.493912443559799.272452148,505089.099672432559810.479434799,505105.664789368559821.746580009,505122.189044209559833.073738793,505138.672218451559844.460761371,505155.114094137559855.907497169,505171.514453852559867.413794827,505187.873080733559878.979502195,505204.189758468559890.604466339,505220.464271299559902.288533539,505236.696404027559914.031549297,505252.885942011559925.833358332,505269.032671176559937.693804589,505285.136378011559949.612731234,505301.196849574559961.589980662,505317.213873498559973.625394498,505333.187237985559985.718813594,505349.116731818559997.870078038,505365.002144361560010.079027153,505380.843265557560022.345499497,505396.639885937560034.66933287,505412.391796622560047.050364312,505428.098789321560059.488430108,505443.760656339560071.983365787,505459.377190578560084.535006127,505474.948185536560097.143185156,505490.473435319560109.807736154,505505.952734632560122.528491657,505521.385878792560135.305283457,505536.772663724560136.586038135,505538.308784621560148.137942603,505552.112885967560161.02629941,505567.406342674560173.970183451,505582.652831619560186.969423569,505597.852151195560200.023847873,505613.004100421560213.133283742,505628.108478939560226.29755783,505643.165087022560239.516496062,505658.173725576560252.789923644,505673.134196139560266.117665058,505688.046300887560279.499544072,505702.909842635560292.935383734,505717.724624841560306.425006381,505732.490451606560319.968233637,505747.207127682 YH点561920.584583174,506944.755043672561929.376900375,506949.097019472561938.350934573,506953.509124556561947.33259918,506957.905676113561956.321677559,506962.28705008561965.317955025,506966.653623403561974.321218797,506971.005774001561983.331257952,506975.34388074561992.347863376,506979.668323402562001.370827715,506983.97948265562010.399945329,506988.277740007562019.435012241,506992.563477819562028.47582609,506996.83707923562037.522186081,507001.098928153562046.573892938,507005.349409241562055.630748851,507009.58890786562064.692557431,507013.81781006562073.759123659,507018.036502551562082.830253835,507022.245372673562091.905755531,507026.444808368562100.985437538,507030.635198161562110.069109819,507034.816931125562119.156583457,507038.99039686562128.247670606,507043.155985468562137.342184442,507047.314087525562146.439939107,507051.465094057562155.540749667,507055.609396517562164.644432055,507059.747386757562173.750803021,507063.879457004562182.859680085,507068.005999839562191.970881484,507072.12740817562201.084226118,507076.244075207562210.199533507,507080.356394442562219.31662373,507084.46475962562228.435317384,507088.569564722562237.555435524,507092.671203934562246.676799619,507096.770071629562255.799231496,507100.866562344562264.922553291,507104.961070751562274.046587398,507109.053991641562283.171156418,507113.145719896562292.296083104,507117.236650468562301.421190314,507121.327178354 HZ点562301.598218,507121.406533243。

坐标正算反算公式讲解坐标正算和反算是地理信息系统(GIS)中两个常用的操作,用于将地理坐标转换为平面坐标(正算)或将平面坐标转换为地理坐标(反算)。
这两个操作在测量、绘图、导航、定位等领域都有广泛的应用。
下面是对坐标正算和反算公式的详细讲解。
一、坐标正算公式坐标正算是将地理坐标(经纬度)转换为平面坐标(XY坐标)。
在坐标正算中,我们需要用到投影坐标系和大地坐标系之间的转换公式。
1.地理坐标系地理坐标系使用经度和纬度来表示地球上的点。
经度是指从地球圆心到其中一点的经线弧度长度与赤道弧度长度的比值,范围为-180到180度;纬度是指从地球赤道到其中一点的纬线弧度长度与半径的比值,范围为-90到90度。
2.投影坐标系投影坐标系是将地理坐标投影到平面坐标系上的一种方法。
根据需要,可以选择不同的投影方式,例如等角、等面积、等距、等分四类等。
每个投影方式都有其特点,选用不同的投影方式可以满足不同的需求。
3.原理坐标正算的原理是根据地理坐标系中点的经纬度和投影坐标系中原点的经纬度之间的差异,通过一定的计算公式将地理坐标系中的点坐标转换为投影坐标系中的点坐标。
4.具体步骤(1)选择合适的投影坐标系,确定原点和偏移量。
(2)计算地理坐标系中点的经纬度与原点经纬度的差值。
(3)利用投影坐标系的转换公式,将差值转换为平面坐标。
5.常用坐标正算公式常用的坐标正算公式包括高程改正公式、大地坐标系转换公式、高斯投影正算公式等。
二、坐标反算公式坐标反算是将平面坐标(XY坐标)转换为地理坐标(经纬度)。
在坐标反算中,我们需要用到投影坐标系和大地坐标系之间的反转换公式。
1.原理坐标反算的原理是根据投影坐标系中点的坐标和大地坐标系中原点的经纬度之间的差异,通过一定的计算公式将平面坐标系中的点坐标转换为地理坐标系中的点坐标。
2.具体步骤(1)选择合适的投影坐标系,确定原点和偏移量。
(2)计算平面坐标系中点的坐标与原点坐标的差值。
(3)利用投影坐标系的反转换公式,将差值转换为地理坐标。
坐标方位角EXCEL计算公式1.计算坐标方位角的基本公式:方位角=ATAN2(y轴坐标差,x轴坐标差)2.公式解释:ATAN2是Excel的一个数学函数,用于计算给定点的反正切值。
其中,y轴坐标差为点的纵坐标与原点纵坐标之差,x轴坐标差为点的横坐标与原点横坐标之差。
3.公式应用示例:假设在A1单元格中输入点的横坐标,B1单元格中输入点的纵坐标,C1单元格中输入原点的横坐标,D1单元格中输入原点的纵坐标。
则在E1单元格中输入如下公式:=ATAN2(B1-$D$1,A1-$C$1)这样就可以得到点相对于原点的坐标方位角。
需要注意的是,Excel中的数学函数ATAN2返回的角度以弧度为单位,如果需要以度数显示,可以使用Excel的DEGREES函数将结果转换为度数。
例如,在F1单元格中输入如下公式:=DEGREES(E1)这样就可以得到以度数表示的坐标方位角。
在使用以上公式计算坐标方位角时,需要确保原点的横纵坐标与点的横纵坐标分别对应。
另外,Excel中的坐标系正方向为向右为x轴正方向,向下为y轴正方向,因此计算得到的方位角范围为-π到π,即-180°到180°。
如果需要将角度值映射到0°到360°的范围,可以使用如下公式:IF(F1<0,F1+360,F1)总结:在Excel中,我们可以使用ATAN2函数来计算坐标方位角,公式为方位角 = ATAN2(y轴坐标差, x轴坐标差)。
在计算得到的结果为弧度时,可以使用DEGREES函数将其转换为度数。
另外,如果需要将角度值映射到0°到360°的范围,可以使用IF函数进行判断和调整。
以上是关于在Excel中计算坐标方位角的基本方法和公式示例。
Excel 在坐标正反算中的应用
周会利;姜有亮
【期刊名称】《四川水泥》
【年(卷),期】2015(000)002
【摘要】Excel是一种专业的电子表格,除了作为一种办公软件被普遍使用之外,Excel在测量数据计算中的应用也在逐步被挖掘。
本文结合测量教学中的坐标正反算案例,阐述了Excel在测量数据计算中的应用过程。
【总页数】1页(P233-233)
【作者】周会利;姜有亮
【作者单位】湖北国土资源职业学院,湖北武汉430090;湖北国土资源职业学院,湖北武汉 430090
【正文语种】中文
【中图分类】K928
【相关文献】
1.Excel在高斯投影坐标正算公式中的应用 [J], 崔学敏;赵雪松;姚继华
2.CASIOfx-4800P计算器在一井定向及坐标正、反算的应用 [J], 钟恢贵
3.后方交会和坐标反算程序在施工测量中的应用 [J], 许凌毅
4.坐标反算法在有砟轨道测量施工中的应用 [J], 王珍
5.编程计算器在坐标正、反算中的应用 [J], 陈先辉
因版权原因,仅展示原文概要,查看原文内容请购买。
利用Excel实现北京54、西安80大地坐标正反算
刘斌
【期刊名称】《大众科技》
【年(卷),期】2012(000)006
【摘要】用最简单最快捷的Excel电子表格实现北京54、西安80坐标系大地坐标与平面坐标的转换。
% with the simplest and most efficient Excel spreadsheet achieved 54 Beijing, Xi'an80 coordinates geodetic coordinates to plane coordinates conversion.
【总页数】2页(P11-12)
【作者】刘斌
【作者单位】安徽省煤田地质局第三勘探队,安徽宿州234000
【正文语种】中文
【中图分类】P226+.3
【相关文献】
1.正形变换实现北京54坐标与西安80坐标之间的转换 [J], 张佃友;覃辉
2.利用4参数法进行北京54坐标至西安80坐标的换算 [J], 程新辉;吴银;吴承兵
3.利用EXCEL实现空间直角坐标与大地坐标间的转换 [J], 王强;鹿罡
4.无控制点实现北京54坐标与西安80坐标系统的转换 [J], 廖晓和
5.利用第三方软件实现西安80坐标地形图在北京54坐标系统下的校正 [J], 张钦云
因版权原因,仅展示原文概要,查看原文内容请购买。