Matlab2012教程--经典教程

●MATLAB R2012a●课后习题答案全解第一章基础准备及入门习题1及解答⏹ 1.数字1.5e2，1.5e3 中的哪个与1500相同吗？〖解答〗1.5e3⏹ 2.请指出如下5个变量名中，哪些是合法的？abcd-2 xyz_3 3chan a变量ABCDefgh〖解答〗2、5是合法的。

⏹ 3.在MATLAB环境中，比1大的最小数是多少？〖解答〗1+eps⏹ 4.设a = -8 , 运行以下三条指令，问运行结果相同吗？为什么？w1=a^(2/3)w2=(a^2)^(1/3)w3=(a^(1/3))^2〖解答〗（1）不同。

具体如下w1=a^(2/3) %仅求出主根w2=(a^2)^(1/3) %求出(-8)^2的主根 w3=(a^(1/3))^2%求出(-8)主根后再平方w1 = -2.0000 + 3.4641iw2 = 4.0000 w3 =-2.0000 + 3.4641i（2）复数的多方根的，下面是求取全部方根的两种方法： （A ）根据复数方根定义a=-8;n=2;m=3;ma=abs(a);aa=angle(a); for k=1:m%m 决定循环次数 sa(k)=(aa+2*pi*(k-1))*n/m;%计算各根的相角 endresult=(ma^(2/3)).*exp(j*sa) %计算各根result =-2.0000 + 3.4641i 4.0000 - 0.0000i -2.0000 - 3.4641i（B ）利用多项式023=-a r 求根p=[1,0,0,-a^2]; r=roots(p) r =-2.0000 + 3.4641i -2.0000 - 3.4641i 4.0000⏹ 5.指令clear, clf, clc 各有什么用处？〖解答〗 clear 清除工作空间中所有的变量。

clf 清除当前图形。

clc 清除命令窗口中所有显示。

⏹ 6.以下两种说法对吗？（1）“MATLAB 进行数值的表达精度与其指令窗中的数据显示精度相同。

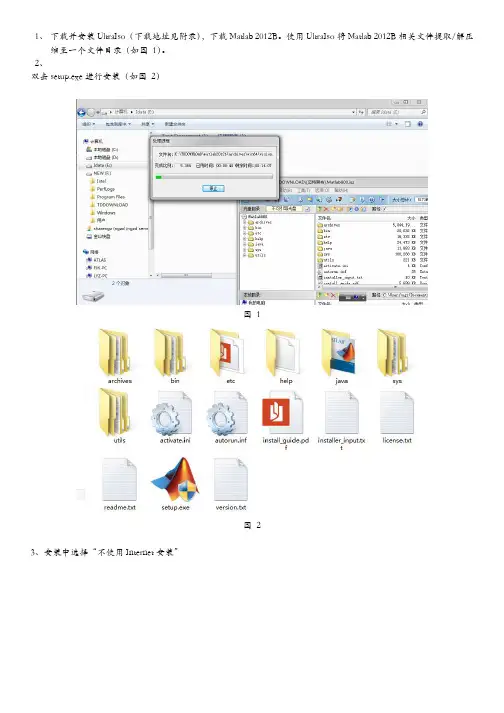
1、下载并安装UltraIso（下载地址见附录），下载Matlab 2012B。

使用UltraIso将Matlab 2012B相关文件提取/解压缩至一个文件目录（如图 1）。

2、双击setup.exe进行安装（如图 2）图 1图 23、安装中选择“不使用Internet安装”图 34、接受许可协议图 45、输入安装密钥：37176-43568-09521-61284-60764-48411-11831-17282-31342-18748-48552-26727-08411图 56、安装类型选择“自定义”图 67、点击“下一步”安装 导入许可协议（附录：Matlab 2012B Crack中的“matlab2012b_std.dat”）图 7 9、设置快捷方式图 8 10、点击“安装”进行安装图 911、等待安装结束图 1012、使用"crack\Usual\install.jar"文件替换"Matlab安装源文件目录\java\jar\install.jar"，重新执行图 2至图 10的相关步骤，其中安装密钥选用“23809-26556-08469-31324”，如图 11，弹出产品选择对话框选择"全否"。

图 11图 1213、所有的安装完成后，可能会遇见这种情况，当你打开后提示你要“激活“，激活文件的搜索路径在你下载的crack 目录下的那个matlab2012b_std.dat，加上就可以了14、另外我安装在Windows xp上，win7或win8会遇到的问题我不知道15、进行完此次安装，Matlab 2012B便安装了除“MATLAB Production Server”之外的所有组件，如果想要安装此组件，将"Matlab安装源文件目录\java\jar\install.jar"用"crack\Usual\install.jar"替换。

Matlab2012教程--经典教程第1章基础准备及入门1.1 最简单的计算器使用法为易于学习，本节以算例方式叙述，并通过算例归纳一些MATLAB最基本的规则和语法结构。

建议读者，在深入学习之前，先读一读本节。

2【例1.3-1】求[122(74)]3的算术运算结果。

本例演示：最初步的指令输入形式和必需的操作步骤。

（1）用键盘在MA TLAB指令窗中输入以下内容>> (12+2*(7-4))/3^2（2）在上述表达式输入完成后，按[Enter] 键，该指令被执行，并显示如下结果。

ans =2〖说明〗本例在指令窗中实际运行的情况参见图 1.3-1。

指令行“头首”的“>>”是“指令输入提示符”，它是自动生成的。

本书在此后的输入指令前将不再带提示符“>>”。

理由是：（A）为使本书简洁；（B）本书用MATLAB 的M-book写成，而在M-book中运行的指令前是没有提示符的。

5MATLAB的运算符（如+、- 等）都是各种计算程序中常见的习惯符号。

一条指令输入结束后，必须按[Enter] 键，那指令才被执行。

由于本例输入指令是“不含赋值号的表达式”，所以计算结果被赋给MATLAB的一个默认变量“ans”。

它是英文“answer”的缩写。

【例1.3-2】“续行输入”法。

本例演示：或由于指令太长，或出于某种需要，输入指令行必须多行书写时，该如何处理。

S=1-1/2+1/3-1/4+ ...1/5-1/6+1/7-1/8S =0.6345〖说明〗MA TLAB用3个或3个以上的连续黑点表示“续行”，即表示下一行是上一行的继续。

本例指令中包含“赋值号”，因此表达式的计算结果被赋给了变量S。

指令执行后，变量S被保存在MA TLAB 的工作空间（Workspace）中，以备后用。

如果用户不用clear 指令清除它，或对它重新赋值，那么该变量会一直保存在工作空间中，直到本MATLAB 指令窗被关闭为止。

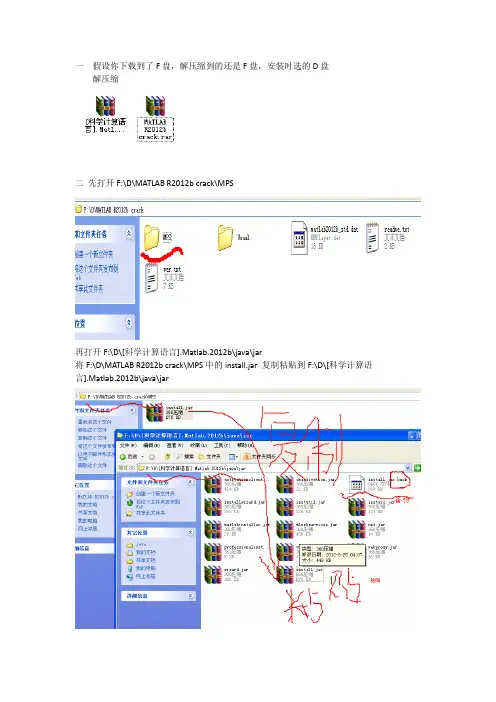
一假设你下载到了F盘，解压缩到的还是F盘，安装时选的D盘解压缩
二先打开F:\D\MATLAB R2012b crack\MPS
再打开F:\D\[科学计算语言].Matlab.2012b\java\jar
将F:\D\MATLAB R2012b crack\MPS中的install.jar复制粘贴到F:\D\[科学计算语言].Matlab.2012b\java\jar
三
打开F:\D\[科学计算语言].Matlab.2012b\bin\win64
先运行vcredist_x64.exe安装好后
再运行setup.exe运行“Setup.exe”→选择“不使用互联网的安装”→输入序列号: 23809-26556-08469-31324
23809-26556-08469-31324
安装到D盘
我安装了有一小时吧。

四安装好后打开
D:\Program Files\MATLAB\MATLAB Production Server\R2012b\bin （假如小美女已经安装到了D盘）运行matlab.exe开始激活
F:\D\MATLAB R2012b crack里找到matlab2012b_std.dat
激活后再次运行
D:\Program Files\MATLAB\MATLAB Production Server\R2012b\bin中的matlab.exe即可打开MATLAB
顺手创建个快捷方式
五将快捷方式放在容易找到的位置
F盘的压缩包和解压缩包都可以删了的。

MATLAB基础——连续时间信号与系统课程安排MATLAB简介连续时间信号与系统离散时间信号与系统MATLAB实验内容连续时间系统的时域分析傅里叶变换拉普拉斯变换、s 域分析内容连续时间系统的时域分析1微分方程式的建立与求解零输入响应与零状态响应冲激响应与阶跃响应微分方程式的建立与求解•连续时间系统的研究方法包括输输法端描法输入－输出法（端口描述法）系统状态变量分析法•输入－输出法LTI系统可以用一元高阶微分方程描述LTI 系统可以用元高阶微分方程描述[17012]b1a = [1,7,0,12];b = 1; %定义微分方程的行矢量sys = tf(b,a)%生成系统描述sys（tf=transfer function）微分方程式的建立与求解•状态变量描述法一个一元高阶微分方程，必然可以化成两个多元一阶微分方程组，即状态方程和输出方程（观测方程）sys = ss(A,B,C,D) %ss=state space，ABCD为状态方程和输出方程的矩阵微分方程式的建立与求解•微分方程的解包括齐次解和特解两部分•齐次解即系统特征方程的根，用roots函数计算p = [1 7 16 12];%定义多项式pa = roots(p);%求解多项式p=0的根aa%打印显示a = -3.0000-2.0000 + 0.0000i-2.0000 -0.0000i微分方程式的建立与求解•特解即系统（采用微分方程表示）在给定信号激励下的输出•用lsim函数进行仿真a = [1,2,3];%定义多项式pb = [1,1];%求解多项式p=0的根asys=tf(b a);sys = tf(b,a);%建立系统描述syst = [0:0.1:10]’;%定义仿真时间为0s到10s，抽样间隔为0.1se1 = t.^2’;%定义激励信号e1r1=lsim(sys e1t);输出为r1 = lsim(sys,e1,t);%用e1激励sys，输出为r1e2 = exp(t);…微分方程式的建立与求解微分方程式的建立与求解•Help polyfunroots -Find polynomial roots.poly -Convert roots to polynomial.polyval-Evaluate polynomial.l l E l t l i lpolyvalm-Evaluate polynomial with matrix argument.residue-Partial-fraction expansion(residues).residue Partial fraction expansion (residues).polyfit-Fit polynomial to data.polyder-Differentiate polynomial.polyint-Integrate polynomial analytically.conv-Multiply polynomials.deconv-Divide polynomials.Divide polynomials零输入响应和零状态响应•lsim函数还可以对带有非零起始状态的LTI 系统进行仿真 y = lsim(sys, u, t, x0)•注意：若用lsim函数仿真非零起始状态响应，则该系统必LTI 系统，lsim函须用状态方程描述（对传递函数描述的LTI系统数无法仿真非零起始状态响应）零输入响应和零状态响应零输入响应和零状态响应•解：采用两种方法•第一种：首先仿真2V电压en作用足够长时间（10秒）后系统进入稳态，从而得到稳态的状态变量值x0，再以其作为起始值仿真4V电压e作用下的输出rf，即是系统的完全响应真作出系应•这种方法还可以得到零状态响应rzs和零输入响应rzi•第二种：构造一个激励信号，先保持2V足够长时间再跳变为4V，然后即可以零初始状态一次仿真得到系统的完全响应r1零输入响应和零状态响应• C = 1; L = 1/4; R1 = 1; R2 = 3/2;%定义器件参数• a = [-1/R1/C,-1/C;1/L,-R2/L];%定义A，B，C，D四个矩阵• b = [1/R1/C;0];• c = [-1/R1,0];• d = [1/R1];•sys = ss(a,b,c,d);建立LTI系统sys()%•tn= [-10:0.01:-0.01]‘;%生成-10s到-0.01s的抽样时间，间隔为0.01s •en = 2*(tn<0);%生成激励信号的抽样值，e(t)=2•xn]=lsim(sys en tn);[rn tn xn]= lsim(sys,en,tn);%仿真t<0时的输出信号•x0 = xn(length(tn),:);%x0记录了起始状态，即0状态的值-•t = [0:0.01:10]‘;%生成从0s到10s的抽样时间，间隔为0.01s • e = 4*(t>=0);%生成激励信号的抽样值，e(t)=4•ezi= 0*(t>=0);%生成零输入信号的抽样值，e(t)=0•rzs= lsim(sys,e,t);%仿真零状态响应•rzi= lsim(sys,ezi,t,x0);%仿真零输入响应•rf= lsim(sys,e,t,x0);%仿真完全响应f l i(t0)•r1 = lsim(sys,[en;e],[tn;t]);%用另一种方法仿真完全响应零输入响应和零状态响应冲激响应和阶跃响应•如果分别用冲激信号和阶跃信号作激励，lsim函数可仿真出冲激响应和阶跃响应•MATLAB 专门提供了impulse(sys) 和step(sys)两个函数直接产生冲激响应和阶跃响应冲激响应和阶跃响应• a = [1, 7, 10];• b = [1, 6, 4];•sys = tf(b,a);%LTI系统模型y(,);定义系统模•t = [0:0.01:3]‘;%生成0到3s，间隔0.01s的抽样时间•h1 = step(sys);%用step函数仿真sys的阶跃响应•x_step= zeros(size(t));%另一种方法：根据定义构造阶跃信号x_step•x_step(t>0) = 1;•x_step(t==0) = 1/2;%lsim函数不支持输入NaN，所以x_step(0)=1/2•lsim(sys,x_step,t);%仿真x_step激励sys的响应lsim(sys x step t);x step•[h2, t2] = impulse(sys, t);%用impulse函数仿真sys的冲激响应并保存在h2中•x delta= zeros(size(t));%另一种方法：根据定义构造冲激响应x delta_(());_•x_delta(t==0) = 100;%lsim函数不支持输入Inf，所以令x_delta(0)=100，因为抽样间隔是%0.01，选择100可保证数值积分为1•[y1,t] = lsim(sys,x_delta,t);%仿真x_delta激励sys的响应并保存在y1中•y2 = y1-x_delta;%从响应中减去一个冲激信号得到y221d lt从响应中减去个冲激信号得到2冲激响应和阶跃响应冲激响应和阶跃响应求系统的响应：卷积求系统的响应卷积•卷积运算的数值近似•MATLAB 提供了w = conv(u,v) 函数实现卷积和求系统的响应：卷积求系统的响应卷积•t = [-1:0.01:4]‘;%生成从-1s到4s，间隔0.01s的抽样时间t • e = (t>-1/2&t<1);%定义激励信号e•h = (t>0&t<2).*t/2;%定义冲激响应h•[r1,t1] = conv1(e,t,h,t);%用卷积计算系统输出r1，相应的抽样时间为t1 [r1t1]=conv1(e t h t);相应的抽样时间为•tr = t1(t1>=-1&t1<=4);%从t1中选择和t相同起止时刻的抽样时间tr•r = r1(t1>=-1&t1<=4);%用类似方法选择tr对应的输出r•function [w,tw] = conv1(u,tu,v,tv)•% 输入参数：u和v表示两个序列，tu和tv分别表示它们的抽样时间•% 返回值：w和wt分别表示卷积结果及其抽样时s间•T = tu(2)-tu(1);T tu(2)tu(1);•w = T*conv(u,v);•tw= tu(1)+tv(1)+T*[0:length(u)+length(v)-2]';求系统的响应：卷积求系统的响应卷积求系统的响应：连续时间信号的数值计算求系统的响应连续时间信号的数值计算•自然界中绝大部分物理量是连续的，数字计算机处理连续信号必须做近似，计算精度取决于算法和数字表示的位数信号必须做近似计算精度取决于算法和数字表示的位数•例如积分运算的简单数值计算方法是分段求和•复杂数值计算方法包括插值、拟合等等•help interp, resample, polyfit, …内容连续时间系统的时域分析傅里叶变换拉普拉斯变换、s 域分析内容傅里叶变换2傅里叶变换周期信号的傅里叶级数分析卷积特性（卷积定理）傅里叶变换•符号方法MATLAB 提供符号函数fourier和ifourier实现傅里叶变换和逆变换符数实傅变换变换syms t%定义符号t(())()F1 = fourier(t*heavisde(t))%计算tu(t)的傅里叶变换F1输出：F1 = i* (pi * dirac(1,w) * w^2 + i) / w^2%dirac(1,w)表示δ’(ω) F2 = fourier(sin(t))输出p(()())()表示()输出：F2 = i* pi * (dirac(w + 1)-dirac(w -1))%dirac(w + 1)δω+1)工程应用中经常需要对抽样数据做傅里叶分析，这种情况下往往无法得到信号的解析表达式，因而数值计算方法是应用傅里叶变换的法得到信号的解析表达式因而数值计算方法是应用傅里叶变换的主要途径傅里叶变换•将傅里叶变换写成离散表示形式Ω=ω2-ω1∆ω=Ω/K•同理写出逆变换傅里叶变换•三种方法二重循环循环+矢量相乘矩阵相乘傅里叶变换•二重循环T = 2;%定义时域抽样区间长度T2N = 200;%定义时域抽样点数t = linspace(-T/2,T/2-T/N,N)‘;%定义时域抽样点f = (t>-1/2&t<1/2);%初始化时域信号OMG16*iOMG = 16*pi;%定义频域抽样区间长度K = 100;%定义频域抽样点数omg= linspace(-OMG/2,OMG/2-OMG/K,K)‘;%定义频域抽样点F = zeros(size(omg));%初始化频谱for k = 1:K%循环计算每个频谱抽样点的频谱算每个频谱样频谱 for n = 1:N%用循环实现公式F(k) = F(k) + T/N*f(n)*exp(-j*omg(k)*t(n));endendfs= zeros(size(t));%初始化合成信号for n = 1:N%循环计算每个时域抽样点的合成信号 for k = 1:K%用循环实现公式fs(n) = fs(n) + OMG/2/pi/K*F(k)*exp(j*omg(k)*t(n));endend傅里叶变换傅里叶变换•矢量计算法傅里叶变换•矩阵相乘法傅里叶变换：程序优化技巧傅里叶变换程序优化技巧•程序优化技巧阵算代替用矩阵运算代替循环变量预定义•举例：计算sin(n), n=1,2,…,10^6举例i()1210^6for n = 1:1e6x(n) sin(n);x(n)=sin(n);endx = zeros(1e6, 1);x = sin([1:1e6]);•时间函数help timefun周期信号的傅里叶级数分析•和傅里叶变换的数值计算方法相似周期信号的傅里叶级数分析卷积特性（卷积定理）•验证卷积定理：时域卷积对应于频域相乘•可用两种方法计算三角脉冲的频谱一是直接对三角脉冲做傅里叶变换二是利用卷积定理，矩形脉冲的卷积是三角脉冲，所以可以先计算矩形脉冲的频谱，再取其平方将两种计算结果绘制在一起，验证卷积定理的正确性卷积特性（卷积定理）卷积特性提高函数的稳定性卷积特性：提高函数的稳定性•考察MATLAB库函数open conv open polyfit function c = conv(a, b)na= length(a);nb= length(b);if na ~= numel(a) || nb ~= numel(b)error('MATLAB:conv:AorBNotVector', 'A and B must be vectors.');endif na> nb[c,zf] = filter(b, 1, a);if nb> 1c(na+1:na+nb-1) = zf;endelse[c,zf] = filter(a, 1, b);if na>1if na> 1c(nb+1:na+nb-1) = zf;endend内容连续时间系统的时域分析傅里叶变换拉普拉斯变换、s 域分析内容拉普拉斯变换拉普拉斯变换、s域分析2拉普拉斯变换和逆变换系统函数H(s)由系统函数分析时频特性拉普拉斯变换和逆变换•用符号函数laplace和ilaplace实现（单边）拉氏变换和逆变换syms t w%定义符号syms s;F1 = laplace(t3)%计算拉氏变换F1 f = ilaplace(10(s+2)(s+5)/s F1=laplace(t^3)f=ilaplace(10*(s+2)*(s+5)/s 输出：F1 = 6/s^4/(s+1)/(s+3)) F2 = laplace(sin(w*t)) %计算拉氏变换F2输出：f = -10/3*exp(-3*t)输出：F2 = w/(s^2+w^2)-20*exp(-t)+100/3拉普拉斯变换和逆变换•用部分分式展开的函数residue 求逆变换r =%两个部分分式系数-12b = [1,5,9,7];a1 = [1,1];2[12]p =%两个极点（特征根）-2-1k =%自由项12a2 = [1,2];a = conv(a1,a2);[r,p,k] = residue(b,a)•解：先用MATLAB 求留数，写出展开式1 2•最后写出时域表达式拉普拉斯变换和逆变换•参考Symbolic Math Toolbox合并同类项collect因式分解factor化简simplify变量替换subs求极限limit微分和求导diff积分int解方程组solve解微分方程组dsolve系统函数H(s)H()•回顾前面介绍的tf函数，可知MATLAB用系统函数H(s)描述LTI系统由电路可知传递函数为H(s)=1/(s+1)sys = tf(1,[0.1 0.1]);%定义系统函数H(s)t = [0:0.01:10]‘;%定义抽样时间te = sin(3*t);%生成激励信号e(t)i= lsim(sys, e, t);%仿真电流信号i(t)系统函数H(s)H()由系统函数分析时频特性•MATLAB用zero(sys) 和pole(sys) 函数直接计算零极点•[p,z] = pzmap(sys) 函数也可以计算零极点不带返回值则绘制出系统的零极点图•[b,a]= zp2tf(z,p,k) 和[z,p,k] = tf2zp(b,a) 两个函数用于在零两个数用于在零极点和传递函数这两种描述方法之间进行转换由系统函数分析时域特性•t = [0:.1:40]‘;%定义抽样时间•figure, id = 1;%生成新图框，定义子图标号id=1•for omega = .5:-.25:0%循环omega=[0.5, -0.25, 0]•for sigma = -.06:.03:.06%循环sigma=[-.06:.03:.06]•p = sigma + j*omega;%定义极点p = sigma + j*omega•if omega ~= 0%如果极点不在实轴上if0•p = [p;p‘];%则再添加一个共轭极点•end•[b a]=zp2tf([]p1);%[b a] zp2tf([],p,1);由零、极点转换为传递函数的多项式系数•subplot(3,5,id);%生成标号为id的子图框•impulse(b,a,t);%绘制抽样时间为t的冲激响应•set(gca,‘YLim’,[-20,20]);%设置Y轴范围以求最好视觉效果•id = id + 1;%子图标号加1•end%内层sigma循环结束•end%外层omega循环结束由系统函数分析时域特性由系统函数分析频域特性•freqs(b,a) 函数用于绘制系统的频率响应（包括幅度响应和相位响应）其中b和a分别是传递函数的分子和分母多项式系数由系统函数分析频域特性•用zp2tf从零、极点求得系统的传递函数b,a•用freqs(b,a)求得频率响应•绘图查看频响特性（低通、高通、带通、带阻）。

matlab使用指导（2012）一、基础知识1.1 常见数学函数如：输入x=[-4.85 -2.3 -0.2 1.3 4.56 6.75]，则：ceil(x)= -4 -2 0 2 5 7fix(x) = -4 -2 0 1 4 6floor(x) = -5 -3 -1 1 4 6round(x) = -5 -2 0 1 5 71.2 系统的在线帮助1 help 命令：1.当不知系统有何帮助内容时，可直接输入help以寻求帮助: >>help（回车）2.当想了解某一主题的内容时，如输入：>> help syntax（了解Matlab的语法规定）3.当想了解某一具体的函数或命令的帮助信息时，如输入：>> help sqrt （了解函数sqrt的相关信息）2 lookfor命令现需要完成某一具体操作，不知有何命令或函数可以完成，如输入：>> lookfor line （查找与直线、线性问题有关的函数）1.3 常量与变量系统的变量命名规则：变量名区分字母大小写；变量名必须以字母打头，其后可以是任意字母，数字，或下划线的组合。

此外，系统内部预先定义了几个有特殊意1 数值型向量（矩阵）的输入1．任何矩阵（向量），可以直接按行方式．．．输入每个元素：同一行中的元素用逗号（，）或者用空格符来分隔；行与行之间用分号（；）分隔。

所有元素处于一方括号（[ ]）内；例1：>> Time = [11 12 1 2 3 4 5 6 7 8 9 10]>> X_Data = [2.32 3.43；4.37 5.98]2上面函数的具体用法，可以用帮助命令help得到。

如help zeros,可查到zeros的具体用法。

例：meshgrid(x,y)输入x=[1 2 3 4]; y=[1 0 5]; [X,Y]=meshgrid(x, y)，则X = Y =1 2 3 4 1 1 1 11 2 3 4 0 0 0 01 2 3 4 5 5 5 5目的是将原始数据x，y转化为矩阵数据X，Y。

第一步安装：
解压→打开MA TLAB→MATLAB_R2012a→双加sepup.exe→选择不使用Internet安装→
选择是（Y），下一步→选择我已有我的许可证的安装密钥→打开文件crack、打开第四幅图将密钥抄写进去，下一步→典型，下一步→安装在C盘默认的（我也是C盘）可以自建的→安装，下一步→完成。

第二步激活：
打开C盘，打开MA TLAB→R1201a→双击bin文件夹中的matlab.exe→选择不使用Internet 手动激活→选择“输入许可证文件的完整路径（包括文件名），点击右侧的浏览（R）打开crack子目录选择lic_standalone.dat→单击下一步，选择(S)按钮→单击下一步（N）激活
最后结束后，在C盘的MATLAB→bin文件夹中右击MATLAB.exe发送桌面快捷方式，这样就可以了！祝你们成功！。

第1讲Matlab基础MATLAB是矩阵实验室（Matrix Laboratory）的简称，是美国MathWorks公司出品的商业数学软件，用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境。

MATLAB和Mathematica、Maple并称为三大数学软件。

MATLAB的基本数据单位是矩阵，它的指令表达式与数学、工程中常用的形式十分相似，故用MATLAB来解决问题要比用C，FORTRAN等语言完成相同的事情简捷得多，并且MATLAB也吸收了像Maple等软件的优点,使MATLAB成为一个强大的数学软件。

主要应用● 数值分析● 数值和符号计算● 工程与科学绘图● 控制系统的设计与仿真● 数字图像处理技术● 数字信号处理技术● 通讯系统设计与仿真● 财务与金融工程一初步认识Matlab的操作1.1 简单操作：功能命令（操作对象，指定格式）。

功能命令指的是需要完成的任务所对应的函数。

操作对象一般为函数、普通方程、微分方程、矩阵表达式等；指定格式一般为操作对象的控制选项。

>> fplot('x*sin(x)',[-pi,pi])>> dsolve('Dy = y^2*(1-y^2)')1.2 复杂操作：编程处理。

这时，没用一个或若干命令完成所需任务。

二Matlab的编辑、查找、数据保存等2.1 各窗口的字体调整：File,Preference,fonts,custom,font to use 2.2 C窗口里修改命令：先用上下键调入，再编辑；X 表示重新调入X字母开头的上下一行；模糊查询：命令前几个字母，在点击tab键删除C窗口里输入：clc回车删除C窗口里命令：clear回车，则所有命令被删除退出C窗口里的输入：按EscC窗口里：Help 功能命令C窗口里：输入功能命令前几个字母，再按一下tap，会跳出子窗口，用上下键寻找所需命令。