下载文档原格式
二进制乘法引言在计算机科学中，二进制乘法是一种重要的计算方法。
它是基于二进制表示的数字进行运算的一种方式，常用于逻辑门电路设计、计算机算术运算以及编程中。
本文将介绍二进制乘法的基本原理、计算方法和应用场景，并提供一些示例来帮助读者更好地理解和应用二进制乘法。
二进制乘法的基本原理二进制乘法实际上是将两个二进制数相乘的方法。
与十进制乘法类似，二进制乘法也是通过逐位相乘和相加的方式进行计算的。
二进制数由0和1组成，表示为二进制位。
在二进制乘法中，我们将乘数和被乘数的每一位逐个相乘，并将结果相加得到最终的乘积。
二进制乘法的计算方法以下是一种常用的二进制乘法计算方法：1.准备两个二进制数，即乘数和被乘数。
保证乘数和被乘数位数相同，不足的部分用0填充。
2.从乘数的最低位（即最右边）开始，逐个乘以被乘数的每一位。
如果乘数位上的数字为1，则将被乘数乘以2的乘数位的位置数次方。
3.将每一个乘积相加，得到最终的乘积。
以下是一个例子，展示了如何进行二进制乘法：乘数: 1011被乘数: 1101011 <- 乘数x 110 <- 被乘数----------------1011 <- 乘数的最低位为1，乘以被乘数，得到被乘数本身+ 0000 <- 乘数的次低位为0，乘以被乘数，得到0+ 1011 <- 乘数的次高位为1，乘以被乘数，得到被乘数的四倍----------------= 10001010 <- 二进制乘法的结果二进制乘法的应用场景二进制乘法广泛应用于计算机科学和数字逻辑电路设计中。
下面列举了二进制乘法的一些常见应用场景：•逻辑门电路设计：二进制乘法在逻辑门电路的设计中非常重要。
通过多个逻辑门的组合，可以实现二进制乘法运算。
•计算机算术运算：在计算机中，二进制乘法常用于数字的乘法运算。
计算机通过电路和算法实现二进制乘法运算，可以进行高效的数字计算。
•编程：在编程语言中，二进制乘法可以用于位运算和数值计算。
二进制的乘法在计算机科学中，二进制是一种非常重要的数制系统。
它只有两个数字，0和1，但却可以表示任意的数字和字符。
在计算机中，二进制的运算也是非常常见的，其中乘法是一种基本的运算。
本文将介绍二进制的乘法，包括乘法的基本原理、算法和应用。
一、二进制的基本原理二进制的基本原理是用0和1表示数字。
在二进制中，每个数字位代表一个权值，从右往左依次为1、2、4、8、16、32、64、128……以2的幂次递增。
例如，二进制数1101表示的数字为13，因为1×1+0×2+1×4+1×8=13。
二进制的乘法基于十进制的乘法，但是只包含0和1两个数字。
在二进制中，乘法的规则与十进制相同，但是只需要记住两个乘数和积的每个位的值即可。
例如，计算二进制数101×11，可以按照如下方法进行计算：101× 11-----1011010------1111在这个例子中，我们将乘数11写在上面，将被乘数101写在下面，然后从右往左依次计算每一位的乘积。
第一位是1×1=1，第二位是1×0=0，第三位是1×1=1，然后将这些乘积相加得到101。
接下来，我们将乘数11向左移动一位，变成110，然后再次计算乘积。
第一位是1×0=0，第二位是1×1=1，第三位是1×0=0，然后将这些乘积相加得到1010。
最后，我们将这两个乘积相加得到1111，即为所求的积。
二、二进制的乘法算法二进制的乘法算法有许多种，下面介绍两种常见的算法：加法法和移位法。
1. 加法法加法法是二进制乘法的最基本算法。
它的原理是将乘数的每一位与被乘数相乘，然后将每个乘积相加得到最终的积。
例如，计算二进制数101×11，可以按照如下方法进行计算：101+ 101-------1010-------1111在这个例子中，我们将乘数11拆分成1和1，然后将乘数的每一位与被乘数相乘，得到101和101。
二进制的乘法在计算机科学中，二进制是一种十分重要的基础概念。
而在二进制中进行乘法运算也是常见的操作。
本文将探讨二进制的乘法运算方法及其应用。
一、二进制概述二进制是一种由0和1组成的数字系统。
与我们熟悉的十进制不同，二进制采用了“逢二进一”的原则。
每一位上的数值表示的是2的幂次方。
例如，二进制数1011，可以表示为：(1 * 2^3) + (0 * 2^2) + (1 * 2^1) + (1 * 2^0) = 11二、二进制的乘法运算与十进制的乘法原理类似，只不过运算的基数变成了2。
下面我们以两个二进制数的乘法为例，来介绍一种简单而常用的计算方法——“逐位相乘法”。
例子：1011× 110步骤一：将被乘数（1011）的末位与乘数（110）的每一位相乘，并记录结果。
```1 0 1 1× 1 1 0----------1 0 1 1（末位）1 0 1 1----------1 1 0 1 0```步骤二：将被乘数的次低位与乘数的每一位相乘，并记录结果。
```1 0 1 1（次低位）× 1 1 0----------1 1 0 1（次低位）1 1 0 1----------1 0 1 1 0 0```步骤三：将被乘数的次高位与乘数的每一位相乘，并记录结果。
```1 0 1 1（次高位）× 1 1 0----------1 0 1 1（次高位）1 0 1 1----------1 1 0 1 0 1 0```步骤四：将被乘数的最高位与乘数的每一位相乘，并记录结果。
```1 0 1 1（最高位）× 1 1 0----------1 0 1 1（最高位）1 0 1 1----------1 1 0 1 0 1 0 1```步骤五：将所有结果相加。
```1 0 1 1（次高位）1 1 0 1（次低位）1 1 0 1（末位）+ 1 0 1 1（最高位）-----------------1 1 1 1 1 0 1 0```因此，二进制数1011乘以二进制数110等于二进制数1111010。
二进制乘法规则二进制乘法是指在二进制数系统中进行乘法运算的规则。
在二进制数系统中，只有0和1两个数字，因此乘法的运算规则也与十进制数系统中的乘法规则有所不同。
在二进制乘法中，乘数和被乘数的每一位都可以是0或1。
乘法的结果是两个二进制数相乘的积。
下面我们来详细介绍二进制乘法的规则。
1. 乘法表我们可以根据乘法表来进行二进制乘法运算。
乘法表列出了0和1相乘的结果，如下所示：0 × 0 = 00 × 1 = 01 × 0 = 01 × 1 = 1根据乘法表，我们可以得出以下结论：- 0乘以任何数都等于0；- 1乘以任何数都等于这个数本身。
2. 单位进位在二进制乘法中，当两个二进制数的位数不同时，需要进行单位进位的操作。
单位进位是指将进位的数值加到下一位的操作。
例如，当乘数为1时，被乘数的每一位都需要乘以1，并将结果相加。
如果某一位的乘积大于1，就需要进行进位操作。
3. 乘法运算步骤下面我们来看一个具体的例子来说明二进制乘法的运算步骤。
假设有两个二进制数：1011和110。
我们将乘数和被乘数对齐，如下所示：1 0 1 1× 1 1 0然后，从右到左，将乘数的每一位与被乘数相乘，并将结果写在相应的位置上：1 0 1 1× 1 1 0__________0 0 0 0 （0 × 1）1 0 1 1 （1 × 1，不需要进位）1 0 1 1 （1 × 0，不需要进位）+____________1 1 1 0 1 0 （结果）我们将所有结果相加得到最终的乘积。
在这个例子中，最终的乘积为111010。
4. 乘法规则总结通过以上例子，我们可以总结出二进制乘法的规则：- 乘数的每一位与被乘数相乘，并将结果写在相应的位置上；- 如果某一位的乘积大于1，就需要进行进位操作；- 将所有结果相加得到最终的乘积。
需要注意的是，在二进制乘法中，进位是非常重要的。
二进制数的乘法和除法运算在计算机科学和数字电路中，二进制数是一种重要的表示方式，它以0和1表示数字。
除了进行基本的加法和减法运算外，二进制数也可以进行乘法和除法运算。
本文将详细介绍二进制数的乘法和除法运算方法。
一、二进制数的乘法运算二进制数的乘法运算方法与十进制数的乘法非常类似，只是运算的基数为2。
下面以两个二进制数A和B的乘法运算来进行说明。
1. 将被乘数A和乘数B对齐，并从右向左逐位相乘。
例如，给定二进制数A=1011和B=110，将它们对齐：1011× 110-------------2. 逐位相乘，得到部分乘积。
如果某一位为0，则相应位的部分乘积为0，如果某一位为1，则相应位的部分乘积等于被乘数。
对于上述例子，我们可以进行如下计算：1011× 110-------------1011 （部分乘积1）+ 0000 （部分乘积2）+ 1011 （部分乘积3）-------------= 10011010 （乘积）3. 对所有部分乘积进行相加，得到最终的乘积。
对于上述例子，我们有：1 0 0 1 1 0 1 0+ 1 0 1 1----------------------= 1 1 0 0 0 0 1 0因此，二进制数1011乘以二进制数110的结果为1100010。
二、二进制数的除法运算二进制数的除法运算同样类似于十进制数的除法运算，下面以被除数A和除数B的除法运算来进行说明。
1. 比较被除数A的高位和除数B。
如果被除数的高位小于除数，则商的对应位为0。
如果被除数的高位大于或等于除数，则商的对应位为1，并将被除数的高位减去除数。
2. 将除数右移一位，并将商左移一位。
再将被除数的下一位与新的除数进行比较：如果被除数的下一位小于除数，则商的对应位为0。
如果被除数的下一位大于或等于除数，则商的对应位为1，并将被除数的下一位减去除数。
3. 重复上述步骤，直到被除数的所有位都比较完毕。
第4讲二进制从5幅国画，3幅油画，2幅水彩画中选取两幅不同类型的画布置教室，问有几种不同的选法？31二进制就是只用0和1两数字，在计数与计算时必须“满二进一”，即每两个相同的单位组成一个和它相邻的最高的单位。
二进制的最大特点是：每个数的各个数位上只有0或只有1两种状态。
二进制与十进制之间可以互相转化。
1，将一个二进制数写成十进制数的步骤是：（1）将二进制数的各数位上数字改写成相应的十进制数；（2）将各数位上对应的十进制数求和，所得结果就是相应的十进制数。
将十进制数改写成二进制数的过程，正好相反。
2，十进制数改写成二进制数的常用方法是：除以二倒取余数。
3，二进制数的计算法则：（1）加法法则：0＋0=0 0＋1=1 1＋0=1 1＋1=10（2）乘法法则：0×0=0 0×1=0 1×0=0 1×1=1改写成十进制数。
例1：把二进制数110（2）分析与解答：十进制有两个特点：（1）它有十个不同的数字符号；（2）满十进1。
二进制有两个特点：（1）它的数值部分，只需用两个数码0和1来表示；（2）它是“满二进一”。
改写成十进制数，只要把它写成2的幂之和的形式，然后按通常的方法把二进制数110（2）进行计算即可。
=1×22＋1×21＋0×20110（2）=1×4＋1×2＋0×1=4＋2＋0=6把下列二进制数分别改写成十进制数。
（1）100（2）（2）1001（2）例2：把十进制数38改写成二进制数。
分析与解答：把十进制数改写成二进制数，可以根据二进制数“满二进一”的原则，用2连续去除这个十进制数，直到商为零为止，把每次所得的余数按相反的顺序写出来，就是所化成的二进制数，这种方法叫做“除以二倒取余数”。
2 38 02 19 (1)2 9 (1)2 4 02 2 01 (1)即：38（10）=100110（2）把下列十进制数分别改写成二进制数。
二进制补码乘法除法二进制补码乘法除法1)二进制乘法 (1) Binary Multiplication)Binary numbers can be multiplied using two methods,二进制数可以使用两种方法相乘，1.Paper method: Paper method is similar tomultiplication of decimal numbers on paper.纸法:纸法类似于十进制数在纸上相乘。
puter method: Computer method is used bydigital machines to multiply the binary numbers.计算机方法:数字计算机使用计算机方法乘以二进制数。
However, both these methods follow the same rule of multiplication which is,但是，这两种方法都遵循相同的乘法规则，即0 * 0 = 00 * 1 = 01 * 0 = 01 * 1 = 1Note: If two binary numbers are of 'n' bits each in magnitude, then their product can be maximum '2n' bits long in magnitude.注意：如果两个二进制数的大小均为'n'位，则它们的乘积最大为'2n'位。
长手乘法/纸张方法 (Long Hand Multiplication/Paper Method)The long Hand Multiplication technique is similar to decimal multiplication that we do on paper.长手乘法技术类似于我们在纸上做的十进制乘法。
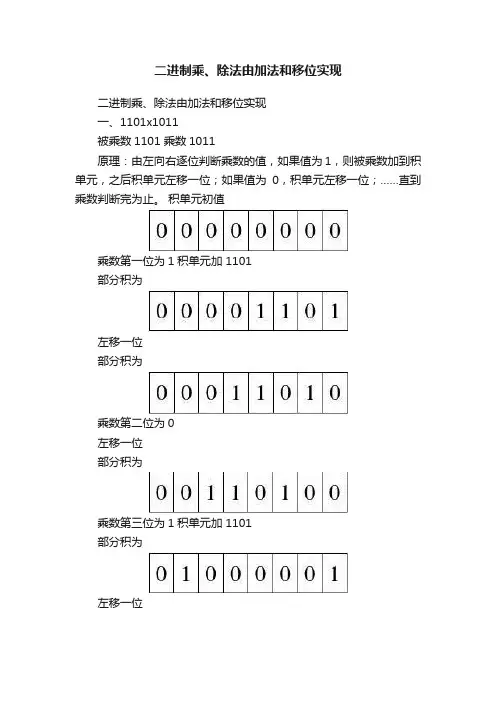
二进制乘、除法由加法和移位实现二进制乘、除法由加法和移位实现一、1101x1011被乘数1101 乘数1011原理：由左向右逐位判断乘数的值，如果值为1，则被乘数加到积单元，之后积单元左移一位；如果值为0，积单元左移一位；……直到乘数判断完为止。
积单元初值乘数第一位为1积单元加 1101部分积为左移一位部分积为乘数第二位为0左移一位部分积为乘数第三位为1积单元加 1101部分积为左移一位乘数第四位为1积单元加 1101部分积为此时乘数判断完毕，不再移位。
积为10001111。
二、1000001÷101被除数1000001 除数101原理：设被除数为A 、除数为B 、商为Q （初值为0）、余数为R （初值为0）。
设置一个Q 单元和R 单元，A 由高位至低位依次左移进入R 单元。
每次移位进入后比较R 单元和B 的值，如果R ≥B ，则将这一位的商单元的值置1，然后从R 中减去B （做补码加法运算），否则不做操作。
商单元与移位同步进行。
……直到A 全部进入R 单元为止。
此时Q 中存放商、R 中存放余数。
A=1000001，B=101，B 的补码1011R 初值Q 初值A=1000001左移入R ，A=000001 R=B=101R<b< p="">Q=A=000001左移入R，A=00001 R=B=101R<b< p="">Q=A=00001左移入R，A=0001 R=B=101R<b< p="">Q=A=0001左移入R ，A=001R=B=101 R ≥B ，则R-B=R+（-B ）1000+1011=0011R=Q=A=001左移入R ，A=01 R=B=101R ≥B ，则R-B=R+（-B ）0110+1011=0001 R=Q=A=01左移入R ，A=1 R=B=101R<b< p="">Q=A=1左移入R R=B=101R ≥B ，则R-B=R+（-B ）0101+1011=0000 R=Q=</b<></b<></b<></b<>。
