理论力学-刚体静力学专门问题
- 格式:doc
- 大小:163.50 KB
- 文档页数:7

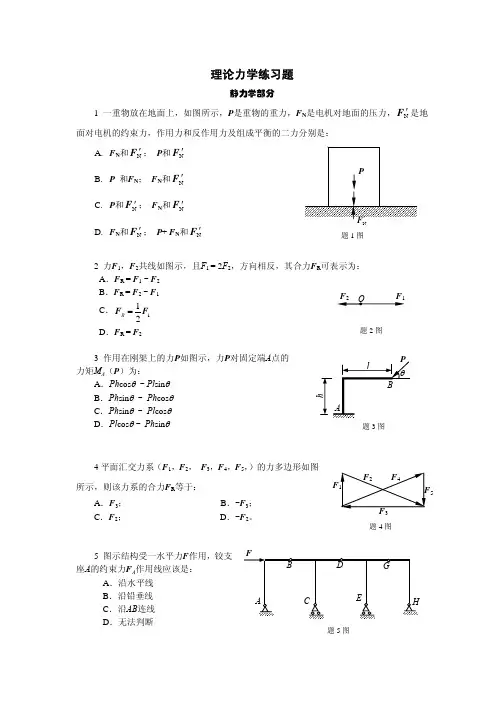
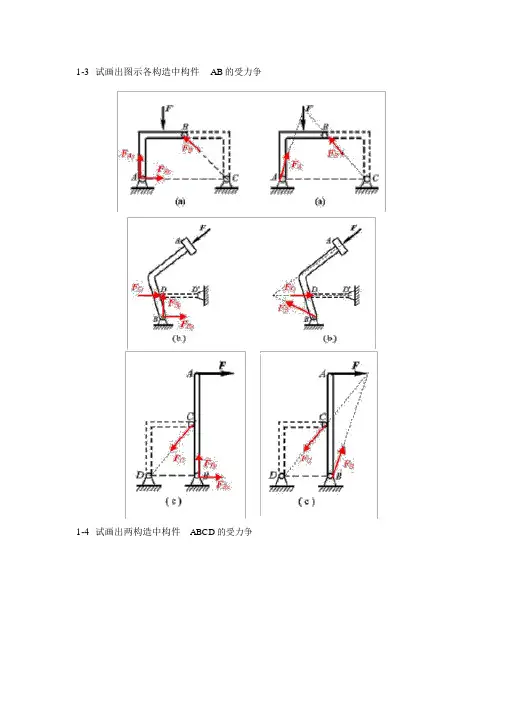
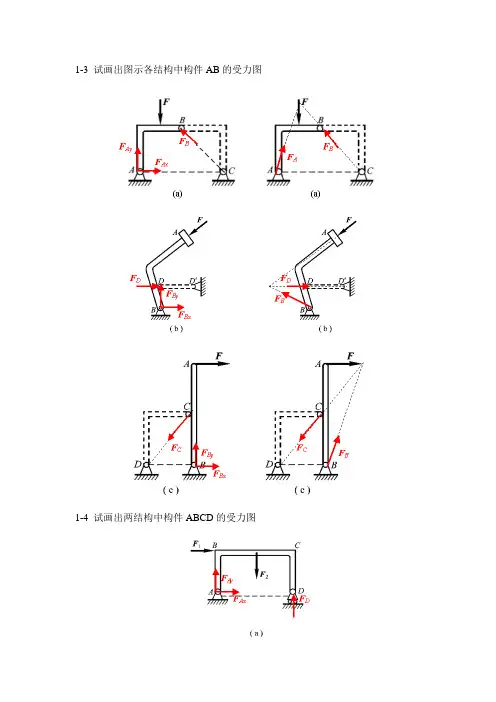
1-3 试画出图示各构造中构件AB的受力争1-4 试画出两构造中构件ABCD的受力争1-5 试画出图 a 和 b 所示刚系统整体各个构件的受力争1-5a1-5b1- 8 在四连杆机构的ABCD的铰链 B 和 C上分别作用有力F1和 F2,机构在图示位置均衡。
试求二力F1和 F2之间的关系。
解:杆 AB,BC, CD为二力杆,受力方向分别沿着各杆端点连线的方向。
解法 1( 分析法 )假定各杆受压,分别选用销钉 B 和 C 为研究对象,受力以下图:yyFBCC xB Fo45BCx30o o F60F2CDF AB F1由共点力系均衡方程,对 B 点有:F x0F2F BC cos4500对 C点有:F x0FBC F1 cos3000解以上二个方程可得:F12 6F2 1.63F23解法 2( 几何法 )分别选用销钉 B 和 C 为研究对象,依据汇交力系均衡条件,作用在 B 和C 点上的力构成关闭的力多边形,以下图。
F F2BCF AB o30o45CD60oFF BC F1对 B 点由几何关系可知:F2F BC cos450对 C 点由几何关系可知:F BC F1 cos300解以上两式可得:F1 1.63F22-3 在图示构造中,二曲杆重不计,曲杆AB 上作用有主动力偶 M。
试求 A 和 C 点处的拘束力。
解: BC为二力杆 ( 受力以下图 ) ,故曲杆 AB 在 B 点处遇到拘束力的方向沿BC 两点连线的方向。
曲杆AB遇到主动力偶M的作用, A 点和 B 点处的拘束力一定构成一个力偶才能使曲杆AB保持均衡。
AB受力以下图,由力偶系作用下刚体的均衡方程有(设力偶逆时针为正):M0 F A10a sin(450 )M 0F A0.354Ma此中:tan 1。
对 BC杆有:F C FB F A0.354M 3aA,C两点拘束力的方向以下图。
2-4解:机构中 AB杆为二力杆,点A,B 出的拘束力方向即可确立。
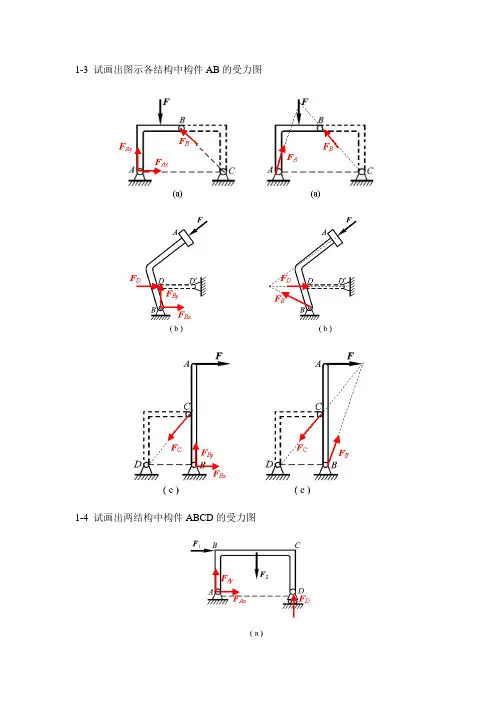
1-3 试画出图示各结构中构件AB的受力图1-4 试画出两结构中构件ABCD的受力图1-5 试画出图a和b所示刚体系整体各个构件的受力图1-5a1-5b1- 8在四连杆机构的ABCD 的铰链B 和C 上分别作用有力F 1和F 2,机构在图示位置平衡。
试求二力F 1和F 2之间的关系。
解:杆AB ,BC ,CD 为二力杆,受力方向分别沿着各杆端点连线的方向。
解法1(解析法)假设各杆受压,分别选取销钉B 和C 为研究对象,受力如图所示:由共点力系平衡方程,对B 点有:∑=0x F 045cos 02=-BC F F对C 点有:∑=0x F 030cos 01=-F F BC解以上二个方程可得:22163.1362F F F ==解法2(几何法)分别选取销钉B 和C 为研究对象,根据汇交力系平衡条件,作用在B 和C 点上的力构成封闭的力多边形,如图所示。
对B 点由几何关系可知:0245cos BC F F =对C 点由几何关系可知:0130cos F F BC =解以上两式可得:2163.1F F =2-3 在图示结构中,二曲杆重不计,曲杆AB 上作用有主动力偶M 。
试求A 和C 点处的约束力。
解:BC 为二力杆(受力如图所示),故曲杆AB 在B 点处受到约束力的方向沿BC 两点连线的方向。
曲杆AB 受到主动力偶M 的作用,A 点和B 点处的约束力必须构成一个力偶才能使曲杆AB 保持平衡。
AB 受力如图所示,由力偶系作用下刚体的平衡方程有(设力偶逆时针为正):0=∑M 0)45sin(100=-+⋅⋅M a F A θ aM F A 354.0=其中:31tan =θ。
对BC 杆有:aM F F F A B C 354.0=== A ,C 两点约束力的方向如图所示。
2-4FF解:机构中AB杆为二力杆,点A,B出的约束力方向即可确定。
由力偶系作用下刚体的平衡条件,点O,C处的约束力方向也可确定,各杆的受力如图所示。

理论力学中的静力学平衡条件与应用在理论力学中,静力学是研究物体处于平衡状态时的力学原理和条件。
静力学平衡条件是判断物体是否处于平衡状态的基本准则。
本文将对理论力学中的静力学平衡条件进行分析,并探讨其在实际应用中的意义。
1. 刚体静力学平衡条件在理论力学中,刚体是指其形状和体积在外力作用下保持不变的物体。
刚体静力学平衡条件是判断刚体是否处于平衡状态的基本原理。
根据刚体静力学平衡条件,一个刚体处于平衡状态需要满足以下两个条件:- 力的平衡条件:合力为零。
即作用在刚体上的所有力的矢量和等于零。
- 力矩的平衡条件:合力矩为零。
即作用在刚体上的所有力矩的代数和等于零。
2. 非刚体静力学平衡条件在实际应用中,许多物体并不是刚体,而是由多个部分组成的弹性体。
对于非刚体的情况,同样存在静力学平衡条件来判断物体是否处于平衡状态。
非刚体静力学平衡条件包括以下几个方面:- 力的平衡条件:合力为零。
即作用在物体上的合外力等于零,物体保持静止。
- 力矩的平衡条件:合力矩为零。
即作用在物体上的合外力矩等于零,物体不会产生旋转。
- 形变平衡条件:物体内部各部分之间应满足力的平衡条件和形变的平衡条件,使得物体整体保持平衡。
3. 静力学平衡条件的应用静力学平衡条件在工程学、建筑学和力学等领域有着广泛的应用。
以下是一些典型的应用场景:- 结构力学:静力学平衡条件可用于判断建筑物、桥梁和机械结构等是否处于稳定的平衡状态,从而确保其安全性。
- 弹性体力学:静力学平衡条件可用于分析和设计材料的弹性性能,求解材料的应力和变形分布。
- 静力学问题求解:通过应用静力学平衡条件,可以解决一些静力学问题,如悬臂梁的荷载计算、桥梁上的力的平衡等。
4. 实例分析以建筑结构为例,应用静力学平衡条件可以分析房屋的支撑结构是否稳定。
在设计房屋的支撑结构时,需要考虑以下几个方面:- 力的平衡条件:房屋所受的重力需要通过支撑结构的柱子、墙壁等来承受,使得合力为零,保持平衡。


第一章静力学基础一、是非题1.力有两种作用效果,即力可以使物体的运动状态发生变化,也可以使物体发生变形。
()2.在理论力学中只研究力的外效应。
()3.两端用光滑铰链连接的构件是二力构件。
()4.作用在一个刚体上的任意两个力成平衡的必要与充分条件是:两个力的作用线相同,大小相等,方向相反。
()5.作用于刚体的力可沿其作用线移动而不改变其对刚体的运动效应。
()6.三力平衡定理指出:三力汇交于一点,则这三个力必然互相平衡。
()7.平面汇交力系平衡时,力多边形各力应首尾相接,但在作图时力的顺序可以不同。
()8.约束力的方向总是与约束所能阻止的被约束物体的运动方向一致的。
()二、选择题1.若作用在A点的两个大小不等的力F1和F2,沿同一直线但方向相反。
则其合力可以表示为。
①F1-F2;②F2-F1;③F1+F2;2.作用在一个刚体上的两个力F A、F B,满足F A=-F B的条件,则该二力可能是。
①作用力和反作用力或一对平衡的力;②一对平衡的力或一个力偶。
③一对平衡的力或一个力和一个力偶;④作用力和反作用力或一个力偶。
3.三力平衡定理是。
①共面不平行的三个力互相平衡必汇交于一点;②共面三力若平衡,必汇交于一点;③三力汇交于一点,则这三个力必互相平衡。
4.已知F1、F2、F3、F4为作用于刚体上的平面共点力系,其力矢关系如图所示为平行四边形,由此。
①力系可合成为一个力偶;②力系可合成为一个力;③力系简化为一个力和一个力偶;④力系的合力为零,力系平衡。
5.在下述原理、法则、定理中,只适用于刚体的有。
①二力平衡原理;②力的平行四边形法则;③加减平衡力系原理;④力的可传性原理;⑤作用与反作用定理。
三、填空题1.二力平衡和作用反作用定律中的两个力,都是等值、反向、共线的,所不同的是。
2.已知力F沿直线AB作用,其中一个分力的作用与AB成30°角,若欲使另一个分力的大小在所有分力中为最小,则此二分力间的夹角为度。
1-3 试画出图示各结构中构件AB的受力图1-4 试画出两结构中构件ABCD的受力图1-5 试画出图a和b所示刚体系整体各个构件的受力图1-5a1-5b1- 8在四连杆机构的ABCD 的铰链B 和C 上分别作用有力F 1和F 2,机构在图示位置平衡。
试求二力F 1和F 2之间的关系。
解:杆AB ,BC ,CD 为二力杆,受力方向分别沿着各杆端点连线的方向。
解法1(解析法)假设各杆受压,分别选取销钉B 和C 为研究对象,受力如图所示:由共点力系平衡方程,对B 点有:∑=0x F 045cos 02=-BC F F对C 点有:∑=0x F 030cos 01=-F F BC解以上二个方程可得:22163.1362F F F ==F 2F BCF ABB45oy xF BCF CDC60o F 130oxy解法2(几何法)分别选取销钉B 和C 为研究对象,根据汇交力系平衡条件,作用在B 和C 点上的力构成封闭的力多边形,如图所示。
对B 点由几何关系可知:0245cos BC F F =对C 点由几何关系可知:0130cos F F BC =解以上两式可得:2163.1F F =2-3 在图示结构中,二曲杆重不计,曲杆AB 上作用有主动力偶M 。
试求A 和C 点处的约束力。
解:BC 为二力杆(受力如图所示),故曲杆AB 在B 点处受到约束力的方向沿BC 两点连线的方向。
曲杆AB 受到主动力偶M 的作用,A 点和B 点处的约束力必须构成一个力偶才能使曲杆AB 保持平衡。
AB 受力如图所示,由力偶系作用下刚体的平衡方程有(设力偶逆时针为正):0=∑M 0)45sin(100=-+⋅⋅M a F A θ aM F A 354.0=其中:31tan =θ。
对BC 杆有:aM F F F A B C 354.0=== A ,C 两点约束力的方向如图所示。
2-4F BCF 60oF 130oF 2F BCF AB45o解:机构中AB 杆为二力杆,点A,B 出的约束力方向即可确定。

静力学知识要点绪论:1.理论力学研究对象:刚体;物体的运动效应(外效应)。
静力学:物体在力的作用下保持平衡条件;2. 三部分内容的研究对象:运动学:只从几何角度研究物体的运动,不研究其运动产生的原因;动力学:研究受力物体力与运动之间的关系;静力学第一章静力学公理和物体受力分析1.四大公理和二大推论的具体内容。
(熟记+理解)2.二力杆的正确判断,受力方向的确定。
3.三力平衡汇交定理的应用。
4.各种常用的约束和约束反力(I)光滑接触面约束作用点在接触点,方向沿公法线,指向受力物体,受压。
(II)柔索约束作用点在接触点,方向沿绳索背离物体,受拉。
(III)光滑圆柱铰链约束a)中间铰:方向不定用两个正交分力来表示;FxFb)固定铰:方向不定用两个正交分力来表示;Fc)滚动铰支座:限制法线方向运动,通过铰链中心垂直于支撑面,指向不定;N F(IV) 轴承约束a) 向心轴承:方向不定,用两个正交分力来表示;FFb) 止推轴承:三个正交分力;y Fz Fx F(V) 固定端约束:5. 正确画出物体或整体的受力分析图:例题1-1,1-2,1-4(注意内力\外力,作用力\反作用力;正确识别二力杆);6. P21页 思考题 1-2、3、4 作业题:1-1(c 、e 、f 、j )、1-2(c 、f )第二章 平面力系几何条件:力多边形自行封闭;1. 平面汇交力系平衡条件 解析条件: Fx ∑=0Fy ∑=02. 应用平衡条件解题(例题2-3)3. 平面力偶系 力矩的定义,方向判别(为负)平行也无合力。
平面力偶的的两个要素:力偶矩的大小;力偶的转向。
力偶的等效定理:力偶可在平面内任意移动,只要力偶矩的大小、方向不变。
i M ∑=0. 具体应用(例题2-5、2-6)4. 平面任意力系的简化 力的平移定理 P39 简化结果讨论 P41-425. 平面 充要条件:R F =0, Mo=0任意 平衡方程:一矩式:Fx ∑=0 Fy ∑=0()O M F ∑=0 (0点任意取) 力系 二矩式:()A M F ∑=0()B M F ∑=0 Fx ∑=0 (x 不垂直AB 连线) 平衡 : ()A M F ∑=0 ()B M F ∑=0()C M F ∑=0(ABC 不共线) P45 例2-8、2-96. 均布载荷 —— 集中力 大小: 围成图形的面积方向:与q 一致作用点:围成图形的几何中心ql l 31 ql 21q =F 7. 物系的平衡 静定/超静定判别未知量多物系平衡求解思路:以整体为对象———— 选个体为对象求个别未知量具体应用:P51. 例2-11、2-12、2-168. 桁架的内力计算 节点法 例2-18截面法 例 2-199.各种平面力系独立平衡方程数目: 平面任意力系(3个);平面汇交力系(2个);平面力偶系(1个);平面平行力系(2个)各种约束 分析力系类型10.静力学步骤:研究对象 画受力分析 列方程 求解 类型反力确定 确定独立方程数目思考题:P61 2-2、2-3、2-5作业题:2-1、2-3、2-7、2-8c 、2-12、2-14b 、2-20、2-21、2-51、2-57第三章 空间力系1. 空间汇交力系 力在坐标轴上的投影 平衡条件:∑Fx=0、∑Fy=0、∑Fz=0P81 例3-2、3-32. 空间力对点之矩和力对轴之矩力对点之矩:()M O ⨯= 为矢量力多轴之矩:x y yF x —F M Z =⎪⎪⎭⎫ ⎝⎛ P84 公式3-12 例3-4 ()[]()M F M Z Z =0 Z 必须经过O 点3. 空间力偶 AB ⨯=r 三要素:力偶矩大小;力偶矢量方向(与作用面垂直);作用面上转向。

理论力学绪论理论力学:是研究物体机械运动一般规律的科学。
机械运动:物体在空间的位置随时间的改变。
静力学:主要研究受力物体平衡时作用力所应满足的条件;同时也研究物体受力的分析方法,以及力系简化的方法。
运动学:只从几何的角度来研究物体的运动(如轨迹、速度、加速度等),而不研究引起物体运动的物理原因。
动力学:研究受力物体的运动和作用力之间的关系。
静力学引言静力学是研究物体的受力分析、力系的等效替换(或简化)、建立各种力系的平衡条件的科学。
1.静力学研究的三个问题⑴物体的受力分析:分析物体(包括物体系)受哪些力,每个力的作用位置和方向,并画出物体的受力图。
⑵力系的等效替换(或简化):用一个简单力系等效代替一个复杂力系。
⑶建立各种力系的平衡条件:建立各种力系的平衡条件,并应用这些条件解决静力学实际问题。
2.基本概念平衡:物体相对惯性参考系(如地面)静止或作匀速直线运动。
质点:具有质量,而其形状、大小可以不计的物体。
质点系:具有一定联系的若干质点的集合。
刚体:在力的作用下,其内部任意两点间的距离始终保持不变的物体。
力:物体间相互的机械作用,作用效果使物体的机械运动状态发生改变。
力的三要素:大小、方向和作用线。
力系:是指作用在物体上的一群力。
等效力系:对同一刚体产生相同作用效应的力系。
合力:与某力系等效的力。
平衡力系:对刚体不产生任何作用效应的力系。
共点力系:力的作用线汇交于一点。
平面汇交(共点)力系:力的作用线在同一平面内。
空间汇交(共点)力系:力的作用线不在同一平面内。
力系的分类:按作用线所在的位置,分为平面力系和空间力系;按作用线之间的相互关系,分为共线力系、平行力系、汇交力系和任意力系。
第一章静力学公理和物体的受力分析§1-1 静力学公理公理1 力的平行四边形法则作用在物体上同一点的两个力,可以合成为一个合力。
合力的作用点也在该点,合力的大小和方向,由这两个力为边构成的平行四边形的对角线确定。
重修班静力学复习题一、是非判断题(10分)1.若两个力的力矢量相等,12F F =r r,则两个力等效。
(×) (若两个力偶的力偶矩矢相等,12M M =r r,则两个力偶等效)(√)2.根据力的可传性原理,可以将构架ABC 上的作用在AB 杆的力F 移至AC 杆图示位置。
2. 图中圆盘处于平衡状态,说明力偶M 与力F 等效。
(×)3. 空间中三个力构成一平衡力系,此三力必共面。
(√)4. 空间任意力系向某一点O 简化,主矢为零,则主矩与简化中心无关。
(√)5. 空间任意力系总可以用二个力来平衡。
(√)6. 力与轴共面则力对轴的矩为零。
(√)7. 空间平行力系不可能简化为力螺旋。
(√)二 选择题(15分)1不经计算,可直接判断出图示桁架结构的零杆数目为 C 个。
A 2; B 3;C 4;D 5PA B C D E F G F F期未试题A :(6分)图示简支桁架,已知力P 、Q ,长度a ,刚杆1,2,3的内力分别为=1T ( 0 ),=2T ( -P ),=3T ( 0 )。
期未试题B (6分) 图示悬臂桁架受到大小均为F 的三个力作用,则杆1内力大小为( 0 ),杆2内力大小为( -F ),杆3内力大小为( 0 )。
2 物块重力大小为5kN G =,与水平面间的摩擦角为020f ϕ=,今用与铅垂线成025角的力F 推动物块,若5kN F G ==,则物块A 。
A 保持静止;B 处于临界状态;C 向右加速滑动;D 向右匀速滑动期未试题:2 物块重力大小为5kN G =,与水平面间的摩擦角为030f ϕ=,今用与铅垂线成050角的力F 推动物块,若5kN F G ==,则物块( A )。
补考试题:物块重力大小为5kN G =,与水平面间的摩擦角为030f ϕ=,今用与铅垂线成065角的力F 推动物块,若5kN F G ==,则物块( C )。
第二、1题图 第二、1题图GF 065G F 025G F 0502fθϕ≤3在正方体的一个侧面,沿AB方向作用一集中力F,则该力对坐标轴的力矩大小为 D 。
一、判断题:1. 力系的合力一定比各分力大。
( )2. 作用与反作用定律只适用于刚体。
〔 〕3. 在同一平面的两个力偶,只要这两个力偶的力偶矩大小相等,那么这两个力偶必然等效。
〔 〕4. 力对于一点的矩不因力沿其作用线移动而改变。
〔 〕5、作用在一个物体上有三个力,当这三个力的作用线汇交于一点时,那么此力系必然平衡。
〔 〕6、二力构件的约束反力,其作用线是沿二受力点连线,指向可任意假设。
( )7、一平面力系的主矢不为零,那么此力系分别向A 、B 两点简化,结果一样。
( )8、由于零力杆不承受力,所以它是无用杆,它的存在与否对桁架构造没有影响。
( )9、作用在一个刚体上的任意两个力成平衡的必要与充分条件是:两个力的作用线一样,大小相等,方向相反。
〔 〕10、在有摩擦的情况下,全约束力与法向约束力之间的夹角称为摩擦角。
〔 〕 11、假设两个力的大小相等,其在同一轴上的投影也一定相等。
( ) 12、力偶无合力,就是说力偶的合力等于零。
( ) 13、但凡两点受力的构件都是二力构件。
( )14、光滑铰链类约束反力,可以用任意两个相互垂直的分力表示。
( )15、在保持力偶矩不变的前提下,力偶可在同一平面,或相互平行的平面任意移动,不改变力偶对刚体的作用效果。
( )16、加减平衡力系原理不但适用于刚体,而且适用于变形体。
〔 〕 17、一力F,沿某一轴的投影是唯一的;沿该方向的分力也是唯一的。
( ) 18.平面任意力系平衡的充要条件是力系的合力等于零。
〔 〕19.假设某力系在任意轴上的投影都等于零,那么该力系一定是平衡力系。
〔 〕 20.不管什么物体,其重心和形心总是在同一点上。
〔 〕 21、力偶只能使刚体转动而不能使刚体移动。
( )22、在任何情况下,摩擦力的大小总等于摩擦系数与正压力的乘积。
〔 〕 23、处于平衡状态的三个力必须共面 〔 〕 24、只要两力大小相等,方向相反,该两力就组成一力偶。
〔〕25、摩擦力是未知约束反力,其大小和方向完全可以平衡方程来确定。
第四章刚体静力学专门问题一、是非题1 .摩擦力的方向总是和物体运动的方向相反。
()2.摩擦力是未知约束反力,其大小和方向完全可以由平衡方程来确定。
()3.静滑动摩擦系数的正切值等于摩擦角。
()4 .在任何情况下,摩擦力的大小总等于摩擦力系数与正压力的乘积。
()5.当考虑摩擦时,支承面对物体的法向反力 N 和摩擦力F 的合力R 与法线的夹角力称为摩擦角。
6. 只要两物体接触面之间不光滑,并有正压力作用,则接触面处摩擦力一定不为零。
7. 在求解有摩擦的平衡问题(非临界平衡情况)时,静摩擦力的方向可以任意假定,而其大小一般是未知的O8. 滚阻力偶的转向与物体滋动的转向相反。
二、选择题1. 五根等长的细直杆皎接成图示杆系结构,各杆重量不计若R A =P C = P,且垂直 BD 则杆BD 的内力 S BE =① -P (压); ② -V3P (压); ③-J3P/3 (压); ④—J3P /2 (压)。
2. 图示(a )、(b )两结构受相同的荷载作用,若不计各杆自重,则两结构 A 支座反 力, B 支座反务 ,杆 AC 内力,杆 BC 内力。
① 相同; r F②不同。
[入 甲3. 若斜面倾角为a ,物体与斜面间的摩擦系数为 f, -欲使物体能静止在斜面上,则必须满足的条件 些 ______________________ 盐 W_14. 已知杆OA 重W 物块M 重Q 杆与物块间有摩擦,而物体 与地面间的摩擦略去不计。
当水平力 P 增大而物块仍然保持平衡 时,杆对物体M 的正压力。
①由小变大;① tg f ② tg f③ tg④ tgV a ;> a ;a V f ;a > f o② 由大变小; ③ 不变。
5 .物A 重100KN,物B 重25KN A 物与地面的摩擦系数为 0.2 ,滑轮处摩擦不计。
则物体 A 与地面间的摩擦 为① 20KN ; ② 16KN ; ③ 15KN ;④ 12KN 。
判断题静力学1. 凡在二力作用下的物体称为二力构件。
2. 在两个力的作用下,使刚体处于平衡的必要条件与充分条件是这两个力等值反向,共线。
3. 力的可传性适用于一般物体4. 合力比分力大5. 凡矢量都可以用平行四边形法则合成6. 汇交的三个力是平衡力系7. 约束力是与主动力有关的力系8. 作用力与反作用力是平衡力系9. 画受力图时,对一般物体力可沿作用线任意的滑动10. 受力图中不应出现内力11. 汇交力系平衡的几何条件是力的多边形封闭12. 两个力F 1,F 2在同一轴上的投影相等,则这两个力大小一定相等13. 力F 在某一轴上的投影等于零,则该力一定为零14. 合力总是大于分力15. 平面汇交力系求合力时,作图时力序可以不同,其合力不变16. 力偶使刚体只能转动,而不能移动17. 任意两个力都可以合成一个力18. 力偶中的两个力在任意直线段上投影的代数和恒为零19. 平面力偶距的大小与矩心点的位置有关20. 力沿其作用线任意滑动不改变它对同一点的矩21. 平面任意力系的主失F R ’=1ni F =∑i ≠0时,则力系一定简化为一个力偶 22. 平面任意力系中只要主失F R ’=1ni F =∑i ≠0,力系总可以简化为一个力23. 平面任意力系中主失的大小与简化中心的位置有关24. 平面任意力系中主矩的大小与简化中心的位置无关25. 作用在刚体上的力可以任意移动,不需要附加任何条件26. 作用在刚体上的任意力系若力的多边形自行封闭,则该力系一定平衡27. 平面任意力系向任意点简化的结果相同,则该力系一定平衡28. 求平面任意力系的平衡时,每选一次研究对象,平衡方程的数目不受限制29. 桁架中的杆是二力杆30. 静滑动摩擦力F S 应是一个范围值31.空间力偶中的两个力对任意投影轴的代数和恒为零32.空间力对点的矩在任意轴上的投影等于力对该轴的矩33.空间力系的主失是力系的合力34.空间力系的主矩是力系的合力偶矩35.空间力系向一点简化所得的主失和主矩与原力系等效36.空间力系的主失为零,则力系简化为力偶37.空间汇交力系的平衡方程只有3个投影形式的方程38.空间汇交力系的三个投影形式的平衡方程,对投影轴没有任何限制39.空间力偶等效只需力偶矩失相等40.空间力偶系可以合成为一个合力运动学1.某瞬时动点的速度为零,则动点的加速度必为零2.某瞬时动点的加速度为零,则动点的速度必为零3.切向加速度是表示动点速度方向对时间的导数4.法向加速度是表示动点速度大小对时间的导数5.点做曲线运动时,法向加速度是不等于零的6.点做直线运动时,法向加速度是等于零的7.点做直线运动时,切向加速度是等于零的8.轨迹曲线的曲率半径为无穷大时,点做直线运动9.点做匀变速运动时,切向加速度大小保持不变10.法向加速度的方向是指向轨迹曲线的曲率中心11.平移刚体上各点的轨迹一定是直线12.在某一瞬时刚体上各点的速度相等,刚体做平移运动13.某瞬时刚体有两点的速度相等,刚体做平移运动14.研究刚体的平移运动用点的运动学知识即可15.平移刚体上各点的轨迹形状相同,同一瞬时刚体上各点的速度相等,各点的加速度相等16.刚体在运动的过程中,存在一条不动的直线,则刚体做定轴转动17.刚体做定轴转动时各点的速度大小与到转轴的距离成正比,各点的加速度大小与到转轴的距离成反比18.刚体做定轴转动时法向加速度a n=r2ω19.齿轮传递时其角速度的比等于半径的正比20.刚体做定轴转动时角速度与角加速度同号时,刚体做加速转动21.绝对运动是运动相对于定系的运动22.相对运动是运动相对于动系的运动23.牵连运动是动点相对于动系的运动24. 动点的绝对运动看成是动点的相对运动和牵连运动的合成25. 动点相对速度对时间的导数等于动点的相对加速度26. 在一般情况下,某瞬时动点的绝对加速度等于动点的相对加速度和牵连加速度的矢量和27. 刚体平面运动为其上任意一点与某一固定平面的距离始终平行的运动28. 平面图形的运动可以看成是随着基点的平移和绕基点转动的合成29. 平面图形上任意两点的速度在某固定轴上投影相等30. 平面图形随基点平移的速度和加速度与基点的选择有关31. 平面图形绕基点转动的角速度和角加速度与基点的选择有关32. 速度瞬心点处的速度为零,加速度也为零33. 刚体的平移也是平面运动动力学1.质点受到的力越大,则速度越大 2.质量是物体的惯性量度 3.质点运动方向与所受的力同向 4.若质点不受力,则质点做惯性运动 5. 牛顿定律适合于任何坐标系6. 质点的动量与冲量是等价的物理量7. 质点系的动量等于外力的主失8. 质点系动量守恒是指质点系内各质点的动量不变9. 质心运动守恒是指质心位置不变10. 质点系动量的变化只与外力有关,与内力无关11. 质点系动量矩定理d/dt*L 0=1n i M =∑0(F i (e))中的矩心点对任意点都成立12. 质点系动量矩的变化与外力有关,与内力无关13. 质点系对某点动量矩守恒,则对过该点的任意轴也守恒14. 当质心的动量与某轴平行时,则质点对该轴的动量矩恒为零15. 质心轴的转动惯量是所有平行于质心轴转动惯量的最大值16. 圆轮纯滚动时,与地面接触点的法向约束力和滑动摩擦力均不做功17. 理想约束,其约束力作功之和恒等于零18. 质点系动能的变化与作用在质点系上的外力有关,与内力无关19. 动能定理的方程是矢量式20.弹簧由其自然位置拉长10cm,再拉长10cm,在这两个过程中弹力作功相等。
第四章 刚体静力学专门问题一、是非题1.摩擦力的方向总是和物体运动的方向相反。
( )2.摩擦力是未知约束反力,其大小和方向完全可以由平衡方程来确定。
( )3.静滑动摩擦系数的正切值等于摩擦角。
( )4.在任何情况下,摩擦力的大小总等于摩擦力系数与正压力的乘积。
( )5.当考虑摩擦时,支承面对物体的法向反力N 和摩擦力的合力与法线的夹角φ称为摩擦角。
( )6.只要两物体接触面之间不光滑,并有正压力作用,则接触面处摩擦力一定不为零。
( )7.在求解有摩擦的平衡问题(非临界平衡情况)时,静摩擦力的方向可以任意假定,而其大小一般是未知的。
( )8.滚阻力偶的转向与物体滋动的转向相反。
( )二、选择题1.五根等长的细直杆铰接成图示杆系结构,各杆重量不计若P A =P C =P ,且垂直BD 。
则杆BD 的内力S BD = 。
① -P (压); ②P 3-(压); ③P 3-/3(压); ④P 3-/2(压)。
2.图示(a )、(b )两结构受相同的荷载作用,若不计各杆自重,则两结构A 支座反力 ,B 支座反务 ,杆AC 内力 ,杆BC 内力 。
① 相同;② 不同。
3.若斜面倾角为α,物体与斜面间的摩擦系数为f ,欲使物体能静止在斜面上,则必须满足的条件是 。
① tg f ≤α;② tg f >α;③ tg α≤f ;④ tg α>f 。
4.已知杆OA 重W ,物块M 重Q 。
杆与物块间有摩擦,而物体与地面间的摩擦略去不计。
当水平力P 增大而物块仍然保持平衡时,杆对物体M 的正压力 。
① 由小变大;②由大变小;③不变。
5.物A重100KN,物B重25KN,A物与地面的摩擦系数为0.2,滑轮处摩擦不计。
则物体A与地面间的摩擦力为。
① 20KN;② 16KN;③ 15KN;④ 12KN。
6.四本相同的书,每本重G,设书与书间的摩擦系数为0.1,书与手间的摩擦系数为0.25,欲将四本书一起提起,则两侧应加之P力应至少大于。
① 10G;② 8G;③ 4G;④ 12.5G。
三、填空题1.图示桁架中,杆①的内力为;杆②的内力为。
2.物体受摩擦作用时的自锁现象是指。
3.已知砂石与皮带间的摩擦系数为f=0.5,则皮带运输机的输送送带的最大倾角α。
4.物块重W=50N,与接触面间的摩擦角φm=30°,受水平力Q作用,当Q=50N时物块处于(只要回答处于静止或滑动)状态。
当Q= N时,物块处于临界状态。
5.物块重W=100KN,自由地放在倾角在30°的斜面上,若物体与斜面间的静摩擦系数f=0.3,动摩擦系数f‘=0.2,水平力P=50KN,则作用在物块上的摩擦力的大小为。
6.均质立方体重P,置于30°倾角的斜面上,摩擦系数f=0.25,开始时在拉力T作用下物体静止不动,逐渐增大力T,则物体先(填滑动或翻倒);又,物体在斜面上保持静止时,T的最大值为。
四、计算题1.图示桁架中已知P1=P2=P=1000KN,试求AC、BC、BD三杆的内力。
2.在图示平面桁架中,已知:P、L。
试求CD杆的内力。
3.图示桁架。
已知:a=2m,b=3m,P1=P2=P=10KN。
试求1、2杆的内力。
4.在图示物块中,已知:Q、θ,接触面间的摩擦角φM。
试问:①β等于多大时拉动物块最省力;②此时所需拉力P为多大。
5.半圆柱体重P,重心C到圆心O点的距离为α=4R/(3π),其中R为半圆柱半径,如半圆柱体与水平面间的静摩擦系数为f。
试求半圆柱体刚被拉动时所偏过的角度θ。
6.图示均质杆,其A端支承在粗糙墙面上,已知:AB=40cm,BC=15cm,AD=25cm,系统平衡时θmin=45°。
试求接触面处的静摩擦系数。
7.已知:物块A、B均重G=10N,力P=5N,A与B、B与C间的静摩擦系数均为f=0.2。
①判断两物块能否运动;②试求各物块所受的摩擦力。
8.一均质物体尺寸如图,重P=1KN,作用在C点,已知:物体与水平地面摩擦f=0.3。
求使物体保持平衡所需的水平力Q的最大值。
9.在图示桌子中,已知:重P,尺寸L1、L2。
若桌脚与地面间的静摩擦系数为f。
试求桌子平衡时,水平拉力应满足的条件。
10.均质杆AD重W,BC杆重不计,如将两杆于AD的中点C搭在一起,杆与杆之间的静摩擦系数f=0.6。
试问系统是否静止。
11.已知:G=100N,Q=200N,A与C间的静摩擦系数f1=1.0,C与D之间的静摩擦系数f2=0.6。
试求欲拉动木块C的P min=?12.曲柄连杆机构中OA=AB,不计OA重量,均质杆AB重P,铰A处作用铅垂荷载2P,滑块B重为Q,与滑道间静滑动摩擦系数为f,求机构在铅垂平面内保持平衡时的最小角度φ。
第四章 刚体静力学专门问题参考答案一、是非题1、错2、错3、错4、错5、错6、错7、对8、对二、选择题1、③2、①①①①3、③4、②5、③6、①三、填空题1、杆①的内力为:Q 2 。
杆②的内力为:Q 。
2、如果作用于物体的全部主动力的合力的作用线在摩擦角之内,则不论这个力怎么大,物体必保持静止的一种现象。
3、α=Arc tg f=26.57°4、滑动;50N 3/35、6.7KN6、翻倒;T=0.683P四、计算题1、解:取整体;Σm A ()=0-2P αcos45°-P αcos45°+3P αcos45°-4αcos °Y E =0∴Y E =1500KNΣY=0 Y A +Y E -P ·3=0 ∴Y A =1500KN用截面I -I 截割留左部分ΣmB ()=0 S AC αsin45°-Y A αcos45°=0S AC =1500KNΣY=0 -S BC sin45°-P+Y A =0 S BC =707KNΣX=0 S AC +S BD +S BC cos45°=0S BD =-2000KN2、解:取整体Σm A =0, Y B ·8L -P ·4L=0∴ Y B =P/2取图示部分 D =2·D E =6LΣmo=0,-Y B ·2L+S CD ·cos45°·4L+S CD ·sin45°·2L=0解得;S CD =0.236P3、解:对整体 Σm A ()=0,-P ·2b+2ap+N E ·5b=0,N E =2P (b -a )/5b部分桁架 Σm H ()=0,S 1 a+N E b=0,S 1=-2P (b -a )/5a节点F ΣX=0, S 2=S 1=-2P (b -a )/5a4、解:用几何法(1)⊥是最省力,此时 β=θ+φm(2)Pmin/sin (φm+θ)=Q/sin90°∴ Pmin=Q ·sin (θ+φm )5、解:选半圆体为研究对象,由:ΣX=0 Q -F m =0ΣY=0 N -P=0Σm A ()=0Pa ·sin θ-Q (R -R ·sin θ)=0F m =Nf由上述方程联立,可求出在临界平衡状态下的θK 为 ⎪⎪⎭⎫ ⎝⎛+=f f K ππθ343arcsin 6、解:对AB 杆。
Σm D (F )=0, N A ·25-W ·cos45°·20=0N A =22W/5Σmc (F )=0, W ·5·21×2+F ·25·21×2-N ·25·21×2=0 F=(22-1)W/5 又F ≤fN ∴f ≥(22-1)/22=0.6467、解:(1)取物块A 为研究对象ΣY=0 N A -G -P ·sin30°=0 N A =12.5N F Amax =N A ·f=2.5N使A 沿B 物块运动的力 Px=P ·cos30°=4.33N Px >F Amax所以A 物块沿B 物块运动取整体为研究对象ΣY=0 N C -2G -P ·sin30°=0N C =22.5NF Bmax =N C ·f=4.5N所以B 物块不动(2)由上面计算可知A 物块上摩擦力为F Amax = 2.5N取B 物块为研究对象,因B 物块不动ΣX=0 F Amax -F B =0F B =F Amax =2.5N8、解:不翻倒时:Σm A ()=0 Q 1·2+P ·0.4=0 此时Q=Q 1= 0.2KN 不滑动时:ΣX=0 F max -Q 2=0ΣY=0 -P+N=0此时Q=Q 2=F max =0.3KN所以物体保持平衡时:Q=Q 1=0.2KN9、解:(一)假设先滑动对桌子 ΣX=0 Q -(F A +F B )=0 ΣY=0 N A +N B -P=0又 F A +F B ≤f (N A +N B )∴ Q ≤fP(二)假设先翻倒对桌子 Σm B =0 P ·L 1-Q ·L 2=0∴ Q=PL 1/L 2∴ 所求之Q 应满足 fP ≤Q ≤L 1 P/L 210、解:取AB 杆,假设AB 杆处于平衡状态Σm A (F )=0,L ·cos60°W+S ·cos30°×L=0 ∴ S=W/3N=S ·cos30°=W/2F=S ·sin30°=0.288WFmax=fN=0.3W ∵F <Fmax ∴系统处于静止状态11、解:取ABΣm B ()=021AB ·sin45°·G -AB ·N ·sin -AB ·Fmax ·sin45°=0 Fmax=Nf 1∴ N=G/2(1+f 1)=25N取CΣY=0, N 1-Q -N '=0∴ N 1=225NΣX=0, Pmin -Fmax '-F 1 max =0∴ P min =160N12、解:取AB ,使φ处于最小F=fN 设AB=L ΣmB (F )=0 L S o A sin φ—2P ·Lcos φ-P ·21Lcos φ=0 S o A=415P/sin φ ΣY=0 N -2P -P -Q+S O A sin φ=0 N=41 7P+Q ΣX=0 -F+ S O A sin φ=0 F=f ·41(7P+4Q ) tg φ=5P/(7Pf+4Qf )φmin =a r c tg[5P/(4Qf+7Pf )]。