框架柱计算长度系数的总结

多层钢结构厂房框架柱平面内计算长度研究何喜洋1 黄长华 宋 扬（广东省电力设计研究院，广州，510663）摘 要：多层钢结构厂房是火电、核电工程主厂房常用的结构形式。

对于钢框架结构设计，我国的钢结构设计规范采用的是计算长度设计法；由于荷载工况和荷载组合的复杂性，对主厂房采用考虑二阶效应的非线性分析方法还有一定难度。

本文在总结各种钢框架柱计算长度系数算法的基础上，从计算长度系数的定义出发，通过三种有代表性的计算长度分析模型的比较研究，提出了一种适用于火电、核电工程钢结构主厂房框架柱计算长度确定方法。

该方法考虑了（包含重力二阶效应的）模型的几何非线性效应和荷载分布情况对计算长度的影响，并能与主厂房建模过程紧密结合，也符合工程设计简单、便利的原则。

最后，本文通过某核电工程常规岛主厂房框架柱计算长度实例分析，阐明了本文提出的方法和步骤，获得了一些有益的结论，供设计人员参考。

关键词：多层钢结构厂房；计算长度；整体稳定；线性屈曲；临界荷载Frame Column Plane Effective Length Study on Multiple-Storey Steel PlantHE Xiyang 1 HUANG Zhanghua SONG Yang（Guangdong Electric Power Design Institute, Guangzhou, 510663, China）Abstract: Multiple-storey steel plant is a general structural system of thermal and nuclear power plant. For steel frame structure design, effective length design method is adopted by steel structure design code in our country; because of the complexity of load case and load combination, it is difficult to use nonlinear analysis method considering two order effects to analyze the plant. In this paper, all kinds of method to calculate the effective of frame column are summarized, starting with the definition of effective length, three representative model are studied and compared with each other, a new method to decide the effective length of thermal and nuclear plant frame column are proposed by the author based on comparison and study. Influence of Geometry nonlinear including gravitational two order effect on effective length is considered in this method, the method is convenient and closely associated with the modeling process. At the end of this paper, an example to calculate the effective length of nuclear plant column is used to describe the steps of the method mentioned above, good effects, which are a useful reference for civil engineer, are acquired during this example.Keywords：Multiple-storey steel plant; effective length; integral stability; linear buckling; critical load前 言多层钢结构厂房是火力发电厂主厂房和核电站常规岛常用的结构形式。

框架梁柱有效高度计算公式在建筑设计和结构设计中，框架梁柱的有效高度是一个非常重要的参数。

它直接影响到结构的稳定性和承载能力，因此需要进行准确的计算。

本文将介绍框架梁柱有效高度的计算公式，并对其进行详细的解析。

框架结构是建筑中常见的一种结构形式，其主要由梁和柱组成。

在设计中，需要确定梁柱的有效高度，以保证结构的稳定性和承载能力。

框架梁柱的有效高度是指在受压状态下，柱子的有效长度。

在计算有效高度时，需要考虑到柱子的侧向稳定性和受压构件的强度，以保证结构的安全性。

框架梁柱有效高度的计算公式如下：\[ L_{eff} = k \cdot L \]其中，\( L_{eff} \)为框架梁柱的有效高度，\( L \)为柱子的实际长度，\( k \)为修正系数。

修正系数\( k \)的计算公式如下：\[ k = 1 \frac{P_{cr}}{P} \]其中，\( P_{cr} \)为柱子的临界压力，\( P \)为柱子的实际受压力。

在实际的设计中，修正系数\( k \)的计算需要考虑到柱子的截面形状、材料性质、受力状态等因素。

通常情况下，可以根据相关的规范和经验值来确定修正系数的取值。

在计算框架梁柱有效高度时，需要注意以下几点：1. 考虑柱子的侧向稳定性。

在计算有效高度时，需要考虑到柱子的侧向稳定性，以保证结构在受压状态下不会出现侧向失稳的情况。

2. 考虑受压构件的强度。

在计算有效高度时，需要考虑到受压构件的强度，以保证结构在受压状态下不会出现破坏的情况。

3. 考虑修正系数的取值。

修正系数\( k \)的取值对于有效高度的计算非常重要，需要根据具体的情况进行合理的选择。

框架梁柱有效高度的计算是结构设计中的重要内容，它直接影响到结构的稳定性和承载能力。

在实际的设计中，需要综合考虑柱子的受力状态、材料性质、截面形状等因素，以保证计算结果的准确性和合理性。

通过合理的有效高度计算，可以有效地提高结构的安全性和经济性，为建筑的设计和施工提供可靠的技术支持。

PKPM-STS钢柱计算长度系数详解钢柱计算长度系数规范的相关修改及程序实现1.1 框架柱计算长度系数的规范变化新钢标中对于有支撑框架结构改进了判断结构是否为强支撑框架的分界准则其中旧钢规中的公式（5.3.3-1）新刚标中变为 (8.3.1-6) 按新钢标设计时，满足上式要求，该楼层可按无侧移考虑，反之应按有侧移考虑。

其中新钢标为支撑结构层侧移刚度，即施加于结构上的水平力与其产生的层间位移角的比值。

分别为第i层无侧移和有侧移框架柱计算长度系数算得的柱轴压稳定承载力之和，与旧钢规相同。

新钢标条文说明中提到考虑到不推荐采用弱支撑框架，因此取消了弱支撑框架相关概念和稳定系数确定公式，如果不满足公式8.3.1-6条要求时，则认为它是无支撑框架结构。

1.2 有无侧移自动判断功能V4.2版本SATWE依据新钢标中规定的强支撑判断原则公式，对于有支撑框架按照公式8.3.1-6进行计算，对于满足条件的楼层按照无侧移框架确定框架柱的计算长度系数，不满足的楼层按照有侧移框架确定计算长度系数，同时该层以上在该方向上均按照有侧移考虑。

该功能如下图，在参数定义—设计信息1中勾选“自动考虑有无侧移”。

图 6.1-1 “自动考虑有无侧移”参数在下图中的设计属性补充定义中可以在此处查看和修改构件的计算长度系数，需要注意的是此处显示计算长度系数并不是程序自动判断有无侧移后确定的计算长度系数结果，程序经过判断后有无侧移的结果要到“计算结果”中去查看。

图 6.1-2 计算长度系数查看和修改1.3 有无侧移自动判断的实现过程1）Sb支撑结构层侧移刚度的确定，程序根据内力计算得到支撑杆件风荷载或地震作用下在该方向上的水平剪力之和，同时得到各层位移角，水平剪力与位移角的比值即为支撑结构层侧移刚度。

2）分别为第i层无侧移和有侧移框架柱计算长度系数算得的柱轴压稳定承载力之和，与旧钢规公式相，其中φ为按照无侧移框架计算长度得到的轴心受压稳定系数，其中为按照有侧移框架计算长度得到的轴心受压稳定系数根据以上各参数的计算方法，以一50米10层带支撑钢框架为例，说明软件计算过程。

1平面外计算长度系数确定
平面外柱子与水平环梁形成钢框架，计算长度系数按照《钢结构设计规范》GB50017-2003附录表D-2有侧移框架柱的计算长度系数μ确定。

2计算结果（考虑Y向有混凝土主楼故经计算Y向可按无侧移钢架考虑。

本次不做详细计算说明。

）
该层相交于柱上端的横梁线刚度之和与柱线刚度之和的比值K1=0.3，该层相交于柱下端的横梁线刚度之和与柱线刚度之和的比值，K2=0.250，查得首层计算长度系数μ=1.95，回转半径i=153.4mm，长细比：1.95*8190/153.4=104，满足规范要求。

端的横梁线刚度之和与柱线刚度之和的比值，K2=0.30，查得首层计算长度系数μ=1.74，回转半径i=153.4mm，长细比：1.74*13600/153.4=154，不满足规范要求。

该层相交于柱上端的横梁线刚度之和与柱线刚度之和的比值K1=0.27，该层相交于柱下端的横梁线刚度之和与柱线刚度之和的比值，K2=0.12，查得首层计算长度系数μ=2.33，回转半径i=153.4mm，长细比：2.33*10500/153.4=159.5，不满足规范要求。

框架柱计算柱长度系数柱长系数是指在使用框架柱计算柱长度时所引入的修正系数。

在结构设计中，为了简化计算，常常将柱视为理想化的杆件，即柱的长度远大于其截面尺寸，忽略了柱的弯曲变形。

然而，在实际工程中，柱的长度与截面尺寸相比并不总是很大，因此需要考虑柱的弯曲变形对结构的影响。

柱长系数的计算是为了修正柱的长度对结构刚度和强度的影响。

一般情况下，柱长系数的计算与柱的端部约束条件有关。

根据柱端部的约束条件的不同，柱长系数可以分为简支柱、固定柱和半固定柱三种情况。

考虑简支柱的情况。

简支柱的两端可以自由转动，不受任何约束。

在这种情况下，柱长系数为1.0，即不需要进行修正。

考虑固定柱的情况。

固定柱的两端被完全约束，不允许任何位移或转动。

在这种情况下，柱的弯曲变形会导致柱的长度变短，从而影响结构的刚度和强度。

为了修正这种影响，需要计算固定柱的柱长系数。

固定柱的柱长系数可以根据柱的截面形状和约束条件来确定。

通常，可以使用公式或图表给出固定柱的柱长系数。

在实际设计中，常常使用柱长系数表格来确定柱的柱长系数。

柱长系数表格会给出不同截面形状和约束条件下的柱长系数，设计人员可以根据具体情况选择合适的柱长系数。

考虑半固定柱的情况。

半固定柱的一端被固定，另一端可以自由转动。

在这种情况下，柱的弯曲变形会导致柱的长度变短，但变形程度会小于固定柱。

为了修正这种影响，同样需要计算半固定柱的柱长系数。

半固定柱的柱长系数也可以通过公式或表格来确定。

设计人员需要根据柱的截面形状和约束条件选择合适的柱长系数。

在实际工程中，柱长系数的计算对于柱的设计至关重要。

柱长系数的选择不当会导致结构刚度和强度的不足或过剩。

因此，设计人员需要根据具体情况进行合理的柱长系数计算，并在设计过程中进行必要的修正。

柱长系数是在使用框架柱计算柱长度时所引入的修正系数。

根据柱的约束条件的不同，柱长系数可以分为简支柱、固定柱和半固定柱三种情况。

设计人员需要根据柱的具体情况选择合适的柱长系数，并进行必要的修正，以保证结构的刚度和强度。

钢柱计算长度系数确定及长细比相关问题答疑钢柱计算长度系数的确定是钢结构常规设计方法中重要的一环,本文对于钢结构中常用的结构形式,门式刚架和钢框架结构结构中的钢柱确定中遇到的几个问题一一解答,希望对设计人员在钢柱计算长度系数确定时能够有所帮助.1、《门式刚架轻型房屋钢结构技术规范》GB51022-2015确定刚架柱的计算长度系数都有哪些算法？按门规附录A.0.1-A.0.5规定的方法以及A.0.8规定的方法,两种方法有何异同？应该如何选择？1）门式刚架规范对于门式刚架柱计算长度系数确定提供了两种算法,一种是按照门式刚架规范附录A.0.1-A.0.5规定的方法确定刚架柱面内的计算长度系数；另一种是按照门式刚架规范附录A.0.8方法确定刚架柱面内的计算长度系数.对于门式刚架规范的两种方法,二维设计程序是通过参数中的勾选项实现的,见下图：图1门式刚架二维设计参数定义勾选该选项后,程序按照门式刚架规范附录A.0.8方法确定刚架柱面内的计算长度系数,不勾选时,程序按照门式刚架规范附录A.0.1-A.0.5规定的方法确定刚架柱面内的计算长度系数.对于存在摇摆柱的门式刚架,在采用两种方法确定计算长度系数时,程序都会按照A.0.6条要求对于刚架柱的计算长度系数进行放大.2）第一种方法即A.0.1-A.0.6这套方法,其基本设计思路与钢规和梁柱线刚度比方法较为相似,采用梁柱线刚度比作为钢柱面内计算长度系数,这种方法对于门式刚架结构形式没有特别要求,可以支持较为复杂的门式刚架带夹层、高低跨、阶形柱等都可以参考此方法计算得到柱的计算长度系数.第二种方法与旧版门式刚架规程中所规定的一阶弹性方法较为接近,程序主要基于公式A.0.8-1确定,即：由公式可以看出其方法的特点是根据整体抗侧刚度以及柱承担的轴向力得到钢柱的计算长度系数,因此可以考虑单层各跨各柱之间的相互支援作用,同时可以看到该方法适用范围较窄,规范规定各跨梁的标高无突变,无高低跨时可用,但通过对应公式可以看出,该方法同样不适用与刚架柱中间增加节点后截面出现变化的情况,或带夹层的情况,如果使用该方法就会出现柱的计算长度系数异常大的现象,例如下图中带夹层的门式刚架模型的1-5号柱,图2门式刚架柱及其位置其中1、2号柱为截面有变化的阶形柱,3-5号柱为夹层位置的柱,其分别按照门规附录的两种方法分别计算上述柱的计算长度系数,得到以下结果,我们会发现,对于分段的阶形柱和夹层柱按照门式刚架规范附录A.0.8方法计算得到的柱面内计算长度系数相较另一种方法差异很大,一般是A.0.1-A.0.5方法的若干倍,明显偏大,所以在出现上述现象,此时A.0.8的这种方法就不太合适了.门式刚架规范两种算法的比较表12在钢柱长细比等指标不满足规范要求时,为什么很多情况下,增大柱截面尺寸后长细比等指标不但没有降低,反而变大了？为了更清楚说明这种现象产生的原因,以如下简单模型中的框架柱为例,只改变中柱的截面,其他条件均不改变的情况下,考察不同柱截面的回转半径、强轴方向的计算长度系数这两个参数,以及长细比的变化趋势.图3钢框架模型轴侧图该模型中柱采用程序中的国标热轧H型截面,其他条件不变,截面依次增大,分别为HW400*400 HW400*408,HW414*405,HW428*407,HW458*417,HW498*432.首先通过下面折线图来看回转半径的变化,我们发现回转半径并不会随着截面的增大而增大,在截面由HW400*400变为HW400*408时,其腹板厚度和翼缘长度均变大了,为什么回转半径反而变小呢？这是由于回转半径i=√（I/A）,它由截面惯性距和截面面积共同控制,当截面变大时,截面面积和惯性矩同时增大,截面面积增大的速率大于截面惯性矩时,则会出现回转半径减小的情况,而总体上,回转半径由于受到这种条件的制约,增大的趋势也非常缓慢.再来看柱计算长度系数的变化趋势,它再一次和我们一般的认知有着相反的趋势,柱的计算长度系数会随着柱截面的加大而增大,出现这种现象的原因我们要从柱计算长度系数确定过程来分析,根据旧钢规和新钢标对于框架柱计算长度系数确定的方法,其主要过程参数为相交于柱上、下端并与之刚接的横梁线刚度之和与柱线刚度之和的比值K1、K2,通过规范附录公式及对应表格,我们得到无论是无侧移框架还是有侧移框架失稳模式,柱计算长度系数,都与K1、K2呈反比关系,而在不改变梁截面的情况下,增大柱截面而不改变梁截面的情况下会使K1、K2这两个参数变小（最底层柱K2不变）,进而柱的计算长度系数始终是呈增大的趋势.最后柱的长细比也是随着截面的增大而变大,究其原因还是由于柱计算长度系数和回转半径的变化趋势和速率导致的,上面我们已经知道柱的计算长度是逐渐增大的趋势,而总体上回转半径也呈缓慢增大的趋势,此时柱的长细比变化趋势由计算长度随着柱截面增大的速率和回转半径增大的速率之间的大小关系决定,计算长度比回转半径增大的快,长细比就会增大,反之则长细比减小,在这个例子中计算长度系数的增速要比回转半径快.综上,单纯的通过调整柱截面来让长细比满足要求可能会付出很高的代价.图4框架柱回转半径、计算长度系数和长细比变化趋势3钢框架柱长细比超限该如何调整？由上一问我们得出在一些情况下我们不能单纯的通过调整柱的截面来调整长细比超限的情况,我们应该从以下几个方面去进行长细比的调整.1）在满足强柱弱梁的前提下,增加梁截面尺寸可以降低柱的长细比水平.在柱截面受到建筑限制或增大截面无效的情况下,可以通过适当增大长细比验算方向的与柱刚接的梁截面尺寸来使首层柱K1增大,其他层柱K1,K2都增大的方式减小柱的计算长度系数,进而减小柱的长细比.2）在条件允许的情况下,对于有支撑结构增加支撑杆件或增加已有支撑杆件的刚度使结构由有侧移框架变为无侧移框架.3）采用规范提供的性能化设计方法或性能化设计思想有效增加长细比限值,使长细比更容易满足.如采用新钢标17章抗震性能化设计方法时,满足了相应性能目标的要求后,其长细比限值有所降低.抗规8.1.3注2：多、高层钢结构房屋,当构件的承载力满足2倍地震作用组合下的内力要求时,7～9度构件抗震等级允许按降低1度确定,通过该条可以使承载力能力用较大富裕度的构件,降低其抗震等级,进而其所对应的长细比限值等指标也有所降低.4在调整钢框架中框架梁截面尺寸后为什么与其相连的计算长度系数没有变化？在钢框架中的框架梁很多情况下需要与框架柱做铰接连接,在这种情况下,根据旧钢规和新钢标的附录中均有当横梁与框架柱刚接时,其横梁线刚度取0,此时铰接横梁的线刚度就与参数K1,K2的确定没有影响了,K1,K2不变,计算长度系数自然不会发生变化.。

钢结构框架柱的计算长度系数该怎么选取呢?是按照程序默认值呢(没有选取P-△二阶效应), 还是改为1 ,1(选取P-△二阶效应),呢?1.如果是高层钢结构：可以按照《高层民用建筑钢结构技术规程》JGJ99-98的6.3.2条执行。

简言之：（1）有支撑或剪力墙的结构，层间位移角小于1/250时，可以取计算长度系数1.0；（2）纯框架体系，层间位移角小于1/1000时，按照无侧移的公式（6.3.2-2）。

2.如果是多层钢结构：可以按照《钢结构设计规范》GB50017-2003的5.3.5条执行。

（1）无支撑纯框架：1）采用一阶弹性分析方法，按照附录D表D-2；2）采用二阶弹性分析方法，即在每层柱顶附加考虑公式3.2.8-1的假象水平力，框架计算长度取1.0（此方法也就是很多人认为的P-△二阶效应）（2）有支撑框架：分为强支撑（无侧移）和弱支撑。

现在谈谈P-△二阶效应计算方法：常用有以下几种：1.《高层民用建筑钢结构技术规程》JGJ99-98第5.2.11的条文说明的方法2.《钢结构设计规范》GB50017-2003第3.2.8条的方法3.《高层建筑混凝土结构技术规程》JGJ3-2002第5.4.3条的方法4.Wilson教授提出的等效几何刚度的方法（可以参看Wilson著《结构静力与动力分析》第11章，也可以参看徐培福等《复杂高层建筑结构设计》第五章第三节，另外也可以参考高小旺等《建筑抗震设计规范理解与应用》2.5节）PKPM等软件考虑P-△二阶效应计算方法采用第4种，即等效几何刚度法。

因此不能将PKPM软件的“P-△二阶效应计算”与柱计算长度系数联系起来。

我个人认为：1.对于高层钢结构，尤其是比较重要的高层钢结构、超高层钢结构，一般需要考虑P-△二阶效应，而且可以使用PKPM计算，即采用Wilson 教授的方法，与计算长度系数没有关系。

2.PKPM讲稿上的计算长度判断方法可以采用:(1)当楼层最大杆间位移小于1/1000时，可以按无侧移设计；(2)当楼层最大杆间位移大于1/1000但小于1/300时，柱长度系数可以按1.0设计；(3)当楼层最大杆间位移大于1/300时，应按有侧移设计。

钢结构框架柱计算长度系数说明很多用户对于STS框架柱的计算长度系数计算都存有疑问，尤其是在框架柱存在跃层柱的时候，有的时候会觉得得软件得出的计算长度系数偏大，或者不准确。

下面我通过一个用户的模型，来详细的讲解一下计算长度系数的问题。

1 跃层柱计算长度系数显示的问题首先我们需要了解一下软件对于跃层柱计算长度系数显示结果的问题用户模型如下：选取其中一根柱子，看一下软件（satwe）对于计算长度系数输出：绕构件X轴的计算长度系数两层分别是 2.55和2.92 ，因为分了标准层，所以输出了两个计算长度系数，但如果我么手算的话，肯定是按照一个柱子来求计算长度系数，那么现在软件输出的计算长度系数，和我们手算的到底有什么区别呢？我们可以利用二维门式钢架计算验证一下，抽取这个立面，形成PK文件，二维门刚计算的计算长度系数如下：二维门刚是按照一整根柱子求出了一个计算长度系数1.36计算长度系数主要涉及到构件长细比的计算，截面是确定的，那我们来看计算长度：Satwe计算结果：下段柱计算长度=2.55*4.8米（层高）=12.24米上段柱计算长度=2.92*4.2米（层高）=12.264米二维门刚计算结果：1.36*（4.8+4.2）=12.24米结论：从上面的计算可以得知，satwe对于跃层柱的计算长度系数，是按照一整根柱来得到的，但是输出的时候是分层输出的，所以对于求得的计算长度系数按照层高做了处理，但是结果是一样的，这个我么在后面可以手算验证。

2 如何核对计算长度系数Satwe对于构件的的计算长度系数的计算是按照《钢规》附录D来计算的，很多用户对软件的计算长度系数存在疑问，但是通过我们的核对，绝大多数的情况，软件还是严格按照规范来计算的，但是对于一些连接情况特别复杂的情况，规范也没有特别说明的的情况，软件也会出现一定的问题，那么我们该怎样核对构件的计算长度系数呢？第一个方法，就是我们上面用到的，抽一榀，用我们的二维门刚来验证。

有侧移框架柱计算长度系数的计算及对《钢规》的一点疑问说明：本文中《钢规》指GB50017-2003《钢结构设计规范》，美标指ANSI/AISC 360-05 Specification for Structural Steel Buildings.《钢规》第2章术语和符号2.1.14对“计算长度”的定义：构件在其有效约束点间的几何长度乘以考虑杆端变形情况和所受荷载情况的系数而得的等效长度，用以计算构件的长细比。

一、概述通常我们在设计验算一个钢框架的稳定性时，都是根据《钢规》中的计算长度法把框架稳定简化成柱子构件的稳定问题来对待，求柱子的计算长度的目的不光是为了验算柱子本身的稳定性，更主要的是验算框架的整体性。

这里，任何一根框架柱都不是孤立存在的，框架中的其它构件对整体的稳定性都是相关的。

《钢规》中在验算压弯构件稳定问题时的几个公式（式5.2.2-1、式5.2.2-3）和强度验算公式相比也只是添加了稳定系数、等效弯矩系数，其它和强度验算是完全一样的，那么如何体现结构的整体稳定性呢？就是通过稳定系数和等效弯矩系数。

而稳定系数又和构件的计算长度是直接相关的。

在与柱翼缘平行的平面内，通常布臵斜撑构成无侧移体系，此种体系的柱子的计算长度系数都小于1，实际应用中简化计算取1，本文只讨论在与柱腹板平行的平面内的柱子的计算长度系数。

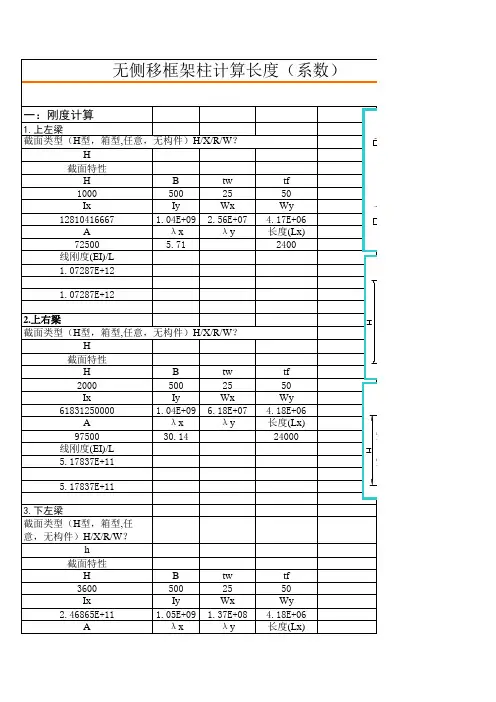
二、规范中的计算方法2.1. 《钢规》中有侧移框架柱计算长度系数的计算方法附录D 表 D-2 注1，对有侧移框架柱的计算长度系数μ值按下式计算：0cos )(6sin 3621221=⋅++⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-μπμπμπμπK K K K 其中1K ，2K 分别为相交于柱上端、柱下端的横梁线刚度之和与柱线刚度之和的比值。

《钢规》条文说明5.3.3中提到，以上计算的基本假定为：1 材料是线弹性的；2 框架只承受作用在节点上的竖向荷载；3 框架中的所有柱子是同时丧失稳定的，即各柱同时达到其临界荷载；4 当柱子开始失稳时，相交于同一点的横梁对柱子提供的约束弯矩，按柱子的线刚度之比分配给柱子；5在无侧移失稳时，横梁两端的转角大小相等方向相反；在有侧移失稳时，横梁两端的转角不但大小相等而且方向亦相同。

钢结构框架柱计算长度系数说明钢结构框架柱的计算是结构设计中的重要一环，而计算长度系数则是框架柱计算中必不可少的一项内容。

本文将对钢结构框架柱的计算长度系数进行详细的说明，包括计算长度系数的定义、计算方法、影响因素、计算示例以及相关规范的规定。

一、计算长度系数的定义钢结构框架柱的计算长度系数是指柱在受压作用下的有效长度与柱的实际长度之比。

它是结构杆件的基本计算参数之一，用于确定柱的稳定性和承载力。

计算长度系数是根据框架体系的刚度、支座条件和加载条件等因素来确定的。

一个合理的计算长度系数能够准确反映柱的实际抗压能力，从而保证结构的安全性。

二、计算长度系数的计算方法计算长度系数的计算方法通常有四种：欧拉临界弯曲法、期限挠度法、极限位移法和有效长度系数法。

1. 欧拉临界弯曲法（Euler's formula）根据欧拉临界弯曲理论，该方法适用于细长柱的计算，其计算长度系数公式为：λe = Klc * Klh * Kld * Ke * Kf * Kp * Kd其中，λe为计算长度系数，Klc为柱端联结系数，Klh为柱顶偏心系数，Kld为桁架柱偏心系数，Ke为结构效应系数，Kf为弯矩分配系数，Kp为单框架层系数，Kd为单框架实心柱系数。

2. 期限挠度法（deflection method）λd = Kkb * Kkc * Kas * Ka * Kd其中，λd为计算长度系数，Kkb为框架柱东西向刚度系数，Kkc为框架柱南北向刚度系数，Kas为桁架柱刚度折减系数，Ka为考虑隔墙效应系数，Kd为刚柱修正系数。

3. 极限位移法（limit displacement method）该方法通过柱的最大位移来计算长度系数，并考虑到极限位移的安全性。

计算长度系数的公式为：λu=Kk*Kh*Ku*Kc*Ka*Kd其中，λu为计算长度系数，Kk为柱边界限抗弯刚度比，Kh为柱高与其极限位移基准长度之比，Ku为柱稳性系数，Kc为柱的构造系数，Ka 为小尺度地震作用系数，Kd为与刚度匹配系数。

（一）规范要求⑴《混凝土结构设计规范》（GB 50010-2002）（以下简称《混凝土规范》）第7.3.11条第2款规定：一般多层房屋梁柱为刚接的框架结构，各层柱的计算长度系数可按表7.3.11-2取用。

⑵第7.3.11条第3款规定：当水平荷载产生的弯矩设计值占总弯矩设计值的75％以上时，框架柱的计算长度l0可按下列两个公式计算，并取其中的较小值：l0＝［l＋0.15（Ψu＋Ψl)]H （7.3.11-1）l0＝（2十0.2Ψmin）H （7.3.11-2）式中：Ψu、Ψl——柱的上端、下端节点处交汇的各柱线刚度之和与交汇的各梁线刚度之和的比值；Ψmin——比值Ψu、Ψl中的较小值；H——柱的高度，按表7.3.11-2的注采用。

（二）工程算例⑴工程概况：某工程为十层框架错层结构，首层层高2m，第二层层高4.5m。

其第一、二层结构平面图、结构三维轴侧图如图1所示。

（图略）（三）SATWE软件的计算结果⑴计算结果表：－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－表1柱1、柱2、柱3按照表7.3.11-2直接取值的计算长度系数柱1／3.25／3.25／1.44／1.44／柱2／1.00／3.25／1.25／1.44／柱3／1.00／1.00／1.25／1.25／－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－表2柱1、柱2、柱3按公式7.3.11-1和7.3.11-2计算的计算长度系数柱1／3.59／3.83／1.60／1.70／柱2／1.33／3.83／1.42／1.70／柱3／1.19／1.12／2.23／2.14／－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－表中数据依次为：柱号／首层Cx／首层Cy／二层Cx／二层Cy／柱1是边柱，首层无梁，二层与三根梁相连；柱2也是边柱，首层下向有一根梁，二层与三根梁相连；柱3是中柱，首层、二层均与四根梁相连。

狗骨式节点连接的钢框架柱计算长度系数【中文摘要】狗骨式节点通过梁翼缘的局部削弱,迫使大震作用下塑性铰偏离脆弱的节点焊缝区,而出现在具有很大延性的梁上,达到减少节点脆性破坏可能性、进步了节点的延性。

然而采用狗骨式节点获得更大塑性转动能力的同时,必然会削弱整个结构的刚度,从而对钢框架的整体稳定产生一定影响。

现阶段通常把平面钢框架的整体稳定简化为柱的稳定来分析,在设计框架柱时,广泛采用计算长度法,即用柱的计算长度代替实际长度来考虑与柱相连构件的约束影响,框架柱计算长度系数可以通过确定其稳定承载力得到。

本文根据框架柱计算长度理论和引进了圆弧形狗骨式节点参数特性,通过改变框架梁柱线刚度比和节点设计参数,建立十二组圆弧形狗骨式节点连接的单层单跨钢框架数值模型。

利用有限元软件ANSYS对这十二组圆弧形狗骨式节点连接的单层单跨钢框架进行特征值屈曲分析,得到圆弧形狗骨式节点三个设计参数对相应钢框架柱稳定承载力的影响规律。

引进结构初始缺陷后,对圆弧形狗骨式节点连接的有侧移和无侧移钢框架模型进行非线性屈曲分析,得到了参数b和参数c对圆弧形狗骨式节点连接的有侧移和无侧移钢框架的非线性屈曲荷载的影响规律。

通过调整梁柱截面和高度,建立不同梁柱线刚度比的RBS节点连接的有侧移钢框架模型,并进行非线性屈曲分析,得到相应的框架柱计算长度系数表。

非线性屈曲分析结果显示,狗骨式节点连接的钢框架柱计算长度系数较常规节点连接的侧移和无侧移框架柱计算长度系数有一定增加,幅值在0.02～14.16%之间。

');【Abstract】 Reduced beam section(RBS) connection can move plastic hinge outward from the beam and column inte***ce to the beam in the earthquake. By trimming beam flanges, the plastic hinge will far away from the welds that have much fracture proneness due to stress concentration and welding sensitivity, reducing the possibility of brittle fracture of connections and improving the ductility of the structure with RBS connections. However, could increased the plastic rotation ability of the connection but weaken the stiffness, and influence the overall stability of the steel frame.At the present time, we usually analysis the stability of steel frame column take the place of entire steel frame in brief. When designing the steel frame column, the widely used method is the column effective length, it means using the effective length of column in stead of actual length to consider the relationship between columns and beams. The coefficient of column effective length can get from the value of its stability bearing capacity.In this ***, based on the column effective length theory of steel frames stability design and the parameter feature of arc-shaped dog-bone connection, through the method of change steel frame beam-columns linear stiffness ratio and the parameter of connection, we build twelve groups numerical model of the single-story and single-bay steel frames with arc-shaped dog-bone connection. After using the finite element software ANSYS to do theeigenvalue buckling analysis of the twelve groups single-story and single-bay steel frames with arc-shaped dog-bone connection, we can get the regular pattern between three parameters of arc-shaped dog-bone connection and the stability bearing capacity of steel frame column. Then under the consideration of steel frame initial defect, we take the mode to do the nonlinear buckling analysis under the different situation of sway frame and non-sway frame, so we get the parameter b and c, which represent the nonlinear buckling load regular pattern of sway frame and non-sway frame separately. After adjusted the section of beam and column, build the different modes of sway frame and non-sway frame with beam-columns linear stiffnessratio of RBS connection, then do the nonlinear buckling analysis, we can get the table of the coefficient of column effective length. The result of nonlinear buckling analysis shows that, the coefficient of column effective length of RBS connection steel frame increased a little, when compared with the regular connection steel frame column, no matter under the situation of sway frame and non-sway frame, and the amplitude between 0.02 and 14.16%.。