求解电源的最大输出功率的几种方法及其规律
- 格式:doc
- 大小:206.50 KB
- 文档页数:4

最大功率原理最大功率原理是电学中的一个重要概念。
它指出,在给定电路中,当电阻与电源连接时,电阻上的功率达到最大值。
这个原理是在19世纪中叶由德国物理学家赫尔曼·冯·亥维兹首次提出的。
根据最大功率原理,当一个电阻连接到一个电源上时,电源会向电路提供电能,而电阻则会将这部分电能消耗掉,形成热能。
在电路中,电流和电压的关系可以用欧姆定律来描述:电流与电压成正比,电阻是比例常数。
根据欧姆定律,我们可以推导出电阻上的功率表达式为P = I^2R,其中P表示功率,I表示电流,R表示电阻。
现在,我们来推导出最大功率原理。
假设我们要找到电路中电阻上的最大功率。
我们可以用微积分的方法,首先计算功率P关于电阻R的导数dP/dR,然后将导数置为零,求得临界点R。
接下来,我们需要判断这个临界点是功率的最大值还是最小值。
经过分析可知,当电流I恰好为电源电动势和电阻之比时,功率P达到最大值,即P = (V^2/R) * R = V^2/R,其中V表示电源电动势。
根据以上推导,我们可以得出结论:在一个电路中,当电源电动势和电阻之间的比值等于电流时,电阻上的功率达到最大值。
这个结果也可以用最大功率定理来表述:给定电源电动势和电阻,连接时达到最大功率的条件是电阻等于电源内阻的复共轭。
在实际应用中,最大功率原理被广泛应用于电子设备的设计和能源管理中。
最大功率原理的应用不仅限于电学领域,类似的思想也可以在其他领域中得到应用。
例如,在机械系统中,最大功率原理可以用于优化机械装置的工作效率。
在化学反应中,最大功率原理可以用来确定反应条件以达到最大产率。
总之,最大功率原理为我们理解和优化能量转换过程提供了一个有效的工具。
需要注意的是,在实际应用中,还需要考虑电路的安全性和稳定性。
特别是在高功率电路中,电流和电压可能达到很高的数值,需要采取相应的保护措施,以防止电路、电源或电器受到损坏,甚至引发火灾或其他事故。
总结起来,最大功率原理是电学中的一个重要概念,它指出在给定电路中,当电阻与电源连接时,电阻上的功率达到最大值。

·中学生·一个推论解决电路的动态分析问题王 坤(济宁市育才中学 山东济宁 272000) 电路的动态分析问题是高考中恒定电流这一部分的重要题型,其特点是:在纯电阻电路中,某一电阻变化,判断其他支路的电压、电流的变化.例1 (2007年宁夏理综卷第19题)在如图1所示的电路中,E为电源电动势,r为电源内阻,R1和R3均为定值电阻,R2为滑动变阻器.当R2的滑动触点在a端时合上开关S,此时三个电表A1、A2和V的示数分别为I1、I2和U.现将R2的滑动触点向b端移动,则三个电表示数的变化情况是A.I1增大,I2不变,U增大B.I1减小,I2增大,U减小C.I1增大,I2减小,U增大D.I1减小,I2不变,U减小这类问题的一般思路是:根据电阻的变化判断总电阻的变化———依据闭合电路欧姆定律判断总电流的变化———依据U=E-Ir判断总电压的变化———依据欧姆定律和串联分压规律判断支路电压的变化———依据欧姆定律和并联分流的规律判断支路电流的变化.如上题:将R2的滑动触点向b端移动,则R2接入电路的电阻减小———电路总电阻减小———总电流变大———总电压变小———R3两端的电压变大所以R1和R2所构成的并联支路的电压变小———R1两端的电压变小所以电流变小———因总电流变大所以通过R2的电流变大,B正确.这一分析过程过于繁琐,我们可以通过一个推论直接得出结果.推论的内容可以表述为:在所接电源电动势不变的情况下,电路的任意一部分支路(包括干路)的电阻增大,则该支路的电压增大、电流减小;电阻减小,则该支路的电压减小、电流增大.用上述推论分析例1,直接可以得出结论:R2减小,则通过R2的电流增大,R2两端的电压减小———所以R1两端电压减小,通过R1的电流减小;R2减小,总电阻减小,则总电压减小,B正确.我们用同样的方法分析一下下面两个例题,大家可以看出这种方法的优越性.例2 (2011年海南卷第2题)如图2,E为内阻不能忽略的电池,R1、R2、R3为定值电阻,S0、S为开关,V与A分别为电压表与电流表.初始时S0与S均闭合,现将S断开,则A.V的读数变大,A的读数变小B.V的读数变大,A的读数变大C.V的读数变小,A的读数变小D.V的读数变小,A的读数变大分析 S断开相当于R2变大,则并联支路的电阻变大,根据推论可得出并联支路的电压变大,所以R3的电压变大、电流变小;R2变大,总电阻变大,则总电压变大,B正确.例3 (2009年广东卷第10题)如图3所示,电动势为E、内阻不计的电源与三个灯泡和三个电阻相接,只合上开关S1,三个灯泡都能正常工作,如果再合上S2,则下列表述正确的是A.电源输出功率减小B.L1上消耗的功率增大C.通过R1上的电流增大D.通过R3上的电流增大分析 电路结构是R3与L3串联,然后与L2、L1、R2并联,并联支路与R1串联.合上S2相当于R2减小,并联支路的总电阻减小,根据推论可得出并联支路的电压减小、电流增大,所以通过R1上的电流增大,通过R3、L1上的电流减小,L1上消耗的功率减小,因通过R1的电流即干路电流增大,内阻不计,电源的输出功率即EI增大,C正确.这个推论把电压和电流的变化直接与电阻的变化联系在一起,在解决问题时既可节省时间,又能避免因复杂的分析过程而容易产生的错误.·08·2012年10月 Vol.30 No.19 中学物理电源输出功率最大值求解六法及比较作者:刘益民作者单位:扬州市宝应县中学 江苏扬州 225800刊名:中学物理(高中版)英文刊名:ZHONGXUE WULI(GAOZHONG BAN)年,卷(期):2012,30(10)引用本文格式:刘益民电源输出功率最大值求解六法及比较[期刊论文]-中学物理(高中版) 2012(10)。

【最新整理,下载后即可编辑】求解电源的最大输出功率的几种方法及其规律太原市第十二中学 姚维明【题目1】如图1所示的电路,若电源的电动势为E ,内电阻为r ,外部电路有滑动变阻器R ,问在什么条件下电源的输出功率最大?设电源的输出功率为P ,端压为U ,流过电源的电流为I 。
方法一:运用P~R 函数关系法:因为UI P =、IR U =和R r EI +=, 所以22)(R r RE P +=,得R r RrE P ++=222。
可见,当R Rr =2,即r R =时P 有最大值,且最大值rE P 42max =。
P~R 的函数图像如图2所示。
①当R=r时,电源的输出功率最大,P m =rE 42。
②当R >r 时,随着R 的增大输出功率减小。
③当R <r 时,随着R 的减小输出功率减小。
方法二:运用P~I 函数关系法因为UI P =、Ir E U -=,所以r I EI P 2-=,推得r E r E I r P 4)2(22+--=。
可见,当r EI 2=时P 有最大值,且最大值rE P 42max =。
P~I 的函数图像如图3所示。
方法三:运用P~U 函数关系因为UI P =、rUE I -=,所以rU U r E P 2-=,图1图4图3图2推得rE E U r P 4)2(122+--=。
可见,当2EU =时P 有最大值,且最大值rE P 42max =。
P~U 的函数图像如图4所示。
【规律总结】当R=r 时电源的输出功率最大,且电源的最大输出功率为rE 42,此时2EU=,rE I 2=。
此时 U ~I 图像如图5所示,图5中斜线部分的“面积”表示了电源的最大输出功率。
“等效电源”解决功率问题【题目2】如图所示,电源的电动势E=2V ,内阻r=1Ω,定值电阻R 0=2Ω,变阻器R 的阻值变化范围为0~10Ω,求:(1)变阻器R 的阻值为多大时,R 0消耗的功率最大?(2)变阻器R 的阻值为多大时,R 上消耗的功率最大?是多少?(3)变阻器R 的阻值为多大时,电源的输出功率最大?是多少?方法:(1)对定值电阻,直接运用公式。

电源最大功率问题的几种解法关于学习的“三部曲”,西方有的学者总结为”3W”,就是“1.是什么(What)2.为什么(Why)3.怎么样(How)”。
中国学者总结为“知其然知其所以然和举一反三”。
把它用到物理学习上,就是说,首先要知道某个知识,还要知道这个知识为什么是这样的,最后,还有应用这个知识解决问题。
但是,有的人知其然不知其所以然,照本宣科,死记硬背,套用公式,就会造成错误。
本文以电源最大输出功率问题为例加以说明。
关于电源最大输出功率问题,1980年代的教科书上有这个实验,以后没有了。
高考也以计算题考过,全国卷考过,江苏卷考过,上海卷考过,每题都不同。
可见此问题的重要。
本文从基本问题谈起。
一、电源最大输出功率问题的基本问题如下图所示,电源电动势为E=6V,内阻为r=2Q,外电路接一滑动变阻器_9R,求电源输出功率最大的条件及其值。
rz_"RE,r【解法1】公式法E-R厂八仟2电源输出功率为P=I2R=------=------2----(R+')2(R t)23R£2当R=r=2Q时,电源输出功率最大值为7^=——=4.5W.4r【解法2】图象法根据p=〃R=E R,=36^2作出p~R图象如下:(R+尸)(R+2)2PR—-PR从图象可以看出,当R=2Q时,电源输出功率最大值为p m=4.5W.【解法3】求导数法电功率表达式:P=-^R,根据求导公式(凹),=凹胃史,得导数:(R+r)2v v2P,(R)=E"(R+r)2_E2R.2(R+r)=E2.(R+r).(r_R),当R=r时,导数的分(R+r)4(R+r)4''A2x9子为零,即此时有极大值,将R=r=2Q代入P式得最大值pg=(二2)2=4.5W.二、变式如下图所示,电源电动势为E=6V,内阻为r=2Q,外电路接一滑动变阻器R和一定值电阻氏=0.50,求:(1)滑动变阻器的功率最大的条件及其最大值。

高中物理闭合电路的欧姆定律常见题型及答题技巧及练习题(含答案)及解析一、高考物理精讲专题闭合电路的欧姆定律1.如图所示,R 为电阻箱,V 为理想电压表.当电阻箱读数为R 1=2Ω时,电压表读数为U 1=4V ;当电阻箱读数为R 2=5Ω时,电压表读数为U 2=5V .求:(1)电源的电动势E 和内阻r .(2)当电阻箱R 读数为多少时,电源的输出功率最大?最大值P m 为多少? 【答案】(1)E =6 V r =1 Ω (2)当R=r =1 Ω时,P m =9 W 【解析】 【详解】(1)由闭合电路欧姆定律E U Ir =+得:111U E U r R =+,代入得44422E r =+=+①, 222U E U r R =+,代入得:5555E r r =+=+②, 联立上式并代入数据解得:E=6V ,r=1Ω(2)当电阻箱的阻值等于电源的内电阻时电源的输出功率最大,即有R=r=1Ω电源的输出功率最大为:22226()92441m E E P I R r W W r r =====⨯;2.有一个100匝的线圈,在0.2s 内穿过它的磁通量从0.04Wb 增加到0.14Wb ,求线圈中的感应电动势为多大?如果线圈的电阻是10Ω,把它跟一个电阻是990Ω的电热器串联组成闭合电路时,通过电热器的电流是多大? 【答案】50V , 0.05A . 【解析】 【详解】已知n =100匝,△t =0.2s ,△Φ=0.14Wb-0.04Wb=0.1Wb ,则根据法拉第电磁感应定律得感应电动势0.1100V=50V 0.2E nt ∆Φ==⨯∆ 由闭合电路欧姆定律得,通过电热器的电流50A=0.05A 10990E I R r ==++3.如图所示,电路中电阻R 10=Ω,电源的内电阻2r =Ω,灯泡L 上标有“3V 0.25A”的字样,闭合开关S ,灯泡正常发光.求:(1)灯泡的功率; (2)电源的电动势; (3)电源的总功率;【答案】(1) 0.75W (2) 6V (3) 1.5W 【解析】 【详解】(1)由题知,灯泡正常发光,则灯泡的电压为 U=3V ,电流为 I=0.25A 所以灯泡的功率为 P=UI=0.75W (2)由闭合电路欧姆定律得:电源的电动势 E=U+I (R+r )=3+0.25×(10+2)=6V (3)电源的总功率:P=IE=0.25×6W=0.5W.4.如图所示,电源电动势E =30 V ,内阻r =1 Ω,电阻R 1=4 Ω,R 2=10 Ω.两正对的平行金属板长L =0.2 m ,两板间的距离d =0.1 m .闭合开关S 后,一质量m =5×10﹣8kg ,电荷量q =+4×10﹣6C 的粒子以平行于两板且大小为 =5×102m/s 的初速度从两板的正中间射入,求粒子在两平行金属板间运动的过程中沿垂直于板方向发生的位移大小?(不考虑粒子的重力)【答案】【解析】根据闭合电路欧姆定律,有:电场强度:粒子做类似平抛运动,根据分运动公式,有:L=v 0ty=at 2 其中:联立解得:点睛:本题是简单的力电综合问题,关键是明确电路结构和粒子的运动规律,然后根据闭合电路欧姆定律和类似平抛运动的分运动公式列式求解.5.如图所示,电路由一个电动势为E 、内电阻为r 的电源和一个滑动变阻器R 组成。

电源最大输出功率的条件论证及应用在闭合电路中,电源提供的功率等于内外电路消耗的功率之和,对于含有可变电阻的纯电阻电路,可变电阻的阻值变化直接影响着电源的总功率,也影响着闭合电路中各部分的功率分配。
电源的最大输出功率是电源性能的重要标志之一,求电源最大输出功率的问题也是电功率这部分内容的难点,学生虽经反复练习,但仍不得其法。
笔者经过调查得知,学生出错的根本原因在于不理解功率取最大值的条件。
这里笔者就电源最大输出功率的条件论证及应用,结合自己的教学实际谈一点粗浅的认识,请同仁指教。
一、基本规律及条件论证1.规律一,当电源电动势E和内电路电阻r一定,外电路的电阻R可变时,电源的输出功率在满足条件的情况下,可取得最大值。
下面用多种方法对此结论加以证明,旨在让中学生读者选择适合自己认识的证法,以加深对电源最大输出功率条件的理解。
1.1 证明方法之一,公式法电源的输出功率,即消耗在外电路电阻上的功率,据闭合电路的欧姆定律有,所以(1)(1)式可变形为(2)根据公式“若a、b均为正数,则a+b≥,当且仅当a=b时,a+b取最小值”可得 (2)式分母中,当(即)时,取最小值,因而,当电源的输出功率有最大值1.2 证明方法之二,解析法可将(1)式变形为(3)当(3)式分母中(即)时,分母取最小值,因而电源有最大输出功率。
1.3 证明方法之三,利用二次函数的极值。
若路端电压为U,电路中电流为I,则外电路中消耗的功率应为,而据闭合电路的欧姆定律有(4)所以电源输出功率可以表示为(5)由(5)式可以看出,输出功率P是电流I的二次函数,且二次项系数为负,因而当电流(此时)时,电源输出功率有最大值1.4 证明方法之四,图像法根据(4)式作出路端电压随电路中电流变化的图像(图1),图像上任意一点N所对应的路端电压为U,电流为I,则这时消耗在外电路上的功率可以用图中矩形(画斜线部分)的面积来表示。
从图中可以看出,当电路中电流很小或者很大时,图中矩形的面积均较小,而只有当时,,矩形面积最大,即电源的输出功率有最大值1.5 证明方法之五,利用导数求极值 (1)式中P 对R 求导可得。


电源的输出功率及有关的几个重要推论摘要:通过对电源输出功率问题的分析研究,总结出比较实用的电源的输出功率及有关的几个重要推论,以便快速准确解题。
关键词:电源输出功率;等效电源;等效内阻;重要推论电源的输出功率问题是高频出现于各类试卷中的典型题目.现就电源的输出功率及有关的几个重要推论简要探讨其后,以便进一步理解和快速解答此类问题.一、电源输出功率的变化规律探讨 1.对于如图1所示的纯电阻电路,电源电动势E ,内阻为r ,当滑动变阻器R 的滑片移动时,试分析电源的输出功率P 出如何变化?因P 出=I 2R =E 2R (R +r )2=E 2(R -r )2R +4r .则电源的输出功率P 出随R 的变化规律大致如图2曲线所示,即:①当R =r 时,电源的输出功率最大为P m =E 24r .②当R >r 时,随着R 的增大输出功率越来越小.③当R <r 时,随着R 的增大输出功率越来越大. 针对电源的最大输出功率,由R =r 和欧姆定律知:④当端电压2E U =时,电源的输出功率最大为P m =E 24r ,⑤当总电流rE I 2=时,电源的输出功率最大为P m =E 24r .2.对于图3所示的电路等,可结合等效电源法用上述推论快速解答问题.即当R 2= r ′(r ′为等效内阻,即r ′=R 1+r )时,滑动变阻器R 2消耗的功率最大,且P 2m =rE '42…特别说明:上述推论成立有条件的,即电路为纯电阻电路,且内阻及等效内阻必须为定值电阻.典例1. 如图3所示的电路,已知电源电动势E =5 V ,内阻=2 Ω,定值电阻R 1=0.5 Ω,滑动变阻器R 2的阻值范围为0~10 Ω.求:(1)当滑动变阻器R 2的阻值为多大时,电阻R 1消耗的功率最大?最大功率是多少? (2)当滑动变阻器的阻值为多大时,滑动变阻器消耗的功率最大?最大功率是多少? (3)当滑动变阻器的阻值为多大时,电源的输出功率最大?最大功率是多少? 解析:(1)定值电阻R 1消耗的电功率为P 1=I 2R 1=E 2R 1(R 1+R 2+r )2,可见当滑动变阻器的阻值R 2=0时,R 1消耗的功率最大,最大功率为P 1m =E 2R 1(R 1+r )2=2 W.· E r SR P 图1 图2图3(2)将定值电阻R 1看做电源内阻的一部分,则等效电源的等效内阻r ′=R 1+r =2.5 Ω,等效电动势仍为E ,故当滑动变阻器的阻值R 2=r′=2.5 Ω时,滑动变阻器消耗的功率最大,最大功率为P 2m =E 24r ′=)(412r R E +=2.5 W.(3)由电源的输出功率与外电阻的关系可知,当R 1+R 2=r ,即R 2=r -R 1=(2-0.5) Ω=1.5 Ω时,电源有最大输出功率,最大功率为P m =E 24r =3.125 W.二、电源输出功率非最大时的电阻、电流和电压的变化规律探讨当P 出<P m 时,每个输出功率P 对应两个外电阻R 1和R 2,两个电流I 1和I 2,两个外电压U 1和U 2,它们的关系如下:①由P=I 2R =R rR E 2)(+,即222Pr Pr)2(+--R E PR =0 ,分别设两个根为R 1、R 2,整理得:r PE R R 2221-=+ 和221r R R =. ②由I Ir E UI P )(-==整理得,02=+-P EI rI ,由韦达定理等得:rEI I =+21和r P I I =21.③ 由UI P ==rU E U)(- 整理得,0Pr 2=+-EU U ,由韦达定理等得:E U U =+21和Pr 21=U U典例2.如图4甲所示电路中,R 为电阻箱,电源的电动势为E ,内阻为r .图乙为电源的输出功率P 与电流表示数I 的关系图象,其中功率P 0分别对应电流I 1、I 2,外电阻R 1、R 2.下列说法中正确的是( )A .I 1+I 2>rE B.r EI I =+21 BC .rR 1>2R r D .r R 1=2R r解析:由闭合电路欧姆定律得:U =E ﹣Ir ,则输出功率为:P =UI =EI ﹣I 2r ,故有,整理得:rEI I =+21,故A 错误,B 正确; 图4根据电功率表达式,P 0==,且rR EI +=,则有:;整理得:221r R R =,则C 错误、D 正确,;故答案为BD .巩固练习:1.在纯电阻电路中,当用一个固定的电源(E 、r 是定值)向变化的外电阻供电时,关于电源的输出功率P 随外电阻R 变化的规律如图5所示,则( )A .当R =r 时,电源有最大的输出功率B .电源有最大的输出功率时电源的效率η=100%C .电源的总功率P ′随外电阻R 的增大而增大D .电源的输出功率P 随外电阻R 的增大而增大2.某同学将一直流电源的总功率P E 、输出功率P R 和电源内部的发热功率P r 随电流I 变化的图线画在同一坐标系内,如图6所示,根据图线可知( )A .反映P r 变化的图线是bB .电源电动势为8 VC .电源内阻为2 ΩD .电源的最大输出功率为2W3. 将阻值相等的R 1和R 2串联后接在一个稳压电源上,两个电阻均是用金属丝绕制而成的,设R 1温度不变,对R 2加热或冷却,则关于R 2的电功率变化情况,下列说法正确的是( )A. 加热变大,冷却变小B. 加热变小,冷却变大C. 加热、冷却都变小D. 加热、冷却都变大4. 在一些电路中,我们常可以将一部分含电源的未知电路等效成一个不知内阻和电动势的电源.如图7所示,电路虚线框内的各元件参数未知但均为定值,当它的输出端a 、b 间分别接入不同阻值的电阻R x 时,电流表有不同读数I ,则(1)表格中①、②的数值应为( ) A .①=28Ω②=0.1A B .①=38Ω②=0.2A C .①=48Ω②=0.3A D .①=58Ω②=0.4A(2)R x 为多大时其消耗的功率最大?最大功率为多少? (3)与10Ω电阻消耗功率相等的另一电阻阻值是多大?5. 如图8所示电路中,R 为电阻箱,电源的电动势为E ,内阻为r 。


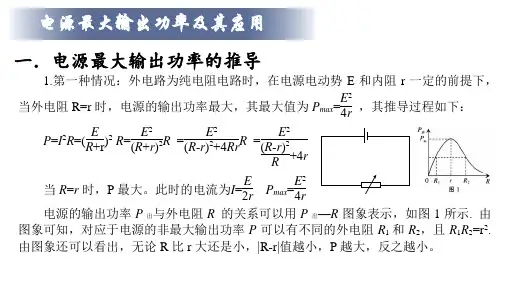
电源最大输出功率及其应用一.电源最大输出功率的推导1.第一种情况:外电路为纯电阻电路时,在电源电动势E 和内阻r 一定的前提下,当外电阻R=r 时,电源的输出功率最大,其最大值为P max =E 24r ,其推导过程如下:P =I 2R =(E R +r )2 R =E 2(R +r )2R =E 2(R -r )2+4Rr R =E 2(R -r )2R +4r当R =r 时,P 最大。
此时的电流为I =E 2r P max =E 24r电源的输出功率P 出与外电阻R 的关系可以用P 出—R 图象表示,如图1所示. 由图象可知,对应于电源的非最大输出功率P 可以有不同的外电阻R 1和R 2,且R 1R 2=r 2. 由图象还可以看出,无论R 比r 大还是小,|R-r|值越小,P 越大,反之越小。
2.第二种情况:外电路为非纯电阻电路时,电源的最大输出功率推导过程如下:P =UI =(E -Ir )I =-rI 2+EI ,这是一个二次函数,有极值,根据数学知识可求得P max =E 24r ,此时电流I =E 2r ,这一结论比第一种情况更具有普遍性,第一种情况是第二种情况的特例。
结论:无论纯电阻还是非纯电阻电路,当I =E 2r ,电源的输出功率最大,最大值为P max =E 24r 。
二.纯电阻电路中最大功率的应用1.定值电阻与滑动变阻器串联例题1:如图所示,电源电动势E =3V ,内阻r =3Ω,定值电阻R 1=1Ω,滑动变阻器R 2的最大阻值为10Ω,求:(1) 当变阻器的阻值为多大时,电源输出功率最大?电源输出的最大功率是多少?电源的效率为多大?(2) 当变阻器的阻值R 2为多大时变阻器消耗功率的最大?变阻器消耗的最大功率是多少?(3) 当滑动变阻器的阻值R 2为多大时,电阻R 1消耗的功率最大?电阻R 1消耗的最大功率是多少?【解析】(1)根据结论可知,当电路内外电阻相等时输出功率最大,即当变阻器的阻值为2Ω时输出功率最大,P max =E 24r =0.75W ,效率为50%(2)在变阻器变化过程中若R 减小时,电路中的电流I 增大,根据P =I 2R 无法直接判断最大功率,我们可以借用以上结论,当我们把R 1看作电源内阻时,R 2就作为外电路了,当内外电路电阻相等时,输出功率最大,所以当R 2与等效内阻(R 1+r )相等时,功率最大,此时R 2应等于4Ω,=916 W(3非常麻烦,也没有必要,大家想一下,当通过R 1的电流最大时,它的功率不就是最大吗?即当R 2=0时,电流最大,R 1的功率也最大,I =E R 1+r =34 A P =I 2R =916 W 2. 定值电阻与滑动变阻器并联例题2 如图所示,电源电动势E =2V ,内阻r =1Ω,电阻R 0=2Ω,滑动变阻器的阻值范围为0~10Ω.求:(1)变阻器R 的阻值为多大时,R 0消耗的功率最大?(2)变阻器R 的阻值为多大时,R 上消耗的功率最大?是多少?(3)变阻器R 的阻值为多大时,电源的输出功率最大?是多少?【解析】(1)当R 0两端的电压最大时,R 0消耗的功率最大,当R 取最大值时,路端电压(即并联电路两端的电压)最大,Ω时R 上消耗的功率最大,最大输出功率为P max =(43)24×23 =23 W(3)当内外电阻相等时,电源的输出功率最大,即R 并=r ,R =2Ω,P max =E 24r =1W 小结:当把定值电阻等效为电源内阻时,串联、并联的区别:电动机刚好正常工作(额定输出功率为P0=2W),甲图电流为I1,乙图电流为I2,则下列选项正确的是()A. I1=2A,I2=1AB. I1=2A,I2=2AC. R1=2Ω,R2=2ΩD. R1=2Ω,R2=1.5ΩD项,把R3看成电源的内阻,ab间为外电路,电压表的示数就可以看作路端电压,故ΔUΔI=r+R3=6Ω,两种情况下比值相等,故D错误。
求解电源的最大输出功率的几种方法及其规律【题目1】如图1所示的电路,若电源的电动势为E ,内电阻为r ,外部电路有滑动变阻器R ,问在什么条件下电源的输出功率最大?设电源的输出功率为P ,端压为U ,流过电源的电流为I 。
方法一:运用P~R 函数关系法:因为UI P =、IR U =和Rr EI +=, 所以22)(R r RE P +=,得R r Rr E P ++=222。
可见,当R Rr =2,即r R =时P 有最大值, 且最大值rE P 42max=。
P~R 的函数图像如图2所示。
①当R=r 时,电源的输出功率最大,P m =rE 42。
②当R >r 时,随着R 的增大输出功率减小。
③当R <r 时,随着R 的减小输出功率减小。
方法二:运用P~I 函数关系法因为UI P =、Ir E U -=,所以r I EI P 2-=, 推得rE r E I r P 4)2(22+--=。
可见,当rEI 2=时P 有最大值, 且最大值rE P 42max=。
P~I 的函数图像如图3所示。
方法三:运用P~U 函数关系因为UI P =、rUE I -=,所以r U U r E P 2-=,推得rE E U r P 4)2(122+--=。
可见,当2EU =时P 有最大值,图1图4图3图2且最大值rE P 42max=。
P~U 的函数图像如图4所示。
【规律总结】当R=r 时电源的输出功率最大,且电源的最大输出功率为r E 42,此时2E U =,rE I 2=。
此时 U ~I 图像如图5所示,图5中斜线部分的“面积”表示了电源的最大输出功率。
“等效电源”解决功率问题【题目2】如图所示,电源的电动势E=2V ,内阻r=1Ω,定值电阻R 0=2Ω,变阻器R 的阻值变化范围为0~10Ω,求:(1)变阻器R 的阻值为多大时,R 0消耗的功率最大?(2)变阻器R 的阻值为多大时,R 上消耗的功率最大?是多少? (3)变阻器R 的阻值为多大时,电源的输出功率最大?是多少?方法:(1)对定值电阻,直接运用公式。
最大功率的计算公式在我们的日常生活和学习中,经常会碰到各种各样与功率相关的问题。
那什么是最大功率呢?最大功率的计算公式又是什么呢?别急,咱们慢慢道来。
最大功率这个概念啊,简单来说,就是在某个特定条件下,一个设备或者系统能够输出的最大能量转换效率。
比如说,一辆汽车发动机能达到的最大动力输出,一个灯泡能发出的最亮光线对应的功率等等。
那最大功率的计算公式到底是啥呢?对于直流电路,最大功率的计算公式是 P = I²R (其中 P 表示功率,I 表示电流,R 表示电阻)。
在交流电路中呢,情况稍微复杂一点,最大功率的计算就需要考虑到电压、电流的相位等因素啦。
我给您讲个事儿吧,就前几天,我家那台用了好些年的空调突然出了点毛病。
制冷效果变得特别差,我就琢磨着是不是功率出了问题。
我找来工具,测了测电流和电阻,想着用最大功率的计算公式算一算,看看是不是功率不足导致制冷不行。
结果发现,还真有可能是电路中的某个电阻出了点小状况,影响了功率输出。
再来说说在物理实验中的应用。
比如我们在做电学实验的时候,经常会通过改变电阻的大小,来观察功率的变化。
这时候,最大功率的计算公式就能派上大用场啦。
通过计算,我们可以准确地知道在什么样的电阻值下,电路能够输出最大功率,从而达到最佳的实验效果。
在实际的工程应用中,比如电力系统的设计,工程师们必须精确计算最大功率,以确保电网能够稳定运行,不会因为过载而出现故障。
想象一下,如果没有准确计算最大功率,一个城市的电力供应可能就会出现大问题,那可就麻烦啦!学习最大功率的计算公式,不仅能帮助我们解决实际生活中的问题,对于我们理解能量转换的原理也非常有帮助。
它就像是一把钥匙,能打开我们对电学世界更深入理解的大门。
不管是在简单的直流电路,还是复杂的交流电路中,只要我们掌握了最大功率的计算公式,再结合实际情况进行分析,就能轻松应对各种与功率相关的问题。
所以啊,别小看这小小的计算公式,它的作用可大着呢!希望大家都能熟练掌握,让它成为我们解决问题的有力工具。
电源输出功率与外电阻的关系之勘阻及广创作一、电源的最大输出功率在电源负载为纯电阻时,电源的输出功率与外电阻R 的关系是:P 出=I 2R=.r 4R)r R (E Rr4)r R (RE )r R (RE 222222+-=+-=+由此式可以看出,当外电阻等于内电阻(即R=r )时,电源输出功率最大,最大输出功率为r 4E P 2m =. 电源的输出功率P 出与外电阻R 的关系可以用P 出—R图象暗示,如图1所示. 由图象可知,对应于电源的非最大输出功率P 可以有分歧的外电阻R 1和R 2,且R 1R 2=r 2(请同学们自己证明). 由图象还可以看出,当R<r 时,若R 增大,则P 出增大;当R>r 时,若R 增大,则P 出减小.注意:1. 推导此关系式时,R 是可变电阻,r 是定值电阻. 当外电阻等于内电阻,即R=r 时,电源输出功率最大,最大输出功率为r 4E P 2m =;若R 与r 不相等,则R 值越接近r 的值,P 出越大.2. 电源的输出功率与电源的效率是完全分歧的物理量. 电源的效率Rr 11rR R)r R (I R I 22+=+=+=η,所以当R 增大时,效率η提高. 当R=r时,电源有最大输出功率,但效率仅为50%,效率其实不高. 二、电源的外特性曲线如图2所示,在电源的外特性曲线上某点纵坐标和横坐标值的乘积为电源的输出功率,图中阴影矩形的面积暗示电源的输出功率,当2E U =时,电源输出功率最大. (请同学们想一想,为什么?)例1、如图3所示,电源的电动势E=2V ,内阻r=1Ω,定值电阻R 0=2Ω,变阻器R 的阻值变更范围为0~10Ω,求:(1)变阻器R 的阻值为多大时,R 0消耗的功率最大?(2)变阻器R 的阻值为多大时,R 上消耗的功率最大?是多少?(3)变阻器R 的阻值为多大时,电源的输出功率最大?是多少?解析(1)R 0消耗的功率20R U P =,由于R 0是定值电阻,故R 0两端的电压越大,R 0消耗的功率P 0越大. 而路端电压随着外电阻的增大而增大,所以当R=10Ω时,R 0消耗的功率最大.(2)可以把电源和定值电阻R 0合起来看作一个等效电源,等效电路图如图4所示,等效电源的电动势E ′=V34V 2122E r R R 00=⨯+=+,等效内阻r ′=Ω=Ω+⨯=+321221r R rR 00,当R=r ′时,即32R =Ω时R 上消耗的功率最大,.W 32W 324)34(r 4E P 22maxR =⨯=''=(3)当外电路电阻与内电路电阻相等时,电源输出功率最大,即rR R RR P 00=+=外时,代入数值得:R=2Ω时,电源输出功率最大. 最大输出功率.W 1W 142r 4E P 22max=⨯==例2、如图5所示的电路中,当电键K 断开和闭合时,电源的输出功率完全相同. 已知R 1=9Ω,R 2Ω,求当K 断开时R 1上消耗的功率P 和K 闭合时R 1上消耗的功率P 1之比.解析:K 闭合时,R 1、R 2并联,其并联电阻为=+=212112R R R R R 4Ω,由于当电键K 断开和闭合时,电源的输出功率完全相同,据2121r R R =可得==121R R r 6Ω,所以有:当K 断开时R 1上消耗的功率21)rR E(P +=·225E 9R 21=;当K 闭合时R 1上消耗的功率925E 4R )R r R E(P 21212121⨯=⋅+=,所以有:.49P P 1=3、(2005江苏物理卷)如图所示,R 为电阻箱,○V 为理想电压表.当电阻箱读数为R 1=2Ω时,电压表读数为U 1=4V ;当电阻箱读数为R 2=5Ω时,电压表读数为U 2=5V .求: (1)电源的电动势E 和内阻r 。
求解电源的最大输出功率的几种方法及其规律
【题目1】如图1所示的电路,若电源的电动势为E ,内电阻为r ,外部电路有滑动变阻器R ,问在什么条件下电源的输出功率最大?
设电源的输出功率为P ,端压为U ,流过电源的电流为I 。
方法一:运用P~R 函数关系法:
因为UI P =、IR U =和R
r E
I +=
, 所以2
2)(R r R
E P +=,得R r R
r E P ++=222。
可见,当R R
r =2
,即r R =时P 有最大值, 且最大值r
E P 42max
=。
P~R 的函数图像如图2所示。
①当R=r 时,电源的输出功率最大,P m =r
E 42。
②当R >r 时,随着R 的增大输出功率减小。
③当R <r 时,随着R 的减小输出功率减小。
方法二:运用P~I 函数关系法
因为UI P =、Ir E U -=,所以r I EI P 2
-=, 推得r
E r E I r P 4)2(2
2+--=。
可见,当r
E
I 2=
时P 有最大值, 且最大值r
E P 42max
=。
P~I 的函数图像如图3所示。
方法三:运用P~U 函数关系
因为UI P =、r
U
E I -=,所以r U U r E P 2-=,
推得r
E E U r P 4)2(12
2+--=。
可见,当2
E
U =
时P 有最大值,
图1
图4
图3
图2
且最大值r
E P 42max
=。
P~U 的函数图像如图4所示。
【规律总结】当R=r 时电源的输出功率最大,且电源的最大输出功
率为r E 42,此时2E U =,r
E I 2=。
此时 U ~I 图像如图5所示,图5中斜线部分的“面积”表示了电源的最大输出功率。
“等效电源”解决功率问题
【题目2】如图所示,电源的电动势E=2V ,内阻r=1Ω,定值电阻R 0=2Ω,变阻器R 的阻值变化范围为0~10Ω,求:
(1)变阻器R 的阻值为多大时,R 0消耗的功率最大?
(2)变阻器R 的阻值为多大时,R 上消耗的功率最大?是多少? (3)变阻器R 的阻值为多大时,电源的输出功率最大?是多少?
方法:(1)对定值电阻,直接运用公式。
R 0消耗的功率0
2
00R U p =,
由于R 0是定值电阻,故R 0两端的电压越大,R 0消耗的功率P 0越大. 而路端电压随着外电阻的增大而增大,所以当R=10Ω时,R 0消耗的功率最大.
(2)对可变电阻,运用等效电源法。
可以把电源和定值电阻R 0合起来看作一个等效电源,等效电路图如图所示。
(断路电压U=E ,短路电流I M =E/r )
等效电源电动势E ′=
V E r R R 3
4
00=+,
等效电源内阻r ′=
Ω=+3
2
00r r R R ,
当R=r ′时,即R=2/3Ω时R 上消耗的功率最大,W r
E p M
32
4/2/==
(3)当外电路电阻与内电路电阻相等时,电源输出功率最大。
即
r R R RR =+0
时,代入数值得:R=2Ω时,电源输出功率最大.
最大输出功率/2
/
4r
E P M ==
1W 【题目3】图中所示的电路中,电源的电动势为E ,内阻为r ,R 1为定值电阻,那么负载电阻R 取何值时,负载R 上将获得最大功率?
方法一:等效电源法。
将定值电阻R 1和电源看成一个等效电源,如图虚线框所示。
E r R
R 1
A
B
E ' r '
则等效电源的电动势E E =',内阻r R r +=1', 由例1的结论可知,当r R r R +==1'时,
)
(4'4'12
2r R E r E P m +=
= 方法二:常规思想法。
)
(4)]([)(12
122
12
r R R
r R R E R r R R E R I P +++-=++==
显然,r R R +=1时,)
(412
r R E P m +=
典型案例:
1.右图所示的电路中,电源的电动势E=5V , r=4Ω,R=90Ω,R 0为可变电阻,在R 0由0增大到400Ω的过程中,求:
⑴可变电阻R 0上消耗热功率最大的条件和最大值。
⑵电源的内阻r 和固定电阻R 上消耗的最小功率之和。
解:(1)当R 0=(R+r )=94Ω时,R 0有最大热功率,P 0=0.066W (2)当R 0=400Ω时,P R +P r 最小。
且P R +P r =()W 0096.0r R R
r R E
2
0=+⎪⎪⎭
⎫ ⎝⎛++ 2.右图所示,直线A 为电源的U —I 图线,直线B 为电阻R 的U —I 图线,用该电源和电阻组成闭合电路时,电源的输出功率和电路的总功率分别是多大?电源的效率η为多大? 解:(1)E=3V ,r=0.5Ω R=1Ω ∴I =2A ,P 出=I 2R =4W P 总=EI =6W
(2)η= P 出/ P 总=66.7%
3.使用等效电源法还能对《用安培表和伏特表测电源的电动势和内电阻》这个实验进行误差分析。
由于电表内阻的影响,采用图7所示的电
路,所测的电动势____于真实值,内阻_____于
真实值;采用图8所示的电路,所测的电动势
____于真实值,内阻_____于真实值。
解:图7中,安培表的示数确为流过电源的电流,但伏特表的示数却不是电源的路端电
压,而是虚线框内等效电源的路端电压,因此,
采用图7所示的电路,测出的是虚线框内等效电源的电动势E '和内阻r '。
R 0
R
E
r
E r 图8
s A V E r 图7 s
A V
即:真测E E E E ===' 真串测r R r r r r A >+==='
图8中,伏特表的示数确为电源两端的路端电压,但安培表的示数却不是流过电源的电流,而是流过虚线框内等效电源的电流,因此,采用图8所示的电路,测出的是虚线框内等效电源的电动势E '和内阻r '。
即:真测E E r R R E E V V <+=
=' 真并测r r r
R R r r r V V
<+==='
故此题的答案为等、大、小、小。