测量平差公式.pdf
- 格式:pdf
- 大小:153.71 KB
- 文档页数:4


测量平差期末复习资料1. 将静止的海水面向整个陆地延伸,用所形成的封闭曲面代替地球表面,形成的重力等位面,这个曲面称为大地水准面。
其特点是水准面上任意一点的铅垂线(重力作用线)都垂直于该点的曲面。
2. 6°带中央子午线经度N=L=6N-3, 3°带中央子午线经度L=3n 。
3. 高程系统:确定该点沿铅垂方向到某基准面的距离。
绝对高程(海拔):指某点沿铅垂线方向到大地水准面的距离,用H表示。
相对高程:某点距假定水准面的铅垂距离。
高差:地面上两点间的高程之差。
4. 地形 :a,地物:地面上固定性物体,如河流、房屋、道路、湖泊等; b.地貌:地面的高低起伏的形态,如山岭、谷地和陡崖等。
5. 线性代数补充知识1) 由n m ⨯个数有次序地排列成m 行n 列的表叫矩阵通常用一个大写字母表示, 如:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⨯mn m m n n n m a a a a a a a a a A212222111211 2)若m=n ,即行数与列数相同,称A 为方阵。
元素a11、a22……ann 称为对角元素。
3)若一个矩阵的元素全为0,称零矩阵,一般用O 表示。
4)对于 的方阵,除对角元素外,其它元素全为零,称为对角矩阵。
如:)(00000022112211nn mn n m a a adiag a aa A=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⨯5)对于 对角阵,若a11=a22=……=ann =1,称为单位阵,一般用E 、I 表示。
6)若aij=aji ,则称A 为对称矩阵.矩阵的基本运算:1)若具有相同行列数的两矩阵各对应元素相同,则: 2)具有相同行列数的两矩阵A 、B 相加减,其行列数与A 、B 相同,其元素等于A 、B 对应元素之和、差。
且具有可交换性与可结合性。
3)设A 为m*s 的矩阵,B 为s*n 的矩阵,则A 、B 相乘才有意义,C=AB ,C 的阶数为m*n 。
O A=A O =O ,IA=AI=A ,A (B+C )=AB+AC ,ABC=A (BC )矩阵的转置:对于任意矩阵Cmn:nn ⨯n n ⨯BA =⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⨯mn m m n n n m c c c c c c c c c C 212222111211将其行列互换,得到一个nm 阶矩阵,称为C 的转置。


坐标平差闭合计算公式一、坐标平差闭合差计算的基本概念。
1. 定义。
- 在测量工作中,由于观测值存在误差,使得由观测值计算得到的结果(如闭合导线的坐标计算)与理论值之间存在差异,这个差异就称为闭合差。
坐标平差闭合差计算是测量平差中的重要内容,其目的是通过一定的方法对观测值进行调整,使得调整后的结果满足理论上的几何关系。
2. 闭合导线坐标计算中的闭合差类型。
- 角度闭合差:对于闭合导线,其内角和理论值根据多边形内角和公式(n - 2)×180^∘(n为多边形边数)计算。
而实际观测的内角和与理论值之间的差值就是角度闭合差f_β,即f_β=∑limits_i = 1^nβ_i-(n - 2)×180^∘。
- 坐标增量闭合差。
- 在平面直角坐标系中,闭合导线各边坐标增量的代数和在理论上应该为零。
设Δ x_i和Δ y_i分别为第i边的纵、横坐标增量,对于闭合导线,∑limits_i =1^nΔ x_i=0,∑limits_i = 1^nΔ y_i=0。
但由于观测误差的存在,实际计算得到的坐标增量代数和∑limits_i = 1^nΔ x_i=f_x,∑limits_i = 1^nΔ y_i=f_y,f_x和f_y分别称为纵、横坐标增量闭合差。
- 坐标增量闭合差的大小反映了观测误差对坐标计算的影响程度。
根据坐标增量闭合差可以计算出导线全长闭合差f_D,f_D=√(f_x)^2+f_{y^2}。
- 为了衡量导线测量的精度,还需要计算导线全长相对闭合差K=frac{f_D}{∑limits_i = 1^nD_i}(其中∑limits_i = 1^nD_i为导线的总长度)。
二、坐标平差闭合差的调整原则和方法。
1. 角度闭合差的调整。
- 调整原则:将角度闭合差反号平均分配到各观测角中。
设角度闭合差为f_β,观测角个数为n,则每个角的改正数v_β=-frac{f_β}{n}。
- 调整后的角度计算:调整后的角度β_i'=β_i+v_β。

测量平差一.测量平差基本知识 1.测量平差定义及目的在设法消除系统误差、粗差影响下,其基本任务是求待定量的最优估量和评定其精度。
人们把这一数据处理的整个过程叫测量平差。
测量平差的目的:一是通过数据处理求待定量的最优估值;二是评定观测成果的质量。
2.协方差传播律及协方差传播律是观测值(向量)与其函数(向量)之间精度传递的规律。
①观测值线性函数的方差: 函数向量:Y=F(X) Z=K(X)其误差向量为:ΔY=F ΔX ΔZ=K ΔX则随机向量与其函数向量间的方差传递公式为⎪⎪⎪⎭⎪⎪⎪⎬⎫====F D K D K D F D K D K D F D F D TXZYTXYZTXZTXY②多个观测值线性函数的协方差阵t×n×n ×t×n T n XX t t ZZ K D K D =③非线性的协方差传播T XX ZZ K KD D =3.权及常用的定权方法①权表示比例关系的数字特征称之为权,也就是权是表征精度的相对指标。
权的意义不在于它们本身数值的大小,而在于它们之间所存在的比例关系。
()n i iiP ,...,2,1220==σσi P 为观测值i L 的权,20σ是可以任意选定的比例常数。
②单位权方差权的作用是衡量观测值的相对精度,称其为相对精度指标。
确定一组权时,只能用同一个0σ,令0σσ=i ,则得:iiP ===02202021σσσσ上式说明20σ是单位权(权为1)观测值的方差,简称为单位权方差。
凡是方差等于20σ的观测值,其权必等于1。
权为1的观测值,称为单位权观测值。
无论20σ取何值,权之间的比例关系不变。
③ ⅰ.水准测量的权NC P h =式中,N 为测站数。
SC P h =式中,S 为水准路线的长度。
ⅱ.距离量测的权ii S C P =式中,i S 为丈量距离。
ⅲ.等精度观测算术平均值的权CP ii N=式中,i N 为i 次时同精度观测值的平均值。




第五章 测量误差及测量平差§5.1 测量误差概述一、测量误差的概念某量的各测量值相互之间或观测值与理论值之间的往往存在着某些差异,说明观测中存在误差。
观测值与真值之差称为测量误差,也叫真误差。
X l i i -=∆ (i =1、2、……、n ) X 为真值。
二、研究测量误差的目的分析测量误差的产生原因、性质和积累规律;正确地处理测量成果,求出最可靠值;评定测量结果的精度;为选择合理的测量方法提供理论依据。
三、测量误差产生的原因1.测量仪器因素2.观测者的因素3.外界条件的因素测量观测条件——测量仪器、观测人员和外界条件这三方面的因素综合起来称为测量观测条件。
等精度观测——测量观测条件相同的各次观测称为等精度观测。
非等精度观测——测量观测条件不相同的各次观测称为非等精度观测。
四、测量误差的分类1.系统误差在相同的观测条件下对某量作一系列观测,如果误差的大小、符号表现出系统性,或按一定的规律变化,或保持不变,这种误差称为系统误差。
其特点:具有累积性,但可以采用适当的观测方法或加改正数来消除或减弱其影响。
2.偶然误差在相同的观测条件下对某量作一系列观测,如果误差的大小和符号不定,表面上没有规律性,但实际上服从于一定的统计规律性,这种误差称为偶然误差。
偶然误差单个的出现上没有规律性,不能采用适当的观测方法或加改正数来消除或减弱其影响。
因此,观测结果中偶然误差占据了主要地位,是偶然误差影响了观测结果的精确性。
五、减少测量误差的措施对系统误差,通常采用适当的观测方法或加改正数来消除或减弱其影响。
对偶然误差,通常采用多余观测来减少误差,提高观测成果的质量。
§5.2 偶然误差的特性一、精度的含义1.准确度准确度是指在对某一个量的多次观测中,观测值对该量真值的偏离程度。
2.精密度精密度是指在对某一个量的多次观测中,各观测值之间的离散程度。
3.精度精度也就是精确度,是评价观测成果优劣的准确度与精密度的总称,表示测量结果中系统误差与偶然误差的综合影响的程度。

测量平差资料第⼀章绪论⼀、观测误差1、为什么要进⾏观测必要观测、多余观测2、误差存在的现象3、误差产⽣的原因观测条件:观测仪器、观测者、外界条件4、误差的分类粗差、系统误差、偶然误差5、误差的处理办法⼆、测量平差的简史和发展三、测量平差的两⼤任务及本课程的主要内容第⼆章误差分布与精度指标⼀、偶然误差的规律性1、随机变量2、偶然误差的分布正态分布3、偶然误差的统计特性由统计分析可以看出,偶然误差具有下列特性:1、在⼀定的观测条件下,偶然误差的绝对值有⼀定的限值,即超过⼀定限值的偶然误差出现的概率为零;2、绝对值较⼩的偶然误差⽐绝对值较⼤的偶然误差出现的概率⼤;3、绝对值相等的正负偶然误差出现的概率相同;4、偶然误差的理论平均值为零⼆、随机变量的数字特征(1)反映随机变量集中位置的数字特征---数学期望(2)反映随机变量偏离集中位置的离散程度----⽅差(3)映两两随机变量x、y相关程度的数字特征---协⽅差3、协⽅差(a) 定义相关系数三、衡量精度的指标1、⽅差和中误差2、平均误差3、或然误差4、极限误差5、相对(中、真、极限)误差四、随机向量的数字特征1、随机向量2、随机向量的数学期望3、随机向量的⽅差-协⽅差阵协⽅差阵的定义协⽅差阵的特点4、互协⽅差阵协⽅差阵的定义协⽅差阵的特点五、精度准确度精确度观测值的质量取决于观测误差(偶然误差、系统误差、粗差)的⼤⼩。
1、精度:描述偶然误差,可从分布曲线的陡峭程度看出精度的⾼低。
2、准确度:描述系统误差和粗差,可⽤观测值的真值与观测值的数学期望之差来描述,即:3、精确度:描述偶然误差、系统误差和粗差的集成,精确度可⽤观测值的均⽅误差来描述,即:即观测值中只存在偶然误差时,均⽅误差就等于⽅差,此时精确度就是精度。
七、⼩结第三章协⽅差传播律⼏个概念1、直接观测量2、⾮直接观测量---观测值的函数⽔准测量导线测量三⾓形内⾓平差值3、独⽴观测值4、⾮独⽴观测值----相关观测值独⽴观测值各个函数之间不⼀定独⽴5、误差传播律6、协⽅差传播律⼀、观测值线性函数的⽅差设观测向量L及其期望和⽅差为:若观测向量的多个线性函数为三、两个函数的互协⽅差阵四、⾮线性函数的情况五、多个观测向量⾮线性函数的⽅差—协⽅差矩阵设观测向量的t个⾮线性函数为:对上式求全微分,得六、协⽅差传播律的应⽤1、⽔准测量的精度2、距离丈量的精度3、同精度独⽴观测值算术平均值的精度七、应⽤协⽅差传播律时应注意的问题(1)根据测量实际,正确地列出函数式;(2)全微分所列函数式,并⽤观测值计算偏导数值;(3)计算时注意各项的单位要统⼀;(4)将微分关系写成矩阵形式;(5)直接应⽤协⽅差传播律,得出所求问题的⽅差-协⽅差矩阵。
水准平差计算公式
平差公式=(闭合差/线路总长)*距离
介绍:
一、水准测量:水准测量是利用一条水平视线,并借助水准尺,来测定地面两点间的高差,这样就可由已知点的高程推算出未知点的高程。
通常由水准原点或任一已知高程点出发,沿选定的水准路线逐站测定各点的高程。
由于不同高程的水准面不平行,沿不同路线测得的两点间高差将有差异,所以在整理国家水准测量成果时,须按所采用的正常高系统加以必要的改正,以求得正确的高程。
二、水准仪的原理
水准测量是利用一条水平视线,并借助水准尺,来测定地面两点间的高差,这样就可由已知点的高程推算出未知点的高程。
三、水准仪的结构
根据水准测量的原理,水准仪的主要作用是提供一条水平视线,并能照准水准尺进行读数。
因此,水准仪构成主要有望远镜、水准器及基座三部分。
任务一(1):列条件方程:⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=''++-+--++-++++=++++=++++=++++0)sin )sin(sin sin sin )sin(1(cot cot ))(cot(cot ))(cot(cos 000387586438866434333878755765454326871ρL L L L L L L L v L v L v v L L v L v v L L v L wc v v v v w v v v v w v v v v b a⎪⎪⎪⎭⎫ ⎝⎛-+++=-+++=-+++=180180180765454326871L L L L w L L L L w L L L L w c b a任务一(2)列条件方程:⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎨⎧-=+-=+-=+-=+-=+-=+-=+-=+428831773266435524412334122411ˆˆˆˆˆˆˆˆˆˆˆˆˆˆX X v h X X v h X X V h X X v h X H v h X X v h X X v h H X v h B A列误差方程:⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧-=--=+-=-=-=+-=-==4283173264352412341241242δδδδδδδδδδδδδδv v v v v v vv误差矩阵:⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡87654321v vv v v v vv =⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-------10100101011011000010001110011000⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡4321δδδδ—⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡--02400200任务二:控制网平差报[平面点位误差表]点名长轴(m) 短轴(m) 长轴方位dms 点位中误差m高程中误差mP1 0.0035 P2 0.0033 P3 0.0045 P4 0.0060 [控制点成果表]点名X(m) Y(m) H(m) 备注A 0.0000 0.0000 20.1230 固定点B 0.0000 0.0000 48.7130 固定点P1 0.0000 0.0000 28.1369P2 0.0000 0.0000 39.0359P3 0.0000 0.0000 54.6017P4 0.0000 0.0000 56.5292数据录入:编辑网的属性:选择计算方案:闭合差计算:平差计算:任务三:点位误差表:[平面点位误差表]点名长轴(m) 短轴(m) 长轴方位dms 点位中误差m高程中误差mP1 0.0191 0.0147 141.1853 0.0241P2 0.0225 0.0195 3.3115 0.0298P3 0.0264 0.0220 12.2823 0.0344P4 0.0250 0.0181 18.1742 0.0309P5 0.0206 0.0186 6.2445 0.0278P6 0.0190 0.0165 112.2220 0.0251[控制点成果表]点名X(m) Y(m) H(m) 备注A 871.1893 220.8223 0.0000 固定点B 632.2173 179.4811 0.0000 固定点C 840.9400 533.4018 0.0000 固定点D 663.4752 570.7100 0.0000 固定点P1 825.8298 272.2452 0.0000P2 740.1267 312.5952 0.0000P3 768.3730 392.2339 0.0000P4 732.0697 470.9076 0.0000P5 681.6516 279.3417 0.0000P6 674.5787 506.1882 0.0000数据录入:编辑网的属性:选择计算方案:闭合差计算:闭合差信息:坐标推算:平差计算:成果:网形分析:平差略图:任务四:控制网平差报告点位误差表:[平面点位误差表]点名长轴(m) 短轴(m) 长轴方位dms 点位中误差m高程中误差mP1 1790.8181 1473.4317 177.3426 2319.0581P2 3623.6005 2557.5139 80.5619 4435.2404控制点成果表:[控制点成果表]点名X(m) Y(m) H(m) 备注A 4899.8460 130.8120 0.0000 固定点B 8781.9450 1099.4430 0.0000 固定点C 4548.7950 7572.6220 0.0000 固定点P1 5656.8640 2475.5593 0.0000P2 663.8174 2944.0183 0.0000数据录入:编辑控制网属性:选择计算方案:闭合差计算:坐标推算:平差计算:精度统计图:平差略图:网形分析:。
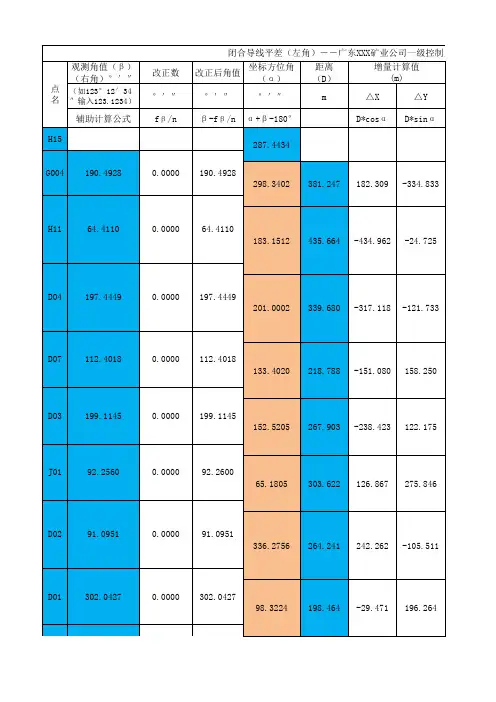
闭合导线坐标计算
闭合导线计算式根据外业观测的边长、夹角和方位角以及其中一个导线点的坐标,结合平差计算,来推算其余各导线点的坐标。
设对闭合导线n 个内角分别进行了观测,各个符号精度要求的观测值为
βi 测,并对闭合多边形的n 个边长分别进行了测量,各个符号精度要求的观测值为
L i ;其中一个导线点的坐标为x i y i ;确定其余各个导线点的坐标x x i 1+,y i 1+
1 角度闭合差的计算也调整
(1)实测角度闭合差的计算
闭合导线n 个实测内角的和
∑测β不等于其理论值(n-2)*180,其差称为角度闭合差以f β
表示:
︒−−=∑180*2)(测n f β
β
(2)实测角度闭合差检核 角度闭合差校核是将实测角度闭合差也同级导线角度闭合差的容许值f 容β,按各级导线测
量主要技术要求比较,以确定角度综合限差是否满足要求。
这里角度综合限差采用图根导线数据,即f 容β=40''n 。
(3)角度闭合差的调整 若f β≤f 容β
,则可以进行角度闭合的调整,否则,应分析情况重测。
角度闭合差的调整原则是,将f β以相反的符号平均分配到各个观测角中,即各点改正数为式 v β=
f β/n 计算时,根据角度的取位的要求,改正数可凑整到1″、6″、10″.若不能均分,一般情况下,因短边角引起的误差较大,因此给短边角的夹角多分配一点,使各角改正数的总和也反号的闭合差相等,即f v ββ−=∑
2、推算各边的坐标方位角
推算各边的坐标方位角目的是为了计算坐标增量。
推算方法根据起始方位角及改正后的
转折角,按式依次推算出各边的坐标方位角。
或
βαα右
−+=+1801i i 1801−+=+βαα左
i i 式中:
αi ----------第i 条边的正方位角 α
1−i ---------第i+1条的正方位角 ββ右左--------分别为第i-1条边与第i 条边间所夹的左右角。
在推算过程中,如果算出αi >360°,则应减去360°如果算出的αi <0°,则应加
上360°
为了发现推算过程中的差错,最后必须推算至起始边的坐标方位角,看其是否与已知值相等,以此作为计算校核。
3 坐标增量闭合差的计算和调整
(1)计算实测各边的坐标增量
设第i 条实测边的终、横坐标增量分别为 αi i i L X cos .=∆
测
αi i i L Y sin .=∆测
(2)确定理论纵、横坐标增量∑△Xi 理、∑△Yi 理
闭合导线的纵横坐标增量总和的理论值应为零,则有
∑△Xi 理=0
∑△Yi 理=0
(3)计算坐标增量闭合差fx.fy
由于测量误差,改正后的角度仍有残余误差,坐标增量总和的测量计算值∑△X 测与∑△Y 测一般都不为零,其值称为坐标增量闭合差,fx.fy 表示,则
fx=∑△Xi 测-∑△Xi 理=∑△Xi 测
fy=∑△Yi 测-∑△Yi 理=∑△Yi 测
(4)计算导线全长闭合差f 并检核全长相对闭合差K
因计算的闭合导线并不闭合,而存在一个缺口,这个缺口的长度称为导线闭合差f fy fx f 22+=
导线越长,全长闭合差也越大。
通常用相对闭合差来衡量导线测量的精度,导线的全长相对
闭合差按 K=∑L f =f L
l ∑
试中∑L 为导线边长的总和。
导线的全长相对闭合差应满足规定。
否则应先检查记录和全部业内作业计算,必要时到现场检查,重测部分或全部结果。
若K 值符合精度要求,则可将增量闭合差fx.fy 以相反符号。
按与边长成正比分配到各个增量中。
(5)计算各条边的改正数
v △xi.v △xi
任意一边分配的改正数v △xi.v △xi 按式
v
△xi=Li Li fx ∑ v △yi=
Li Li fy ∑ 改正数应按增量取位的要求凑整至cm 或mm ,并且必须使改正数的总和与反符号闭合差相等,即
f v
x x −=∑∆
f v x
y −=∑∆ (6)确定各个边长改正后的坐标增量-------坐标增量计算值(△Xi 算、△yi 算)又式
v X X
xi i i ∆+=∆∆测算 v Y Y
yi i i ∆+=∆∆测算 4、计算各个导线点的坐标X i+1. Y i+1. X X X
i i i ∆+=+算1 Y Y Y i i i ∆+=+算1
闭合导线坐标计算是按一定得次序在表中进行,如果导线未与高级控制点连接,则起算点的坐标可自行假设。
为了检查坐标推算中的差错,最后还应推回到起算的坐标,看其是否和已知值相等,以此作为计算校核。