(完整版)拉普拉斯变换

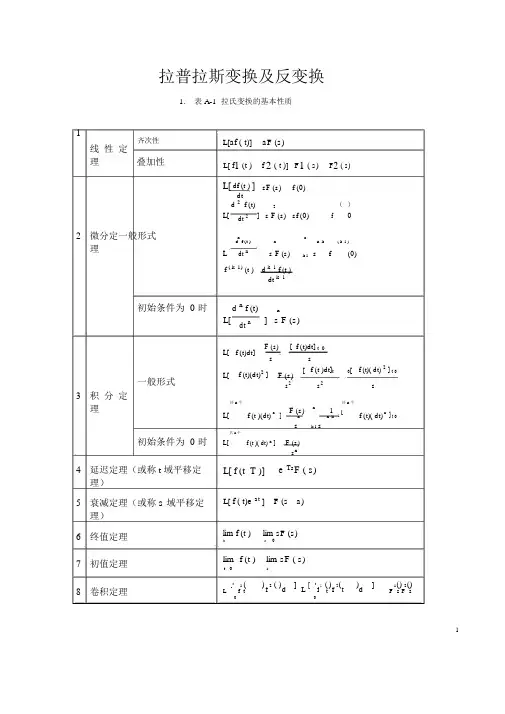
拉普拉斯变换及反变换1. 表 A-1 拉氏变换的基本性质1齐次性线性定理叠加性2微分定一般形式理L[af ( t)] aF (s)L[ f1 (t ) f 2 ( t )] F1 ( s) F2 ( s) L[ df (t ) ] sF (s) f (0)dtL[d 2 f (t) 2f（）dt 2 ] s F (s) sf (0) 0n nd f (t ) n n k ( k 1 )L dt n s F (s) k 1 s f (0) f ( k 1) (t ) d k 1 f (t )dt k 1初始条件为 0 时一般形式3积分定理初始条件为 0 时4延迟定理（或称 t 域平移定理）5衰减定理（或称 s 域平移定理）6终值定理7初值定理8卷积定理L[d n f (t) ndt n ] s F (s)L[ f (t)dt]F (s) [ f (t)dt] t 0s sL[ f (t)(dt)2 ] F (s)[ f (t )dt]t 0[ f (t)( dt) 2 ] t 0s2 ss2共 n个n共 n个nF (s) 1 nL[ f (t )(dt) ] 1 [ f (t)( dt) ] t 0nk 1 sn ks共 n个F (s)L[ f (t )( dt) n ]s nL[ f (t T )] e Ts F ( s)L[ f ( t)e at ] F (s a)lim f (t ) lim sF (s)t s0lim f (t ) lim sF ( s)t 0 st 1 ( ) 2 ( ) ] [ t 1 ( ) 2 ( ) ] 1() 2()[ f d L f f t dL f t t F s F s0 012．表 A-2 常用函数的拉氏变换和z 变换表拉氏变换E(s)111 e Ts1s12s13s1s n 11s a1( s a) 2as( s a)b a( s a)(s b)s2 2ss2 2( s a) 2 2s a( s a)2 21s (1 / T ) ln a 时间函数 e(t)δ(t)T (t )(t nT )n01(t )tt 22ntn!e atte at1 e ate at e btsin tcos te at sin te at cos ta t / T23．用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开，然后逐项查表进行反变换。

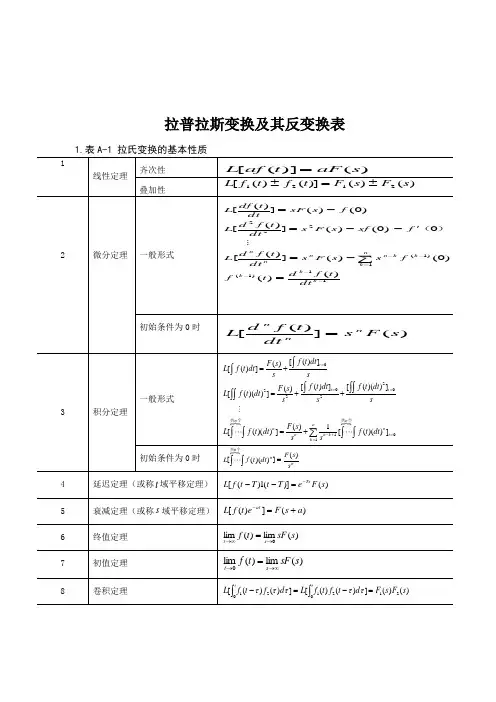
拉普拉斯变换及其反变换表3． 用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开，然后逐项查表进行反变换。

设)(s F 是s 的有理真分式11n 1n nn11m 1m mmas a s a s a b s b s b s b )s (A )s (B )s (F ++++++++==---- （m n >）式中系数n1n 1a ,a ,...,a ,a-，m1m 1b ,b ,b ,b - 都是实常数；n m ,是正整数。

按代数定理可将)(s F 展开为部分分式。

分以下两种情况讨论。

① 0)(=s A 无重根这时，F(s)可展开为n 个简单的部分分式之和的形式。

∑=-=-++-++-+-=n1i iinnii2211ss cs s c s s c s s c s s c )s (F 式中，Sn 2S 1S ，，， 是特征方程A(s)＝0的根。

i c 为待定常数，称为F(s)在i s 处的留数，可按下式计算： )s (F )s s (lim c is s i-=→或is s i)s (A )s (B c='=式中，)(s A '为)(s A 对s 的一阶导数。

根据拉氏变换的性质，从式（F-1）可求得原函数[]t s n 1i i n 1i i i 11i e c s s cL )s (F L )t (f -==--∑∑=⎥⎦⎤⎢⎣⎡-==② 0)(=s A 有重根设0)(=s A 有r 重根1s ，F(s)可写为())s s ()s s ()s s ()s (B s F n1r r 1---=+=nnii1r 1r 111r 11r r 1rss cs s c s s c )s s (c )s s (c )s s (c -++-++-+-++-+-++-- 式中，1s 为F(s)的r 重根，1+r s ，…, n s 为F(s)的n-r 个单根；其中，1+r c ，…, n c 仍按式(F-2)或(F-3)计算，r c ，1-r c ，…, 1c 则按下式计算：)s (F )s s (lim c r1s s r-=→)]s (F )s s ([dsdlim c -=)s (F )s s (dsd lim !j 1c -=)s (F )s s (dsdlim )!1r (1c --=原函数)(t f 为 [])()(1s F L t f -=⎥⎦⎤⎢⎣⎡-++-++-+-++-+-=s s cs s c s s c )s s (c )s s (c )s s (c L e c e c t c t )!2r (c t )!1r (c ∑+⎥⎦⎤⎢⎣⎡+++-+-= （F-6）。

第一章 拉普拉斯变换1 拉普拉斯变换的概念定义1 设函数()t f 为[)+∞,0上的实（或复）函数，且积分()dt et f st-+∞⎰0（s 为复参量）收敛，则由此积分所确定的函数()()dt et f s F st-+∞⎰=()1称为函数()t f 的拉普拉斯变换（简称为拉式变换）．记作()()[]t f L s F =()2()s F 称为()t f 的拉氏变换（或称为象函数）．如果()s F 是()t f 的拉普拉斯变换，则称()t f 为()s F 的逆变换（或称为象原函数），记作()()[]s F Lt f 1-=．由拉普拉斯变换的定义，可以求得一些常用函数的拉普拉斯变换． 例1 求阶跃函数()⎩⎨⎧<≥=0,00,t t k t f 的拉普拉斯变换.（图1）解 根据拉普拉斯变换的定义有 ()[]()dt et f t f L st-+∞⎰=0dt e k st-+∞⎰=dt ek st⎰+∞-=0积分dt est⎰+∞-0在()0Re >s 时收敛，且有sesdt e st st110=-=∞+-+∞-⎰所以()[]sk t f L =()()0Re >s ．当1=k 时，阶跃函数称为单位阶跃函数，记作()⎩⎨⎧<≥=0,00,t t k t u ，此时有()[]st u L 1=()()0Re >s ．例2 求指数函数()ate tf =的拉普拉斯变换.(a 为复数)解 由()1.2式可得()()dt edt ee s F ta s stat ⎰⎰+∞---+∞==as -=1()()()a s Re Re >．例3 求正弦函数()kt t f sin =的拉普拉斯变换．(k 为复数) 解 []dt kt ekt L st⎰+∞-=0sin sin()dt eee istiktikt-+∞-⎰-=21⎪⎭⎫⎝⎛+--=ik s ik s i 112122ksk +=()()()()()iks ik s ik s Re Re ,0Re 0Re >>->+即且．同理可得余弦函数kt cos 的拉普拉斯变换． []22cos kss kt L +=()()()()()ik s ik s ik s Re Re ,0Re 0Re >>->+即且．2 拉普拉斯变换的存在定理定理1 若函数()t f 在[)+∞,0上满足下列条件： ()1 ()t f 在的任一有限区间上分段连续； ()2 存在常数0,0>>c M ，使得()ctMe t f ≤，则()t f 的拉普拉斯变换 ()()dt et f s F st-+∞⎰=在半平面()c s >Re 上一定存在，此时右端的积分绝对且一致收敛，而在这半平面内，()s F为解析函数．定理的条件是充分的，物理学和工程技术中常见的函数大多都满足定理的条件，因此拉普拉斯变换有着广泛的应用．但是定理的条件不是必要的，即在不满足定理条件的前提下，拉普拉斯变换仍可能存在．如函数21-t 在0=t 处不满足定理的条件()1，但从下面的例子可知它的拉普拉斯变换为sπ．例4 求幂函数()mt t f =（常数1->m ）的拉普拉斯变换．解 根据()1.2式，有[]dt et tL stm m-+∞⎰=0，令u st =，du sdt 1=，从而有du sesu dt et umm stm10-∞+-∞+⎰⎰=()11111+Γ==++∞-+⎰m sdu eu sm um m故()()111+Γ=+m stL m m()()0Re >s ．当m 为正整数时，有 ()1+=m msm t L ！ ()()0Re >s ．当21-=m 时，由于π==⎰⎰+∞-+∞-022dx edu eu xum，()u x =故sdt et stπ=-∞+-⎰21．前用我们利用拉普拉斯变换的定义求得一些较简单的函数的拉氏变换．但仅用这些来求函数的变换是并不方便的，有的甚至求不出来．本节的性质将有助于求函数的拉普拉斯变换．为叙述方便，假设所要求进行拉氏变换的函数的拉氏变换都存在，且记 ()[]()s F t f L =， ()[]()s G t g L =． １. 线性性质()()[]()[]()[]t g L t f L t g t f L βαβα+=+； ()3()()[]()[]()[]s G Ls F Ls G s F L111---+=+βαβα， ()4其中，βα,是常数．此性质的证明可由拉式变换，拉式逆变换的定义直接导出． 例5 求函数()kt e kt kt t f ++=cos sin的拉氏变换．解 ()[][][][]kte L kt L kt L tf L ++=cos sinks ksk s -+++=122()()()()()k s ik s Re Re Re Re >>且２. 微分性质()[]()()0f s sF t f L -=' ()5()()[]()()()()()000121-----'--=n n n nn ff sf ss F s t fL ()()c s >Re ()6证 根据拉氏变换的定义，有 ()[]()dt e t f t f L st-+∞⎰'='0．对右端积分利用分部积分法可得()()()dt et f s et f dt e t f ststst -+∞∞+--+∞⎰⎰+='0()[]()0f t f sL -=． 所以()[]()()0f s sF t f L -='．若利用()5式两次，可得 ()[]()[]{}''=''t f L t f L()[]()0f t f sL '-'=()()()002f sf s F s '--=．由此类推，便可得 ()()[]()()()()()000121-----'--=n n n nn ff sf ss F s t fL ()()c s >Re ．特别地，当初值()()()()00001==='=-n f f f 时，有()[]()()[]()()()[]()s F s t f L s F s t f L s sF t f L n n ==''=',,,2，()()c s >Re ．对于象函数，由拉普拉斯变换存在定理可知()s F 在()c s >Re 内解析，因而 ()()dt et f dsd s F st-+∞⎰='0()[]dt e t f dsd st-+∞⎰=0()dt et tf st-+∞⎰-=()[]t tf L -=,即 ()()[]t tf L s F -=' ()()c s >Re ()7 用同样方法可求得 ()()()()[]()2,≥-=n t f t L s Fnn ， ()()c s >Re()8因此，求象函数()s F 的导数转化为求象原函数()t f 乘以()nt -的拉氏变换，亦可反过来求解问题．例6求函数()kt t f sin =的拉式变换解 因为()kt k kt cos sin ='，()kt k kt sin sin 2-="，于是有()00=f ，()k f ='0，()00=''f ，从而 []()[]()()()00sin 22f sf s F s t f L kt k L '--=''=-，即 [][]k kt L s kt L k -=-sin sin 22．所以 []22s i n ksk ktL += ()()()()0Re Re >>s k ik s 为实数时，，Re ．例7求函数()kt k t f sin =的拉氏变换．解 已知[]22sin ksk kt L +=，等式两边对s 求导，得[]()()222222sin ks ks ks kds d dskt L d +-=⎪⎭⎫⎝⎛+=．则由()7.2式知，[]()[][]kt t L kt t L dskt L d sin sin sin -=-=．比较上述两式即得 []()2222sin kskskt t L +=．同理可得[]()22222c o s ksk sktt L +-=．3. 积分性质()()s F sdt t f L t10=⎥⎦⎤⎢⎣⎡⎰ ()9()()s F s dt t f dt dt L n n t t t 1000=⎥⎦⎤⎢⎣⎡⎰⎰⎰次()10 证 设()()dtt f t h t⎰=，则()()t f t h ='，()00=h ． 由微分性质，有()[]()[]()()[]t h sL h t h sL t h L =-='0， 即()()[]()s F st f L sdt t f L t110==⎥⎦⎤⎢⎣⎡⎰．重复应用()9.2式，可得 ()()s F s dt t f dt dtL n n ttt1000=⎥⎦⎤⎢⎣⎡⎰⎰⎰ 次． 由此，我们可以把象原函数的积分运算转化为对象函数的代数运算． 另外，根据拉氏变换的存在定理，对于象函数可证得下述积分性质：()()ds s F t t f L s⎰∞=⎥⎦⎤⎢⎣⎡ ()11()()ds s F ds ds t t f L n s s s n 次⎰⎰⎰∞∞∞=⎥⎦⎤⎢⎣⎡ ()12特别地，当0,1==s n 时，有 ()()ds s F dt tt f ⎰⎰∞+∞+=． ()13 例 8 求函数()⎰=td t f 0sin τττ的拉氏变换．解 由式()9可得()[]⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=⎰t t L s d L t f L t sin 1sin 0τττ， 又由式()11可得[]ds t L t t L s⎰∞=⎥⎦⎤⎢⎣⎡sin sin ds ss⎰∞+=112s arctan 2-=π．故⎪⎭⎫⎝⎛-=⎥⎦⎤⎢⎣⎡⎰s s d L t arctan 21sin 0πτττ． 且有211sin 02π=+=⎰⎰+∞+∞ds sdt tt ．例9 计算积分dt te ebtat⎰∞+---0．解 由()13可得[]ds eeL dt te ebtatbtat⎰⎰∞+--∞+---=-0a b ds b s a s ln 11=⎪⎭⎫ ⎝⎛+-+=⎰∞+．4. 延迟性质当0<t 时，()0=t f ，则对任一非负实数0t ，有 ()[]()s F e t t f L st 00-=-， ()14()[]()01t t f s F eLst -=--． ()15证 由式()1可知， ()[]()dt e t t f t t f L st⎰+∞--=-000()()dt et t f dt et t f stt stt -+∞-⎰⎰-+-=0000()dt et t f stt -+∞⎰-=0 ()()00=<t f t 时()du eu f e sust -+∞-⎰=0()0t t u -=令()s F e st 0-=．故有()[]()s F et t f L st 00-=-．比较函数()t f 与()0t t f -，前者在0≥t 时有非零数值，而后者在0t t ≥时有非零数值，即向后延迟了时间0t ．从图形上来看，()t f 沿t 轴向右平移0t 就可得到()0t t f -．此性质表明，时间函数延迟0t 的拉氏变换等于它的象函数乘以指数因子0st e-．例 10 求函数()⎩⎨⎧≤≥=-000,0,1t t t t t t u 的拉氏变换． 解 因为()[]st u L 1=，所以由()14式可得()[]010st est t u L -=-．5.位移性质()()[]t f e L a s F at=- ()16()[]()t f ea s F Lat=--1()17证 由拉氏变换定义知 ()[]()dt et f et f e L statat-+∞⎰=()()()a s F dt et f ta s -==--+∞⎰．此性质表明：一个函数乘以指数函数ate 后的拉氏变换等于其象函数作位移a ． 例11 求[]matte L ．解 已知()()111+Γ=+m stL m m，由()16可知，[]()()111+Γ-=+m a s te L m mat．例12 求[]kt e L atsin ．解 因为[]22sin ksk kt L +=，所以由()16可得， []()22sin ka s kkt eL at+-=．同理可得 []()22cos ka s skt e L at +-=．6.相似性质()[]⎪⎭⎫⎝⎛=a s F a at f L 1()0>a ()18 证 令at u =，则 ()[]()dt eat f at f L st-+∞⎰=()du eu f auas -∞+⎰=1⎪⎭⎫ ⎝⎛=a s F a 1．7.卷积与卷积定理定义2 若函数()t f 1，()t f 2在0<t 时均为零，则积分()()τττd t f f t-⎰201称为函数()t f 1与()t f 2的卷积，记作()()t f t f 21*，即 ()()()()τττd t f f t f t f t-=*⎰20121． ()19由卷积定义，可证明卷积具有如下性质：()1交换律：()()()()t f t f t f t f 1221*=* ()2结合律： ()()()[]()()[]()t f t f t f t f t f t f 321321**=**()3分配律：()()()[]()()()()t f t f t f t f t f t f t f 3121321*+*=+*例 13 求函数()t t f =1和()t t f sin 2=的卷积． 解 由卷积定义可知， ()()()τττd t t f t f t⎰-=*021s i n()()ττττd t t tt ⎰---=0cos cos()t t t 0sin τ-+=t t sin -= 定理 2 （卷积定理）若()[]()s F t f L 11=，()[]()s F t f L 22=，则()()[]()()s F s F t f t f L 2121=* ()20 ()()[]()()t f t f s F s F L21211*=- ()21卷积定理表明两个函数卷积的拉氏变换等于它们各自的拉式变换的乘积．证明略． 以上卷积定理可推广到n 个函数卷积的情形． 推论 若()[]()()n k s F t f L k k ,,2,1 ==，则()()()[]()()()s F s F s F t f t f t f L n n 2121=*** ()22 例14 求函数()t t f =1和()t t f sin 2=的卷积的拉氏变换．解一 由例13知()()[][]t t L t f t f L sin 21-=*，故[][][]()11111sin sin 2222+=+-=-=*sssst L t L t t L ．解二 由卷积定理可得， [][][]()11111s i n s i n 2222+=+==*sssst L t L t t L ．8.初值定理设()[]()s F t f L =，且()[]t f L '存在，则()()s sF t f s t ∞→→=+lim lim 0()23若定义()()t f f t +→+=lim 0（假定极限存在），则称()+f 为()t f 的初值．9.终值定理设()[]()s F t f L =，()[]t f L '存在，且()s sF 的一切奇点都在s 平面的左半平面，则 ()()∞+=→f s sF s 0lim ()24其中()()t f f t +∞→=∞+lim （假定极限存在），我们也称()∞+f 为()t f 的终值．前面我们讨论了函数()t f 在拉氏变换下的象函数()s F 的问题，反过来，若已知拉氏变换下的象函数()s F ，求象原函数()t f ，此问题就是拉式逆变换问题．下面给出拉普拉斯逆变换的定义：定义3 若()[]()s F t f L =，则积分 ()()ds e s F i t f sti i ⎰∞+∞-=ααπ21（α为s 的实部） ()25建立的从()s F 到()t f 的对应称作拉普拉斯逆变换（简称拉式逆变换）．记作 ()[]()t f s F L=-1．它与拉式变换构成了一个拉式变换对．由拉普拉斯变换存在定理可得：定理 3 若()t f 满足拉普拉斯变换存在定理的条件，即()()[]t f L s F =．则()t f 在连续点处有()()ds e s F it f sti i ⎰∞+∞-=ααπ21.在()t f 的间断点处，上式右端收敛于()()[]0021-++t f t f ，其中()c s >=αRe ．若由定义来求拉式逆变换是相当困难的，下面我们介绍一些方法．（1） 利用拉式变换性质求拉式逆变换 例15 求()()()()b a b s a s s F ≠--=1的拉式逆变换．解 因为 ()()⎪⎭⎫ ⎝⎛----=b s a s b a s F 111，所以由拉式变换的线性性质及拉式变换表知 ()[]⎪⎪⎭⎫ ⎝⎛⎥⎦⎤⎢⎣⎡--⎥⎦⎤⎢⎣⎡--=---b s L a s L b a s F L 11111 ()btateeba --=1．()()()()[]b a s Re ,Re max Re >例16 求()⎥⎦⎤⎢⎣⎡+-1121s s L ． 解 利用高等数学中关于有理真分式的分解知识可知()11111122+++-=+s sss s，故由式()4及拉式变换表可得()⎥⎦⎤⎢⎣⎡++⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡+----111111121121s L s L s L s s L tet -++-=1． ()()0Re >s通过上述两个例子，我们发现，若()s F 为有理真分式时，可将()s F 进行适当分解，进一步通过查表得到每个分解式的拉式逆变换，然后利用拉式变换的线性性质求处()s F 的拉式逆变换．这种方法也可称为象原函数的部分分式法．例16求函数()11ln+-=s s s F 的拉式逆变换．解 由拉式变换的微分性质可知 ()[]()t tf s F L -='-1，而()1111+--='s s s F ，所以()⎥⎦⎤⎢⎣⎡+---=-111111s s Ltt f ． 查拉式变换表可得 ()()tteet t f -=-1sht t2-= ()()1Re >s例17 求函数()922-=-sse s F s的拉式逆变换．解 因为t ch s s L 3921=⎥⎦⎤⎢⎣⎡-- ()()0Re >s ， ()922-=-ss e s F s，故由拉式变换的延迟性质有 ()[]()231-=-t ch s F L．例18 求函数()()223252+++=s s s F 的拉式逆变换．解 因为()()()2232122++++=s s s F ，由拉式变换的位移性质可知()[]()()⎥⎦⎤⎢⎣⎡++++=--221132122s s Ls F L⎥⎦⎤⎢⎣⎡++=--2212312s s Let⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡++⎥⎦⎤⎢⎣⎡+=---2212212333132s L s s L e t， 查拉式变换表可得 ()[]⎪⎭⎫⎝⎛+=--t t es F Lt3sin 313cos 221．例19 求函数()()2211ss s F +=的拉式逆变换．解 因为 ()11122+=sss F ，故由卷积定理知 ()[]⎥⎦⎤⎢⎣⎡+=--1112211s s Ls F Lt t sin *= t t sin -=例20 求函数()()2221+=sss F 的拉式逆变换．解 因为()()11122222+∙+=+=ss ss sss F ，故由卷积定理知 ()[]⎥⎦⎤⎢⎣⎡+∙+=--112211s s s sLs F Lt t cos cos *= ()()[]τττττd t t d t tt⎰⎰-+=-=2cos cos 21cos cos()02sin 21cos 21t t t ⎥⎦⎤⎢⎣⎡-+=ττ ()t t t sin cos 21+=．（2） 利用留数方法此方法主要依据下面的定理．定理 4 若n s s s ,,,21 是函数()s F 的所有奇点（适当选取α使这些奇点全在()α<s Re 的范围内），且当∞→s 时，()0→s F ，则有()()[]∑⎰=∞+∞-=nk k ststi i s es F s ds e s F i 1,Re 21ααπ，即()()[]∑==nk k sts e s F s t f 1,Re ()0>t ．()26例21求⎥⎦⎤⎢⎣⎡+--16221s se L s ．解 由定理2.4可知 ∑=---⎥⎦⎤⎢⎣⎡+=⎥⎦⎤⎢⎣⎡+nk k sts s s e s se s s se L122221,16Re 16．而i s 41=，i s 42-=为函数1622+-sse s的两个一阶极点，()()()it st s t e i s e i s se s 2422221424,16Re ---===⎥⎦⎤⎢⎣⎡+，()()()it st s t e i s e i s se s 2422221424,16Re ----=-==⎥⎦⎤⎢⎣⎡-+，故()()[]it i t s e e s se L24242212116-----+=⎥⎦⎤⎢⎣⎡+ ()24cos -=t ()2>t ．以上介绍的这些方法可根据()s F 的特点灵活选择使用，也可根据具体情况将各种方法结合起来使用．我们主要介绍拉普拉斯变换在求解微分方程（组）及电学上的应用根据拉式变换的线性和微分性质可知，一个微分方程通过拉氏变换可以转换为象函数的代数方程．如果能从代数方程中解出象函数，则通过求象函数的逆变换，就可以得到原微分方程的解．因此拉式变换可用来解微分方程，下面举例说明．例 1 求微分方程133=+'+''+'''y y y y 满足初始条件()()()0000=''='=y y y 的特解．解 设()()[]t y L s Y =，方程两边取拉式变换，并结合初始条件，可得()()()()ss Y s sY s Y s s Y s 13323-=+++，解之，有()()311+=s s s Y()()321111111+-+-+-=s s s s，取逆变换得到()tttet teet y ------=2211．例2 求方程t ydt y y t=+-'⎰044满足初始条件()00=y 的解．解 设()()[]t y L s Y =，方程两边取拉式变换，则原方程变为 ()()()2144ss Y ss Y s sY =+-即()()221-=s s s Y()222124141-+--=s s s，取拉式逆变换可得()ttteet y 22214141+-=．例3求微分方程组()()2930x x x y y y ''''''-+-++= ()()2750x x x y y y ''''''++--+=满足初始条件: (0)(0)1,(0)(0)0x x y y ''====的解.解 对以上微分方程组作拉氏变换, 记()()X p L x t =⎡⎤⎣⎦, ()()Y p L y t =⎡⎤⎣⎦, 并注意初始条件: (0)(0)1,(0)(0)0x x y y ''====, 有()()1L x t p X p '=-⎡⎤⎣⎦, ()()21L x t p Xp p ''=--⎡⎤⎣⎦, ()()L y t p Yp '=⎡⎤⎣⎦, ()()2L y t p Yp ''=⎡⎤⎣⎦, 因而得()()()()2229321p p X p p p Y p p -+-++=+ ()()()()2227523pp Xp pp Yp p ++--+=+将以上两式相加和相减, 得()()()()21122,41p Xp Y p Xp Y p p p +-=+=+-于是有()2211221313434pXp p p p =++-++()2221221313434pYp p p p =---++再作拉氏逆变换, 便得()()111221122112co s 2sin 23134343t p x t LL L e t t p p p ---⎡⎤⎡⎤⎡⎤=++=++⎢⎥⎢⎥⎢⎥-++⎣⎦⎣⎦⎣⎦()()1112221221122co s 2sin 23134343tp y t LL L e t t p p p ---⎡⎤⎡⎤⎡⎤=--=--⎢⎥⎢⎥⎢⎥-++⎣⎦⎣⎦⎣⎦其次, 用拉氏变换来处理一些电路中所反映出的微分方程问题.对于RLC 串联电路(见图5.2.1), 电流()i t 与电阻R 上的电压()R u t 、电感L 上的电压()L u t 及电容C 上的电压()C u t 满足如下的关系式()()()(),,R L d i t u t R i t u t Ld t==()()001,tC u t i t d t q c ⎡⎤=+⎢⎥⎣⎦⎰ (1) 这里0q 表示0t =时电容C 上的电量. 以()I p 表示()i t 的拉氏变换, 或叫运算电流, 又以()RU p 、()L U p 、()C U p 分别表示()R u t 、()L u t 、()C u t 的拉氏变换, 它们都叫运算电压. 由(1.3) 、(1.10) 、(1.13)与(1.16), 有()()()()()()00,1,RL C U p R I p U p L p Ip i U p Ip q C p⎧==-⎡⎤⎣⎦⎪⎨=+⎡⎤⎪⎣⎦⎩(2)其中0i 表示初始时刻0t =电路中的电流. 由于电源电压()()()()R L C u t u t u t u t =++, 如果000i q ==, 则()u t 的拉氏变换为()()()()()()()1R L C Up U p U p U p R L p Ip Zp I p C p ⎡⎤=++=++=⎢⎥⎣⎦(3)此处()1Z p R L p C p=++称为总运算阻抗, 而R 、L p 、1C p分别称为电阻R 、电感L 、电容C 的运算阻抗.一般地说, 当两个运算阻抗为()1Z p 、()2Z p 的元件串联时, 则两个元件上电压的拉氏变换为()()()11U p Z p I p =、()()()22U p Z p I p =,而总电压的拉氏变换为()()()()()()()()1212Up U p U p Z p Z p I p Zp I p =+=+=⎡⎤⎣⎦. (4)类似地, 当两个运算阻抗为()1Z p 、()2Z p 的元件并联时, 总电压的拉氏变换为()()()()()1122Up Z p I p Z p I p ==, (5)而总电流的拉氏变换为()()()()()()()()12121212Up Up Z Z Ip I p I p Up Z p Z p Z Z +=+=+=, (6)所以()()1212Z Z Up Ip Z Z =+. (7)例4 设RLC 串联电路接上电压E 的直流电源, 由在初始时刻0t =的电路中的电流00i =, 电容C 上没有电量即00q =, 求电路中电流()i t 的变化规律?解 由于()()()R L C u t u t u t E ++=, 又000i q ==, 从(2.1), 有()01td i R i Li t d t E d t c++=⎰. (8)由性质, 可知电压E 的拉氏变换为E p, 又由(3), 知(8)式左边的拉氏变换为,()()()()1Up Zp I p R L p Ip C p ⎡⎤==++⎢⎥⎣⎦,所以有()()21111EUp E p I p R L R L p R L p p p C p C p L C L===++++++(9)()()()121212111E ELp p L p p λλλλλλ⎡⎤==-⎢⎥-----⎣⎦, 这里记21,2R L L Cαβ==,而12λαλα=-+=--是代数方程210R p p LC L++=的两个根.1) 当αβ>,即R >,则从(1.6)式,可求得()I p 的拉氏逆变换,即()1212(),0.ttE i t e et L λλλλ⎡⎤=-≥⎣⎦- （10） 2) 当αβ<,即R <时, 12,λλ是一对共轭复数,即12j λαλα=-+=--=此时同样可得()1212()ttE i t e eL λλλλ⎡⎤=-⎣⎦-((ttE e eαα-+-⎡⎤=-⎢⎥⎣⎦(11)sin ,0.tEt α-=≥3) αβ=,即R =, 12λλα==-,则有2211()1()E E I p R L L p p p L C Lα==+++.从而可求得()I p 的拉氏逆变换 (),0tE i t tet L α-=≥. （12）如果R L C 串联电路的电源是正弦式电压0()sin u t u t ω=, 而()u t 的拉氏变换为[]022()u L u t p ωω=+,则由微分方程001()sin ,0,t d i R i Li t d t u t t d t Cω++=≥⎰(13)即初始条件:000,0i q ==, 可得 , 0222()()1()()()u p A p I p B p p L p R p Cωω==+++(14)这里0()A p u p ω=,2221()()()B p p L p R p Cω=+++都是实系数的多项式, ()B p的根是00,,),)22R R i i p p L Lωω--+=--=,若设2110,()04R L CLω>->,则02()1()2()u A i B i L R i Cωωωωω='-++00022000()()()(2)A p u pB p p L p R ωω='++,再由(1.22)式, 便得()I p 的拉式逆变换(2.15)000222001()R e 2R e ,1()(2)p t i tp i t u e e t o p L p R L R i C ωωωωω⎡⎤⎢⎥=+≥⎢⎥++⎢⎥-++⎣⎦.例1 对于图5.2.2所示的电路, 输入电压即电源电压为E (常数), 又初始时刻0t =的电流00i =,电容上的电量00q =, 求输出电压()u t 出.解 已知输入电压(),0u t E t =>入, 要求输出电压(),0u t t >出, 用()U p 入, ()U p 出分别表示()u t 入, ()u t 出的拉氏变换, 而()E U p p=入, 以()i t 表示通过电路的总电流(见图5.2.2), ()I p 是()i t 的拉氏变换. 因电阻1R 与电容1C 是并联着的, 其运算抗阻为11111111111111R C R C p R R Z R C ppR C pτ===+++,这里111R C τ=, 又设222R C τ=, 则电阻2R 与电容2C 是并联运算抗阻为222222211RC R R Z R C ppτ==++于是电路的总运算阻抗为()()()11221212211212121111R C RC R R R R pR R Z Z Z ppp p ττττττ+++=+=+=++++,而输出运算电压()U p 入与输入运算电压()U p 出之比()()()()()()()()2222221212111RC RC R Z p I p Z p U p p R R U p Zp I p Zp ppτττ+===+++出入 (16)11211122122111111pR p R R p R pR R τττττ+==+⎛⎫++++ ⎪+⎝⎭上述函数称为此电路的传递函数, 它描述了整个电路的特征. 从(2.16)式, 并注意()U p E p =入, 又设121a R R =+, 1212b R R ττ=+, 可得()()()()1111111E b a E b a p p E E E a U p U p a b pp a b pa pa b ppp a bττττ--++===+=+++++入出(17)虽然这里没有列出描述电路的微分方程, 但仍得到了输出运算电压()U p 出的具体表示式, 这显示了用拉氏变换处理线性电路问题的优点. 对(17)式, 作拉氏逆变换, 即得输出电压. ()11,0at b Eu t E e t a ba τ-⎛⎫=+-> ⎪⎝⎭出. (18)1)当12ττ=时, ()201212,01R E E u t u t R R R R ===>++出；2) 当1τ《2τ时, ()121200,0R R tR R u t u u e t +-≈->出；3)当1τ》2τ时, ()12121012,0R R tR R R E u t u e t R R +-≈+>+出，从以上情况可以看出: 当111222R C R C ττ===时, 便是无失真的输出, 电压幅度衰减为)(212R R R +倍, 因此上述电路可用来作为衰减器.。

完整版拉普拉斯变换表拉普拉斯变换是一种用来描述动态系统的数学工具。

它可以将时间域的函数转换为复频域的函数，使得复杂的微积分运算变得简单。

下面是拉普拉斯变换常用的函数表。

1. 常数函数拉普拉斯变换表达式：L{1} = 1/s解释：常数函数的拉普拉斯变换等于1除以s。

这个表达式可以直接从拉普拉斯变换的定义得出。

2. 单位阶跃函数拉普拉斯变换表达式：L{u(t)} = 1/s解释：单位阶跃函数是在t=0处取值为0，t>0处取值为1的函数。

它的拉普拉斯变换等于1除以s。

因为当s>0时，1/s表示连续求导的意义，也就是说，一个单位阶跃函数的拉普拉斯变换就是一个连续求导的过程。

3. 指数函数拉普拉斯变换表达式：L{e^at} = 1/(s-a)解释：指数函数的拉普拉斯变换等于1除以s减去指数函数的指数。

这个表达式可以通过对指数函数求拉普拉斯变换的定义进行求解。

4. 正弦函数拉普拉斯变换表达式：L{sin(at)} = a/(s^2 + a^2)解释：正弦函数的拉普拉斯变换等于a除以s平方加上正弦函数的频率a的平方。

这个表达式可以通过对正弦函数求拉普拉斯变换的定义进行求解。

5. 余弦函数拉普拉斯变换表达式：L{cos(at)} = s/(s^2 + a^2)解释：余弦函数的拉普拉斯变换等于s除以s平方加上余弦函数的频率a的平方。

这个表达式可以通过对余弦函数求拉普拉斯变换的定义进行求解。

6. 阻尼正弦函数拉普拉斯变换表达式：L{e^(-bt)sin(at)} = a/(s^2 + (a+b)^2)解释：阻尼正弦函数的拉普拉斯变换等于a除以s平方加上阻尼正弦函数的频率a加上阻尼b的平方。

这个表达式可以通过对阻尼正弦函数求拉普拉斯变换的定义进行求解。

7. 阻尼余弦函数拉普拉斯变换表达式：L{e^(-bt)cos(at)} =(s+b)/(s^2 + (a+b)^2)解释：阻尼余弦函数的拉普拉斯变换等于s加上阻尼余弦函数的频率a加上阻尼b的平方，除以s平方加上阻尼余弦函数的频率a加上阻尼b的平方。

Laplace拉氏变换公式表1. 常数变换：对于常数C，其拉普拉斯变换为C/s，其中s是复数频率。

2. 幂函数变换：对于幂函数t^n，其中n为实数，其拉普拉斯变换为n!/s^(n+1)。

3. 指数函数变换：对于指数函数e^(at)，其中a为实数，其拉普拉斯变换为1/(sa)。

4. 正弦函数变换：对于正弦函数sin(at)，其中a为实数，其拉普拉斯变换为a/(s^2+a^2)。

5. 余弦函数变换：对于余弦函数cos(at)，其中a为实数，其拉普拉斯变换为s/(s^2+a^2)。

6. 双曲正弦函数变换：对于双曲正弦函数sinh(at)，其中a为实数，其拉普拉斯变换为a/(s^2a^2)。

7. 双曲余弦函数变换：对于双曲余弦函数cosh(at)，其中a为实数，其拉普拉斯变换为s/(s^2a^2)。

8. 指数衰减正弦函数变换：对于指数衰减正弦函数e^(at)sin(bt)，其中a和b为实数，其拉普拉斯变换为b/(s+a)^2+b^2。

9. 指数衰减余弦函数变换：对于指数衰减余弦函数e^(at)cos(bt)，其中a和b为实数，其拉普拉斯变换为s+a)/(s+a)^2+b^2。

10. 指数增长正弦函数变换：对于指数增长正弦函数e^(at)sin(bt)，其中a和b为实数，其拉普拉斯变换为b/(sa)^2+b^2。

Laplace拉氏变换公式表11. 幂函数与指数函数的乘积变换：对于函数t^n e^(at)，其中n为实数，a为实数，其拉普拉斯变换为n!/(sa)^(n+1)。

12. 幂函数与正弦函数的乘积变换：对于函数t^n sin(at)，其中n为实数，a为实数，其拉普拉斯变换可以通过分部积分法得到。

13. 幂函数与余弦函数的乘积变换：对于函数t^n cos(at)，其中n为实数，a为实数，其拉普拉斯变换可以通过分部积分法得到。

14. 指数函数与正弦函数的乘积变换：对于函数e^(at) sin(bt)，其中a和b为实数，其拉普拉斯变换为b/(sa)^2+b^2。