阴影部分面积47

【史上最全小学求暗影部分面积专题—含答案】小学及小升初温习专题-圆与求暗影部分面积----完全答案在最后面目的：经由过程专题温习,增强学生对于图形面积盘算的灵巧应用.并加深对面积和周长概念的懂得和区分.面积求解大致分为以下几类：c重难点：不雅察图形的特色,依据图形特色选择适合的办法求解图形的面积.能灵巧应用所学过的根本的平面图形的面积求暗影部分的面积.例2.正方形面积是7平方厘米,求暗影部分的面积.例1.求暗影部分的面积.(单位:厘米)(单位:厘米)例3.求图中暗影部分的面积.(单位:厘例4.求暗影部分的面积.(单位:厘米)米)例5.求暗影部分的面积.(单位:厘米) 例6.如图：已知小圆半径为2厘米,大圆半径是小圆的3倍,问：空白部分甲比乙的面积多若干厘米？例7.求暗影部分的面积.(单位:厘米)例8.求暗影部分的面积.(单位:厘米)例9.求暗影部分的面积.(单位:厘米)例10.求暗影部分的面积.(单位:厘米)例11.求暗影部分的面积.(单位:厘米)例12.求暗影部分的面积.(单位:厘米)例13.求暗影部分的面积.(单位:厘米)例14.求暗影部分的面积.(单位:厘米)例15.已知直角三角形面积是12平方厘米,求暗影部分的面积.例16.求暗影部分的面积.(单位:厘米)例17.图中圆的半径为5厘米,求暗影部分的面积.(单位:厘米)例18.如图,在边长为6厘米的等边三角形中挖去三个同样的扇形,求暗影部分的周长.例19.正方形边长为2厘米,求暗影部分的面积.例20.如图,正方形ABCD的面积是36平方厘米,求暗影部分的面积.例21.图中四个圆的半径都是1厘米,求暗影部分的面积.例22.如图,正方形边长为8厘米,求暗影部分的面积.例23.图中的4个圆的圆心是正方形的4个极点,,它们的公共点是该正方形的中间,假如每个圆的半径都是1厘米,那么暗影部分的面积是若干？例24.如图,有8个半径为1厘米的小圆,用他们的圆周的一部分连成一个花瓣图形,图中的黑点是这些圆的圆心.假如圆周π率取3.1416,那么花瓣图形的的面积是若干平方厘米？例25.如图,四个扇形的半径相等,求暗影部分的面积.(单位:厘米)例26.如图,等腰直角三角形ABC和四分之一圆DEB,AB=5厘米,BE=2厘米,求图中暗影部分的面积.例27.如图,正方形ABCD的对角线AC=2厘米,扇形ACB是以AC为直径的半圆,扇形DAC是以D为圆心,AD为半径的圆的一部分,求暗影部分的面积.例28.求暗影部分的面积.(单位:厘米)例29.图中直角三角形ABC 的直角三角形的直角边AB=4厘米,BC=6厘米,扇形BCD地点圆是以B为圆心,半径为BC的圆,∠CBD=,问：暗影部分甲比乙面积小若干？例30.如图,三角形ABC是直角三角形,暗影部分甲比暗影部分乙面积大28平方厘米,AB=40厘米.求BC的长度.例31.如图是一个正方形和半圆所构成的图形,个中P 为半圆周的中点,Q为正方形一边上的中点,求暗影部分的面积.例32.如图,大正方形的边长为6厘米,小正方形的边长为4厘米.求暗影部分的面积.例33.求暗影部分的面积.(单位:厘米)例34.求暗影部分的面积.(单位:厘米)例35.如图,三角形OAB是等腰三角形,OBC是扇形,OB=5厘米,求暗影部分的面积.触类旁通★巩固演习【专1】下图中,大小正方形的边长分离是9厘米和5厘米,求暗影部分的面积.【专1-1】.右图中,大小正方形的边长分离是12厘米和10厘米.求暗影部分面积.【专1-2】.求右图中暗影部分图形的面积及周长.【专2】已知右图暗影部分三角形的面积是5平方米,求圆的面积.【专2-1】已知右图中,圆的直径是2厘米,求暗影部分的面积.【专2-2】求右图中暗影部分图形的面积及周长.【专2-3】求下图中暗影部分的面积.（单位：厘米）【专3】求下图中暗影部分的面积.【专3-1】求右图中暗影部分的面积.【专3-2】求右图中暗影部分的面积.【专3-3】求下图中暗影部分的面积.完全答案例1解：这是最根本的办法：圆面积减去等腰直角三角形的面积,×-2×1=1.14（平方厘米）例2解：这也是一种最根本的办法用正方形的面积减去圆的面积.设圆的半径为 r,因为正方形的面积为7平方厘米,所以=7,所以暗影部分的面积为：7-=7-例3解：最根本的办法之一.用四个圆构成一个圆,用正方形的面积减去圆的面积,所以暗影部分的面积：2×2-π＝0.86平方厘米.例4解：同上,正方形面积减去圆面积, 16-π()=16-4π例5解：这是一个用最经常应用的办法解最罕有的题,为便利起见,我们把暗影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π(别的：此题还可以算作是1题中暗影部分的8倍.例6解：两个空白部分面积之差就是两圆面积之差（全加上暗影部分）π-π()=100.48平方厘米（注：这和两个圆是否订交.交的情形若何无关）例7解：正方形面积可用(对角线长×对角线长÷2,求)所以暗影面积为：π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割.补.增.减变形)例8解：右面正方形上部暗影部分的面积,等于左面正方形下部空白部分面积,割补今后为圆,所以暗影部分面积为：π(例9解：把右面的正方形平移至左边的正方形部分,则暗影部分合成一个长方形,所以暗影部分面积为：2×3=6平方厘米例10解：同上,平移阁下两部分至中央部分,则合成一个长方形,所以暗影部分面积为2×1=2平方厘米(注: 8.9.10三题是简略割.补或平移)例11解：这种图形称为环形,可以用两个齐心圆的面积差或差的一部分来求.（π -π）×=例12.解：三个部分拼成一个半圆面积．π(例13解: 连对角线后将"叶形"剪开移到右上面的空白部分,凑成正方形的一半.所以暗影部分面积为：8×8÷2=32平方厘米例14解：梯形面积减去圆面积,(4+10)×4-π=28-4π=15.44平方厘米 . 例15.剖析: 此题比上面的题有必定难度,这是"叶形"的一个半.解: 设三角形的直角边长为r,则=12,=6圆面积为：π÷2=3π.圆内三角形的面积为12÷2=6,暗影部分面积为：(3π-6)×例16解：［π＋π－π］ =例17解：上面的暗影部分以AB为轴翻转后,全部暗影部分成为梯形减去直角三角形,或两个小直角三角形AED.BCD面积和.例18解：暗影部分的周长为三个扇形弧,拼在一路为一个半圆弧,例19解：右半部分上面部分逆时针,下面部分顺时针扭转到左半部分,构成一个矩形.所以面积为：1×2=2平方厘米例20解：设小圆半径为r,4=36, r=3,大圆半径为R,=2=18,将暗影部分经由过程迁移转变移在一路构成半个圆环,所以面积为:π(-例21.解：把中央部分分成四等分,分离放在上面圆的四个角上,补成一个正方形,边长为2厘米,所以面积为：2×2=4平方厘米例22解法一: 将左边上面一块移至右边上面,补上空白,则左边为一三角形,右边一个半圆.暗影部分为一个三角形和一个半圆面积之和. π(解法二: 补上两个空白为一个完全的圆.所以暗影部分面积为一个圆减去一个叶形,叶形面积为:π()÷2-4×4=8π-16所以暗影部分的面积为:π(例23解：面积为４个圆减去８个叶形,叶形面积为：π-1×1=π-1所以暗影部分的面积为:4π-8(π-1)=8平方厘米例24剖析：衔接角上四个小圆的圆心构成一个正方形,各个小圆被切去个圆,这四个部分正好合成３个整圆,而正方形中的空白部分合成两个小圆．解：暗影部分为大正方形面积与一个小圆面积之和．例25剖析：四个空白部分可以拼成一个以２为半径的圆．所以暗影部分的面积为梯形面积减去圆的面积,4×(4+7)÷2-π例26解: 将三角形CEB以B为圆心,逆时针迁移转变90度,到三角形ABD地位,暗影部分成为三角形ACB面积减去个小圆面积,为: 5×5÷2-π例27解: 因为2==4,所以=2以AC为直径的圆面积减去三角形ABC面积加上弓形AC面积,π-2×2÷4+[π÷4-2]=π-1+(π-1)例28解法一：设AC中点为B,暗影面积为三角形ABD面积加弓形BD的面积,弓形面积为:[π解法二：右上面空白部分为小正方形面积减去小圆面积,其值为：5×5-π=25-π暗影面积为三角形ADC减去空白部分面积,为：10×5÷2-（25-π）=例29.解: 甲.乙两个部分同补上空白部分的三角形后合成一个扇形BCD,一个成为三角形ABC,此两部分差即为：π×－例30.解：两部分同补上空白部分后为直角三角形ABC,一个为半圆,设BC长为X,则40X÷2-π÷2=28例31.解：连PD.PC转换为两个三角形和两个弓形,两三角形面积为：△APD面积+△QPC面积=两弓形PC.PD面积为：π-5×5所以暗影部分的面积为：37.5+π-25=51.75平方厘例32解：三角形DCE的面积为:×4×10=20平方厘米梯形ABCD的面积为:(4+6)×4=20平方厘米从而知道它们面积相等,则三角形ADF面积等于三角形EBF面积,暗影部分可补成圆ABE的面积,其面积为：π米例33.解:用大圆的面积减去长方形面积再加上一个以2为半径的圆ABE面积,为(π+π)-6=×13π-6例34解：两个弓形面积为：π-3×4÷2=π-6暗影部分为两个半圆面积减去两个弓形面积,成果为π+π-（π-6）=π（4+-）+6=6平方厘米例35解：将两个同样的图形拼在一路成为圆减等腰直角三角形[π÷4-×5×5]÷2=（π-触类旁通★巩固演习-answer【专1】（5+9）×5÷2+9×9÷2－（5+9）×5÷2=40.5（平方厘米）【专1-1】（10+12）×10÷×12×12÷4－（10+12）×10÷2=113.04（平方厘米）【专1-2】面积：6×（6÷×（6÷2）×（6÷2）÷2=3.87（平方厘米）×6÷2+6＋（6÷2）×2=21.42（厘米）【专2】2r×r÷2=5 即r×r=5×5=15.7（平方厘米）【专2-1】×（2÷2）×（2÷2）－2×2÷2=1.14（平方厘米）【专2-2】×6×6÷×（6÷2）×（6÷2）÷2=14.13 （平方厘米）周长：2××6÷×6÷2+6=24.84 （厘米）【专2-3】（6+4）×4÷2－（4××4×4÷4）=16.56（平方厘米）【专3】6×3－3×3÷2=13.5（平方厘米）【专3-1】8×（8÷2）÷2=16（平方厘米）【专3-2】×4×4÷4－4×4÷2=4.56（平方厘米）【专3-3】5×5÷2=12.5（平方厘米）。

总结：对于不规则图形面积的计算问题一般将它转化为若干基本规蒈则图形的组合，分析整体与部分的和、差关系，问题便得到解决.常用的基本方法有：蒇一、相加法：这种方法是将不规则图形分解转化成几个基本规则图形，分别计算它们的面袁例如，下图中，要求整个图形的面积，只要先求出上面积，然后相加求出整个图形的面积..半圆的面积，再求出下面正方形的面积，然后把它们相加就可以了薀衿羅二、相减法：这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积袄.例如，下图，若求阴影部分的面积，只需先求出正方形面积再减去里面圆的面积即可差.蚀羆蚇蚃三、直接求法：这种方法是根据已知条件，从整体出发直接求出不规则图形面积.如下页右螀的三角形，其面积直42、高是上图，欲求阴影部分的面积，通过分析发现它就是一个底是1?2?4?4。

：接可求为|2莇莂四、重新组合法：这种方法是将不规则图形拆开，根据具体情况和计算上的需要，重新组袀例如，欲求下图中阴影部分面积，可以.合成一个新的图形，设法求出这个新图形面积即可. 把它拆开使阴影部分分布在正方形的4个角处，这时采用相减法就可求出其面积了螈蒅袆袀五、辅助线法：这种方法是根据具体情况在图形中添一条或若干条辅助线，使不规则图膈如下图，求两个正方形中转化成若干个基本规则图形，然后再采用相加、相减法解决即可..此题虽然可以用相减法解决，但不如添加一条辅助线后用直接法作更简便阴影部分的面积.芄膃羀六、割补法：这种方法是把原图形的一部分切割下来补在图形中的另一部分使之成为基本蕿例如，如下图，欲求阴影部分的面积，只需把右边弓形切.规则图形，从而使问题得到解决.割下来补在左边，这样整个阴影部分面积恰是正方形面积的一半肆羂七、平移法：这种方法是将图形中某一部分切割下来平行移动到一恰当位置，使之组合成肀例如，如下图，欲求阴影部分面积，可先沿中间切.一个新的基本规则图形，便于求出面积开把左边正方形内的阴影部分平行移到右边正方形内，这样整个阴影部分恰是一个正方形。

小学五年级数学求阴影部分面积习题1、三角形ABC的面积是24平方厘米，AE＝BC＝8厘米，CD＝4厘米，求阴影部分面积。

2、正方形ABCD的周长是48厘米，已知AE的长度是EB的3倍，求阴影部分面积。

3、如图，一个直角梯形的上底是10厘米，下底是6厘米，面积是40平方厘米，把它分成一个平行四边形和直角三角形后，三角形的面积是多少平方厘米。

4、下面直角梯形的面积是49平方分米，求阴影部分的面积。

5、求整个图形的面积。

（单位：厘米）6、下图所示梯形，如果它的上底增加4厘米，面积就增加18平方厘米，这梯形原来的面积是多少平方厘米？7、求下面图形中阴影部分的面积。

（单位：厘米）8、下图由大小不等的两个正方形拼成，小正方形的边长是6厘米，阴影部分面积是60 厘米，求图中空白部分的面积。

9、求正方形中阴影部分的面积。

10、在下图中，已知平行四边形ABED的面积是30平方厘米，BE长6厘米，EC长4厘米。

求梯形ABCD的面积。

11、图中空白部分是一个面积为30平方厘米的平行四边形，求阴影部分面积。

12、如图：在直角梯形ABCD中，AB＝4分米。

CD＝9分米，空白部分面积为10平方分米，求阴影部分面积。

13、求阴影部分的面积（单位：厘米）：14、图中三角形DEC的面积是2.7平方米，AD＝4.4米，AB＝2米。

求平行四边形CDFG中阴影部分的面积。

15、如图，在梯形ABCD中，CD＝4厘米，AB＝2DC，AECD为平行四边形，已知梯形面积为66平方厘米，求阴影部分面积。

16、图中三角形ABC的面积是24平方厘米，AE＝BC＝8厘米，CD＝4厘米，求阴影部分的面积。

17、图中空白部分是一个面积为30平方厘米的平行四边形，求阴影部分面积。

18、图中，阴影部分的面积是56平方厘米，BD＝14厘米，求梯形ABCD 的面积。

19、梯形ABCD面积是96平方厘米，AB＝6厘米，中位线EF＝12厘米，求阴影部分面积。

20、求这个组合图形的面积。

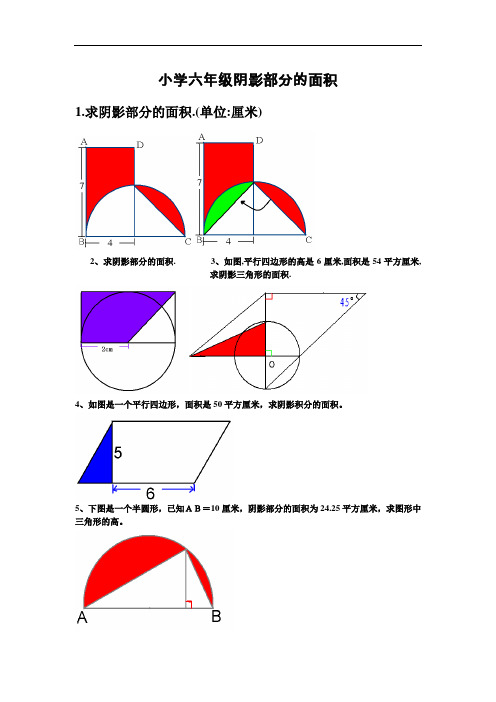
小学六年级阴影部分的面积1.求阴影部分的面积.(单位:厘米)2、求阴影部分的面积.3、如图,平行四边形的高是6厘米,面积是54平方厘米,求阴影三角形的面积.4、如图是一个平行四边形，面积是50平方厘米，求阴影积分的面积。

5、下图是一个半圆形，已知ＡＢ＝10厘米，阴影部分的面积为24.25平方厘米，求图形中三角形的高。

6、如图，一个长方形长是10cm,宽是4cm,以A点和C点为圆心各画一个扇形,求画中阴影部分的面积是多少平方厘米?7、如图，正方形的面积是10平方厘米，求圆的面积。

8、如图，已知梯形的两个底分别为4厘米和7厘米，梯形的面积是多少平方厘米？9、如图，ABCD是一个长方形,AB=10厘米,AD=4厘米,E、F分别是BC、AD的中点，G 是线段CD上任意一点，求阴影部分的面积。

10、如图，阴影部分的面积是空白部分的2倍，求阴影部分三角形的底。

（单位：厘米）11、如图，梯形的面积是60平方厘米，求阴影部分的面积。

12、求阴影部分的面积。

13、已知平行四边形的面积是20平方厘米，A是底边上的中点，求阴影部分的面积。

14、如图，已知半圆的面积是31.4平方厘米，求长方形的面积。

15、求下图中阴影部分的面积和周长。

（单位：厘米）16、如图，求阴影部分①比阴影部分②的面积多多少？（单位：厘米）17、求阴影部分的面积。

18、如图所示，正方形ABCD的边AB=4厘米，EC=10厘米，求阴影部分的面积。

19、如图，在边长为6cm的正方形内有一个三角形BEF，线段AE=3cm，DF=2cm，求三角形BEF的面积。

20、已知梯形ABCD的面积是27.5平方厘米，求三角形ACD的面积。

21、如图，已知一个四边形的两条边的长度和三个角的度数，这个四边形的面积是多少？（单位：厘米）22、求下图阴影部分的面积。

23、求图中阴影部分的面积。

（单位：厘米）24、求下图中阴影部分的面积。

（单位：厘米）25、求阴影部分的面积。

六年级阴影部分的面积1.求阴影部分的面积。

(单位:厘米)解：割补后如右图，易知，阴影部分面积为一个梯形。

梯形上底DE=7-4=3厘米，1S =S =DE AB)AD 2⨯+⨯阴梯形（=137)42⨯+⨯（=20(平方厘米)2、求阴影部分的面积。

解：S =S 阴梯形，梯形的上底是圆的直径，下底、高是圆的半径，S =S 阴梯形=124)22⨯+⨯（=6(2cm )3、如图，平行四边形的高是6厘米，面积是54平方厘米，求阴影三角形的面积。

解：S =AD AO ⨯ABCD =54平方厘米，且AO=6厘米，所以AD=9厘米。

由图形可知AED∆是等腰直角三角形，所以AE=AD ，OE=OF=AE-AO=9-6=3cm ，BO=BC-OC=9-3=6cm 。

1S =BO OF 2⨯⨯阴=1S =632⨯⨯阴=92cm 。

4、如图是一个平行四边形，面积是50平方厘米，求阴影积分的面积。

解：方法一：过C 点作CF AD ⊥交AD 于点F ，可知AECF 是长方形，面积=5×6=302cm ，ABE CFD S =S ∆∆=(50-30)÷2=102cm 。

方法二：BC=S ABCD ÷AE=50÷5=10cm ，BE=BC-EC=10-6=4cm ，ABE S ∆=BE ×AE ÷2 =4×5÷2=102cm5、下图是一个半圆形，已知ＡＢ＝10厘米，阴影部分的面积为24.25平方厘米，求图形中三角形的高。

解：S =S -S ∆阴半圆=21AB 22π⎛⎫⨯⨯ ⎪⎝⎭-24.25=21103.1422⎛⎫⨯⨯ ⎪⎝⎭-24.25=152cm ， 三角形的高=2S ∆÷AB=2×15÷10=3cm 。

6、如图，一个长方形长是10cm ，宽是4cm ，以A 点和C 点为圆心各画一个扇形，求画中阴影部分的面积是多少平方厘米?解：BECD 1S =S -S 4阴大圆=ABCD 11S -S S 44⎛⎫- ⎪⎝⎭大圆小圆=ABCD 11S +S -S 44大圆小圆=()2213.1410-4-1044⨯⨯⨯ =25.942cm 。

小学六年级求阴影部分面积试题和答案题目一：下图中，阴影部分是一个由三个不完整的矩形组成的图形，请计算阴影部分的面积，并写出计算过程。

解答：首先，我们需要计算每个不完整的矩形的面积，然后将它们相加得到阴影部分的总面积。

矩形一：长 = 6 cm宽 = 4 cm面积 = 长 ×宽 = 6 cm × 4 cm = 24 cm²矩形二：长 = 3 cm宽 = 5 cm面积 = 长 ×宽 = 3 cm × 5 cm = 15 cm²矩形三：长 = 4 cm宽 = 2 cm面积 = 长 ×宽 = 4 cm × 2 cm = 8 cm²将三个矩形的面积相加得到阴影部分的总面积：总面积 = 24 cm² + 15 cm² + 8 cm² = 47 cm²所以，阴影部分的面积为 47 cm²。

题目二：下图是一个由一个圆和一个矩形组成的图形，其中阴影部分为矩形内的部分。

请计算阴影部分的面积，并写出计算过程。

解答：首先，我们需要计算矩形的面积，然后计算圆的面积，并用矩形的面积减去圆的面积得到阴影部分的面积。

矩形：长 = 8 cm宽 = 5 cm面积 = 长 ×宽 = 8 cm × 5 cm = 40 cm²圆：半径 = 2 cm面积= π × 半径² = 3.14 × 2 cm × 2 cm ≈ 12.56 cm²阴影部分的面积 = 矩形的面积 - 圆的面积阴影部分的面积 = 40 cm² - 12.56 cm² ≈ 27.44 cm²所以，阴影部分的面积为约 27.44 cm²。

题目三：下图中，阴影部分是图形中心的圆与边界的三个小圆相交形成的部分。

请计算阴影部分的面积，并写出计算过程。

六年级数学上册典型例题系列之第五单元圆：求阴影部分的面积专项练习（解析版）专项练习一：S整体-S空白=S阴影1.求图中阴影部分的面积（单位：厘米）。

解析：图一：S阴影=S半圆-S三角形半径：10÷2=5（cm）3.14×52÷2-5×5÷2=39.25-12.5=26.75（平方厘米）图二：S阴影=S梯形-S扇形（8+4）×4÷2-3.14×42÷4=24-12.56=11.44（平方厘米）图三：S阴影=S梯形-S半圆（6+10）×3÷2-3.14×32÷2=24-14.13=9.87（平方厘米）2.求图中阴影部分的面积（单位：厘米）。

解析：S阴影=S正方形-S圆4×4-3.14×22=3.44（平方厘米）3.下图中，正方形的边长是2厘米，四个圆的半径都是1厘米，圆心分别是正方形的四个顶点。

求出阴影部分的面积。

解析：S阴影=S正方形-S圆2×2-3.14×12=0.86（平方厘米）4.如图，正方形ABCD的对角线AC=2厘米，扇形ACB是以AC为直径的半圆，扇形DAC是以D为圆心，AD为半径的圆的一部分，求阴影部分的面积。

解析：S阴影=S扇形+S半圆-S正方形S半圆：3.14×（2÷2）2÷2=1.57（平方厘米）S扇形：3.14×2÷4=1.57（平方厘米）S正方形：2×2÷2=2（平方厘米）S阴影：1.57+1.57-2=1.14（平方厘米）专项练习二：割补法1.求图中阴影部分的面积（单位：厘米）。

解析：8×4÷2=26（平方厘米）2.如图，大正方形的边长是4cm，求图中阴影部分的面积（单位：厘米）。

解析：4×2=8（平方厘米）3.如图，正方形边长为2厘米，求阴影部分的面积。

最新人教版六年级数学几何典型题解：阴影部分的面积1.求阴影部分的面积。

(单位:厘米)解：割补后如右图，易知，阴影部分面积为一个梯形。

梯形上底DE=7-4=3厘米，1S =S =DE AB)AD 2⨯+⨯阴梯形（=137)42⨯+⨯（=20(平方厘米)2、求阴影部分的面积。

解：S =S 阴梯形，梯形的上底是圆的直径，下底、高是圆的半径，S =S 阴梯形=124)22⨯+⨯（=6(2cm )3、如图，平行四边形的高是6厘米，面积是54平方厘米，求阴影三角形的面积。

解：S =AD AO ⨯ABCD =54平方厘米，且AO=6厘米，所以AD=9厘米。

由图形可知AED ∆是等腰直角三角形，所以AE=AD ，OE=OF=AE-AO=9-6=3cm ，BO=BC-OC=9-3=6cm 。

1S =BO OF 2⨯⨯阴=1S =632⨯⨯阴=92cm 。

4、如图是一个平行四边形，面积是50平方厘米，求阴影积分的面积。

解：方法一：过C 点作CF AD ⊥交AD 于点F ，可知AECF 是长方形，面积=5×6=302cm ，ABE CFD S =S ∆∆=(50-30)÷2=102cm 。

方法二：BC=S ABCD ÷AE=50÷5=10cm ，BE=BC-EC=10-6=4cm ，ABE S ∆=BE ×AE ÷2 =4×5÷2=102cm5、下图是一个半圆形，已知ＡＢ＝10厘米，阴影部分的面积为24.25平方厘米，求图形中三角形的高。

解：S =S -S ∆阴半圆=21AB 22π⎛⎫⨯⨯ ⎪⎝⎭-24.25=21103.1422⎛⎫⨯⨯ ⎪⎝⎭-24.25=152cm ， 三角形的高=2S ∆÷AB=2×15÷10=3cm 。

6、如图，一个长方形长是10cm ，宽是4cm ，以A 点和C 点为圆心各画一个扇形，求画中阴影部分的面积是多少平方厘米?解：BECD 1S =S -S 4阴大圆=ABCD 11S -S S 44⎛⎫- ⎪⎝⎭大圆小圆=ABCD 11S +S -S 44大圆小圆=()2213.1410-4-1044⨯⨯⨯ =25.942cm 。

小学奥数练习卷（知识点：等积变形）注意事项：1．答题前填写好自己的姓名、班级、考号等信息2．请将答案正确填写在答题卡上第Ⅰ卷（选择题）一．选择题（共6小题）1．如图，在由1×1的正方形组成的网格中写有2015四个数字（阴影部分），其边线要么是水平或竖直的直线段，要么是连接1×1的正方形相邻两边中点的线段，或者是1×1 的正方形的对角线，则图中2015四个数字（阴影部分）的面积是（）A．47B．C．48D．2．如图，大正六边形内部有7个完全一样的小正六边形，已知阴影部分的面积是180平方厘米．那么大正六边形的面积是（）平方厘米．A．240B．270C．300D．3603．如图中，正八边形ABCDEFGH的面积为1，其中有两个正方形ACEG和PQRS．那么正八边形中阴影部分的面积（）A．B．C．D．4．如图，大正方形的边长为14，小正方形的边长为10，阴影部分的面积之和是（）A．25B．40C．49D．505．大、中、小三个正方形，边长都是整数厘米，小正方形的周长比中正方形的边长小，把这两个正方形放在大正方形上（如图），大正方形露出的部分的面积是10平方厘米（图中阴影部分）．那么，大正方形的面积是（）平方厘米．A．25B．36C．49D．646．如图所示，在5×8的方格中，阴影部分的面积为37cm2．则非阴影部分的面积为（）cm2．A．43B．74C．80D．111第Ⅱ卷（非选择题）二．填空题（共35小题）7．如图，形ABCDEF．如果正六边形ABCDEF的面积为80平方厘米，那么用来组成正六边形ABCDEF的所有菱形的面积总和是平方厘米．8．如图，已知梯形ABCD中，CD=10，梯形ABCD的高是4，那么阴影部分的面积是．9．正方形A、B、C、D的边长依次是15，b，10，d（b，d都是自然数），若它们的面积满足S A=S B+S C+S D，则b+d=．10．两个正六边形的面积都是2016，中间连接一个正方形，那么图中阴影三角形的面积是．11．如图，正十二边形的面积是2016平方厘米，那么图中阴影部分的面积是平方厘米．12．如图，直角三角形ABC中，∠ABC=90°，AC=14，四边形BCDE和四边形ABFG 都是正方形，连结AD与BC相交于点H，如果GH与AC平行，那么阴影四边形BEDH的面积是．13．一个容积是100立方厘米的水杯（即这个水杯装满水时，水的体积是100立方厘米），内有一部分水，盛盛向杯中放入了一个小正方体，水溢出了20立方厘米；盛盛又向杯中放入了一个相同的小正方体，水又溢出了30立方厘米（如图），那么，原来水杯中装有立方厘米的水．14．如图是由两个直径为2的圆和四个腰长为2的等腰直角三角形组成，则图中的阴影部分面积是．（π=3）15．如图所示，已知大圆的半径为2，则阴影部分的面积为（圆周率用π表示）．16．如图中三个正方形的边长从左到右依次减半，小正方形的边长为3，那么图中阴影部分的面积是．17．长方形ABCD被CE、DF分成四块，已知其中3块的面积分别是5、16、20平方厘米，那么四边形ADOE的面积是平方厘米．18．如图所示，长方形ABCD中，AD﹣AB=9厘米，梯形ABCE的面积是三角形ADE面积的5倍，三角形ADE的周长比梯形ABCE 的周长短68厘米．长方形ABCD的面积是平方厘米．19．如图，正六边形ABCDEF面积是2014平方厘米，在AB、BC、DE、EF上分别取中点G、H、I、J，四边形GHIJ的面积是平方厘米．20．如图，ABCD和ABEF都是长方形，如果长方形ABEF的面积是30平方厘米，那么阴影部分的面积是平方厘米．21．如图所示，四边形ABCD是梯形，四边形ABED是平行四边形，四边形FGHI 是长方形，E、F、G分别是边CD、AD、BC的中点．如果平行四边形ABED的面积是48平方厘米，那么，长方形FGHI的面积是平方厘米．22．如图所示，正方形ABCD的对角线BD长20厘米，BDFE是长方形．那么，五边形ABEFD的面积是平方厘米．23．直角三角形的两条直角边分别是3与9，以三角形的每条边长作为正方形的边长，分别可以画出三个正方形（如图），这个多边形的面积是．24．右图是由甲乙丙丁拼成的正方形，其中甲与丁都是边长为整数厘米数的正方形，乙与丙都是长方形，且甲与丁的面积之和为100平方厘米，那么长方形乙与丙的面积之和为平方厘米．25．在平行四边形ABCD中，EF∥AH、HG∥AD．如果平行四边形AHPE的面积是5平方厘米．平行四边形PFCG的面积是16平方厘米．那么三角形PBD的面积是平方厘米．26．勾股定理又称为“毕达哥拉斯定理”，是一个有着悠悠4000多年历史的重要几何定理．它揭示了这样一个事实：对任何一个直角三角形而言，以它的两条直角边的长度为边长的正方形的面积之和，等于以斜边的长度为边长的正方形的面积．关于勾股定理，人们发现了400多种证明，甚至连美国总统也曾加入到证明一者的队伍中．在众多证明方法中，我国古代数学家刘徽给出的证明简单直观，耐人寻味（如图所示）这个证明实际上给出了一个通过有限次直线切割，将两个正方形拼补为一个更大的正方形的方法．设两个小正方形的边长分别为3和4，按照刘徽的方法，这两个小正方形被切割成5部分，请分别计算出这5部分的面积，并按从小到大的顺序写在下面：．27．四个正方形A、B、C、D如图放置，其中正方形A的周长是12厘米，正方形D的周长是60厘米，则阴影部分的面积会为平方厘米．28．如图，在一块长为10米，宽为5米的矩形草地上，有一条弯曲的柏油小路，小路任何地方的水平宽度都是1米．则空白部分的草地的面积是平方米．29．在一个长为100米，宽为88米的长方形湖中，有一座宽为2米的九曲回廊，如图，九曲回廊拐弯处均为直角，请问，没有被九曲回廊覆盖的湖水面积为平方米．30．如图，已知一个四边形的两条边的长度和它的三个角的度数．那么这个四边形的面积是平方厘米．31．如图，直角梯形A BCD的上底与高相等，正方形DEFH的边长等于6厘米，阴影部分的面积是平方厘米．32．三个正方形ABCD、BEFG、CHIJ如下图所示摆放，已知ABCD的边长为10，BEFG的边长为6，阴影部分的面积是．33．如图，正方形ABCD中，等腰直角三角形AEF的面积是1，长方形EFGH的面积是10，那么，正方形ABCD的面积是．34．如图，三个同心圆分别被直径AB，CD，EF，GH八等分，那么，图中阴影部分面积与非阴影部分面积之比是．35．图形的面积是cm2．36．如图，5个等腰直角三角形叠放在一起，它们的斜边都在一条直线上，已知最小的等腰直角三角形的斜边长是4厘米，其余等腰三角形的斜边依次多4厘米，则图中阴影部分的面积是平方厘米．37．如图，校园中有两个大小相同的正方形花坛（图中阴影部分），花坛的四周是1米宽的水泥路．如果水泥路的总面积是41平方米，那么一个花坛的面积是平方米．38．如图所示，小正方形EFGH在大正方形ABCD的内部，阴影部分的总面积为124平方厘米，E、H在边AD上，O为线段CF的中点．则四边形BOGF的面积为平方厘米．39．如图，在直角三角形中有一个正方形，已知BD=10厘米，DC=7厘米，阴影部分的面积是．40．如图所示，在大长方形中放入六个形状大小相同的小长方形，图中阴影部分的面积是．41．在一个边长50米的正方形菜园里修二纵二横四条宽2米的小路（如图），则剩下可以种菜的面积是平方米．三．解答题（共9小题）42．四边形ABCD中，M为AB的中点，N为CD的中点，如果四边形ABCD的面积是80平方厘米，求阴影部分BNDM面积是多少？43．熙熙军团的胸章是如图所示的正八边形图案，已知正八边形的边长为18，那么阴影部分的面积是多少？44．5个相同的长方形放在一个正方形内，所有长方形的边都平行于正方形的对应边，正方形的边长为24厘米，求：单个长方形的面积．45．如图，ABCD是个梯形，其对角线的交点为O，延长AC至点E，满足CE=AO，延长DB至点F，满足BF=DO．若△BFG的面积为2015平方厘米．求：△CGE 的面积．46．如图，E为正方形ABCD的边AB的延长线上一点，F为线段DE上一点，FA=50，S△FCE=75，S△FBC=175，交BC于点G、ED交BC于点H，已知S△FBE（1）直接写出BH：HC；（2）求S；△ABF（3）求正方形ABCD的面积；（4）求梯形AGHD的面积．47．如图，正方形ABCD的面积为1，E、F分别为BC、CD的中点，AE和BF相交于点O．求：（1）△ABE的面积；（2）AO：OE；（3）△AOB的面积；（4）△COD的面积．48．如图，已知一个四边形的两条边的长度和三个角的度数，这个四边形的面积是多少平方厘米？（单位：厘米）49．如图，大正方形的周长比小正方形的周长多80厘米，阴影部分的面积为880平方厘米，那么，大正方形的面积是多少平方厘米？50．某校科技小组有一块长方形试验田，已知这块试验田的面积是7.79平方米，并且长比宽多2.2米，这个长方形的周长是米．参考答案与试题解析一．选择题（共6小题）1．如图，在由1×1的正方形组成的网格中写有2015四个数字（阴影部分），其边线要么是水平或竖直的直线段，要么是连接1×1的正方形相邻两边中点的线段，或者是1×1 的正方形的对角线，则图中2015四个数字（阴影部分）的面积是（）A．47B．C．48D．【分析】将每个数字中的阴影小三角形进行位置的移动，组合成小正方形，然后数出一共有多少个小正方形，即可求出阴影部分的面积．【解答】解：据分析可知：将小三角形移到空白处补全完整正方形，共47.5个，所以阴影部分的面积是47；故选：B．【点评】解答此类题目，一般都是将阴影部分转化成规则的图形，再根据规则图形的面积公式进行解答．2．如图，大正六边形内部有7个完全一样的小正六边形，已知阴影部分的面积是180平方厘米．那么大正六边形的面积是（）平方厘米．A．240B．270C．300D．360【分析】按题意，显然可以将图进行分割，分割后阴影部分有六个面积相等的小正六边形，而空白部分是3个面积相等的小正六边形，利用面积之比不难求得大正六边形的面积．【解答】解：如图所示，将图分割成面积相等的小正三角形，显然，图中的空白部分的面积和等于3个小正六边形．而阴影部分由6个小正六边形组成，所以，大正六边形是由9个小正六边形组成的．一个小正六边形的面积为：180÷6=30（平方厘米），大正六边形的面积为：30×9=270（平方厘米），故选：B．【点评】本题考查了等积变形，突破点是：利用等积变形，求得每个个正六边形的面积，最后不难求得大正六边形的面积．3．如图中，正八边形ABCDEFGH的面积为1，其中有两个正方形ACEG和PQRS．那么正八边形中阴影部分的面积（）A．B．C．D．【分析】可以将图中阴影部分进行等积变形，将一部分进行平移，等积变形后不难发现阴影部分和空白部分的面积刚好相等．【解答】解：根据分析，将图中阴影部分进行等积变形，由图不难发现，阴影部分和空白部分的面积刚好相等，正八边形中阴影部分的面积占：故选：A．【点评】考查了等积变形，突破点是：利用等积变形，不难求得结果．4．如图，大正方形的边长为14，小正方形的边长为10，阴影部分的面积之和是（）A．25B．40C．49D．50【分析】按题意，将图①逆时针旋转90°，阴影部分可拼成一等腰直角三角形，不难求得阴影部分的面积．【解答】解：根据分析，如下图所示，图①逆时针旋转90°，阴影部分可拼成一等腰直角三角形，S=142÷4=49故选：C．【点评】本题考查了等积变形，突破点是：将图①逆时针旋转90°，阴影部分可拼成一等腰直角三角形．5．大、中、小三个正方形，边长都是整数厘米，小正方形的周长比中正方形的边长小，把这两个正方形放在大正方形上（如图），大正方形露出的部分的面积是10平方厘米（图中阴影部分）．那么，大正方形的面积是（）平方厘米．A．25B．36C．49D．64【分析】一条阴影部分的面积为10÷2=5平方厘米．因为边长都是整数，所以只能为1×5．故可以求得大正方形的边长为1+5，大正方形面积不难求得．【解答】解：根据分析，一条阴影部分的面积为10÷2=5平方厘米．因为都是整数，所以只能为1×5．故，大正方形面积=（1+5）×（1+5）=6×6=36平方厘米．故选：B．【点评】本题考查了等积变形，突破点是：利用边长都是整数，而乘积为5的特点求出正方形的边长，从而求得面积．6．如图所示，在5×8的方格中，阴影部分的面积为37cm2．则非阴影部分的面积为（）cm2．A．43B．74C．80D．111【分析】如图所示，在5×8的方格中，阴影部分占了18.5个格，非阴影就分占21.5格；阴影面积为37cm2，据此可求出每格的面积，进而求出则非阴影部分的面积．【解答】解：如图，阴影部分占了18.5个格，面积为37cm2，每格的面积是：37÷18.5=2（cm2）；非阴影就分占21.5格，其面积是：21.5×2=43（cm2）；答：则非阴影部分的面积为43cm2；故选：A．【点评】解答此题的关键是看阴影部分占多少格，由阴影部分所占的面积及格数即可求出每格的面积，进而求出非阴影部分的面积．二．填空题（共35小题）7．如图，形ABCDEF．如果正六边形ABCDEF的面积为80平方厘米，那么用来组成正六边形ABCDEF的所有菱形的面积总和是45平方厘米．【分析】按题意，可以将图形等积变形，再图中用虚线标出所有的小棱形，再数一下有多少个小棱形，即可求得棱形的面积．【解答】解：根据分析，如图，将正六边形ABCDEF分割成若干个面积相等的小棱形，共有48个小棱形，每个小棱形的面积为：80÷48=平方厘米，则画实线的棱形面积为：=45平方厘米．即：那么用来组成正六边形ABCDEF的所有菱形的面积总和是45平方厘米．故答案是：45．【点评】本题考查了等积变形，本题突破点是：将图形等积变形，只要数出小棱形的个数，即可算出所有棱形的面积．8．如图，已知梯形ABCD中，CD=10，梯形ABCD的高是4，那么阴影部分的面积是20．【分析】如下图：连接AC，△AEC和△BEC如果都以EC为底，那么它们属于同底等高的两个三角形，故，它们的面积相同；这样整个阴影部分的面积就等于△ADC的面积．【解答】解：如上图所示：连接AC，△AEC和△BEC如果都以EC为底，那么它们属于同底等高的两个三角形，故，它们的面积相同；这样整个阴影部分的面积就等于△ADC的面积，而△ADC的高等于梯形的高；即：阴影部分面积=△ADC的面积=DC×高÷2=10×4÷2=20．故：应该填20．【点评】等积变换重点找和部分阴影面积相等的图形．9．正方形A、B、C、D的边长依次是15，b，10，d（b，d都是自然数），若它们的面积满足S A=S B+S C+S D，则b+d=13或15．【分析】按题意，则有：S A=S B+S C+S D⇒152=b2+102+d2，故可以求得b和d的平方和，根据b和d是自然数，可以得到b和d的值，从而求得b+d的值．【解答】解：根据分析，S A=S B+S C+S D⇒152=b2+102+d2，⇒b2+d2=125，∵b和d是自然数，∴①b=2，d=11，b+d=13；②b=10，d=5，b+d=15，故答案是：13或15．【点评】本题考查了等积变形，本题突破点是：可以求得b和d的平方和，根据b和d是自然数，可以得到b和d的值，从而求得b+d的值．10．两个正六边形的面积都是2016，中间连接一个正方形，那么图中阴影三角形的面积是672．【分析】如下图，进行登积变形，将正六边形六等分，一份的面积为2016÷6=336，由此即可解决问题．【解答】解：如下图，进行登积变形，将正六边形六等分，一份的面积为2016÷6=336，所以阴影部分的面积=336×2=672．故答案为672．【点评】本题考查三角形的面积、正六边形的性质、等积变形等知识，解题的关键是学会用转化的思想思考问题．11．如图，正十二边形的面积是2016平方厘米，那么图中阴影部分的面积是672平方厘米．【分析】据观察，可以将阴影部分的面积等积变形，画在图中，标上字母，不难求得阴影部分的面积．【解答】解：根据分析，如图，首先将阴影部分等积变形成下图形状，并设正三角形面积为a，四边形面积为b，整个正十二边形是由12个a这样的正三角形和6个b这样的四边形组成，而阴影部分是由4个a这样的正三角形和2个b这样的四边形组成，恰好是整个正十二边形的，故阴影部分面积=2016×=672平方厘米．故答案是：672．【点评】本题考查了等积变形，本题突破点是：将阴影部分面积等积变形，不难求得阴影部分的面积．12．如图，直角三角形ABC中，∠ABC=90°，AC=14，四边形BCDE和四边形ABFG 都是正方形，连结AD与BC相交于点H，如果GH与AC平行，那么阴影四边形BEDH的面积是98．【分析】首先需要将阴影部分的不规则的图形变成规则图形，考虑连接BD，再根据蝴蝶定理有梯形两翼面积相等，最后跟正方形ABFG联系起来．恰好是两个正方形面积的一半．根据勾股定理即可求解．【解答】解：根据梯形两翼面积相等（蝴蝶定理）．S△ADE=S△BCE．=S△ACH．本题中：连接BD，AB平行CD，S△BDHS△ACH=S△AGH，根据S△AGH是正方形ABFG面积的一半．S阴=S△BED+S△BDH，又S△BED是正方形BCDE面积的一半．S阴就是两个正方形面积和的一半．S阴=+===98．故答案为：98【点评】本题中只给出了数据有一个垂直，一个斜边，最后一定是用这个斜边即可求出本题问题．首先需要知道梯形两翼面积相等，再根据勾股定理求出了两个正方形的面积，一半就是本题答案问题解决．13．一个容积是100立方厘米的水杯（即这个水杯装满水时，水的体积是100立方厘米），内有一部分水，盛盛向杯中放入了一个小正方体，水溢出了20立方厘米；盛盛又向杯中放入了一个相同的小正方体，水又溢出了30立方厘米（如图），那么，原来水杯中装有90立方厘米的水．【分析】首先放入的木块水溢出20cm3，此时容器是满的，再加入相同的木块水溢出30cm3，说明木块的体积是30cm3，而不是20cm3．说明第一次加入时候容器是有空余的．做差即可．【解答】解：根据木块的体积相同，第二次加入时候水溢出30．第一次水溢出20．证明原路容器中有30﹣20=10cm3空余部分．这个容器共100cm3，原来的水共有100﹣10=90cm3．故答案为：90【点评】根据两次水溢出的水量不同判断第二次才是木块的体积，第一次容器中水没有装满，根据条件做差即可求解．问题解决．14．如图是由两个直径为2的圆和四个腰长为2的等腰直角三角形组成，则图中的阴影部分面积是 4.5．（π=3）【分析】将右边阴影部分补到左边对应位置上，可以补成大等腰三角形，面积为2×（2×2）÷2=4；还有两个弓形，刚好是半圆减去小等腰三角形的面积，半圆面积为3×（2÷2）2÷2=1.5，小等腰三角形面积为2×（2÷2）÷2=1，那么弓形面积为1.5﹣1=0.5；从而求出整体阴影面积为4+0.5=4.5，据此解答即可．【解答】解：见上图，根据分析可得，大等腰三角形面积为：2×（2×2）÷2=4，半圆面积为：3×（2÷2）2÷2=1.5，小等腰三角形面积为：2×（2÷2）÷2=1，弓形面积为：1.5﹣1=0.5，整体阴影面积为：4+0.5=4.5，答：图中的阴影部分面积是 4.5．故答案为：4.5．【点评】本题关键是在保证面积不变的情况下通过旋转平移使的问题简单化．解答这种类型的问题往往利用“割补结合”等积变形：观察图形，把图形分割，再进行移补，形成一个容易求得的图形．15．如图所示，已知大圆的半径为2，则阴影部分的面积为4π﹣8（圆周率用π表示）．【分析】把中间四个“树叶”形的阴影部分，每个都平均分成两份，然后补到正方形的外面，那么阴影部分的总面积=圆的面积﹣正方形的面积，据此根据圆和正方形的面积公式（对角线的长度×对角线的长度÷2）解答即可．【解答】解：π×22﹣（2×2）×（2×2）÷2=4π﹣8答：阴影部分的面积为4π﹣8．故答案为：4π﹣8．【点评】解答这种类型的问题往往利用“割补结合”等积变形：观察图形，把图形分割，再进行移补，形成一个容易求得的图形．16．如图中三个正方形的边长从左到右依次减半，小正方形的边长为3，那么图中阴影部分的面积是13.5．【分析】连接AB、BD，则AB∥CD，所以图中阴影部分ACD的面积就等于三角形BCD的面积，三角形BCD的底是3×2+3，高是3，然后根据三角形的面积公式解答即可．【解答】解：根据分析可得，（3×2+3）×3÷2=9×3÷2=13.5答：图中阴影部分的面积是13.5．故答案为：13.5．【点评】本题考查了面积的等积变形，关键根据等底等高的三角形面积相等转化．17．长方形ABCD被CE、DF分成四块，已知其中3块的面积分别是5、16、20平方厘米，那么四边形ADOE的面积是19平方厘米．=2S△EOF=10，∴S△EDF=S长【分析】连ED，则由题意，EF=DC，FO=DO，S△EDO=5+10=15，可得S长方形ABCD=60，即可求出四边形ADOE的面积．方形ABCD【解答】解：连ED，则由题意，EF=DC，FO=DO∴S=2S△EOF=10，∴S△EDF=S长方形ABCD=5+10=15，△EDO=60，∴S长方形ABCD∴四边形ADOE的面积是60﹣5﹣20﹣16=19，故答案为19．【点评】本题考查等积变形，考查四边形面积的计算，考查学生分析解决问题的能力，属于中档题．18．如图所示，长方形ABCD中，AD﹣AB=9厘米，梯形ABCE的面积是三角形ADE面积的5倍，三角形ADE的周长比梯形ABCE 的周长短68厘米．长方形ABCD的面积是3060平方厘米．【分析】如图，作EM⊥AB于M．首先证明△BCE的面积是△ADE面积的两倍，推出EC=2DE，设DE=x，则EC=2x，AB=CD=3x，因为三角形ADE的周长比梯形ABCE 的周长短68厘米，列出方程求出x即可解决问题．【解答】解：如图，作EM⊥AB于M．因为四边形ABCD是长方形，易知四边形ADEM，四边形BCEM都是长方形，所以△DEA与△AEM的面积相等，△BEC与△BEM的面积相等，因为梯形ABCE的面积是三角形ADE面积的5倍，所以△BCE的面积是△ADE面积的两倍，所以EC=2DE，设DE=x，则EC=2x，AB=CD=3x，因为三角形ADE的周长比梯形ABCE 的周长短68厘米，所以3x+2x﹣x=68，所以x=17cm，AB=51因为AD﹣AB=9厘米，所以AD=51+9=60cm，所以矩形ABCD的面积为51×60=3060cm2．故答案为3060．【点评】本题考查长方形的性质、三角形的面积等知识，解题的关键是学会添加常用辅助线，学会利用参数，构建方程解决问题．19．如图，正六边形ABCDEF面积是2014平方厘米，在AB、BC、DE、EF上分别取中点G、H、I、J，四边形GHIJ的面积是1007平方厘米．【分析】把正六边形按照如图分割，可见整体是24份，阴影部分占12份，由此即可解决问题．【解答】解：把正六边形按照如图分割，可见整体是24份，阴影部分占12份，∴S阴=S正六边形=×2014=1007，故答案为1007．【点评】本题考查等积变形，解题的关键是学会利用分割法解决问题．20．如图，ABCD和ABEF都是长方形，如果长方形ABEF的面积是30平方厘米，那么阴影部分的面积是15平方厘米．【分析】设内部交点为O，如下图，只要证明则阴影部分面积等于△ABF的面积即可；【解答】解：设内部交点为O，如下图，通过等积变形可知△FOD的面积和△FOC的面积相等，则阴影部分变成了△AFC 的面积，再通过等积变形可知△AFC的面积和△ABF的面积相等；△ABF的面积为长方形ABEF的一半，即30×=15平方厘米．故答案为15．【点评】本题考查长方形的性质、等积变形、等高模型等知识，解题的关键是灵活掌握等高模型解决问题，学会用转化的思想思考问题．21．如图所示，四边形ABCD是梯形，四边形ABED是平行四边形，四边形FGHI 是长方形，E、F、G分别是边CD、AD、BC的中点．如果平行四边形ABED的面积是48平方厘米，那么，长方形FGHI的面积是36平方厘米．【分析】作AP⊥CD于P，设FG交BE于K．设AB=a，AP=b，想办法求出FI、FG 的长（用a、b表示）即可解决问题．【解答】解：作AP⊥CD于P，设FG交BE于K．设AB=a，AP=b，由题意ab=48，∵四边形ABED是平行四边形，∴AB∥CD，AB=DE=a，∵ED=EC=a，AF=DF，BG=GC，∴FG∥AB，∴BK=KE，FK=AB=a，∵BG=GC，∴KG=a，FG=a，∵FI∥AP，AF=DF，∴DI=IP，∴FI=AP=b，∴S=b•a=ab=36长方形FGHI故答案为36．【点评】本题考查平行四边形的性质、梯形的性质、长方形的性质，三角形中位线定理，平行线等分线段定理等知识，解题的关键是学会利用参数解决问题．22．如图所示，正方形ABCD的对角线BD长20厘米，BDFE是长方形．那么，五边形ABEFD的面积是300平方厘米．【分析】如图所示，连接AC，与BD交于O，则图中的6个直角三角形的面积相等，即可得出结论．【解答】解：如图所示，连接AC，与BD交于O，则图中的6个直角三角形的面积相等，所以五边形ABEFD的面积=6个△ABO的面积=6×=300平方厘米，故答案为300．【点评】本题考查五边形ABEFD的面积的计算，考查等积变形，考查学生分析解决问题的能力，属于中档题．23．直角三角形的两条直角边分别是3与9，以三角形的每条边长作为正方形的边长，分别可以画出三个正方形（如图），这个多边形的面积是193.5．【分析】直角三角形的两条直角边分别是3与9，由勾股定理可得斜边的平方为9+81，求出两个小正方形的面积与直角三角形的面积，即可得出结论．【解答】解：直角三角形的两条直角边分别是3与9，由勾股定理可得斜边的平方为9+81，为大正方形的面积，所以总面积为9+81+（9+81）+3×9÷2=193.5，故答案为193.5．【点评】本题考查勾股定理，等积变形，考查学生的转化能力，求出是大正方形的面积关键．24．右图是由甲乙丙丁拼成的正方形，其中甲与丁都是边长为整数厘米数的正方形，乙与丙都是长方形，且甲与丁的面积之和为100平方厘米，那么长方形。

组合图形面积应用1．求下面图形的面积（1）（2）（1）解：8×6＋（8＋12）×3÷2=48＋20×3÷2=48＋60÷2=48＋30=78（平方米）（2）解：5.4×4.2＋5.4×6÷2=22.68＋32.4÷2=22.68＋16.2=38.88（平方厘米）2．工厂制作一些流动红旗，式样如图，制作一面流动红旗需要多少平方厘米的布料？解：60×30-30×（60-45）÷2=60×30-30×15÷2=1800-450÷2=1800-225=1575（平方厘米）答：制作一面流动红旗需要1575平方厘米的布料。

3．友谊公园的中心有一块长方形草坪，草坪里有一条宽1米的曲折小路。

草坪的实际面积有多大？解：（12-1）×（10-1）=11×9=99（平方米）答：草坪的实际面积有99平方米。

4．李叔叔家原来有一块边长12米的正方形菜地，今年他将这块菜地进行了扩建（如图中的涂色部分）。

（1）原来这块菜地的面积是多少平方米？（2）李叔叔今年扩建了多少平方米的菜地？（1）解：12×12=144（平方米）答：原来这块菜地的面积是144平方米。

（2）解：（12＋7）×（12＋2）-144=19×14-144=266-144=122（平方米）答：李叔叔今年扩建了122平方米的菜地。

5．求出下面图形的面积。

（1）如图，已知梯形的面积是60米2，那么，阴影部分（三角形）的面积是多少米"？（2）求出下面组合图形的面积。

（单位：厘米）（1）解：（60×2）÷（8＋12）=120÷20=6（米）8×6÷2=48÷2=24（平方米）答：阴影部分（三角形）的面积是24平方米。